Как доказать что 3 медианы пересекаются. Медиана треугольника. Теоремы связанные с медианами треугольника. Формулы для нахождения медиан
Медианой именуется отрезок, проведенный из вершины треугольника на середину противоположной стороны, то есть делит ее точкой пересечения пополам. Точка, в которой медиана пересекает противоположную вершине, из которой она выходит, сторону, именуется основанием. Через одну точку, называемую точкой пересечения, проходит каждая медиана треугольника. Формула длины ее может выражаться несколькими способами.
Формулы для выражения длины медианы
- Зачастую в задачах по геометрии ученикам приходится иметь дело с таким отрезком, как медиана треугольника. Формула ее длины выражается через стороны:
где a, b и c — стороны. Причем с является стороной, на которую медиана опускается. Таким образом выглядит самая простая формула. Медианы треугольника иногда требуется проводить для вспомогательных расчетов. Есть и другие формулы.
Есть и другие формулы.
- Если при расчете известны две стороны треугольника и определенный угол α, находящийся между ними, то длина медианы треугольника, опущенной к третьей стороне, будет выражаться так.
Основные свойства
- Все медианы имеют одну общую точку пересечения O и ею же делятся в отношении два к одному, если вести отсчет от вершины. Такая точка носит название центра тяжести треугольника.
- Медиана разделяет треугольник на два других, площади которых равны. Такие треугольники называются равновеликими.
- Если провести все медианы, то треугольник будет разделен на 6 равновеликих фигур, которые также будут треугольниками.
- Если в треугольнике все три стороны равны, то в нем каждая из медиан будет также высотой и биссектрисой, то есть перпендикулярна той стороне, к которой она проведена, и делит надвое угол, из которого она выходит.
- В равнобедренном треугольнике медиана, опущенная из вершины, которая находится напротив стороны, не равной никакой другой, будет также высотой и биссектрисой.
 Медианы, опущенные из других вершин, равны. Это также является необходимым и достаточным условием равнобедренности.
Медианы, опущенные из других вершин, равны. Это также является необходимым и достаточным условием равнобедренности. - Если треугольник является основанием правильной пирамиды, то высота, опущенная на данное основание, проецируется в точку пересечения всех медиан.
- В прямоугольном треугольнике медиана, проведенная к наибольшей стороне, равняется половине ее длины.
- Пусть O — точка пересечения медиан треугольника. Формула, приведенная ниже, будет верная для любой точки M.
- Еще одним свойством обладает медиана треугольника. Формула квадрата ее длины через квадраты сторон представлена ниже.
Свойства сторон, к которым проведена медиана
- Если соединить любые две точки пересечения медиан со сторонами, на которые они опущены, то полученный отрезок будет являться средней линией треугольника и составлять одну вторую от стороны треугольника, с которой она не имеет общих точек.
- Основания высот и медиан в треугольнике, а также середины отрезков, соединяющих вершины треугольника с точкой пересечения высот, лежат на одной окружности.

В заключение логично сказать, что одним из самых важных отрезков является именно медиана треугольника. Формула ее может использоваться при нахождении длин других его сторон.
Урок 1
Медианы треугольника. Точка пересечения медиан.
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Доказательство:
Точка пересечения медиан треугольника является центром тяжести этого треугольника.
Задача 1 Точка пересечения медиан треугольника отстоит от его вершин на расстояния, равные 4, 6 и 8. Найти длины медиан треугольника.
Решение. Пусть в треугольнике АВС AM, BE и CD — медианы, К – точка их пересечения, KС=4, KА=6 и КВ=8.
https://pandia.ru/text/78/182/images/image004_34.gif»>, то есть на отрезок КА приходится 2 части, а на отрезок КМ – одна часть, то вся медиана АМ состоит из трех равных частей и https://pandia. ru/text/78/182/images/image006_24.gif»>.
ru/text/78/182/images/image006_24.gif»>.
Аналогично,
,
Ответ: 6, 9 и 12
Задача 2 Медианы AM и СК треугольника АВС взаимно перпендикулярны и равны соответственно 6 и 9 . Вычислить длины сторон АВ и ВС.
https://pandia.ru/text/78/182/images/image010_15.gif»>,
поэтому и
, .
Кроме того
, .
Вычислим по теореме Пифагора длины отрезков AK и СМ, получаем
Теперь вычислим длины сторон АВ и ВС:
АВ=2АК=10, ВС=2СМ=.
Ответ : 10;.
Тест для самоконтроля.
1. Медиана треугольника делит пополам (выбрать один из вариантов ответов)
1) угол треугольника
2) сторону треугольника
3) две стороны треугольника
2. В каком отношении точка пересечения медиан треугольника делит каждую из медиан треугольника (выбрать правильные варианты ответов).
1) 2:1 считая от основания треугольника
2) 1:2 считая от вершины треугольника
3) 2:1 считая от вершины треугольника
4) 1:2 считая от основания треугольника
5) на две равные части
3.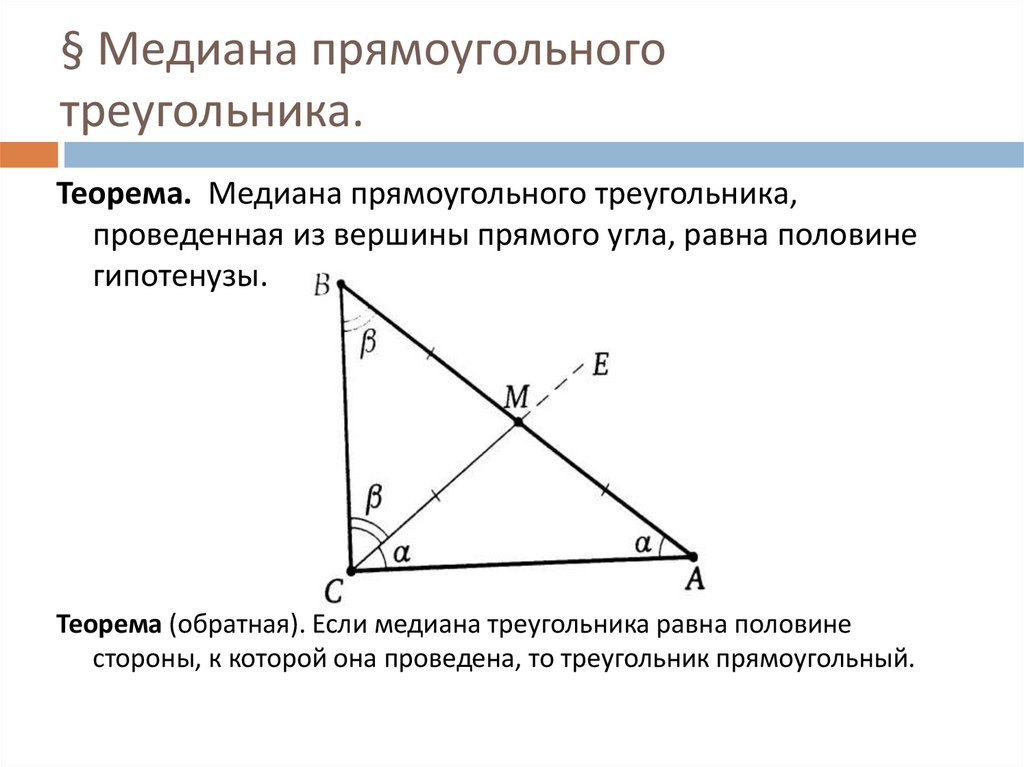 Если в треугольнике АВС проведена медиана АM и Р – точка пересечения медиан треугольника, то какую часть медианы АМ составляет отрезок АР? (выбрать один из вариантов ответов)
Если в треугольнике АВС проведена медиана АM и Р – точка пересечения медиан треугольника, то какую часть медианы АМ составляет отрезок АР? (выбрать один из вариантов ответов)
4. В треугольнике АВС проведена медиана АM и Р – точка пересечения медиан треугольника. Какую часть медианы АМ составляет отрезок РМ? (выбрать один из вариантов ответов)
5.
В треугольнике АВС проведена медиана АM и Р – точка пересечения медиан треугольника. Какую часть отрезка АР составляет отрезок РМ? (выбрать один из вариантов ответов)Посмотреть правильные ответы.
Задачи для самостоятельного решения.
1. Точка пересечения медиан треугольника отстоит от его вершин на расстояния, равные 6 см, 8 см и 12 см. Найдите длины медиан треугольника.
Посмотреть решение.
2. Медианы ВM и СК треугольника АВС взаимно перпендикулярны и равны соответственно 15 и 36 . Найдите длины сторон АВ и АС.
Посмотреть решение.
3. Медианы треугольника равны 6, 9 и 12. На каком расстоянии от вершин находится точка пересечения медиан треугольника?
На каком расстоянии от вершин находится точка пересечения медиан треугольника?
Посмотреть решение.
4. Медианы треугольника равны 9, 12 и 18. Найдите расстояния от середин сторон треугольника до центра тяжести данного треугольника.
Посмотреть решение.
5. Центр тяжести треугольника отстоит от середин его сторон на расстояния. Равные 5, 6 и 7. Найдите медианы данного треугольника.
Посмотреть решение.
6. Точка пересечения медиан треугольника удалена от середин его сторон на расстояния, равные 2, 3 и 4. На каких расстояниях от вершин треугольника находится эта точка?
Посмотреть решение.
Медиана и высота треугольника – это одна из самых увлекательных и интересных тем геометрии. Термин «Медиана» означает прямую или отрезок, который соединяет вершину треугольника с его противоположной стороной. Другими словами, медиана – это линия, которая проходит из середины одной стороны треугольника в противоположную вершину этого же треугольника. Поскольку у треугольника только три вершины и три стороны, значит и медианы может быть только три.
Поскольку у треугольника только три вершины и три стороны, значит и медианы может быть только три.
Свойства медианы треугольника
- Все медианы треугольника пересекаются в одной точке и разделяются этой точкой в соотношении 2:1, считая от вершины. Таким образом, если нарисовать в треугольнике все три медианы, то точка их пересечения будет делить их на две части. Часть, которая располагается ближе в вершине, будет составлять 2/3 всей линии, а часть, которая располагается ближе к стороне треугольника – 1/3 линии. Пересекаются медианы в одной точке.
- Три медианы, проведенные в одном треугольнике, делят этот треугольник на 6 маленьких треугольников, чья площадь будет равна.
- Чем больше сторона треугольника, от которой исходит медиана, тем меньше эта медиана. И наоборот, самая короткая сторона имеет самую длинную медиану.
- Медиана в прямоугольном треугольнике имеет ряд собственных характеристик. Например, если вокруг такого треугольника описать окружность, которая будет проходить через все вершины, то медиана прямого угла, проведенная к гипотенузе, станет радиусом описанной окружности (то есть ее длина будет составлять расстояние от любой точки окружности до ее центра).

Уравнение длины медианы треугольника
Формула медианы исходит из теоремы Стюарта и гласит, что медиана – это квадратный корень из отношения квадратов суммы сторон треугольника, которые образуют вершину, за вычетом квадрата стороны, к которой проведена медиана к четырем. Другими словами, чтобы узнать длину медианы нужно возвести в квадрат показатели длины каждой стороны треугольника, а затем записать это в виде дроби, в числителе которой будет сумма квадратов сторон, которые образуют угол, откуда исходит медиана, минус квадрат третьей стороны. В качестве знаменателя здесь выступает цифра 4. Затем из данной дроби нужно извлечь корень квадратный, и тогда мы получим длину медианы.
Точка пересечения медиан треугольника
Как мы писали выше, всем медианы одного треугольника пересекаются в одной точке. Эту точку называют центром треугольника. Он делит каждую медиану на две части, длина которым соотносится как 2:1. При этом центр треугольника является и центром описанной вокруг него окружности.
Координаты точки пересечения медиан треугольника
Чтобы найти координаты пересечения медиан одного треугольника, воспользуемся свойством центроида, согласно которому он делит каждую медиану на отрезки 2:1. Обозначаем вершины как как A(x 1 ;y 1), B(x 2 ;y 2), C(x 3 ;y 3),
и вычисляем координаты центра треугольника по формуле: x 0 = (x 1 + x 2 + x 3)/3; y 0 = (y 1 + y 2 + y 3)/3.
Площадь треугольника через медиану
Все медианы одного треугольника делят этот треугольник на 6 равных треугольников, а центр треугольника делит каждую медиану в соотношении 2:1. Поэтому если известны параметры каждой медианы, можно вычислить и площадь треугольника через площадь одного из маленьких треугольников, а затем увеличить этот показатель в 6 раз.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.

- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Медиана треугольника — это отрезок, соединяющий верщину треугольника с серединой противолежащей стороны этого треугольника.
Свойства медиан треугольника
1. Медиана разбивает треугольник на два треугольника одинаковой площади.
2. Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника (центроидом).
3. Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.
Длина медианы проведенной к стороне: (док-во достроением до параллелограмма и использованием равенства в параллелограмме удвоенной суммы квадратов сторон и суммы квадратов диагоналей )
Т1. Три медианы треугольника пересекаются в одной точке М, которая делит каждую из них в отношении 2:1, считая от вершин треугольника. Дано: ∆ABC, СС 1 , АА 1 , ВВ 1 — медианы
∆ABC . Доказать: и
Д-во: Пусть М — точка пересечения медиан СС 1 , АА 1 треугольника ABC. Отметим A 2 — середину отрезка AM и С 2 — середину отрезка СМ. Тогда A 2 C 2 — средняя линия треугольника АМС. Значит,А 2 С 2 || АС
и A 2 C 2 = 0,5*АС. С 1 А 1 — средняя линия треугольника ABC. Значит, А 1 С 1 || АС и А 1 С 1 = 0,5*АС.
С 1 А 1 — средняя линия треугольника ABC. Значит, А 1 С 1 || АС и А 1 С 1 = 0,5*АС.
Четырехугольник А 2 С 1 А 1 С 2 — параллелограмм, так как его противоположные стороны А 1 С 1 и А 2 С 2 равны и параллельны. Следовательно, А 2 М = МА 1 и С 2 М = МC 1 . Это означает, что точки А 2 и M делят медиану АА 2 на три равные части, т. е. AM = 2МА 2 . Аналогично СМ = 2MC 1 . Итак, точка М пересечения двух медиан АА 2 и CC 2 треугольника ABC делит каждую из них в отношении 2:1, считая от вершин треугольника. Совершенно аналогично доказывается, что точка пересечения медиан АА 1 и BB 1 делит каждую из них в отношении 2:1, считая от вершин треугольника.
На медиане АА 1 такой точкой является точка М, следовательно, точка М и есть точка пересечения медиан АА 1 иBB 1.
Таким образом, n
T2. Докажите, что отрезки, которые соединяют центроид с вершинами треугольника, делят его на три равновеликие части. Дано: ∆ABC , — его медианы.
Дано: ∆ABC , — его медианы.
Доказать:S AMB =S BMC =S AMC . Доказательство. В, у них общая. т.к. равны их основания и высота, проведенная из вершины М, у них общая. Тогда
Аналогичным образом доказывается, чтоS AMB = S AMC . Таким образом,S AMB = S AMC = S CMB . n
Биссектриса треугольника.Теоремы связанные с биссектрисами треугольника. Формулы для нахождения биссектрис
Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.
Биссектриса угла есть геометрическое место точек внутри угла, равноудалённых от сторон угла.
Свойства
1. Теорема о биссектрисе: Биссектриса внутреннего угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон
2. Биссектрисы внутренних углов треугольника пересекаются в одной точке — инцентре — центре вписанной в этот треугольник окружности.
3. Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса).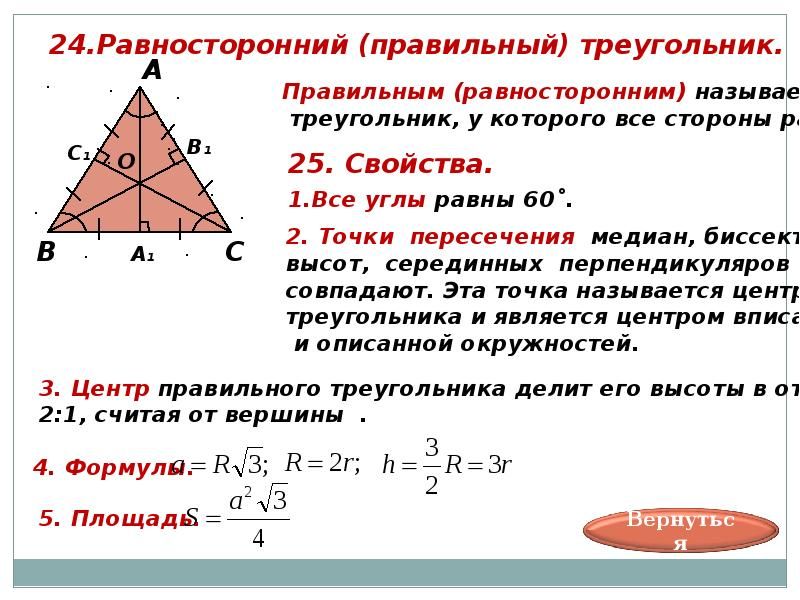
Вычисление длины биссектрисы
l c — длина биссектрисы, проведённой к стороне c,
a,b,c — стороны треугольника против вершин A,B,C соответственно,
p — полупериметр треугольника,
a l ,b l — длины отрезков, на которые биссектриса l c делит сторону c,
α,β,γ — внутренние углы треугольника при вершинах A,B,C соответственно,
h c — высота треугольника, опущенная на сторону c.
Метод площадей.
Характеристика метода. Из названия следует, что главным объектом данного метода является площадь. Для ряда фигур, например для треугольника, площадь довольно просто выражается через разнообразные комбинации элементов фигуры (треугольника). Поэтому весьма эффективным оказывается прием, когда сравниваются различные выражения для площади данной фигуры. В этом случае возникает уравнение, содержащее известные и искомые элементы фигуры, разрешая которое мы определяем неизвестное. Здесь и проявляется основная особенность метода площадей – из геометрической задачи он «делает» алгебраическую, сводя все к решению уравнения (а иногда системы уравнений).
1) Метод сравнения: связан с большим кол-вом формул S одних и тех же фигур
2) Метод отношения S: основан на след опорных задачах:
Теорема Чевы
Пусть точки A»,B»,C» лежат на прямых BC,CA,AB треугольника. Прямые AA»,BB»,CC» пересекаются в одной точке тогда и только тогда, когда
Доказательство.
Обозначим через точку пересечения отрезков и . Опустим из точек С и А перпендикуляры на прямую ВВ 1 до пересечения с ней в точках Kи L соответственно (см. рисунок).
Поскольку треугольники и имеют общую сторону , то их площади относятся как высоты, проведенные на эту сторону, т.е. AL иCK:
Последнее равенство справедливо, так как прямоугольные треугольники и подобны по острому углу.
Аналогично получаем и
Перемножим эти три равенства:
что и требовалось доказать.
Замечание. Отрезок (или продолжение отрезка), соединяющий вершину треугольника с точкой, лежащей на противоположной стороне или ее продолжении, называется чевианой.
Теорема (обратная теорема Чевы) . Пусть точки A»,B»,C» лежат на сторонах BC,CA и AB треугольника ABC соответственно. Пусть выполняется соотношение
Тогда отрезки AA»,BB»,CC» и пересекаются в одной точке.
Теорема Менелая
Теорема Менелая. Пусть прямая пересекает треугольник ABC, причем C 1 – точка ее пересечения со стороной AB, A 1 – точка ее пересечения со стороной BC, и B 1 – точка ее пересечения с продолжением стороны AC. Тогда
Доказательство . Проведем через точку C прямую, параллельную AB. Обозначим через K ее точку пересечения с прямой B 1 C 1 .
ТреугольникиAC 1 B 1 иCKB 1 подобны (∟C 1 AB 1 = ∟KCB 1 , ∟AC 1 B 1 = ∟CKB 1). Следовательно,
ТреугольникиBC 1 A 1 иCKA 1 такжеподобны (∟BA 1 C 1 =∟KA 1 C, ∟BC 1 A 1 =∟CKA 1). Значит,
Из каждого равенства выразим CK:
Откуда что и требовалось доказать.
Теорема (обратная теорема Менелая). Пусть дан треугольник ABC. Пусть точка C 1 лежит на стороне AB, точка A 1 – на стороне BC, а точка B 1 – на продолжении стороны AC, причем выполняется соотношение
Пусть точка C 1 лежит на стороне AB, точка A 1 – на стороне BC, а точка B 1 – на продолжении стороны AC, причем выполняется соотношение
Тогда точки A 1 ,B 1 и C 1 лежат на одной прямой.
Треугольник. Формулы и свойства треугольников
Формулы по геометрии треугольника
Определение. Треугольник — фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.
Типы треугольников
По величине углов
По числу равных сторон
Вершины, углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°:
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
Если α > β, тогда a > b
Если α = β, тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
A + b > c
B + c > a
C + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| A | = | B | = | C | = 2R |
| Sin α | Sin β | Sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
A 2 = b 2 + c 2 — 2 bc · cos α
B 2 = a 2 + c 2 — 2 ac · cos β
C 2 = a 2 + b 2 — 2 ab · cos γ
Теорема о проекциях
Для остроугольного треугольника:
A = b cos γ + c cos β
B = a cos γ + c cos α
C = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Медианы треугольника
Определение. Медиана треугольника ― отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.
Свойства медиан треугольника:
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
Медиана треугольника делит треугольник на две равновеликие части
Треугольник делится тремя медианами на шесть равновеликих треугольников.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
Ma = 1 2 √ 2 b 2 +2 c 2 — a 2
Mb = 1 2 √ 2 a 2 +2 c 2 — b 2
Mc = 1 2 √ 2 a 2 +2 b 2 — c 2
Биссектрисы треугольника
Свойства биссектрис треугольника:
Биссектрисы треугольника пересекаются в одной точке, равноудаленной от трех сторон треугольника, — Центре вписанной окружности.
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
La = 2√ bcp ( p — a ) b + c
Lb = 2√ acp ( p — b ) a + c
Lc = 2√ abp ( p — c ) a + b
Где p = a + b + c 2 — полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
La = 2 bc cos α 2 b + c
Lb = 2 ac cos β 2 a + c
Lc = 2 ab cos γ 2 a + b
Высоты треугольника
Определение.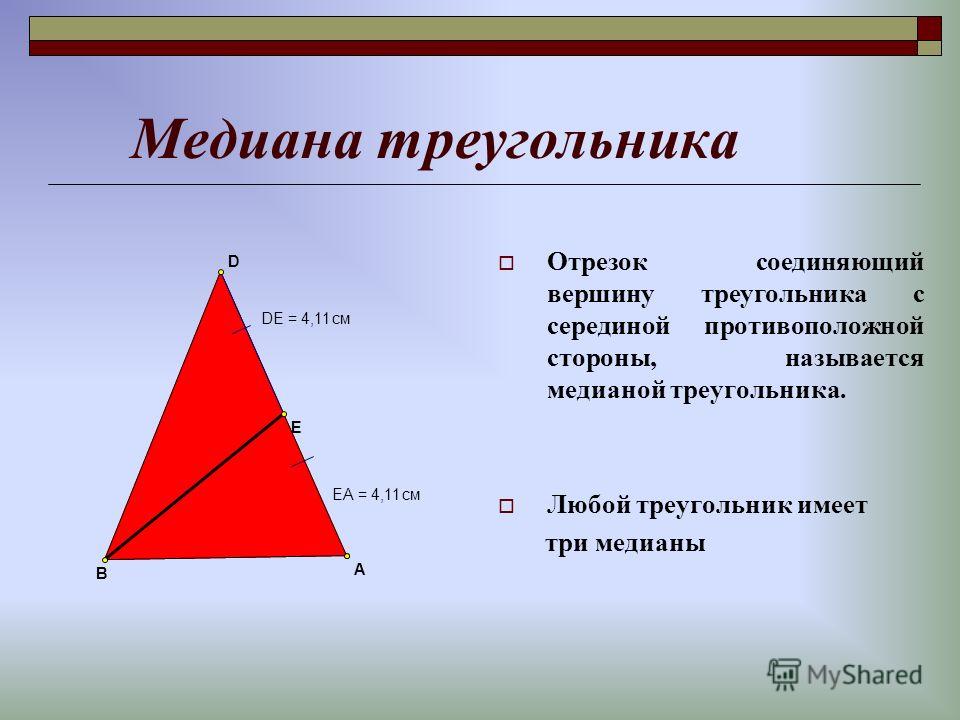 Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.
Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.
- внутри треугольника — для остроугольного треугольника; совпадать с его стороной — для катета прямоугольного треугольника; проходить вне треугольника — для острых углов тупоугольного треугольника.
Свойства высот треугольника
Формулы высот треугольника
Ha = b sin γ = c sin β
Hb = c sin α = a sin γ
Hc = a sin β = b sin α
Окружность вписанная в треугольник
Свойства окружности вписанной в треугольник
Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.
Формулы радиуса окружности вписанной в треугольник
R = ( a + b — c )( b + c — a )( c + a — b ) 4( a + b + c )
Окружность описанная вокруг треугольника
Определение. Окружность называется Описанной вокруг треугольника, если она содержит все вершины треугльника.
Свойства окружности описанной вокруг треугольника
Центр описанной вокруг треугольника окружности лежит на пересечении серединных перпендикуляров к его сторонам.
Центр описанной окружности лежит внутри остроугольного треугольника, снаружи тупоугольнго треугольника, на середине гипотенузы прямоугольного треугольника.
Формулы радиуса окружности описанной вокруг треугольника
R = S 2 sin α sin β sin γ
R = a 2 sin α = b 2 sin β = c 2 sin γ
Связь между вписанной и описанной окружностями треугольника
Средняя линия треугольника
Свойства средней линии треугольника
MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC
MN || AC KN || AB KM || BC
3. Средняя линия отсекает треугольник, подобный данному, площадь которого равна четвёрти площади исходного треугольника
4. При пересечении всех трёх средних линий образуются 4 равных треугольника, подобных (даже гомотетичных) исходному с коэффициентом 1/2.
Признаки. Если отрезок параллелен одной из сторон треугольника и соединяет середину стороны треугольника с точкой, лежащей на другой стороне треугольника, то этот отрезок — средняя линия.
Если отрезок параллелен одной из сторон треугольника и соединяет середину стороны треугольника с точкой, лежащей на другой стороне треугольника, то этот отрезок — средняя линия.
Периметр треугольника
Периметр треугольника ∆ ABC равен сумме длин его сторон
Формулы площади треугольника
Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты
Формула Герона
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
| S = | A · b · с |
| 4R |
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
Равенство треугольников
Свойства. У равных треугольников равны и их соответствующие элементы. (В равных треугольниках против равных сторон лежат равные углы, против равных углов лежат равные стороны)
Признаки равенства треугольников
Первый признак равенства треугольников — по двум сторонам и углу между ними
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Третий признак равенства треугольников — по трем сторонам
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Подобие треугольников
Определение. Подобные треугольники — треугольники соответствующие углы которых равны, а сходственные стороны пропорциональны.
Подобные треугольники — треугольники соответствующие углы которых равны, а сходственные стороны пропорциональны.
∆АВС ~ ∆MNK => α = α 1, β = β 1, γ = γ 1 и AB MN = BC NK = AC MK = k,
Где k — коэффициент подобия
Признаки подобия треугольников
Первый признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
Второй признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
Третий признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого, а углы, между этими сторонами, равны, то такие треугольники подобны.
Определение. Треугольник — фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.
По величине углов
По числу равных сторон
Формулы биссектрис треугольника через две стороны и угол.
Ru. onlinemschool. com
21.06.2019 2:57:30
2019-06-21 02:57:30
Источники:
Https://ru. onlinemschool. com/math/formula/triangle/
Все формулы для треугольника » /> » /> .keyword { color: red; }
Формулы по геометрии треугольника
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
A , B , C — стороны произвольного треугольника
Α , Β , Γ — противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), ( A ):
* Внимательно, при подстановке в формулу, для тупого угла ( Α >90), cos Α принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), ( A):
2.
 Как узнать сторону прямоугольного треугольника
Как узнать сторону прямоугольного треугольникаЕсть следующие формулы для определения катета или гипотенузы
A , B — катеты
C — гипотенуза
Α , Β — острые углы
Формулы для катета, ( A ):
Формулы для катета, ( B ):
Формулы для гипотенузы, ( C ):
Формулы сторон по теореме Пифагора, ( A, b ):
3. Формулы сторон равнобедренного треугольника
Вычислить длину неизвестной стороны через любые стороны и углы
B — сторона (основание)
A — равные стороны
Α — углы при основании
Β — угол образованный равными сторонами
Формулы длины стороны (основания), (B ):
Формулы длины равных сторон, (A):
4.
 Найти длину высоты треугольника
Найти длину высоты треугольникаВысота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется — Ортоцентр.
H — высота треугольника
A — сторона, основание
B, c — стороны
Β , Γ — углы при основании
P — полупериметр, p=(a+b+c)/2
R — радиус описанной окружности
S — площадь треугольника
Формула длины высоты через стороны, ( H ):
Формула длины высоты через сторону и угол, ( H ):
Формула длины высоты через сторону и площадь, ( H ):
Формула длины высоты через стороны и радиус, ( H ):
5.
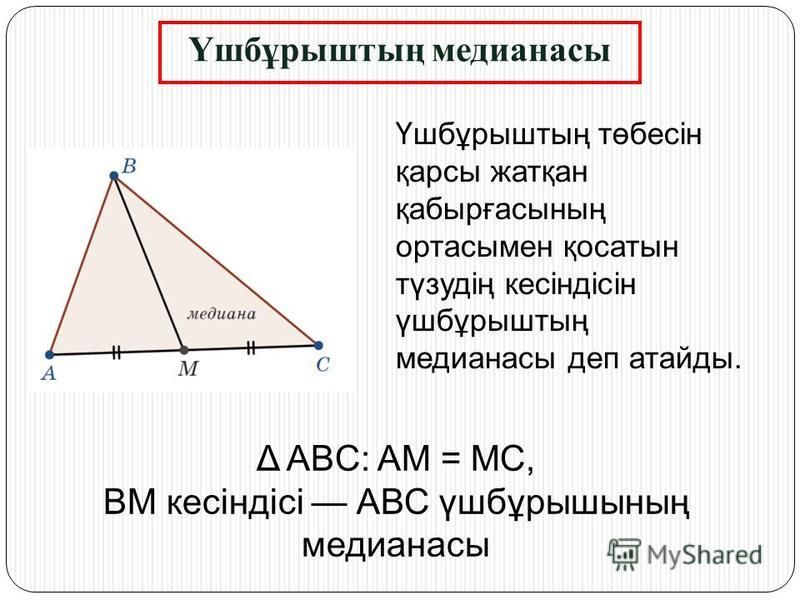 Формулы высоты прямого угла в прямоугольном треугольнике
Формулы высоты прямого угла в прямоугольном треугольникеВ прямоугольном треугольнике катеты, являются высотами. Ортоцентр — точка пересечения высот, совпадает с вершиной прямого угла.
H — высота из прямого угла
A, b — катеты
С — гипотенуза
C 1 , C 2 — отрезки полученные от деления гипотенузы, высотой
Α , Β — углы при гипотенузе
Формула длины высоты через стороны, ( H ):
Формула длины высоты через гипотенузу и острые углы, ( H ):
Формула длины высоты через катет и угол, ( H ):
Формула длины высоты через составные отрезки гипотенузы, ( H ):
6. Найти длину биссектрисы в треугольнике
L — биссектриса, отрезок |OB|, который делит угол ABC пополам
A, b — стороны треугольника
С — сторона на которую опущена биссектриса
D, e — отрезки полученные делением биссектрисы
Γ — угол ABC , разделенный биссектрисой пополам
P — полупериметр, P =(A+b+ c )/2
Длина биссектрисы через две стороны и угол, ( L ):
Длина биссектрисы через полупериметр и стороны, ( L ):
Длина биссектрисы через три стороны, ( L ):
Длина биссектрисы через стороны и отрезки D , E , ( L ):
Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.
7. Биссектриса прямоугольного треугольника
1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:
L — биссектриса, отрезок ME, исходящий из прямого угла (90 град)
A, b — катеты прямоугольного треугольника
С — гипотенуза
Α — угол прилежащий к гипотенузе
Формула длины биссектрисы через катеты, ( L ):
Формула длины биссектрисы через гипотенузу и угол, ( L ):
2. Найти по формулам длину биссектрисы из острого угла на катет:
L — биссектриса, отрезок ME, исходящий из острого угла
A, b — катеты прямоугольного треугольника
С — гипотенуза
Α, β — углы прилежащие к гипотенузе
Формулы длины биссектрисы через катет и угол, ( L ):
Формула длины биссектрисы через катет и гипотенузу, ( L ):
8.
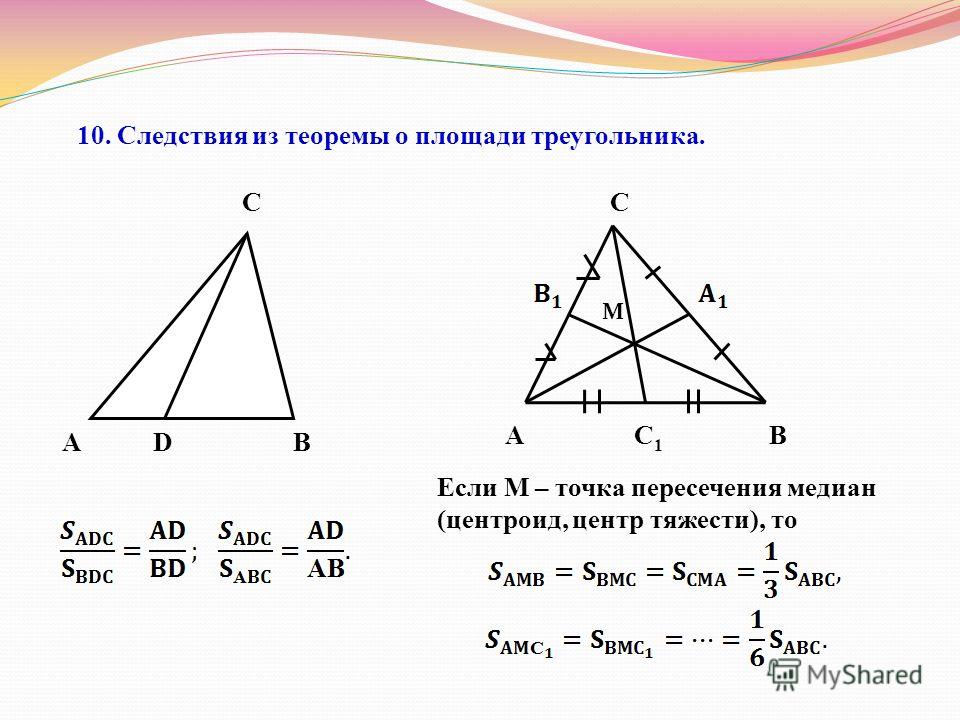 Длина биссектрисы равнобедренного треугольника
Длина биссектрисы равнобедренного треугольникаL — высота = биссектриса = медиана
A — одинаковые стороны треугольника
B — основание
Α — равные углы при основании
Β — угол образованный равными сторонами
Формулы высоты, биссектрисы и медианы, через сторону и угол, ( L ):
Формула высоты, биссектрисы и медианы, через стороны, ( L ):
9. Найти медиану биссектрису высоту равностороннего треугольника
Формула для вычисления Высоты = биссектрисы = медианы.
В равностороннем треугольнике: все Высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.
L — высота=биссектриса=медиана
A — сторона треугольника
Формула длины высоты, биссектрисы и медианы равностороннего треугольника, ( L ):
10.
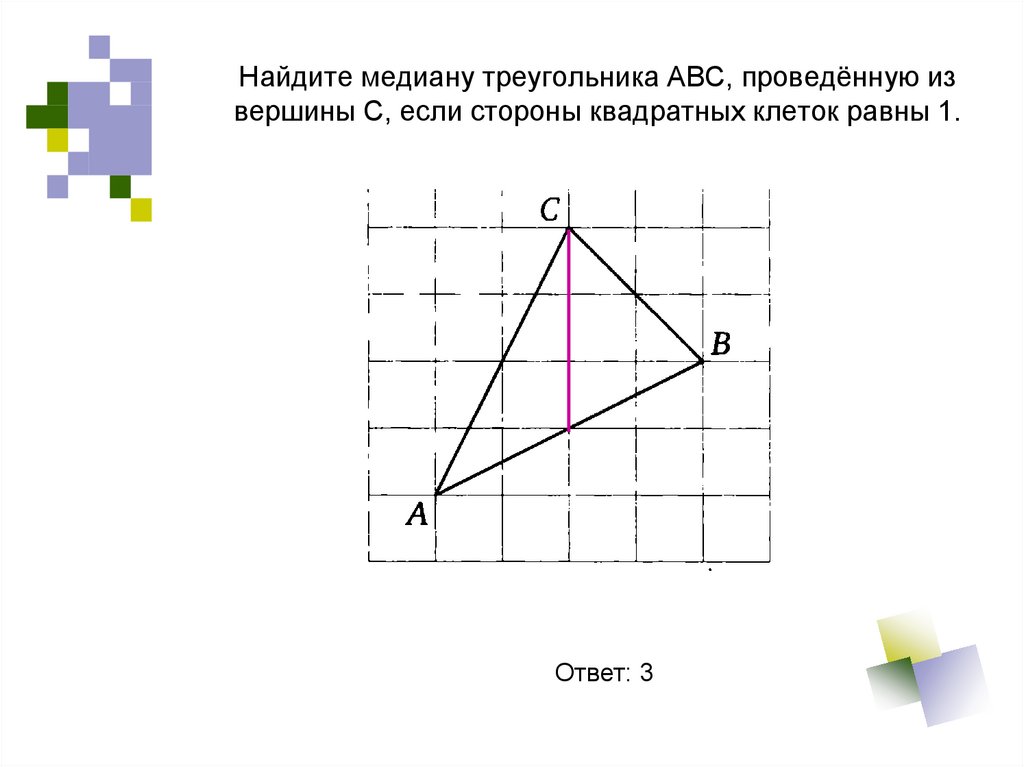 Найти длину медианы треугольника по формулам
Найти длину медианы треугольника по формуламМедиана — отрезок |AO|, который выходит из вершины A и делит противолежащею сторону C пополам.
Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.
M — медиана, отрезок |AO|
C — сторона на которую ложится медиана
A, b — стороны треугольника
Γ — угол CAB
Формула длины медианы через три стороны, ( M ):
Формула длины медианы через две стороны и угол между ними, ( M ):
11. Длина медианы прямоугольного треугольника
Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу C , пополам.
Медиана в прямоугольном треугольнике ( M ), равна, радиусу описанной окружности ( R ).
H — высота из прямого угла
Как узнать сторону прямоугольного треугольника
Есть следующие формулы для определения катета или гипотенузы
A , B — катеты
C — гипотенуза
Α , Β — острые углы
Формулы для катета, ( A ):
Формулы для катета, ( B ):
Формулы для гипотенузы, ( C ):
Формулы сторон по теореме Пифагора, ( A, b ):
H — высота треугольника
Точка их пересечения, является центром вписанной окружности.
Www-formula. ru
12.06.2020 1:15:09
2020-06-12 01:15:09
Источники:
Https://www-formula. ru/2011-10-09-11-08-41
ru/2011-10-09-11-08-41
Формулы треугольника, с примерами » /> » /> .keyword { color: red; }
Формулы по геометрии треугольника
Здесь – радиус описанной окружности.
Теоремы треугольника
Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними
Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Коэффициент пропорциональности равен диаметру описанной окружности:
Теорема тангенсов. Разность двух сторон треугольника относится к их сумме, как тангенс полуразности противолежащих углов к тангенсу полусуммы этих углов:
Равносторонний треугольник со стороной :
– радиус описанной окружности,
– радиус вписанной окружности,
– высота, совпадающая с медианой и биссектрисой,
– площадь треугольника.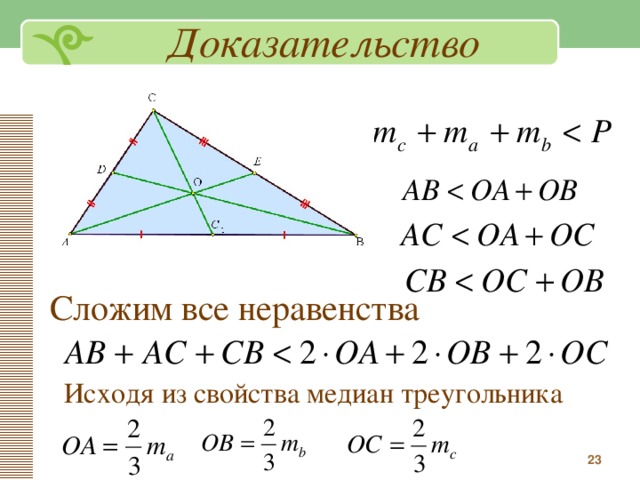
Формулы прямоугольного треугольника
В прямоугольном треугольнике с, гипотенузой и катетами и
Примеры решения задач
| Задание | В равностороннем треугольнике со стороной см найти площадь и радиусы вписанной и описанной окружностей. |
| Решение | Площадь равностороннего треугольника найдем по формуле, подставив : |
Тогда искомые радиусы вписанной и описанной окружностей
| Задание | В треугольнике стороны см см, а. Найти все стороны и все углы треугольника. |
| Решение | Сделаем рисунок. |
Воспользуемся теоремой синусов и найдем угол :
Откуда, т. е. . Следовательно, треугольник является прямоугольным. Значит,
Найдем сторону по теореме Пифагора:
см
см
Здесь – радиус описанной окружности.
Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними
Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Коэффициент пропорциональности равен диаметру описанной окружности:
Стороны треугольника пропорциональны синусам противолежащих углов. Коэффициент пропорциональности равен диаметру описанной окружности:
Теорема тангенсов. Разность двух сторон треугольника относится к их сумме, как тангенс полуразности противолежащих углов к тангенсу полусуммы этих углов:
Равносторонний треугольник со стороной :
– радиус описанной окружности,
– радиус вписанной окружности,
– высота, совпадающая с медианой и биссектрисой,
– площадь треугольника.
Разность двух сторон треугольника относится к их сумме, как тангенс полуразности противолежащих углов к тангенсу полусуммы этих углов.
Ru. solverbook. com
19.06.2018 16:06:54
2018-06-19 16:06:54
Источники:
Http://ru. solverbook. com/spravochnik/formuly-po-geometrii/treugolnik/formuly-treugolnika/
Вычисление медиан и биссектрис 11 класс онлайн-подготовка на Ростелеком Лицей
Введение
Наверняка за то время, что вы изучаете геометрию, вы решили множество задач, в условии которых встречались медианы или биссектрисы. Обычно наличие таких слов предполагало лишь формальное использование определения медианы или биссектрисы, то есть то, что какая-то сторона либо какой-то угол разделены пополам.
Обычно наличие таких слов предполагало лишь формальное использование определения медианы или биссектрисы, то есть то, что какая-то сторона либо какой-то угол разделены пополам.
Чуть реже мы использовали специфические свойства медиан и биссектрис. Но что делать, если нужно найти длину самой медианы или биссектрисы? Сейчас мы об этом и поговорим.
[00:0:54/Теорема о сторонах и диагоналях параллелограмма]
Докажем сначала полезную вспомогательную теорему о параллелограмме.
Теорема
В параллелограмме сумма квадратов диагоналей равна сумме квадратов сторон: .
Доказательство
Рассмотрим треугольники и (Рис. 1).
Рис. 1. Иллюстрация к доказательству теоремы
По теореме косинусов для треугольника имеем .
По теореме косинусов для треугольника имеем .
Теперь заметим, что и – секущая, то есть углы и – внутренние односторонние, а значит, их сумма равна . Следовательно, их косинусы равны по модулю и противоположны по знаку: .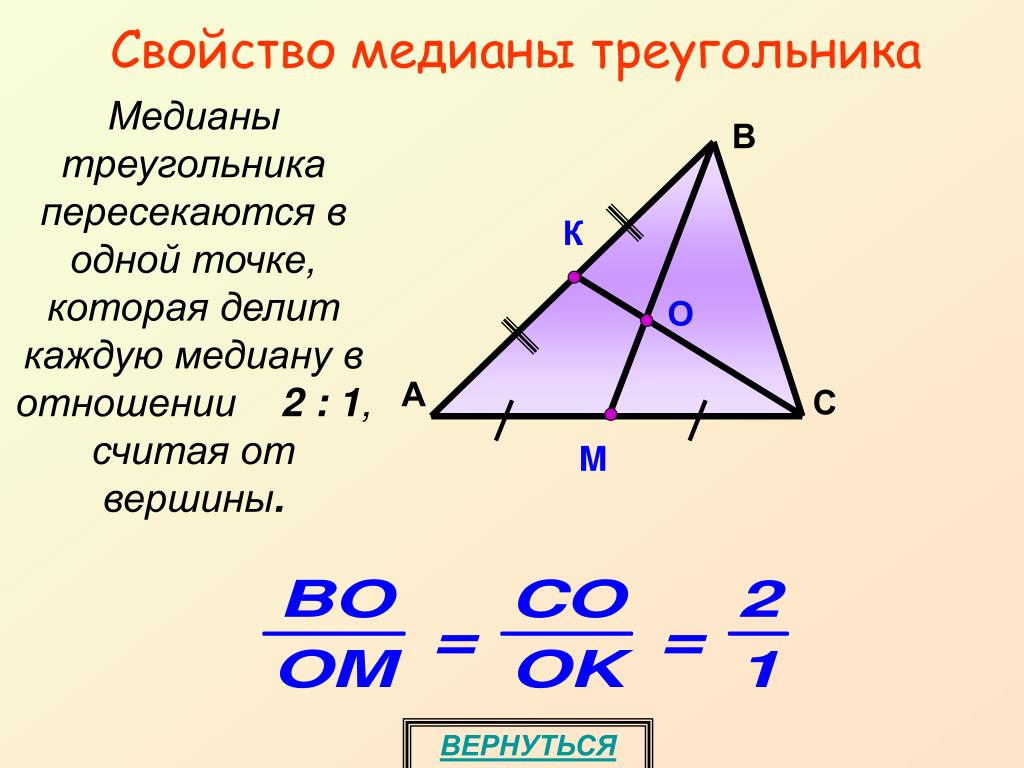 Учитывая это, сложим два равенства, получаем: .
Учитывая это, сложим два равенства, получаем: .
Теорема доказана.
Длина медианы
Эта теорема и сама по себе довольно полезна, потому что с ее помощью можно быстро найти недостающую сторону или диагональ параллелограмма. Но для нас сейчас особенно важно, что именно с помощью этой теоремы мы получим формулу для вычисления длины медианы треугольника. Для этого воспользуемся одним полезным стандартным приёмом при решении геометрических задач – удвоением медианы.
Теорема
Длину медианы треугольника можно вычислить по формуле: (Рис. 2).
Рис. 2. Иллюстрация к теореме о длине медианы треугольника
Доказательство
Продлим медиану на ее длину за точку – получим точку . Заметим, что – параллелограмм по признаку: диагонали делятся точкой пересечения пополам (Рис. 3).
Рис. 3. Удвоение медианы
Значит, к нему можно применить доказанную нами теорему о сторонах и диагоналях параллелограмма:
Теорема доказана.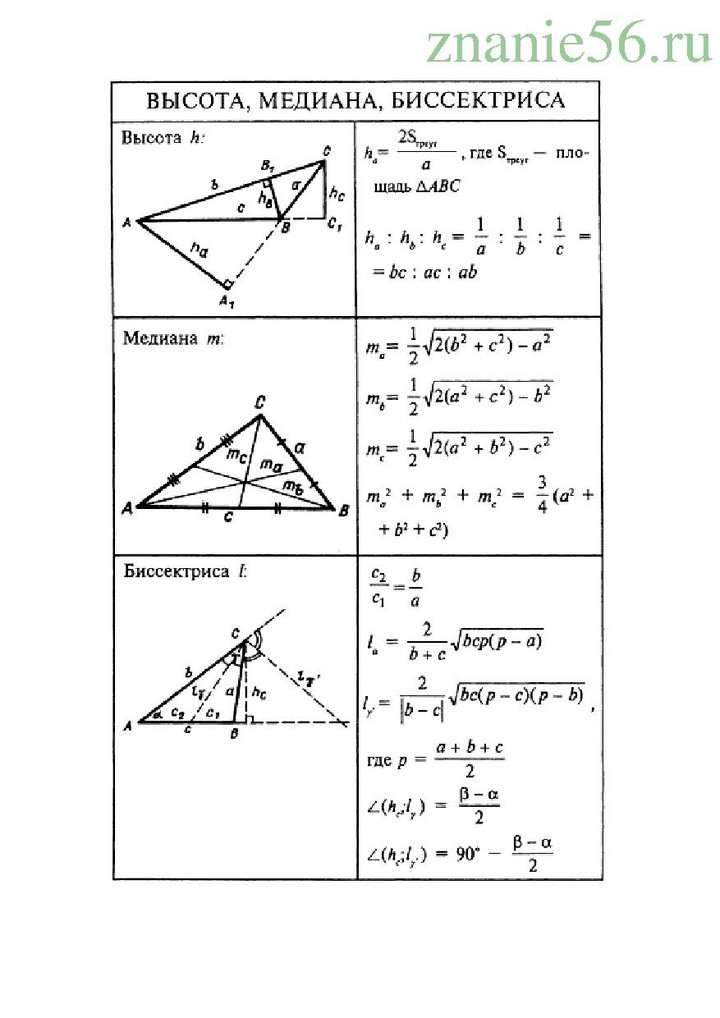
Итак, теперь мы умеем находить медиану треугольника, зная длины трёх его сторон. Воспользуемся этим для решения различных задач.
Примеры
Пример 1
Стороны треугольника равны и . Найти медиану, проведенную к большей стороне.
Решение
Воспользуемся формулой для длины медианы: .
Подставляем в неё известные из условия длины сторон:
Ответ: .
Пример 2
В треугольнике : , , медиана . Найти .
Решение
Воспользуемся формулой для длины медианы и подставим в неё данные из условия:
Ответ: .
Формула длины медианы применяется и для доказательства теорем.
Доказательство теоремы
Теорема
Если в треугольнике две медианы равны, то он равнобедренный.
Доказательство
Пусть (Рис. 1).
Рис. 1. Иллюстрация к теореме
1. Иллюстрация к теореме
Выразим длины обеих медиан через длины сторон треугольника и приравняем полученные формулы:
.
Получаем, что треугольник равнобедренный. Что и требовалось доказать.
Длина биссектрисы
Длину биссектрисы ищут гораздо реже. Однако формула для вычисления её длины может быть полезна для решения некоторых задач.
Теорема
Длину биссектрисы треугольника можно вычислить по формуле: (Рис. 4).
Рис. 4. Иллюстрация к теореме
Доказательство
Воспользуемся методом площадей. Запишем формулы для вычисления площади некоторых треугольников:
С другой стороны, площадь треугольника равна сумме площадей двух непересекающихся треугольников, из которых он состоит: . Тогда
Теорема доказана.
Пример
Рассмотрим задачу, которую можно решить, используя полученную формулу.
Задача
Пусть в треугольнике , , . Требуется найти биссектрису (Рис. 5).
Рис. 5. Иллюстрация к задаче
Решение
Воспользуемся полученной формулой для длины биссектрисы:
Нахождение биссектрисы по трём сторонам
Можно ли найти длину биссектрисы, если известны только длины трёх сторон треугольника? Конечно, можно по теореме косинусов найти косинус соответствующего угла треугольника, а затем по формуле косинуса двойного угла найти косинус половины угла и применить доказанную нами формулу длины биссектрисы. Но есть и другой алгоритм.
Пример
Пусть в треугольнике : и . Найти биссектрису (Рис. 1).
Рис. 1. Иллюстрация к условию задачи
Решение
1. Первым делом найдем . Заметим, что по свойству биссектрисы , значит, .
2. Далее по теореме косинусов для треугольника находим косинус угла :
3. Теперь применим теорему косинусов к треугольнику :
Теперь применим теорему косинусов к треугольнику :
Если этот метод вам понравился больше, то можно использовать для нахождения длины биссектрисы и его. Впрочем, в формулу подставлять гораздо проще.
Кстати, если даны три стороны, то есть еще одна формула, позволяющая найти длину биссектрисы: где и – отрезки, на которые сторона делится биссектрисой (Рис. 6).
Рис. 6. Нахождение биссектрисы по трем сторонам
Доказательство
Пусть – точка пересечения продолжения биссектрисы и окружности, описанной около (Рис. 1).
Рис. 1. Иллюстрация к доказательству
Тогда треугольники и подобны (одна пара углов равна по определению биссектрисы, а углы и – вписанные и опираются на одну дугу).
Значит, , то есть .
Осталось заметить, что по теореме о пересекающихся хордах: , подставив это в полученное равенство, получим требуемое:
Заключение
На этом уроке мы познакомились с формулами для вычисления длины медианы и биссектрисы в треугольнике. Помимо этого, доказали важную теорему о сторонах и диагоналях параллелограмма и решили несколько задач на применение выведенных формул.
Помимо этого, доказали важную теорему о сторонах и диагоналях параллелограмма и решили несколько задач на применение выведенных формул.
Список рекомендованной литературы
- Геометрия. Учебник для 10-11 классов. Атанасян Л.С. и др. 18-е изд. – М.: Просвещение, 2009.
- Геометрия 11 класс, А.В. Погорелов. М.: Просвещение, 2002.
- Геометрия. 11 класс. Рабочая тетрадь. Бутузов В.Ф., Глазков Ю.А., Юдина И.И. 8-е изд. – М.: Просвещение, 2013.
Рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «syl.ru» (Источник)
- Интернет-портал «www-formula.ru» (Источник)
- Интернет-портал «zdesformula.ru» (Источник)
Домашнее задание
- Вычислите длину биссектрисы треугольника , проведённую из вершины , если .
- Длины катетов прямоугольного треугольника равны и . Найдите длину биссектрисы прямого угла треугольника.

- В равнобедренном треугольнике длина боковой стороны равна . Медиана, проведённая к боковой стороне, равна . Найдите длину основания треугольника.
Как найти сторону треугольника если известны 2 его стороны
Обновлено: 28.09.2022
Вычисление длины стороны треугольника по двум другим и углу между ними согласно теореме косинусов.
После написания калькулятора Длина стороны прямоугольного треугольника по запросу пользователя вдруг вспомнил, что теорема Пифагора есть частный случай теоремы косинусов:
Воистину, тема треугольника неисчерпаема, как атом. На сайте уже был один калькулятор, который использовал теорему косинусов — Нахождение углов треугольника по заданным сторонам, а вот и второй, который просто находит длину противолежащей стороны.
Примеры решения задач
После того как изучены и рассмотрены основные понятия, свойства и теоремы для различного рода треугольников, можно переходить к решению геометрических задач. 0,5 ≈ 15,556 см.
0,5 ≈ 15,556 см.
Поскольку половина диагонали в два раза меньше гипотенузы, то искомым ответом на задачу будет число c/2 ≈ 7,778 см.
Две высоты и угол
Дан треугольник ABC. Известно, что при вершине C угол составляет 37 °. Из вершин A и B проведены высоты к сторонам этого треугольника, их длины составляют h2 = 10 см и h3 = 8 см, соответственно. Необходимо узнать длину стороны фигуры, которая лежит против угла C.
Из условия задачи можно найти длины сторон AC и BC. Для этого следует увидеть, что каждая из высот с двумя другими сторонами треугольника образует прямоугольную фигуру. Воспользовавшись тригонометрическими равенствами, можно получить следующие результаты:
- AC = h2/sinC = 10/sin (37 °) ≈ 16,616 см;
- BC = h3/sinC = 8/sin (37 °) ≈ 13,293 см.
Против угла C лежит сторона AB, которую следует найти. Получается, что известны две стороны треугольника (AC и BC) и угол между ними. Остается применить теорему косинусов, чтобы получить ответ:
AB = (AC 2 + BC 2 — 2*AC*BC*cosC)^0,5 = (16,616 2 + 13,293 2 — 2* 16,616 * 13,293 *cos (37 °))^0,5 ≈ 10 см.
Полученный результат свидетельствует о том, что высота h2 совпадает со стороной AB с рассчитанной точностью, то есть исходный треугольник являлся прямоугольным.
Таким образом, для нахождения стороны треугольника, если известны две другие его стороны или иные отрезки, следует воспользоваться теоремами. Основными из них являются теорема косинусов и синусов, а также Пифагора и Аполлония.
4. Найти длину высоты треугольника
Высота- перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.
H — высота треугольника
a — сторона, основание
b, c — стороны
β , γ — углы при основании
p — полупериметр, p=(a+b+c)/2
R — радиус описанной окружности
S — площадь треугольника
Формула длины высоты через стороны, ( H ):
Формула длины высоты через сторону и угол, ( H ):
Формула длины высоты через сторону и площадь, ( H ):
Формула длины высоты через стороны и радиус, ( H ):
5.
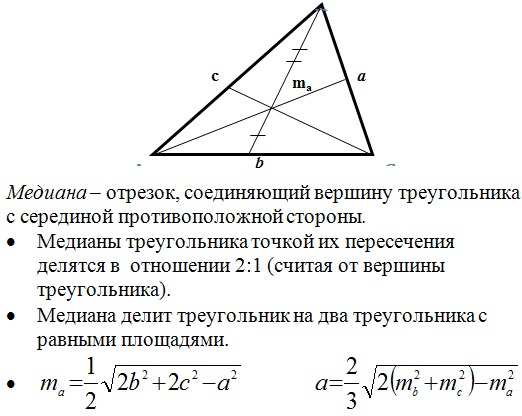 Формулы высоты прямого угла в прямоугольном треугольнике
Формулы высоты прямого угла в прямоугольном треугольникеВ прямоугольном треугольнике катеты, являются высотами. Ортоцентр — точка пересечения высот, совпадает с вершиной прямого угла.
H — высота из прямого угла
a, b — катеты
с — гипотенуза
c 1 , c 2 — отрезки полученные от деления гипотенузы, высотой
α , β — углы при гипотенузе
Формула длины высоты через стороны, ( H ):
Формула длины высоты через гипотенузу и острые углы, ( H ):
Формула длины высоты через катет и угол, ( H ):
Формула длины высоты через составные отрезки гипотенузы , ( H ):
10. Найти длину медианы треугольника по формулам
Медиана — отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.
Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.
M — медиана, отрезок |AO|
c — сторона на которую ложится медиана
a, b — стороны треугольника
γ — угол CAB
Формула длины медианы через три стороны, ( M ):
Формула длины медианы через две стороны и угол между ними, ( M ):
7.
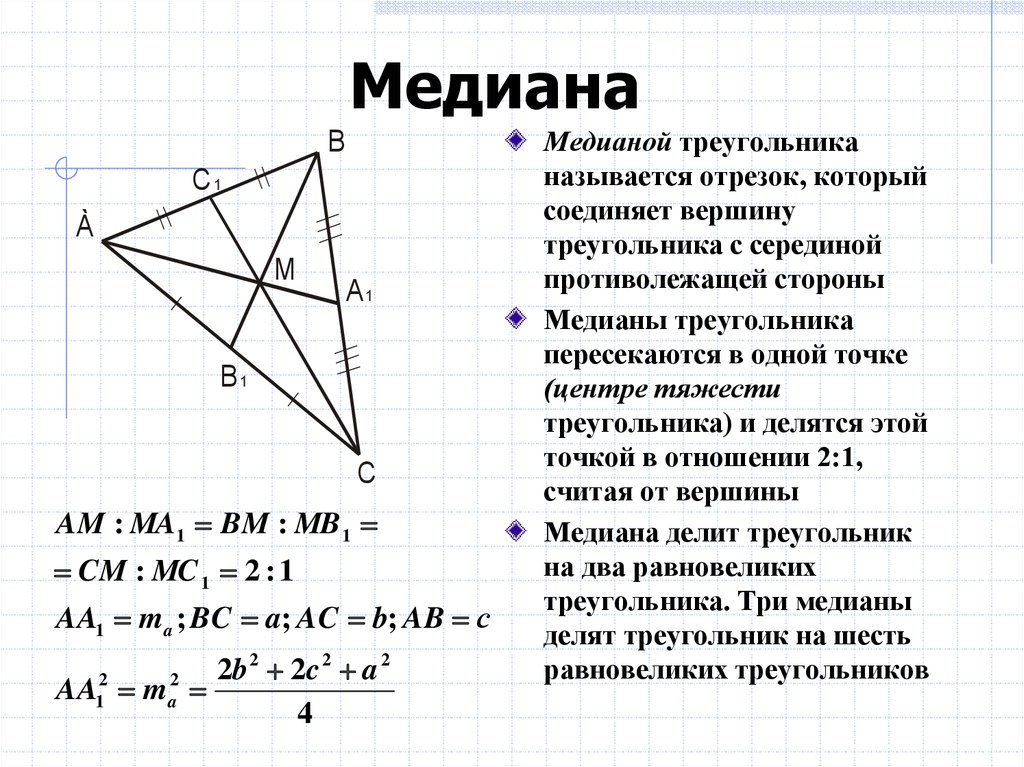 Биссектриса прямоугольного треугольника
Биссектриса прямоугольного треугольника1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:
L — биссектриса, отрезок ME , исходящий из прямого угла (90 град)
a, b — катеты прямоугольного треугольника
с — гипотенуза
α — угол прилежащий к гипотенузе
Формула длины биссектрисы через катеты, ( L ):
Формула длины биссектрисы через гипотенузу и угол, ( L ):
2. Найти по формулам длину биссектрисы из острого угла на катет:
L — биссектриса, отрезок ME , исходящий из острого угла
a, b — катеты прямоугольного треугольника
с — гипотенуза
α , β — углы прилежащие к гипотенузе
Формулы длины биссектрисы через катет и угол, ( L ):
Формула длины биссектрисы через катет и гипотенузу, ( L ):
Все формулы для треугольника
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a , b , c — стороны произвольного треугольника
α , β , γ — противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), ( a ):
* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), ( a):
11. Длина медианы прямоугольного треугольника
Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c , пополам.
Медиана в прямоугольном треугольнике ( M ), равна, радиусу описанной окружности ( R ).
3. Формулы сторон равнобедренного треугольника
Вычислить длину неизвестной стороны через любые стороны и углы
b — сторона (основание)
a — равные стороны
α — углы при основании
β — угол образованный равными сторонами
Формулы длины стороны (основания), (b ):
Формулы длины равных сторон , (a):
9.
 Найти медиану биссектрису высоту равностороннего треугольника
Найти медиану биссектрису высоту равностороннего треугольникаФормула для вычисления высоты = биссектрисы = медианы.
В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.
L — высота=биссектриса=медиана
a — сторона треугольника
Формула длины высоты, биссектрисы и медианы равностороннего треугольника, ( L ):
6. Найти длину биссектрисы в треугольнике
L — биссектриса, отрезок |OB|, который делит угол ABC пополам
a, b — стороны треугольника
с — сторона на которую опущена биссектриса
d, e — отрезки полученные делением биссектрисы
γ — угол ABC , разделенный биссектрисой пополам
p — полупериметр, p =(a+b+ c )/2
Длина биссектрисы через две стороны и угол, ( L ):
Длина биссектрисы через полупериметр и стороны, ( L ):
Длина биссектрисы через три стороны, ( L ):
Длина биссектрисы через стороны и отрезки d , e , ( L ):
Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.
Важные теоремы
Знание теорем для рассматриваемой фигуры позволяет понять, как найти сторону, зная 2 стороны треугольника. Прежде всего применяются две базовые теоремы:
К этим двум теоремам следует добавить еще два важных равенства, которые связаны с именами древнегреческих философов.
Первое выражение базируется на знаменитой теореме Пифагора, которая устанавливает связь между длинами двух катетов (меньшие стороны) и гипотенузы (большая сторона) в треугольнике с прямым углом. Если гипотенузу обозначить буквой c, тогда будет выполняться следующее равенство:
Если известные любые две стороны, то для определения третьей достаточно взять под квадратный корень соответствующую сумму или разницу квадратов.
Вторая из дополнительных теорем носит название философа Аполлония Пергского. Соответствующее ей математическое выражение выглядит так:
a 2 + b 2 = ½*c 2 + 2*Mc 2 .
Здесь Mc — это медиана, проведенная к стороне c из вершины C. Это равенство также называют в математике теоремой медианы.
Это равенство также называют в математике теоремой медианы.
Как определить вид треугольника
Онлайн калькулятор поможет узнать по сторонам, является ли треугольник прямоугольным, равнобедренным, равносторонним или разносторонним.
Как определить, что треугольник прямоугольный: по Теорема Пифагора — сумма квадратов длин катетов равна квадрату длины гипотенузы c 2 = a 2 + b 2
Как определить, что треугольник равнобедренный: один из признаков равнобедренного треугольника — две стороны равны.
Как определить, что треугольник равносторонний: все стороны равны.
Принято выделять три типа треугольников:
тупоугольные — один из углов более 90 градусов,
прямоугольные — один из угол равен 90 градусов,
остроугольные — все углы менее 90 градусов.
Это классификация по типу углов.
В геометрии первая фигура, которую школьники начинают изучать, это треугольник. Он является одним из самых распространенных и простых замкнутых объектов. Знание свойств фигуры и необходимых теорем позволяет решать разные задачи о том, как найти третью сторону треугольника на плоскости.
Знание свойств фигуры и необходимых теорем позволяет решать разные задачи о том, как найти третью сторону треугольника на плоскости.
2. Как узнать сторону прямоугольного треугольника
Есть следующие формулы для определения катета или гипотенузы
a , b — катеты
c — гипотенуза
α , β — острые углы
Формулы для катета, ( a ):
Формулы для катета, ( b ):
Формулы для гипотенузы, ( c ):
Формулы сторон по теореме Пифагора, ( a , b ):
8. Длина биссектрисы равнобедренного треугольника
L — высота = биссектриса = медиана
a — одинаковые стороны треугольника
b — основание
α — равные углы при основании
β — угол образованный равными сторонами
Формулы высоты, биссектрисы и медианы, через сторону и угол, ( L ):
Формула высоты, биссектрисы и медианы, через стороны, ( L ):
Фигура из шести элементов
Под геометрическим элементом полагают какой-либо объект, который имеет определенную меру и является составляющей частью некоторой фигуры. Например, для сферы основными образующими элементами являются радиус и центр.
Например, для сферы основными образующими элементами являются радиус и центр.
Как известно, треугольник — это фигура, которая состоит из трех отрезков и такого же количества вершин. При этом все отрезки попарно пересекаются. Из определения фигуры следует, что ее образуют два типа элементов, общее количество которых составляет 6:
Обычно треугольник обозначают большими латинскими буквами, например, ABC, PQM и так далее. Каждая буква — это название вершины (точка пересечения двух отрезков). AB, BC и CA, которые являются длинами сторон, принято обозначать маленькими латинскими буквами по названию противоположных им вершин, то есть c, a и b, соответственно.
Дополнительные отрезки
Несмотря на всю простоту построения фигуры, она обладает большим количеством дополнительных элементов, которые ее могут определять. Среди них самыми важными являются следующие:
Виды треугольников
Разработана достаточно развитая классификация рассматриваемых фигур. Главными ее пунктами являются значения углов треугольника и взаимоотношение между его отрезками. Так, если в фигуре все углы острые, то она называется остроугольной. Если же один из углов больше 90 °, то треугольник полагается тупоугольным. Чаще всего в задачах рассматривают следующие виды:
Главными ее пунктами являются значения углов треугольника и взаимоотношение между его отрезками. Так, если в фигуре все углы острые, то она называется остроугольной. Если же один из углов больше 90 °, то треугольник полагается тупоугольным. Чаще всего в задачах рассматривают следующие виды:
Основные свойства и понятия
Треугольник является одной из самых изученных фигур в геометрии. Для него известны многие теоремы, которые с успехом используются при решении задач. Существует два основных свойства фигуры, которые следуют из характеристик евклидового пространства:
Помимо названных свойств, следует знать о треугольнике еще такое понятие, как подобие. Его суть состоит в том, что одна из рассматриваемых фигур является точной копией в миниатюре другой. Для подобных треугольников все углы равны попарно, а все три стороны относятся соответственно попарно друг к другу с одним и тем же коэффициентом подобия.
Еще одной полезной характеристикой рассматриваемой фигуры является ее качество (CT). Вычисляется оно по следующей формуле:
Вычисляется оно по следующей формуле:
CT = (a + b — c)*(b + c — a)*(c + a — b)/(a*b*c).
Величина CT лежит в пределах от 0 до 1. Она показывает степень близости фигуры к равностороннему, то есть к наиболее симметричному объекту. Если CT < 0,5, то треугольник считается вырожденным (один из его углов будет тупым, причем чем меньше CT, тем больше величина этого угла), если же CT > 0,5, то фигура характеризуется, как имеющая хорошее качество.
Величина CT применяется для алгоритмов, которые разделяют какую-либо изучаемую геометрическую поверхность на сетку треугольников. Если в этой сетке генерируется много низкокачественных фигур, то будет велика ошибка аппроксимации рассматриваемой величины.
Читайте также:
- Сколько по времени устанавливается симс 4
- Как устроиться в ib
- Виталий пропионат в реальной жизни кто это
- Сталкер как вступить в долг вертолет узнать судьбу военных
- Кожа боевого медведя wow где собирать
Как найти вершину треугольника формула
Типы треугольников
По величине углов
По числу равных сторон
Вершины углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°:
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
Против равных сторон лежат равные углы:
если α > β , тогда a > b
если α = β , тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 – 2 bc · cos α
b 2 = a 2 + c 2 – 2 ac · cos β
c 2 = a 2 + b 2 – 2 ab · cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Медианы треугольника
Свойства медиан треугольника:
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
Медиана треугольника делит треугольник на две равновеликие части
Треугольник делится тремя медианами на шесть равновеликих треугольников.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 1 2 √ 2 b 2 +2 c 2 – a 2
mb = 1 2 √ 2 a 2 +2 c 2 – b 2
mc = 1 2 √ 2 a 2 +2 b 2 – c 2
Биссектрисы треугольника
Свойства биссектрис треугольника:
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
la = 2√ bcp ( p – a ) b + c
lb = 2√ acp ( p – b ) a + c
lc = 2√ abp ( p – c ) a + b
где p = a + b + c 2 – полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2 bc cos α 2 b + c
lb = 2 ac cos β 2 a + c
lc = 2 ab cos γ 2 a + b
Высоты треугольника
Свойства высот треугольника
Формулы высот треугольника
ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Окружность вписанная в треугольник
Свойства окружности вписанной в треугольник
Формулы радиуса окружности вписанной в треугольник
r = ( a + b – c )( b + c – a )( c + a – b ) 4( a + b + c )
Окружность описанная вокруг треугольника
Свойства окружности описанной вокруг треугольника
Формулы радиуса окружности описанной вокруг треугольника
R = S 2 sin α sin β sin γ
R = a 2 sin α = b 2 sin β = c 2 sin γ
Связь между вписанной и описанной окружностями треугольника
Средняя линия треугольника
Свойства средней линии треугольника
MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC
MN || AC KN || AB KM || BC
Периметр треугольника
Периметр треугольника ∆ ABC равен сумме длин его сторон
Формулы площади треугольника
Формула Герона
| S = | a · b · с |
| 4R |
| S = p · r |
Равенство треугольников
Признаки равенства треугольников
Первый признак равенства треугольников — по двум сторонам и углу между ними
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Третий признак равенства треугольников — по трем сторонам
Подобие треугольников
∆MNK => α = α 1, β = β 1, γ = γ 1 и AB MN = BC NK = AC MK = k ,
где k – коэффициент подобия
Признаки подобия треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool. 2) ) перпендикулярен AB и имеет длину 1, а вектор (-q/l*L, p/l*L) (где L — рассчитанная раньше длина CM ) перпендикулярен AB и имеет длину, равную длине MC .
2) ) перпендикулярен AB и имеет длину 1, а вектор (-q/l*L, p/l*L) (где L — рассчитанная раньше длина CM ) перпендикулярен AB и имеет длину, равную длине MC .
Таким образом, у нас есть вектор MC . Прибавляя его координаты к координатам точки M , мы получаем точку C .
Заметьте, что у нас возможно 2 решения, отличающиеся знаком вектора MC : для получения второго решения поменяйте знак у MC из первого решения.
Эта и другие подобные задачи будут кодироваться очень легко, если в вашем арсенале есть классы, представляющие точку, вектор, и определены операции над ними. Например, в моём коде обычно решение выглядит так (C#):
1. Как найти неизвестную сторону треугольника
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a , b , c – стороны произвольного треугольника
α , β , γ – противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), ( a ):
* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), ( a):
2.
 Как узнать сторону прямоугольного треугольника
Как узнать сторону прямоугольного треугольникаЕсть следующие формулы для определения катета или гипотенузы
a , b – катеты
c – гипотенуза
α , β – острые углы
Формулы для катета, ( a ):
Формулы для катета, ( b ):
Формулы для гипотенузы, ( c ):
Формулы сторон по теореме Пифагора, ( a , b ):
3. Формулы сторон равнобедренного треугольника
Вычислить длину неизвестной стороны через любые стороны и углы
b – сторона (основание)
a – равные стороны
α – углы при основании
β – угол образованный равными сторонами
Формулы длины стороны (основания), (b ):
Формулы длины равных сторон , (a):
4.
 Найти длину высоты треугольника
Найти длину высоты треугольникаВысота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.
H – высота треугольника
a – сторона, основание
b, c – стороны
β , γ – углы при основании
p – полупериметр, p=(a+b+c)/2
R – радиус описанной окружности
S – площадь треугольника
Формула длины высоты через стороны, ( H ):
Формула длины высоты через сторону и угол, ( H ):
Формула длины высоты через сторону и площадь, ( H ):
Формула длины высоты через стороны и радиус, ( H ):
|
Отношение между медианой и сторонами треугольника
Содержание:
- Первое отношение между медианой и сторонами треугольника: Сумма двух сторон больше медианы из общей вершины.

- Второе соотношение между медианой и сторонами треугольника: Трижды сумма квадратов длин сторон равна четырехкратному квадрату медиан треугольника.
- Коэффициент сегментации медиан в центре тяжести: Каждая медиана сегментирована по центроиду в соотношении 2 : 1 большим сегментом по направлению к вершине.
- Свойства центроида: Три медианы треугольника всегда пересекаются в одной точке внутри треугольника. Эта точка пересечения медиан является центроидом.
Медианы образуют один из наиболее важных наборов компонентов в треугольнике, тесно связанном с треугольником независимо от любой другой геометрической формы.
Например, другая пара важных компонентов, центр и радиус внутри, наследуют все свойства окружности, чтобы обогатить концепцию треугольника, в то время как медианы и точка их пересечения, центроид, проливают больше света на треугольник, не зависящий от любая другая геометрическая форма.
На этом занятии мы рассмотрим важные понятия, связанные с медианами, а также механизмы или доказательства, лежащие в основе этих понятий.
Что такое медианы и центр тяжести
При любом обсуждении геометрии первое, что нам нужно, это геометрическая фигура. На следующем рисунке показаны интересующие нас объекты, медианы.
Медиана определяется следующим образом:
Медиана — это отрезок, соединяющий вершину треугольника и середину противоположной стороны.
Другими словами, медиана — это биссектриса стороны, проходящая через вершину. На приведенном выше рисунке медианы трех вершин A, B и C равны соответственно AD, BE и CF, где D, E и F — середины сторон BC, CA и AB соответственно.
Три медианы проходят или пересекаются друг с другом в одной точке внутри треугольника G (на нашем рисунке). Эта точка пересечения медиан лежит внутри треугольника и называется центроидом.
Понятия о медианах и центроиде
Важными понятиями о медианах и центроидах являются:
- Медиана — это отрезок , проходящий от вершины треугольника до середины противоположной стороны.
 Это по определению.
Это по определению. - Три медианы треугольника пересекаются в одной точке, которая называется Центроидом. Имя точки пересечения — центроид по определению, но концепция пересечения одной точки нуждается в доказательстве, которое мы обсудим здесь.
- Центроид всегда будет лежать внутри треугольника, никогда не будет за его пределами. Это свойство центроида требует доказательства, которое мы обсудим здесь.
- Центроид называется центром тяжести треугольника. Вкратце это означает, что если вы рассматриваете треугольник как тонкую металлическую пластину абсолютно одинаковой толщины и плотности, вы можете сбалансировать треугольную металлическую пластину горизонтально на вертикальном карандаше с центром тяжести, расположенным на кончике карандаша, по крайней мере, теоретически .
- Центроид делит каждую медиану на два сегмента с соотношением длины 2 : 1, более длинная сторона обращена к вершине.
 Это свойство нуждается в доказательстве, которое мы обсудим здесь.
Это свойство нуждается в доказательстве, которое мы обсудим здесь. - Сумма длин двух смежных сторон треугольника всегда больше длины медианы из общей вершины двух сторон. Это требует доказательств, и мы их покажем.
- Периметр треугольника всегда будет больше, чем сумма длин трех медиан. Это следует из предыдущего свойства, и его доказательство последует автоматически.
- Трижды сумма квадратов трех сторон треугольника равна четырехкратной сумме квадратов длин медиан. Обсудим его доказательство.
Три медианы пересекаются в одной внутренней точке, которая делит каждую медиану на сегменты в отношении длины 2 : 1, механизм и доказательство
Мы будем использовать следующий рисунок для объяснения этих основных понятий о медианах и центроиде.
Здесь мы докажем три концепции:
- Точка пересечения медиан делит каждую медиану в отношении 2 : 1, причем больший сегмент лежит к вершине, а меньший — к основанию,
- Три медианы пересекаются в одной точке, центроиде и
- Центроид всегда лежит внутри треугольника.

Первый этап решения
В $\треугольнике ABC$ рассмотрим две медианы AD и CF, пересекающие друг друга в точке G. Поскольку F и D являются серединами двух сторон треугольника, отрезок, соединяющий их две точки FD в этом случае всегда будут параллельны основанию AC. Следовательно, два треугольника $\треугольник BAC$ и $\треугольник BFD$ будут подобны друг другу. Это богатая концепция, для доказательства которой вы можете обратиться к нашему обсуждению 9.0055 Базовые и расширенные понятия геометрии, часть 1, точки, линии и треугольники.
Поскольку эти два треугольника подобны, отношения соответствующих сторон равны между собой. То есть
$\displaystyle\frac{BF}{BA}=\frac{BD}{BC}=\frac{FD}{AC}=\frac{1}{2}$.
Нам нужна была в первую очередь информация о том, что FD является половиной AC , и мы ее получили.
Второй этап решения
Теперь сосредоточим внимание на двух треугольниках $\triangle FDG$ и $\triangle ACG$. АС ФД || AC противоположные внутренние углы равны,
АС ФД || AC противоположные внутренние углы равны,
$\angle DFG=\angle ACG$,
$\angle FDG = \angle CAG$,
так что третьи углы тоже равны,
$\angle DGF = \angle CGA$.
Таким образом, два треугольника также подобны (три угла равны, удовлетворяет критерию подобия ААА). Мы воспользовались свойством FD || АС с первой стадии решения. Это использование более общего принципа передачи геометрических свойств. Параллелизм между двумя прямыми FD и AC возникает в треугольниках $\треугольник BAC$ и $\треугольник BFD$ и передается второй паре треугольников $\треугольник FDG$ и $\треугольник ACG$. В геометрии частое использование этого принципа быстро приводит нас к решению.
Из-за подобия двух треугольников, $\triangle FDG$ и $\triangle ACG$, отношения соответствующих сторон равны, то есть
$\displaystyle\frac{GF}{CG}=\frac{ GD}{AG}=\frac{FD}{AC}=\frac{1}{2}$.
Значит, каждая из двух медиан AD и CF делится на два отрезка в отношении 2 : 1 в точке их пересечения G, причем больший отрезок направлен к вершине.
Третий этап решения
На этом заключительном этапе мы рассмотрим теперь пару медиан AD и BE и таким же образом можем доказать, что их точка пересечения, скажем, $G_1$ делит две медианы на отрезки соотношение 2 : 1 с большим сегментом, лежащим к вершине. Но поскольку и $G$, и $G_1$ находятся на расстоянии, равном одной трети расстояния AD от точки A до точки D, эти две точки совпадают. Эта единственная точка пересечения трех медиан называется центроидом.
Поскольку центроид всегда лежит на медиане между вершиной и серединой противоположной стороны, он всегда будет лежать внутри треугольника.
Подобно понятию центра окружности как центра тяжести окружности, центроид также может рассматриваться как центр тяжести асимметричной формы треугольника. Мы не будем обсуждать этот момент здесь и рассмотрим следующую концепцию, чтобы показать вам механизм, стоящий за ним.
Первое соотношение между медианой и сторонами треугольника: сумма двух сторон больше медианы из общей вершины
Это богатая концепция, связывающая сумму длин двух сторон с длиной медианы общей точки. Мы будем использовать следующий рисунок, чтобы показать механизм этой богатой концепции.
Мы будем использовать следующий рисунок, чтобы показать механизм этой богатой концепции.
В единственном порядке степенного единства длины сторон треугольника связаны с длинами медиан двумя способами, которые сами по себе являются взаимозависимыми. Один порядок означает степень длины сторон и медиан в отношении 1.
два отношения мы докажем теперь по отношению к приведенной выше фигуре,
- $AB + AC \gt 2AD$, и то же самое для двух других медиан и соответствующих пар сторон. В описательной форме это означает, что сумма смежных сторон больше, чем удвоенная длина медианы от вершины, общей для двух сторон.
- $AB + BC + CA > AD + BE + CF$. В описательных терминах это означает, что сумма длин сторон больше суммы длин медиан.
Давайте возьмем первое соотношение, чтобы увидеть, как эта концепция оказывается истинной.
Решение первого этапа На приведенном выше рисунке $\треугольник BPC$ является зеркальным отражением $\треугольника ABC$, образованного сближением сторон BP || АС и КП || AB образует параллелограмм ABPC с двумя диагоналями AP и BC, которые делятся пополам в точке пересечения D (из свойств параллелограмма).
н.э. является здесь медианой интереса.
Согласно основным свойствам треугольника, в $\triangle ABP$ сумма любых двух сторон больше третьей,
$AB + BP \gt AP$.
Но, во-первых, поскольку в параллелограмме противоположные стороны равны по длине,
$BP = AC$.
А также, поскольку диагонали делятся пополам в точке их пересечения,
$DP = AD$,
Или, $AP = 2AD$.
Таким образом, объединив эти результаты, мы получим
$AB + AC \gt 2AD$.
Решение второго этапаАналогично,
$BC + BA \gt 2BE$, и
$CB + CA \gt 2CF$.
Суммируя три неравенства,
$2(AB + BC + CA) \gt 2(AD + BE + CF)$,
Или $AB + BC + CA \gt AD + BE + CF$.
Таковы механизмы двух отношений первого порядка между сторонами треугольника и медианами.
Второе соотношение между медианой и сторонами треугольника: суммы квадратов медиан и квадратов сторон
Медианы и стороны треугольника связаны уравнением квадратов второго порядка, что является неожиданностью и немного продвинутой концепцией.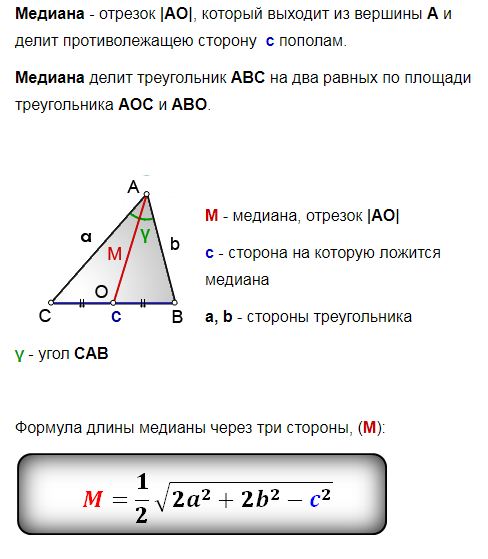 Тем не менее мы постараемся максимально упростить доказательство этой важной богатой концепции, полагаясь только на самые основные геометрические концепции.
Тем не менее мы постараемся максимально упростить доказательство этой важной богатой концепции, полагаясь только на самые основные геометрические концепции.
В описательных терминах соотношение второго порядка между сторонами и медианами треугольника:
Трижды сумма квадратов длин сторон равна четырехкратному квадрату медиан треугольника.
Мы покажем, как это происходит, используя следующий рисунок:
С помощью отношения второго порядка относительно приведенного выше рисунка, где D, E и F — середины трех сторон BC, CA и AB $\треугольника ABC$ и медианы AD, BE и CF, 92)$.
Решение основано на очень простых концепциях, а сам процесс достаточно прост, чтобы любой мог его понять и поверить. Вера в новую концепцию жизненно важна для полезного знания.
Вы можете обратиться к другим доказательствам теоремы Аполлония, чтобы иметь сравнительное представление о различных подходах к проблеме.
Мы закончим это обсуждение проблемой на уровне экзамена SSC CGL.
Задача о соотношении медианных сторон
В $\треугольнике ABC$ с медианами AD, BE и CF (D, E и F — середины сторон BC, CA и AB соответственно) верно следующее, 92)$
Анализ проблемы и решение.
Рисунок, изображающий проблему, показан ниже.
Богатая концепция отношения медианы к длине стороны в треугольнике утверждает, что
Трижды сумма квадратов трех сторон треугольника равна четырехкратной сумме квадратов его медиан.
Чтобы сформулировать концепцию в терминах алгебраического соотношения, по отношению к рисунку выше верно следующее соотношение между суммой сторон и суммой медиан, 92)$.
Ключевые используемые концепции: Расширенная концепция Отношение медианы к длине стороны второго порядка — Анализ неравенства.
Примечание: Будучи ПОЛЬЗОВАТЕЛЯМИ знаний для наилучшего решения проблем, мы должны как можно более ясно знать механизм, стоящий за концепцией. Ясность понимания понятия имеет большое значение для укрепления нашей веры в понятие и, следовательно, нашей способности использовать понятие, когда оно действительно необходимо.
Ясность понимания понятия имеет большое значение для укрепления нашей веры в понятие и, следовательно, нашей способности использовать понятие, когда оно действительно необходимо.
Пошаговая справка по геометрии в Suresolv
Чтобы получить наилучшие результаты из широкого спектра статей учебных пособий , вопросов и решений по Геометрия в Suresolv, 9,0950 следуйте инструкциям
Suresolv Geometry Reading and Practice Guide for SSC CHSL, SSC CGL, SSC CGL Tier II и других конкурсных экзаменов.
Список статей включает ВСЕ статьи по геометрии и соответствующие темы в Suresolv и обновлены.
← →
Теорема Аполлония – формула, доказательство, приложения, примеры
Теорема Аполлония – важная теорема в геометрии . Он соединяет длин сторон треугольника с длинами медиан .
Что такое Теорема Аполлония?
медиана треугольника — это отрезок, соединяющий вершина треугольника к середине противоположной стороны. Теорема Аполлония связывает длину медианы с длинами стороны, разделенной пополам, и двух других сторон.
Это эквивалентно закону параллелограмма элементарной геометрии.
Теорема Аполлония Формула
Пусть \(a\), \(b\) и \(c\) — длины трех сторон треугольника, а \(d\) — длина медианы, которая делит сторону пополам. \(а\). Пусть \(m = \frac{a}{2}\) будет длиной половины, разделенной пополам. 92)\)
Это называется формулой теоремы Аполлония .
Другими словами, Сумма квадратов двух сторон равна два раза T Сумма квадратов Медиана между ними и Полово .
Вывод теоремы Аполлония
Мы можем вывести и дать доказательство теоремы Аполлония, используя Закон косинусов 2)\)
Что доказывает Теорема Аполлония Формула .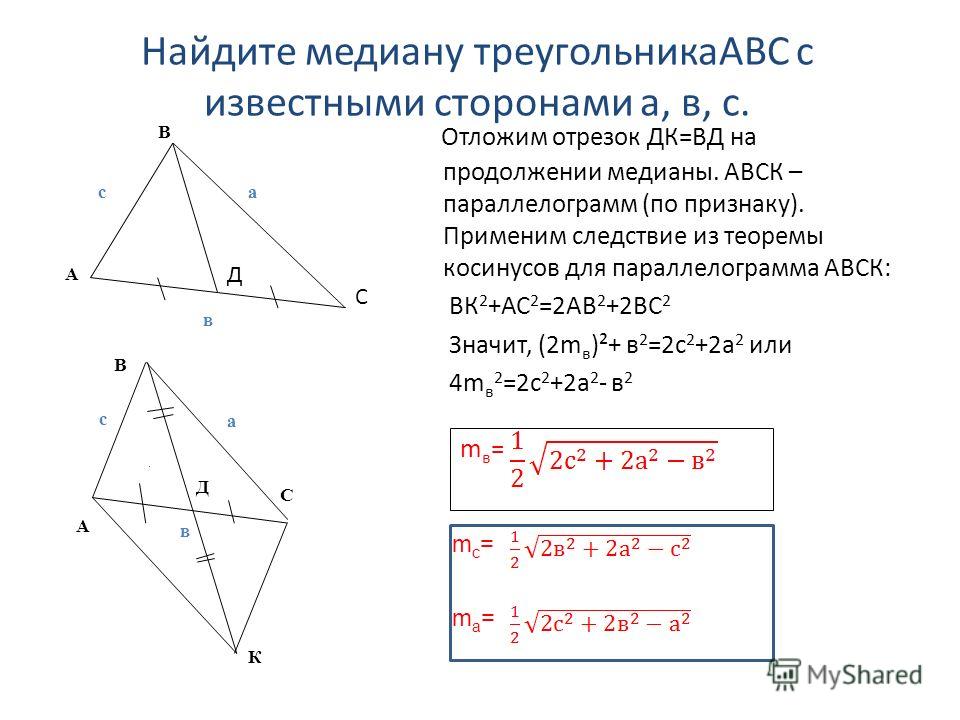
Приложения
Теорема Аполлония — теорема элементарной геометрии, аналогичная Теореме Пифагора . Полезно вычислить длину медианы треугольника.
Эквивалентно Закону о параллелограмме , как указано выше. Это означает, что его можно использовать для нахождения длины одной диагонали параллелограмма, если другой диагонали и двух сторон .
Это также частный случай теоремы Стюарта , которая имеет дело с более общей ситуацией чевиан . Чевиана, как и медиана, представляет собой отрезок, соединяющий одну вершину и противоположную сторону треугольника. Однако, в отличие от медианы, ей не нужно делить пополам другую сторону.
Решенные примеры
Вопрос 1. Стороны треугольника 7, 6 и 10 см. Найдите длину медианы стороны, длина которой 10 см. 92 = 35 \\
d = \sqrt{\frac{35}{2}} \\
d = 4,183 \text{см} \\
\)
Таким образом, длина медианы равна \(d = 4,183 \text{ см}\).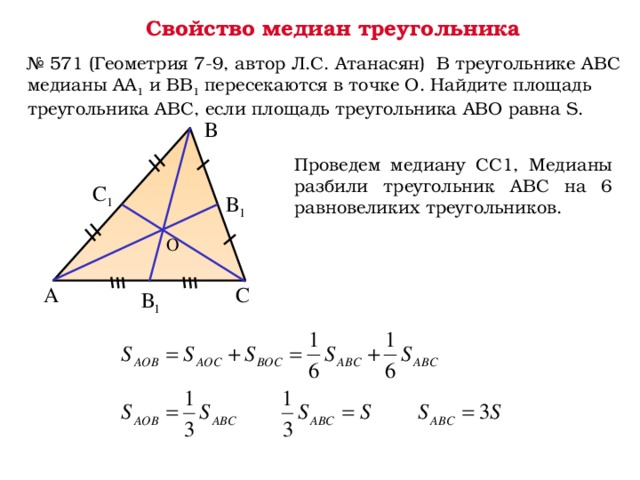
Вопрос 2. Параллелограмм имеет стороны 6 см и 4 см. Найдите длину другой диагонали, если длина одной диагонали равна 8 см.
Раствор. Эта ситуация очень похожа на случай с треугольником. Две стороны и одна диагональ образуют три стороны треугольника . Другая диагональ равна 9.\prime = 2d = 6,32 \text{см}\).
Часто задаваемые вопросы
Что такое теорема Аполлония?
Теорема Аполлония связывает длины сторон треугольника с длинами медианы.
Прописью утверждает, что сумма квадратов двух сторон равна дважды t сумма квадратов медианы между ними и половина третьей стороны . 92)\)
Это Теорема Аполлония.
Почему важна теорема Аполлония?
Теорема Аполлония дает нам способ вычисления медианных длин в треугольниках , если мы знаем их стороны.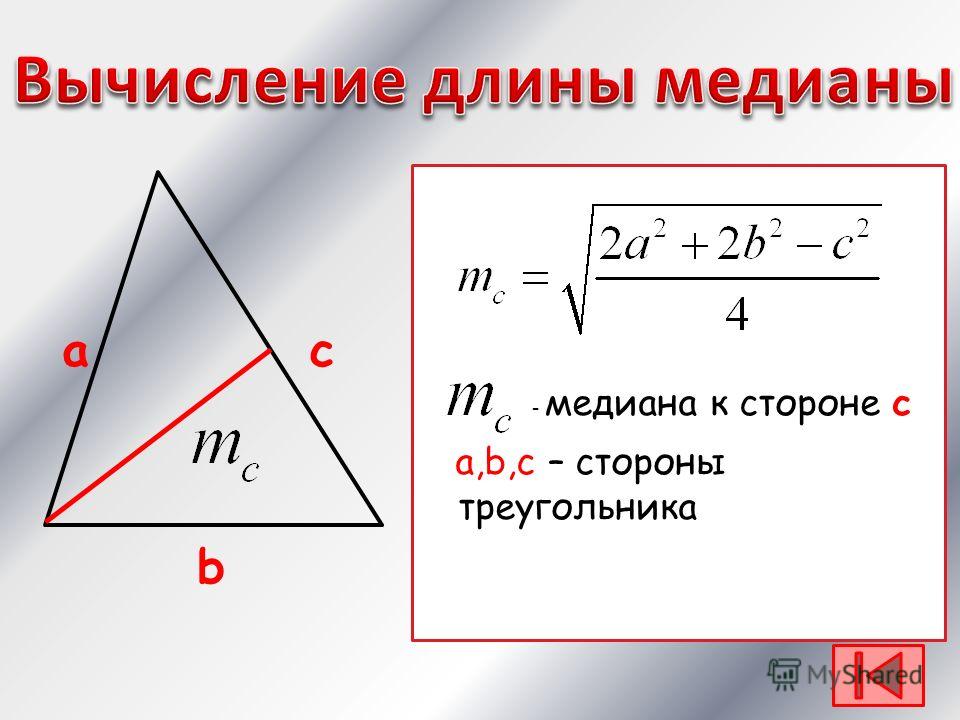 Это поможет нам решить треугольник.
Это поможет нам решить треугольник.
Как теорема Пифагора связана с теоремой Аполлония?
Теорему Пифагора можно рассматривать как частный случай теоремы Аполлония, когда у нас есть 92\)
Это просто теорема Пифагора в прямоугольном треугольнике \(ADB\).
Чем медиана отличается от биссектрисы угла?
Медиана — это отрезок прямой от одной вершины до противоположной стороны, который делит противоположную сторону пополам.
Биссектриса угла — это отрезок от одной вершины до противоположной стороны, который делит пополам угол при вершине.
В общем случае они не совпадают с , если только вершина не находится между равными сторонами, т.е. в равнобедренный треугольник.
Калькулятор медианы стороны C треугольника
✖Сторона треугольника A — это длина стороны A трех сторон треугольника. | +10% -10% |
✖Сторона B треугольника – это длина стороны B трех сторон. | +10% -10% |
✖Сторона C треугольника равна длине стороны C трех сторон. | +10% -10% |
✖Медиана треугольника – это отрезок, соединяющий вершину с серединой противоположной стороны и делящий эту сторону пополам. | А.У. of LengthAlnAngstromArpentAstronomical UnitAttometerBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (UK)DecameterDecimeterEarth-Moon DistanceEarth’s Distance from SunEarth’s Equatorial RadiusEarth’s Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkLong CubitLong ReedMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedRodRoman ActusRopeRussian ArchinSpan (Cloth)Sun’s RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter | ⎘ Копировать |
👎
Формула
Перезагрузить
👍
Медиана на стороне C решения треугольника
ШАГ 0: Сводка предварительного расчета
ШАГ 1: Преобразование входных данных в базовую единицу
Сторона A треугольника: 9 метров —> 9 метров Преобразование не требуется
Сторона B треугольника: 13 метров —> 13 метров Преобразование не требуется
Сторона C треугольника: 14 метров —> 14 метров Преобразование не требуется
ШАГ 2: вычисление формулы
ШАГ 3: преобразование результата в единицу измерения
8. 7177978000308135 Преобразование требуется —> нет
7177978000308135 Преобразование требуется —> нет
Что такое треугольник?
Треугольник — это тип многоугольника, который имеет три стороны и три вершины. Это двухмерная фигура с тремя прямыми сторонами. Треугольник считается трехсторонним многоугольником. Сумма всех трех углов треугольника равна 180°. Треугольник содержится в одной плоскости. Основываясь на сторонах и измерении углов, треугольник имеет шесть типов.
92)/2 для вычисления медианы треугольника. Медиана на стороне C треугольника определяется как длина отрезка, соединяющего вершину, содержащую угол C, с серединой стороны C, противоположной этой вершине. Медиана треугольника обозначается символом M . Как рассчитать медиану стороны C треугольника с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для расчета медианы на стороне C треугольника, введите Сторона A треугольника (S a ) , Сторона B треугольника 92)/2 . Сторона А треугольника — это длина стороны А трех сторон треугольника. Другими словами, сторона треугольника А — это сторона, противоположная углу А. Сторона треугольника В — это длина стороны В трех сторон. Другими словами, сторона треугольника B — это сторона, противоположная углу B, а сторона C треугольника — это длина стороны C трех сторон. Другими словами, сторона C треугольника — это сторона, противоположная углу C.
Сторона А треугольника — это длина стороны А трех сторон треугольника. Другими словами, сторона треугольника А — это сторона, противоположная углу А. Сторона треугольника В — это длина стороны В трех сторон. Другими словами, сторона треугольника B — это сторона, противоположная углу B, а сторона C треугольника — это длина стороны C трех сторон. Другими словами, сторона C треугольника — это сторона, противоположная углу C.
Как вычислить медиану на стороне C треугольника? 92)/2 . Чтобы вычислить медиану на стороне C треугольника, вам понадобится сторона A треугольника (S a ) , сторона B треугольника (S b ) и сторона C треугольника (S c ) . С помощью нашего инструмента вам нужно ввести соответствующее значение для стороны A треугольника, стороны B треугольника и стороны C треугольника и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.
Доля
Скопировано!
Создание пользовательских рабочих листов по предварительной алгебре, алгебре 1, геометрии, алгебре 2, предварительному исчислению и математическому анализу
Неограниченное количество вопросов
Создав задание, вы можете повторно сгенерировать все его вопросы одним щелчком мыши.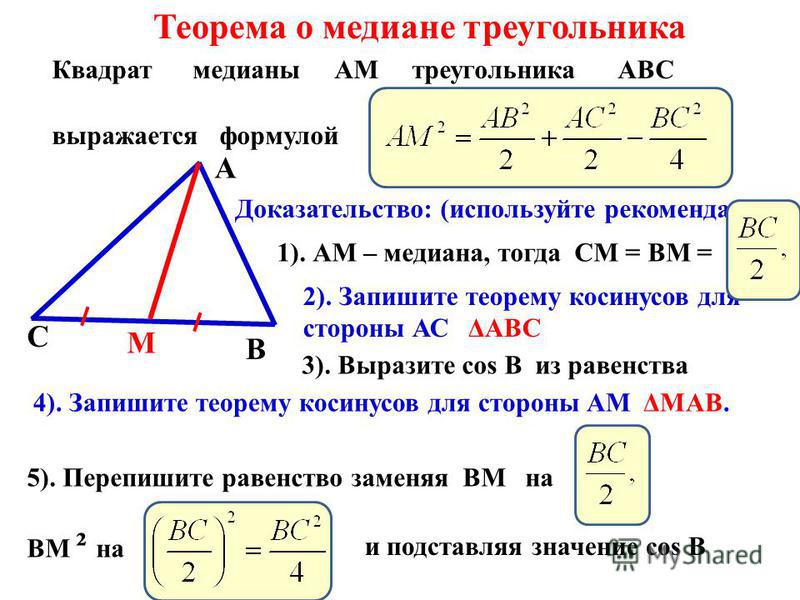 Новые вопросы будут соответствовать тем же параметрам, что и исходные вопросы, но они будут
совершенно новый. Эта функция лежит в основе нашего программного обеспечения и делает его таким мощным: вы
выбирайте свойства вопросов, а не сами вопросы. Когда вопрос заменяется,
вы получаете новый, похожий на исходный вопрос. Как это
работает. Вы можете регенерировать целые задания, определенные группы вопросов или отдельные
вопросы.
Новые вопросы будут соответствовать тем же параметрам, что и исходные вопросы, но они будут
совершенно новый. Эта функция лежит в основе нашего программного обеспечения и делает его таким мощным: вы
выбирайте свойства вопросов, а не сами вопросы. Когда вопрос заменяется,
вы получаете новый, похожий на исходный вопрос. Как это
работает. Вы можете регенерировать целые задания, определенные группы вопросов или отдельные
вопросы.
Easy Spacing
Изменить интервал всего назначения до нужной длины одним щелчком мыши. Легко дайте своим ученикам достаточно места, чтобы показать свою работу, увеличив интервал. Или вы можете сэкономить бумагу, уменьшив интервал.
Расстояние также можно регулировать вручную.
Режим презентации
Очень полезен в качестве учебного пособия при использовании в сочетании с ЖК-проектором или другим дисплеем
система.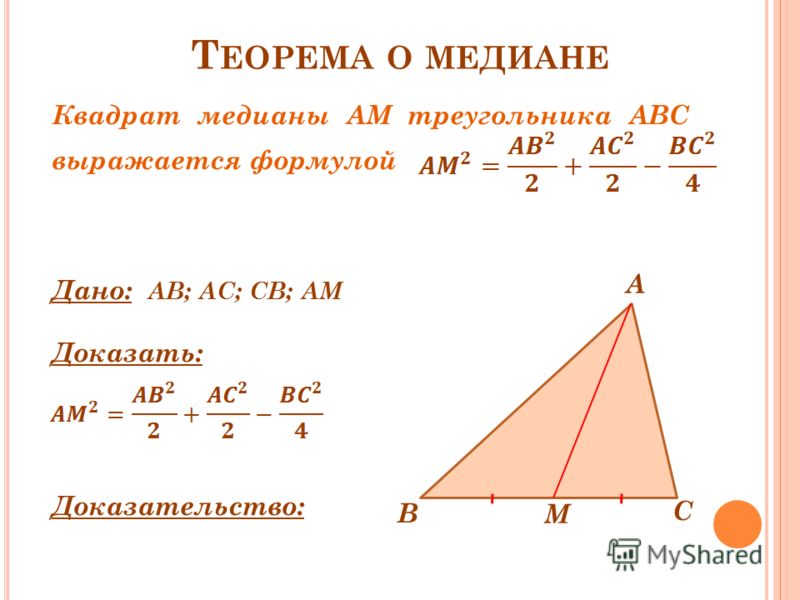 На экране одновременно отображаются от одного до четырех вопросов.
На экране одновременно отображаются от одного до четырех вопросов.
Используйте эту функцию во время обучения. Подготовьте свои примеры с помощью программного обеспечения, а затем используйте проектор для отображения вопросов на доске. Это экономит время при планировании и во время урок, и это позволяет очень легко представить длинные вопросы или вопросы с графиками и диаграммами. С одним отображаемым вопросом вы можете:
- Изменить уровень масштабирования, чтобы учащиеся сзади могли его прочитать
- Нарисуйте линии рядом с вопросом, чтобы помочь вам организовать свою работу, если вы решите вопрос
- Перейти к другому вопросу — полезно при просмотре домашнего задания
- Раскройте ответ
- Показать/скрыть номер вопроса и указания.
Печать нескольких версий
Печать нескольких версий задания.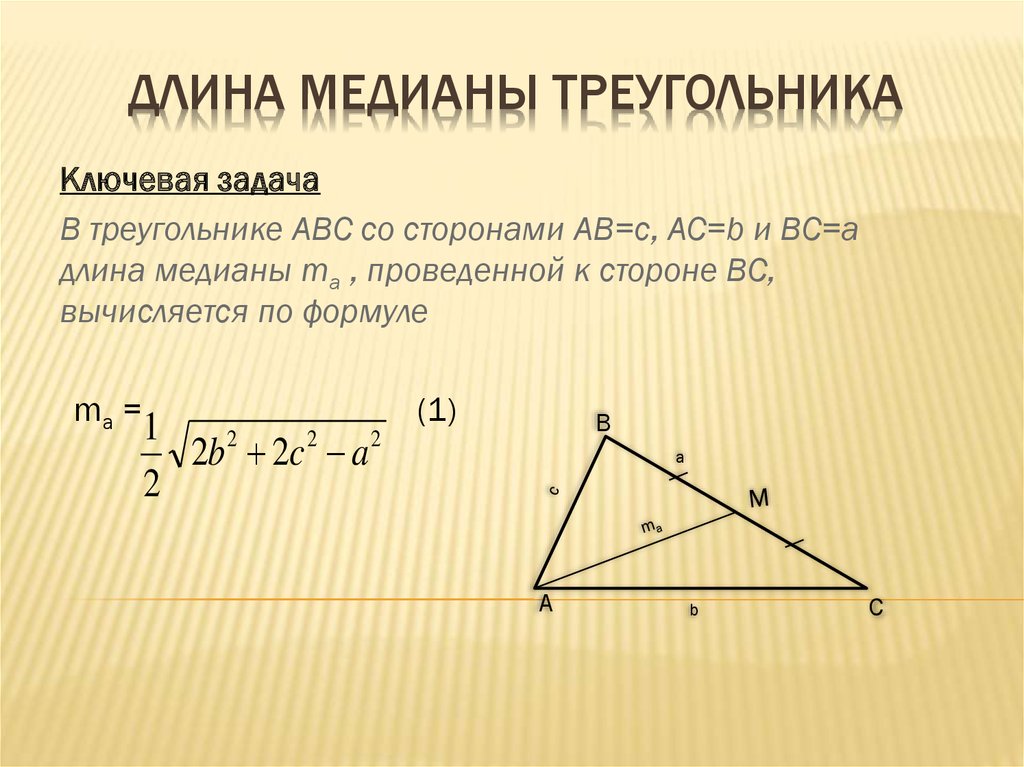 Вы контролируете, как создается каждая новая версия: скремблировать
варианты, перепутать вопросы или составить совершенно новые вопросы. Вы также можете сохранять каждый новый
версию после ее создания.
Вы контролируете, как создается каждая новая версия: скремблировать
варианты, перепутать вопросы или составить совершенно новые вопросы. Вы также можете сохранять каждый новый
версию после ее создания.
Масштаб задания
Пропорционально увеличить или уменьшить количество вопросов в задании. это очень полезно при планировании урока. Вы можете создать несколько вопросов для использования в качестве примеров, а затем масштабировать номер вопроса для создания домашнего задания. Вопросы по домашнему заданию будут полностью новые, но точно вытекающие из урока — и вам не нужно заново составлять вопросы.
Экспорт вопросов
Экспорт вопросов в виде растровых изображений и вставка их в ваш любимый текстовый редактор.
Вопросы, созданные с помощью наших продуктов, можно добавлять к существующим заданиям, которые вы создали с помощью других
программы. Или вы можете освежить старые задания, заменив старые вопросы новыми.
Или вы можете освежить старые задания, заменив старые вопросы новыми.
Все вопросы доступны для экспорта.
Хорошие вопросы с несколькими вариантами ответов
Каждый вопрос, который вы создаете, можно переключать между форматом свободного ответа и множественным выбором. Вопросы с несколькими вариантами ответов содержат умные, потенциально вводящие в заблуждение варианты. Некоторые из них основаны на общих ошибки, которые допускают учащиеся, в то время как другие случайны, но близки к правильному ответу.
Вы управляете количеством вариантов ответа на каждый вопрос, от двух до пяти.
Объединить задания
Объединить два или более заданий в одно. Легко создавайте викторины, тесты и обзоры, объединяя назначения из единицы, а затем масштабирование общей суммы до соответствующей длины. Вопросы будут новое, точно следуя тому, чему вы учили.
Диаграммы, нарисованные в масштабе
Все диаграммы нарисованы точно, за исключением случаев, когда ответ будет выдан.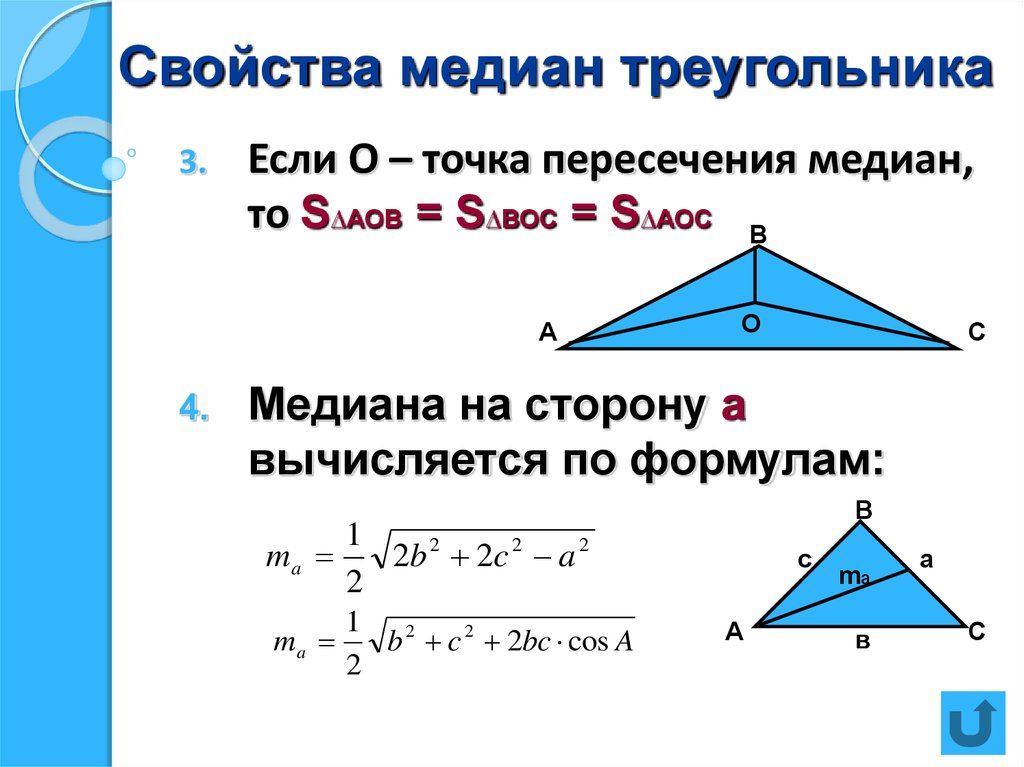 Если угол
помечены как 30°, тогда это действительно 30°. Если стороны треугольника обозначены цифрами 3, 4 и 5, то его
длины действительно находятся в соотношении 3:4:5. Наблюдение за точными диаграммами помогает учащимся интуитивно понять
понимание углов и измерений.
Если угол
помечены как 30°, тогда это действительно 30°. Если стороны треугольника обозначены цифрами 3, 4 и 5, то его
длины действительно находятся в соотношении 3:4:5. Наблюдение за точными диаграммами помогает учащимся интуитивно понять
понимание углов и измерений.
Формат ответа
При печати задания вы выбираете, как будут представлены ответы:
- На листе ответов
- На листе ответов только шансы
- В контексте (рядом с вопросом или внутри вопроса)
- Нет листа ответов
Утилита для работы с графиками и миллиметровой бумагой
Дополните свои уроки высококачественными графиками и миллиметровой бумагой любого размера. Каждый граф может иметь
от нуля до двух функций, изображенных на нем. Графики могут быть любого логического и физического размера. Вы также можете
Мозаичные графики по всей странице, чтобы максимально использовать бумагу.
Вы также можете
Мозаичные графики по всей странице, чтобы максимально использовать бумагу.
Пользовательские направления и пользовательские вопросы
Введите свои собственные направления для создания новых типов задач. Слева показан стандартный заказ вопрос операций, который был изменен, чтобы быть более аналитическим. Вы можете изменить направление на любой тип вопроса.
Время от времени вам нужно будет ввести свой вопрос. Вот для чего нужны пользовательские вопросы. Они могут быть как со свободным ответом, так и с несколькими вариантами ответов и могут содержать текст в математическом формате (уравнения, выражения и др.).
Изменить автоматически сгенерированные вопросы
Большинство автоматически сгенерированных вопросов можно изменить вручную. Если есть выбор, ты не
вроде можно поменять. Если вы хотите, чтобы вопрос был немного другим, вы можете изменить его.

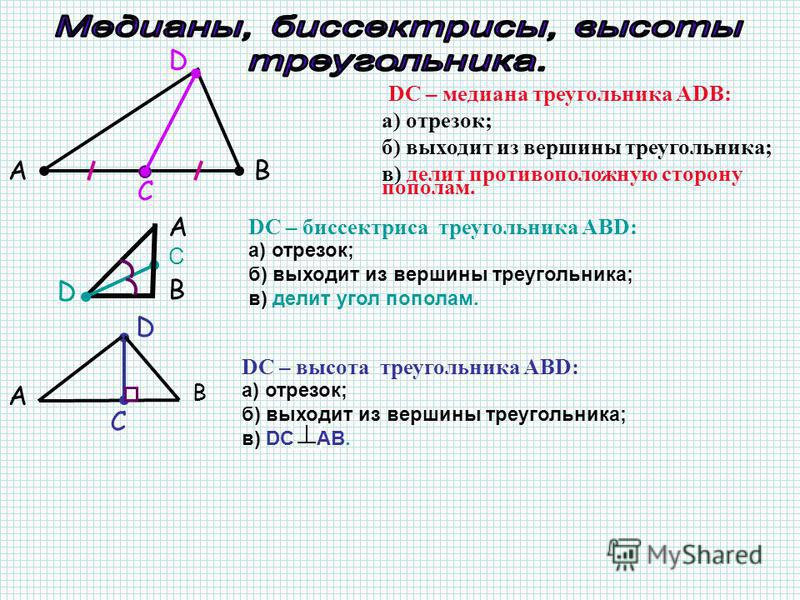 Медианы, опущенные из других вершин, равны. Это также является необходимым и достаточным условием равнобедренности.
Медианы, опущенные из других вершин, равны. Это также является необходимым и достаточным условием равнобедренности.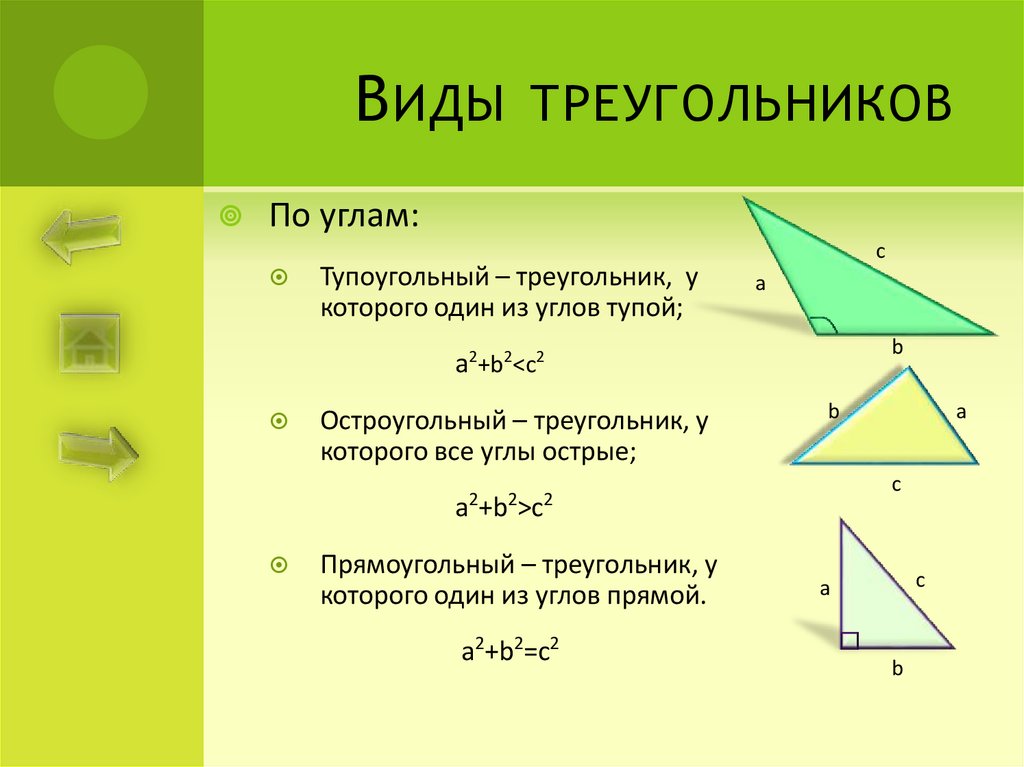
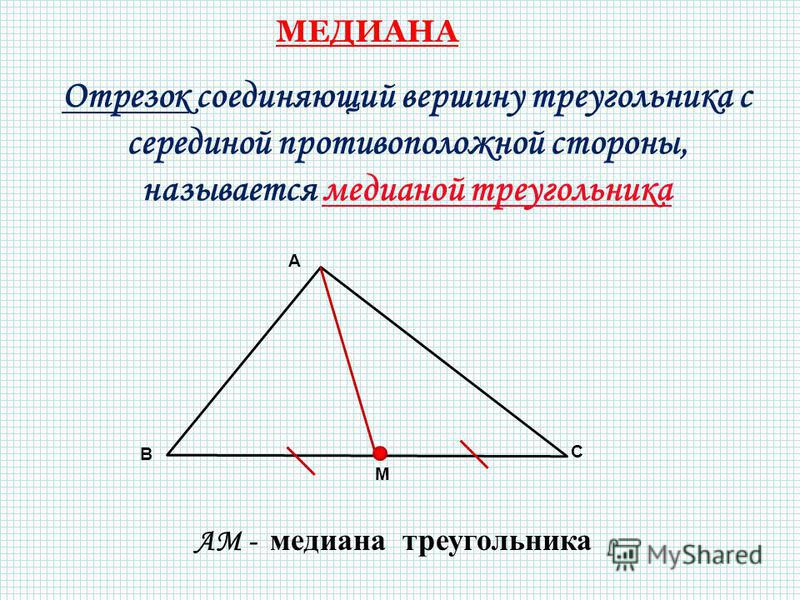


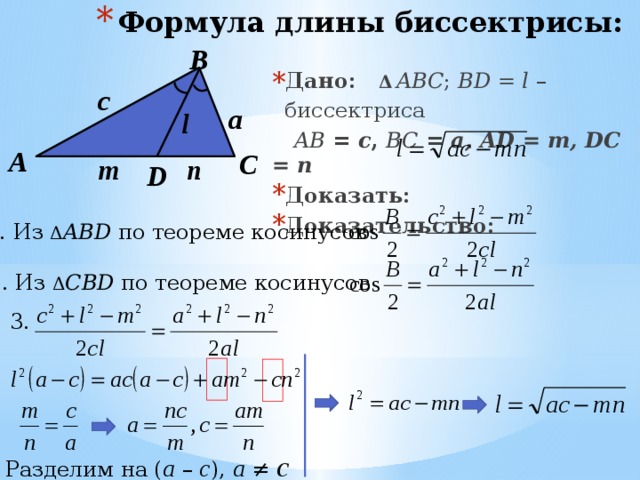
 ..
..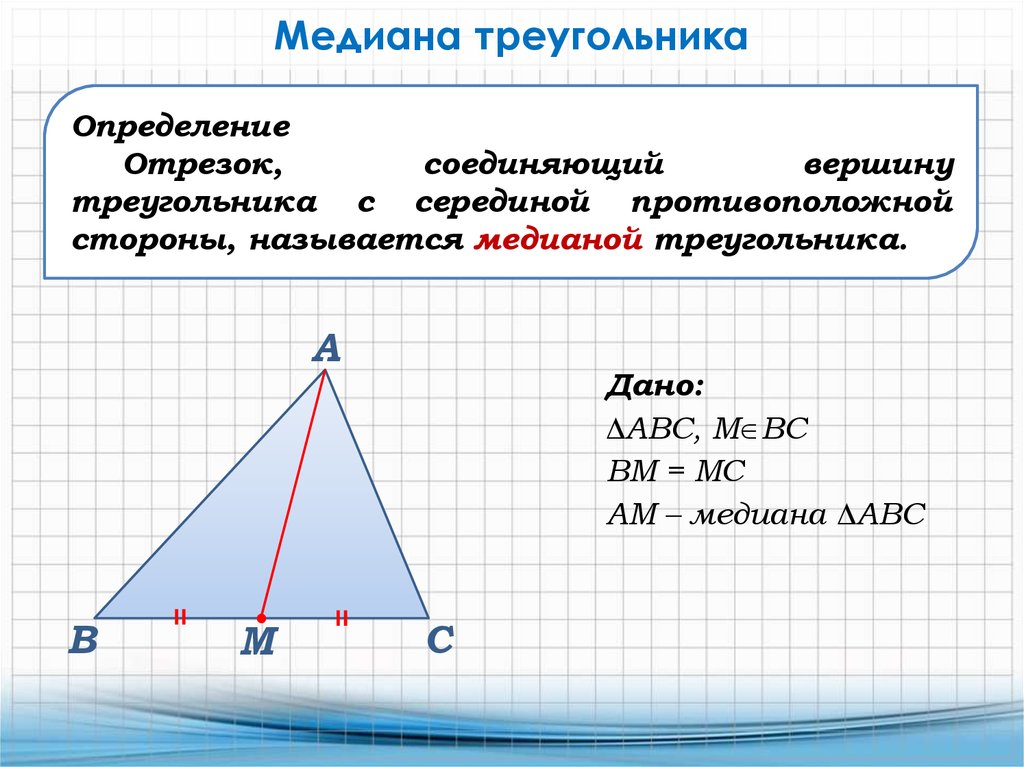
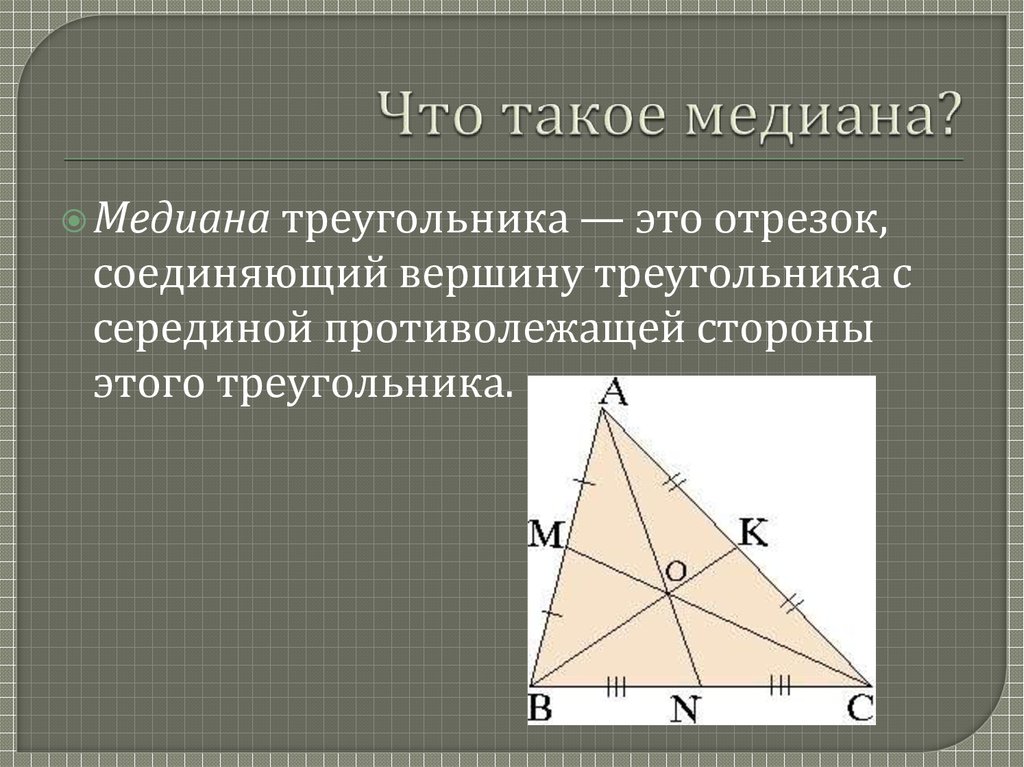
 Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.
Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.
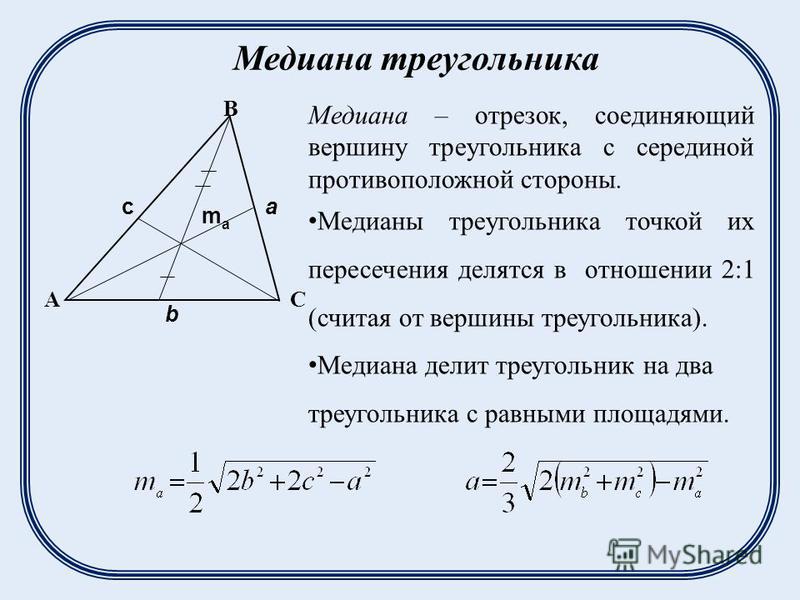 Ортоцентр — точка пересечения высот, совпадает с вершиной прямого угла.
Ортоцентр — точка пересечения высот, совпадает с вершиной прямого угла.
 Это по определению.
Это по определению. Это свойство нуждается в доказательстве, которое мы обсудим здесь.
Это свойство нуждается в доказательстве, которое мы обсудим здесь.
 Другими словами, сторона A треугольника — это сторона, противоположная углу A. of LengthAlnAngstromArpentAstronomical UnitAttometerBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (UK)DecameterDecimeterEarth-Moon DistanceEarth’s Distance from SunEarth’s Equatorial RadiusEarth’s Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkLong CubitLong ReedMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedRodRoman ActusRopeRussian ArchinSpan (Cloth)Sun’s RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter
Другими словами, сторона A треугольника — это сторона, противоположная углу A. of LengthAlnAngstromArpentAstronomical UnitAttometerBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (UK)DecameterDecimeterEarth-Moon DistanceEarth’s Distance from SunEarth’s Equatorial RadiusEarth’s Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkLong CubitLong ReedMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedRodRoman ActusRopeRussian ArchinSpan (Cloth)Sun’s RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter Другими словами, сторона треугольника B — это сторона, противоположная углу B. of LengthAlnAngstromArpentAstronomical UnitAttometerBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (UK)DecameterDecimeterEarth-Moon DistanceEarth’s Distance from SunEarth’s Equatorial RadiusEarth’s Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkLong CubitLong ReedMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedRodRoman ActusRopeRussian ArchinSpan (Cloth)Sun’s RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter
Другими словами, сторона треугольника B — это сторона, противоположная углу B. of LengthAlnAngstromArpentAstronomical UnitAttometerBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (UK)DecameterDecimeterEarth-Moon DistanceEarth’s Distance from SunEarth’s Equatorial RadiusEarth’s Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkLong CubitLong ReedMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedRodRoman ActusRopeRussian ArchinSpan (Cloth)Sun’s RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter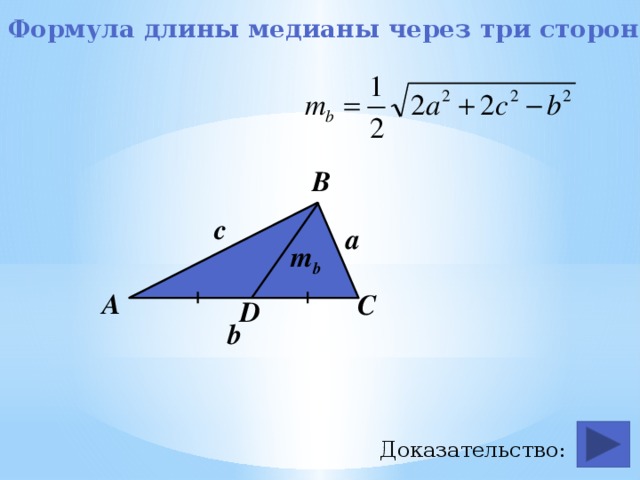 Другими словами, сторона C треугольника — это сторона, противоположная углу C. of LengthAlnAngstromArpentAstronomical UnitAttometerBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (UK)DecameterDecimeterEarth-Moon DistanceEarth’s Distance from SunEarth’s Equatorial RadiusEarth’s Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkLong CubitLong ReedMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedRodRoman ActusRopeRussian ArchinSpan (Cloth)Sun’s RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter
Другими словами, сторона C треугольника — это сторона, противоположная углу C. of LengthAlnAngstromArpentAstronomical UnitAttometerBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (UK)DecameterDecimeterEarth-Moon DistanceEarth’s Distance from SunEarth’s Equatorial RadiusEarth’s Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkLong CubitLong ReedMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedRodRoman ActusRopeRussian ArchinSpan (Cloth)Sun’s RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter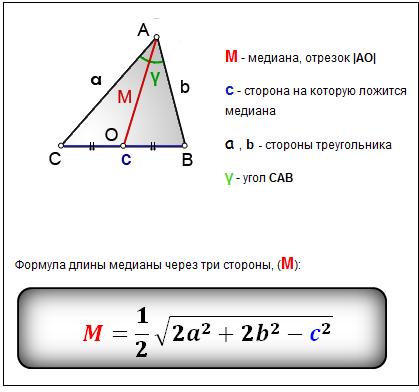 ⓘ Медиана стороны C треугольника [M]
ⓘ Медиана стороны C треугольника [M]