Как начертить параболу y x2: Функция y=x2 и ее график

Содержание

Функция y = x2 и её график

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Тема: Функция y = x2 и её график.

*
y=
2
x
Назовите координаты точек, симметричных данным точкам
относительно оси y :
y
(- 2; 6)
( 2; 6)
(- 1; 4)
(1; 4)
(0; 0)
(0; 0)
(- 3; — 5)
(3; — 5)
х
На графике видно, что ось OY делит параболу на симметричные
левую и правую части (ветви параболы), в точке с координатами (0; 0)
(вершине параболы) значение функции x 2 — наименьшее.

Наибольшего значения функция не имеет. Вершина параболы — это
точка пересечения графика с осью симметрии OY .
На участке графика при x ∈ (– ∞; 0 ] функция убывает,
а при x ∈ [ 0; + ∞) возрастает.
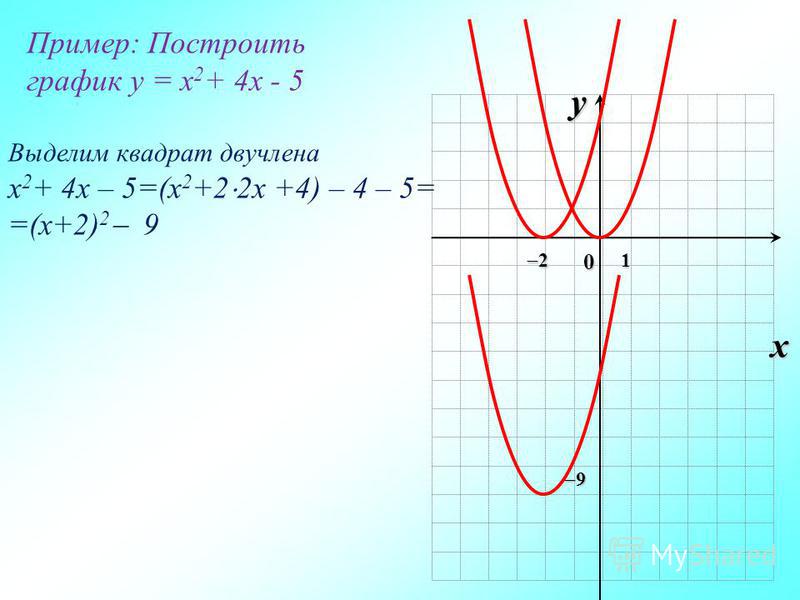
График функции y = x 2 + 3 — такая же парабола, но её
вершина находится в точке с координатами (0; 3) .
Найдите значение функции
y = 5x + 4, если:
х=-1
y = — 1 y = 19
х=-2
y=-6
y = 29
х=3
х=5
Укажите
область определения функции:
y = 16 – 5x
10
y
х
х – любое
число
х≠0
1
y
х 7
4х 1
y
5
х≠7
Постройте графики функций:
1).У=2Х+3
2).У=-2Х-1;
3).
Математическое
исследование
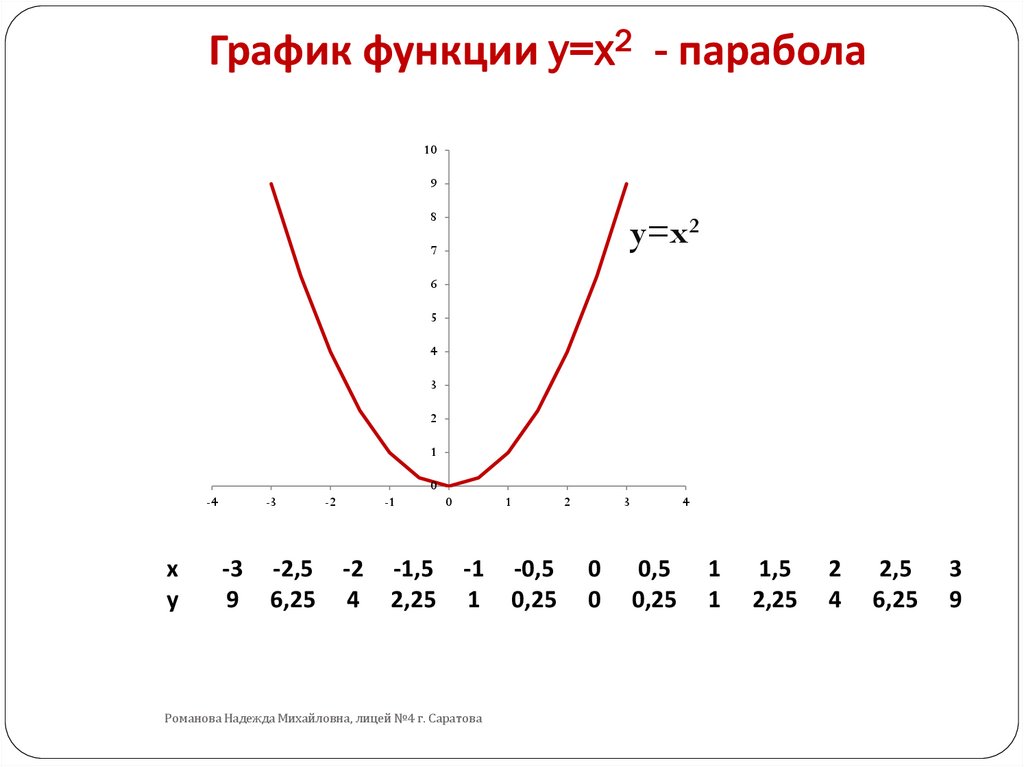
Тема: Функция y = x2
Постройте
график
функции
y = x2
Алгоритм построения параболы..
1.Заполнить таблицу значений Х и У.
2.Отметить в координатной плоскости точки,
координаты которых указаны в таблице.
3.Соедините эти точки плавной линией.
Невероятно,
но факт!
Перевал Парабола
Знаете ли вы?
Траектория камня, брошенного под
углом к горизонту, будет лететь по
параболе.

15. Свойства функции y = x2

*
Свойства функции
y=
2
x
*Область определения
функции D(f):
х – любое число.
*Область значений
функции E(f):
все значения у ≥ 0.
*Если
х = 0, то у = 0.
График функции
проходит через
начало координат.
II
I
*Если
х ≠ 0,
то у > 0.
Все точки графика
функции, кроме точки
(0; 0), расположены
выше оси х.
*Противоположным
значениям х
соответствует одно
и то же значение у.
График функции
симметричен
относительно оси
ординат.
Геометрические
свойства параболы
*Обладает симметрией
*Ось разрезает параболу на
две части: ветви
параболы
*Точка (0; 0) – вершина
параболы
*Парабола касается оси
абсцисс
Ось
симметрии
Найдите у, если:
«Знание – орудие,
а не цель»
Л. Н. Толстой
х = 1,4
— 1,4
у = 1,96
х = 2,6
-2,6
у = 6,76
х = 3,1
— 3,1
у = 9,61
Найдите х, если:
у=6
у=4
х ≈ 2,5 х ≈ -2,5
х=2 х=-2
постройте в одной
системе координат
графики двух функций
1.

Случай :
у=х2
У=х+1
2. случай:
У=х2
у= -1
Найдите
несколько значений
х, при которых
значения функции :
меньше 4
больше 4

• Принадлежит ли графику функции у = х2 точка:
P(-18; 324)
R(-99; -9081)
принадлежит
не принадлежит
S(17; 279)
не принадлежит
• Не выполняя вычислений, определите, какие из
точек не принадлежат графику функции у = х2:
(-1; 1)
*
(-2; 4)
(0; 8)
(3; -9)
(1,8; 3,24)
При каких значениях а точка Р(а; 64) принадлежит графику функции у = х2.
а = 8; а = — 8
(16; 0)
Алгоритм решения уравнения
графическим способом
1. Построить в одной системе
координат графики функций, стоящих
в левой и правой части уравнения.
2. Найти абсциссы точек пересечения
графиков. Это и будут корни
уравнения.
3. Если точек пересечения нет, значит,
уравнение не имеет корней
Удачи вам!

English Русский Правила

Как дискриминант влияет на параболу.

ГИА. Квадратичная функция

На уроках математики в школе Вы уже познакомились с простейшими свойствами и графиком функции y = x 2 . Давайте расширим знания по квадратичной функции

Задание 1.

Построить график функции y = x 2 . Масштаб: 1 = 2 см. Отметьте на оси Oy точку F (0; 1/4). Циркулем или полоской бумаги измерьте расстояние от точки F до какой-нибудь точки M параболы. Затем приколите полоску в точке M и поверните ее вокруг этой точки так, чтобы она стала вертикальной. Конец полоски опустится немного ниже оси абсцисс (рис. 1) . Отметьте на полоске, насколько она выйдет за ось абсцисс. Возьмите теперь другую точку на параболе и повторите измерение еще раз. Насколько теперь опустился край полоски за ось абсцисс?

Результат: какую бы точку на параболе y = x 2 вы не взяли, расстояние от этой точки до точки F(0; 1/4) будет больше расстояния от той же точки до оси абсцисс всегда на одно и то же число – на 1/4.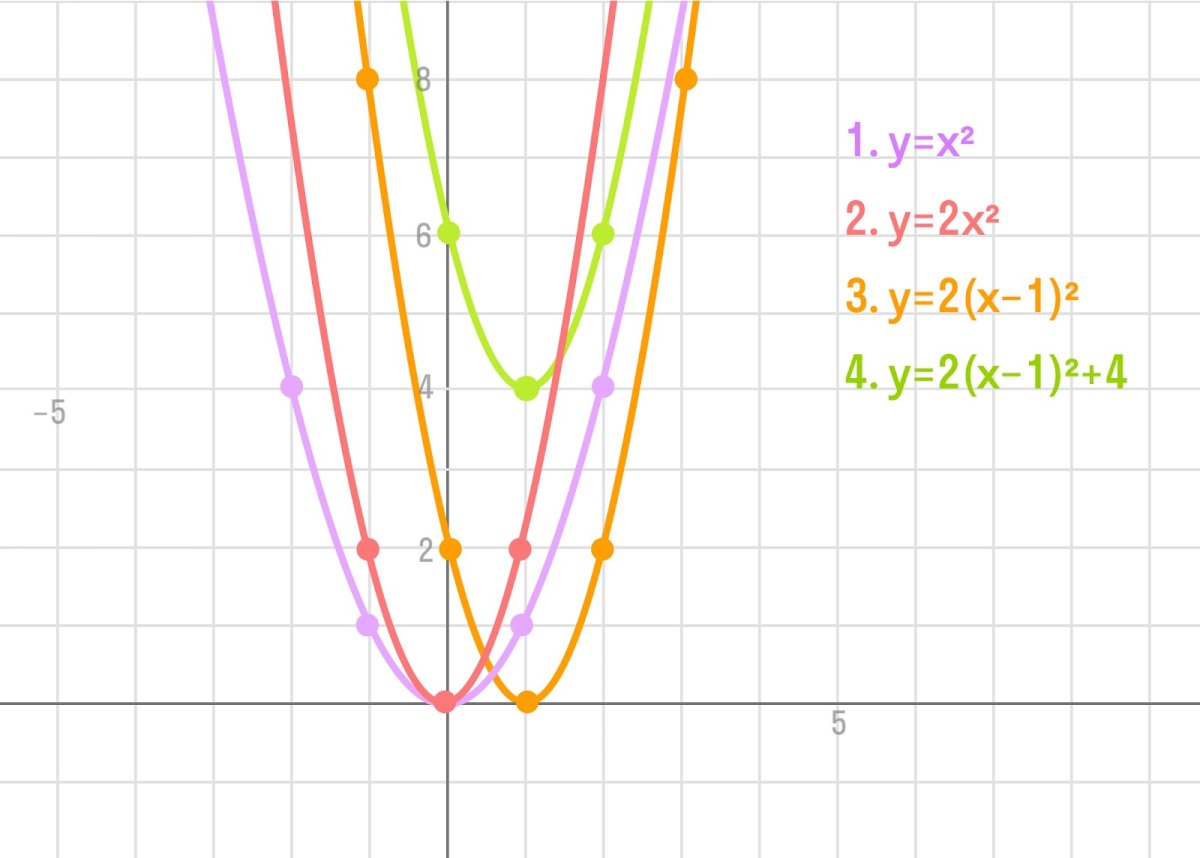

Можно сказать иначе: расстояние от любой точки параболы до точки (0; 1/4) равно расстоянию от той же точки параболы до прямой y = -1/4. Эта замечательная точка F(0; 1/4) называется

фокусом параболы y = x 2 , а прямая y = -1/4 – директрисой этой параболы. Директриса и фокус есть у каждой параболы.

Интересные свойства параболы:

1. Любая точка параболы равноудалена от некоторой точки, называемой фокусом параболы, и некоторой прямой, называемой ее директрисой.

2. Если вращать параболу вокруг оси симметрии (например, параболу y = x 2 вокруг оси Oy), то получится очень интересная поверхность, которая называется параболоидом вращения.

Поверхность жидкости во вращающемся сосуде имеет форму параболоида вращения. Вы можете увидеть эту поверхность, если сильно помешаете ложечкой в неполном стакане чая, а потом вынете ложечку.

3. Если в пустоте бросить камень под некоторым углом к горизонту, то он полетит по параболе (рис. 2).

Если пересечь поверхность конуса плоскостью, параллельной какой-либо одной его образующей, то в сечении получится парабола (рис. 3) .

5. В парках развлечений иногда устраивают забавный аттракцион «Параболоид чудес». Каждому, из стоящих внутри вращающегося параболоида, кажется, что он стоит на полу, а остальные люди каким-то чудом держаться на стенках.

6. В зеркальных телескопах также применяют параболические зеркала: свет далекой звезды, идущий параллельным пучком, упав на зеркало телескопа, собирается в фокус.

7. У прожекторов зеркало обычно делается в форме параболоида. Если поместить источник света в фокусе параболоида, то лучи, отразившись от параболического зеркала, образуют параллельный пучок.

Построение графика квадратичной функции

На уроках математики вы изучали получение из графика функции y = x 2 графиков функций вида:

1) y = ax 2 – растяжение графика y = x 2 вдоль оси Oy в |a| раз (при |a| рис. 4 ).

2) y = x 2 + n – сдвиг графика на n единиц вдоль оси Oy, причем, если n > 0, то сдвиг вверх, а если n

3) y = (x + m) 2 – сдвиг графика на m единиц вдоль оси Ox: если m 0, то влево, (рис.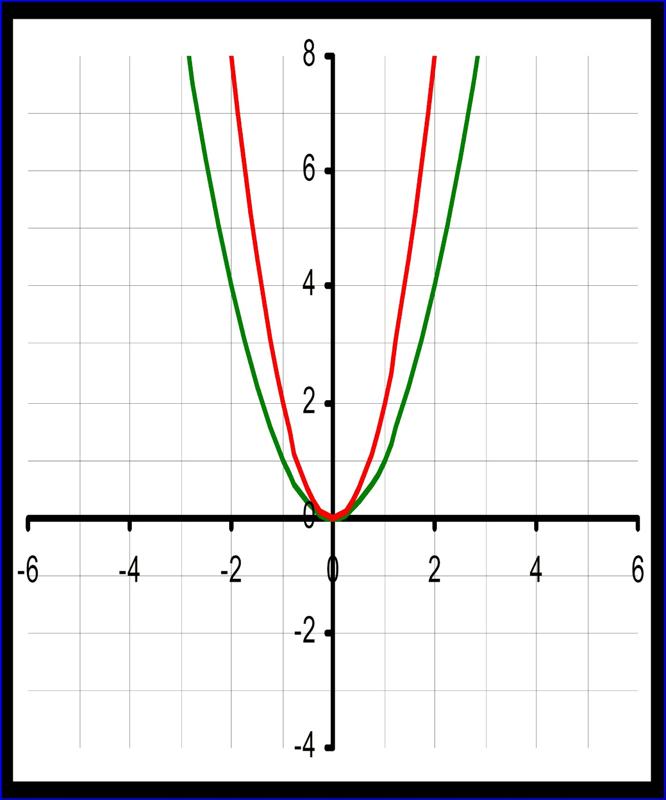 5) .

4) y = -x 2 – симметричное отображение относительно оси Ox графика y = x 2 .

Подробнее остановимся на построении графика функции y = a(x – m) 2 + n .

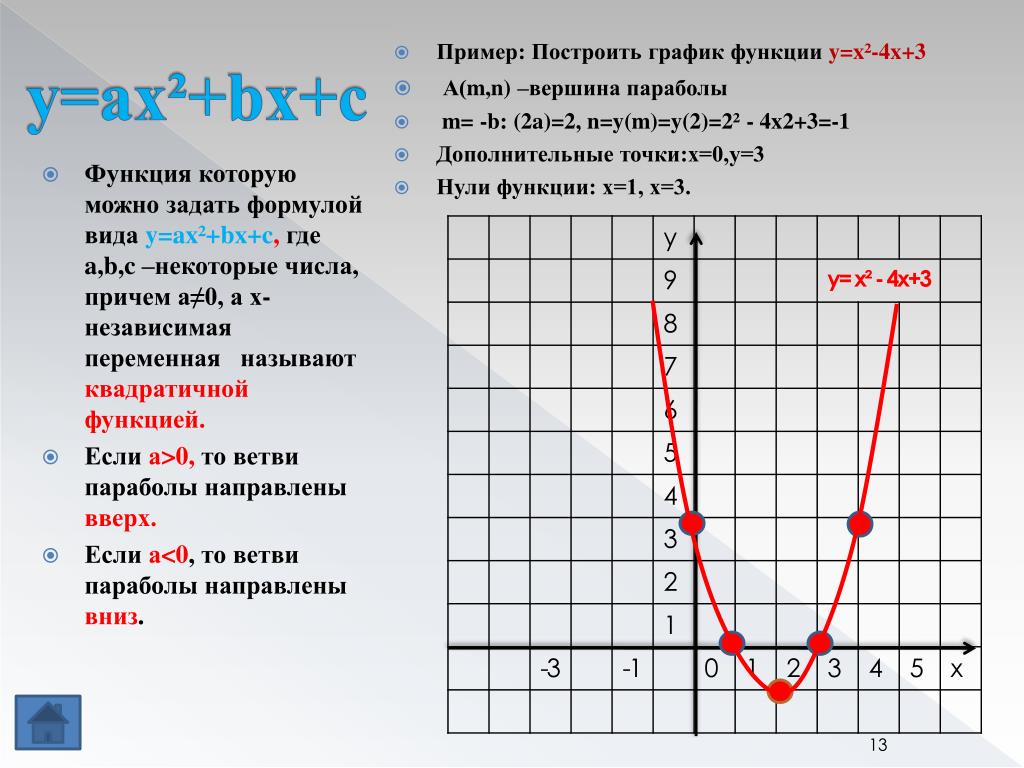
Квадратичную функцию вида y = ax 2 + bx + c всегда можно привести к виду

y = a(x – m) 2 + n, где m = -b/(2a), n = -(b 2 – 4ac)/(4a).

Докажем это.

Действительно,

y = ax 2 + bx + c = a(x 2 + (b/a) x + c/a) =

A(x 2 + 2x · (b/a) + b 2 /(4a 2) – b 2 /(4a 2) + c/a) =

A((x + b/2a) 2 – (b 2 – 4ac)/(4a 2)) = a(x + b/2a) 2 – (b 2 – 4ac)/(4a).

Введем новые обозначения.

Пусть m = -b/(2a) , а n = -(b 2 – 4ac)/(4a) ,

тогда получим y = a(x – m) 2 + n или y – n = a(x – m) 2 .

Сделаем еще замены: пусть y – n = Y, x – m = X (*).

Тогда получим функцию Y = aX 2 , графиком которой является парабола.

Вершина параболы находится в начале координат. X = 0; Y = 0.

Подставив координаты вершины в (*), получаем координаты вершины графика y = a(x – m) 2 + n: x = m, y = n.

Таким образом, для того, чтобы построить график квадратичной функции, представленной в виде

y = a(x – m) 2 + n

путем преобразований, можно действовать следующим образом:

a) построить график функции y = x 2 ;

б) путем параллельного переноса вдоль оси Ox на m единиц и вдоль оси Oy на n единиц – вершину параболы из начала координат перевести в точку с координатами (m; n) (рис. 6) .

Запись преобразований:

y = x 2 → y = (x – m) 2 → y = a(x – m) 2 → y = a(x – m) 2 + n.

Пример.

С помощью преобразований построить в декартовой системе координат график функции y = 2(x – 3) 2 – 2.

Решение.

Цепочка преобразований:

y = x 2 (1) → y = (x – 3) 2 (2) → y = 2(x – 3) 2 (3) → y = 2(x – 3) 2 – 2 (4) .

Построение графика изображено на рис. 7 .

Вы можете практиковаться в построении графиков квадратичной функции самостоятельно.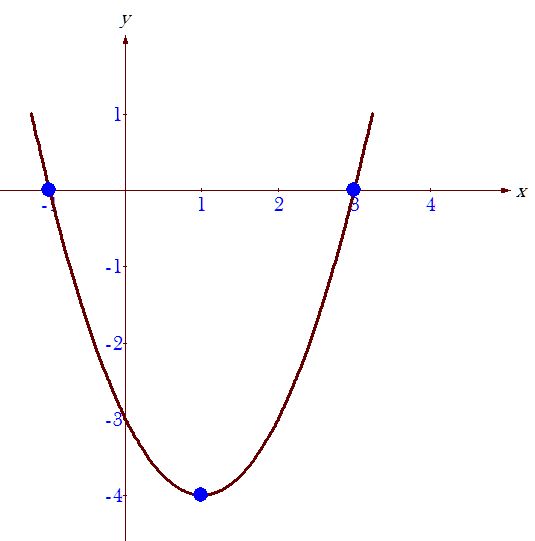 Например, постройте в одной системе координат с помощью преобразований график функции y = 2(x + 3) 2 + 2. Если у вас возникнут вопросы или же вы захотите получить консультацию учителя, то у вас есть возможность провести бесплатное 25-минутное занятие с онлайн репетитором после регистрации . Для дальнейшей работы с преподавателем вы сможете выбрать подходящий вам тарифный план.

Остались вопросы? Не знаете, как построить график квадратичной функции?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

График параболы с использованием Matplotlib в Python

спросил 7 лет, 5 месяцев назад

Изменено 10 месяцев назад

Просмотрено 72к раз

Я пытаюсь нарисовать простую параболу в matplotlib , и я не понимаю, как я должен отображать точки на параболе.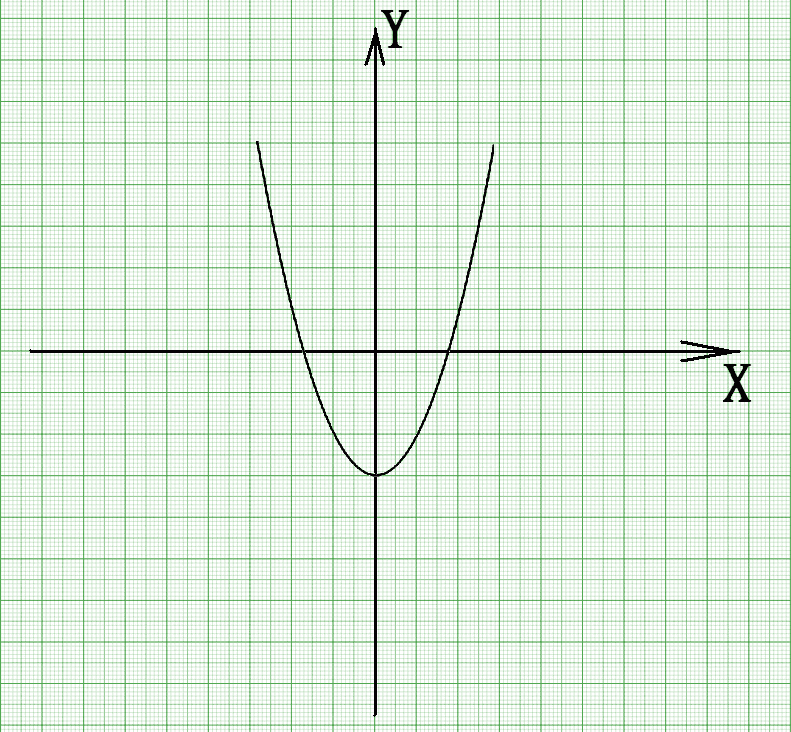 На данный момент это то, что у меня есть: 92+2*х+2 а=[х] б=[у] рис= plt.figure() оси = fig.add_subplot (111) axes.plot(a,b) plt.show() х= х+1

python
python-2.7
matplotlib

Это должно делать:

 импортировать matplotlib.pyplot как plt
импортировать numpy как np
# создать 1000 равноотстоящих точек между -10 и 10
х = np.linspace (-10, 10, 1000)
# вычисляем значение y для каждого элемента вектора x
у = х**2 + 2*х + 2
рис, топор = plt.subplots()
ax.plot (х, у)

Это ваш подход с минимальными изменениями, чтобы заставить его работать (потому что ясно, что вы новичок, и это упражнение для обучения). Я сделал следующие изменения:

Переместил plt.figure и другие графические операторы из цикла. Цикл теперь дает вам данные для построения, а затем вы рисуете их после завершения цикла.
Изменено 9от 2 до x**2
.
Изменено в то время как на для в операторе управления основным циклом.
Закомментировал несколько строк, которые ничего не делали. Все они имели один и тот же источник ошибки (или, на самом деле, бесполезности): в цикле for x задается в строке управления циклом, а затем y вычисляется напрямую, поэтому вам не нужно давать им начальные значения или приращение x , хотя вам пришлось бы выполнять эти шаги для цикла while.

Здесь код:

 импортировать matplotlib.pyplot как plt
а=[]
б=[]
# у=0
# х=-50
для x в диапазоне (-50,50,1):
    у=х**2+2*х+2
    а. добавить (х)
    б.добавлять(у)
    #х=х+1
рис= plt.figure()
оси = fig.add_subplot (111)
axes.plot(a,b)
plt.show()

Привет, я думаю, что вы можете использовать этот

import matplotlib.pyplot как plt импортировать numpy как np ''' Установите значения в переменной x Функция arange помогает сгенерировать массив с следующие параметры упорядочиваются (начало, конец, приращение) ''' х = np.

arange (-100,100,1) ''' Теперь задайте формулу в переменной y ''' у = х**2 ''' Затем добавьте пару (x, y) на график ''' plt.plot(x,y) ''' Наконец покажите график ''' plt.show() 9 ' и ' b o '

Я думаю, вы можете использовать понимание списка для этого.

 импортировать matplotlib.pyplot как plt
из математического импорта sqrt, pow
plt.style.use('приморская-темная сетка')
рис, топор = plt.subplots()
# Определение диапазона для входных значений по горизонтальной оси
x_values = [x для x в диапазоне (-50, 50)]
# Вычисление значений квадратного уравнения для разных значений x_values
y_values = [(pow(x,2)+4*x+4) для x в x_values]
ax.plot (x_values, y_values, ширина линии = 2)
plt.show()

график, сгенерированный python с использованием библиотеки matplotlib

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта 92}$
При $y = 0$ $x = 2$, поэтому точка пересечения у параболы равна $\left( {2,0} \right)$.
Расстояние вершины от направляющей $d$, равно $\dfrac{1}{{4a}}$, здесь $a$ равно 1, из данного уравнения параболы.
$ \Rightarrow d = \dfrac{1}{{4a}}$
$\следовательно d = \dfrac{1}{4}$
$\because a = 1$
Мы знаем, что длина латуса параболы rectum равно $4d$, из приведенных выше выражений значение $4d = 1$, здесь $d$ — расстояние от фокуса до вершины. 92} = 4ay$ , вершина - это начало координат, которое является точкой $\left( {0,0} \right)$.

Недавно обновленные страницы

Рассчитать изменение энтропии, связанное с конверсией Химия класса 11 JEE_Main

Закон, сформулированный доктором Нернстом, является первым законом термодинамики Класс 11 химии JEE_Main

Для реакции при rm0rm0rmC и нормальном давлении A класс 11 химия JEE_Main

Двигатель, работающий между rm15rm0rm0rmC и rm2rm5rm0rmC класс 11 химия JEE_Main

Для реакции rm2Clg в rmCrmlrm2rmg знаки химического класса 11 JEE_Main

Изменение энтальпии перехода жидкой воды в химический класс 11 JEE_Main

Рассчитайте изменение энтропии при переходе 11 химического класса JEE_Main

Закон, сформулированный Д-р Нернст – это Первый закон термодинамики.