Как начертить угол 75 градусов без транспортира: Как построить угол в 75 градусов с помощью циркуля и линейки?

Научно-исследовательская работа «Измеряем углы без транспортира»

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА с. РУССКИЙ КАМЕШКИР

(МБОУ СОШ с. Русский Камешкир)

Измерение углов без транспортира

Исследовательско — практическая работа

Работу выполнила ученица 6 Б класса

Прасулова Кристина

Научный руководитель: Скосырева Лилия Васильевна

Предмет: математика

2019 г

Содержание

1. Введение

2. Цели и задачи

3. Обзор литературы по данной теме

4. Методика работы

5. Описание работы

6. Выводы

7. Используемые ресурсы

8. Приложения

Объект исследования:
углы с различными градусными мерами; инструменты для измерения углов.

Предмет исследования:
процесс измерения углов без использования транспортира.
Гипотеза:
можно предположить, что существуют углы разных градусных мер, которые

можно измерить без применения транспортира, а только пользуясь линейкой без мерных делений, клетчатой бумагой и другими подручными материалами

Методы исследования:
— поисковый метод с использованием научной и учебной литературы, а также поиск необходимой информации в сети Интернет;
— графическое моделирование, анализ и классификация полученных результатов.

Целью работы:
является знакомство с инструментами для измерения углов, исследование метода измерения углов заданной градусной меры без использования транспортира.

Задачи:

1. Провести практическую работу по построению острых углов заданной градусной меры (от 10° до 80°, кратных 10) и выявлению «контрольных» точек – узлов для лучей каждого угла.

2. Проанализировать полученные результаты и систематизировать их

3. Определить группы задач, которые можно решить с помощью исследованного метода построения углов.

4. Сделать вывод о подтверждении или опровержении выдвинутой гипотезы.

Актуальность:

 в курсе геометрии при решении задач часто приходится строить иллюстративные чертежи различных фигур по заданному условию. Владение методом построения углов на клетчатой бумаге позволяет чертить заданные углы с достаточной точностью, не требует наличия транспортира и экономит время на выполнение чертежа.

Содержание:

1. Введение.

2. Построение углов: история и современность.

3. Практическая часть. Построение углов без помощи транспортира.

1) Построение угла 45° без помощи транспортира.

2) Построение острых углов с градусной мерой, кратной 10° без помощи транспортира.

3) Построение тупых углов с градусной мерой, кратной 10°, от 100° до 170°

без помощи транспортира.

4) Построение углов с помощью угольников.

5) Построение углов 30°, 45°, 60°, 90° в практической жизни.

6) Измерение углов по пальцам рук.

4. Выводы и заключение.

5. Литература.

1.ВВЕДЕНИЕ

Увлечение отдельной областью математики часто начинается с размышления над какой-то особенно понравившейся задачей. При изучении в 5 классе на уроках математики темы «Построение угла заданной величины», мы научились строить углы с помощью транспортира.

И сразу обнаружили, что некоторые углы гораздо быстрее и более точно можно начертить в тетрадке с помощью одной только линейки.

Углы с градусными мерами 90° и 180° можно построить, проведя луч по горизонтальным или вертикальным линиям тетради, а углы в 135° и 45° — по диагоналям клеток.

Именно тогда я и заинтересовалась вопросом, а можно ли построить и другие углы, используя только клетчатую бумагу и линейку?

Так появилась моя исследовательская работа «Строим углов без транспортира».

Казалось бы, что увлекательного можно найти на клетчатой плоскости, то есть, на листке бумаги, расчерченном на одинаковые квадратики?

Оказывается, задачи, связанные с бумагой в клеточку, достаточно разнообразны.

Своё исследование я решила начать с изучения ответа на вопрос, как решались задачи на построение углов, начиная с древних времен и до сегодняшнего времени.

2. ПОСТРОЕНИЕ УГЛОВ: ИСТОРИЯ И СОВРЕМЕННОСТЬ

Понятие градуса и появление первых инструментов для измерения углов связывают с развитием цивилизации в древнем Вавилоне, хотя само слово градус имеет латинское происхождение (градус–от лат. gradus- “шаг, ступень”). Градус получится, если, разделить окружность на 360 частей.

Возникает вопрос – а почему древние вавилоняне делили именно на 360 частей.

Дело в то, что в Вавилоне была принята шестидесятиричная система счисления. Более того, число 60 считалось священным. Поэтому все вычисления были связаны с числом 60.

История не сохранила имя ученого, который изобрел транспортир – возможно в древности этот инструмент имел совсем другое название.

Современное название происходит от французского слова ”ТRANSPORTER”, что означает “переносить”.

Первые задачи на построение углов возникли в глубокой древности. Возникли они из хозяйственных потребностей человека. Уже древними архитекторами и землемерами приходилось решать простейшие задачи на построение, связанные с их профессией.

Первые греческие ученые, которые занимались решением геометрических задач на

построение, были: Фалес Милетский (624 – 547 гг. до н.э.), Пифагор (ок. 580 – 500 гг. до н.э.), Платон (427 – 347 гг. до н.э.).

Самые первые задачи на построение, по-видимому, решались непосредственно на

местности и заключались в проведении прямых линий и построения прямого угла.

К задачам на построение прибегали древние инженеры, когда составляли рабочий чертеж того или иного сооружения и решали вопросы, связанные с отысканием красивых геометрических форм сооружения и его наибольшей вместимости.

Задачи на построение помогали людям в их хозяйственной жизни, их решения формулировались в виде ‘практических правил», исходя из наглядных соображений.

Именно эти задачи и были основой возникновения наглядной геометрии, нашедшей довольно широкое развитие у древних народов Египта, Вавилона, Индии и др.

Платон и его ученики считали построение геометрическим, если оно выполнилось при помощи циркуля и линейки, то есть путем проведения окружностей и прямых линий.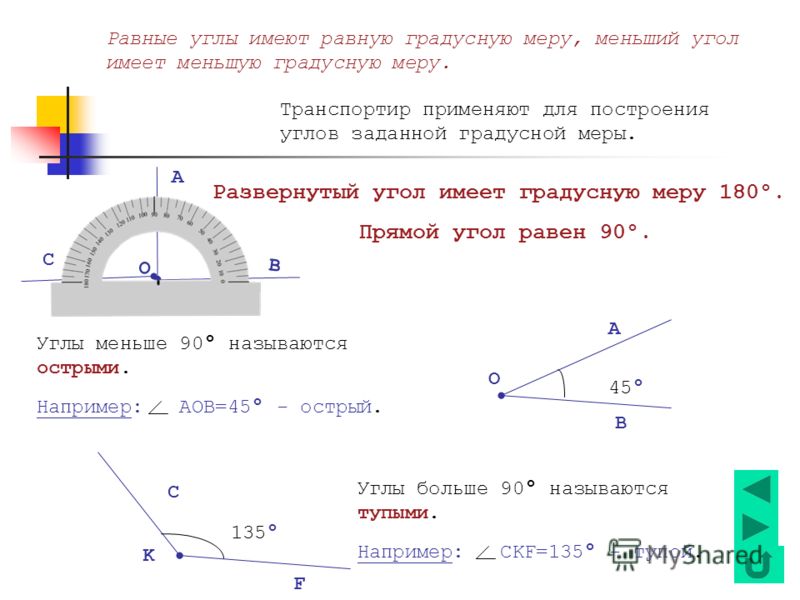 Если же в процессе построения использовались другие чертежные инструменты, например транспортир, то построение не считалось геометрическим.

Древние греки вслед за Платоном стремились к геометрическим построениям и считали их идеалом в геометрии.

Но древние ученые производили измерения не только транспортиром – ведь этот

инструмент был неудобен для измерений на местности и решения задач прикладного

характера. А именно прикладные задачи и являлись главным предметом интереса древних геометров.

Изобретение первого инструмента, позволяющего измерять углы на местности,

связывают с именем древнегреческого ученого Герона Александрийского (I в. до н.э). Он описал инструмент “диоптр”, позволяющий измерять углы на местности и решать множество прикладных задач.

Но прогресс не стоит на месте и в ХVII веке был изобретен прибор нивелир, а в следующем веке английским механиком Джессе Рамсденом был изобретен другой прибор – теодолит.

теодолит

Сегодня теодолит – сложный прибор. Многие работы (в том числе и строительство) требуют предварительной консультации геодезистов измерений с помощью теодолита.

Однако усовершенствование инструментов для измерения углов связано не только с

проведением строительных работ. С древнейших времен люди путешествовали, познавая окружающий мир. Путешественниками необходимо было уметь ориентироваться в пространстве. На долгие века основным ориентиром путешественников стали звезды.

Появился первый инструмент путешественников – астролябия. Астролябия(греч. astrolabion, от astron — «звезда» и labe – “схватывание»; лат. astrolabium) — угломерный прибор, служивший до начала XVIII в. для определения положений светил на небе.

Секстант — это наиболее совершенный прибор для измерения угловых координат небесных тел того времени. Его изобретение приписывается Исааку Ньютону. Секстант позволял измерять как широту, так и долготу точки наблюдения, причем с довольно высокой точностью.

В настоящее время широко используются современные приборы для измерения углов на местности.

Геодезический инструмент для измерения углов при съёмках на местности, специальный вид компаса- буссоль.

Простейший геодезический инструмент, служащий для измерения углов наклона местности с точностью до десятых долей градуса- эклиметр.

Первый в мире транспортир

Необычный объект, который мы можем наблюдать на фото, был найден в гробнице древнеегипетского архитектора Ха (Kha). Без малого столетие прошло с тех пор, как историки впервые задались вопросом о предназначении странного артефакта.

Недавно предположение о возможном способе использования объекта выдвинула ученая-физик. Гипотеза, предложенная Амелией Спаравигной (Amelia Sparavigna) из Туринского политехнического университета (Turin Polytechnic), базируется на числовых отметках, якобы присутствующих на поверхности артефакта.

Архитектор Ха известен тем, что во времена 18-той династии (приблизительно 1400 год до нашей эры) он был задействован в строительстве гробницы фараона. Собственную же усыпальницу Ха нашли 1906 году неподалеку от Долины Царей — это открытие принадлежит археологу Эрнесто Скьяпарелли (Ernesto Schiaparelli). Среди вещей, когда-то принадлежащих архитектору, удалось идентифицировать измерительные пруты длиной в локоть (45 см), инструмент, напоминающий современный угольник, а также неизвестное полое деревянное орудие. По мнению Скьяпарелли, это был инструмент для выставления уровня.

Детально осмотрев старую находку, Амелия Спаравигна пришла к выводу, что на самом деле этот последний объект служил в качестве транспортира — в пользу такой версии свидетельствуют 16 лепестков, расположенных по окружности и находящихся на равном расстоянии друг от друга. Эти лепестки окружены круглым узором, имеющим 36 углов. Очевидно, продолговатая ровная часть инструмента устанавливалась на поверхность, после чего, с помощью уровня, можно было определить угол наклона того или иного объекта.

Числа, присутствующие на находке, якобы соответствовали двум измерительным системам, применявшимся в древнем Египте. Первая, внутренняя часть узора, соответствует шестнадцатичной счетной системе (соответствует современной десятичной). Вторая отображает 36 созвездий, известных египтянам.

Современные угломеры

Транспорти́р (фр. transporteur, от лат. transporto «переношу») — инструмент для построения и измерения углов. Транспортир состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы), разделённого на градусы от 0 до 180°. В некоторых моделях — от 0 до 360°.

Разновидности транспортиров

• Полукруговые (180 градусов) — наиболее простые и древние транспортиры.

• Круговые (360 градусов).

• Геодезические, которые бывают двух типов: ТГ-А — для построения и измерения углов на планах и картах; ТГ-Б — для нанесения точек на чертежной основе по известным углам и расстояниям. Цена деления угломерной шкалы — 0,5°, прямолинейной — 1 миллиметр.

• Улучшенные типы транспортиров, которые необходимы для более точных построений и измерений. Например, существуют специальные транспортиры с прозрачной линейкой с угломерным нониусом, которая вращается вокруг центра.

Транспортиры изготавливаются из стали, пластмассы, дерева и других материалов. Точность транспортира прямо пропорциональна его размеру (чем больше транспортир, тем меньше цена одного деления).

Полукруговой транспортир Круговой транспортир Геодезический транспортир

Угломер электронный Угломер строительный

Изобретение Леонида Чижевского — командирский угломер

Угломер Чижевского представлял собой треногу, на которой крепился круг с делениями, на его оси — подвижная алидада с указателем и визирная трубка на ней. Был еще и компас для ориентирования прибора. Измерив угловые расстояния между своей батареей и целью, командир производит геометрические расчеты и передает необходимые данные по телефону или через связных на свою батарею. Используя их, обученные наводчики направляют орудия на цель. Во время стрельбы командир батареи с помощью бинокля корректирует точность попадания снарядов в цель. Новый способ стрельбы с закрытых позиций давал возможность нанести удар по врагу не одним выстрелом из одного орудия, а со всех орудий разом широким фронтом огня – веером, сохранив при этом людей и технику.

Вот такая история возникновения различных приборов для измерения углов не только на чертежах, но и на любой местности, включая даже небесное пространство!

Таким образом, я выяснила, что на современном этапе существует множество приборов, позволяющих измерять и строить углы с различной степенью точности, которые применяются людьми самых разнообразных профессий, а при изучении курса геометрии в школе для построения углов заданной градусной меры в основном используется циркуль, линейка и транспортир.

3.ПРАКТИЧЕСКАЯ ЧАСТЬ.

1)Построение угла 45° без помощи транспортира.

Угол 45 градусов в геометрии встречается часто.

Рассмотрим, как легко можно построить угол 45 градусов без транспортира, пользуясь только линейкой, карандашом и клеточками тетради.

Легче всего строить прямой угол.

 

Для этого из одной точки по клеточкам строим горизонтальный и вертикальный лучи. 

Градусная мера прямого угла — 90 градусов. 45 градусов — половина от 90º. Значит, чтобы построить угол 45 градусов, нужно взять половину прямого угла.

Сделать это очень легко. Выбираем вершину угла на пересечении клеточек. Одну сторону угла, например, горизонтальный луч, проводим с помощью линейки по клеточкам. Для построения второй стороны угла 45º каждую клеточку делим по диагонали (отмечаем несколько точек):

Затем с помощью линейки и карандаша через эти точки проводим второй луч.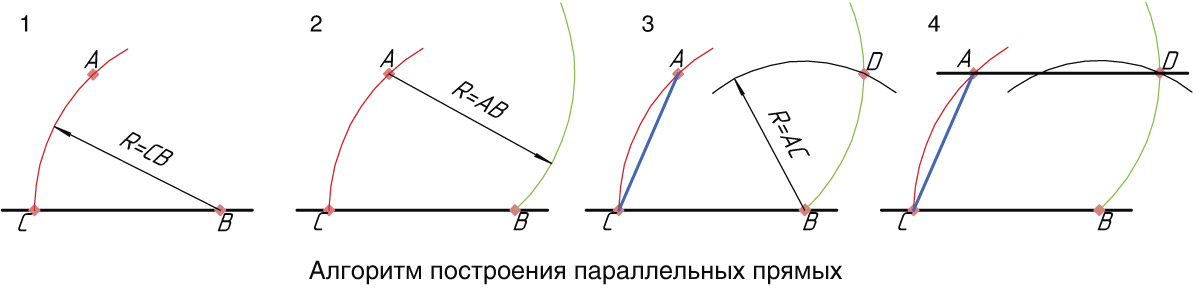 Получили угол 45 градусов:

2)Построение острых углов с градусной мерой, кратной 10° без помощи транспортира.

Для проведения исследования я на листке клетчатой бумаги построила острые углы,

начиная от 10° до 80°, с интервалом в 10°. Центр угла был расположен в узле клеток. Один из лучей, образующих угол, провела горизонтально слева направо.

Далее с помощью транспортира начертила лучи для всех исследуемых углов.

Если второй луч проходил точно через узел клеток, то информацию об этом угле заносила в таблицу.

Положение «контрольного» узла относительно вершины данного угла отмечалось следующим образом: сначала указывалось количество целых клеток вверх, затем вправо.

В результате получилась такая таблица:

Проанализировав данные таблицы для построения углов, можно заметить, что для углов

от 20° до 70° количество клеток вверх на единицу превышает количество десятков в

градусной мере угла. Причем сумма клеток вверх и вправо для всех этих углов равна 11.

Величина острого угла	Количество клеток вверх от вершины угла	Количество клеток вправо от вершины угла
10°	1	6
20°	3	8
30°	4	7
40°	5	6
50°	6	5
60°	7	4
70°	8	3
80°	6	1

То есть, чтобы знать все «контрольные» узлы, полученные в таблице достаточно

запомнить только точку для угла в 10° –(1;6), и для угла 80°- ей служит противоположная(6;1).

А все остальные «контрольные» точки лучей (для углов от 20° до 70°, кратных 10)

подчиняются несложному правилу: «Если прибавить к числу десятков искомого угла единицу, то получим количество клеток по вертикали. Если это число отнять от 11, то получим количество клеток по горизонтали от вершины угла.»

Например, для построения угла в 70° нужно отступить 8 (7+1) клеток по вертикали и 3(11-8) клетки по горизонтали в сторону первого луча.

Анализ данных в полученной таблице еще раз убеждает нас в существовании красоты, закона симметрии и порядка в науке математике.

3)Построение тупых углов с градусной мерой, кратной 10°, от 100° до 170° без помощи транспортира.

Исследованный метод построения углов позволяет решать следующую геометрическую задачу: построение тупых углов от 100° до 170° с шагом в 10°.

Смежные углы имеют общий луч. Поэтому для построения тупых углов можно

пользоваться «контрольной» точкой смежного ему острого угла из таблицы. Только

отсчет клеток по горизонтали выбирается в противоположном горизонтальному лучу

направлении (в нашем случае влево).

4)Построение углов с помощью угольников.

Я исследовала чертёжные инструменты – угольники.

Угольник — линейка в форме прямоугольного треугольника, как правило, с миллиметровой шкалой и с пустотой в форме уменьшенного подобного треугольника внутри.

Наиболее распространены угольники двух видов: с острыми углами по 30 и 60 градусов и равнобедренными с одинаковыми острыми углами по 45 градусов. Угольники используются в черчении для построения некоторых углов без помощи транспортира.

При использовании двух угольников можно построить больший набор углов, прикладывая их друг к другу, например, угол в 75 градусов (30+45), 120 градусов (90+30) и т. д. Покажу, как это сделать…

Понадобятся два вида угольников: первый с углами по 45 градусов, а второй — по 30 и 60.
1)75 градусов можно построить следующим образом: сначала построить угол в 30, а затем от него отложить 45 градусов.

2) 135 градусов: построить прямой угол, затем от него отложить 45 градусов.
3) 25 градусов: построить угол в 60 градусов,  затем от луча внутри угла отложить 45 градусов.

С помощью угольников можно построить углы 105◦, 15◦ и другие.

105= 60+45, 15=60-45 и так далее.

5)Построение углов 30°, 45°, 60°, 90° в практической жизни.

Часто домашнему мастеру необходимо срочно произвести какое либо измерение или сделать разметку под определенным углом, а под рукой нет либо угольника, либо транспортира. В этом случае его выручат несколько простых правил.

Угол 90 градусов.

Если нужно срочно построить прямой угол, а угольника нет, можно воспользоваться любым печатным изданием. Угол бумажного листа — очень точный прямой угол (90 град.). Резательные (вырубочные) машины в типографиях настроены очень точно. Иначе исходный рулон бумаги начнет резаться вкривь и вкось. Поэтому вы можете быть уверены, что этот угол — именно прямой.

А если нет даже печатного издания или необходимо построить угол на местности, например при разметке фундамента или листа фанеры с неровными краями? В этом случае нам поможет правило золотого (или египетского) треугольника.

Золотым (или египетским, или Пифагоровым) треугольником называется треугольник со сторонами, которые соотносятся друг с другом как 5:4:3. По теореме Пифагора, у прямоугольного треугольника квадрат гипотенузы равен сумме квадратов катетов. Т.е. 5х5 = 4х4 + 3х3. 25=16+9 и это неоспоримо.

Поэтому для построения прямого угла достаточно на заготовке провести прямую линию длиной 5 (10,15,20 и т.д. кратной 5 см). А затем, из краев этой линии начать отмерять с одной стороны 4 (8,12,16 и т. д кратно 4 см), а с другой — 3 (6,9,12,15 и т.д. кратно 3 см) расстояния. Должны получиться дуги с радиусом 4 и 3 см. Где эти дуги пересекутся между собой и будет прямой (90 градусов) угол.

Угол 45 градусов.

Такие углы обычно применяют при изготовлении прямоугольных рамок. Материал из которого делается рамка (багет) пилится под углом 45 градусов и стыкуется. Если под рукой нет стусла или транспортира, получить шаблон угла в 45 градусов можно следующим образом. Необходимо взять лист писчей бумаги или любого печатного издания и согнуть его так, что бы линия сгиба проходила точно через угол, а края загнутого листа совпадали. Получившийся угол и будет равен 45 градусам.

Угол 30 и 60 градусов.

Угол в 60 градусов требуется для построения равносторонних треугольников. Например, вам надо напилить такие треугольники для декоративных работ или точно установить силовой укос. Угол в 30 градусов редко применяется в чистом виде. Однако с его помощью (и с помощью угла в 90 градусов) строится угол 120 градусов. А это угол, необходимый для построения равносторонних шестиугольников, фигуры весьма популярной у столяров.

Для построения весьма точного шаблона этих углов в любой момент необходимо запомнить константу (число) 173. Они вытекает из соотношений синусов и косинусов этих углов.

Возьмите лист бумаги из любого печатного издания. Его угол равен точно 90 градусам. От угла по одной стороне отмерьте 100 мм (10 см.), а по другой — 173 мм (17,3 см). Соедините эти точки. Таким образом мы и получили шаблон, у которого один угол 90 градусов, один 30 градусов и один 60 градусов. Можете проверить на транспортире — все точно!

Запомните это число — 173, и вы всегда сможете построить углы в 30 и 60 градусов.

6)Измерение углов по пальцам рук.

Итак, смотрим на свою руку, которая есть у каждого человека. Уточнение! — левша должен снимать показания углов с правой руки, а правша с левой. Причина проста — приоритет действующей руки со временем деформирует кости, суставы и сильнее растягивает мышцы. Поэтому у правшей левая рука менее деформирована и разработана, а у левшей наоборот.

Теперь растопыриваем в стороны пальцы, как только можете за счет усилия только руки, ничем их раздвигать не нужно — только максимальное мышечное усилие. Богом так заложено у человека и это правда, что у здорового человека с нормальной рукой растопыренные пальцы — это полноценно действующий и относительно точный транспортир.

Угол между большим и безымянным пальцами равен 90 гр.

Угол между большим и указательным пальцами равен 45 гр.

Угол между безымянным и средним пальцами равен 22.5 гр.

Угол между безымянным и мизинцем равен 15 гр. — солнечному часу.

4.ВЫВОДЫ И ЗАКЛЮЧЕНИЕ.

Своей исследовательской работой мне хотелось бы доказать, что построение углов очень интересное и познавательное занятие, совсем не сложное и трудоемкое, как может показаться на первый взгляд.

Поработав с материалом и подготовив его к применению на практике, я сделала

следующие выводы:

1. Обычный лист бумаги в клетку может выполнять функцию своеобразного инструмента для построения углов.

2. Угольники можно использовать для построения некоторых углов без использования транспортира.

Таким образом, методы построения углов без помощи транспортира актуальны для школьников, так как большинство задач оформляется на листке тетради в клетку и большинство задач в учебнике геометрии связано с построением фигур с углами, градусная мера которых кратна10°.

5 ЛИТЕРАТУРА.

1. В.В. Вавилов, А.В. Устинов. Задачи на клетчатой бумаге. – М.: Школа им. А.Н.

Колмогорова, 2006. – 183 с

2. Ганьшин В.Н. Простейшие измерения на местности. 3-е изд., перераб. и доп., М.,

Недра, 1983, 108 с., ил.

3.Смирнов В.А, Смирнова И.М. Геометрия на клетчатой бумаге. М., МЦНМО, 2009

4. Большая советская энциклопедия

5. ГОСТ 13494-80. Транспортиры геодезические. Технические условия (с Изменениями N 1-4).

6. Большой энциклопедический политехнический словарь 2004

Список интернет-ресурсов:

http://allencyclopedia.ru/17254 Большая Советская энциклопедия/ Геодезические

инструменты

http://journal.kuzspa.ru/articles/95/ -Электронный научный журнал «Информационно-

коммуникационные технологии в педагогическом образовании»

http://sm-shihova.ucoz.ru/Komu_interesno/Komuinteresno_6. pdf — Математика, 5-6: книга для учителя Автор/создатель: Суворова С.Б., Кузнецова Л.В., Минаева С.С., Рослова Л.О.

http://enc-dic.com/word/t/Transportir-4655.html [энциклопедии и словари]

http://www.gs-market.ru/index.php?show_aux_page=70 [угломеры электронный, строительный]

http://znaika.ru/catalog/5-klass/matematika/Izmerenie-uglov.-Transportir. [история возникновения приборов измерения углов]

http://virtoo.ru/almanach/nepoznannoe/pervyj-v-mire-transportir-izobreli-eg.html [первый в мире транспортир изобрели египтяне]

http://www.vest-news.ru/article.php?id=18508 [угломер Чижевского Л.В.]
http://astro.uni-altai.ru/picture/src/0+1066279852/ [средневековые угломерные инструменты]

.

Изображение и построение углов

1. При помощи ЧП. Повернув головку на заданное число градусов, можно построить любой угол.
2. При помощи транспортира. Приложив центр транспортира к заданной вершине А искомого угла и отметив около шкалы транспортира нулевую точку и точку, соответствующую заданному числу градусов, соединяем обе эти точки с точкой А.
3. При помощи рейсшины и угольников. На Чертеже-№110, а показаны приемы построения углов в 15°, 30°, 45°, 60°, 75° и 90° и дополнительные к ним до 180°.
4. При помощи циркуля и линейки. Таким приемом удобно строить углы, показанные на Чертеже — №110, б.

Деление углов на равные части

Деление произвольного угла пополам. Наиболее удобным приемом деления произвольного угла пополам является деление при помощи циркуля и линейки; последовательность построения биссектрисы угла показана на Чертеже-№111.
Деление прямого угла на три равные части:

1. При помощи ЧП. На Чертеже — №112, а показано, что вдоль кромки линейки, повернутой на 30°. проведен из вершины А луч, а вдоль кромки линейки, повернутой на угол 60°, проведен из вершины А второй луч; получились три угла по 30°.
2. При помощи транспортира. Приложив центр транспортира к вершине А и деление 90° совместив с вертикальной стороной данного прямого угла, намечаем точки против делений в 30° и 60° и соединяем их с вершиной А.
3. При помощи рейсшины и угольника в 30° — 60° — 90°.
На Чертеже — №112, б показано проведение из вершины А луча, наклоненного на угол 60°, и проведение луча, наклоненного на угол 30°.
4. При помощи циркуля и линейки. Построение сводится к проведению двух засечек D и Е и лучей через них из вершины А; радиус R берется произвольный. Порядок построения показан цифрами в кружках.

Уклоны и конусность

Уклоны. Уклоном прямой по отношению к какой-либо другой прямой называется величина се наклона к этой прямой, выраженная через тангенс угла между ними. Следовательно, уклоном прямой АС относительно прямой АВ называется отношение i = h ÷ l = tg α.
Уклоны обычно выражают отношением двух чисел, например 1 : 6.
Как видно из чертежа — №113, а, уклон линии выявляется отношением величин двух катетов прямоугольного треугольника ABC, один из которых, например АВ, имеет направление линии, по отношению к которой задан уклон; гипотенузой является отрезок АС прямой заданного уклона. При обозначении уклона перед размерным числом пишут слово «уклон» параллельно линии, по отношению к которой он задан.

Взамен слова «уклон» допускается применять знак <, вершина угла которого должна быть направлена в сторону уклона (чертеж — №113, в).

Этот знак рекомендуется применять, когда направление уклона неясно выражено.
Проведение через точку А прямой заданного уклона h : l (по отношению к горизонтальной линии). На чертеже — №113, г показаны приемы вспомогательных построений для проведения прямой заданного уклона через заданную точку А: из данной точки А проводят горизонтальный луч и на нем от точки А откладывают длину L (равную числовому значению делителя данного уклона) — получают точку К, через которую проводят вертикальную линию и на ней от точки К откладывают длину h (равную числовому значению делимого данного уклона) — получают точку В. Прямая, проведенная через точки А и В, будет иметь требуемый уклон. Построение можно начинать с проведения вертикального луча из точки А и откладывания на нем величины h.
На чертеже — №113, д показан пример применения уклонов на контуре прокатной стали.

УПРАЖНЕНИЕ 3

Начертить контур шаблона с применением построения уклона (чертеж-№113, е).
Конусность. Конусностью называется отношение диаметра D основания конуса к его высоте h. Перед размерным числом конусности следует писать знак >, вершина которого должна быть направлена в сторону вершины конуса (чертеж-№114, а).
Если на чертеже направление конусности выявлено вполне ясно, допускается взамен знака писать слово «конусность» (параллельно оси конуса).
Числовое значение конусности усеченного конуса определяют по формуле (D — d) ÷ L (чертеж-№114, б).
Определение конусности по чертежу и проведение наклонных линий — образующих конуса — согласно данному числовому значению конусности аналогично определению уклонов и проведению прямых заданного уклона.

На чертеже-№114,в показан пример применения построения конусности при изображении детали — пробки.

УПРАЖНЕНИЕ 4

Пример 1. Начертить изображение конической втулки С применением построений, указанных конусностей, согласно чертежу-№114, г.
Пример 2. Перечертить один из вариантов по заданным размерам с построением указанной конусности (чертеж-№114, д).

Угловые (пропорциональные) масштабы

Угловыми (пропорциональными) масштабами называют графически выраженные числовые масштабы, о которых было сказано (на стр. Масштабы и компоновка чертежей )
Угловые (пропорциональные) масштабы применяют для замены вычислений линейных размеров в том случае, когда чертеж надо выполнить с применением масштаба уменьшения или увеличения. Например, при выполнении чертежа контура пластины в масштабе 1 : 2,5 надо каждую линию предмета изобразить уменьшенной в 2,5 раза. Вычисление уменьшенных размеров каждой линии отнимает много времени.

Вместо этого применяют угловой масштаб (чертеж-№115, а), т. е. прямоугольный треугольник (выполненный обычно на миллиметровой бумаге), вертикальный катет ВС которого относится к горизонтальному АС как 1 : 2,5.

Для уменьшения линий чертежа (чертеж-№115,б) отмеряем разметочным циркулем размер стороны α и, отложив его от вершины А на горизонтальной стороне углового масштаба 1 : 2,5 поворачиваем циркуль вокруг правой иглы и берем по вертикальному направлению до гипотенузы размер α₁, который будет равен α ÷ 2,5
Этот размер переносим на проведенную из заранее намеченной точки К₁ вертикальную линию. Из верхней конечной точки проводим вправо горизонтальный луч; на нем откладываем размер стороны b, уменьшенный в 2,5 раза, т. е. b

1 (полученный аналогично размеру α₁; из конечной точки проводим вниз вертикальную линию и на ней откладываем размер с₁ и т. д. В результате получим чертеж данной фигуры, выполненный в масштабе 1 : 2,5.
Чтобы не чертить каждый раз требуемый угловой масштаб, рекомендуется выполнить на миллиметровой бумаге общий угловой масштаб для уменьшений 1 : 2; 1 : 2,5; 1 : 4; 1 : 5; 1 : 10, такой же, какой показан на чертеже-№115, в.

Чертежи используемые в данной главе: >>> Чертежи №110 №111 №112 >>> Чертеж №113 >>> Продолжение чертежа №114 >>> Чертеж №115 >>> Смотри далее Окружность дуга и многоугольник…..



 

Построение углов — Использование транспортира и циркуля, этапы построения, примеры

LearnPracticeDownload

Построение углов является одним из наиболее важных аспектов геометрии и представляет собой «чистую» форму геометрического построения. Термин «конструирование» в геометрии относится к точному рисованию форм, линий или углов с помощью математических инструментов. Для построения углов вам понадобится только циркуль или транспортир, линейка (прямая) и карандаш.

1.	Типы углов
2.	Построение углов с помощью транспортира
3.	Построение углов с помощью циркуля и линейки
4.	Часто задаваемые вопросы по конструкции углов

Типы углов

Когда две линии пересекаются и имеют общую конечную точку, то есть когда образуется угол. Изучение углов в геометрии очень важно. Ниже приведены 6 типов углов в геометрии, а также градусное измерение углов.

• Острый угол → Угол меньше 90° .
• Прямой угол → Угол, равный ровно 90°.
• Прямой угол → Угол, размер которого равен 180 градусам и выглядит как прямая линия.
• Тупой угол → Угол, размер которого больше 90°, но меньше 180°.
• Угол рефлекса → Угол, который всегда больше 180° (т. е. половина окружности), но меньше 360°.
• Полный угол поворота → угол, равный точно 360°.

Построение углов с помощью транспортира

Угол можно построить либо с помощью транспортира и линейки, либо с помощью циркуля и линейки. Давайте теперь посмотрим на шаги построения угла 50 ° с помощью транспортира.

• Шаг 1 — Нарисуйте отрезок OA.
• Шаг 2 — Поместите центр транспортира в точку O.
• Шаг 3 — Начиная с точки А по часовой стрелке и отметьте точку под углом 50 градусов, глядя на внешний круг транспортира. Обозначьте эту точку как B.

∠BOA — необходимый угол 50°.

Построение углов с помощью циркуля и линейки

Давайте научимся строить угол с помощью циркуля и линейки. В шагах, показанных ниже, мы построим угол 90°, а затем построим биссектрису угла, чтобы разделить пополам 9 градусов.0°, так что мы получим угол 45°.

• Шаг 1: Нарисуйте луч AB.
• Шаг 2: Используя A в качестве центра и любой ширины в качестве радиуса, нарисуйте дугу полукруга, которая касается отрезка AB, и обозначьте ее как Q.
• Шаг 3: Без изменения радиуса нарисуйте еще одну дугу с Q в центре и обозначьте эту точку как D.
• Шаг 4: Повторите тот же процесс с D в качестве центра и обозначьте нарисованную дугу буквой E.
• Шаг 5: Теперь с тем же радиусом и с E и D в качестве центров нарисуйте дуги, которые пересекаются друг с другом в точке, и обозначьте ее как F.
• Шаг 6: Теперь соедините точки A и F. Эта линия называется перпендикулярной и составляет 90 градусов с отрезком AB.
• Шаг 7: Обозначьте точку пересечения дуги полукруга с линией AF как P.
• Шаг 8: Теперь, используя тот же радиус, что и для дуги на шаге 2, нарисуйте две дуги с центрами P и Q. Обозначим точку пересечения этих дуг как R. Теперь соединим точки A и R. Теперь ∠RAB и ∠FAR равны 45° каждая.

Темы, связанные с построением углов

Ознакомьтесь с некоторыми интересными статьями, связанными с построением углов.

• Построение биссектрисы угла
• Геометрическая конструкция
• Пары уголков
• Биссектриса угла
• Уголки

 

Примеры построения углов

1. Пример 1: Постройте угол 75° с помощью циркуля и линейки.

   Решение:

   Шаг 1: Проведите луч AB. Используя A в качестве центра и любого радиуса, нарисуйте дугу, пересекающую AB в точке C.
   Шаг 2: Используя C в качестве центра и того же радиуса, мы рисуем дугу, пересекающую первую дугу в точке D, а D — в с центром и тем же радиусом, нарисуйте дугу, которая пересекает первую дугу в точке E
   . Шаг 3: С точками E и D в качестве центров и с одинаковым радиусом мы рисуем две дуги, пересекающие друг друга в точке F. Соедините AF. Линия AF составляет 90° с отрезком AB.
   Шаг 4: Отметьте точку, где линия AF касается дуги полукруга, как G. Теперь, используя G и D в качестве центров, нарисуйте две дуги, снова пересекающие друг друга в точке H. Теперь мы соединяем AH. ∠HAB= 75°.

   Конструкция уголка 75° показана ниже.

2. Пример 2: Как построить угол 105 градусов?

   Решение:
   Шаг 1: Проведите луч AB. Используя A в качестве центра и любую ширину в качестве радиуса, нарисуйте дугу, пересекающую AB в точке C.
   Шаг 2: Используя C в качестве центра и того же радиуса, мы рисуем дугу, пересекающую первую дугу в точке D, и, используя D в качестве центра и того же радиуса, рисуем другую дугу, снова пересекающую первую дугу в точке G.
   Шаг 3: Используя D и G в качестве центров и с одинаковым радиусом, мы рисуем две дуги, пересекающие друг друга в точке F. Соединяем AF, который составляет 90°. Отметьте точку, где дуга полукруга пересекает линию AF, как E.
   Шаг 4: С точками G и E в качестве центров и с одинаковым радиусом нарисуйте две дуги, пересекающие друг друга в точке H. Теперь соедините точки A и H.
   ∠НАВ = 105°.
   

перейти к слайдуперейти к слайду

Отличное обучение в старшей школе с использованием простых подсказок

Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.

Записаться на бесплатный пробный урок

Практические вопросы по построению углов

 

перейти к слайдуперейти к слайдуперейти к слайду

Часто задаваемые вопросы по построению углов

Что такое построение углов?

Построение углов относится к построению различных углов, таких как 30°, 45°, 60°, 90°, с использованием циркуля, транспортира, линейки и карандаша. Это считается «чистой» формой геометрических построений.

Как построить прямой угол?

Прямой угол – это угол, градусная мера которого равна 90 градусам. Чтобы построить прямой угол, выполните шаги, указанные ниже:

• Начертите отрезок AB и, используя A в качестве центра и произвольного радиуса, нарисуйте дугу так, чтобы она пересекала AB в точке C.
• Теперь, используя C в качестве центра и с тем же радиусом, что и в предыдущем шаге, нарисуйте дугу, пересекающую ранее нарисованную дугу в точке D.
• С D в центре и с тем же радиусом, нарисуйте дугу так, чтобы она пересекала дугу в точке E.
• С центрами D и E и одинаковым радиусом нарисуйте две дуги, пересекающиеся в точке F. Соедините F и A. Теперь ∠FAB — прямой угол, равный 90 градусам.

Как построить угол с помощью транспортира?

Любой угол от 0° до 180° можно легко построить с помощью транспортира. Например, мы можем построить угол 60 ° с помощью транспортира, выполнив шаги, указанные ниже.

• Нарисуем отрезок АВ любой подходящей длины.
• Теперь поместим транспортир на отрезок АВ.
• Затем поместим середину транспортира в точку А.
• На AB справа начнем отсчет с 0° против часовой стрелки и, наконец, отметим точку C, показывающую 60° на полукруглом ребре транспортира.
• Убираем транспортир и присоединяем АС.
• Получаем искомый угол ∠CAB = 60°.

Как построить биссектрису угла?

Биссектриса делит заданный угол на два равных угла. Чтобы построить биссектрису угла, выполните следующие шаги:

• Начертите заданный угол с помощью транспортира (скажем, 60°). Назовем вершины угла A, B и C так, что угол ABC = 60 градусов.
• С B в качестве центра и с более чем половиной BC в качестве радиуса нарисуйте дугу на обоих плечах, то есть AB и BC, и отметьте эти точки, где дуга касается сегментов линии, как D и E соответственно.
• Теперь, используя D и E в качестве центров, нарисуйте две дуги так, чтобы они пересекались в одной точке. Обозначьте эту точку как F.
.
• Соедините F и B. FB — это биссектриса угла, и теперь ∠ABF и ∠FBC будут измерять по 30 градусов каждая.

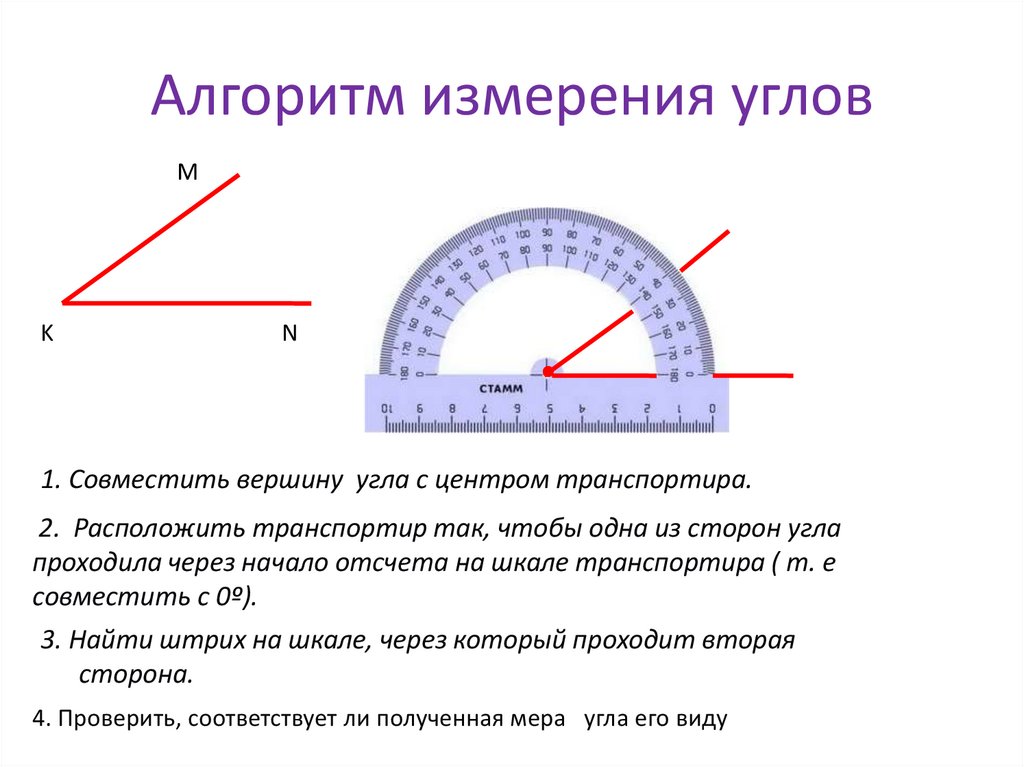
Как измерять и строить углы?

Угол можно измерить с помощью транспортира, который представляет собой полукруглый диск, используемый для рисования и измерения углов. Большинство транспортиров измеряют углы в градусах и делятся на 180 равных частей. Их можно непосредственно использовать для измерения любого угла в диапазоне от 0° до 180° с помощью маркировки. Мы можем использовать либо транспортир, либо компас, чтобы построить углы определенного измерения.

Как строятся углы?

Чтобы построить угол любой степени, нам нужно использовать геометрический инструмент, называемый циркулем. После того, как луч нарисован, циркуль используется для обозначения дуг в соответствии с любым измеренным радиусом. Эти дуги пересекаются друг с другом в различных точках, образуя перпендикулярные линии, образующие угол. Для получения более подробных инструкций ознакомьтесь с разделом построения угла с помощью компаса и линейки в этой статье.

Как построить угол с помощью компаса?

Угол можно построить с помощью двух геометрических инструментов: циркуля и линейки. Вот шаги, чтобы построить угол с компасом:

• Нарисуйте любой отрезок AB.
• Удерживая острие компаса на A, нарисуйте дугу, пересекающую отрезок в точке S. Компас может быть любого измерения.
• Сохраняя те же размеры, заостренный конец помещается в точку S и пересекает первую дугу в точке R.
• Используя линейку, начертите линию, начинающуюся с точки A и соединяющую точку R, чтобы образовался угол.
• Используйте транспортир для измерения угла.

Скачать БЕСПЛАТНЫЕ учебные материалы

Рабочие листы по углам

Рабочие листы по математике и визуальные учебные программы

Как построить угол 60 градусов — GCSE Maths

Введение

Как построить угол 30, 60, 45, 90 градусов?

Как построить угол 60 градусов

Как построить рабочий лист угла 60 градусов

Как построить угол 30 градусов

Как построить угол 90 градусов

Как построить угол 45 градусов

Распространенные заблуждения

Потренируйтесь составлять вопросы под углами 30, 60, 45, 90 градусов

Как построить угол 30, 60, 45, 90 градусов вопросы GCSE

Контрольный список обучения

Следующие уроки

Все еще застряли?

Индивидуальные занятия по математике, созданные для успеха KS4

Теперь доступны еженедельные онлайн-уроки повторения математики GCSE

Узнать больше

Введение

Как построить угол 30, 60, 45, 90 градусов?

Как построить угол 60 градусов

Как построить рабочий лист с углом 60 градусов

Как построить угол 30 градусов

Как построить угол 90 градусов

Как построить угол 45 градусов

Распространенные заблуждения

Потренируйтесь составлять вопросы под углами 30, 60, 45, 90 градусов

Как построить угол 30, 60, 45, 90 градусов вопросы GCSE

Контрольный список обучения

Следующие уроки

Все еще застряли?

Здесь мы узнаем, как построить 30, 60, 45 и 9Угол 0 градусов с помощью карандаша, линейки и циркуля.

Существуют также рабочие листы по конструированию на основе экзаменационных вопросов Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.

Что мы подразумеваем под углом 30, 60, 45, 90 градусов?

Построение углов 30, 60, 45, 90 градусов точное построение этих углов без использования транспортира.

Для этого нам понадобится карандаш, линейка (линейка) и циркуль.

Напр.

Угол 60 градусов можно построить, начертив равносторонний треугольник.
Тогда биссектриса угла образует угол в 30 градусов.

Угол 90 градусов можно построить с помощью биссектрисы.
Тогда биссектриса угла образует угол 45 градусов.

Что такое построение угла 30, 60, 45, 90 градусов?

Как построить угол 60 градусов

Чтобы построить угол 60 градусов:

1. Нарисовать линию.
2. С одного конца линии нарисуйте дугу.
3. От места пересечения дуги с линией нарисуйте еще одну дугу.
4. Соедините конечную точку линии с пересечением двух дуг.

Как построить угол 60 градусов

Как построить рабочий лист с углом 60 градусов

Получите бесплатный рабочий лист из 20+ вопросов и ответов, включая построение 30º, 60º, 9Углы 0º без транспортира. Рассуждения и прикладные вопросы.

СКОРО

Икс

Как построить рабочий лист с углом 60 градусов

Получите бесплатный рабочий лист из 20+ вопросов и ответов, включая построение углов 30º, 60º, 90º без транспортира. Рассуждения и прикладные вопросы.

СКОРО

Как построить угол 60 градусов, пример

Пример 1: построить угол 60 градусов

Построить угол 60°

1. Нарисовать линию.

Карандашом и линейкой проведите прямую линию

2 От одного конца линии проведите дугу.

Используйте циркуль с центром на одном конце линии, начертите дугу.

3 От места пересечения дуги с линией нарисуйте еще одну дугу.

Держите компасы в одном и том же положении. Новая дуга должна пересекать первую дугу.

4 Соедините конечную точку линии с пересечением двух дуг.

Используйте линейку, чтобы соединить конечную точку, использованную в шаге 2, с пересечением двух дуг.

Как построить угол 30 градусов

Чтобы построить угол 30 градусов:

1. Построить угол 60 градусов.
2. Постройте биссектрису угла 60 градусов.

Как построить угол 30 градусов

Как построить угол 30 градусов пример

Пример 2: построить угол 30 градусов

построить угол 30°

построить угол 60 градусов.

Выполните действия из примера 1, чтобы построить угол 60 градусов

Угол ABC равен 60°

Постройте биссектрису угла 60 градусов.

Поместите острие компаса в точку А и начертите дугу. Держите циркуль в том же положении и повторите, поместив точку в C и нарисовав другую дугу. Используя линейку, соедините точку, где дуги пересекаются друг с другом, с вершиной B .

Угол в 60 градусов был разделен пополам на два равных угла по 30 градусов.

Как построить угол 90 градусов

Чтобы построить угол 90 градусов:

1. Нарисуйте линию.
2. Построить серединный перпендикуляр.

Как построить угол 90 градусов

Пример построения угла 90 градусов

Пример 3: построить угол 9Угол 0 градусов

Построение угла 90°

Начертите линию.

Построить серединный перпендикуляр.

Установите циркуль примерно на три четверти длины линии. Поместите острие циркуля на одну из конечных точек линии и нарисуйте дугу. Удерживая компасы в том же положении, нарисуйте еще одну дугу из другой конечной точки. Наконец, используйте линейку, чтобы соединить два пересечения дуг.

Новая линия является серединным перпендикуляром к исходному сегменту линии.

Как построить угол 45 градусов

Чтобы построить угол 45 градусов:

1. Построить угол 90 градусов.
2. Построить биссектрису угла 90 градусов.

Как построить угол 45 градусов

Как построить угол 45 градусов пример

Пример 4: построить угол 45 градусов

Построить угол 45°

Построить угол 90 градусов.

Выполните действия из примера 3, чтобы построить угол 90 градусов

Постройте биссектрису угла 90 градусов.

Поместите острие циркуля в центр А и начертите дугу. Поместите острие циркуля в точку B и начертите дугу. Держите компасы в том же положении, поместите циркуль в точку С и начертите другую дугу, пересекая дугу, сделанную в точке В. Используя линейку, соедините точку, где дуги пересекаются друг с другом, с центром A.

Угол 90 градусов был разделен пополам на два равных угла по 45 градусов.

Распространенные заблуждения

• Карандаш должен быть острым

Острый карандаш поможет вашей диаграмме быть точной. Использование маленького карандаша в компасе также может быть полезным.

Практика построения угла 30, 60, 45, 90 градусов вопросы

Построение должно производиться с использованием компасов с одинаковой настройкой для обеих дуг. Строительные дуги должны быть видны. Линии следует проводить линейкой.

Построение должно быть выполнено с использованием компасов с одинаковой настройкой для обеих последних дуг. Строительные дуги должны быть видны. Линии следует проводить линейкой.

Построение должно быть выполнено с использованием компаса с одинаковой настройкой для обеих последних дуг. Строительные дуги должны быть видны. Линии должны быть начерчены с помощью линейки. Построение должно быть выполнено с помощью циркуля, установленного на одну и ту же настройку для обеих последних дуг. Строительные дуги должны быть видны. Линии следует проводить линейкой. 9{\circ} угол.

 

(3 балла)

Показать ответ

Для построения вспомогательных дуг под углом 60 градусов

(1)

Для рисования дуг для построения биссектрисы угла

( 1)

Для завершения построения угла 30 градусов

(1)

Учебный контрольный список

Теперь вы научились:

• Построение угла 60 градусов
• Построить угол 30 градусов
• Построить угол 90 градусов
• Построить угол 45 градусов

Все еще зависает?

Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning.