| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | сфера (4) | | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | ||
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | 3/9 | ||
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0. 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
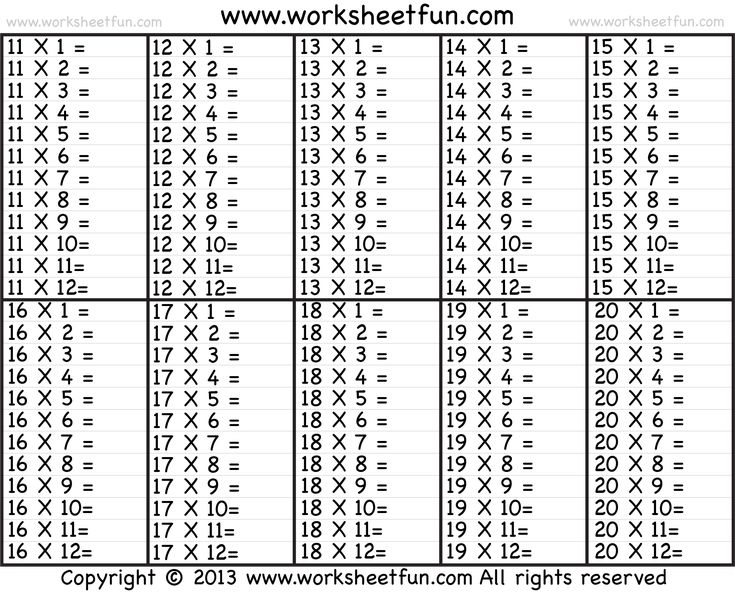
Умножение на 2 | Таблица умножения
На этой странице представлены примеры, описывающие умножение на 2 и умножение числа 2, деление, некоторые способы записи и произношения, таблица умножения на 2 без ответов, в конце статьи — картинки для скачивания, с помощью которых можно распечатать таблицу умножения и деления на 2.
Умножение на 2:
1 x 2 = 2
2 x 2 = 4
3 x 2 = 6
4 x 2 = 8
5 x 2 = 10
6 x 2 = 12
7 x 2 = 14
8 x 2 = 16
9 x 2 = 18
10 x 2 = 20
Первый вариант произношения:
1 x 2 = 2 (1 умножить на 2, равно 2)
2 x 2 = 4 (2 умножить на 2, равно 4)
3 x 2 = 6 (3 умножить на 2, равно 6)
4 x 2 = 8 (4 умножить на 2, равно 8)
5 x 2 = 10 (5 умножить на 2, равно 10)
6 x 2 = 12 (6 умножить на 2, равно 12)
7 x 2 = 14 (7 умножить на 2, равно 14)
8 x 2 = 16 (8 умножить на 2, равно 16)
9 x 2 = 18 (9 умножить на 2, равно 18)
10 x 2 = 20 (10 умножить на 2, равно 20)
Второй вариант произношения:
1 x 2 = 2 ( по 1 взять 2 раза, получится 2)
2 x 2 = 4 ( по 2 взять 2 раза, получится 4)
3 x 2 = 6 ( по 3 взять 2 раза, получится 6)
4 x 2 = 8 ( по 4 взять 2 раза, получится 8)
5 x 2 = 10 ( по 5 взять 2 раза, получится 10)
6 x 2 = 12 ( по 6 взять 2 раза, получится 12)
7 x 2 = 14 ( по 7 взять 2 раза, получится 14)
8 x 2 = 16 ( по 8 взять 2 раза, получится 16)
9 x 2 = 18 ( по 9 взять 2 раза, получится 18)
10 x 2 = 20 ( по 10 взять 2 раза, получится 20)
Иногда еще произносят, например, так:
2 ∙ 2 = 4 (дважды два — четыре)
От перемены мест множителей значение произведения не меняется, поэтому, зная результаты умножения на 2, можно легко найти результаты умножения числа 2.
В качестве знака умножения в разных источниках используют разные символы. Выше был показан пример с (x), в этот раз сделаем запись с помощью приподнятой точки ( ∙ )
Умножение числа 2:
2 ∙ 1 = 2
2 ∙ 2 = 4
2 ∙ 3 = 6
2 ∙ 4 = 8
2 ∙ 5 = 10
2 ∙ 6 = 12
2 ∙ 7 = 14
2 ∙ 8 = 16
2 ∙ 9 = 18
2 ∙ 10 = 20
Варианты произношения:
2 ∙ 1 = 2 (по 2 взять 1 раз, получится 2)
2 ∙ 2 = 4 (по 2 взять 2 раза, получится 4)
2 ∙ 3 = 6 (по 2 взять 3 раза, получится 6)
2 ∙ 4 = 8 (по 2 взять 4 раза, получится 8)
2 ∙ 5 = 10 (по 2 взять 5 раз, получится 10)
2 ∙ 6 = 12 (по 2 взять 6 раз, получится 12)
2 ∙ 7 = 14 (по 2 взять 7 раз, получится 14)
2 ∙ 8 = 16 (по 2 взять 8 раз, получится 16)
2 ∙ 9 = 18 (по 2 взять 9 раз, получится 18)
2 ∙ 10 = 20 (по 2 взять 10 раз, получится 20)
2 ∙ 1 = 2 (2 умножить на 1, равно 2)
2 ∙ 2 = 4 (2 умножить на 2, равно 4)
2 ∙ 3 = 6 (2 умножить на 3, равно 6)
2 ∙ 4 = 8 (2 умножить на 4, равно 8)
2 ∙ 5 = 10 (2 умножить на 5, равно 10)
2 ∙ 6 = 12 (2 умножить на 6, равно 12)
2 ∙ 7 = 14 (2 умножить на 7, равно 14)
2 ∙ 8 = 16 (2 умножить на 8, равно 16)
2 ∙ 9 = 18 (2 умножить на 9, равно 18)
2 ∙ 10 = 20 (2 умножить на 10, равно 20)
Деление на 2:
2 ÷ 2 = 1 (2 разделить на 2, равно 1)
4 ÷ 2 = 2 (4 разделить на 2, равно 2)
6 ÷ 2 = 3 (6 разделить на 2, равно 3)
8 ÷ 2 = 4 (8 разделить на 2, равно 4)
10 ÷ 2 = 5 (10 разделить на 2, равно 5)
12 ÷ 2 = 6 (12 разделить на 2, равно 6)
14 ÷ 2 = 7 (14 разделить на 2, равно 7)
16 ÷ 2 = 8 (16 разделить на 2, равно 8)
18 ÷ 2 = 9 (18 разделить на 2, равно 9)
20 ÷ 2 = 10 (20 разделить на 2, равно 10)
Картинка:
Деление.
Картинка:
Таблица умножения и деления на 2 без ответов (по порядку и вразброс):
| 1 ∙ 2 = | 7 ∙ 2 = | 2 ÷ 2 = | 10 ÷ 2 = |
| 2 ∙ 2 = | 8 ∙ 2 = | 4 ÷ 2 = | 2 ÷ 2 = |
| 3 ∙ 2 = | 9 ∙ 2 = | 6 ÷ 2 = | 4 ÷ 2 = |
| 4 ∙ 2 = | 10 ∙ 2 = | 8 ÷ 2 = | 6 ÷ 2 = |
| 5 ∙ 2 = | 1 ∙ 2 = | 10 ÷ 2 = | 8 ÷ 2 = |
| 6 ∙ 2 = | 2 ∙ 2 = | 12 ÷ 2 = | 16 ÷ 2 = |
| 7 ∙ 2 = | 3 ∙ 2 = | 14 ÷ 2 = | 18 ÷ 2 = |
| 8 ∙ 2 = | 4 ∙ 2 = | 16 ÷ 2 = | 12 ÷ 2 = |
| 9 ∙ 2 = | 5 ∙ 2 = | 18 ÷ 2 = | 14 ÷ 2 = |
| 10 ∙ 2 = | 6 ∙ 2 = | 20 ÷ 2 = | 4 ÷ 2 = |
Эта часть таблицы обычно бывает если не первой, то одной из первых в изучении.
Мы уже говорили о способах записи, теперь рассмотрим пример с умножением на 2, связать старые знания с новыми
5 x 2 = 10.
Большинство авторов книг вкладывают в такую запись на сегодняшний день следующий смысл: 5 умножить на 2 равно 10; если по 5 взять два раза, то получится 10.
Здесь 5 — это первый множитель, 2 — второй множитель, а 10 — значение произведения
Часто в качестве знака умножения также используют приподнятую точку (5 ∙ 2) и «звездочку» или «снежинку» (5 * 2) , можно встретить и другие обозначения.
Мы уже говорили в основной части о том, что, если записать таблицу умножения на числа от 1 до 10, то можно увидеть, что при перемене мест множителей значение произведения не меняется (на основании этого формулируют переместительный закон умножения), поэтому можно выучить только половину таблицы умножения и, зная её, быстро найти ответы для оставшейся половины. Кстати, есть еще и другие способы быстро выучить таблицу, а также способы быстро считать без заучивания таблицы.
Итак, мы только что сказали, что при умножении числа 2 на 5 получится такое же число как и при умножении 5 на 2:
5 x 2 = 2 x 5 = 10.
Но здесь нужно быть очень внимательными, когда дело доходит уже не просто до чисел, а до конкретных задач и примеров. Во многих учебниках рекомендуют с помощью первого множителя обозначать то, что складывают, а с помощью второго указывать, сколько раз.
Приведем в качестве примера такую ситуацию: Вася и Петя собирались рисовать. Мама дала каждому по 5 листов бумаги, значит всего листов будет 10. Это можно записать привычным способом с помощью знака плюс (5 + 5 = 10), а можно записать с помощью двух множителей и знака умножения.
5 x 2 = 10 .
Исходя из того, что каждый множитель при записи выполняет определенную роль, можно прийти к выводу о том, что, если от перемены мест множителей значение произведения не меняется, то это еще не значит, что всегда можно записывать множители в любом порядке. О порядке записи множителей периодически разгораются жаркие споры, надеемся, что скоро по этому вопросу будет достигнуто взаимопонимание.
Также может возникнуть вопрос: зачем вообще нужна такая запись? Зачем вводить новый способ записи, если уже есть «плюс»?
В принципе в данном случае по удобству записи «5 x 2» мало отличается от «5 + 5». А вот если бы по 5 листов бумаги нужно было бы раздать 10 детям?
Тогда пришлось бы записывать 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 = 50. А если нужно было бы раздать по 5 листов целому классу? С помощью сложения записывать это было бы уже не очень удобно. Итак, если нужно раздать по пять листов десяти детям, с помощью знака умножения это можно записать коротко:
Но вернемся пока к основной теме.Способы записи таблицы умножения на 2:
| x | Приподнятая точка | * | Знак не указан |
|---|---|---|---|
| 1 x 2 = 2 | 1 ∙ 2 = 2 | 1 * 2 = 2 | 1 __ 2 = 2 |
| 2 x 2 = 4 | 2 ∙ 2 = 4 | 2 * 2 = 4 | 2 __ 2 = 4 |
| 3 x 2 = 6 | 3 ∙ 2 = 6 | 3 * 2 = 6 | 3 __ 2 = 6 |
| 4 x 2 = 8 | 4 ∙ 2 = 8 | 4 * 2 = 8 | 4 __ 2 = 8 |
| 5 x 2 = 10 | 5 ∙ 2 = 10 | 5 * 2 = 10 | 5 __ 2 = 10 |
| 6 x 2 = 12 | 6 ∙ 2 = 12 | 6 * 2 = 12 | 6 __ 2 = 12 |
| 7 x 2 = 14 | 7 ∙ 2 = 14 | 7 * 2 = 14 | 7 __ 2 = 14 |
| 8 x 2 = 16 | 8 ∙ 2 = 16 | 8 * 2 = 16 | 8 __ 2 = 16 |
| 9 x 2 = 18 | 9 ∙ 2 = 18 | 9 * 2 = 18 | 9 __ 2 = 18 |
| 10 x 2 = 20 | 10 ∙ 2 = 20 | 10 * 2 = 20 | 10 __ 2 = 20 |
Способы записи таблицы деления на 2:
| / | : | ÷ | Без знака |
|---|---|---|---|
| 2 / 2 = 1 | 2 : 2 = 1 | 2 ÷ 2 = 1 | 2 __ 2 = 1 |
| 4 / 2 = 2 | 4 : 2 = 2 | 4 ÷ 2 = 2 | 4 __ 2 = 2 |
| 6 / 2 = 3 | 6 : 2 = 3 | 6 ÷ 2 = 3 | 6 __ 2 = 3 |
| 8 / 2 = 4 | 8 : 2 = 4 | 8 ÷ 2 = 4 | 8 __ 2 = 4 |
| 10 / 2 = 5 | 10 : 2 = 5 | 10 ÷ 2 = 5 | 10 __ 2 = 5 |
| 12 / 2 = 6 | 12 : 2 = 6 | 12 ÷ 2 = 6 | 12 __ 2 = 6 |
| 14 / 2 = 7 | 14 : 2 = 7 | 14 ÷ 2 = 7 | 14 __ 2 = 7 |
| 16 / 2 = 8 | 16 : 2 = 8 | 16 ÷ 2 = 8 | 16 __ 2 = 8 |
| 18 / 2 = 9 | 18 : 2 = 9 | 18 ÷ 2 = 9 | 18 __ 2 = 9 |
| 20 / 2 = 10 | 20 : 2 = 10 | 20 ÷ 2 = 10 | 20 __ 2 = 10 |
Умножение на:
‹ Умножение на 10 Вверх Умножение на 3 ›
3-8 целиком .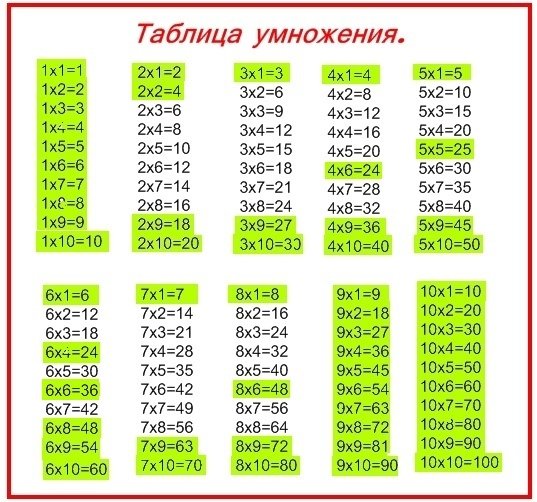
На прошлом уроке вы научились складывать и вычитать дроби. Но это не единственный вид математики, который вы можете делать с дробями. Бывают случаи, когда полезно будет умножать и дроби.
Просмотрите слайд-шоу, чтобы узнать, как написать задачу на умножение с дробями.
Давайте составим пример умножения с дробями. Предположим, вы выпиваете 2/4 чашки кофе каждое утро.
Но ваш врач только что сказал вам, что вам нужно сократить потребление кофе на вдвое .
Теперь вам нужно выяснить, сколько стоит 1/2 от 2/4 кофейника.
Это может не выглядеть как задача на умножение. Но когда вы видите слово из с дробями, значит нужно умножать.
Чтобы настроить пример, мы просто заменим слово из знаком умножения.
Теперь наш пример готов к решению.
В отличие от обычного умножения, которое дает на большее число .
..В отличие от обычного умножения, которое дает на большее число … умножение дробей обычно дает меньший номер .
Итак, когда мы умножаем 1/2 на 2/4…
Итак, когда мы умножаем 1/2 на 2/4… наш ответ будет меньше, чем 2/4.
Вот еще один пример. Допустим, у вас есть 3/5 чашки шоколадной начинки.
Вы хотите положить одинаковое количество начинки в каждый из этих 4 кексов.
Можно сказать, что вы хотите положить 1/4 от 3/5 чашки начинки в каждый кекс.
Как и раньше, мы изменим слово из числа на знак умножения.
Теперь наши дроби готовы к умножению.
..Попробуйте!
Попробуйте решить приведенную ниже задачу на умножение. Пока не беспокойтесь о ее решении!
Рецепт требует 2/3 стакана молока. Вы хотите сократить рецепт вдвое.
Примечание : Хотя в нашем примере правильный ответ 2/3 x 1/2, помните, что порядок умножения не имеет значения.
1/2 х 2/3 тоже будет правильно.
Решение задач на умножение с дробями
Теперь, когда мы знаем, как решать задачи на умножение с дробями, давайте попрактикуемся в решении некоторых из них. Если вам удобно умножать целые числа, вы готовы к умножению дробей.
Щелкните слайд-шоу, чтобы узнать, как умножать две дроби.
Давайте умножим, чтобы найти 1/2 от 7/10.
Как и раньше, мы заменим слово из числа знаком умножения. Теперь мы готовы к умножению.
Сначала мы умножим числители: 1 и 7.
1 умножить на 7 равно 7, поэтому мы напишем 7 справа от числителей.
Когда мы сложили дробей, знаменатели остались прежними. Но когда мы умножаем, знаменатели тоже умножаются.
2 умножить на 10 равно 20, поэтому мы напишем 20 справа от знаменателя.
Теперь мы знаем, что 1/2 умножить на 7/10 равно 7/20.
Можно также сказать, что 1/2 от 7/10 равно 7/20.
Давайте попробуем другой пример: 3/5 умножить на 2/3.
Сначала умножим наши числители. 3 умножить на 2 равно 6.
Далее мы умножим наши знаменатели. 5 умножить на 3 равно 15.
Итак, 3/5 умножить на 2/3 равно 6/15.
Попробуйте!
Попробуйте решить приведенные ниже задачи на умножение.
Умножение дроби на целое число
Умножение дроби на целое число аналогично умножению двух дробей. Есть только один дополнительный шаг: прежде чем вы сможете умножать, вам нужно превратить целое число в дробь. Это слайд-шоу покажет вам, как это сделать.
Щелкните слайд-шоу, чтобы узнать, как умножать дробь и целое число.
Умножим 2 раза на 1/3. Помните, это всего лишь еще один способ спросить: «Сколько будет 1/3 от 2?»
Прежде чем мы начнем, нам нужно убедиться, что эти числа готовы к умножению.
Мы не можем умножить целое число на дробь, поэтому нам придется записать 2 как дробь.
Как вы узнали из раздела «Введение в дроби», мы также можем записать 2 как 2/1. Это потому, что 2 можно дважды разделить на 1.
Теперь мы готовы к умножению!
Во-первых, мы умножим числители : 2 и 1.
2 умножить на 1 равно 2. Выровняем 2 с числителями.
Далее мы умножим знаменателей: 1 и 3.
1 умножить на 3 равно 3. Выровняем 3 со знаменателями.
Итак, 2/1 умножить на 1/3 равно 2/3. Мы могли бы также сказать, что 1/3 от 2 равно 2/3.
Попробуем другой пример: 4 раза по 1/5.
Прежде чем мы начнем, нам придется записать 4 в виде дроби.
Перепишем 4 как 4/1. Теперь мы готовы к умножению.
Сначала умножим числители: 4 и 1.
4 умножить на 1 равно 4, поэтому числитель нашего ответа равен 4.
Далее умножим знаменатели: 1 и 5.
1 умножить на 5 равно 5, поэтому 5 — знаменатель нашего ответа.
Итак, 4/1 умножить на 1/5 равно 4/5.
Попробуйте!
Попробуйте решить приведенные ниже задачи на умножение.
Разделение дробей
На последних нескольких страницах вы узнали, как умножать дробей. Вы, наверное, уже догадались, что на можно разделить и дробей. Вы делите дроби, чтобы увидеть, сколько частей чего-то содержится в чем-то еще. Например, если вы хотите узнать, сколько четвертей дюйма составляет четыре дюйма, вы можете разделить 4 на 1/4.
Давайте попробуем другой пример. Представьте, что рецепт требует 3 стакана муки, но ваш мерный стакан вмещает только 1/3, или одну треть 9.0914 , чашки. Сколько третей стакана нужно добавить?
Нам нужно выяснить, сколько третей стакана приходится на три стакана.
Другими словами, нам нужно разделить три на одну треть.
Мы запишем задачу так:
3 ÷ 1/3
Попробуйте!
Попробуйте решить эти задачи на деление с дробями. Не беспокойтесь об их решении!
Рецепт требует 3/4 стакана воды. У вас есть только мерный стакан 1/8.
Решение задач на деление с дробями
Теперь, когда мы знаем, как писать задачи на деление, давайте потренируемся, решая несколько задач. Деление дробей очень похоже на умножение. Просто требуется один дополнительный шаг. Если вы можете умножать дроби, вы можете их и делить!
Просмотрите слайд-шоу, чтобы узнать, как разделить целое число на дробь.
Разделим 3 на 1/3. Помните, это всего лишь еще один способ спросить: «Сколько третей в числе 3?»
В нашем уроке о делении вы научились писать знак деления вот так (/).
При делении дробей полезно использовать другой символ для деления (÷), чтобы мы не приняли его за дробь.
Как и при умножении, мы начнем с поиска любых целых чисел в нашей задаче. Есть один: 3.
Помните, 3 — это то же самое, что 3/1.
Прежде чем мы сможем разделить, нам нужно сделать еще одно изменение.
Мы поменяем местами числитель и знаменатель дроби, на которую мы делим : 1/3 в этом примере.
Итак, 1/3 становится 3/1.
Это называется нахождением обратной или мультипликативной обратной , дроби.
Так как мы меняем исходную дробь, мы также заменим знак деления (÷) на 9.0913 умножение знак (х).
Это потому, что умножение — это , обратное делению.
Теперь мы можем рассматривать это как обычную задачу на умножение.
Сначала мы умножим числители: 3 и 3.
3 умножить на 3 равно 9, поэтому мы напишем это рядом с числителями.
Далее умножаем знаменатели: 1 и 1.
1 умножить на 1 равно 1, поэтому мы напишем 1 рядом со знаменателем.
Как видите, 3/1 х 1/3 = 9/1.
Помните, что любая дробь больше 1 также может быть выражена как целое число . Итак, 9/1 = 9.
3 ÷ 1/3 = 9. Другими словами, в 3 содержится 9 третей .
Давайте попробуем другой пример: 5 разделить на 4/7.
Как всегда, мы перепишем любые целые числа, чтобы 5 стало 5/1.
Далее мы найдем , обратное числа 4/7. Это дробь, на которую мы делим.
Для этого мы поменяем местами числитель и знаменатель, так что 4/7 станет 7/4.
Затем мы изменим знак деления (÷) на знак умножения (x).
Теперь мы можем умножать, как обычно. Сначала умножим числители: 5 и 7.
5 умножить на 7 равно 35, поэтому мы напишем это рядом с числителями.
Далее мы умножим знаменатели: 1 и 4.
1 умножить на 4 равно 4, поэтому мы напишем это рядом со знаменателями.
Итак, 5/1 х 4/7 = 35/4.
Как вы узнали ранее, мы можем преобразовать нашу неправильную дробь в смешанное число , чтобы наш ответ было легче читать.
35/4 = 8 3/4. Итак, 5 ÷ 4/7 = 8 3/4.
Попробуйте!
Попробуйте решить эти задачи на деление. Пока не беспокойтесь об уменьшении ответа.
Деление двух дробей
Мы только что научились делить целое число на дробь . Вы можете использовать тот же метод, чтобы разделить на две дроби .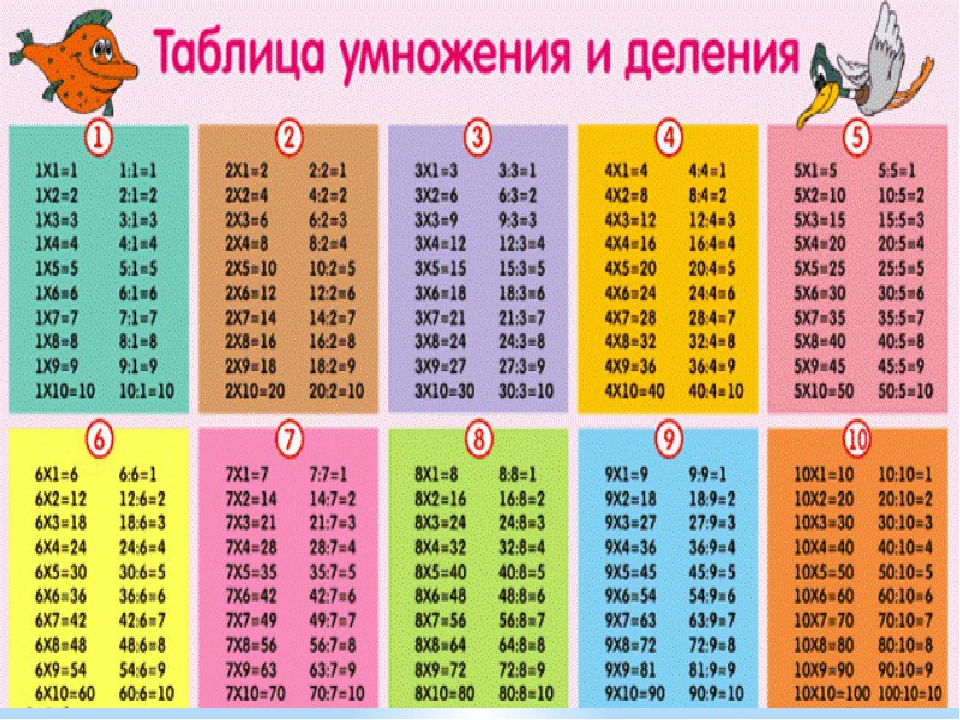
Щелкните слайд-шоу, чтобы узнать, как делить на две дроби.
Давайте попробуем решить задачу с двумя дробями: 2/3 ÷ 3/4. Здесь мы хотим знать, сколько 3/4 в 2/3.
Сначала мы найдем , обратное дроби, на которую мы делим: 3/4.
Для этого мы поменяем местами числитель и знаменатель. Таким образом, 3/4 становится 4/3.
Далее мы изменим знак деления (÷) на знак умножения (x).
Теперь умножим числители. 2 x 4 = 8, поэтому мы напишем 8 рядом с верхними числами.
Далее мы умножим знаменатели. 3 x 3 = 9, поэтому мы напишем 9 рядом с нижними числами.
Итак, 2/3 х 4/3 = 8/9.
Мы могли бы также записать это как 2/3 ÷ 3/4 = 8/9.
Давайте попробуем другой пример: 4/7 разделить на 2/9.
Целых чисел нет, поэтому найдем обратное дроби, на которую мы делим.
Это 2/9.Для этого мы поменяем местами числитель и знаменатель. Таким образом, 2/9 становится 9/2.
Теперь мы изменим знак деления (÷) на знак умножения (x) и умножим как обычно.
Сначала умножим числители. 4 x 9 = 36.
Далее мы умножим знаменатели. 7 х 2 = 14,
Итак, 4/7 х 9/2 = 36/14. Как и раньше, вы можете преобразовать эту неправильную дробь в смешанное число.
Итак, 4/7 ÷ 2/9 = 2 8/14.
Это 2/9.Попробуйте!
Попробуйте решить эти задачи на деление. Пока не беспокойтесь об уменьшении ответа.
Умножение и деление смешанных чисел
Как бы вы решили подобную задачу?
Как вы узнали из предыдущего урока, всякий раз, когда вы решаете задачу с помощью смешанный номер вам нужно сначала преобразовать его в неправильную дробь .
Затем вы можете умножать или делить, как обычно.
Использование отмены для упрощения задач
Иногда вам может понадобиться решить такие задачи:
Обе эти дроби включают больших чисел . Вы можете умножать эти дроби так же, как и любые другие дроби. Однако такие большие числа трудно понять. Можете ли вы представить 21/50 или двадцать одна пятидесятая , у тебя в голове?
21/50 x 25/14 = 525/700
Даже ответ кажется сложным. Это 525/700, или пятьсот двадцать пять семисотых . Какой глоток!
Если вам не нравится работать с большими числами, вы можете упростить подобную задачу, используя метод, называемый отменой . Когда вы отменяете дроби в задаче, вы сокращаете их обе одновременно.
Сначала отмена может показаться сложной, но мы покажем вам, как это сделать шаг за шагом. Давайте еще раз взглянем на пример, который мы только что видели.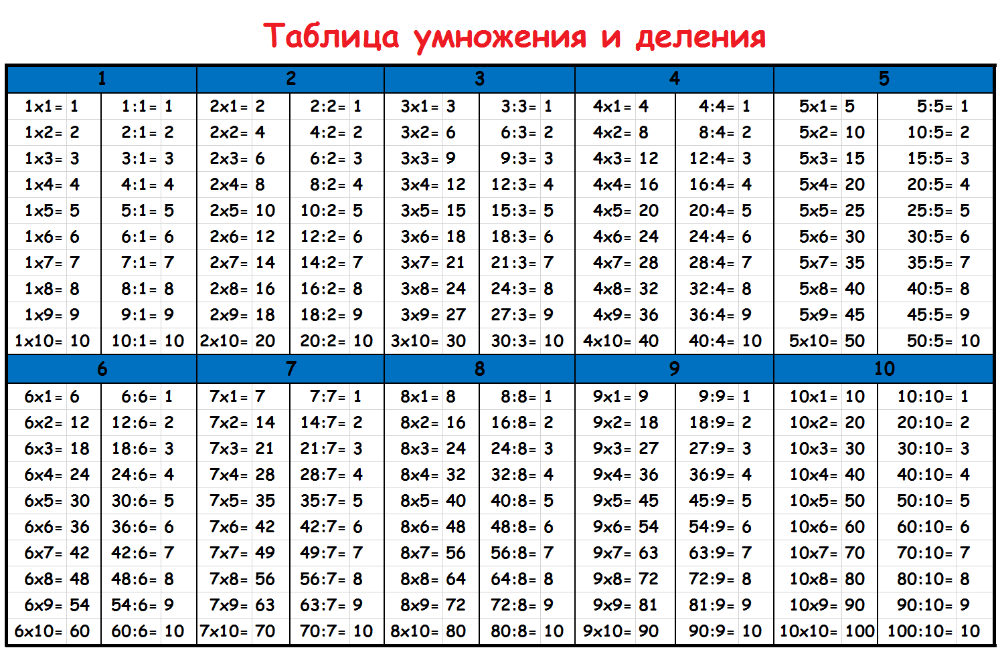
Шаг 1
Во-первых, посмотрите на числитель первой дроби и знаменатель второй. Мы хотим посмотреть, можно ли разделить на одно и то же число.
В нашем примере похоже, что и 21, и 14 можно разделить на 7.
Шаг 2
Далее мы разделим 21 и 14 на 7. Сначала мы разделим наше верхнее число слева: 21.
21 ÷ 7 = 3
Затем разделим нижнее число справа: 14.
14 ÷ 7 = 2
Ответы на каждую задачу запишем рядом с числами, которые мы разделили. Поскольку 21 ÷ 7 равно 3, мы напишем 3 там, где было 21. 14 ÷ 7 равно 2, поэтому мы напишем 2 там, где было 14. Мы можем вычеркнуть или отменить , числа, с которых мы начали.
Теперь наша задача выглядит намного проще, не так ли?
Шаг 3
Давайте посмотрим на другие числа дроби. На этот раз мы рассмотрим знаменатель первой дроби и числитель второй.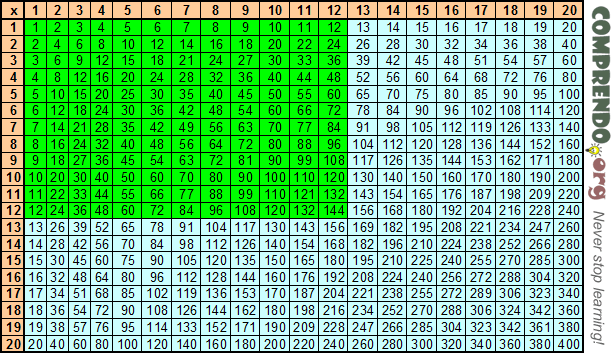
Можно ли разделить на одно и то же число?
Обратите внимание, что их можно разделить на 25! Вы могли также заметить, что они оба могут делиться на 5. Мы могли бы также использовать 5 , но обычно, когда вы отменяете, вы хотите найти наибольшее число , на которое можно разделить оба числа. Таким образом, вам не придется снова сокращать дробь в конце.
Шаг 4
Затем мы отменим так же, как мы делали это в шаге 2.
Мы разделим наше нижнее число слева: 50.
50 ÷ 25 = 2
Затем мы разделим верхнее число на справа: 25.
25 ÷ 25 = 1
Мы запишем ответы на каждую задачу рядом с числами, которые мы разделили.
Шаг 5
Теперь, когда мы отменили исходные дроби, мы можем умножить наши новые дроби, как обычно. Как всегда, сначала умножьте числители:
3 x 1 = 3
Затем умножьте знаменатели:
2 x 2 = 4
Итак, 3/2 x 1/2 = 3/4, или три четверти .