Виды распределения дискретных случайных величин. Закон больших чисел (для детей)
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Виды распределения дискретных случайных величин
10.3.2.16 распознавать видыраспределения дискретных
случайных величин: биномиальное
распределение
Трансформация данных
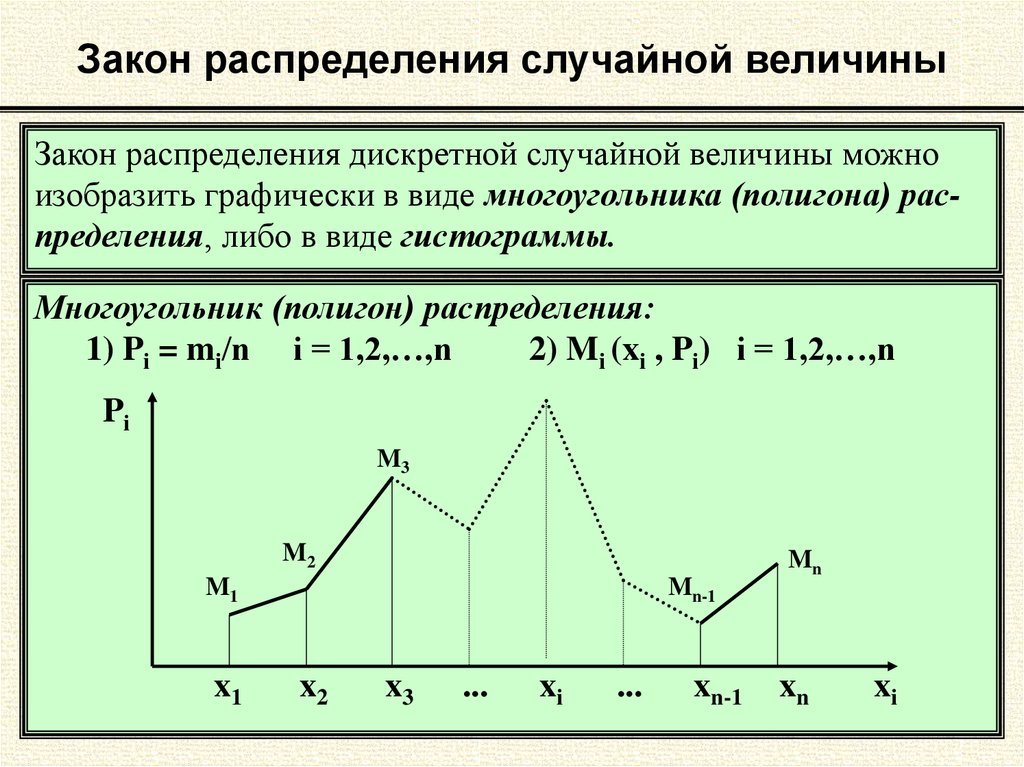
Какие бывают распределения:
1. Равномерное (uniform)
2. Случайное (random)
Могут быть и дискретными, и непрерывными
Трансформация данных
3.
 Биномиальное распределение
Биномиальное распределение(дискретное).
Пример: рассмотрим выводки из 6 детёнышей
каждый.
Возможное соотношение самцов и самок в выводке:
6:0; 5:1; 4:2; 3:3; 2:4; 1:5; 0:6
Трансформация данных
Биномиальное распределение
Вероятность такого
выводка
распределение количества «успехов» (самцов) в
последовательности из N независимых случайных
экспериментов, таких что вероятность «успеха»
(рождения самца) в каждом из них постоянна и равна p.
Количество самцов в
выводке из 6 зверьков
5. Биномиальное распределение
О случайной величине — числе «успехов» в n испытанияхБернулли — говорят, что она имеет биномиальное
распределение с параметрами n и p и обозначают
Х∼B(n,p)
6. При решении примера 1 (о трех выстрелах срелка) мы фактически находим закон распределения случайной величины X — числа
Пример 1. Стрелок производит три независимыхвыстрела по мишени. Вероятность попадания при каждом
выстреле равна 0,9.
 Найти вероятность того, что стрелок
Найти вероятность того, что стрелокровно два раза попадет в цель.
При решении примера 1 (о трех выстрелах срелка) мы
величины
X — числа попаданий при трех выстрелах:
То есть Х имеет биномиальное распределение с параметрами
n=3 и p=0,9 или Х∼B(3,0.9)
xi
0
1
2
3
pi
0,001
0,027
0,243
0,729
Пример 3. Составьте ряд распределения
величины, распределенной по
биномиальному закону с параметрами n=4,
1
p= .
3
Производится серия из n=4 опытов. Случайная
величина Х — число опытов, в которых может
произойти событие А, может принимать
значения 0, 1, 2, 3, 4.
Соответствующие
вероятности
находятся
по
формуле Бернулли при n=4, p=1/3, q=1-1/3=2/3.
m
1
p ( X m) C
3
Вероятность того, что событие
ни в одном опыте (m=0):
m
4
0
4 m
2
3
А не произойдет
4
16
1 2
p ( X 0) C
81
3 3
0
4
Вероятность того, что событие А произойдет
в одном опыте (m=1):
1
3
32
2
1 1
p ( X 1) C4
81
3 3
Аналогично находим вероятности того, что это
событие произойдет в двух (m=2), в трех
(m=3) и в четырех (m=4) опытах:
2
2
24
1 2
p ( X 2) C
81
3 3
2
4
3
1
8
1 2
p ( X 3) C
81
3 3
3
4
4
0
1
1 2
p ( X 4) C44
81
3 3
Таким образом, ряд распределения случайной
величины Х будет выглядеть так:
Хm
0
1
2
3
4
Pm
16/81
32/81
24/81
8/81
1/81
Можно убедиться, что суммарная вероятность
действительно равна 1.

Найдем математическое ожидание случайной
величины,
распределенной
по
биномиальному закону.
Х — число опытов в серии из n, в которых
произошло событие А.
Введем для каждого i=1,2…n случайную
Пусть Zi принимает всего два значения: 1 — если
событие А произойдет в i-ом опыте и 0 — если
событие А не произойдет в i-ом опыте.
Тогда событие Х выразится через сумму событий
Zi :
Х= Z1 +Z2 +…+Zn
Тогда математическое ожидание случайной
величины Х:
M[X]=M[Z1]+M[Z2]+…+M[Zn]
Найдем математическое ожидание Zi
Ряд распределения Zi имеет вид:
Zi
0
1
Pi
q
p
Тогда M[Zi ]=p и M[X]=np.
Найдем дисперсию случайной величины Zi
D[ Z i ] (0 p) q (1 p) p pq
2
Так
как
случайные
независимы, то
2
величины
Zi
D[ X ] D[ Z1 ] D[ Z 2 ] … D[ Z n ]
n D[ Z n ] n p q
Таким образом, для случайной величины,
распределенной по биномиальному закону
M[X ] n p
D[ X ] n p q
English Русский Правила
Распределения случайной величины в EXCEL.
 Примеры и описание Распределения случайной величины в EXCEL. Примеры и описание
Примеры и описание Распределения случайной величины в EXCEL. Примеры и описаниеhistory 23 октября 2016 г.
- Группы статей
- Распределения вероятностей
В статье приведен перечень распределений вероятности, имеющихся в MS EXCEL 2010 и в более ранних версиях. Даны ссылки на статьи с описанием соответствующих функций MS EXCEL.
Приведенные ниже распределения случайной величины часто встречаются в задачах по статистике. Ниже даны ссылки на статьи с описанием соответствующих функций MS EXCEL. В этих статьях построены графики плотности вероятности и функции распределения , приведены примеры решения задач и применение этих распределений на практике.
Также в статьях рассмотрены вопросы генерации случайных величин, имеющих соответствующее распределение, точечная оценка параметров этих распределений и формулы для расчета
среднего значения
,
дисперсии, стандартного отклонения
,
моды
,
медианы
и других показателей распределения.
Распределения MS EXCEL для моделирования поведения случайных величин, встречающихся на практике
Непрерывные распределения
- Нормальное распределение : функции НОРМ.РАСП() , НОРМ.СТ.РАСП() , НОРМ.ОБР() и др.
- Непрерывное равномерное распределение : функция СЛЧИС()
- Экспоненциальное распределение : функция ЭКСП.РАСП()
- Гамма распределение : функции ГАММА.РАСП() и ГАММА.ОБР()
- Логнормальное распределение : функции ЛОГНОРМ.РАСП() и ЛОГНОРМ.ОБР()
- Распределение Вейбулла : функция ВЕЙБУЛЛ.РАСП()
- Бета-распределение : функции БЕТА.РАСП() и БЕТА.ОБР()
Дискретные распределения
- Биномиальное распределение
: функции
БИНОМ.
 РАСП()
,
БИНОМ
.ОБР()
РАСП()
,
БИНОМ
.ОБР() - Распределение Пуассона : функция ПУАССОН.РАСП()
- Равномерное дискретное распределение : функция СЛУЧМЕЖДУ()
- Геометрическое распределение : функция ОТРБИНОМ.РАСП()
- Гипергеометрическое распределение : функция ГИПЕРГЕОМ.РАСП()
- Отрицательное биномиальное распределение : функция ОТРБИНОМ.РАСП()
Распределения MS EXCEL для целей математической статистики
В математической статистике, например для проверки гипотез или для построения доверительных интервалов , наиболее часто используются:
- Нормальное распределение : функции НОРМ.РАСП() , НОРМ.СТ.РАСП() , НОРМ.ОБР() и др.
- Распределение Стьюдента (t-распределение)
: функции
СТЬЮДЕНТ.РАСП()
,
СТЬЮДЕНТ.
 ОБР()
и др.
ОБР()
и др. - Распределение Фишера (F-распределение) : функции F.РАСП() , F.ОБР() и др.
- Хи-квадрат распределение : функции ХИ2.РАСП() , ХИ2.ОБР() и др.
Все эти распределения связаны с нормальным распределением .
© Copyright 2013 — 2023 Excel2.ru. All Rights Reserved
Распределение вероятностей в науке о данных
Введение
Добро пожаловать в мир вероятности в науке о данных! Позвольте мне начать с интуитивного примера. Представьте, что вы аналитик данных или кто-то, кто создает модели машинного обучения или работает над алгоритмами или скриптами Python, и вам нужно анализировать тенденции. Тем не менее, у вас недостаточно данных, чтобы проанализировать тенденцию в вашем наборе данных. В этой статье давайте найдем способ решить эту проблему, используя распределение вероятностей.
Цели обучения
- В этом уроке мы узнаем об общих типах данных.

- Вы также узнаете о различных типах распределений и функции плотности вероятности.
- Наконец-то вы узнаете о взаимосвязях этих дистрибутивов.
Содержание
- Понимание основ вероятности
- Общие типы данных
- Типы дистрибутивов
- Функция распределения вероятности
- Отношения между дистрибутивами
- Проверьте свои знания
- Заключение
Понимание основ вероятности
Давайте начнем с примера. Предположим, вы преподаете в университете. После проверки заданий в течение недели вы выставили оценки всем ученикам. Вы дали эти оценочные работы специалисту по вводу данных в университете и сказали ему создать электронную таблицу, содержащую оценки всех студентов. Но парень хранит только оценки, а не соответствующих учеников.
Он сделал еще одну ошибку; он в спешке пропустил несколько записей, и мы понятия не имеем, чьи оценки отсутствуют. Один из способов выяснить это — визуализировать оценки и посмотреть, сможете ли вы найти тенденцию в данных.
График, который вы построили, называется частотным распределением данных. Вы видите плавную кривую структуру, которая определяет наши данные, но заметили ли вы аномалию? У нас аномально низкая частота в определенном диапазоне баллов. Таким образом, лучшим предположением будет наличие отсутствующих значений, которые устранят вмятину в распределении.
Вот как вы пытаетесь решить реальную проблему с помощью анализа данных. Распределение является обязательным понятием для любого специалиста по данным, студента или практикующего специалиста. Он обеспечивает основу для аналитики и выводной статистики.
В то время как концепция вероятности или равной вероятности дает нам математические расчеты, распределения помогают нам на самом деле визуализировать то, что происходит внутри.
В этой статье я рассмотрел некоторые важные типы вероятностных распределений, которые объясняются ясным и исчерпывающим образом.
Примечание. В этой статье предполагается, что у вас есть базовые знания о вероятности. Если нет, вы можете обратиться к этому распределению вероятностей или к следующим основам вероятности.
Если нет, вы можете обратиться к этому распределению вероятностей или к следующим основам вероятности.
Вероятность систематического рассмотрения результатов случайного эксперимента . Например, когда мы подбрасываем монету, возможны два исхода — орел или решка. Каждый из этих вариантов имеет одинаковую вероятность количества успехов, происходящих во время каждого броска. Вероятность выпадения орла или решки при одном подбрасывании монеты равна ½, что является симметричным распределением вероятности.
Общие типы данных
Прежде чем мы перейдем к объяснению распределений, давайте посмотрим, с какими данными мы можем столкнуться. Данные могут быть дискретными или непрерывными.
Дискретные данные , как следует из названия, могут принимать только указанные значения. Например, когда вы бросаете кубик, возможные результаты: 1, 2, 3, 4, 5 или 6, а не 1,5 или 2,45. (Дискретное распределение вероятностей)
Непрерывные данные могут принимать любое значение в заданном диапазоне. Диапазон может быть конечным или бесконечным. Например, вес или рост девушки, длина дороги. Вес девушки может быть любым – 54 кг, 54,5 кг или 54,5436 кг. (Непрерывное распределение вероятностей)
Диапазон может быть конечным или бесконечным. Например, вес или рост девушки, длина дороги. Вес девушки может быть любым – 54 кг, 54,5 кг или 54,5436 кг. (Непрерывное распределение вероятностей)
Теперь начнем с типов дистрибутивов.
Типы дистрибутивов
Распределение Бернулли
Начнем с самого простого распределения — распределения Бернулли. На самом деле это легче понять, чем кажется!
Все вы, любители крикета! В начале любого матча по крикету, как вы решаете, кто будет бить или мяч? Бросок! Все зависит от того, выиграете вы или проиграете жеребьевку, верно? Допустим, если в результате броска выпала голова, вы выиграли. Иначе ты проиграешь. Нет середины.
Распределение Бернулли имеет только два испытания Бернулли или возможных исходов, а именно 1 (успех) и 0 (неудача), и одно испытание. Таким образом, случайная величина X с распределением Бернулли может принимать значение 1 с вероятностью успеха, скажем, p, и значение 0 с вероятностью неудачи, скажем, q или 1-p.
Здесь появление головы означает успех, а появление хвоста означает неудачу.
Вероятность выпадения орла = 0,5 = Вероятность выпадения решки, поскольку возможны только два исхода.
Функция массы вероятности определяется как: px(1-p)1-x где x € (0, 1).
Может также записываться как
Вероятность успеха и неудачи не обязательно должна быть равновероятной, как результат боя между Гробовщиком и мной. Он почти наверняка выиграет. Значит, в данном случае вероятность моего успеха равна 0,15, а моей неудачи — 0,85
.Здесь вероятность успеха(p) не совпадает с вероятностью отказа. Итак, на диаграмме ниже показано распределение Бернулли нашего боя.
Здесь вероятность успеха = 0,15, а вероятность отказа = 0,85. Ожидаемое значение именно то, на что это похоже. Если я ударю тебя, я могу ожидать, что ты ударишь меня в ответ. В основном ожидаемое значение любого распределения является средним значением распределения. Ожидаемое значение случайной величины X из распределения Бернулли находится следующим образом:
Е(Х) = 1*р + 0*(1-р) = р
Дисперсия случайной величины из распределения Бернулли:
V(X) = E(X²) – [E(X)]² = p – p² = p(1-p)
Существует множество примеров распределения Бернулли, например, будет ли завтра дождь или нет, где дождь означает успех, а отсутствие дождя означает неудачу, а также выигрыш (успех) или проигрыш (неудача) в игре.
Равномерное распределение
Когда вы бросаете правильный кубик, выпадает от 1 до 6. Вероятности получения этих результатов равновероятны, что является основой равномерного распределения. В отличие от распределения Бернулли, все n возможных исходов равномерного распределения равновероятны.
Говорят, что переменная X распределена равномерно, если функция плотности:
График кривой равномерного распределения выглядит как
Вы можете видеть, что форма кривой Равномерного распределения прямоугольная, поэтому Равномерное распределение называется прямоугольным.
Для равномерного распределения a и b являются параметрами.
Количество букетов, продаваемых ежедневно в цветочном магазине, распределяется равномерно, максимум 40 и минимум 10.
Давайте попробуем рассчитать вероятность того, что ежедневные продажи упадут между 15 и 30.
Вероятность того, что дневные продажи упадут между 15 и 30, равна (30-15)*(1/(40-10)) = 0,5
Аналогично, вероятность того, что ежедневные продажи превышают 20, равна = 0,667
Среднее значение и дисперсия X после равномерного распределения составляют:
Среднее -> E(X) = (a+b)/2
Дисперсия -> V(X) = (b-a)²/12
Стандартная однородная плотность имеет параметры a = 0 и b = 1, поэтому PDF для стандартной однородной плотности определяется как:
Биномиальное распределение
Вернемся к крикету. Предположим, вы выиграли жеребьевку сегодня, что свидетельствует об успешном событии. Вы снова бросаете, но на этот раз проигрываете. Если вы выиграете жеребьевку сегодня, это не обязательно, что вы выиграете жеребьевку завтра. Давайте назначим случайную величину, скажем, X, количеству раз, когда вы выиграли жеребьевку. Каким может быть возможное значение X? Это может быть любое число в зависимости от того, сколько раз вы подбрасывали монету.
Предположим, вы выиграли жеребьевку сегодня, что свидетельствует об успешном событии. Вы снова бросаете, но на этот раз проигрываете. Если вы выиграете жеребьевку сегодня, это не обязательно, что вы выиграете жеребьевку завтра. Давайте назначим случайную величину, скажем, X, количеству раз, когда вы выиграли жеребьевку. Каким может быть возможное значение X? Это может быть любое число в зависимости от того, сколько раз вы подбрасывали монету.
Возможны только два исхода. Голова означает успех, а хвост — неудачу. Следовательно, вероятность получения головы = 0,5, а вероятность отказа легко вычислить как: q = 1-p = 0,5.
Распределение, при котором возможны только два исхода, такие как успех или неудача, выигрыш или проигрыш, выигрыш или проигрыш, и при котором вероятность успеха и неудачи одинакова для всех испытаний, называется биномиальным распределением.
Исходы не обязательно должны быть равновероятными. Помните пример драки между Гробовщиком и мной? Итак, если вероятность успеха в эксперименте равна 0,2, то вероятность неудачи легко вычислить как q = 1 – 0,2 = 0,8.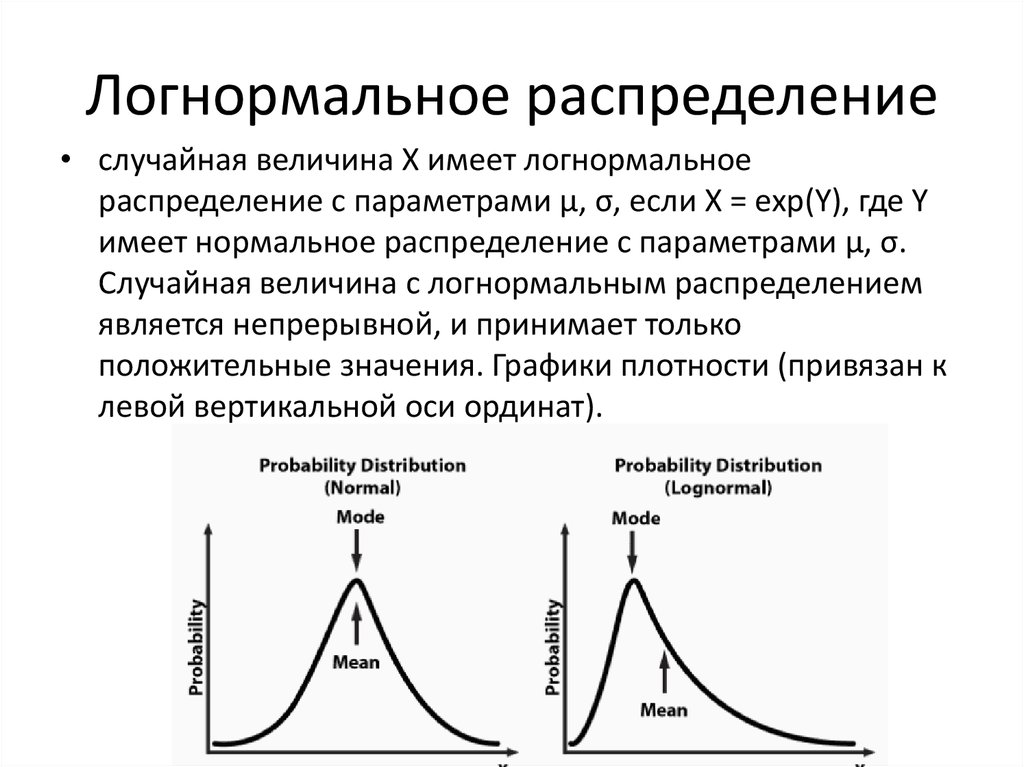
Каждое испытание является независимым, поскольку результат предыдущего броска не определяет и не влияет на результат текущего броска. Опыт с двумя возможными исходами, повторяемый n раз, называется биномиальным. Параметры биномиального распределения — n и p, где n — общее количество испытаний, а p — вероятность успеха в каждом испытании.
На основании приведенного выше объяснения биномиальное распределение имеет следующие свойства:
- Каждое испытание является независимым.
- В испытании возможны только два исхода: успех или провал.
- Всего проведено n идентичных испытаний.
- Вероятность успеха и неудачи одинакова для всех испытаний. (Испытания идентичны.)
Математическое представление биномиального распределения:
Граф биномиального распределения, в котором вероятность успеха не равна вероятности неудачи, выглядит следующим образом.
Теперь, когда вероятность успеха = вероятность неудачи, в такой ситуации график биномиального распределения выглядит как
Среднее значение и дисперсия биномиального распределения определяются по формуле:
Среднее -> µ = n*p
Дисперсия -> Var(X) = n*p*q
Нормальное распределение или распределение Гаусса
Нормальное распределение представляет собой поведение большинства ситуаций во вселенной (Вот почему оно называется «нормальным» распределением. Наверное!). Большая сумма (малых) случайных величин часто оказывается нормально распределенной, что способствует ее широкому применению. Любое распределение известно как нормальное распределение, если оно имеет следующие характеристики:
Наверное!). Большая сумма (малых) случайных величин часто оказывается нормально распределенной, что способствует ее широкому применению. Любое распределение известно как нормальное распределение, если оно имеет следующие характеристики:
- Среднее значение, медиана и мода распределения совпадают.
- Кривая распределения имеет колоколообразную форму и симметрична относительно линии x=µ.
- Общая площадь под кривой равна 1.
- Ровно половина значений находится слева от центра, а другая половина справа.
Нормальное распределение сильно отличается от биномиального распределения. Однако если число испытаний приближается к бесконечности, то формы будут очень похожими.
PDF случайной величины X при нормальном распределении определяется как:
Среднее значение и дисперсия случайной величины X, которая, как говорят, имеет нормальное распределение, определяются по формуле: 92
Здесь µ (среднее значение) и σ (стандартное отклонение) являются параметрами.
График случайной величины X ~ N (µ, σ) показан ниже.
Стандартное нормальное распределение определяется как распределение со средним значением 0 и стандартным отклонением 1. В таком случае PDF принимает вид:
Распределение Пуассона
Предположим, вы работаете в колл-центре; примерно, сколько звонков вы получаете в день? Это может быть любое число. Теперь все количество звонков в колл-центр за день моделируется распределением Пуассона. Еще несколько примеров:
- Количество вызовов скорой помощи, зарегистрированных в больнице за день.
- Количество краж, зарегистрированных в районе за день.
- Количество клиентов, приходящих в салон в час.
- Количество зарегистрированных самоубийств в определенном городе.
- Количество ошибок печати на каждой странице книги.
Теперь вы можете придумать множество примеров, следуя одному и тому же курсу. Распределение Пуассона применимо в ситуациях, когда события происходят в случайные моменты времени и пространства, когда нас интересует только количество появлений события.
Распределение называется распределением Пуассона , если верны следующие предположения:
1. Любое успешное событие не должно влиять на исход другого успешного события.
2. Вероятность успеха на коротком интервале должна равняться его вероятности на более длинном интервале.
3. Вероятность успеха в интервале приближается к нулю, когда интервал становится меньше.
Теперь, если какое-либо распределение подтверждает приведенные выше предположения, то это распределение Пуассона. Некоторые обозначения, используемые в распределении Пуассона:
- λ — скорость, с которой происходит событие,
- t — длина временного интервала,
- А X — количество событий в этом временном интервале.
Здесь X называется случайной величиной Пуассона, а распределение вероятности X называется распределением Пуассона.
Пусть µ обозначает среднее число событий в интервале длины t. Тогда µ = λ*t.
PMF X после распределения Пуассона определяется как:
Среднее значение µ является параметром этого распределения. µ также определяется как λ, умноженное на длину этого интервала. График распределения Пуассона показан ниже:
µ также определяется как λ, умноженное на длину этого интервала. График распределения Пуассона показан ниже:
График, показанный ниже, иллюстрирует сдвиг кривой из-за увеличения среднего значения.
Заметно, что по мере увеличения среднего значения кривая смещается вправо.
Среднее значение и дисперсия X после распределения Пуассона:
Среднее -> E(X) = µ
Дисперсия -> Var(X) = µ
Экспоненциальное распределение
Давайте еще раз рассмотрим пример с колл-центром. А как насчет интервала времени между звонками? Здесь нам на помощь приходит экспоненциальное распределение. Экспоненциальное распределение моделирует интервал времени между вызовами.
Другие примеры:
1. Промежуток времени между прибытиями в метро
2. Промежуток времени между прибытиями на заправку
3. Срок службы кондиционера
Экспоненциальное распределение широко используется для анализа выживаемости. От ожидаемого срока службы машины до ожидаемого срока службы человека экспоненциальное распределение успешно дает результат.
Говорят, что случайная величина X имеет экспоненциальное распределение с PDF:
f(x) = { λe -λx , x ≥ 0
А параметр λ>0, который еще называют скоростью.
Для анализа живучести λ называется интенсивностью отказов устройства в любой момент времени t при условии, что оно выдержало до t.
Среднее значение и дисперсия случайной величины X после экспоненциального распределения:
Среднее -> E(X) = 1/λ
Дисперсия -> Var(X) = (1/λ)²
Кроме того, чем больше скорость, тем быстрее падает кривая, а чем ниже скорость, тем более пологая кривая. Это лучше поясняется графиком, показанным ниже.
Для облегчения вычислений ниже приведены некоторые формулы.
P{X≤x} = 1 – e-λx соответствует площади под кривой плотности слева от x.
P{X>x} = e-λx соответствует площади под кривой плотности справа от x.
P{x1
Функция распределения вероятности
В теории вероятности функция плотности вероятности непрерывной случайной величины — это функция, значение которой в любой заданной выборке (или точке) в наборе данных или пространстве выборки может быть интерпретировано как обеспечивающее относительную вероятность , что значение случайной величины будет равно этой выборке. PDF — это вероятность на единицу длины. Другими словами, в то время как абсолютная вероятность того, что непрерывная случайная величина примет любое конкретное значение, равна 0, значение PDF для двух разных выборок можно использовать для вывода, насколько более вероятно, что случайная величина будет близко к одному образцу по сравнению с другим образцом.
Отношения между дистрибутивами
Связь между Бернулли и биномиальным распределением
- Распределение Бернулли — это частный случай биномиального распределения с одним испытанием.
- Есть только два возможных исхода бернуллиевского и биномиального распределения, а именно успех и неудача.

- И Бернулли, и биномиальное распределение имеют независимые испытания.
Связь между распределением Пуассона и биномиальным распределением
Распределение Пуассона является предельным случаем биномиального распределения при следующих условиях:
- Количество попыток неопределенно велико или n → ∞.
- Вероятность успеха для каждого испытания одинакова и бесконечно мала или p → 0.
- np = λ, конечно.
Связь между нормальным и биномиальным распределением и нормальным распределением и распределением Пуассона
Нормальное распределение — это еще одна предельная форма биномиального распределения при следующих условиях:
- Количество попыток бесконечно велико, n → ∞.
- И p, и q не бесконечно малы.
Нормальное распределение также является предельным случаем распределения Пуассона с параметром λ →∞.
Связь между экспоненциальным распределением и распределением Пуассона
Если время между случайными событиями подчиняется экспоненциальному распределению со скоростью λ, то общее количество событий за период времени длины t подчиняется распределению Пуассона с параметром λt.
Проверьте свои знания
Вы зашли так далеко. Теперь вы можете ответить на следующие вопросы? Позвольте мне знать в комментариях ниже!
1. Формула для расчета стандартной нормальной случайной величины:
а. (x+µ) / σ
б. (x-µ) / σ
c. (х-σ) / мк
2. В распределении Бернулли формула для расчета стандартного отклонения имеет вид:
а. р (1 – р)
б. SQRT(p(p – 1))
c. SQRT(p(1 – p))
3. Для нормального распределения увеличение среднего будет:
а. сдвинуть кривую влево
b. сдвинуть кривую вправо
с. сгладить кривую
4. Срок службы батареи имеет экспоненциальное распределение с λ = 0,05 в час. Вероятность того, что батарея проработает от 10 до 15 часов, составляет:
а.0.1341
б.0.1540
в.0.0079
Заключение
Распределения вероятностей распространены во многих секторах, включая страхование, физику, инженерию, информатику и даже социальные науки, где студенты психологии и медицины широко используют распределения вероятностей. Он имеет простое применение и широкое использование. В этой статье выделено и объяснено применение шести важных распределений, наблюдаемых в повседневной жизни. Теперь вы сможете идентифицировать, соотносить и различать эти распределения.
Он имеет простое применение и широкое использование. В этой статье выделено и объяснено применение шести важных распределений, наблюдаемых в повседневной жизни. Теперь вы сможете идентифицировать, соотносить и различать эти распределения.
Для получения более подробной информации об этих дистрибутивах вы можете обратиться к этому ресурсу.
Ключевые выводы
- Вероятность обычно используется специалистами по обработке и анализу данных для моделирования ситуаций, когда эксперименты, независимые события, проводимые в схожих обстоятельствах, дают разные результаты, например, бросание игральной кости или монеты.
- Дискретные случайные величины и непрерывные случайные величины — это два типа количественных переменных. Дискретные переменные представляют количество, например, количество объектов в коллекции, тогда как непрерывные переменные представляют измеримые количества, например, объем или вес воды.
- Нормальное распределение, распределение хи-квадрат, биномиальное распределение, распределение Пуассона и равномерное распределение — вот некоторые из многих различных классификаций вероятностных распределений.

Часто задаваемые вопросы
Q1. Какое распределение наиболее часто используется в науке о данных?
A. Распределение Гаусса (нормальное распределение) известно своей колоколообразной формой и является одним из наиболее часто используемых распределений в науке о данных или для проверки гипотез.
Q2. Какие 6 распространенных распределений вероятностей должен знать каждый специалист по науке о данных?
A. 6 общих вероятностных распределений: Бернулли, Равномерное, Биномиальное, Нормальное, Пуассона и Экспоненциальное распределение.
Q3. В чем разница между дискретным и непрерывным распределением?
A. Дискретное распределение — это распределение, при котором данные могут принимать только определенные значения, а непрерывное распределение — это распределение, при котором данные могут принимать любое значение в заданном диапазоне.
7 типов статистических распределений с практическими примерами
Статистические распределения помогают нам лучше понять проблему, присваивая диапазон возможных значений переменным, что делает их очень полезными в науке о данных и машинном обучении.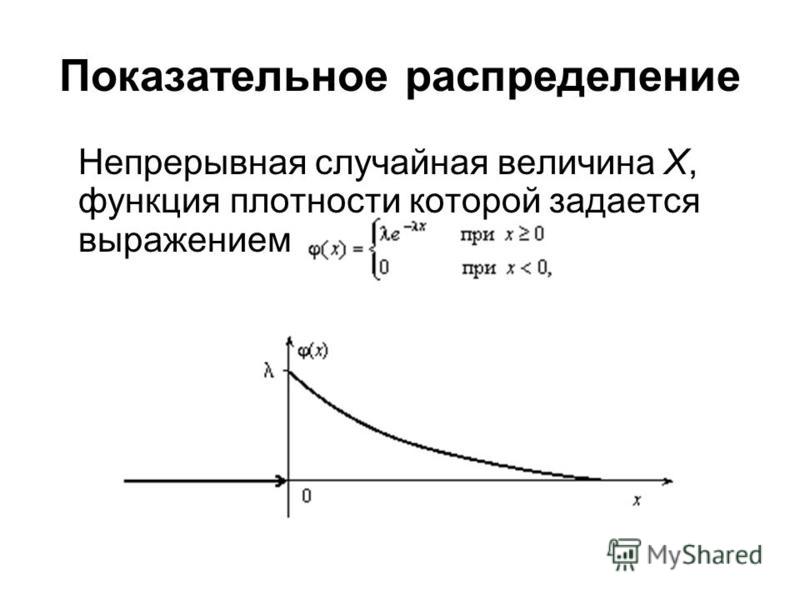 Вот 7 типов распределений с интуитивно понятными примерами, которые часто встречаются в реальных данных.
Вот 7 типов распределений с интуитивно понятными примерами, которые часто встречаются в реальных данных.
Угадываете ли вы, будет ли завтра дождь, делаете ставку на спортивную команду, которая выиграет выездной матч, составляете полис для страховой компании или просто пытаете удачу в блэкджеке в казино, вероятность и распределения вступают в действие во всех аспектах жизни, чтобы определить вероятность событий.
Хороший статистический опыт может оказаться невероятно полезным в повседневной жизни специалиста по данным. Вероятность является одним из основных строительных блоков науки о данных и машинного обучения. В то время как концепция вероятности дает нам математические расчеты, статистические распределения помогают нам визуализировать то, что происходит внутри.
Хорошее владение статистическим распределением значительно упрощает изучение нового набора данных и поиск закономерностей в нем. Это помогает нам выбрать подходящую модель машинного обучения, соответствующую нашим данным, и ускоряет весь процесс в целом.
Это помогает нам выбрать подходящую модель машинного обучения, соответствующую нашим данным, и ускоряет весь процесс в целом.
СОВЕТ ПРОФЕССИОНАЛА: Присоединяйтесь к нашему учебному курсу по науке о данных сегодня, чтобы усовершенствовать свои навыки работы с данными!
В этом блоге мы рассмотрим различные типы данных, общие распределения для каждого из них и убедительные примеры их применения в реальной жизни.
Прежде чем мы продолжим, если вы хотите узнать больше о распределении вероятностей, посмотрите это видео ниже:
Распространенные типы данных
Объяснение различных распределений становится более управляемым, если мы знакомы с типом данных, которые они используют. В повседневных экспериментах мы сталкиваемся с двумя разными исходами: конечным и бесконечным исходом.
В повседневных экспериментах мы сталкиваемся с двумя разными исходами: конечным и бесконечным исходом.
Когда вы бросаете кубик или выбираете карту из колоды, у вас есть ограниченное количество возможных результатов. Этот тип данных называется дискретными данными, которые могут принимать только определенное количество значений. Например, при прокатке штампа указанные значения равны 1, 2, 3, 4, 5 и 6.
Точно так же мы можем видеть примеры бесконечных результатов дискретных событий в нашей повседневной жизни. Время записи или измерение роста человека имеет бесконечно много значений в заданном интервале. Этот тип данных называется непрерывными данными, которые могут иметь любое значение в заданном диапазоне. Этот диапазон может быть конечным или бесконечным.
Предположим, вы измеряете вес арбуза. Это может быть любое значение от 10,2 кг, 10,24 кг или 10,243 кг. Делая его измеримым, но не счетным, следовательно, непрерывным. С другой стороны, предположим, что вы считаете количество мальчиков в классе; поскольку значение является счетным, оно является дискретным.
С другой стороны, предположим, что вы считаете количество мальчиков в классе; поскольку значение является счетным, оно является дискретным.
Типы статистических распределений
В зависимости от типа данных, которые мы используем, мы сгруппировали распределения в две категории: дискретные распределения для дискретных данных (конечные результаты) и непрерывные распределения для непрерывных данных (бесконечные результаты).
Дискретное распределение
Дискретное равномерное распределение: Все исходы равновероятныРавномерное распределение в статистике относится к статистическому распределению, при котором все исходы равновероятны. Рассмотрим бросок шестигранного кубика. У вас есть равная вероятность получить все шесть чисел при следующем броске, т. е. получить ровно одно из 1, 2, 3, 4, 5 или 6, что равно вероятности 1/6, отсюда и пример дискретного равномерного распределения. .
В результате диаграмма равномерного распределения содержит столбцы одинаковой высоты, представляющие каждый результат.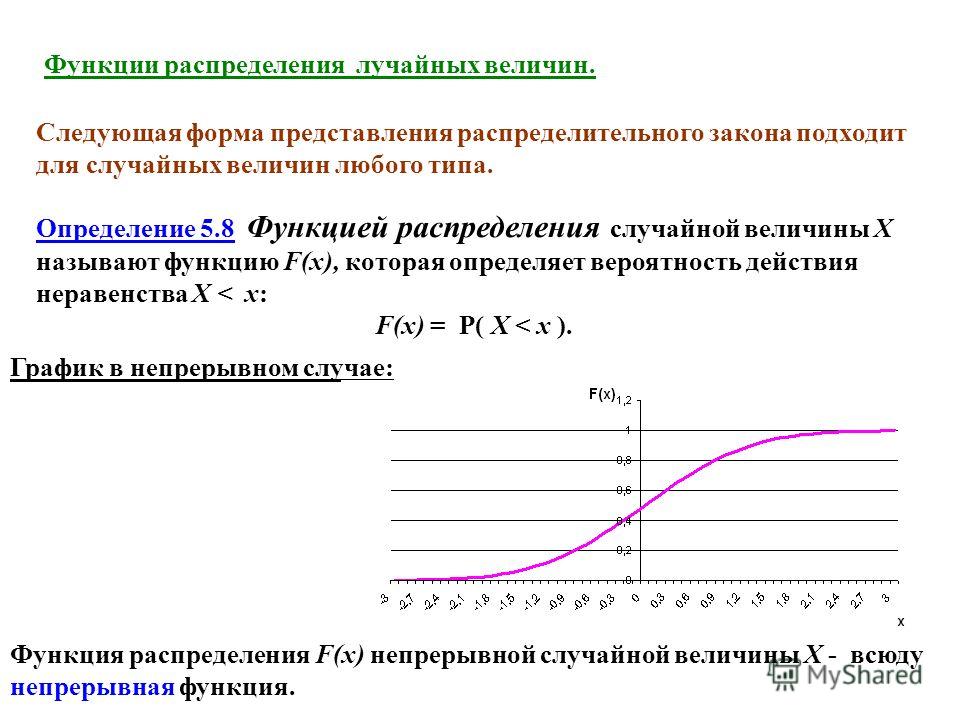 В нашем примере высота — это вероятность 1/6 (0,166667).
В нашем примере высота — это вероятность 1/6 (0,166667).
Равномерное распределение представлено функцией U(a, b), где a и b представляют начальное и конечное значения соответственно. Подобно дискретному равномерному распределению, существует непрерывное равномерное распределение для непрерывных переменных.
Недостаток этого дистрибутива в том, что он часто не предоставляет нам необходимой информации. Используя наш пример с бросающейся игральной костью, мы получаем ожидаемое значение 3,5, что не дает нам точной интуиции, поскольку на игральной кости не бывает половины числа. Поскольку все значения равновероятны, это не дает нам реальной предсказательной силы.
Распределение Бернулли: Одно испытание с двумя возможными исходами Распределение Бернулли — одно из самых простых для понимания распределений. Его можно использовать в качестве отправной точки для получения более сложных распределений.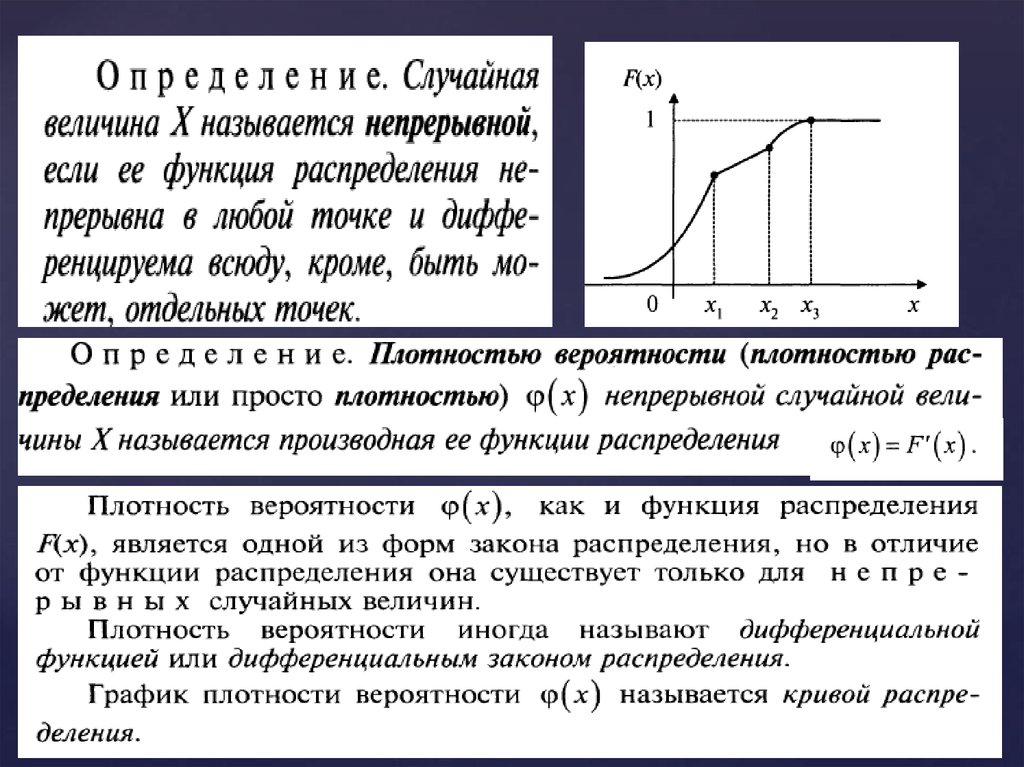 Любое событие с одним испытанием и только двумя исходами подчиняется распределению Бернулли. Подбрасывание монеты или выбор между «Истина» и «Ложь» в викторине — примеры распределения Бернулли.
Любое событие с одним испытанием и только двумя исходами подчиняется распределению Бернулли. Подбрасывание монеты или выбор между «Истина» и «Ложь» в викторине — примеры распределения Бернулли.
У них одно испытание и только два результата. Предположим, вы подбрасываете монету один раз; это одна тропа. Единственных двух исходов — либо орел, либо решка. Это пример распределения Бернулли.
Обычно, следуя распределению Бернулли, мы имеем вероятность одного из исходов (p). Из (p) мы можем вывести вероятность другого исхода, вычитая ее из общей вероятности (1), представленной как (1-p).
Обозначается bern(p), где p — вероятность успеха. Ожидаемое значение испытания Бернулли «x» представлено как E (x) = p, и, аналогично, дисперсия Бернулли равна Var (x) = p (1-p).
Загруженная монета График распределения Бернулли График распределения Бернулли легко читается. Он состоит только из двух столбцов, один из которых увеличивается до соответствующей вероятности p, а другой — до 1-p.
Биномиальное распределение можно рассматривать как сумму результатов события, следующего за распределением Бернулли. Поэтому биномиальное распределение используется в событиях с бинарным исходом, и вероятность успеха и неудачи одинакова во всех последовательных испытаниях. Примером биномиального события может быть многократное подбрасывание монеты для подсчета количества орлов и решек.
Биномиальное распределение и распределение Бернулли.
Разницу между этими дистрибутивами можно объяснить на примере. Представьте, что вы пытаетесь пройти викторину, содержащую 10 вопросов «Верно/Неверно». Попытка ответить на один вопрос T/F будет считаться испытанием Бернулли, в то время как попытка пройти всю викторину из 10 вопросов T/F будет классифицирована как биномиальное испытание. Основные характеристики биномиального распределения:
- При множественных испытаниях каждое из них не зависит от другого.
 То есть результат одного испытания не влияет на другое.
То есть результат одного испытания не влияет на другое. - Каждое испытание может привести только к двум возможным результатам (например, выигрыш или проигрыш) с вероятностями p и (1 – p).
Биномиальное распределение представлено B (n, p), где n — количество испытаний, а p — вероятность успеха в одном испытании. Распределение Бернулли можно представить в виде биномиального испытания как B (1, p), поскольку оно имеет только одно испытание. Ожидаемое значение биномиального испытания «x» — это количество успешных попыток, представленное как E(x) = np. Точно так же дисперсия представлена как Var (x) = np (1-p).
Рассмотрим вероятность успеха (p) и количество попыток (n). Затем мы можем рассчитать вероятность успеха (x) для этих n испытаний, используя следующую формулу:
Например, предположим, что кондитерская компания производит шоколадные батончики как из молочного, так и из темного шоколада. Всего продукты содержат половину плиток молочного шоколада и половину плиток темного шоколада.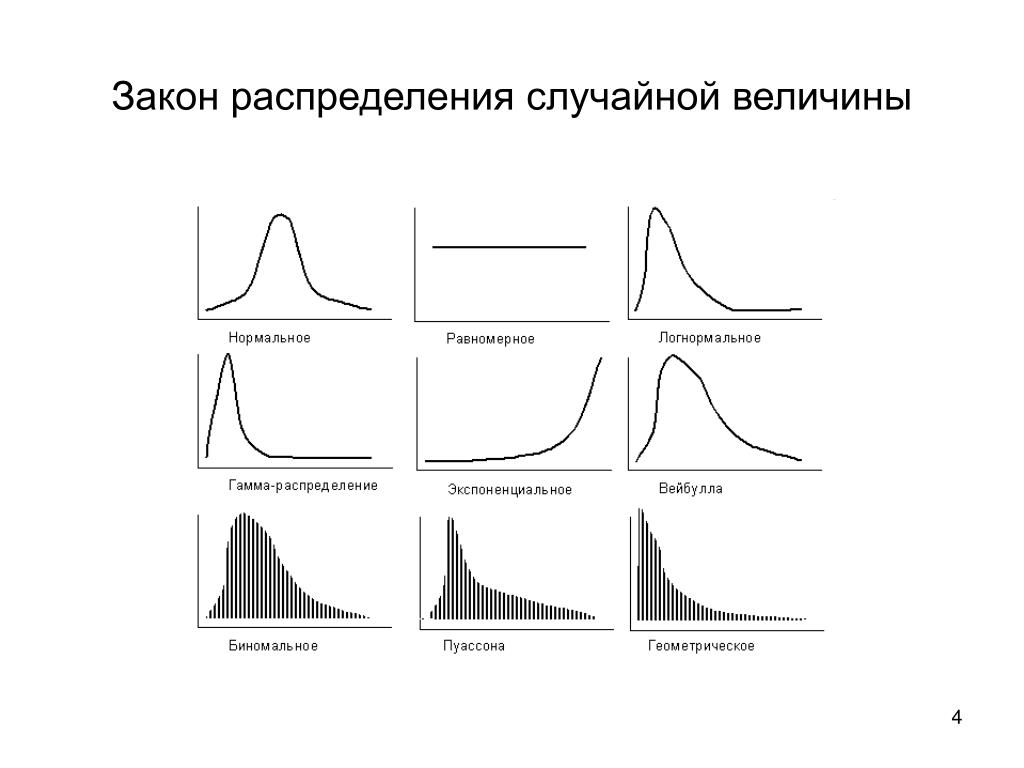 Скажем, вы выбираете десять шоколадных батончиков наугад, и выбор молочного шоколада определяется как успех. Распределение вероятностей количества успехов в этих десяти испытаниях с p = 0,5 показано здесь на графике биномиального распределения:
Скажем, вы выбираете десять шоколадных батончиков наугад, и выбор молочного шоколада определяется как успех. Распределение вероятностей количества успехов в этих десяти испытаниях с p = 0,5 показано здесь на графике биномиального распределения:
Распределение Пуассона относится к частоте, с которой событие происходит в течение определенного интервала. Вместо вероятности события распределение Пуассона требует знания того, как часто оно происходит в определенный период или на определенном расстоянии. Например, сверчок чирикает в среднем два раза за 7 секунд. Мы можем использовать распределение Пуассона, чтобы определить вероятность того, что он чирикнет пять раз за 15 секунд.
Процесс Пуассона представлен обозначением Po(λ), где λ представляет собой ожидаемое количество событий, которые могут произойти за период. Ожидаемое значение и дисперсия процесса Пуассона равны λ.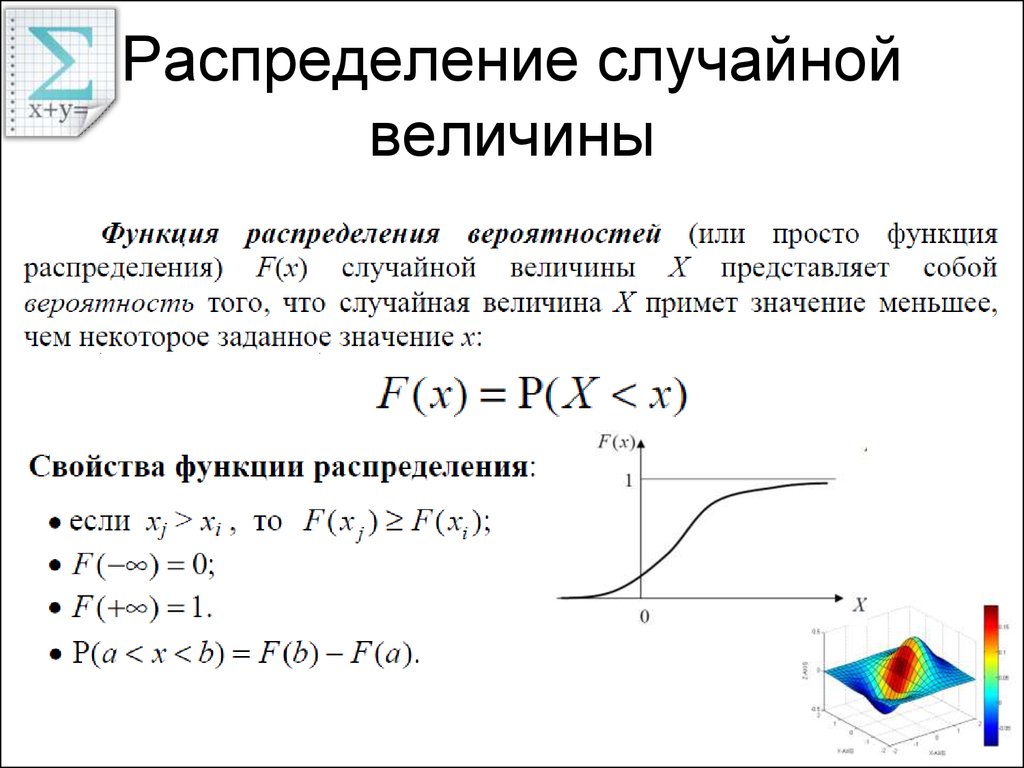 X представляет собой дискретную случайную величину. Распределение Пуассона можно смоделировать, используя следующую формулу.
X представляет собой дискретную случайную величину. Распределение Пуассона можно смоделировать, используя следующую формулу.
Основные характеристики, описывающие процессы Пуассона:
- События независимы друг от друга.
- Событие может произойти любое количество раз (в течение определенного периода).
- Два события не могут происходить одновременно.
График распределения Пуассона показывает количество случаев, когда событие происходит за стандартный интервал времени, и вероятность каждого из них.
Непрерывное распределение
Нормальное распределение: Симметричное распределение значений вокруг среднего Нормальное распределение является наиболее часто используемым распределением в науке о данных. В графе нормального распределения данные распределены симметрично без перекоса. На графике данные имеют форму колокола, при этом большинство значений группируются вокруг центральной области и сужаются по мере удаления от центра.
Нормальное распределение часто проявляется в природе и жизни в различных формах. Например, результаты викторины подчиняются нормальному распределению. Многие студенты набрали от 60 до 80 баллов, как показано на графике ниже. Конечно, учащиеся с баллами, выпадающими из этого диапазона, отклоняются от центра.
График колоколообразной кривой нормального распределенияЗдесь вы можете наблюдать «колоколообразную» кривую вокруг центральной области, указывающую на то, что там находится большинство точек данных. Нормальное распределение представлено здесь как N(µ, σ2), µ представляет собой среднее значение, а σ2 представляет собой дисперсию, одна из которых в основном предоставляется. Ожидаемое значение нормального распределения равно его среднему значению. Некоторые из характеристик, которые могут помочь нам распознать нормальное распределение:
- Кривая симметрична в центре. Следовательно, среднее значение, мода и медиана равны одному и тому же значению, при этом все значения распределяются симметрично вокруг среднего значения.

- Площадь под кривой распределения равна 1 (сумма всех вероятностей должна равняться 1).
68-95-99.7 Правило
При построении графика нормального распределения 68% всех значений лежат в пределах одного стандартного отклонения от среднего. В приведенном выше примере, если среднее значение равно 70, а стандартное отклонение равно 10, 68% значений будут находиться в диапазоне от 60 до 80. Аналогично, 95% значений лежат в пределах двух стандартных отклонений от среднего, а 99,7% лежат в пределах трех стандартных отклонений от среднего. Этот последний интервал охватывает почти все вопросы. Если точка данных не включена, это, скорее всего, выброс.
Плотность вероятности и правило 68-95-99.7 Распределение критерия Стьюдента: нормальное распределение с колоколообразной формой, но с более тяжелыми хвостами. Распределение t используется вместо нормального распределения при небольшом размере выборки. Кривая распределения t-критерия Стьюдента Например, предположим, что мы имеем дело с общим количеством яблок, проданных владельцем магазина за месяц. В этом случае мы будем использовать нормальное распределение. Тогда как, если мы имеем дело с общим количеством яблок, проданных за день, то есть с меньшей выборкой, мы можем использовать t-распределение.
В этом случае мы будем использовать нормальное распределение. Тогда как, если мы имеем дело с общим количеством яблок, проданных за день, то есть с меньшей выборкой, мы можем использовать t-распределение.
Прочтите этот блог, чтобы узнать о 7 лучших статистических методах для лучшего анализа данных. для раздачи. В статистике количество степеней свободы — это количество значений в окончательном расчете статистики, которые могут свободно изменяться. Распределение Стьюдента t представлено как t(k), где k представляет количество степеней свободы. Для k=2, т. е. 2 степеней свободы, ожидаемое значение совпадает со средним.
Таблица Т-распределенияСтепени свободы указаны в левой колонке таблицы Т-распределения.
В целом, t-распределение Стьюдента часто используется при проведении статистического анализа и играет важную роль при проверке гипотез на ограниченных данных.
Экспоненциальное распределение: Модель времени, прошедшего между двумя событиями Экспоненциальное распределение является одним из широко используемых непрерывных распределений.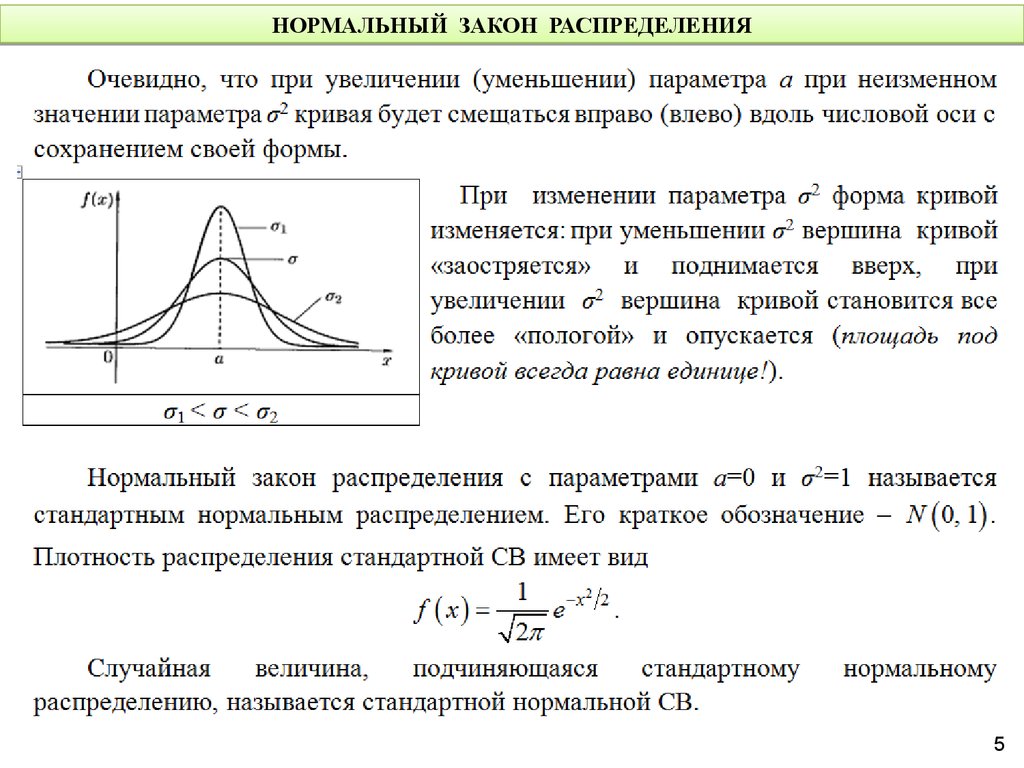 Он используется для моделирования времени, прошедшего между различными событиями. Например, в физике его часто используют для измерения радиоактивного распада; в машиностроении для измерения времени, связанного с получением бракованной детали на конвейере; и в финансах, чтобы измерить вероятность следующего дефолта для портфеля финансовых активов. Еще одно распространенное применение экспоненциального распределения в анализе выживания (например, ожидаемый срок службы устройства/машины).
Он используется для моделирования времени, прошедшего между различными событиями. Например, в физике его часто используют для измерения радиоактивного распада; в машиностроении для измерения времени, связанного с получением бракованной детали на конвейере; и в финансах, чтобы измерить вероятность следующего дефолта для портфеля финансовых активов. Еще одно распространенное применение экспоненциального распределения в анализе выживания (например, ожидаемый срок службы устройства/машины).
Прочитайте 10 лучших книг по статистике, чтобы узнать о статистике
Экспоненциальное распределение обычно представляется как Exp(λ), где λ — параметр распределения, часто называемый параметром скорости. Мы можем найти значение λ по формуле = 1/µ, где µ — среднее значение. Здесь стандартное отклонение совпадает со средним значением. Var (x) дает дисперсию = 1/λ2
Кривая экспоненциального распределения Экспоненциальный график представляет собой изогнутую линию, показывающую экспоненциальное изменение вероятности.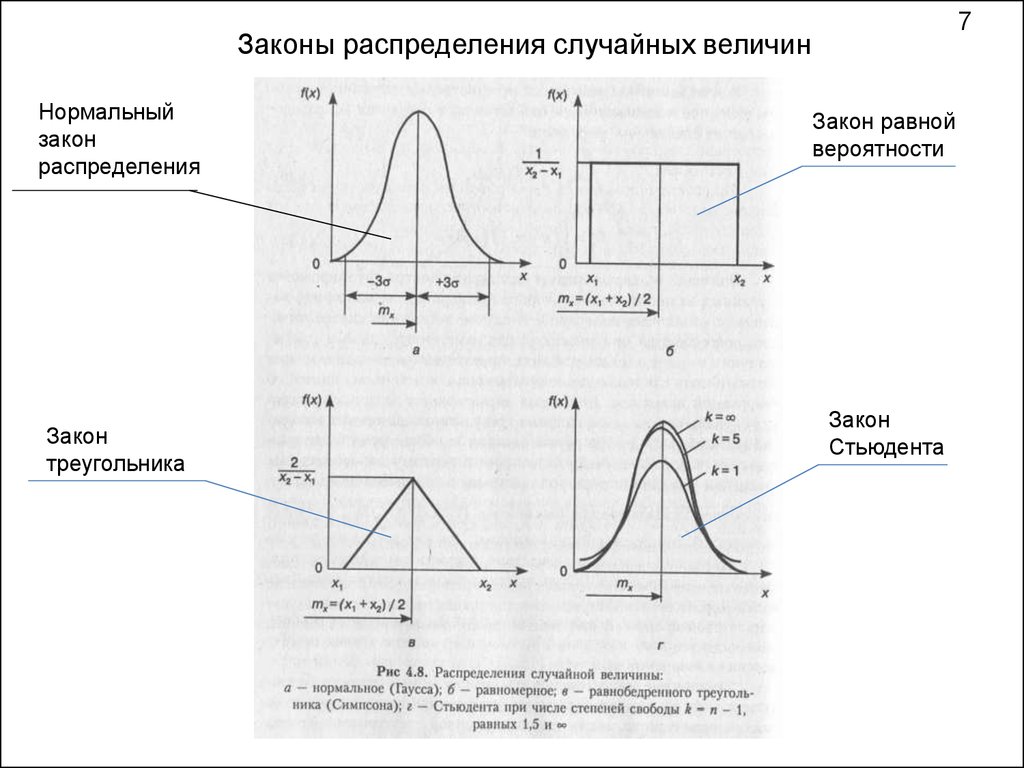

 РАСП()
,
БИНОМ
.ОБР()
РАСП()
,
БИНОМ
.ОБР() ОБР()
и др.
ОБР()
и др.

 То есть результат одного испытания не влияет на другое.
То есть результат одного испытания не влияет на другое.