Как находить дифференциал функции: определения, формулы и примеры решений

Дифференциал функции: основные понятия и определения

Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Главная Справочник Производные Дифференциал функции: основные понятия и определения

Пусть функция в точке имеет отличную от нуля производную

   

Тогда в некоторой окрестности этой точки отношение

   

где при Тому приращение функции можно представить в виде:

   

При этом величина является бесконечно малой более высокого порядка, чем и бесконечно малая поэтому величину называют главной частью приращения функции .

Замечание. Дифференциал называют также дифференциалом первого порядка.

Найдем дифференциал независимой переменной то есть дифференциал функции Так как получаем, что

   

то

   

То есть дифференциал независимой переменной равен ее приращению:

   

Тогда формула для дифференциала перепишется в виде:

   

Таким образом, дифференциал функции равен произведению производной указанной функции на дифференциал независимой переменной.

Геометрический и механический смыслы дифференциала функции

Геометрически дифференциал функции в точке равен приращению ординаты касательной к графику функции в рассматриваемой точке, когда переменная получает приращение .

Механический смысл дифференциала. Пусть материальная точка двигается по закону Дифференциал функции равен:

   

Для фиксированных значений и – это тот путь, который бы прошла материальная точка за время в случае, если она будет двигаться равномерно и прямолинейно с постоянною скоростью

Стоит отметить, что фактический путь в случае неравномерного движения материальной точки, в отличии от дифференциала не является линейной функцией времени а поэтому отличается от пути Но все же, если время является достаточно малым, то скорость движения существенно не изменяется и поэтому движение точки на промежутке времени от до есть практически равномерным.

Основные формулы дифференциала

Основные формулы, которые связаны с дифференциалами, можно получить, используя связь между дифференциалом функции и ее производной, то есть тот факт, что а также соответствующие формулы для производных.

Рассмотрим две дифференцируемые функции и Тогда имеют место следующие равенства:

Понравился сайт? Расскажи друзьям!

Дифференциалы первого порядка.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Определение. Функция $y=f(x)$ называется дифференцируемой в точке $x_0,$ если ее приращение $\Delta y(x_0, \Delta x)$ может быть представлено в виде $$\Delta y(x_0, \Delta x)=A\Delta x+o(\Delta x).$$

 

Главная линейная часть $A\Delta x$ приращения $\Delta y$ называется дифференциалом этой функции в точке $x_0,$ соответствующим приращению $\Delta x,$ и обозначается символом $dy(x_0, \Delta x). 2}.$

Ответ: $\frac{x+y}{x-y}dx.$

 

 

 

4.1 Основы дифференциальных уравнений. Расчет, том 2

Цели обучения

• 4.1.1 Определите порядок дифференциального уравнения.
• 4.1.2 Объясните, что понимается под решением дифференциального уравнения.
• 4.1.3 Различают общее решение и частное решение дифференциального уравнения.
• 4.1.4 Определите проблему начального значения.
• 4.1.5 Определите, является ли данная функция решением дифференциального уравнения или задачи с начальным значением.

Исчисление — это математика изменений, а скорости изменений выражаются производными. Таким образом, один из наиболее распространенных способов использования исчисления состоит в том, чтобы составить уравнение, содержащее неизвестную функцию y=f(x)y=f(x) и ее производную, известную как дифференциальное уравнение . Решение таких уравнений часто дает информацию о том, как изменяются величины, и часто дает представление о том, как и почему происходят изменения.

Методы решения дифференциальных уравнений могут принимать различные формы, включая прямое решение, использование графиков или компьютерные вычисления. Мы вводим основные идеи в этой главе и опишем их более подробно позже в ходе курса. В этом разделе мы изучаем, что такое дифференциальные уравнения, как проверять их решения, некоторые методы, которые используются для их решения, и некоторые примеры распространенных и полезных уравнений.

Общие дифференциальные уравнения

Рассмотрим уравнение y′=3×2,y′=3×2, которое является примером дифференциального уравнения, поскольку оно включает производную. Существует связь между переменными xx и y:yy:y — неизвестная функция x.x. Кроме того, левая часть уравнения является производной от y.y. Поэтому мы можем интерпретировать это уравнение следующим образом: начнем с некоторой функции y=f(x)y=f(x) и возьмем ее производную. Ответ должен быть равен 3×2,3×2. Какая функция имеет производную, равную 3×2?3×2? Одной из таких функций является y=x3,y=x3, поэтому эта функция считается решением дифференциального уравнения.

Определение

Дифференциальное уравнение — это уравнение, содержащее неизвестную функцию y=f(x)y=f(x) и одну или несколько ее производных. Решением дифференциального уравнения является функция y=f(x)y=f(x), которая удовлетворяет дифференциальному уравнению, когда ff и его производные подставляются в уравнение.

СМИ

Посетите этот веб-сайт, чтобы узнать больше по этой теме.

Некоторые примеры дифференциальных уравнений и их решений представлены в таблице 4.1.

Уравнение	Решение
у’=2ху’=2х	у=х2у=х2
у’+3у=6х+11у’+3у=6х+11	у=е-3х+2х+3у=е-3х+2х+3
y′′−3y′+2y=24e−2xy′′−3y′+2y=24e−2x	y=3ex-4e2x+2e-2xy=3ex-4e2x+2e-2x

Стол 4. 1 Примеры дифференциальных уравнений и их решения

Обратите внимание, что решение дифференциального уравнения не обязательно уникально, прежде всего потому, что производная константы равна нулю. Например, y=x2+4y=x2+4 также является решением первого дифференциального уравнения в таблице 4.1. Мы вернемся к этой идее немного позже в этом разделе. А пока давайте сосредоточимся на том, что означает, что функция является решением дифференциального уравнения.

Пример 4.1

Проверка решений дифференциальных уравнений

Проверка того, что функция y=e−3x+2x+3y=e−3x+2x+3 является решением дифференциального уравнения y′+3y=6x+11.y′+3y =6х+11.

Решение

Чтобы проверить решение, мы сначала вычисляем y′y′, используя цепное правило для производных. Это дает y′=−3e−3x+2.y′=−3e−3x+2. Затем подставляем yy и y′y′ в левую часть дифференциального уравнения:

(−3e−3x+2)+3(e−3x+2x+3). (−3e−3x+2) +3(е-3х+2х+3).

Полученное выражение можно упростить, сначала распределив его, чтобы исключить скобки, что даст

−3e−3x+2+3e−3x+6x+9,−3e−3x+2+3e−3x+6x+9.

Объединение одинаковых членов приводит к выражению 6x+11,6x+11, равному правой части дифференциального уравнения. Этот результат подтверждает, что y=e−3x+2x+3y=e−3x+2x+3 является решением дифференциального уравнения.

Контрольно-пропускной пункт 4.1

Убедитесь, что y=2e3x−2x−2y=2e3x−2x−2 является решением дифференциального уравнения y′−3y=6x+4.y′−3y=6x+4.

Удобно определять характеристики дифференциальных уравнений, чтобы было легче говорить о них и классифицировать их. Наиболее основной характеристикой дифференциального уравнения является его порядок.

Определение

Порядок дифференциального уравнения — это наивысший порядок любой производной неизвестной функции, входящей в уравнение.

Пример 4.2

Определение порядка дифференциального уравнения

Каков порядок каждого из следующих дифференциальных уравнений?

1. у’-4у=х2-3х+4у’-4у=х2-3х+4
2. x2y‴−3xy″+xy′−3y=sinxx2y‴−3xy″+xy′−3y=sinx
3. 4xy(4)−6x2y″+12x4y=x3−3×2+4x−124xy(4)−6x2y″+12x4y=x3−3×2+4x−12

Решение

1. Наибольшая производная в уравнении равна y′,y′, поэтому порядок равен 1,1.
2. Наибольшая производная в уравнении равна y‴,y‴, поэтому порядок равен 3,3.
3. Наибольшая производная в уравнении равна y(4),y(4), поэтому порядок равен 4,4.

Контрольно-пропускной пункт 4.2

Каков порядок следующего дифференциального уравнения?

(x4−3x)y(5)−(3×2+1)y′+3y=sinxcosx(x4−3x)y(5)−(3×2+1)y′+3y=sinxcosx

Общие и частные решения

Мы уже отмечали, что дифференциальное уравнение y′=2xy′=2x имеет по крайней мере два решения: y=x2y=x2 и y=x2+4.y=x2+4. Единственная разница между этими двумя решениями заключается в последнем члене, который является константой. Что, если последний член является другой константой? Будет ли это выражение по-прежнему решением дифференциального уравнения? На самом деле любая функция вида y=x2+C,y=x2+C, где CC представляет любую константу, также является решением. Причина в том, что производная x2+Cx2+C равна 2x,2x, независимо от значения C.C. Можно показать, что любое решение этого дифференциального уравнения должно иметь вид y=x2+C.

y=x2+C. Это пример общего решения дифференциального уравнения. График некоторых из этих решений приведен на рис. 4.2. ( Примечание : на этом графике мы использовали четные целые значения для CC в диапазоне от -4−4 до 4,4. На самом деле ограничений на значение C;C нет; это может быть целое число или нет.)

Рисунок 4.2 Семейство решений дифференциального уравнения y′=2x.y′=2x.

В этом примере мы можем выбрать любое желаемое решение; например, y=x2−3y=x2−3 является членом семейства решений этого дифференциального уравнения. Это называется частным решением дифференциального уравнения. Конкретное решение часто может быть однозначно идентифицировано, если нам предоставляется дополнительная информация о проблеме.

Пример 4.3

Поиск частного решения

Найдите частное решение дифференциального уравнения y′=2xy′=2x, проходящего через точку (2,7).(2,7).

Решение

Любая функция вида y=x2+Cy=x2+C является решением этого дифференциального уравнения. Чтобы определить значение C,C, мы подставляем значения x=2x=2 и y=7y=7 в это уравнение и решим для C:C:

y=x2+C7=22+C=4+CC= 3.y=x2+C7=22+C=4+CC=3.

Следовательно, частное решение, проходящее через точку (2,7)(2,7), равно y=x2+3.y=x2+3.

Контрольно-пропускной пункт 4.3

Найдите частное решение дифференциального уравнения

y′=4x+3y′=4x+3

, проходящее через точку (1,7),(1,7), при условии, что y=2×2+3x+Cy =2×2+3x+C является общим решением дифференциального уравнения.

Проблемы с начальным значением

Обычно данное дифференциальное уравнение имеет бесконечное число решений, поэтому естественно спросить, какое из них мы хотим использовать. Чтобы выбрать одно решение, необходимо больше информации. Некоторая конкретная информация, которая может быть полезна, — это начальное значение, представляющее собой упорядоченную пару, которая используется для поиска определенного решения.

Дифференциальное уравнение вместе с одним или несколькими начальными значениями называется начальной задачей. Общее правило состоит в том, что количество начальных значений, необходимых для начальной задачи, равно порядку дифференциального уравнения. Например, если у нас есть дифференциальное уравнение y′=2x,y′=2x, то y(3)=7y(3)=7 является начальным значением, и вместе эти уравнения образуют начальную задачу. Дифференциальное уравнение y″−3y′+2y=4exy″−3y′+2y=4ex имеет второй порядок, поэтому нам нужны два начальных значения. В задачах с начальным значением порядка больше единицы для независимой переменной следует использовать одно и то же значение. Примером начальных значений для этого уравнения второго порядка могут быть y(0)=2y(0)=2 и y′(0)=−1.y′(0)=−1. Эти два начальных значения вместе с дифференциальным уравнением образуют начальную задачу. Эти проблемы названы так потому, что часто независимой переменной в неизвестной функции является t, t, которая представляет время. Таким образом, значение t=0t=0 представляет собой начало проблемы.

Пример 4.4

Проверка решения задачи с начальными значениями

Проверка того, что функция y=2e−2t+ety=2e−2t+et является решением задачи с начальными значениями

y′+2y=3et,y( 0)=3. y′+2y=3et,y(0)=3.

Решение

Чтобы функция удовлетворяла начальной задаче, она должна удовлетворять как дифференциальному уравнению, так и начальному условию. Чтобы показать, что yy удовлетворяет дифференциальному уравнению, мы начнем с вычисления y′.y′. Это дает y′=−4e−2t+et.y′=−4e−2t+et. Затем мы подставляем как yy, так и y′y′ в левую часть дифференциального уравнения и упрощаем:

y′+2y=(−4e−2t+et)+2(2e−2t+et)=−4e−2t+et+4e−2t+2et=3et.y′+2y=(−4e−2t +et)+2(2e-2t+et)=-4e-2t+et+4e-2t+2et=3et.

Это равно правой части дифференциального уравнения, поэтому y=2e−2t+ety=2e−2t+et решает дифференциальное уравнение. Далее вычисляем y(0):y(0):

y(0)=2e−2(0)+e0=2+1=3.y(0)=2e−2(0)+e0=2 +1=3.

Этот результат подтверждает исходное значение. Следовательно, данная функция удовлетворяет начальной задаче.

Контрольно-пропускной пункт 4.4

Проверить, что y=3e2t+4sinty=3e2t+4sint является решением задачи о начальных значениях

y′−2y=4cost−8sint,y(0)=3. y′−2y=4cost−8sint,y (0)=3.

В примере 4.4 начальная задача состояла из двух частей. Первая часть представляла собой дифференциальное уравнение y′+2y=3ex,y′+2y=3ex, а вторая часть представляла собой начальное значение y(0)=3.y(0)=3. Эти два уравнения вместе образуют начальную задачу.

В целом то же самое. Начальная задача будет состоять из двух частей: дифференциального уравнения и начального условия. Дифференциальное уравнение имеет семейство решений, а начальное условие определяет значение C.C. Семейство решений дифференциального уравнения в примере 4.4 задается формулой y=2e−2t+Cet.y=2e−2t+Cet. Это семейство решений показано на рис. 4.3, где конкретное решение y=2e−2t+ety=2e−2t+et помечено.

0 функция меняет направление и плавно возрастает по мере того, как t стремится к бесконечности. Большие значения C имеют более узкую кривую ближе к оси y и при более высоком значении y. Для C = 0 функция стремится к 0, когда t стремится к бесконечности. Для С

Рисунок 4. 3 Семейство решений дифференциального уравнения y′+2y=3et.y′+2y=3et. Частное решение y=2e−2t+ety=2e−2t+et помечено.

Пример 4,5

Решение задачи с начальными значениями

Решите следующую задачу с начальными значениями:

y′=3ex+x2−4,y(0)=5.y′=3ex+x2−4,y(0)=5.

Решение

Первым шагом в решении этой задачи с начальными значениями является поиск общего семейства решений. Для этого найдем первообразную обеих частей дифференциального уравнения

∫y′dx=∫(3ex+x2−4)dx,∫y′dx=∫(3ex+x2−4)dx,

а именно ,

y+C1=3ex+13×3−4x+C2.y+C1=3ex+13×3−4x+C2.

(4.1)

Мы можем интегрировать обе стороны, потому что член и появляется сам по себе. Обратите внимание на две константы интегрирования: C1C1 и C2.C2. Решение уравнения 4.1 для yy дает

y=3ex+13×3-4x+C2-C1.y=3ex+13×3-4x+C2-C1.

Поскольку C1C1 и C2C2 являются константами, C2-C1C2-C1 также является константой. Таким образом, мы можем определить C=C2−C1,C=C2−C1, что приводит к уравнению

y=3ex+13×3−4x+C.y=3ex+13×3−4x+C.

Далее мы определяем значение C.C. Для этого подставим x=0x=0 и y=5y=5 в уравнение 4.1 и решим для C:C:

5=3e0+1303−4(0)+C5=3+CC=2,5=3e0+ 1303−4(0)+C5=3+CC=2.

Теперь подставим значение C=2C=2 в уравнение 4.1. Решение начальной задачи: y=3ex+13×3−4x+2.y=3ex+13×3−4x+2.

Анализ

Разница между общим решением и частным решением заключается в том, что общее решение включает набор функций независимой переменной, определенных явно или неявно. Начальное значение или значения определяют, какое конкретное решение в семействе решений удовлетворяет желаемым условиям.

Контрольно-пропускной пункт 4,5

Решить начальную задачу

y′=x2−4x+3−6ex,y(0)=8.y′=x2−4x+3−6ex,y(0)=8.

В физике и инженерных приложениях мы часто рассматриваем силы, действующие на объект, и используем эту информацию для понимания результирующего движения, которое может произойти. Например, если мы начнем с объекта на поверхности Земли, основной силой, действующей на этот объект, будет гравитация. Физики и инженеры могут использовать эту информацию вместе со вторым законом движения Ньютона (в форме уравнения F=ma, F=ma, где FF представляет силу, mm представляет массу, а aa представляет собой ускорение), чтобы вывести уравнение, которое можно решить. .

Рисунок 4.4 Для бейсбольного мяча, падающего в воздухе, на него действует только сила тяжести (без учета сопротивления воздуха).

На рис. 4.4 мы предполагаем, что единственная сила, действующая на бейсбольный мяч, — это сила тяжести. Это предположение игнорирует сопротивление воздуха. (Сила, вызванная сопротивлением воздуха, будет рассмотрена позже.) Ускорение силы тяжести на поверхности Земли, g, g, составляет приблизительно 9,8 м/с2,9,8 м/с2. Введем систему отсчета, где поверхность Земли находится на высоте 0 метров. Пусть v(t)v(t) представляет собой скорость объекта в метрах в секунду. Если v(t)>0,v(t)>0, мяч поднимается, а если v(t)<0,v(t)<0, мяч падает (рис. 4.5).

0, а стрелка, указывающая вниз, помечена как v(t)

Рисунок 4,5 Возможные скорости подъема/падения бейсбольного мяча.

Наша цель — определить скорость v(t)v(t) в любой момент времени t.t. Для этого поставим задачу с начальным значением. Предположим, что масса мяча равна m,m, где mm измеряется в килограммах. Мы используем второй закон Ньютона, который гласит, что сила, действующая на объект, равна его массе, умноженной на его ускорение (F=ma).(F=ma). Ускорение является производной скорости, поэтому a(t)=v′(t).a(t)=v′(t). Следовательно, сила, действующая на бейсбольный мяч, определяется выражением F=mv′(t).F=mv′(t). Однако эта сила должна быть равна силе тяжести, действующей на объект, которая (опять же с использованием второго закона Ньютона) определяется формулой Fg=-mg, Fg=-mg, поскольку эта сила действует в направлении вниз. Поэтому мы получаем уравнение F=Fg,F=Fg, которое становится mv′(t)=−mg. mv′(t)=−mg. Разделив обе части уравнения на мм, мы получим уравнение 9.0019

v'(t)=-g.v'(t)=-g.

Обратите внимание, что это дифференциальное уравнение остается неизменным независимо от массы объекта.

Теперь нам нужно начальное значение. Поскольку мы ищем скорость, в контексте задачи имеет смысл предположить, что мы знаем начальную скорость или скорость в момент времени t=0.t=0. Это обозначается как v(0)=v0.v(0)=v0.

Пример 4.6

Скорость движущегося бейсбольного мяча

Бейсбольный мяч брошен вверх с высоты 33 метра над поверхностью Земли с начальной скоростью 10 м/с, 10 м/с, и единственная сила, действующая на него, — сила тяжести. Мяч имеет массу 0,15 кг 0,15 кг на поверхности Земли.

1. Найдите скорость v(t)v(t) бейсбольного мяча в момент времени t.t.
2. Какова его скорость через 22 секунды?

Решение

1. Исходя из предыдущего обсуждения, дифференциальное уравнение, которое применяется в этой ситуации, имеет вид с2. Начальное условие: v(0)=v0,v(0)=v0, где v0=10м/с, v0=10м/с. Следовательно, начальная задача имеет вид v′(t)=−9,8 м/с2, v(0)=10 м/с. v′(t)=−9,8 м/с2, v(0)=10 м/с.
   Первым шагом в решении этой задачи с начальными значениями является получение первообразной обеих частей дифференциального уравнения. Это дает

   ∫v′(t)dt=∫−9,8dtv(t)=−9,8t+C.∫v′(t)dt=∫−9,8dtv(t)=−9,8t+C.

   
   Следующим шагом является решение для C.C. Для этого подставьте t=0t=0 и v(0)=10:v(0)=10:

   v(t)=-9,8t+Cv(0)=-9,8(0)+C10=C.v( t)=-9,8t+Cv(0)=-9,8(0)+C10=C.

   
   Следовательно, C=10C=10, а функция скорости определяется выражением v(t)=−9,8t+10,v(t)=−9,8t+10.
2. Чтобы найти скорость через 22 секунды, подставьте t=2t=2 в v(t).v(t).

   v(t)=-9,8t+10v(2)=-9,8(2)+10v(2)=-9,6.v(t)=-9,8t+10v(2)=-9,8(2)+10v (2)=-9,6.

   
   Единицы скорости — метры в секунду. Поскольку ответ отрицательный, объект падает со скоростью 9,6 м/с. 9,6 м/с.

Контрольно-пропускной пункт 4.6

Предположим, что камень падает из состояния покоя с высоты 100100 метров, и единственная сила, действующая на него, — сила тяжести. Найдите уравнение для скорости v(t)v(t) как функции времени, измеряемой в метрах в секунду.

Естественный вопрос, который возникает после решения задачи такого типа, заключается в том, на какой высоте объект будет находиться над поверхностью Земли в данный момент времени. Пусть s(t)s(t) обозначает высоту объекта над поверхностью Земли, измеряемую в метрах. Поскольку скорость является производной положения (в данном случае высоты), это предположение дает уравнение s′(t)=v(t).s′(t)=v(t). Необходимо начальное значение; в этом случае хорошо работает начальная высота объекта. Пусть начальная высота задана уравнением s(0)=s0.s(0)=s0. Вместе эти предположения дают начальную задачу

s′(t)=v(t),s(0)=s0.s′(t)=v(t),s(0)=s0.

Если известна функция скорости, то можно найти и функцию положения.

Пример 4.7

Высота движущегося бейсбольного мяча

Бейсбольный мяч брошен вверх с высоты 33 метра над поверхностью Земли с начальной скоростью 10 м/с, 10 м/с, и единственная сила, действующая на него, — сила тяжести. Мяч имеет массу 0,150,15 кг на поверхности Земли.

1. Найдите положение s(t)s(t) бейсбольного мяча в момент времени t.t.
2. Какова его высота через 22 секунды?

Решение

1. Мы уже знаем, что функция скорости для этой задачи равна v(t)=−9,8t+10,v(t)=−9,8t+10. Начальная высота бейсбольного мяча 33 метра, поэтому s0=3.s0=3. Следовательно, исходная задача для этого примера равна
   . Чтобы решить начальную задачу, сначала найдем первообразные:

   ∫s′(t)dt=∫−9,8t+10dts(t)=−4,9t2+10t+ C.∫s′(t)dt=∫−9,8t+10dts(t)=−4,9t2+10t+C.

   
   Далее подставляем t=0t=0 и находим C:C:

   s(t)=-4,9t2+10t+Cs(0)=-4,9(0)2+10(0)+C3=C.s(t)=-4,9t2+10t+Cs(0)=-4,9( 0)2+10(0)+С3=С.

   
   Следовательно, функция положения равна s(t)=−4,9t2+10t+3.s(t)=−4,9t2+10t+3.
2. Высота бейсбольного мяча после 2s2s определяется как s(2):s(2):

   s(2)=−4,9(2)2+10(2)+3=−4,9(4)+23=3,4 .s(2)=-4,9(2)2+10(2)+3=-4,9(4)+23=3,4.

   
   Следовательно, бейсбольный мяч находится на высоте 3,43,4 метра над поверхностью Земли через 22 секунды. Стоит отметить, что в процессе решения задачи масса шара полностью нейтрализовалась.

Раздел 4.1 Упражнения

Определите порядок следующих дифференциальных уравнений.

1.

у’+у=3у2у’+у=3у2

2.

(у’)2=у’+2у(у’)2=у’+2у

3.

y‴+y″y′=3x2y‴+y″y′=3×2

4.

y′=y″+3t2y′=y″+3t2

5.

dydt=tdydt=t

6.

dyx+d2ydx2=3x4dydx+d2ydx2=3×4

7.

(dydt)2+8dydt+3y=4t(dydt)2+8dydt+3y=4t

Убедитесь, что следующие функции являются решениями данного дифференциального уравнения.

8.

y=x33y=x33 решает y′=x2y′=x2

9.

y=2e−x+x−1y=2e−x+x−1 решает y′=x−yy′=x−y

10.

y=e3x−ex2y=e3x−ex2 решает y′=3y+exy′=3y+ex

11.

y=11−xy=11−x решает y′=y2y′=y2

12.

y=ex2/2y=ex2/2 решает y′=xyy′=xy

13.

y=4+lnxy=4+lnx решает xy′=1xy′=1

14.

y=3−x+xlnxy=3−x+xlnx решает y′=lnxy′=lnx

15.

y=2ex−x−1y=2ex−x−1 решает y′=y+xy′=y+x

16.

y=ex+sinx2−cosx2y=ex+sinx2−cosx2 решает y′=cosx+yy′=cosx+y

17.

y=πe−cosxy=πe−cosx решает y′=ysinxy′=ysinx

Проверьте следующие общие решения и найдите частное решение.

18.

Найдите частное решение дифференциального уравнения y′=4x2y′=4×2, которое проходит через (−3,−30),(−3,−30), учитывая, что y=C+4x33y=C+4×33 является общим решение.

19.

Найдите частное решение дифференциального уравнения y′=3x3y′=3×3, которое проходит через (1,4.75),(1,4.75), при условии, что y=C+3x44y=C+3×44 является общим решением.

20.

Найдите частное решение дифференциального уравнения y′=3x2yy′=3x2y, которое проходит через (0,12),(0,12), при условии, что y=Cex3y=Cex3 является общим решением.

21.

Найдите частное решение дифференциального уравнения y′=2xyy′=2xy, которое проходит через (0,12),(0,12), при условии, что y=Cex2y=Cex2 является общим решением.

22.

Найдите частное решение дифференциального уравнения y′=(2xy)2y′=(2xy)2, которое проходит через (1,−12),(1,−12), учитывая, что y=−3C+4x3y=− 3С+4х3 — общее решение.

23.

Найдите частное решение дифференциального уравнения y′x2=yy′x2=y, которое проходит через (1,2e),(1,2e), при условии, что y=Ce−1/xy=Ce−1/x равно общее решение.

24.

Найдите частное решение дифференциального уравнения 8dxdt=−2cos(2t)−cos(4t)8dxdt=−2cos(2t)−cos(4t), которое проходит через (π,π),(π,π), при заданных что x=C−18sin(2t)−132sin(4t)x=C−18sin(2t)−132sin(4t) является общим решением.

25.

Найдите частное решение дифференциального уравнения dudt=tanududt=tanu, проходящее через (1,π2),(1,π2), при условии, что u=sin−1(eC+t)u=sin−1(eC+ т) является общим решением.

26.

Найдите частное решение дифференциального уравнения dydt=e(t+y)dydt=e(t+y), которое проходит через (1,0),(1,0), при условии, что y=−ln(C− et)y=−ln(C−et) является общим решением.

27.

Найдите частное решение дифференциального уравнения y′(1−x2)=1+yy′(1−x2)=1+y, которое проходит через (0,−2),(0,−2), учитывая, что y=Cx+11−x−1y=Cx+11−x−1 является общим решением.

Для следующих задач найдите общее решение дифференциального уравнения.

28.

у’=3x+exy’=3x+ex

29.

y’=lnx+tanxy’=lnx+tanx

30.

y’=sinxecosxy’=sinxecosx

31.

у’=4xy’=4x

32.

у’=sin-1(2x)y’=sin-1(2x)

33.

у’=2tt2+16y’=2tt2+16

34.

x’=cotht+lnt+3t2x’=cotht+lnt+3t2

35.

х’=t4+tx’=t4+t

36.

у’=уу’=у

37.

у’=уху’=ух

Решите следующие начальные задачи, начиная с y(0)=1y(0)=1 и y(0)=−1.y(0)=−1. Нарисуйте оба решения на одном графике.

38.

dydt=2tdydt=2t

39.

dydt=-tdydt=-t

40.

dydt=2ydydt=2y

41.

dydt=-ydydt=-y

42.

dydt=2dydt=2

Решите следующие начальные задачи, начиная с y0=10.y0=10. В какой момент yy увеличивается до 100 100 или падает до 1–1?

43.

dydt=4tdydt=4t

44.

dydt=4ydydt=4y

45.

dydt=−2ydydt=−2y

46.

dydt=e4tdydt=e4t

47.

dydt=e-4tdydt=e-4t

Напомним, что семейство решений включает в себя решения дифференциального уравнения, отличающиеся на константу. Для следующих задач используйте свой калькулятор, чтобы построить график семейства решений данного дифференциального уравнения. Используйте начальные условия от y(t=0)=-10y(t=0)=-10 до y(t=0)=10y(t=0)=10, увеличивая на 2,2. Есть ли критическая точка, в которой поведение решения начинает меняться?

48.

[Т] у’=у(х)у’=у(х)

49.

[Т] ху’=уху’=у

50.

[Т] y’=t3y’=t3

51.

[T] y’=x+yy’=x+y ( Подсказка: y=Cex-x-1y=Cex-x-1 является общим решением)

52.

[Т] у’=xlnx+sinxy’=xlnx+sinx

53.

Найдите общее решение, описывающее скорость мяча массой 1 фунт 1 фунт, брошенного вверх со скоростью aa фут/сек.

54.

В предыдущей задаче, если начальная скорость мяча, брошенного в воздух, равна a=25a=25 фут/с, запишите частное решение скорости мяча. Решите, чтобы найти время, когда мяч коснется земли.

55.

Вы бросаете вверх в воздух два объекта с разными массами m1m1 и m2m2 с одинаковой начальной скоростью aa фут/с. Как изменится их скорость через 11 секунд?

56.

[Т] Вы бросаете мяч массой 11 кг вверх со скоростью a=25a=25 м/с на Марс, где ускорение свободного падения g=−3,711g=−3,711 м/с ² . С помощью калькулятора вычислите, насколько дольше мяч находится в воздухе на Марсе, чем на Земле, где g=-9,8 м/с2g=-9,8 м/с2.

57.

[T] В предыдущей задаче с помощью калькулятора вычислите, насколько выше поднялся мяч на Марсе, где g=-9,8 м/с2g=-9,8 м/с2.

58.

[T] Автомобиль на автостраде ускоряется по закону a=15cos(πt),a=15cos(πt), где tt измеряется в часах. Составьте и решите дифференциальное уравнение, чтобы определить скорость автомобиля, если его начальная скорость равна 5050 миль в час. Какова скорость водителя после 4040 минут вождения?

59.

[T] Для автомобиля из предыдущей задачи найдите выражение для расстояния, пройденного автомобилем за время t,t, при условии, что начальное расстояние равно 0,0. За какое время автомобиль проедет 100100 км? Округлите ответ до часов и минут.

60.

[T] В предыдущей задаче найдите общее расстояние, пройденное за первый час.

61.

Подставьте y=Be3ty=Be3t в y′−y=8e3ty′−y=8e3t, чтобы найти конкретное решение.

62.

Подставьте y=acos(2t)+bsin(2t)y=acos(2t)+bsin(2t) в y′+y=4sin(2t)y′+y=4sin(2t), чтобы найти конкретное решение.

63.

Подставьте y=a+bt+ct2y=a+bt+ct2 в y′+y=1+t2y′+y=1+t2, чтобы найти конкретное решение.

64.

Подставьте y=aetcost+betsinty=aetcost+betsint в y′=2etcosty’=2etcost, чтобы найти конкретное решение.

65.

Решить y′=ekty′=ekt с начальным условием y(0)=0y(0)=0 и решить y′=1y′=1 с тем же начальным условием. Когда kk приближается к 0,0, что вы замечаете?

Область определения дифференциального уравнения

Недавно читатель попросил меня написать ответ на несколько вопросов о дифференциальных уравнениях:

Описание курса AP Calculus 2016 года теперь включает новое утверждение об ограничениях области для решений дифференциальных уравнений. В частности, в EK 3.5A3 говорится: «Решения дифференциальных уравнений могут подвергаться ограничениям предметной области». [Текущий CED 2020 года использует ту же формулировку в заявлении Essential Knowledge FUN-7. E.3] Не могли бы вы написать сообщение в блоге, в котором обсуждается (1) пример того, как определить ограничение домена; (2) предположение о том, будет ли отведена одна из точек дифференциального уравнения на свободный отклик для уточнения ограничения; и (3) размышление о том, может ли это понятие появиться при множественном выборе, и если да, то как.

Во-первых, позвольте мне похвалить его за то, что он заметил EK 3.5A3. Я упустил это из виду и еще не видел, чтобы кто-то понял это. Кажется, это новый пункт в описании курса. Не паникуйте. В текущем CED 2020 EK FUN-7.E.3 указано

Один вопрос с вопросом о домене и диапазоне задавался раньше, но некоторое время назад. В частности, 2000 AB6 и 2006 AB 5 запрашивали область решения дифференциального уравнения (см. ниже для обоих). Это единственные случаи, которые я могу найти, требующие от студентов найти область решения.

С 2008 года многие стандарты подсчета очков включали домен, но они не требовали получения каких-либо баллов.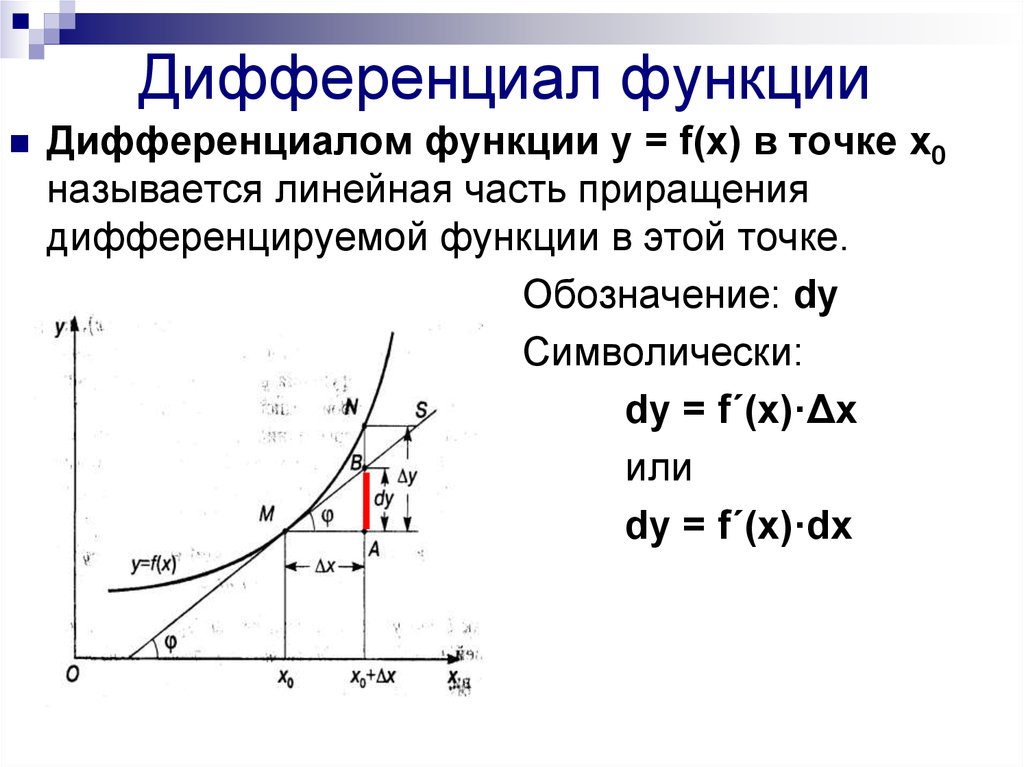 Они обсуждаются ниже. Домены были включены в решение, я подозреваю, потому что стандарты обнародованы, а читатели хотят опубликовать максимально полный ответ.

Что требуется от домена?

Общепринятые требования заключаются в том, что решение дифференциального уравнения должно быть функцией , областью определения которой (1) должен быть открытый интервал, (2) на котором дифференциальное уравнение истинно, и (3) содержит начальное условие. Комментарии:

• Интервал должен быть открытым, так как производные не определены в конечных точках интервалов. Производная — это двусторонний предел, и к конечной точке можно подойти только с одной стороны. Хотя односторонние производные могут быть определены, они являются более обременительным требованием и не являются необходимыми.
• На практике это означает, что решение не может пересекать вертикальную асимптоту или проходить через точку, в которой функция не определена; он должен оставаться на той стороне, где находится начальное условие.
• Дифференциальное уравнение должно быть истинным в том смысле, что подстановка решения и его производной (производных) в дифференциальное уравнение должна привести к тождеству. (См. 2007 AB 4(b) для практики).
• И, конечно же, координата x исходной точки должна быть в домене.

Учителя иногда спрашивают, почему мы не можем просто пропустить асимптоту или неопределенную точку. Когда вы делаете это, вы работаете с кусочной функцией. Здесь нет проблем, но учтите, что на элементах вне домена, как описано выше, у вас может быть любая функция, которую вы хотите, и при этом соответствовать трем требованиям, указанным выше.

Поиск домена.

Вот несколько примеров. Обратите внимание, что учитываются дифференциальное уравнение, его решение и начальное условие.

2000 AB 6: После нахождения решения нахождение области является предварительным расчетным вопросом, требующим решения простого неравенства . Домен .

2006 AB 5 : будет обсуждаться ниже в ответ на другой заданный им вопрос.

2008 АВ 5 : Дифференциальное уравнение не определено при x = 0, а начальное условие находится справа от него. Итак, домен состоит из всех положительных чисел.

2011 AB5/BC5 : Домен указан в основе; Время начинается сейчас, и дифференциальное уравнение применяется «на следующие 20 лет», поэтому 0 <  x < 20

2013 AB 6 : Решение таково, Таким образом, домен имеет все размеры x , так что x = 1 (начальное условие) и для которого . Дальнейшее упрощение не было дано. По графическому калькулятору диапазон составляет около .

2013 BC 5 : Решение содержит вертикальную асимптоту x = –1. Поскольку начальное условие равно (0, –1), домен равен x > –1; сторона асимптоты, содержащая начальное условие.

2014 AB 6 : Ни уравнение, ни решение не имеют значений, для которых x не определено; Итак, домен состоит из всех действительных чисел.

2016 AB 4 : Дифференциальное уравнение с f (2) = 3. Решение , имеет вертикальную асимптоту, где знаменатель равен 0, а именно , и не определено (из-за логарифма) для . Самый большой открытый интервал, содержащий начальное условие, находится между этими двумя значениями, а именно

2017 AB 4: Конечные точки домена указаны в основе задачи. Время t начинается, когда картофель вынимают из духовки, поэтому t > 0, а дифференциальное уравнение в (c) дается для t < 10. Таким образом, область значений 0 < t < 10,

2018 AB 6 : И дифференциальное уравнение, и его общее решение определены для всех действительных чисел: 

Все они не требуют «исчисления» — это вопросы «найти область» из предварительного исчисления с заботой о вертикали. асимптоты. Есть и другие соображения. Более подробное и более подробное обсуждение этого вопроса можно найти в «Области решений дифференциальных уравнений» бывшего главного читателя Ларри Риддла.

Думаю, это ответ на первый вопрос моего читателя. Что касается его второго и третьего вопросов, я думаю, что ответ положительный. В какой-то момент учащимся будет предложено указать область определения дифференциального уравнения. Я предполагаю, что это будет довольно простая часть вопроса со свободным ответом, состоящая из одного пункта. Если решение дифференциального уравнения необходимо, то оно кажется слишком длинным для вопроса с несколькими вариантами ответов. Это все догадки с моей стороны; Я не знаю, что будет на будущих экзаменах.

2019 AB 4: Решение представляет собой многочлен и справедливо для всех действительных чисел.

2021 AB 6: Решение содержит мощность эл. Домен состоит из действительных чисел.

2021 BC 4: Решение содержит члены с ln( x ). Домен — все x > 0.

2022 AB 5 : Домен — все реальные числа

---

Мой читатель также спрашивал об абсолютном значении

Еще один вопрос, который может быть связан с этой темой, касается релевантности знаков модуля в решениях дифференциальных уравнений. Когда их можно оставить в растворе, а когда они избыточны?

Абсолютные значения могут сильно запутать детей. Смотрите мои посты «Абсолютно» и «Абсолютно ценно». Предварительные темы, да, но они возвращаются снова и снова.

Вот два примера с абсолютными значениями и доменами:

2005 AB 6 : После разделения переменных и применения начального условия получаем . Это не функция; его график представляет собой эллипс. Мы не можем просто написать , так как это тоже не функция. С начальным условием  f (1) = –1, имеем . Затем выберите половину эллипса, где y  – отрицательное значение и . Домен .

2006 АВ 5 . Вопрос о начальной ценности должен решить .

Через несколько шагов мы приходим к . В точке начального условия  и, следовательно, . Продолжая, приходим к . Для экзамена AP мы можем остановиться здесь, так как у нас есть функция и алгебраическое упрощение не требуется.

Был запрошен домен.