Как находить площадь трапеции — ответ на Uchi.ru
Ответ или решение2
К
В предложенном задании нас просят рассказать, каким образом можно найти площадь трапеции. Для выполнения этого задания сначала разберёмся, что же такое трапеция.
Трапеция
Трапеция — это геометрическая фигура, которая представляет собой выпуклый четырёхугольник с двумя сторонами параллельными друг другу и двумя не параллельными сторонами. При этом параллельные стороны треугольника называют основаниями трапеции, а две другие боковыми сторонами трапеции. Трапеция может быть:
- Прямоугольной. Прямоугольной называют трапецию, в которой два угла из четырёх равны 90 градусам.
- Равнобедренной. Равнобедренной называют трапецию, в которой боковые стороны и пары углов у каждого из оснований равны.
Площадь трапеции
В математике существует несколько способов нахождения площади трапеции в зависимости от данных величин. Рассмотри эти формулы:
- Площадь через основание и высоту.
Если нам даны величины оснований трапеции и её высота, то для нахождения площади используем следующую формулу: S = 1/2 * h (a + b).
Если нам даны величины оснований трапеции и её высота, то для нахождения площади используем следующую формулу: S = 1/2 * h (a + b).- Площадь через среднюю линию и высоту. Если нам даны величины двух оснований и высоты или только высоты и средней линии, которая равна полусумме оснований, то можем найти площадь трапеции по следующей формуле: S = m * h.
- Площадь через прямоугольник и два треугольника. Если провести трапеции вершины из углов при меньшем основании, то трапеция разделится на прямоугольник и два треугольника, следовательно, площадь такой трапеции будет равна сумме площадей этих фигур: S (трапеции) = S (квадрата) + S (треугольника 1) + S (треугольника 2).
К
Площадь трапеции будет равна полусумме ее оснований, умноженной на высоту. В виде формулы это записывается в виде выраженияS = ( ( a + b ) * h ) / 2где S — площадь трапеции, a,b — длина каждого из оснований трапеции, h — высота трапеции.
Есть еще одна простая формула для подсчета ее площади.
Согласно ней площадь трапеции равна произведению ее средней линии на высоту трапеции и записывается в виде: S = m * h, где S — площадь, m — длина средней линии, h — высота трапеции. Данная формула больше подходит для задач по математике, чем для бытовых задач, так как в реальных условиях вам не будет известна длина средней линии без предварительных расчетов. А известны вам будут только длины оснований и боковых сторон.
S = ( ( a + b ) / 2 ) * √ c2 — ( ( b — a )2 + c2 — d2 / 2 ( b — a ) )2
где S — площадь, a,b — основания, c,d — боковые стороны трапеции.
Знаешь ответ?
Как написать хороший ответ?Как написать хороший ответ?
Будьте внимательны!
- Копировать с других сайтов запрещено. Стикеры и подарки за такие ответы не начисляются. Используй свои знания. 🙂
- Публикуются только развернутые объяснения. Ответ не может быть меньше 50 символов!
0 /10000
Формула площади трапеции
В статье понятно и доступно разберем
Трапеция это геометрическая четырехугольная фигура, состоящая из двух параллельных линий называющихся основанием и двух боковых линии не являющиеся параллельными, называющиеся боковые стороны.
Линия которая соединяет стороны как основные так и боковые посередине, называется — средней линией, высота выводится под углом 900.
Площадью трапеции называется участок на плоскости, который ограничен данной фигурой, обозначается в единицах квадратных.
В случае если мы знаем величину средней линии k, формула меняется на более легкую, она приравнивается к половине суммы длины основных линий
В случае когда мы знаем длину всех сторон, можно рассчитать площадь используя данную формулу
Если разобрать данную формулу на примере, то мы получим следующее:
Рассмотрим для ясности: трапеция с длиной боковых линий х = 5 см, g = 4 см, основные линии y = 3 см, z = 7 см. Требуется найти S = ?.
Трапеция бывает однобокой, ещё ее называют равнобедренной — так как диагонали равны между собой.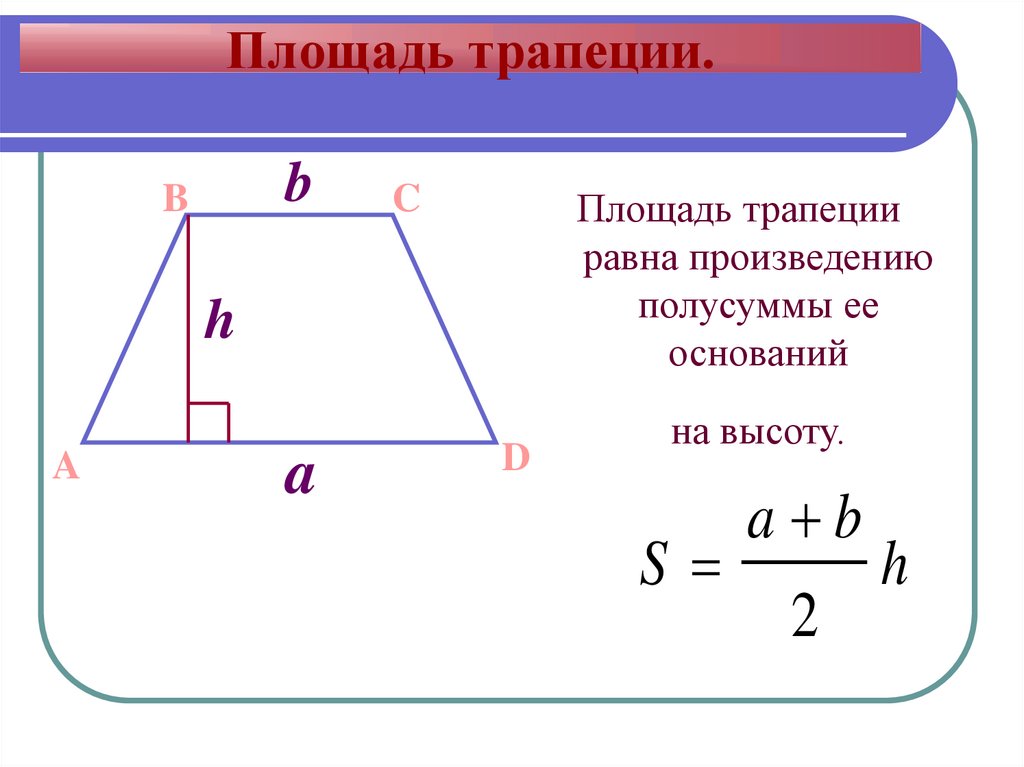
Для нее формула может складываться через радиус вписанной в нее окружности, диагонали и углы прилегающие к основанию.
В случае когда мы знаем длину диагоналей и угол находящийся между ними:
В том случае когда выводим формулу с помощью боковых сторон и углов прилегающих к основанию. Формула будет выглядеть так:
Вывод: Если нам известно одно основание из двух и величины углов принадлежащие этому основанию, мы без труда сможем узнать площадь трапеции.
Трапеция бывает криволинейной — это тогда, когда трапеция находится на оси координат, ограничена графиком продолжительной функции.
В случае когда основание трапеции находится на оси х и ограничено точками x1 = z, x2 = y. Вычислить площадь трапеции помогут интегралы
где F (z) — значение в точке z
F (y) — значение в точке y
Разберем для наглядности: Криволинейная трапеция, ограниченная функцией y = f(x).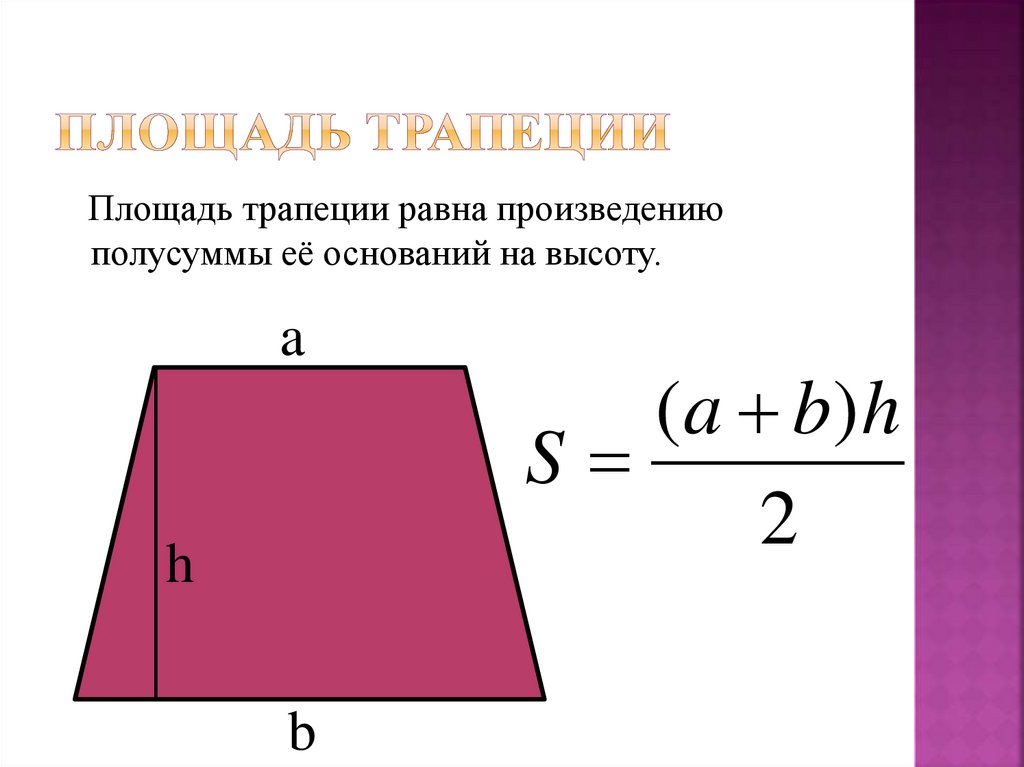
Функция F(x) = — x3 — 27×2 — 240x — 8. Нужно найти S = ?. Фигура ограничивается: графиком сверху y = f(x)., снизу ОХ осью, слева х = (-10), справа х = (-8).
В условиях задачи дана функция. С помощью нее найдем значения точек.
1) F(-8) = -(-8)3 — 27 х (-8)2 — 240 х (-8) — 8 = 24-1728+1920 — 8 = 696
2) F(-10) = -(-10)3 — 27 х (-10)2 — 240 х (-10) — 8 = 1000-2700+240 — 8 = 692
3) F(-8) — F (-10) = 696 — 692 = 4
Ответ: S = 4
Вот собственно и всё по формулам площади для разных видов трапеций. Если у вас появились какие то вопросы, обязательно пишите их в комментариях. Успехов в учебе.
vamsochinenie.ru — база сочинений на самые разные темы.
Площадь трапеции: Формула и примеры
Давайте узнаем, как найти площадь трапеции .
Что такое трапеция?
Трапеция представляет собой четырехстороннюю плоскую фигуру с одной парой параллельных сторон, называемых ее основаниями . Высота (также называемая высотой ) трапеции перпендикулярна ее основаниям. Две другие непараллельные стороны называются ножками . Примерами предметов в форме трапеции являются цветочные горшки, сумки, ведра и другие архитектурные вещи.
См. иллюстрацию трапеции ниже.
Как найти площадь трапеции
Площадь двумерной фигуры относится к общему объему пространства, заключенного внутри этой фигуры. Он измеряется в кубических единицах, таких как м 2 , см 2 , км 2 , а в 2 . Перед вычислением убедитесь, что все единицы одинаковы.
Связанные материалы: Площадь круга – формула и примеры
Чтобы найти площадь трапеции , умножьте среднее значение двух оснований (параллельных сторон) трапеции на ее высоту, как указано в этой формуле: 2 • H
Где:
A = область трапеции
A = длина основания трапеции 1
B = высота из базы трапсоидов 2
H = высота трапециевида 2
H = высота.
трапеция
Пример #1: Нахождение площади трапеции при заданных измерениях в одних и тех же единицах измерения
Найдите площадь трапеции при следующих измерениях:
a = 10 см, b = 8 см, h = 6 см
Решение примера №1:
Шаг 1. Запишите данные числа: a = 10 см, b = 8 см, h = 6 см.
Шаг 2. Подставьте цифры в формулу. Аналог 10см для a , 8 см для b и 6 см для ч .
A = ( a + b ) / 2 • h
= (10см + 8см) / 2 • (6см) Шаг 0 Упрощение.
A = 18см / 2 • (6см)
= 9см • 6см
A = 54см 2
0 Следовательно, площадь трапеции
04 это
54см 2 .
Пример #2: Нахождение площади трапеции при заданных измерениях в разных единицах измерения
Найдите площадь трапеции, приведенной ниже.
Решение примера №2:
Шаг 1. Запишите данные измерения: a = 5 ярдов, b = 126 дюймов, ч = 4 ярда.
Шаг 2 . Поскольку все единицы измерения должны быть одинаковыми, преобразуйте 126 дюймов в ярды.
Напомним: 1 ярд = 36 дюймов. Запишите преобразование в виде дроби, равной 1: (1 ярд / 36 дюймов) = 1,
126IN • (1YD / 36IN) = 126 в • (1 YYD / 36 в ) = 126YD / 36 = 3,5 года
Следовательно, конвертированное значение B — 3,5 YD .
Шаг 3. Подставьте измерения в формулу. Замените 5yd на a , 3.5yd на b и 4yd на h 9004.
А = ( а + б ) / 2 • h
= (5 ярдов + 3,5 ярда) / 2 • (4 ярда)
Шаг 4. Упростить.
A = 8.5yd / 2 • (4yd)
= 4.25yd • 4yd
A = 17yd 2
Therefore, the area of the trapezoid is 17yd 2 .
Пример №3. Нахождение основания трапеции
Найдите другое основание трапеции площадью 71,5 см 2 , высота 6,5 см, основание 9 см.
Решение примера №3:
Шаг 1. Напишите формулу площади трапеции: A = ( a + b ) / 2 • 4 ч = ( a + b )h / 2.
Используйте последнее, чтобы найти недостающее основание.
Шаг 2. Пусть a будет недостающим основанием. Подставьте данные измерения в формулу.
Временно удалите юниты, чтобы избежать путаницы.
A = ( a + b )h / 2
71,5 = ( a + 9) (6,5) / 2
Шаг 3. Упростить.
Сначала умножьте 6,5 см на выражение ( a + 9).
71,5 = (6,5 a + 58,5) / 2
Умножьте обе части уравнения на 2. a + 58,5
Вычтите 58,5 с обеих сторон.
143 – 58,5 = 6,5 a + 58,5 – 58,5
85 = 6,5 a
Разделите обе части на 6,5.
85 / 6,5 = 6,5 a / 6,5
13 = a
Следовательно, длина другого основания равна 04см.
Проверка решения примера №3:
Подставьте измерения в формулу площади трапеции.
A = ( a + b ) ч / 2
71,5 см 2 = [(13 см + 9 см) (6,5 см)] /2
71,5 см 2 = [(22 см) (6,5 см)] / 2
Упростить.
71,5 см 2 = 143 см 2 / 2
71,5 см 2 = 71,5 см 2
Спасибо за внимание.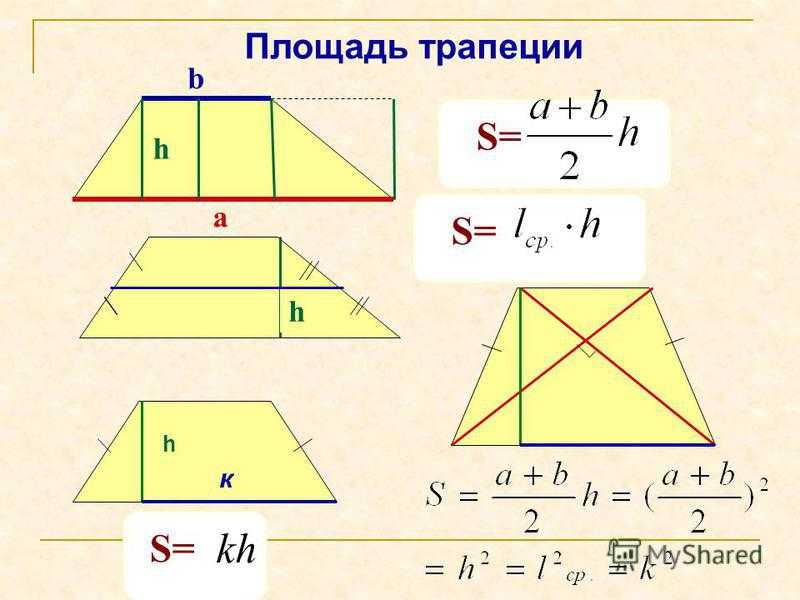
Мы надеемся, что это эффективно! Всегда не стесняйтесь возвращаться на эту страницу, если у вас возникнут вопросы о площади трапеции .
Ознакомьтесь с некоторыми другими сообщениями в нашем блоге или инвестируйте в свое будущее с помощью одного из наших курсов самообучения!
Щелкните здесь, чтобы ознакомиться с руководством по подготовке к экзамену AP по программе Calculus AB 2021 !Площадь трапеции — веб-формулы
Трапеция – это четырехугольник, у которого только одна пара сторон параллельна. Чтобы вычислить площадь трапеции, возьмите среднее значение оснований и умножьте его на высоту.
Площадь трапеции определяется как:
A = (a + b) ∙ h /2
a: длина вершины
б: длина основания
h: высота
Когда a = 0, форма становится треугольником.
Пример 1:
Какова площадь трапеции с основаниями 5 см и 8 см и высотой 6 см?
Раствор :
Используя формулу площади трапеции, получим:
Площадь трапеции = 0,5 × h × (a + b)
Площадь трапеции = 0,5 × 6 × (5 + 8)
Площадь трапеции = 0,5 × 6 × 13
Площадь трапеции = 39 см 2
Пример 2:
Площадь трапеции равна 52 см 2 , а основания соответственно 11 дюймов и 15 дюймов.
Найдите его высоту.
Решение : Мы знаем, что площадь трапеции определяется как:
Площадь трапеции = 0,5× h × (a + b), где h — высота, выделив h из формулы, мы сможем определить ее высоту
52 = 0,5 × (11 + 15) × ч
52 = 0,5 × 26 × ч
52 = 13ч
Таким образом:
h = 52/13 = 4 дюйма
Пример 3: Площадь трапеции 15 см 2 и расстояние между параллельными основаниями 6 см. Если одно из параллельных оснований равно 3 см, то какова длина другого параллельного основания?
Решение : Пусть a будет длиной неизвестной параллельной стороны, а b будет известным основанием.
Площадь трапеции = 0,5 × высота × (a+b) = 15 см 2
Подставив значения получим:
(0,5) × 6 × (3 + а) = 15
Умножьте каждую сторону на 2
6 х (3 + а) = 30
Разделив каждую сторону на 6, получим
.
3 + а = 5
а = 2 см
Следовательно, длина другой параллельной стороны равна 2 см.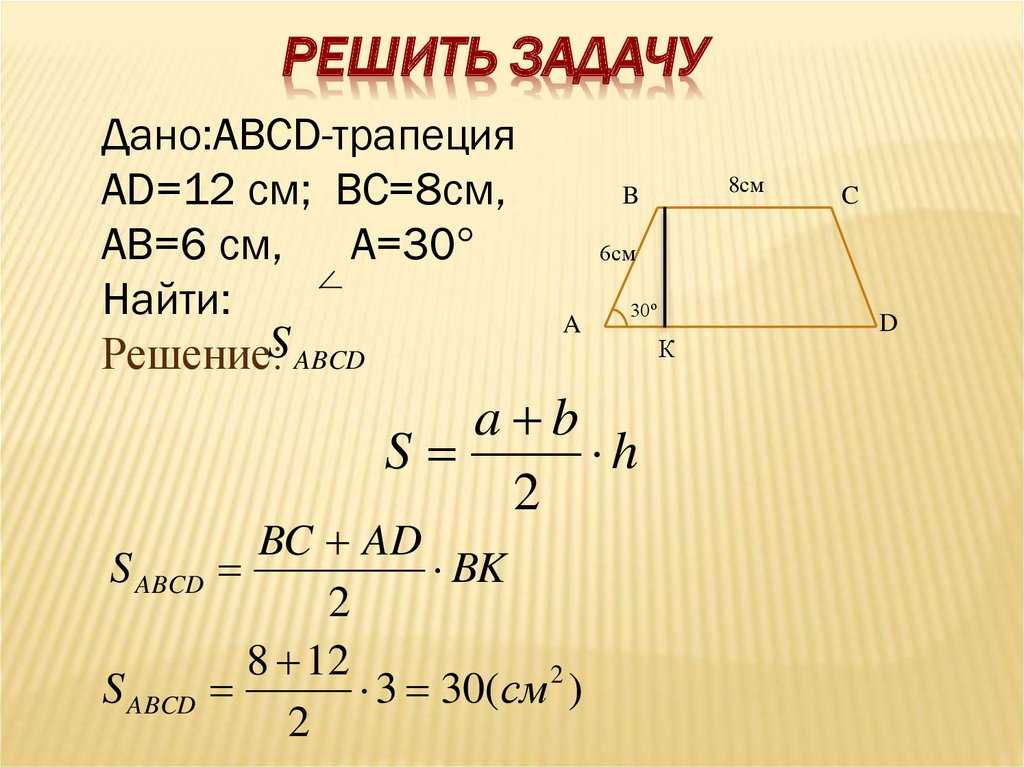
Пример 4: Каковы длины параллельных сторон трапеции, если ее площадь 18 см 2 , высота 4 см, а длина более короткой стороны на 5 см короче длинной стороны?
Решение : Пусть у будет длина большей стороны.
Длина меньшей стороны равна (y — 5) см, так как короткая сторона на 5 см короче длинной.
Площадь трапеции = 18 см 2
По формуле площади трапеции имеем:
(0,5) × 4 × [y + (y — 5)] = 18
Умножьте каждую сторону на 2,
4 × (2у — 5) = 36
Разделите каждую сторону на 4,
2г — 5 = 9
Упростим уравнение, получим:
2y = 14 и y = 7 см
Таким образом, длина большей стороны равна y = 7 см, тогда как длина меньшей стороны равна y — 5 = 7 — 5 = 2 см
Пример 5: Площадь трапеция 160 см2. Параллельные стороны равны 18 см и 14 см. Найдите расстояние между параллельными сторонами.
Решение :
Дано A = 160 см 2 , a = 18 см и b = 14 см.