Как находить область определения функции 11 класс: Как найти область определения функции?

Область определения и множество значений тригонометрических функций

Урок 1. Алгебра 11 класс ФГОС

В этом видеоуроке мы вспомним, как устанавливается соответствие между действительными точками и точками окружности с помощью поворота точки окружности, а также вспомним, что называют синусом, косинусом и тангенсом произвольного угла. Скажем, какие функции называются тригонометрическими функциями. Выясним, что является областью определения и множеством значений тригонометрических функций.

Конспект урока «Область определения и множество значений тригонометрических функций»

Сегодня на уроке мы с вами вспомним, как устанавливается соответствие между действительными точками и точками окружности с помощью поворота точки окружности, а также вспомним, что называют синусом, косинусом и тангенсом произвольного угла. Скажем, какие функции называются тригонометрическими функциями. Выясним, что является областью определения и множеством значений тригонометрических функций.

Прежде чем приступить к рассмотрению новой темы, давайте возьмём окружность единичного радиуса с центром в начале координат и отметим на ней точку .

Тогда при повороте точки  на угол  радиан мы получим точку . При этом помним, что ордината точки  – это синус угла , а абсцисса этой точки – это косинус угла .

Далее считаем, что все углы измерены в радианной мере, и поэтому обозначение «радиан», как правило, опускается. Договорившись считать единицу измерения углов (1 радиан) фиксированной, определяем, например, синус числа x как синус угла в x радиан; косинус числа x как косинус угла в x радиан и так далее.

Так, каждому действительному числу x поставлены в соответствие числа синус x и косинус x, то есть на множестве действительных чисел определены функции  и .

Получается, что областью определения функций игрек  и  является множество  всех действительных чисел.

Давайте найдём множество значений функции . Для этого надо выяснить, какие значения может принимать

y при различных значениях x, то есть надо установить, для каких значений y существуют такие значения x, при которых  равен y.

Мы знаем, что уравнение  имеет корни, если . И уравнение не имеет корней, если . Из этого следует, что множеством значений функции  является отрезок .

Найдём множество значений функции . Для этого надо выяснить, какие значения может принимать y при различных значениях x, то есть надо установить, для каких значений y существуют такие значения x, при которых  равен y.

Знаем, что уравнение  имеет корни, если . И уравнение не имеет корней, если .

А значит, множеством значений функции  является отрезок .

Таким образом, можно сказать, что функции  и  являются ограниченными.

Теперь поговорим про функцию . Она определяется формулой .

 не должен обращаться в нуль, так как делить на нуль нельзя.

Функция  определена при тех значениях x, для которых .

Мы знаем, что решением уравнения  является .

Тогда областью определения функции  является множество  всех действительных чисел, кроме .

Известно, что уравнение  имеет корни при любом действительном значении . Следовательно, множеством значений функции  является множество  всех действительных чисел.

Осталось выяснить, что является областью определения и множеством значений функции . Запишем: . Здесь  не должен обращаться в нуль, так как делить на нуль нельзя. А значит, функция  определена при тех значениях x, для которых .

Корнем уравнения  является . Тогда областью определения функции  является множество  всех действительных чисел, кроме , .

Уравнение  имеет корни при любом действительном значении

a, а значит, множеством значений функции  является множество  всех действительных чисел.

Таким образом, мы с вами выяснили, что является областью определения и множеством значений функций , ,  и . Эти функции называются тригонометрическими функциями.

А сейчас давайте выполним несколько заданий.

Задание первое. Найдите область определения функций:

а) ; б) ; в) .

Решение.

Задание второе. Найдите множество значений функций:

а) ; б) .

Решение.

Задание третье. Найдите наибольшее и наименьшее значения функции

.

Решение.

Следующий урок 2 Чётность, нечётность, периодичность тригонометрических функций

Получите полный комплект видеоуроков, тестов и презентаций Алгебра 11 класс ФГОС

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

«Область определения функции»

Урок разноуровневого

обобщающего повторения

по алгебре и началам анализа

для учащихся 11 класса

по теме:

«Область определения функции»

Герасимова Татьяна Геннадьевна

2017 год

На основе открытого урока

Н. Б.Кононовой (Краснодарский край, Крымский район, ст. Нижнебаканская)

Разноуровневый урок обобщающего повторения в 11 классе с применением

мультимедийного проектора.

Длительность урока 40 минут.

Урок разработан для учащихся 11 класса. Тема урока выбрана на основании анализа результатов всех краевых диагностических работ в данном классе, которые показали, что в заданиях этой темы учащиеся часто допускают ошибки и не в полной мере усвоили тему «Область определения функции».

В классе 6 учеников.

Перед началом урока учащиеся рассаживаются в соответствии с двумя уровнями подготовки — по вариантам ( 1 вариант слабее, 2 вариант сильнее)

Форма урока:

Фронтальный опрос, дифференцированный опрос, работа с разноуровневыми группами, самостоятельная работа.

Цель урока: Обобщить теоретические знания по теме « Область определения

функции», рассмотреть методы нахождения области определения сложных функций в заданиях базового и повышенного уровня. Организовать работу учащихся по указанной теме на уровне, соответствующем уровню уже сформированных знаний.

Задачи урока:

образовательные:

формирование умений находить область определения различных функций

закрепление навыков в нахождении области определения изученных

ранее функций

развивающие:

развитие аналитического мышления, творческого подхода при выпол-

нении заданий

активизация познавательной деятельности учащихся с помощью

интерактивных средств обучения

воспитательные:

формирование ответственности перед сдачей ЕГЭ

Оборудование:

мультимедийное оборудование ,компьютер ,доска,

индивидуальные карточки с тестами, бланки ответов.

Ход урока.

I этап урока — организационный ( 1 минута)

Учитель сообщает учащимся тему урока, цель и поясняет, что во время урока постепенно будет использоваться тот раздаточный материал, который находится у них на партах.

Слайд №1

Обращение к учащимся:

«В ходе урока вы будете работать как у доски, так и самостоятельно выполнять задания теста, составленного на два уровня сложности: 1 вариант более лёгкий, 2 вариант сложнее. У каждого ученика тест и бланк для ответов , в котором будут фиксироваться ответы к заданиям А и выполняться задания В и С. В бланке ответов есть дополнительное задание, которое можно выполнять в течение урока при наличии

свободного от других заданий времени».

II этап урока — общие свойства функций. (5 мин)

Учитель обращается к учащимся с вопросом: «Что такое функция? С какими свойствами функций мы знакомились на уроках математики ?»

Учащиеся дают ответы.

Далее проводится устная работа по графику функции.

Слайд №2

Учащиеся отвечают на вопросы:

1. Что такое множество значений функции? Найти множество значений функции,

график которой изображён на рисунке.

2. Сколько нулей имеет функция? Определить нули функции.

3. Определить промежутки возрастания функции.

4. Определить промежутки убывания функции.

5. Определить промежутки, на которых функция принимает положительные

значения.

6.Определить промежутки, на которых функция принимает неположительные значения.

7.Найти значение аргумента, при котором функция принимает наименьшее значение.

8. Чему равно наименьшее значение функции? Чему равно наибольшее значение?

9. С помощью графика функции решить неравенство ƒ(х) 2

10. Что такое область определения функции? Найти область определения данной функции.

Итак, сегодня на уроке мы более подробно остановимся на последнем из рассмотренных нами свойств функций и обобщим понятие – область определения функции.

Ученикам предлагается выполнить задание А1 в тестах ( по графику)

( ответы вносятся в бланк ответов)

1 вариант 2 вариант

А1.Найти область определения функции, график которой изображён на рисунке

А1.Укажите количество целых значений аргумента, принадлежащих области определения функции, график которой изображён на рисунке

1) [ – 4; 3 ] 2) ( 1; 4 ] 3) [ –4; –1 ) ( –1; 3 4) ( – 4; –1 ) (– 1; 3 )

1) 8 2) 10 3) 9 4) 3

III этап урока ( 2 мин)

Учитель сообщает учащимся, что если функция задана формулой и область определения её не указана, то считают, что область определения состоит из всех значений независимой переменной , при которых эта формула (функция) имеет смысл (определена).

Учитель напоминает учащимся, какие элементарные функции определены на всей числовой прямой.

Слайд №3

у = P_n(x) , где P_n(x) – многочлен n ^ой степени

( у = 5х⁶ – 3х⁴+2х³–1; у = 3х⁵–11х )

у = — корень нечётной степени

(у = ; у = )

у =, у =

у =а^х

Далее учитель обращает внимание учащихся на то, что необходимо чётко разграничивать понятия область определения функции и множество значений функции.

IVэтап урока (20 мин )

Учитель напоминает учащимся, что для нахождения области определения функции, заданной формулой, следует исключить те значения аргумента, при которых указанные действия невозможно выполнить. Невозможно, например, делить на нуль; извлекать корень чётной степени из отрицательного числа; вычислять логарифм отрицательного числа и нуля; вычислять логарифм по отрицательному основанию и основанию, равному нулю и единице; возводить нуль в степень нуля; возводить отрицательное число в иррациональную степень; вычислять аrcsin x‚ arccos x, если .

А теперь рассмотрим более подробно перечисленные случаи.

Слайд №4 (1мин)

Учащимся предлагается устно найти область определения следующих функций:

у= ; у = ; у =

Слайд №5 (5 мин)

у = D(у) = [ 0; +)

Учитель обращается к учащимся:

«Часто приходится работать с функциями, представляющими собой комбинации нескольких функций, поэтому область определения таких функций содержит несколько условий».

Разбирается решение следующих заданий у доски:

Задания а) и б) выполняют слабые учащиеся, задание в) — сильный ученик

а)Найти наименьшее натуральное число, входящее в область определения функции у = Ответ: 1 (–;

б)Найти наибольшее целое число, входящее в область определения функции у = Ответ: –2 (–;

в) Найти целые числа, входящие в область определения функции у = Ответ: 3 (2; 4)

Далее учащимся предлагается выполнить задание А2 в тестах. (2 мин)

1 вариант:

А2. Найти область определения функции у =

1) ( 1; + 2) (– 3) (– 4) [1; +

2 вариант:

А2. Найти область определения функции у =

1) [ –2; 0 ] 2) [ 0; 2 ] 3) ( – 4) [ –2; 2 ]

Слайд №6

у = D(у) = ( 0; + при а и 1

Устная работа с классом:

Какова область определения следующих функций?

а) у = б) у =

После чего выполняется решение следующих заданий у доски:

Найти область определения функции:

а) для слабого ученика б) для сильного ученика

у = у =

( ответы : а) ( 0; 4) б) ( 2; 3) )

По окончании работы у доски, выполняется задание А3 в тестах.(2 мин)

1 вариант.

А3. Какое из следующих чисел входит в область определения функции

1) 2 2) 2,01 3) 3 4) 4

2 вариант.

А3. Найти область определения функции у =

1) ( 0,5; + 2) ( 0,75; + 3) ( 0,5; 0,75 ) 4) [ 0,5; +

Слайд №7 (4 мин)

Область определения функции у = : х

Область определения функции у х

У доски разбирается решение следующих заданий ( у доски 3 ученика)

Найти область определения функции:

а) для слабого ученика б), в) для сильных учеников

а) у = 5 б) у = в) у =

(ответы: а) ; б) в) ; )

Далее самостоятельно выполняется задание А4 в тестах:(2 мин)

1 вариант.

А4. Найти область определения функции у = tg3х

1) х 2) х

3) х + 4) х

2вариант.

А4. Найти область определения функции у = ctg3х·

1) ( – 2) х 3) х 4) х

Слайд №8

Учитель просит учащихся вспомнить обратные тригонометрические функции.

Область определения обратных тригонометрических функций:

у = D (

у = D (

у =

у = D(у) = R

Разбирается у доски решение следующих заданий на нахождение

области определения функций:

а) для слабого ученика б) для сильного ученика

а) у = (2х –3) б) у =

( ответ: [1;2] ) (ответ: [ 0,1; 10 ] )

По окончании решения выполняется задание А5 в тестах.(2мин)

1 вариант.

А5. Найти область определения функции у = аrccos

1) [–1;1] 2) ( 1; 5 ) 3) [ 1; 5 ] 4) ( –

2 вариант.

А5. Найти область определения функции у =

1) ( – 2) х 3) х 4) [ –1; )

Vэтап урока . (5 мин)

После выполнения последнего задания в тестах переходим ко второй части работы.

На доске обсуждаем решение заданий уровня В1 для 1 варианта и С1 для 2 варианта.

1 вариант: В 1: Найти область определения функции:

2 вариант: С 1: Найти область определения функции:

Решение :

1 вариант.

х

2 вариант.

VI этап урока ( 5 мин)

Далее ученики приступают к самостоятельному выполнению заданий В1 и С1 в бланках ответов ( приводят полное решение задания)

Задание В1: (1 вариант)

Найти область определения функции

Задание С1: ( 2 вариант )

Найти область определения функции

По окончании решения учащиеся сдают бланк ответов, после чего на доске высвечивается таблица ответов и учащиеся проверяют своё решение. (2 мин)

Слайд №9

1 вариант

А1	А2	А3	А4	А5	В1
3	4	2	3	3	(–3; –2)(–2;]

2 вариант

А1	А2	А3	А4	А5	С1
2	1	2	3	4	[–3; –1) (–1; 0]

Слайд №10 Критерии оценки:

Каждое задание А – 1 балл, задание В – 1 балл, задание С – 2 балла.

0 –3 балла —- «2»

4 балла —- «3»

5 баллов —- «4»

6 и 7 баллов—- «5»

VII этап урока (1 мин)

Итог урока: Учитель ещё раз обращает внимание учащихся на те теоретические факты, которые вспоминали на уроке, говорит о необходимости выучить их.

Комментирует ответы учащихся, обсуждает предварительные оценки.

Окончательные результаты будут объявлены после проверки работ учащихся

VIII этап урока ( 1 мин)

Д/З: раздать тесты краевой контрольной работы №6

и индивидуальные карточки следующего содержания :

В1. Найти область определения функции

У =

В2. Найти область определения функции

У =

В3. На каком множестве совпадают функции

У = и у = –

Задание С: Найти область определения функции

Тесты и бланки ответов прилагаются.

1 вариант.

А1 . Найти область определения функции , график которой изображён на рисунке .

1) [ – 4; 3 ] 2) ( 1; 4 ] 3) [ –4; –1 ) ( –1; 3 ] 4) ( – 4; –1 ) (– 1; 3 )

А2. Найти область определения функции у =

1) ( 1; + 2) (– 3) (– 4) [1; +

А3. Какое из следующих чисел входит в область определения функции

1) 2 2) 2,01 3) 3 4) 4

А4. Найти область определения функции у = tg3х

1) х 2) х

3) х + 4) х

А5. Найти область определения функции у = аrccos

1) [–1;1] 2) ( 1; 5 ) 3) [ 1; 5 ] 4) ( –

2 вариант.

А1. Укажите количество целых значений аргумента, принадлежащих области определения функции, график которой изображён на рисунке

1) 8 2) 10 3) 9 4) 3

А2. Найти область определения функции у =

1) [ –2; 0 ] 2) [ 0; 2 ] 3) ( – 4) [ –2; 2 ]

А3. Найти область определения функции у =

1) ( 0,5; + 2) ( 0,75; + 3) ( 0,5; 0,75 ) 4) [ 0,5; +

А4. Найти область определения функции у = ctg3х·

1) ( – 2) х 3) х 4) х

А5. Найти область определения функции у =

1) ( – 2) х 3) х 4) [ –1; )

Бланк ответов.

Фамилия , имя________________________________

1 вариант

А1	А2	А3	А4	А5	В1

Задание В1: Найти область определения функции

Решение:

Дополнительное задание: Найти область определения функции

Бланк ответов.

Фамилия , имя________________________________

2 вариант

А1	А2	А3	А4	А5	С1

Задание С1: Найти область определения функции

Решение:

Дополнительное задание: Найти область определения функции

11B: переменная область видимости | Computer Science Circles

Урок 11 состоит из трех частей A, B, C, которые можно выполнять в любом порядке.

В этом уроке мы объясним концепцию под названием переменной области видимости . Основная идея состоит в том, что можно иметь две разных переменных с одним и тем же именем всякий раз, когда они имеют разные области видимости. Это значительно упрощает написание и редактирование программ, особенно больших. Это также необходимый компонент в более поздней теме, рекурсии.

Пример переменной области видимости

Для этого примера частью нашей программы будет следующая функция:

 def Square(x):
   значение = х * х
   возвращаемое значение 

Это функция, которая вычисляет квадрат числа x , например, квадрат(5) возвращает 25 . Теперь предположим, что мы вызываем Square из другой части программы, которая также использует переменную value для другой цели:

 # здесь начинается основная часть программы
значение = 17
пять в квадрате = квадрат (5)
печать (пять квадратов, значение) 

Вопрос, что будет напечатано в этом сценарии? Есть две возможности, если мы не знаем, как работает Python:

1. Одна из возможностей состоит в том, что Python распознает, что две переменные value должны быть каким-то образом «разделены». Таким образом, вызов в квадрате вернет 25, но значение value в основной части останется равным 17, и мы увидим вывод 25 17 .
2. Другая возможность состоит в том, что когда квадрат , выполняется, перезаписывает существующее значение значением на 25, и мы видим вывод 25 25 .

Посмотрим, что будет на самом деле!

Мы видим, что поведение Python соответствует варианту №1. На самом деле, всякий раз, когда вы вызываете функцию, вы не можете влиять на какие-либо переменные, определенные вне этой функции. Вместо этого любые операторы, присваивающие значения переменным, влияют только на «локальную» переменную, которая находится «внутри» вызова функции.

причина того, что Python и большинство других языков работают таким образом, заключается в том, что он значительно упрощает написание длинных программ с множеством функций. В частности, когда мы определяем новую функцию, нам всегда разрешается использовать любые имена переменных внутри функции (включая общие, такие как result,   temp и i ), даже если они используются где-то еще для других целей. .

Чтобы увидеть это подробнее, посмотрите «Шаг 6 из 8» в визуализаторе. Обратите внимание, что есть два разных значение переменных: одна внутри функции квадрата и одна снаружи (в «глобальной» области).

Упражнение с множественным выбором: внутреннее и внешнее

Что выводит следующая программа?

 x = "внешний" 
 def xReplace(значение): 
 x = значение 
 xReplace("внутренний") 
 print(x) 

Ваш выбор: Выберите одинПрограмма вызывает ошибку.innerouter

Правильно! Оператор x = значение влияет только на локальную версию переменной 9. 0021 x внутри функции. Глобальная версия x не меняется. (Поэтому функция xReplace бесполезна и никогда не дает никакого эффекта.)

Еще одна концепция, аналогичная области действия , — это пространство имен ;  пространство имен похоже на область действия пакета. Таким образом, даже если вы импортируете пакет (например, math ), в котором где-то используется имя переменной

x , оно не пересекается с переменной x , используемой вашей программой, поскольку они находятся в разных пространствах имен.

Правила области видимости: наблюдение

Бывают ситуации, когда мы хотим смешивать переменные из локальной и глобальной области видимости. Одним из распространенных примеров является случай, когда у вас есть некоторая общая переменная, инициализированная один раз в начале программы, но вы также хотите, чтобы ваши функции могли читать эту переменную.

Пример

Чтение глобальной переменной из функции

favouriteTopping=’пепперони’ def orderПицца(n): print(«Хочу», str(n), favouriteTopping, «пицца») заказатьПиццы(3)

Здесь локальная область видимости не содержала переменную с именем favouriteTopping , , но это не вызвало ошибку . Правило Python для оценки переменных заключается в том, что если необходимо оценить переменную, которая не существует в локальной области видимости, она ищет ее в глобальной области видимости. В нашем случае он действительно нашел

избранное, опережая в глобальной области видимости. (В более общем случае, когда одно тело функции вызывает другую функцию, у вас будет три области видимости; Python всегда сначала проверяет «самую локальную» область и переходит пошагово к глобальной области видимости, пока не будет найдена переменная.)

Два приведенных выше примера с orderPizzas и xReplace почти синтаксически идентичны. Почему Python создает новую локальную переменную x в xReplace , но не создает новую избраннуюВверх в orderPizzas ? Правило Python следующее: если вы только читаете переменную, то новая локальная переменная не создается; но если вы запишете переменную хотя бы один раз, то переменная будет рассматриваться как локальная во всем теле функции.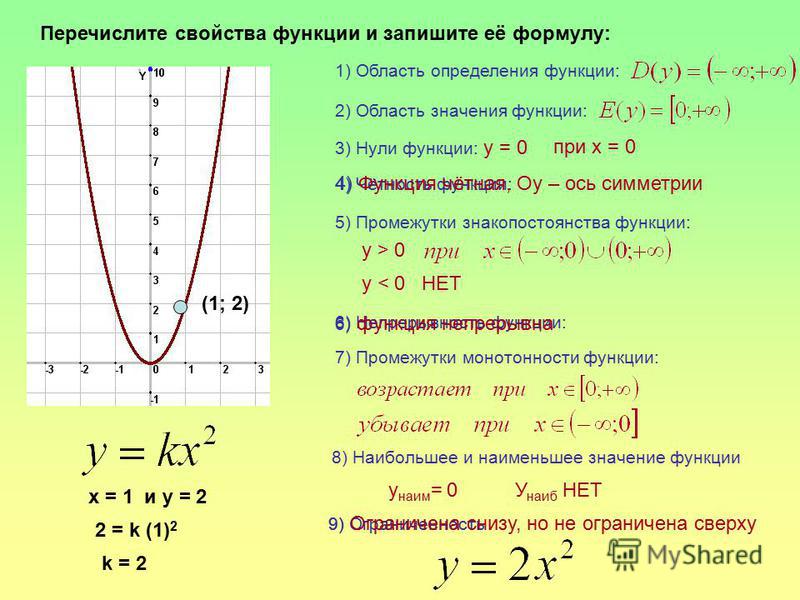 (Это наиболее частая причина UnboundLocalError : см. эти два вопроса [1, 2] в официальной документации по Python. g  до 0 , но терпит неудачу). глобальный  Изменения Как и многие другие вещи, описанный выше нормальный поток работает в 99% всех ситуаций. Но в оставшемся 1% случаев вы действительно можете захотеть изменить глобальную переменную из функции. Python позволяет вам сделать это с помощью глобальный оператор . Это модификация более раннего примера xReplace . Обратите внимание, что мы объявляем переменную как global в функции. Это позволяет изменять глобальное значение внутри функции. Повторяю: внутри функции присвоение имени переменной, определенной в глобальной области, фактически создает отдельную новую переменную локальной области с тем же именем вместо изменения переменной глобальной области (например, resetToZero ). Если вы хотите обновить глобальную переменную, вы должны включить оператор global «variable-name»  внутри функции (например, фиксированный пример xReplace ). Затем Python понимает, что изменения в «имя переменной» в функции предназначены для ссылки на существующую переменную глобальной области видимости. Как мы упоминали ранее, чтение глобальной переменной не требует использования оператора global ; только пишет . На этом урок окончен! Что такое переменная в компьютерном программировании? Переменные используются для хранения информации, на которую можно ссылаться и которой можно манипулировать в компьютерной программе. Они также предоставляют способ маркировки данных описательным именем, чтобы наши программы могли быть более понятными читателю и нам самим. Полезно думать о переменных как о контейнерах, содержащих информацию. Их единственная цель — маркировать и хранить данные в памяти. Затем эти данные можно использовать во всей вашей программе. Присвоение имен переменным известно как одна из самых сложных задач в компьютерном программировании. Когда вы даёте имена переменным, хорошо подумайте об именах. Приложите все усилия, чтобы убедиться, что имя, которое вы присваиваете своей переменной, точно описательно и понятно другому читателю. Иногда этот другой читатель — это вы сами, когда вы пересматриваете программу, написанную месяцами или даже годами ранее. При присвоении переменной используется символ = . Имя переменной идет слева, а значение, которое вы хотите сохранить в переменной, идет справа. irb :001 > first_name = 'Джо' => "Джо" Здесь мы присвоили значение 'Джо' , которое является строкой, переменной first_name . Теперь, если мы хотим сослаться на эту переменную, мы можем это сделать. irb :002 > имя_имя => "Джо" Как видите, теперь мы сохранили строку 'Joe' в памяти для использования во всей программе. Примечание. Убедитесь, что вы не путаете оператор присваивания ( = ) с оператором равенства ( == ). Отдельный символ = присваивает значение, а символ == проверяет, равны ли две вещи. Давайте попробуем кое-что. Посмотрите на следующий сеанс irb. ирб :001 > а = 4 => 4 ирб :002 > б = а => 4 ирб :003 > а = 7 => 7 Каково значение b на данный момент? Попробуйте предположить, а затем введите этот сеанс в irb, чтобы узнать. Вы заметите, что значение b осталось 4, а a было переназначено на 7. Это показывает, что переменные указывают на значения в памяти и не сильно связаны друг с другом. Если это сбивает с толку, не волнуйтесь, у нас есть много упражнений для вас, чтобы сделать эту информацию ясной и очевидной. А если сомневаетесь, всегда пробуйте в irb. До сих пор вы могли назначать данные переменным только из программы. Однако на практике вам нужно, чтобы другие люди могли интересным образом взаимодействовать с вашими программами. Для этого мы также должны позволить пользователю хранить информацию в переменных. Затем мы можем решить, что нам делать с этими данными. Один из способов получить информацию от пользователя — вызвать метод gets . получает означает «получить строку», и это очень весело. Когда вы используете его, программа ждет, пока пользователь 1) введет информацию и 2) нажмет клавишу ввода. Давайте попробуем. Введите эти примеры в irb, чтобы получить представление и немного поэкспериментировать с ними, если хотите. irb :001 > имя = получает Боб => "Боб\n" После кода name = gets компьютер ждал, пока мы введем некоторую информацию. Мы набрали «Боб», а затем нажали ввод, и программа вернула 9.0021 «Боб\n» . \n в конце является символом «новой строки» и представляет собой клавишу ввода. Но мы не хотим, чтобы это было частью нашей строки. Мы будем использовать chomp , связанную с gets , чтобы избавиться от этого — вы можете поместить .chomp после любой строки, чтобы удалить символы возврата каретки в конце. irb:001 > имя = gets.chomp Боб => "Боб" Вот так! Это намного красивее. Теперь мы можем использовать переменную name по своему усмотрению. irb:001 > имя = gets.chomp Боб => "Боб" irb :002 > имя + 'супер здорово!' => "Боб просто супер!" Область действия переменной определяет, где в программе переменная доступна для использования. Область действия переменной определяется тем, где переменная инициализируется или создается. В Ruby область действия переменной определяется определением метода или блоком . У них разное поведение, когда дело доходит до области видимости переменных. Определения области видимости переменных и методов Мы узнаем о методах в следующей главе. На данный момент вы можете думать о методах как о фрагментах многократно используемого кода, которые ваша программа может выполнять много раз во время своего выполнения. Определения методов выглядят следующим образом: имя = 'Кто-то еще' def print_full_name(first_name, last_name) имя = имя_имя + ' ' + фамилия ставит имя конец Как только мы определили метод, мы можем вызывать его столько раз, сколько нам нужно, с разными значениями для first_name и last_name : print_full_name 'Питер', 'Генри' # печатает Питер Генри print_full_name 'Линн', 'Блейк' # печатает Линн Блейк print_full_name 'Kim', 'Johansson' # печатает Ким Йоханссон вставляет имя # печатает Somebody Else С точки зрения переменной области действия, методы имеют автономную область действия. Это означает, что из тела метода можно ссылаться или изменять только переменные, инициализированные в теле метода. Кроме того, переменные, инициализированные внутри тела метода, недоступны вне тела метода. Это немного похоже на непроницаемый пузырь. Таким образом, в приведенном выше коде мы не можем использовать или изменить имя переменная из строки 1 внутри метода print_full_name . Однако мы можем создать и использовать переменную с другим именем , которая локально привязана к методу. Вот почему строки 4 и 5 работают без изменения значения name из строки 1. Область действия переменных и блоки Блок — это фрагмент кода, который следует за вызовом метода, разделенный фигурными скобками {} или сделать/завершить : всего = 0 [1, 2, 3].каждый { |число| всего += число } ставит тотал # 6 всего = 0 [1, 2, 3].each do |number| всего += число конец ставит тотал # 6 В приведенных выше примерах { |число| . .. } — это блок, как и do |number| ... конец . Хотя они выглядят по-разному, поведение идентично. В обоих случаях код может получать доступ и изменять переменные, определенные вне блока. Таким образом, оба блока могут получить доступ и изменить всего . Однако любые переменные, инициализированные внутри блока (например, номер ) не может быть доступен с помощью внешнего кода. Для блоков одно правило, которое мы хотим подчеркнуть, заключается в следующем: Внутренняя область может обращаться к переменным, инициализированным во внешней области, но не наоборот. Взглянув на код, вы проясните это. Допустим, у нас есть файл с именем scope.rb . #scope.rb a = 5 # переменная инициализируется во внешней области видимости 3.раз сделать |n| # вызов метода с блоком a = 3 # доступен здесь, во внутренней области видимости? конец ставит Каково значение a при выводе на экран? Попробуйте. Значение a равно 3. Это связано с тем, что a доступно для внутренней области, созданной 3.times do ... end , что позволило коду переназначить значение a . На самом деле три раза переназначал на 3. Попробуем что-нибудь другое. Мы изменим исходный код scope.rb : # scope.rb а = 5 3.раз сделать |n| # вызов метода с блоком а = 3 b = 5 # b инициализируется во внутренней области видимости конец ставит puts b # доступен ли b здесь, во внешней области видимости? Какой результат вы получили при запуске этой программы? Вы должны были получить сообщение об ошибке примерно такого содержания: scope.rb:11:in ` ': неопределенная локальная переменная или метод `b' для main:Object (ИмяОшибка) Это связано с тем, что переменная b недоступна вне вызова метода с блоком, в котором она инициализирована. Когда мы вызываем , помещаем b , он недоступен в этой внешней области. Прежде чем двигаться дальше, вы должны знать, что существует пять типов переменных. Константы, глобальные переменные, переменные класса, переменные экземпляра и локальные переменные. Хотя вам пока не следует слишком сильно беспокоиться об этих темах, вот краткое описание каждой из них. Константы объявляются путем написания каждой буквы в имени переменной заглавной в соответствии с соглашением Ruby. Они используются для хранения данных, которые никогда не нужно изменять. В то время как большинство языков программирования не позволяют изменять значение, присвоенное константе, Ruby позволяет. Однако он выдаст предупреждение, информирующее вас о том, что для этой переменной было предыдущее определение. То, что вы можете, не означает, что вы должны изменить значение. На самом деле, вы не должны. Константы не могут быть объявлены в определениях методов и доступны во всех областях вашего приложения. Пример объявления константы: MY_CONSTANT = 'Я доступен во всем вашем приложении. ' Глобальные переменные объявляются, когда имя переменной начинается со знака доллара ( $ ). Эти переменные доступны во всем приложении, переопределяя все границы области. Рубисты стараются держаться подальше от глобальных переменных, так как при их использовании могут возникнуть неожиданные сложности. Пример объявления глобальной переменной: $var = 'Я также доступен в вашем приложении.' Переменные класса объявляются путем начала имени переменной с двух знаков @ . Эти переменные доступны экземплярам вашего класса, а также самому классу. Когда вам нужно объявить переменную, связанную с классом, но каждому экземпляру этого класса не требуется собственное значение для этой переменной, вы используете переменную класса. Переменные класса должны быть инициализированы на уровне класса, вне каких-либо определений методов. Затем их можно изменить с помощью определений методов класса или экземпляра. Пример объявления переменной класса: @@instances = 0 Переменные экземпляра объявляются путем начала имени переменной с одного знака @ . Эти переменные доступны во всем текущем экземпляре родительского класса. Переменные экземпляра могут пересекать некоторые границы области, но не все из них. Вы узнаете об этом больше, когда доберетесь до тем ООП, и не должны использовать переменные экземпляра, пока не узнаете о них больше. Пример объявления переменной экземпляра: @var = 'Я доступен во всем текущем экземпляре этого класса.' Локальные переменные — это наиболее распространенные переменные, с которыми вы столкнетесь, и они подчиняются всем границам области видимости. Эти переменные объявляются, начиная имя переменной ни с $ , ни с @ , а также не используя заглавные буквы во всем имени переменной. Пример объявления локальной переменной: var = 'Я должен пройти через границы области видимости.' В этой главе мы говорили о том, как использовать переменные для хранения информации для последующего использования и как получить информацию от пользователя. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт