Как находить определитель матрицы 3 порядка: Найти определитель матрицы третьего порядка

Содержание

3. Определитель третьего порядка. Вычисление определителя с помощью алгеб-раических дополнений (вывод).

Определителем матрицы 3-го порядка это число равное сумме произведений элементов любой строки (столбца) на алгебраические дополнения элементов этой строки ((-1)^ikA_ik).

При вычисление определителя 3-го порядка удобно пользоваться правилом треугольника.

Минором некоторого элемента a_ij определителя k-го порядка называется определитель

n-1 порядка получающегося из одной путем вычеркивания строки и столбца на пересечение которых находятся элементы a_ij . Алгебраическим дополнением a_ijназывается минор умноженный на (-1)ⁱ⁺^jA_ij=(-1)ⁱ⁺^j*M_ij.

Знаки миноров:

Разложение определителя по элементам строки или столбца: Определитель = сумме произведений элементов некоторой строки (столбца) на соответствующие алгебраические дополнения.

4. Обратная матрица (определение, вывод формулы).

Если определитель квадратной матрицы не равен 0, то такая матрица называется не выраженной, в противном случае выраженной. Матрица обратная квадратной матрице А – это квадратная матрица В удовлетворяющая равенству АВ=ВА. Обратная матрица существует только для квадратной и имеет тот же порядок. Обозначается А^-1.

АА^-1=А^-1А=Е. Алгоритм нахождения обратной матрицы: 1) Найти определитель матрицы А(∆А). Если ∆А = 0, то А^-1не существует. Если ∆А≠0, то А^-1существует, то переходим к п.2. 2) Составляем матрицу алгебраических дополнений элементов матрицы А. 3) Записать обратную матрицу А^-1А^-1= 1/∆A*Ã

5. Системы линейных уравнений, основные понятия.

Системой линейных уравнений (СЛУ) состоящий из m – уравнений и n – неизвестных называется система вида:

(1)

где a_ij (i=1,m , j=1,n) – коэффициенты, b_i – свободные члены, x_j – неизвестное.

Систему (1) можно записывать в матричной форме (А*Х=В) (2), где

Расширенной матрицей системы (1) называется матрица (Ã(А|В)) дополненная свободным столбцам.

Решить систему значит найти все её неизвестные. Решением системы называют такой набор значений x₁=  ₁, x₂=  ₂, … , x_n=  _n, при котором все уравнения систем (1) обращаются в верные равенства. Решение систем можно так же записать матрицу столбца. СЛУ называется совместной, если она имеет хотя бы 1 решение и не совместной если она не имеет решений.

6. Решение систем линейных уравнений матричным способом.

Матричный способ: А*Х=В (2) домножим обе части равенства (2) на матрицу А^-1 слева.

А^-1*А*Х= А^-1*В ≡ Е*Х= А^-1*В ≡ Х= А^-1*В (3). Отыскивание решения по формуле (3) называется матричным способом.

7. Решение систем линейных уравнений методом Крамера (вывод).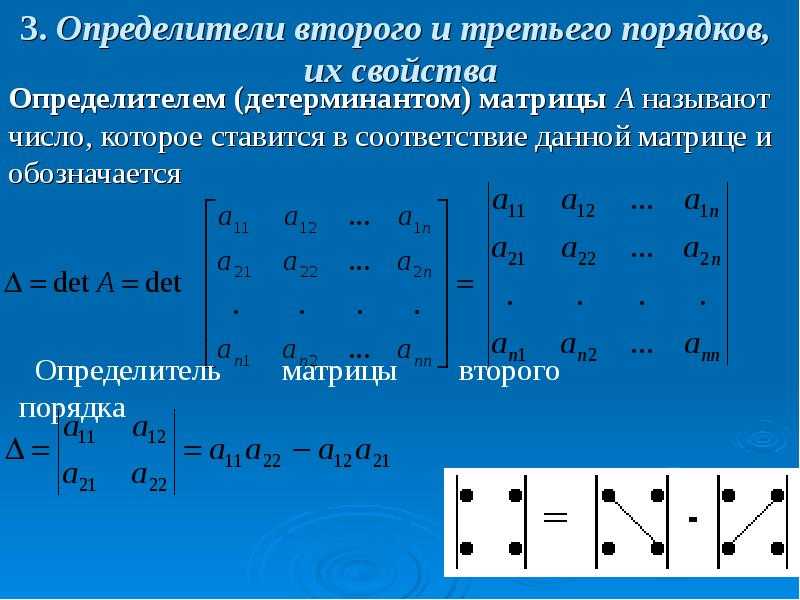

Для решения СЛУ при m=n можно использовать метод Крамера. Рассмотрим случай m=n=3:

если ∆≠0, то решение существует и одно ( )
если ∆=0, но ∆₁≠0, ∆₂≠0, ∆₃≠0, то решения нет
если все ∆=∆₁=∆₂=∆₃=0, то решений бесконечное множество.

8. Ранг матрицы, вычисление ранга матрицы.

Минором k-го порядка произвольной матрицы А называется определитель, составленный из элементов матрицы, расположенных на пересечении каких либо

k-строк k-столбцов. Рангом матрицы А называется наибольший из порядков её миноров отличных от нуля.

Теорема 1:

При элементарных преобразованиях ранг матрицы не изменяется.

Теорема 2:

Ранг ступенчатой матрицы равен количеству её не нулевых строк

Следствие:

Ранг произвольной матрицы равен рангу соответствующей ей ступенчатой матрицы.

9. Решение систем линейных уравнений методом Жордана-Гаусса. Теорема Кронекера-Капелли.

Метод Гаусса – это универсальный способ решения СЛУ с произвольным количеством уравнений и неизвестных.

Достоинство:

1. Менее трудоемкий чем другие методы

2. Позволяет однозначно установить наличие или отсутствие решения, а в случае совместимости найти единственное решение ии бесконечное множество решений.

3. Определяет ранг матрицы системы.

В методе Гаусса применяют прямой и обратный ход. Прямой ход: расширенная матрица системы приводится к ступенчатому виду. Обратный ход: последовательное определения неизвестных из ступенчатой системы соответствующей ступенчатой матрицы.

Теорема Кронекера – Капели: СЛУ (1) совместно имеет решение тогда и только тогда, когда ранг матрицы систем равен рангу расширенной матрицы этой системы.

rang(A) = rang(A|B)

Решение приведением только расширенной матрицы к ступенчатому виду, результаты исследования можно представить в виде схемы:

Если r < n т.е. количество ненулевых строк, а значит количество уравнений меньше количества неизвестных. Пусть r переменных: x₁,x₂,…,x_r соответствуют найденному рангу, тогда их называют основными (или базисными) оставшиеся n-r переменных x_r₊₁,x_r₊₂,…,x_n называются неосновными или свободными. Свободные переменные могут принимать произвольные значения. Если всем свободным значениям придать значение = 0, то найденное решение называется базисным. Выражая все базисные переменные через свободные можно получить общее решение системы придовая при этом свободным переменным произвольные значения, тогда общее решение будет иметь вид:

Определитель матрицы 3 порядка: как считать, формула

Содержание:

Определитель матрицы 3 порядка, описание
Правила для нахождения
Нахождение методом треугольника
Метод Саррюса
Свойства определителя

Содержание

Определитель матрицы 3 порядка, описание

Правила для нахождения
Нахождение методом треугольника
Метод Саррюса
Свойства определителя

Определитель матрицы 3 порядка, описание

Детерминант или определитель матрицы третьего порядка вида $A=\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{pmatrix}$ является сопоставляемое с ним число

$\left|A\right|=\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}=a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-(a_{13}a_{22}a_{31}+a_{12}a_{21}a_{33}+a_{11}a_{23}a_{32})$

Для обозначения данной величины используют символы: |А|, Δ, det A.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Правила для нахождения

Для вычисления детерминанта матрицы 3×3 не нужно заучивать формулу. Данное число можно найти с помощью двух способов:

правила треугольников;
правила Саррюса.

Нахождение методом треугольника

Правило основывается на том, что произведение диагональных составляющих и произведения вершин двух треугольников уменьшаемой матрицы суммируются. Произведение диагональных элементов и произведения вершин треугольников в вычитаемой матрице записываются со знаком минус.

Схематическое изображение рассматриваемого правила выглядит так:

По схеме можно восстановить формулу нахождения определителя матрицы третьего порядка, которая приведена в определении детерминанта:

$a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{13}a_{22}a_{31}-a_{12}a_{21}a_{33}-a_{11}a_{23}a_{32}=a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-(a_{13}a_{22}a_{31}+a_{12}a_{21}a_{33}+a_{11}a_{23}a_{32})$

Пример

Найти определитель матрицы:

$A=\begin{pmatrix}1&3&4\\0&2&1\\1&5&-1\end{pmatrix}$

Решение

$\left|A\right|=\begin{vmatrix}21&12&14\\21&12&56\\25&12&14\end{vmatrix}=21\times12\times14+12\times56\times25+14\times12\times21-14\times12\times25-12\times56\times21-21\times12\times14=2016$

Метод Саррюса

Для нахождения определителя матрицы 3×3 необходимо соблюсти условия в следующей последовательности:

два первых столбца приписать по левую сторону от детерминанта;
произведения компонентов главной диагонали и ей параллельных записать с положительным знаком;
произведения элементов, расположенных на побочной и параллельных ей диагоналях, записать с отрицательным знаком.

Вычисление определителя матрицы по рассматриваемому правилу схематически можно изобразить так:

Пример

Рассчитать по методу Сюрраса детерминант матрицы

$A=\begin{pmatrix}1&2&3\\4&5&6\\7&8&9\end{pmatrix}$

Решение

$\left|A\right|=\begin{vmatrix}1&2&3\\4&5&6\\7&8&9\end{vmatrix}\;=\begin{vmatrix}1&2&3\\4&5&6\\7&8&9\end{vmatrix}\begin{array}{c}1\\4\\7\end{array}\begin{array}{c}2\\5\\8\end{array}=1\times5\times9+2\times6\times7+3\times4\times8-3\times5\times7-1\times6\times8-2\times4\times9=0$

Свойства определителя

Преобразование столбцов и строк незначительными действиями не оказывает влияния на значение детерминанта.
Перемена строк и столбцов местами влечет за собой изменение значения детерминанта на противоположное.
Детерминант треугольной матрицы можно вычислить путем умножения составляющих, находящихся на главной диагонали.

Насколько полезной была для вас статья?

Рейтинг: 2.00 (Голосов: 4)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

Видео с вопросами: Вычисление определителя третьего порядка заданной матрицы

Стенограмма видео

Найдите определитель матрицы один, два, три; три, два, два; ноль, девять, восемь.

Итак, в этой задаче нас просят найти определитель матрицы три на три. Теперь, чтобы найти определитель матрицы три на три, у нас есть общее правило. Итак, если мы посмотрим сюда, у нас есть матрица три на три 𝑎, 𝑏, 𝑐; 𝑑, 𝑒, 𝑓; 𝑔, ℎ, 𝑖. Таким образом, эти вертикальные линии говорят нам, что мы смотрим на определитель. Они означают определитель матрицы 𝑎, 𝑏, 𝑐; 𝑑, 𝑒, 𝑓; 𝑔, ℎ, 𝑖.

И чтобы найти определитель, он равен 𝑎 — потому что это первый член в первой строке — умноженный на определитель подматрицы, которая образуется, когда мы удаляем строку и столбец, в которых находится 𝑎. Таким образом, это будет подматрица 𝑒, 𝑓, ℎ, 𝑖, поэтому 𝑎 умножается на член в этой подматрице. Тогда минус 𝑏. И это потому, что у нас есть шаблон с нашими коэффициентами. Таким образом, мы выбираем каждый из первых терминов в первой строке. Но они следуют шаблону положительный, отрицательный, положительный.

Таким образом, как я уже сказал, это минус 𝑏, умноженный на подматрицу два на два, образованную, если вы удалите столбец и строку, в которой находится 𝑏. Плюс 𝑐, умноженный на подматрицу два на два, определитель этой , то есть 𝑑, 𝑒, 𝑔, ℎ. Итак, отлично, теперь мы знаем, как это решить. Давайте продолжим и найдем определитель нашей матрицы.

Таким образом, используя наше правило, мы можем сказать, что определитель матрицы один, два, три; три, два, два; ноль, девять, восемь можно вычислить как единицу, умноженную на определитель подматрицы два на два два, два, девять, восемь минус два, умноженную на определитель подматрицы два на два три, два, ноль, восемь плюс три умножается на определитель подматрицы три, два, ноль, девять. И я собираюсь просмотреть третий раздел, просто чтобы напомнить нам, как мы его нашли.

Итак, мы выбрали три, потому что это третий термин в верхней строке. И это положительно, потому что наш шаблон говорит, что первый столбец положительный, второй столбец отрицательный, третий столбец положительный и так далее. И мы нашли подматрицу три, два, ноль, девять, удалив строку и столбец, в которых была тройка. И тогда у нас осталось три, два, ноль, девять.

Хорошо, отлично. Итак, давайте теперь узнаем значение этого. Итак, чтобы вычислить значение нашего определителя матрицы три на три, нам нужно найти определители наших подматриц два на два. Мы делаем это, используя это общее правило. Если у нас есть определитель матрицы 𝑎, 𝑏, 𝑐, 𝑑, он равен 𝑎, умноженному на 𝑑 минус 𝑏, умноженному на 𝑐. Итак, мы собираемся использовать это, чтобы найти значение определителя нашей матрицы три на три.

Итак, прежде всего, умножим единицу на. Тогда у нас есть два, умноженные на восемь — потому что это наши 𝑎 и наши 𝑑 — минус два, умноженные на девять, наши 𝑏 и наши 𝑐. И тогда у нас будет минус два, умноженное на три, умноженное на восемь, минус два, умноженное на ноль, и, наконец, плюс три, умноженное на три, умноженное на девять, минус два, умноженное на ноль.

Хорошо, отлично. Итак, у нас теперь есть форма, в которой мы можем теперь просто продолжить и вычислить значение нашего определителя. Так что это даст нам отрицательную двойку. И это потому, что два, умноженные на восемь, равно 16, 16 минус 18, потому что два, умноженные на девять, равно 18, дают минус два. И это, умноженное на один, равно минус двум. Итак, это минус два минус 48 плюс 81, что равно 31. Следовательно, мы можем сказать, что определитель матрицы один, два, три; три, два, два; ноль, девять, восемь равно 31.

Миноры матрицы 3×3

Математические сомнения
Матрицы
Несовершеннолетние

Определитель квадратной подматрицы второго порядка при выходе из строки и столбца элемента называется минором этого элемента в квадратной матрице третьего порядка.

Квадратная матрица три на три содержит девять элементов, расположенных в трех строках и трех столбцах. При вычислении младшего элемента остальные записи в этой строке и столбце не учитываются. Он образует квадратную матрицу два на два с оставшимися элементами, и определитель этой матрицы называется минором соответствующего элемента. Таким образом, для девяти элементов матрицы порядка $3$ можно вычислить девять миноров.

$D$ $\,=\,$ $\begin{bmatrix} d_{11} & d_{12} & d_{13} \\ d_{21} & d_{22} & d_{23} \\ d_{31} & d_{32} & d_{33} \\ \end{bmatrix}$

Теперь научимся находить минор каждого элемента матрицы $D$ порядка $3 \times 3$ . Для нахождения миноров элементов в матрице порядка $3$ необходимы знания по нахождению определителя матрицы второго порядка.

Миноры для элементов первой строки

Посмотрите на элементы первой строки матрицы $D$. Элементы $d_{11}$, $d_{12}$ и $d_{13}$ — это элементы первой строки матрицы $D$. Их миноры обозначаются $M_{11}$, $M_{12}$ и $M_{13}$ соответственно. Теперь давайте узнаем, как найти минор каждого элемента в первой матрице $3 \times 3$.

Младший элемент записи в первой строке и первом столбце

Запись $d_{11}$ является элементом первой строки и первого столбца. Оставьте элементы в первой строке и записи в первом столбце. Остальные элементы образуют квадратную матрицу порядка $2$.

Затем найдите определитель матрицы для вычисления минора элемента $d_{11}$, который в матричной алгебре обозначается как $M_{11}$.

$M_{11}$ $\,=\,$ $\begin{vmatrix} d_{22} & d_{23} \\ d_{32} & d_{33} \\ \end{vmatrix}$

$\поэтому\,\,\,$ $M_{11}$ $\,=\,$ $d_{22} \times d_{33}\,-\,d_{23} \times d_{32 }$

Минор записи в первой строке и втором столбце

Элемент $d_{12}$ является записью в первой строке и втором столбце. Оставьте записи в первой строке и записи во втором столбце. Оставшиеся элементы образуют квадратную матрицу порядка $2\times 2$.

Теперь вычислите определитель матрицы для нахождения минора элемента $d_{12}$, который в математике обозначается как $M_{12}$.

$M_{12}$ $\,=\,$ $\begin{vmatrix} d_{21} & d_{23} \\ d_{31} & d_{33} \\ \end{vmatrix}$

$\следовательно\,\,\,$ $M_{12}$ $\,=\,$ $d_{21} \times d_{33}\,-\,d_{23} \times d_{31} $

Минор записи в первой строке и третьем столбце

Запись $d_{13}$ является элементом в первой строке и третьем столбце. Оставьте элементы в первой строке и записи в третьем столбце. Оставшиеся элементы образуют квадратную матрицу второго порядка.

Теперь найдите определитель матрицы для вычисления минора элемента $d_{13}$, который в матрицах просто представлен как $M_{13}$.

$M_{13}$ $\,=\,$ $\begin{vmatrix} d_{21} & d_{22} \\ d_{31} & d_{32} \\ \end{vmatrix}$

$\поэтому\,\,\,$ $M_{13}$ $\,=\,$ $d_{21} \times d_{32}\,-\,d_{22} \times d_{31} $

Миноры для элементов второй строки

Сосредоточьтесь на элементах второй строки матрицы $D$. Элементы $d_{21}$, $d_{22}$ и $d_{23}$ являются элементами второй строки матрицы $D$. Миноры этих элементов представлены $M_{21}$, $M_{22}$ и $M_{23}$ соответственно. Теперь давайте узнаем, как найти минор каждой записи во второй строке матрицы третьего порядка.

Минор записи во второй строке и первом столбце

Элемент $d_{21}$ является записью во второй строке и первом столбце. Оставьте элементы во второй строке и элементы в первом столбце. По остальным элементам он образует матрицу порядка $2\times 2$.

Теперь найдите определитель матрицы для вычисления минора элемента $d_{21}$, который обозначается $M_{21}$ в этой матричной алгебре.

$M_{21}$ $\,=\,$ $\begin{vmatrix} d_{12} & d_{13} \\ d_{32} & d_{33} \\ \end{vmatrix}$

$\поэтому\,\,\,$ $M_{21}$ $\,=\,$ $d_{12} \times d_{33}\,-\,d_{13} \times d_{32 }$

Минор записи во второй строке и втором столбце

Элемент $d_{22}$ является элементом второй строки и второго столбца. Записями во второй строке и записями во втором столбце пренебречь. Оставшиеся элементы образуют квадратную матрицу второго порядка.

Затем оцените определитель матрицы, чтобы найти минор элемента $d_{22}$. В математике это обозначается как $M_{22}$.

$M_{22}$ $\,=\,$ $\begin{vmatrix} d_{11} & d_{13} \\ d_{31} & d_{33} \\ \end{vmatrix}$

$\поэтому\,\,\,$ $M_{22}$ $\,=\,$ $d_{11} \times d_{33}\,-\,d_{13} \times d_{31} $

Минор записи во второй строке и третьем столбце

Запись $d_{23}$ является элементом во второй строке и третьем столбце. Теперь оставьте элементы во второй строке и записи в третьем столбце. Таким образом, из остальных элементов получается квадратная матрица порядка $2\times 2$.

Найдите определитель матрицы, чтобы найти минор элемента $d_{23}$ и обозначается $M_{23}$ просто в матрицах.

$M_{23}$ $\,=\,$ $\begin{vmatrix} d_{11} & d_{12} \\ d_{31} & d_{32} \\ \end{vmatrix}$

$\поэтому\,\,\,$ $M_{23}$ $\,=\,$ $d_{11} \times d_{32}\,-\,d_{12} \times d_{31} $

Миноры для элементов третьей строки

Наконец, сосредоточимся на элементах в третьей строке матрицы $D$. Элементы $d_{31}$, $d_{32}$ и $d_{33}$ являются элементами третьей строки матрицы $D$. Миноры этих записей обозначаются $M_{31}$, $M_{32}$ и $M_{33}$ соответственно. Теперь давайте узнаем, как оценить младшие из них в третьей строке матрицы.

Второстепенная запись в третьей строке и первом столбце

Элемент $d_{31}$ является элементом в третьей строке и первом столбце. Оставьте записи в третьей строке и записи в первом столбце. Из оставшихся элементов он образует квадратную матрицу размером $2 \times 2$.

Затем найдите определитель матрицы для вычисления минора элемента $d_{31}$, который в матричной алгебре обозначается как $M_{31}$.

$M_{31}$ $\,=\,$ $\begin{vmatrix} d_{12} & d_{13} \\ d_{22} & d_{23} \\ \end{vmatrix}$

$\поэтому\,\,\,$ $M_{31}$ $\,=\,$ $d_{12} \times d_{23}\,-\,d_{13} \times d_{22 }$

Минор записи в третьей строке и втором столбце

Элемент $d_{32}$ является записью в третьей строке и втором столбце. Не учитывать записи в третьей строке и записи во втором столбце. По остальным элементам образует квадратную матрицу порядка $2\times 2$.