Sin 75 вычислить: Mathway | Популярные задачи

36Risolvere per ?cos(x)=1/27Risolvere per xsin(x)=-1/28Преобразовать из градусов в радианы2259Risolvere per ?cos(x)=( квадратный корень из 2)/210Risolvere per xcos(x)=( квадратный корень из 3)/211Risolvere per xsin(x)=( квадратный корень из 3)/212Графикg(x)=3/4* корень пятой степени из x 13Найти центр и радиусx^2+y^2=914Преобразовать из градусов в радианы120 град. 2+n-72)=1/(n+9)

sin 75 градусов и cos 75 градусов , заменяя 75 градусов на 45 градуса + 30 градусов — Знания.site

Последние вопросы

• Алгебра

  32 минут назад

  Доведіть, що 3¹² — 3¹⁰ кратне 8.

• Алгебра

  42 минут назад

  помогите пожалуйста сделать контрольную работу!умоляю!!!!​

• Алгебра

  52 минут назад

  Найди сочетательное свойство умножения рациональных чисел

• Алгебра

  57 минут назад

  Заполни пропуски так, чтобы получилось сочетательное свойство умножения. Запиши числа в полях ответа. 

• Алгебра

  1 час назад

  √12-6√3+√3 = помогите пожалуйста

• Алгебра

  1 час назад

  f(x) = 3cos x — 4 корінь 3 степеня з х

• Алгебра

  1 час назад

  √4-2√3-√3= помогите пожалуйста

• Алгебра

  1 час назад

  Помогите пожалуйста!!! Знайти корені рівняння 2х2 ( в квадрате) — х + 3 = 0

• Алгебра

  1 час назад

  Одне з натуральних чисел на 12 більше за друге, а їх добуток дорівнює 405. 2-2x=0 Помогите пж

• Алгебра

  2 часа назад

  Задача по математике

• Алгебра

  2 часа назад

  СРОЧНО!!!(m=n)2 m чення при m = n (n-m)2 + m2-n2 + 5m +3n m+n​

• Алгебра

  2 часа назад

  Один із катетів прямокутного трикутника на 9 см менший від гіпотенузи, а другий на 7 см більший, ніж перший. Знайдіть гіпотенузу.Срочно !!!!!​

Все предметы

English

United States

Polski

Polska

Bahasa Indonesia

Indonesia

English

India

Türkçe

Türkiye

English

Philippines

Español

España

Português

Brasil

Русский

Россия

How much to ban the user?

1 hour 1 day 100 years

Калькулятор — sin(75) — Солуматы

Sin, расчет онлайн

Резюме:

Тригонометрическая функция sin для вычисления синуса угла в радианах, градусов или градианов.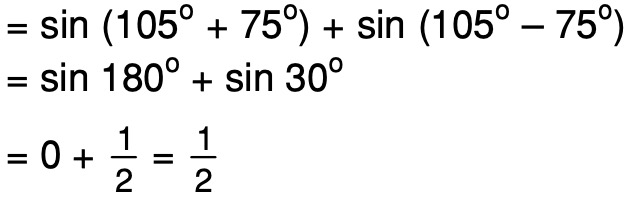

sin online

---

Описание:

Калькулятор позволяет использовать большинство из тригонометрических функций , есть возможность вычислить синус , косинус и касательная угла через одноименные функции.

Тригонометрическая функция синус отметил синус , позволяет вычислить

синус угла онлайн , можно использовать разные угловые единицы: градус, градус и радианы, которые по умолчанию являются угловыми единицами.

1. Расчет синуса

Вычисление синуса угла в радианах

Калькулятор синуса позволяет с помощью функции sin вычислить онлайн синус синус угла в радианах, вы должны сначала выберите нужную единицу, нажав на кнопку параметров расчетного модуля. После этого можно приступать к расчетам.

Чтобы вычислить синус онлайн от `pi/6`, введите sin(`pi/6`), после вычисления результат `1/2` возвращается.

Обратите внимание, что функция синуса способна распознавать некоторые специальные углы и делать расчеты со специальными связанными значениями в точной форме.

Вычислить синус угла в градусах

Чтобы вычислить синус угла в градусах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.

Чтобы вычислить синус 90, введите sin(90). результат 1 возвращается.

Вычислить синус угла в градусах

Чтобы вычислить синус угла в градианах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.

Чтобы вычислить синус 50, введите sin(50), после вычисления, возвращается результат `sqrt(2)/2`.

Обратите внимание, что функция синуса способна распознавать некоторые специальные углы и выполнять исчисление со специальными ассоциированными точными значениями.

2. Таблица специальных синусоидальных значений

Синус допускает некоторые специальные значения, которые калькулятор может определить в точных формах. Вот таблица значений общего синуса :

sin(`2*pi`)	`0`
sin(`pi`)	`0`
sin(`pi/90 `2`)	7
sin(`pi/4`)	`sqrt(2)/2`
sin(`pi/3`)	`sqrt(3)/2`
sin(`pi/6`)	`1/2`
sin(`2*pi/3`)	`sqrt(3) /2`
sin(`3*pi/4`)	`sqrt(2)/2`
sin(`5*pi/6`)	`1/2`
sin(`0`)	`0`
sin(`-2*pi`)	`0`
sin(`-pi`) 7 0907 8 `		sin(`pi/2`)	`-1`
sin(`-pi/4`)	`-sqrt(2)/2`
sin(`-pi/3`)	`-sqrt(3)/2`
sin(`-pi/6`)	`-1/2`
sin(`-2*pi/3`)	`-sqrt(3)/2`
sin( `-3*pi/4`)	`-sqrt(2)/2`
sin(`-5*pi/6`)	`-1/2`

3. Основные свойства

`AA x в RR, k в ZZ`,

• `sin(-x)= -sin(x)`
• `sin(x+2*k*pi)=sin(x)`
• `sin(pi-x)=sin(x)`
• `sin(pi+x)=-sin(x)`
• `sin(pi/2-x)=cos(x)`
• `sin(pi/2+x)=cos(x)`

Производная синуса

Производная синуса равна cos(x).

Первообразная синуса

Первообразная синуса равна -cos(x).

Свойства функции синуса

Функция sine является нечетной функцией, для каждого действительного x `sin(-x)=-sin(x)`. Следствием для кривой, представляющей синусоидальную функцию, является то, что она допускает начало отсчета как точку симметрии.

Уравнение с синусом

Калькулятор имеет решатель, который позволяет решать уравнение с синусом вида cos(x)=a . Расчеты для получения результата детализированы, поэтому можно будет решать уравнения типа `грех(х)=1/2` или `2*sin(x)=sqrt(2)` с этапами расчета.

Синтаксис:

sin(x), где x — мера угла в градусах, радианах или градах.

---

Примеры:

sin(`0`), возвращает 0

---

Производный синус:

можно использовать калькулятор производной, который позволяет вычислить производную функции синуса

производная sin(x) является производной(`sin(x)`)=`cos(x)`

---

Синус первообразной :

Калькулятор первообразной позволяет вычислить первообразную функции синуса.

Первопроизводная sin(x) является первообразной(`sin(x)`)=`-cos(x)`

---

Предел синуса :

Калькулятор предела позволяет вычислить пределы функции синуса.

предел sin(x) is limit(`sin(x)`)

---

Обратная функция синуса :

обратная функция синуса — это функция арксинуса, отмеченная как arcsin.

---

---

Графический синус :

Графический калькулятор может отображать синусоидальную функцию в заданном интервале.

---

---

Свойство функции синуса:

Функция синуса является нечетной функцией.

---

Расчет онлайн с синусом (sine)

См. также

Список связанных калькуляторов:

• Арккосинус : arccos. Функция arccos позволяет вычислять арккосинус числа. Функция arccos является обратной функцией функции косинуса.
• Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
• Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
• Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
• Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
• Косеканс: косеканс Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
• Котангенс : котан. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
• Тригонометрическое расширение: expand_trigo. Калькулятор позволяет получить тригонометрическое разложение выражения.
• Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
• Упростить калькулятор: упростить. Калькулятор, который может упростить алгебраическое выражение онлайн.
• Секанс : сек. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
• Синус : синус. Тригонометрическая функция sin для вычисления греха угла в радианах, градусов или градианов.
• Тангенс: коричневый. Тригонометрическая функция тангенса для вычисления тангенса угла в радианах, градусов или градианов.

Прочие ресурсы

• Исправленные упражнения на числовые функции
• Бесплатные онлайн математические игры про функции — производная — примитив — f(x)=0
• Расчет с использованием обычных математических функций

 

Найти значение sin 75°

Дата последнего обновления: 28 февраля 2023 г.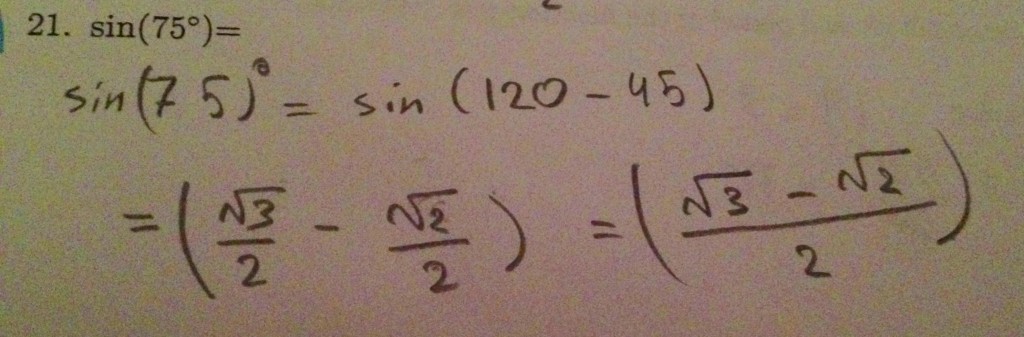

•

Всего просмотров: 268,5 тыс.0002 Просмотров сегодня: 4.53k

Ответить

Проверено

268.5k+ просмотров

Подсказка: Чтобы решить этот вопрос, мы будем использовать тригонометрические отношения составных углов. Прежде всего, разберемся, что такое составные углы и каковы различные тригонометрические соотношения составных углов. Затем подберем тригонометрическое отношение синусов составных углов. Таким образом, мы можем найти значение sin 75°.

Полный пошаговый ответ:
Угол называется составным углом, если этот угол образован сложением или вычитанием двух углов.
Например, если один из углов равен ∠A, а другой угол равен ∠B, то ∠(A + B) является примером составного угла. Другой составной угол, который можно составить из ∠A и ∠B, может быть ∠(A – B).
Тригонометрические отношения составных углов не обладают свойством ассоциирования.
Например, tan (A + B) $\ne $ tan A + tan B.
Существуют специальные формулы для составных углов. Формулы сложных углов синусов, косинусов и тангенсов тригонометрических соотношений даны следующим образом:
sin (A + B) = sin A $\times $ cos B + cos A $\times $ sin B
sin (A ─ B) = sin A $\times $ cos B + cos A $\times $ sin B
cos (A + B) = cos A $\times $ cos B ─ sin A $\times $ sin B
sin (A ─ B) = cos A $\times $ cos B + sin A $\times $ sin B
tan (A + B) = $\dfrac{\operatorname{tanA}+tanB}{1-\operatorname{tanAtanB}}$
tan (A ─ B) = $\dfrac{\operatorname{tanA}-tanB} {1+\operatorname{tanAtanB}}$
Нам нужно найти значение sin 75°. 75 также можно записать как 30 + 45.
$\Rightarrow $ sin 75° = sin (30° + 45°)
Применим тригонометрические отношения сложных углов.
$\Rightarrow $ sin 75° = sin 30° $\times $ cos 45° + cos 30° $\times $ sin 45°
Мы знаем, что sin 30° = $\dfrac{1}{2}$, cos 45° = sin 45° = $\dfrac{1}{\sqrt{2}}$ и cos 30° = $\dfrac{\sqrt{3}}{2}$.
$\Rightarrow $ sin 75° = $\dfrac{1}{2}\times \dfrac{1}{\sqrt{2}}+\dfrac{\sqrt{3}}{2}\times \dfrac{ 1}{\sqrt{2}}$

$\Rightarrow $ sin 75° = $\dfrac{1+\sqrt{3}}{2\sqrt{2}}$

Примечание: Студентам рекомендуется наизусть выучить формулы тригонометрических отношений сложных углов.