Радиус вписанной окружности в прямоугольный треугольник формула. Формулы радиусов вписанных и описанных окружностей правильных многоугольников
Очень часто при решении геометрических задач приходится совершать действия со вспомогательными фигурами. Например, находить радиус вписанной или описанной окружности и т.д. Данная статья покажет, как находить радиус окружности, описанной около треугольника. Или, иными словами, радиус окружности, в которую вписан треугольник.
Как найти радиус окружности, описанной около треугольника – общая формула
Общая формула выглядит следующим образом: R = abc/4√p(p – a)(p – b)(p – c), где R – радиус описанной окружности, p – периметр треугольника поделенный на 2 (полупериметр). a, b, c – стороны треугольника.
Найти радиус описанной окружности треугольника, если a = 3, b = 6, c = 7.
Таким образом, исходя из вышеприведенной формулы, вычисляем полупериметр:
p = (a + b + c)/2 = 3 + 6 + 7 = 16. => 16/2 = 8.
Подставляем значения в формулу и получаем:
R = 3 × 6 × 7/4√8(8 – 3)(8 – 6)(8 – 7) = 126/4√(8 × 5 × 2 × 1) = 126/4√80 = 126/16√5.
Ответ: R = 126/16√5
Как найти радиус окружности, описанной около равностороннего треугольника
Для нахождения радиуса окружности, описанной около равностороннего треугольника, существует довольно простая формула: R = a/√3, где a – величина его стороны.
Пример: Сторона равностороннего треугольника равна 5. Найти радиус описанной окружности.
Так как у равностороннего треугольника все стороны равны, для решения задачи нужно всего лишь вписать ее значение в формулу. Получим: R = 5/√3.
Ответ: R = 5/√3.
Как найти радиус окружности, описанной около прямоугольного треугольника
Формула выглядит следующим образом: R = 1/2 × √(a² + b²) = c/2, где a и b – катеты и c – гипотенуза. Если сложить квадраты катетов в прямоугольном треугольнике, то получим квадрат гипотенузы. Как видно из формулы, данное выражение находится под корнем. Вычислив корень из квадрата гипотенузы, мы получим саму длину. Умножение получившегося выражения на 1/2 в итоге приводит нас к выражению 1/2 × c = c/2.
Пример: Вычислить радиус описанной окружности, если катеты треугольника равны 3 и 4. Подставим значения в формулу. Получим: R = 1/2 × √(3² + 4²) = 1/2 × √25 = 1/2 × 5 = 2.5.
В данном выражение 5 – длина гипотенузы.
Ответ: R = 2.5.
Как найти радиус окружности, описанной около равнобедренного треугольника
Формула выглядит следующим образом: R = a²/√(4a² – b²), где a – длина бедра треугольника и b – длина основания.
Пример: Вычислить радиус окружности, если его бедро = 7, а основание = 8.
Решение: Подставляем в формулу данные значения и получаем: R = 7²/√(4 × 7² – 8²).
R = 49/√(196 – 64) = 49/√132. Ответ можно записать прямо так.
Ответ: R = 49/√132
Онлайн ресурсы для вычисления радиуса окружности
Можно очень легко запутаться во всех этих формулах. Поэтому при необходимости можно воспользоваться онлайн калькуляторами, которые помогут вам в решении задач на нахождение радиуса. Принцип работы таких мини-программ очень прост.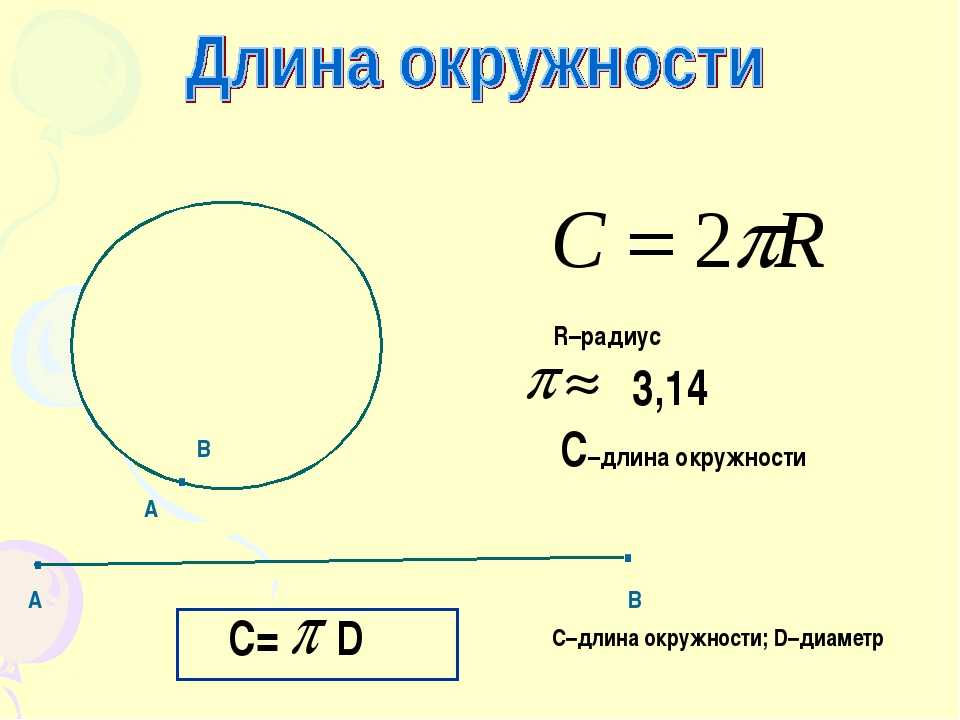 Подставляете значение стороны в соответствующее поле и получаете готовый ответ. Можно выбрать несколько вариантов округления ответа: до десятичных, сотых, тысячных и т.д.
Подставляете значение стороны в соответствующее поле и получаете готовый ответ. Можно выбрать несколько вариантов округления ответа: до десятичных, сотых, тысячных и т.д.
Окружность, вписанная в треугольник
Существование окружности, вписанной в треугольник
Напомним определение биссектрисы угла .
Определение 1 . Биссектрисой угла называют луч, делящий угол на две равные части.
Теорема 1 (Основное свойство биссектрисы угла) . Каждая точка биссектрисы угла находится на одном и том же расстоянии от сторон угла (рис.1).
Рис. 1
Доказательство D , лежащую на биссектрисе угла BAC , и DE и DF на стороны угла (рис.1). Прямоугольные треугольники ADF и ADE равны , поскольку у них равны острые углы DAF и DAE , а гипотенуза AD – общая. Следовательно,
Следовательно,
DF = DE,
что и требовалось доказать.
Теорема 2 (обратная теорема к теореме 1) . Если некоторая , то она лежит на биссектрисе угла (рис.2).
Рис. 2
Доказательство . Рассмотрим произвольную точку D , лежащую внутри угла BAC и находящуюся на одном и том же расстоянии от сторон угла. Опустим из точки D перпендикуляры DE и DF на стороны угла (рис.2). Прямоугольные треугольники ADF и ADE равны , поскольку у них равны катеты DF и DE , а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.
Определение 2 . Окружность называют окружностью, вписанной в угол , если она сторон этого угла.
Теорема 3 . Если окружность вписана в угол, то расстояния от вершины угла до точек касания окружности со сторонами угла равны.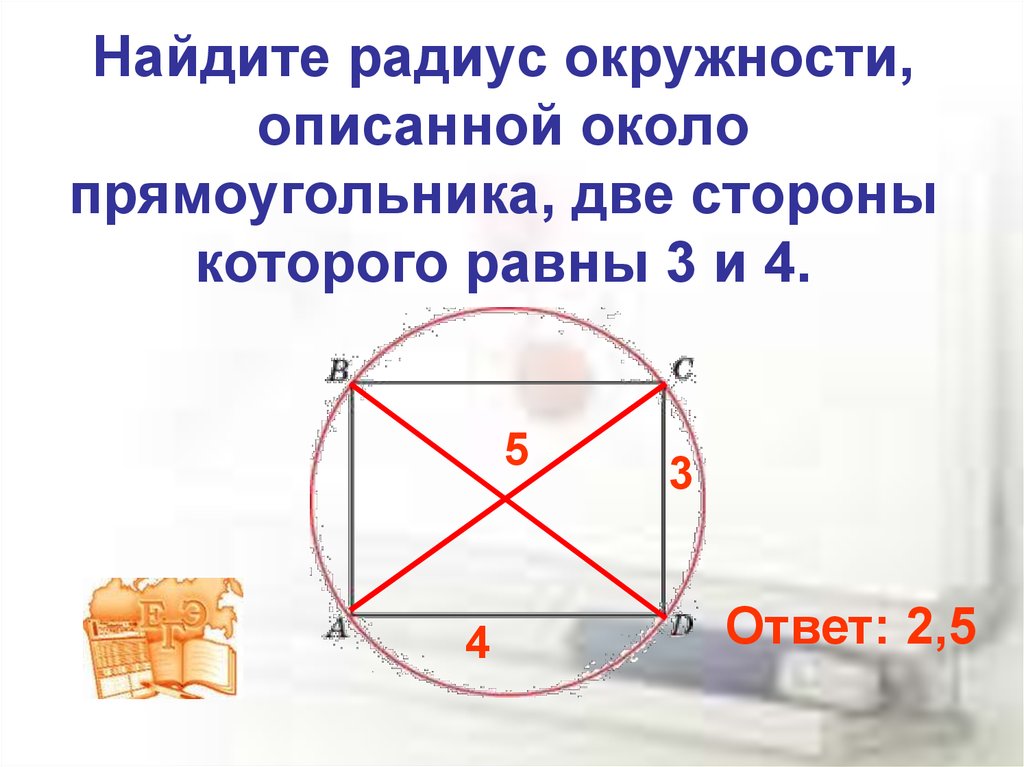
Доказательство . Пусть точка D – центр окружности, вписанной в угол BAC , а точки E и F – точки касания окружности со сторонами угла (рис.3).
Рис.3
a , b , c – стороны треугольника, S –площадь,
r – радиус вписанной окружности, p – полупериметр
.
Посмотреть вывод формулы
a – боковая сторона равнобедренного треугольника , b – основание, r – радиус вписанной окружности
a r – радиус вписанной окружности
Посмотреть вывод формул
,
где
,
то, в случае равнобедренного треугольника, когда
получаем
что и требовалось.
Теорема 7 . Для справедливо равенство
где a – сторона равностороннего треугольника, r –
радиус вписанной окружности (рис.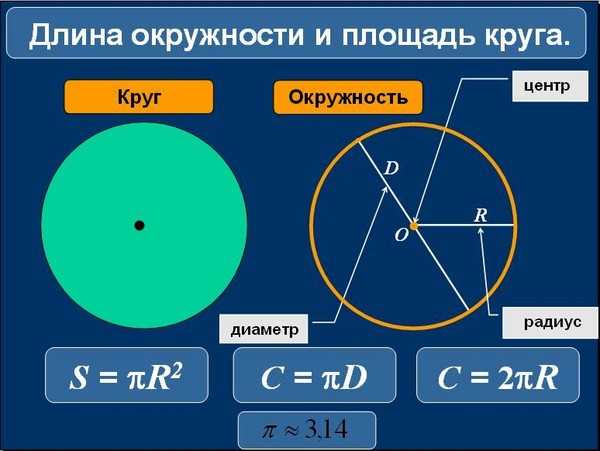 8).
8).
Рис. 8
Доказательство .
,
то, в случае равностороннего треугольника, когда
b = a,
получаем
что и требовалось.
Замечание . Я рекомендую вывести в качестве упражнения формулу для радиуса окружности, вписанной в равносторонний треугольник, непосредственно, т.е. без использования общих формул для радиусов окружностей, вписанных в произвольный треугольник или в равнобедренный треугольник.
Теорема 8 . Для прямоугольного треугольника справедливо равенство
где a , b – катеты прямоугольного треугольника, c – гипотенуза , r – радиус вписанной окружности.
Доказательство . Рассмотрим рисунок 9.
Рис. 9
Поскольку четырёхугольник CDOF является
, у которого соседние стороны DO и OF равны, то этот прямоугольник –
.
СВ = СF= r,
В силу теоремы 3 справедливы равенства
Следовательно, принимая также во внимание , получаем
что и требовалось.
Подборка задач по теме «Окружность, вписанная в треугольник».
1.
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
2.
3
В треугольнике ABC АС=4, ВС=3, угол C равен 90º. Найдите радиус вписанной окружности.
4.
Катеты равнобедренного прямоугольного треугольника равны 2+. Найдите радиус окружности, вписанной в этот треугольник.
5.
Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 2. Найдите гипотенузу c этого треугольника. В ответе укажите с(–1).
Приведем ряд задач из ЕГЭ с решениями.
Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен . Найдите гипотенузу c этого треугольника. В ответе укажите .
Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен . Тогда гипотенуза равна .
Запишем площадь треугольника АВС двумя способами:
Приравняв эти выражения, получим, что . Поскольку , получаем, что . Тогда .
В ответ запишем .
Ответ: .
Задача 2.
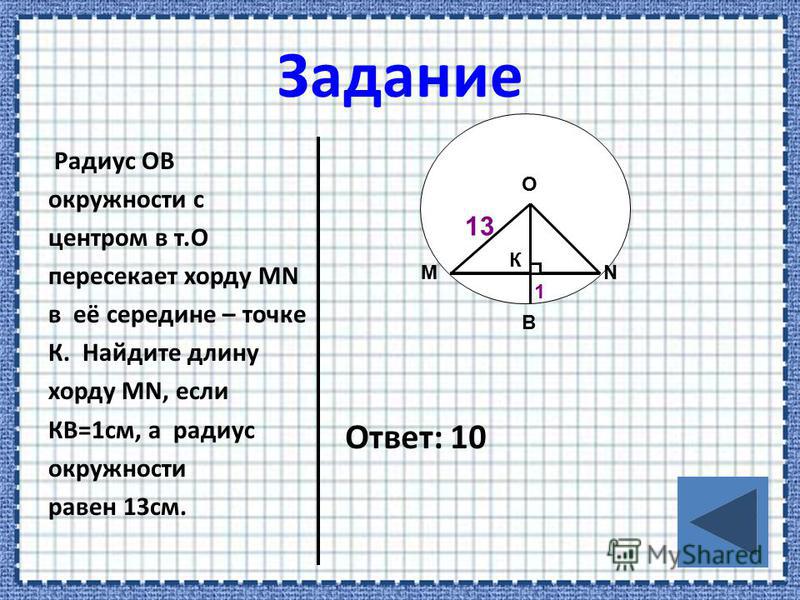
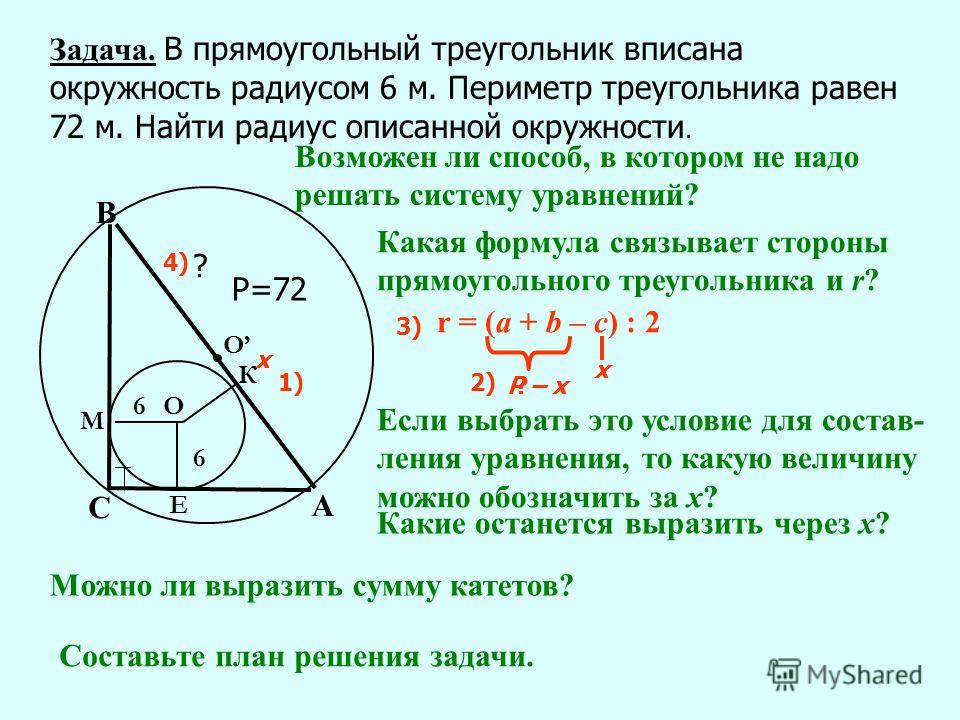
1. В произвольном две боковые стороны 10см и 6см (AB и BC). Найти радиусы описанной и вписанной окружностей
Задача решается самостоятельно с комментированием.
Решение:
В .
1) Найти:
2) Доказать:
и найти СK
3) Найти: радиусы описанной и вписанной окружностей
Решение:
Задача 6.
Найти : ОС=?
Решение : в данном случае задачу можно решить, воспользовавшись либо теоремой Пифагора, либо формулой для R. Второй случай будет проще, поскольку формула для R выведена из теоремы.
Второй случай будет проще, поскольку формула для R выведена из теоремы.
Задача 7.
Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен 2. Найдите гипотенузу с этого треугольника. В ответе укажите .
S – площадь треугольника
Нам неизвестны ни стороны треугольника, ни его площадь. Обозначим катеты как х, тогда гипотенуза будет равна:
А площадь треугольника будет равна 0,5х 2 .
Значит
Таким образом, гипотенуза будет равна:
В ответе требуется записать:
Ответ: 4
Задача 8.
В треугольнике ABC АС = 4, ВС = 3, угол C равен 90 0 . Найдите радиус вписанной окружности.
Воспользуемся формулой радиуса окружности вписанной в треугольник:
где a, b, c – стороны треугольника
S – площадь треугольника
Две стороны известны (это катеты), можем вычислить третью (гипотенузу), также можем вычислить и площадь.
По теореме Пифагора:
Найдём площадь:
Таким образом:
Ответ: 1
Задача 9.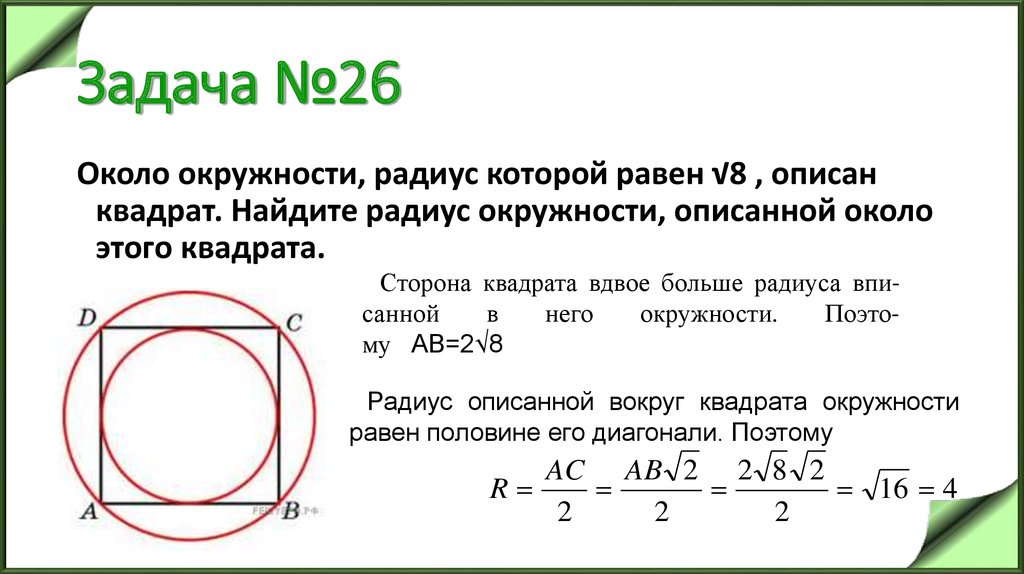
Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.
Воспользуемся формулой радиуса окружности вписанной в треугольник:
где a, b, c – стороны треугольника
S – площадь треугольника
Известны все стороны, вычислим и площадь. Её мы можем найти по формуле Герона:
Тогда
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Ромб – это параллелограмм, у которого все стороны равны. Следовательно, он наследует все свойства параллелограмма. А именно:
- Диагонали ромба взаимно перпендикулярны.
- Диагонали ромба являются биссектрисами его внутренних углов.
Окружность можно вписать в четырехугольник тогда и только тогда, когда суммы противоположных сторон равны.
Следовательно, в любой ромб можно вписать окружность. Центр вписанной окружности совпадает с центром пересечения диагоналей ромба.
Радиус вписанной окружности в ромб можно выразить несколькими способами
1 способ. Радиуса вписанной окружности в ромб через высоту
Высота ромба равна диаметру вписанной окружности. Это следует из свойства прямоугольника, который образуют диаметр вписанной окружности и высота ромба – у прямоугольника противолежащие стороны равны.
Это следует из свойства прямоугольника, который образуют диаметр вписанной окружности и высота ромба – у прямоугольника противолежащие стороны равны.
Следовательно формула радиуса вписанной окружности в ромб через высоту:
2 способ. Радиус вписанной окружности в ромб через диагонали
Площадь ромба можно выразить через радиус вписанной окружности
, где Р – периметр ромба. Зная, что периметр это сумма всех сторон четырехугольника имеем P= 4×а. Тогда
Но площадь ромба также равна половине произведения его диагоналей
Прировняв правые части формул площади, имеем следующее равенство
В результате получаем формулу, позволяющую вычислить радиус вписанной окружности в ромб чрез диагонали
Пример расчета радиуса окружности вписанной в ромб, если известны диагонали
Найти радиус окружности вписанной в ромб, если известно, что длина диагоналей 30 см и 40 см
Пусть ABCD -ромб, тогда AC и BD его диагонали.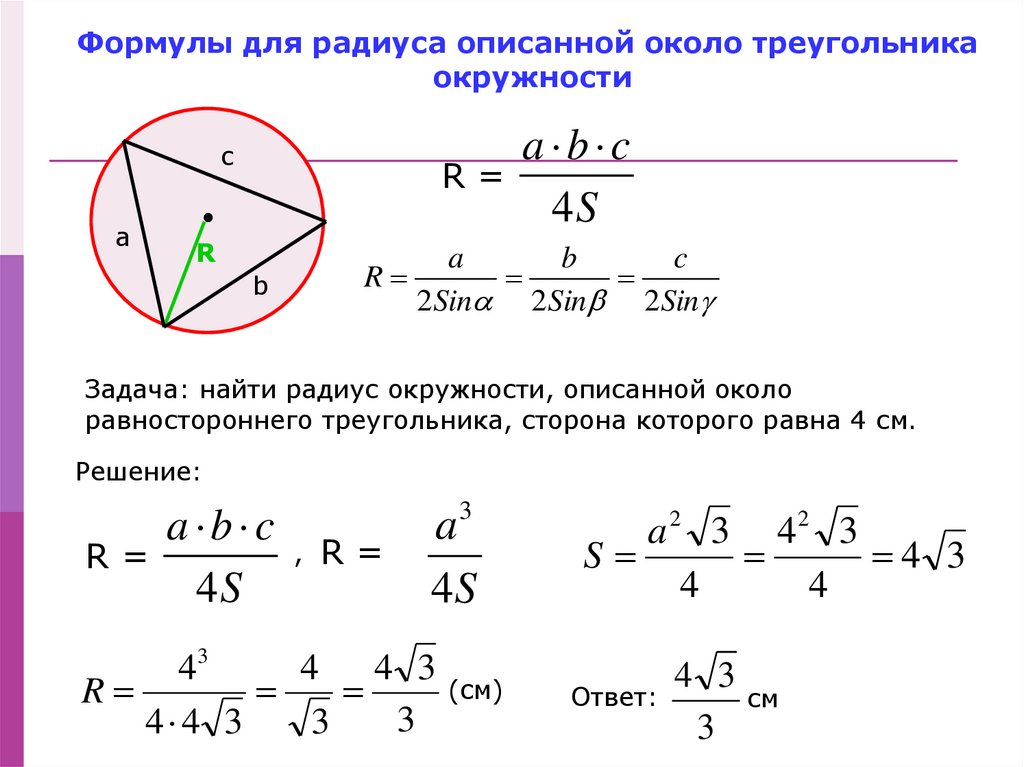 AC= 30 см, BD =40 см
AC= 30 см, BD =40 см
Пусть точка О – это центр вписанной в ромб ABCD окружности, тогда она будет также являться и точкой пересечения его диагоналей, делящих их пополам.
т.к диагонали ромба пересекаются под прямым углом, то треугольник AOB прямоугольный. Тогда по теореме Пифагора
, подставляем в формулу ранее полученные значения
AB = 25 см
Применив ранее выведенную формулу для радиуса описанной окружности в ромб, получаем
3 способ. Радиус вписанной окружности в ромб через отрезки m и n
Точка F – точка касания окружности со стороной ромба, которая делит ее на отрезки AF и BF . Пусть AF= m, BF=n.
Точка O – центр пересечения диагоналей ромба и центр вписанной в него окружности.
Треугольник AOB – прямоугольный, так как диагонали ромба пересекаются под прямым углом.
, т.к. является радиусом, проведенным в точку касания окружности. Следовательно OF – высота треугольника AOB к гипотенузе.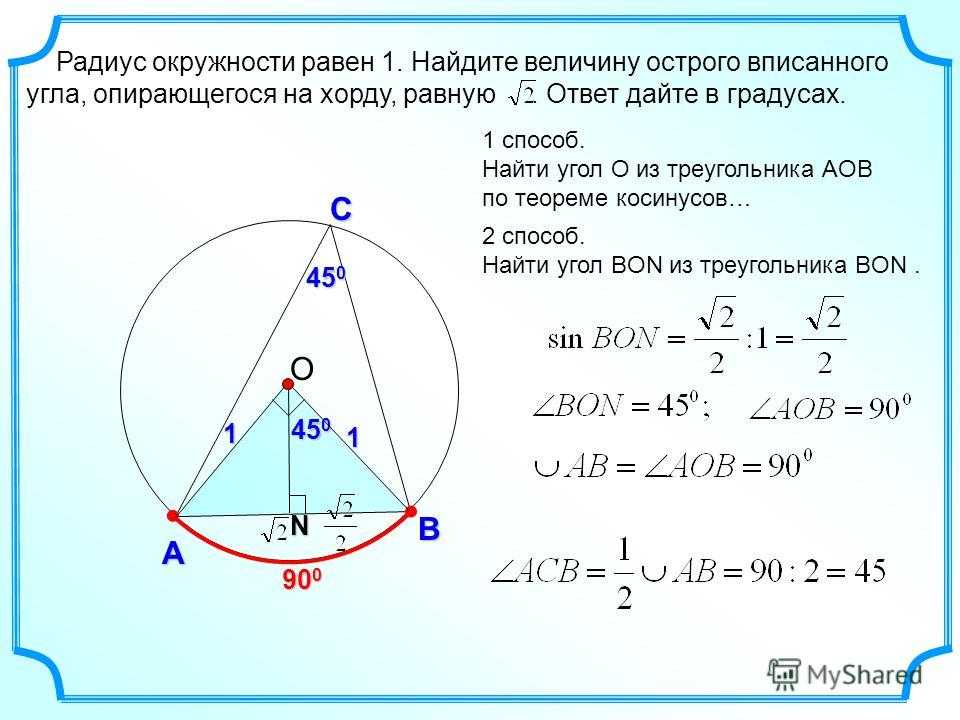 Тогда AF и BF – проекции катетов на гипотенузу.
Тогда AF и BF – проекции катетов на гипотенузу.
Высота в прямоугольном треугольнике, опущенная на гипотенузу есть среднее пропорциональное между проекциями катетов на гипотенузу.
Формула радиуса вписанной окружности в ромб через отрезки равна корню квадратному из произведения этих отрезков, на которые делит сторону ромба точка касания окружности
Как найти радиус окружности? Этот вопрос всегда актуален для школьников, изучающих планиметрию. Ниже мы рассмотрим несколько примеров того, как можно справиться с поставленной задачей.
В зависимости от условия задачи радиус окружности вы можете найти так.
Формула 1: R = Л / 2π, где Л — это а π — константа, равная 3,141…
Формула 2: R = √(S / π), где S — это величина площади круга.
Формула 1: R = В/2, где В — гипотенуза.
Формула 2: R = М*В, где В — гипотенуза, а М — медиана, проведенная к ней.
Как найти радиус окружности, если она описана вокруг правильного многоугольника
Формула: R = А / (2 * sin (360/(2*n))), где А — длина одной из сторон фигуры, а n — количество сторон в данной геометрической фигуре.
Как найти радиус вписанной окружности
Вписанной окружность называется тогда, когда она касается всех сторон многоугольника. Рассмотрим несколько примеров.
Формула 1: R = S / (Р/2), где — S и Р — площадь и периметр фигуры соответственно.
Формула 2: R = (Р/2 — А) * tg (а/2), где Р — периметр, А — длина одной из сторон, а — противолежащий этой стороне угол.
Как найти радиус окружности, если она вписана в прямоугольный треугольник
Формула 1:
Радиус окружности, которая вписана в ромб
Окружность можно вписать в любой ромб, как равносторонний, так и неравносторонний.
Формула 1: R = 2 * Н, где Н — это высота геометрической фигуры.
Формула 2: R = S / (А*2), где S — это а А — длина его стороны.
Формула 3: R = √((S * sin А)/4), где S — это площадь ромба, а sin А — синус острого угла данной геометрической фигуры.
Формула 4: R = В*Г/(√(В² + Г²), где В и Г — это длины диагоналей геометрической фигуры.
Формула 5: R = В*sin (А/2), где В — диагональ ромба, а А — это угол в вершинах, соединяющих диагональ.
Радиус окружности, которая вписана в треугольник
В том случае, если в условии задачи вам даны длины всех сторон фигуры, то сначала высчитайте (П), а затем полупериметр (п):
П = А+Б+В, где А, Б, В — длин сторон геометрической фигуры.
Формула 1: R = √((п-А)*(п-Б)*(п-В)/п).
А если, зная все те же три стороны, вам дана еще и то можете рассчитать искомый радиус следующим образом.
Формула 2: R = S * 2(А + Б + В)
Формула 3: R = S/п = S / (А+Б+В)/2), где — п — это полупериметр геометрической фигуры.
Формула 4: R = (п — А) * tg (А/2), где п — это полупериметр треугольника, А — одна из его сторон, а tg (А/2) — тангенс половины противолежащего этой стороне угла.
А ниже приведенная формула поможет отыскать радиус той окружности, которая вписана в
Формула 5: R =А * √3/6.
Радиус окружности, которая вписана в прямоугольный треугольник
Если в задаче даны длины катетов, а также гипотенуза, то радиус вписанной окружности узнается так.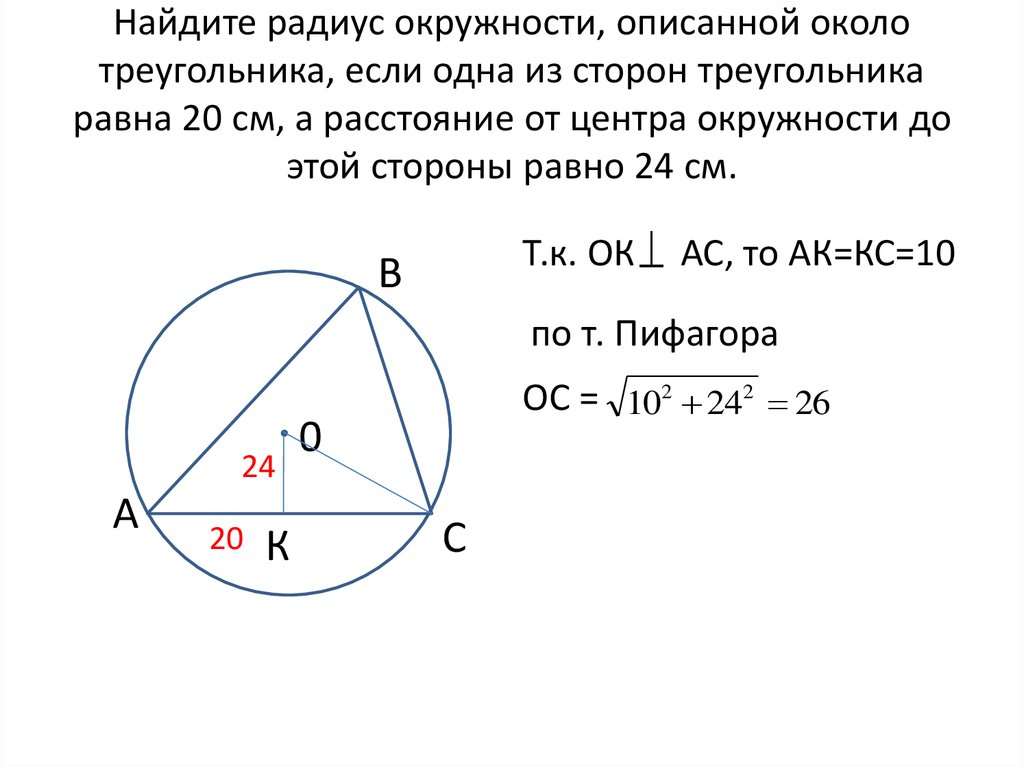
Формула 1: R = (А+Б-С)/2, где А, Б — катеты, С — гипотенуза.
В том случае, если вам даны только два катета, самое время вспомнить теорему Пифагора, чтобы гипотенузу найти и воспользоваться вышеприведенной формулой.
С = √(А²+Б²).
Радиус окружности, которая вписана в квадрат
Окружность, которая вписана в квадрат, делит все его 4 стороны ровно пополам в точках касания.
Формула 1: R = А/2, где А — длина стороны квадрата.
Формула 2: R = S / (Р/2), где S и Р — площадь и периметр квадрата соответственно.
Радиус окружности
Для начала дадим определение радиуса. В переводе с латинского radius – это «луч, спица колеса». Радиус окружности – это отрезок прямой, соединяющий центр окружности с точкой, которая находится на ней. Длина данного отрезка – это значение радиуса. В математических расчётах для обозначения данной величины используют латинскую букву R.
Советы по нахождению радиуса:
- Диаметр окружности является отрезком прямой, проходящей через ее центр и соединяющей точки, лежащие на окружности, которые максимально удалены друг от друга.
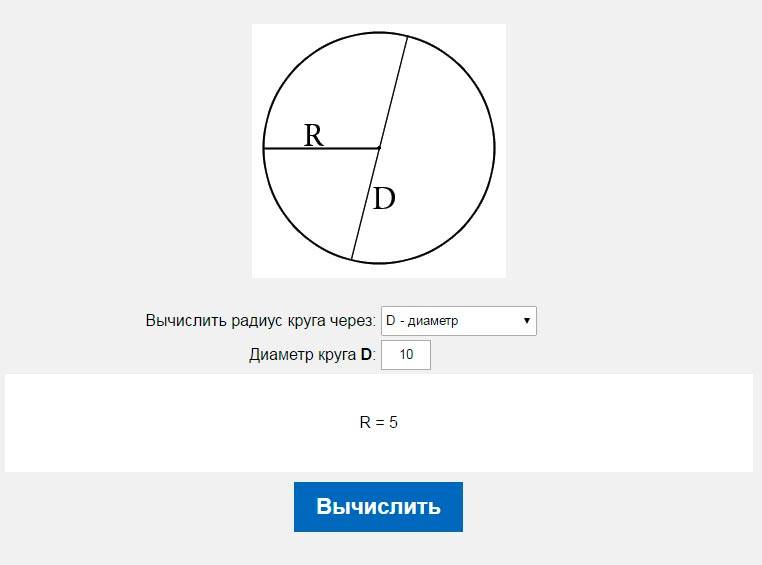
 Радиус окружности равняется половине её диаметра, следовательно, если вам известен диаметр окружности, то для нахождения её радиуса следует применить формулу: R = D/2, где D – диаметр.
Радиус окружности равняется половине её диаметра, следовательно, если вам известен диаметр окружности, то для нахождения её радиуса следует применить формулу: R = D/2, где D – диаметр. - Длина закрытой кривой, которая образуется на плоскости – это длина окружности. Если вы знаете ее длину, то для нахождения радиуса окружности вы можете применить универсальную в своем роде формулу: R = L/(2*π), где L является длиной окружности, а π – константой, равной 3,14. Константа π представляет собой отношение длины окружности к длине ее диаметра, она одинакова для всех окружностей.
- Круг представляет собой геометрическую фигуру, являющуюся частью плоскости, ограниченной кривой – окружностью. В том случае, если вы знаете площадь какого либо круга, то радиус окружности может быть найден по специальной формуле R = √(S/π), где S является площадью круга.
- Радиус вписаной окружности (в квадрат) находится следующим образом: r = a/2, где а является стороной квадрата.
- Радиус описанной окружности (вокруг прямоугольника) вычисляют по формуле: R = √ (a2 + b 2)/2, где а и b являются сторонами прямоугольника.

- В том случае, если вы не знаете длину окружности, но знаете высоту и длину какого-либо ее сегмента, то вид формулы будет таков:
R = (4*h3 + L2)/8*h, где h является высотой сегмента, а L является его длиной.
Находим радиус окружности, вписанной в треугольник (прямоугольный). В треугольник, какой бы вид он не имел, может быть вписана лишь одна-единственная окружность, центр которой будет одновременно той точкой, где пересекаются биссектрисы его углов. Прямоугольный треугольник имеет множество свойств, которые должны быть учтены, когда вычисляется радиус вписанной окружности. В задаче могут быть приведены различные данные, следовательно, требуется выполнить дополнительные вычисления, необходимые для ее решения.
Советы по нахождению радиуса вписанной окружности:
- Сначала нужно построить треугольник с теми размерами, которые уже были заданы в вашей задаче. Это необходимо делать, зная размеры всех трёх сторон или двух сторон и угла между ними. Так как размер одного угла вам уже известен, то в условии должны быть два катета.
 Катеты, которые противолежат углам, должны быть обозначены, как а и b, а гипотенуза – как с. Что касается радиуса вписанной окружности, то он обозначается как r.
Катеты, которые противолежат углам, должны быть обозначены, как а и b, а гипотенуза – как с. Что касается радиуса вписанной окружности, то он обозначается как r. - Для применения стандартной формулы определения радиуса вписанной окружности требуется найти все три стороны прямоугольного треугольника. Зная размеры всех сторон, вы сможете найти полупериметр треугольника из формулы: p = (a + b+ c)/2.
- Если вы знаете один угол и катет, то вам следует определить, прилежащий он или противолежащий. Если он прилежащий, то гипотенузу можно вычислить, используя теорему косинусов: c = a/cosCBA. Если он противолежащий, то тогда требуется воспользоваться теоремой синусов: c=a/sinCAB.
- Если у вас есть полупериметр, то вы можете определить радиус вписанной окружности. Вид формулы для радиуса будет таким: r=√(p-b)(p-a)(p-c)/p.
- Следует отметить, что найти радиус можно по формуле: r = S/p. Так что если вам известны два катета, то процедура вычисления будет более лёгкой. Гипотенуза, требуемая для полупериметра, может быть найдена по сумме квадратов его катетов.
 Вычислить площадь вы можете, перемножив все имеющиеся катеты и разделив надвое число, которое вы получили.
Вычислить площадь вы можете, перемножив все имеющиеся катеты и разделив надвое число, которое вы получили.
Какой радиус? — Learning Street
Каков радиус? Радиус — это расстояние от центра круга до внешнего края круга.
Это показано на диаграмме ниже:
Зная радиус круга, вы также можете вычислить диаметр, так как диаметр — это расстояние прямо через центр круга. Диаметр всегда вдвое больше длины радиуса.
Когда дети узнают о радиусе?Изучив 2D- и 3D-фигуры в 1-м и 2-м классах, дети познакомятся с различными частями круга в 6-м классе.
Учителя попросят детей измерить радиус и диаметр различных кругов и могут также дать Нити, чтобы можно было измерить окружность круга.
Какие вопросы будут заданы детям относительно радиуса? Как только дети узнают, что диаметр круга в два раза больше радиуса, их можно познакомить с формулой «C = 2 x π x r», которая поможет им точнее рассчитать длину окружности. Вот пример использования формулы в вопросе:
Вот пример использования формулы в вопросе:
Вопрос: Вычислите длину окружности, где π = 3,14.
Ответ:
Нам сказали, что радиус окружности равен 50 см, поэтому теперь мы можем подставить это в формулу C = 2 x π x r:
2 x 3,14 x 50 = 314 см
Окружность = 314 см
Если бы на диаграмме был указан только диаметр круга, то дети могли бы найти радиус по половине диаметра или использовать формулу C = π x d.
Учителя также могут дать детям формулу для вычисления площади круга: π x r ². Это можно использовать так:
Вопрос: Вычислите площадь этого круга, где π = 3,14.
Ответ:
Нам сказали, что радиус окружности равен 14 см, поэтому теперь мы можем подставить это значение в формулу A = π x r²:
3,14 x 14 x 14 = 615,44 см²
Площадь = 615,44 см² ( единицы площади всегда записываются в виде квадратов, например см² и м²).
Как помочь детям с радиусом?
Важно, чтобы дети уделяли достаточно времени изучению определений различных частей круга, чтобы они не путались при выполнении практических вопросов.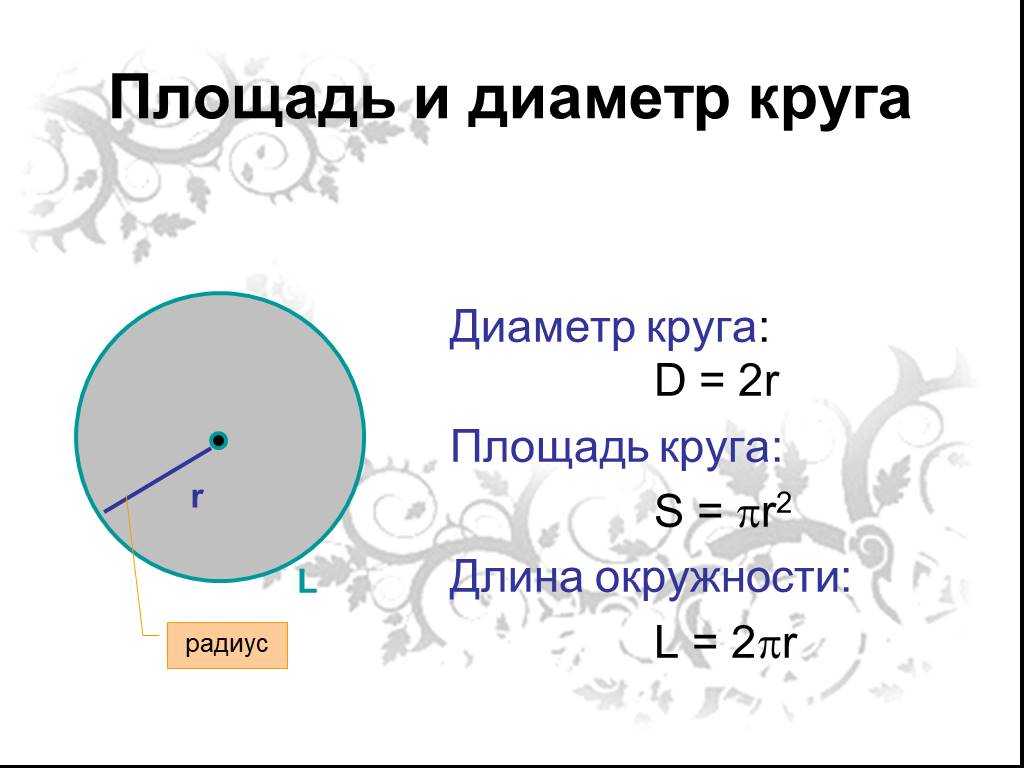 Наличие доступа к помеченной диаграмме круга может помочь детям укрепить уверенность, когда они впервые изучают определения.
Наличие доступа к помеченной диаграмме круга может помочь детям укрепить уверенность, когда они впервые изучают определения.
Иногда детям будут давать практические вопросы, основанные на сценариях, без нарисованных диаграмм. В ответ на эти вопросы полезно предложить детям самим нарисовать диаграмму, чтобы они могли визуализировать то, что вопрос ожидает от них.
Например:
У Ребекки в саду за домом есть круглый пруд. Расстояние от середины пруда до края 145 см. Какова окружность пруда?
Ответ:
Сначала начертите круг пруда и напишите на нем указанные размеры.
Затем для вычисления окружности используйте формулу 2 x π x r (где π = 3,14):
2 x 3,14 x 145 = 910,6 см
Окружность пруда 910,6 см
с радиусом? Наши специализированные курсы по математике познакомят детей с радиусом одновременно с тем, что они узнают об этом в школе, чтобы помочь им в обучении. Их учат этому, а затем у них есть вопросы и упражнения для практики, чтобы они могли делать это на экзаменах.
Тесты могут включать SAT, конкурсные тесты 11 Plus или выборочные экзамены независимой школы.
Наши курсыНажмите, чтобы ознакомиться с курсами, которые у нас есть
- Независимая школа 11 Plus Курсы подготовки к экзаменам
- Начальная школа 11 Plus Курсы подготовки к экзаменам
- Курсы усовершенствования/развития начальной школы
Радиус круга – определение, формулы, примеры
Что такое радиус круга
Радиус круга – это расстояние от центра круга до любой точки на его окружности. Это половина длины диаметра круга.
Ниже показан радиус окружности.
Радиус кругаРадиус против диаметра круга
Как мы знаем, диаметр в два раза больше радиуса круга, или, говоря словами, радиус равен половине диаметра. Взгляните на диаграмму ниже, чтобы понять, как они связаны.
Радиус и диаметр окружностиФормулы
Существует четыре различных способа определения радиуса окружности. Все дают один и тот же результат, но они используются на основе предоставленной информации. Обсудим каждый из них отдельно.
Все дают один и тот же результат, но они используются на основе предоставленной информации. Обсудим каждый из них отдельно.
Как найти радиус окружности по окружности
Когда длина окружности известна, уравнение для расчета радиуса выводится ниже.
As we know,
Circumference ( C ) = 2 πr , here r = radius, and π = 3.141 = 22/7
=> r = C /2 π
Таким образом,
Радиус ( r ) = C / 2π
Давайте решим пример, чтобы лучше проиллюстрировать концепцию.
Найдите радиус окружности с длиной окружности 64 см.
Решение:
Как мы знаем,
Радиус (r) = C/2π, здесь C = 64 см, π = 3,141
= 64/(2 × 3,141)
= 10,19 см
Как найти Радиус круга из площади
Когда площадь круга известна, уравнение для получения радиуса выводится ниже.
Как известно,
Площадь ( A ) = πr 2 , here r = radius, and π = 3.141 = 22/7
r 2 = A / π
r = √ A / π
Давайте решим пример, чтобы лучше проиллюстрировать концепцию.
Рассчитайте радиус круга площадью 166 м 2 .
Решение:
Как мы знаем,
r = √A/π, здесь A = 166 м 2 ,π = 3,141
= √166/3,141
= √52,84
= 7,26 м
Как найти радиус окружности, используя диаметр радиус получен ниже.
Как мы знаем,
Диаметр (d) = 2 × радиус (r)
r = d/2
Давайте решим пример, чтобы лучше проиллюстрировать концепцию.
Найдите радиус круга диаметром 12 дюймов.
Решение:
Как мы знаем,
r = d/2, здесь d = 12 дюймов
= 12/2
= 6 дюймов.

 Радиус окружности равняется половине её диаметра, следовательно, если вам известен диаметр окружности, то для нахождения её радиуса следует применить формулу: R = D/2, где D – диаметр.
Радиус окружности равняется половине её диаметра, следовательно, если вам известен диаметр окружности, то для нахождения её радиуса следует применить формулу: R = D/2, где D – диаметр.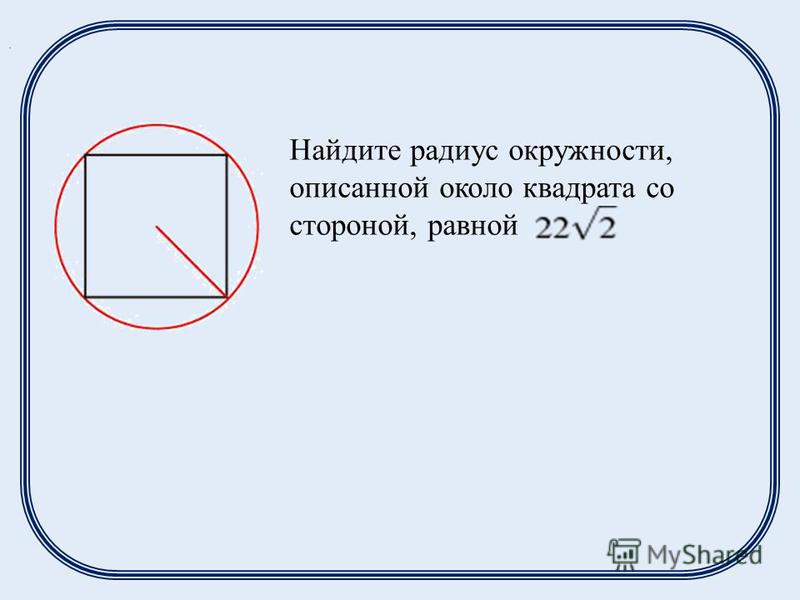
 Катеты, которые противолежат углам, должны быть обозначены, как а и b, а гипотенуза – как с. Что касается радиуса вписанной окружности, то он обозначается как r.
Катеты, которые противолежат углам, должны быть обозначены, как а и b, а гипотенуза – как с. Что касается радиуса вписанной окружности, то он обозначается как r. Вычислить площадь вы можете, перемножив все имеющиеся катеты и разделив надвое число, которое вы получили.
Вычислить площадь вы можете, перемножив все имеющиеся катеты и разделив надвое число, которое вы получили.