Найти синус, косинус и тангенс в таблицах Google
Тригонометрические функции — синус, косинус и касательная — основаны на прямоугольном треугольнике (треугольник, содержащий угол, равный 90 градусам).
В математическом классе эти триггерные функции найдены с использованием различных тригонометрических соотношений, сравнивающих длину соседних и противоположных сторон треугольника с расстоянием гипотенузы или друг с другом.
В электронных таблицах Google эти триггерные функции можно найти с помощью функций SIN, COS и TAN для углов, измеренных в радиан .
01 из 03
Степени против Радианов
Использование вышеуказанных тригонометрических функций в электронных таблицах Google может быть проще, чем делать это вручную, но, как уже упоминалось, важно понимать, что при использовании этих функций угол необходимо измерять в радиан скорее, чем степени — это единица, с которой большинство из нас не знакомы.
Радианы связаны с радиусом окружности, причем один радиан приблизительно равен 57 градусам.
Чтобы упростить работу с функциями триггера, используйте функцию Google Spreadsheets RADIANS, чтобы преобразовать угол, измеряемый от градусов к радианам, как показано в ячейке B2 на изображении выше, где угол 30 градусов преобразуется в 0,5235987756 радианов.
Другие варианты преобразования от градусов к радианам включают:
- вложение функции RADIANS внутри функции SIN — как показано в строке 3 в примере;
- с помощью Google Spreadsheets Функция ПИ в формуле: угол (градусы) * PI () / 180 как показано в строке 4 в примере.
Продолжить чтение ниже
02 из 03
Синтаксис и аргументы функций Trig
Синтаксис функции относится к компоновке функции и включает имя функции, скобки и аргументы.
Синтаксис функции SIN:
= SIN (угол)
Синтаксис функции COS:
= COS (угол)
Синтаксис функции TAN:
= TAN (угол)
угол — вычисляемый угол — измеряется в радианах— размер угла в радианах может быть введен для этого аргумента или, альтернативно, ссылка ячейки на местоположение этих данных на листе. В этом примере описаны шаги, используемые для ввода функции SIN в ячейку C2 на изображении выше, чтобы найти синус 30-градусного угла или 0.5235987756 радиан. Эти же шаги могут быть использованы для вычисления косинуса и касательной для угла, как показано в строках 11 и 12 на изображении выше. Таблицы Google не используют диалоговые окна для ввода аргументов функции, которые можно найти в Excel. Вместо этого он имеет автоматический предложить который появляется, когда имя функции вводится в ячейку. Продолжить чтение ниже Как видно на изображении выше, аргумент функции SIN вводится после открытой круглой скобки. Функция SIN отображает #ЗНАЧЕНИЕ! если ссылка, используемая как аргумент функции, указывает на ячейку, содержащую текст. В пятой строке вышеприведенного примера вы можете увидеть это, где ссылка на ячейку указывает на текстовую метку: Угол (радианы). Если ячейка указывает на пустую ячейку, функция возвращает нулевое значение (см. \(\
\operatorname{ctg} \beta=\frac{B C}{A C}=\frac{a}{b}
\), \(\
\operatorname{ctg} \alpha=\frac{A C}{B C}=\frac{b}{a}
\)
Рассмотрим окружность радиуса 1 с центром в начале координат. Выберем произвольный угол \(\
\alpha
\) , которому на окружности соответствует точка \(\
A\left(x_{0}, y_{0}\right)
\) Опустим перпендикуляры на оси координат, тогда \(\
\operatorname{ctg} \alpha=\frac{O B}{A B}=\frac{x_{0}}{y_{0}}
\) т.е. котангенсом угла есть отношение абсциссы точки \(\
\mathrm{A}
\) к ее ординате. Так как синус угла равен значению ординаты точки \(\
\mathrm{A}
\), а косинус угла равен значению абсциссы, то \(\
\operatorname{ctg} \alpha=\frac{x_{0}}{y_{0}}=\frac{\cos \alpha}{\sin \alpha}
\) Функция \(\
y=\operatorname{ctg} x
\) является периодической с периодом \(\
T=\pi
\) , т. \(\
\operatorname{ctg}(\pi+\alpha)=\operatorname{ctg} \alpha
\) Примеры решения задач ПРИМЕР 1 В прямоугольном треугольнике \(\
A B C
\) с катетами \(\
A B=3 \mathrm{см}
\) и \(\
A C=5 \mathrm{см}
\) найти котангенсы углов \(\
B
\) и \(\
C
\) Так как котангенс острого угла в прямоугольном треугольнике равен отношению прилежащего катета к противолежащему, то можем записать, что \(\
\operatorname{ctg} \angle B=\frac{A B}{A C}=\frac{3}{5}
\), \(\
\operatorname{ctg} \angle C=\frac{A C}{A B}=\frac{5}{3}
\)
Пример: Использование функции таблиц SST в Google Spreadsheets
Ввод аргумента функции
#ЗНАЧЕНИЕ! Ошибки и результаты пустых ячеек
{\circ}
\), \(\
\angle A=\alpha
\), \(\
\angle B=\beta
\) , гипотенузой \(\
A B=c
\) и катетами \(\
A C=b
\) и \(\
\mathrm{BC}=\mathrm{a}
\) (рис.1). Тогда
е.
\(\ \operatorname{ctg} \angle B=\frac{3}{5} \), \(\ \operatorname{ctg} \angle C=\frac{5}{3} \)
ПРИМЕР 2
Найти \(\ \operatorname{ctg} \alpha \) , если
\(\ \frac{4 \sin \alpha+\cos \alpha}{\cos \alpha-2 \sin \alpha}=3 \)
Преобразуем заданное выражение следующим образом:
\(\ 4 \sin \alpha+\cos \alpha=3(\cos \alpha-2 \sin \alpha) \)
или
\(\ -2 \cos \alpha=-10 \sin \alpha \Rightarrow \frac{\cos \alpha}{\sin \alpha}=\frac{10}{2}=5 \)
Так как \(\ \operatorname{ctg} \alpha=\frac{\cos \alpha}{\sin \alpha} \) , то имеем, что
\(\ \operatorname{ctg} \alpha=5 \)
\(\ \operatorname{ctg} \alpha=5 \)
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Тангенс 45 градусов Теорема тангенсов Сумма тангенсов Тангенс угла
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПринимаю Политику конфиденциальности
Подпишись на рассылку, чтобы не пропустить информацию об акциях
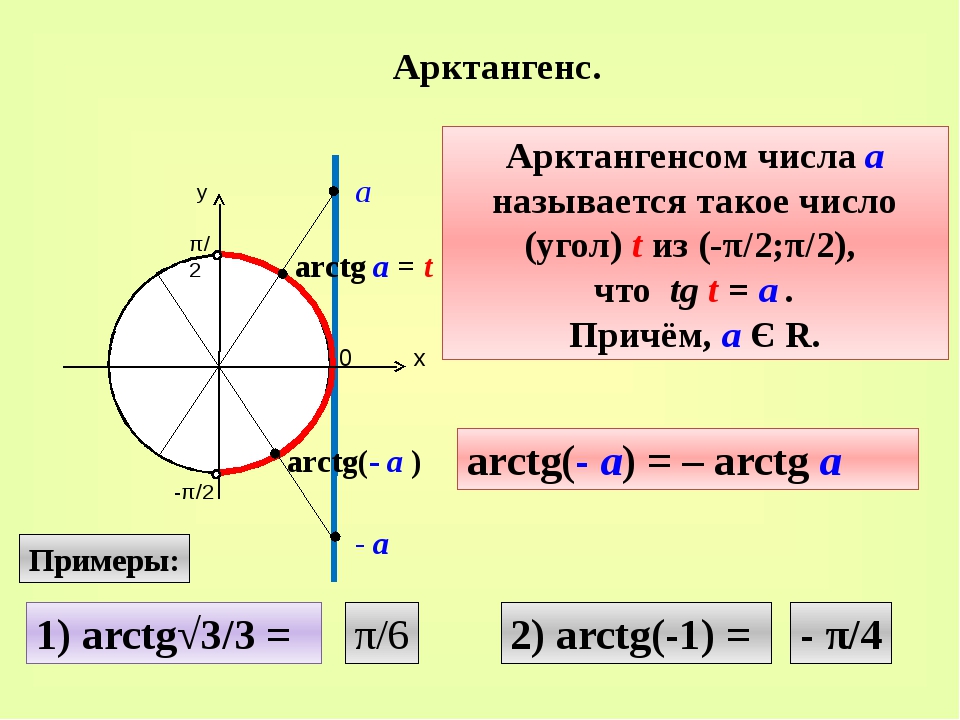
Предварительное исчисление алгебры — Тригонометрия — Найти значение cos($\theta$) по заданной кроватке($\theta$)
спросил
Изменено 4 года, 11 месяцев назад
Просмотрено 1к раз
$\begingroup$
Мне нужно найти cos($\theta$) в квадранте I, если задано cot($\theta$) = 23.
Книга показывает ответ как: 92+1}} = \sqrt{\frac{529}{530}} = 0,998113207$$
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Формула котангенса — GeeksforGeeks
Тригонометрия — важный раздел математики, изучающий соотношение между длинами сторон и углами прямоугольного треугольника. Синус, косинус, тангенс, косеканс, секанс и котангенс — это шесть тригонометрических соотношений или функций. Где тригонометрическое отношение изображается как отношение между сторонами прямоугольного треугольника.
- sin θ = противолежащая сторона/гипотенуза
- cos θ = прилежащая сторона/гипотенуза
- tan θ = противолежащая сторона/прилежащая сторона
- cosec θ = 1/sin θ = гипотенуза/противоположная сторона
- sec θ = 1/cos θ = гипотенуза/прилежащая сторона
- cot θ = 1/tan θ = прилежащая сторона /обратная сторона
Формула котангенса
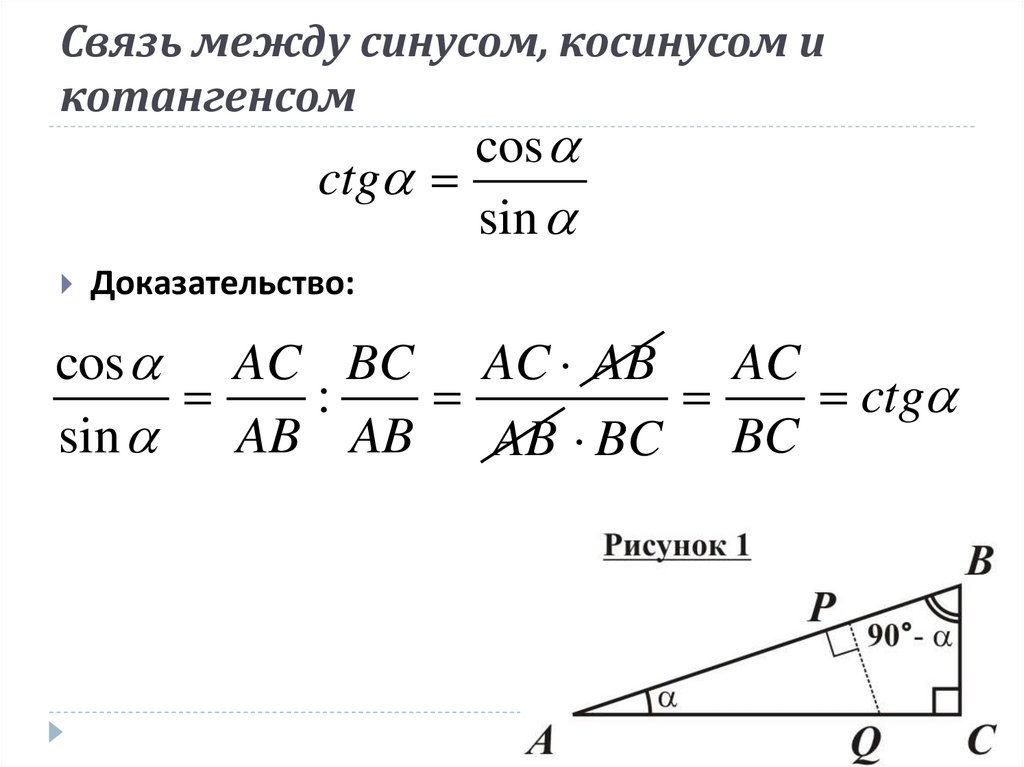
Функция котангенса является обратной функцией данной функции тангенса. Величина котангенса угла в прямоугольном треугольнике равна отношению длины стороны, прилежащей к данному углу, к длине стороны, противолежащей данному углу.
Запишем функцию котангенса как «кроватка».
Треугольник ABC
Теперь формула котангенса для угла θ: квадранты и отрицательные во втором и четвертом квадрантах.
- раскладушка (2π + θ) = раскладушка θ (1 st квадрант) (3 рд квадрант)
- кроватка (2π – θ) = – кроватка θ (4 -й квадрант)
- Функция котангенса является отрицательной функцией, поскольку котангенс отрицательного угла является отрицательным значением котангенса положительного угла.
COT (-θ) =-COT θ
- С точки зрения тангентной функции, функция Cotangent записана,
Cot θ/1/TAN θ
COT θ/1/TAN θ
COT или)
cot θ = tan (90° – θ) (или) tan (π/2 – θ)
- Функция котангенса в терминах функций синуса и косинуса может быть записана как
cot θ = cos θ/sin θ
Мы знаем, что cot θ = смежная сторона/противоположная сторона
Теперь разделим числитель и знаменатель на гипотенузу
⇒ cot θ = (прилежащая сторона/гипотенуза) / (противоположная сторона/гипотенуза)
Мы знаем, что sin θ = противолежащая сторона/гипотенуза
cos θ = смежная сторона/гипотенуза
Следовательно, cot θ = cos θ/sin θ
- Функция котангенса в терминах функции синуса может быть записана как
cot sin θ = (√9 1 2 θ)/sin θ
Мы знаем, что cot θ = cos θ/sin θ
Из пифагорейских тождеств мы имеем;
cos 2 θ + sin 2 θ = 1
⇒ cos θ = √1 – sin 2 θ
Следовательно, cot θ = 909137 0138
- Функция котангенса через функцию косинуса может быть записана как /sin θ
Из пифагорейских тождеств мы имеем;
COS 2 θ + sin 2 θ = 1
sin θ = √1 — cos 2 θ
Следовательно, Cot θ =
- Cotangen пишется как 9
Мы имеем )
⇒ Cot θ = cosec θ/sec θ
- Котангентская функция с точки зрения функции Cosecant может быть записана как:
Cot θ = √ (Cosec 2 — 1)
9000 2
9000 2 от Пифагорейские тождества, мы имеем,
cosec 2 θ – cot 2 θ = 1
⇒ cot 2 θ = 1 – cosec 2 – 1
Следовательно, cot θ = √(cosec 2 – 1)
- функция котангенса может быть записана30 как функция секанса30: 909029
Cot θ = 1/(√sec 2 θ — 1)
Из пифагорских идентичностей,
Sec 2 θ — TAN 2 θ = 1
θ θ θ θ = TAN θ θ θ =
θ.
sec 2 θ – 1Мы знаем, что cot θ = 1/tan θ
Следовательно, COT θ =
Тригонометрическое соотношение Таблица
Тригонометрическое соотношение таблицы
Котэнг -закон. Законодательство по котэнгсу
Котэнг -закон. Законодательство по котэнгсу
Котэнг -закон. Законодательство по котэнгсу
Котэнгент Законодательство
. углы. Закон котангенсов описывает отношение между длинами сторон треугольника и котангенсами половин трех углов. Рассмотрим треугольник ABC, где a, b и c — длины сторон треугольника.
Закон котангенсов гласит, что,
Где s — полупериметр треугольника ABC, а r — его внутренний радиус вписанной окружности треугольника.
s = (a + b + c)/2
r =
Примеры задач
Задача 1.
Решение:
Учитывая данные, tan θ = 3/4
Мы знаем, что cot θ = 1/tan θ
⇒ кроватка θ = 1/(3/4) = 4/3
Итак, кроватка θ = 4/3
Задача 2. Найти значение кроватки α, sin α = 1/3 и cos α = 2√2/3.
Решение:
При данных данных sin α = 1/3 и cos α = 2√2/3
Мы знаем, что cot α = cos α/sin α
⇒ 900 (2√2/3) / (1/3) = 2√2
Следовательно, значение кроватки α = 2√2
Задача 3. Мальчик, стоящий в 15 м от дерева, смотрит на 30-метровую -градусный угол к вершине дерева. Какова высота дерева?
Решение:
Диаграмма по заданным данным
При данных данных расстояние между мальчиком и подножием дерева = 15 м и θ = 30°
Пусть высота дерева равна ‘h’
Имеем, кроватка θ = соседняя/противоположная сторона
⇒ кроватка 30° = 15/ч
⇒ √3 = 15/ч [так как, кроватка 30° = √3]
⇒ 900 h = 15/√3
⇒ h = 5√3 м
Следовательно, высота дерева = 5√3 м
Задача 4.
Найдите значение cot x, если sec x = 6/5. Решение:
Данные, г. X = 6/5
Мы имеем, Sec 2 X — TAN 2 x = 1
Я (6/5) 2 2 2 2 2 2 2 2 2 2 2 2 x = 1
— Tan 2 x = 1
⇒ 36/25 — TAN 2 X = 1
⇒ TAN 2 X = 36/25 — 1
⇒ TAN 2 X = 11/25
⇒ тангенс x = √(11/25) = √11/5
Мы знаем, что cot x = 1/tan x
⇒ cot x = 1/(√11/5) = 5/√11
Следовательно, cot x = 5/√11
Задача 5 : Найдите значение cot θ, если cosec θ = 25/24.
Решение:
Данные данные, Cosec θ = 25/24
Мы знаем, что, Cot θ = √ (Cosec 2 — 1)
⇒ Кот. ) 2 – 1
⇒ детская кроватка θ =√(625 – 576)/576 = √49/576
⇒ детская кроватка θ = 7/24
Следовательно, значение кроватки θ = 7/24
Задача 6: Найдите значение кроватки β, если sin β = 5/13.
- Cotangen пишется как 9
sec 2 θ – 1
Найдите значение cot x, если sec x = 6/5. 