Параллельна ли средняя линия трапеции ее основаниям. Средняя линия трапеции
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Понятие средней линии трапеции
Для начала вспомним, какую фигуру называют трапецией.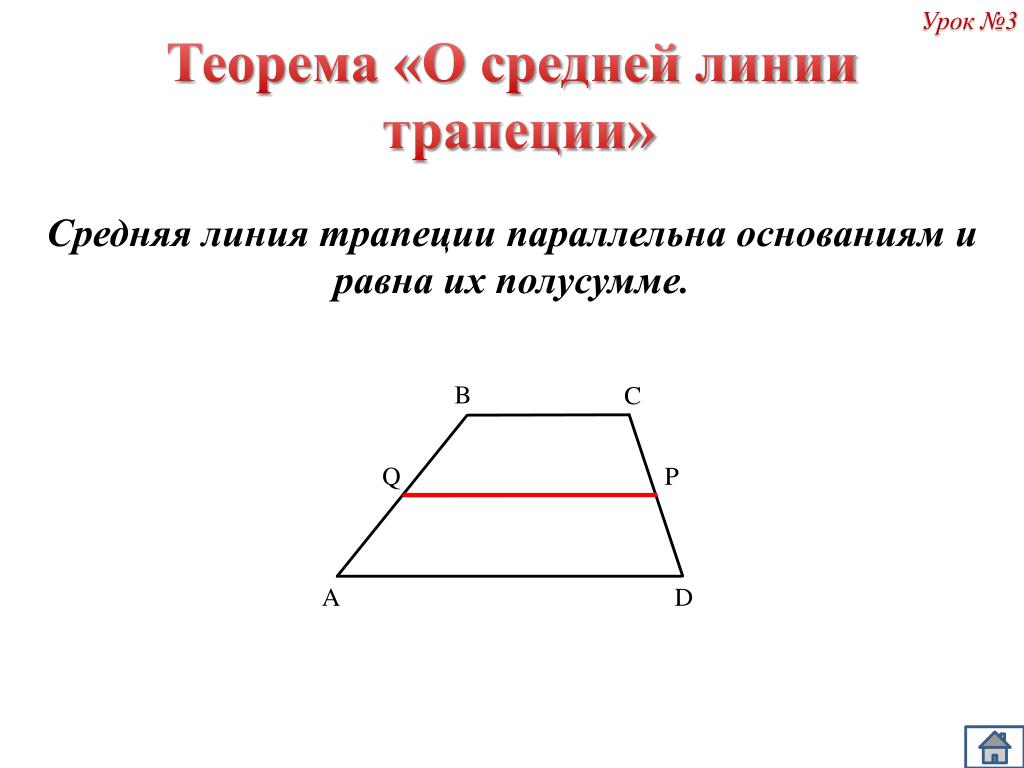
Определение 1
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
При этом параллельные стороны называются основаниями трапеции, а не параллельные — боковыми сторонами трапеции.
Определение 2
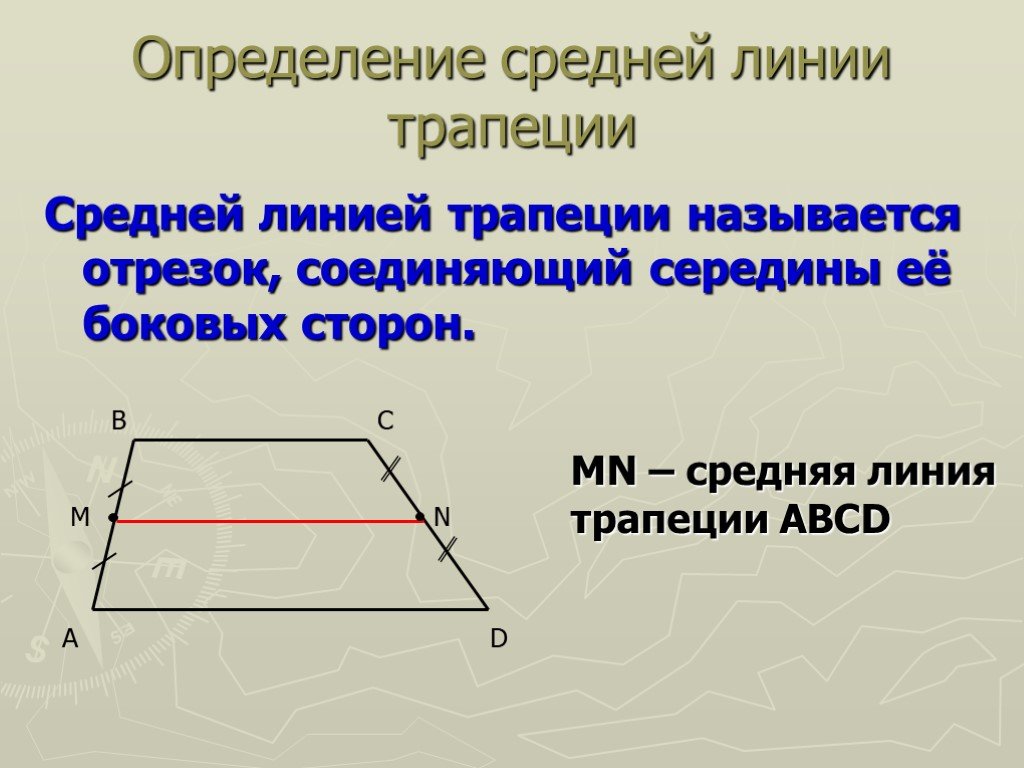
Средняя линия трапеции — это отрезок, соединяющий середины боковых сторон трапеции.
Теорема о средней линии трапеции
Теперь введем теорему о средней линии трапеции и докажем её вектор ным методом.
Теорема 1
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство.
Пусть нам дана трапеция $ABCD$ с основаниями $AD\ и\ BC$. И пусть $MN$ — средняя линия этой трапеции (рис. 1).
Рисунок 1. Средняя линия трапеции
Докажем, что $MN||AD\ и\ MN=\frac{AD+BC}{2}$.
Рассмотрим вектор $\overrightarrow{MN}$. Используем далее правило многоугольника для сложения векторов. С одной стороны получим, что
С другой стороны
Сложим два последних равенства, получим
Так как $M$ и $N$ — середины боковых сторон трапеции, то будем иметь
Получаем:
Следовательно
Из этого же равенства (так как $\overrightarrow{BC}$ и $\overrightarrow{AD}$ сонаправлены, а, следовательно, коллинеарны) получаем, что $MN||AD$.
Теорема доказана.
Примеры задач на понятие средней линии трапеции
Пример 1
Боковые стороны трапеции равны $15\ см$ и $17\ см$ соответственно. Периметр трапеции равен $52\ см$. Найти длину средней линии трапеции.
Решение.
Обозначим среднюю линию трапеции через $n$.
Сумма боковых сторон равна
Следовательно, так как периметр равен $52\ см$, сумма оснований равна
Значит, по теореме 1, получаем
Ответ: $10\ см$.
Пример 2
Концы диаметра окружности удалены от его касательной соответственно на $9$ см и $5$ см. Найти диаметр этой окружности.
Решение.
Пусть нам дана окружность с центром в точке $O$ и диаметром $AB$. Проведем касательную $l$ и построим расстояния $AD=9\ см$ и $BC=5\ см$. Проведем радиус $OH$ (рис. 2).
Рисунок 2.
Так как $AD$ и $BC$ — расстояния до касательной, то $AD\bot l$ и $BC\bot l$ и так как $OH$ — радиус, то $OH\bot l$, следовательно, $OH|\left|AD\right||BC$.
Понятие средней линии трапеции
Для начала вспомним, какую фигуру называют трапецией.
Определение 1
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
При этом параллельные стороны называются основаниями трапеции, а не параллельные — боковыми сторонами трапеции.
Определение 2
Средняя линия трапеции — это отрезок, соединяющий середины боковых сторон трапеции.
Теорема о средней линии трапеции
Теперь введем теорему о средней линии трапеции и докажем её вектор ным методом.
Теорема 1
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство.
Пусть нам дана трапеция $ABCD$ с основаниями $AD\ и\ BC$. И пусть $MN$ — средняя линия этой трапеции (рис. 1).
Рисунок 1. Средняя линия трапеции
Докажем, что $MN||AD\ и\ MN=\frac{AD+BC}{2}$.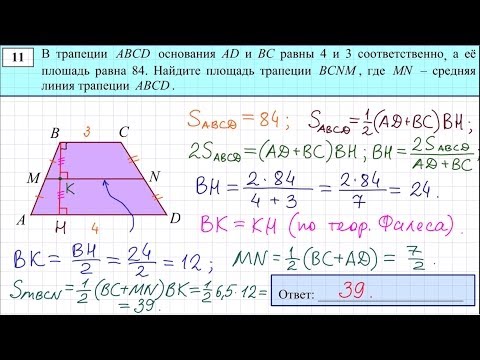
Рассмотрим вектор $\overrightarrow{MN}$. Используем далее правило многоугольника для сложения векторов. С одной стороны получим, что
С другой стороны
Сложим два последних равенства, получим
Так как $M$ и $N$ — середины боковых сторон трапеции, то будем иметь
Получаем:
Следовательно
Из этого же равенства (так как $\overrightarrow{BC}$ и $\overrightarrow{AD}$ сонаправлены, а, следовательно, коллинеарны) получаем, что $MN||AD$.
Теорема доказана.
Примеры задач на понятие средней линии трапеции
Пример 1
Боковые стороны трапеции равны $15\ см$ и $17\ см$ соответственно. Периметр трапеции равен $52\ см$. Найти длину средней линии трапеции.
Решение.
Обозначим среднюю линию трапеции через $n$.
Сумма боковых сторон равна
Следовательно, так как периметр равен $52\ см$, сумма оснований равна
Значит, по теореме 1, получаем
Ответ: $10\ см$.
Пример 2
Концы диаметра окружности удалены от его касательной соответственно на $9$ см и $5$ см.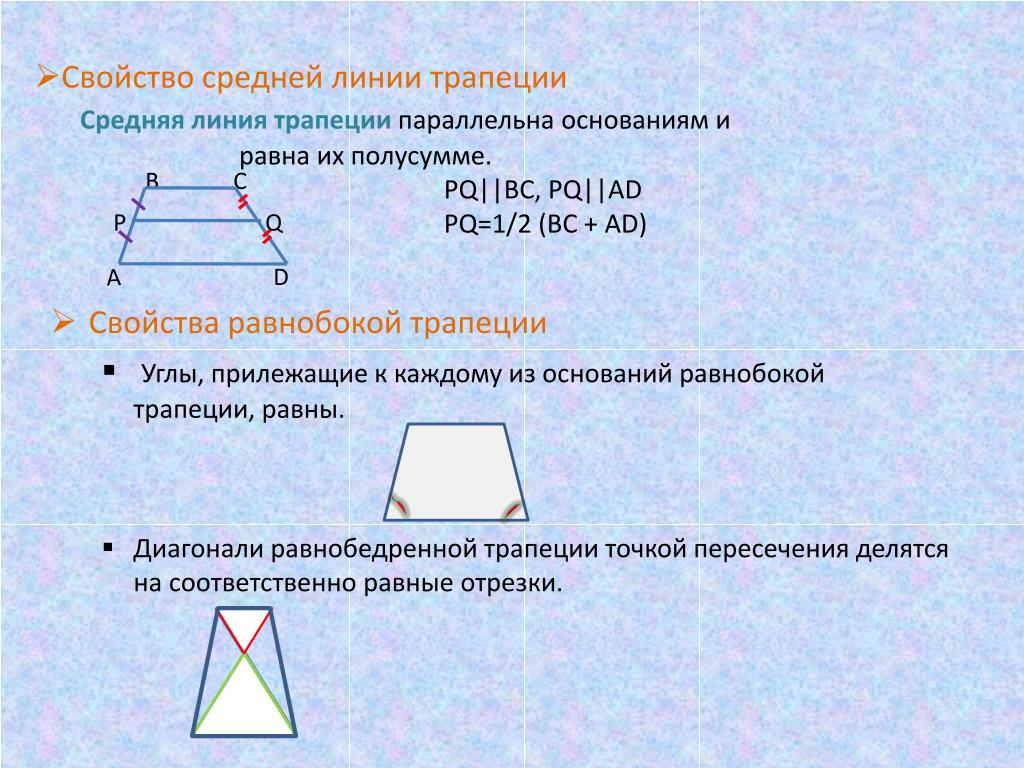 Найти диаметр этой окружности.
Найти диаметр этой окружности.
Решение.
Пусть нам дана окружность с центром в точке $O$ и диаметром $AB$. Проведем касательную $l$ и построим расстояния $AD=9\ см$ и $BC=5\ см$. Проведем радиус $OH$ (рис. 2).
Рисунок 2.
Так как $AD$ и $BC$ — расстояния до касательной, то $AD\bot l$ и $BC\bot l$ и так как $OH$ — радиус, то $OH\bot l$, следовательно, $OH|\left|AD\right||BC$. Из этого всего получаем, что $ABCD$ — трапеция, а $OH$ — ее средняя линия. По теореме 1, получаем
- Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
- Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
- Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
- Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
- Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
- Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции
Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.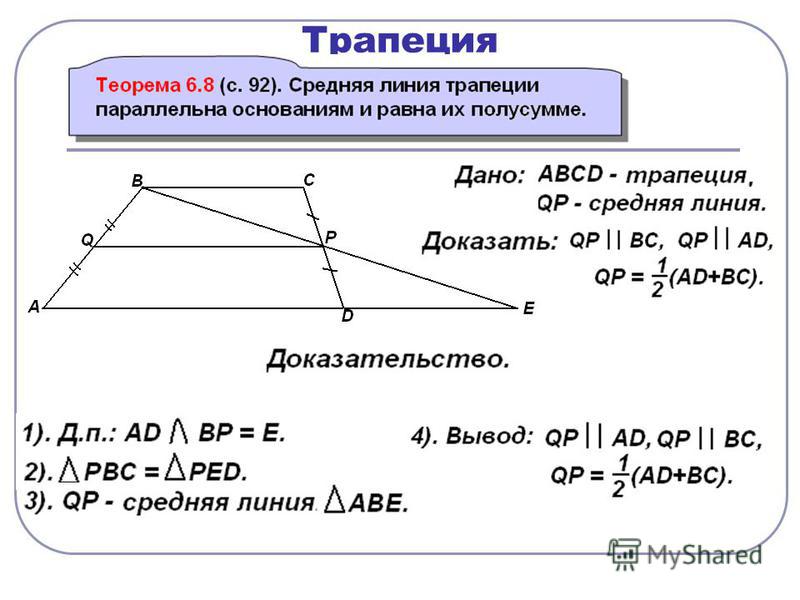
Отрезок, соединяющий середины диагоналей трапеции,
Данный отрезок параллелен основаниям трапеции .
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.
LM = (AD — BC)/2
или
LM = (a-b)/2
Свойства треугольников, образованных диагоналями трапеции
Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными .
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.
Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны , то есть треугольники являются равновеликими.
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований .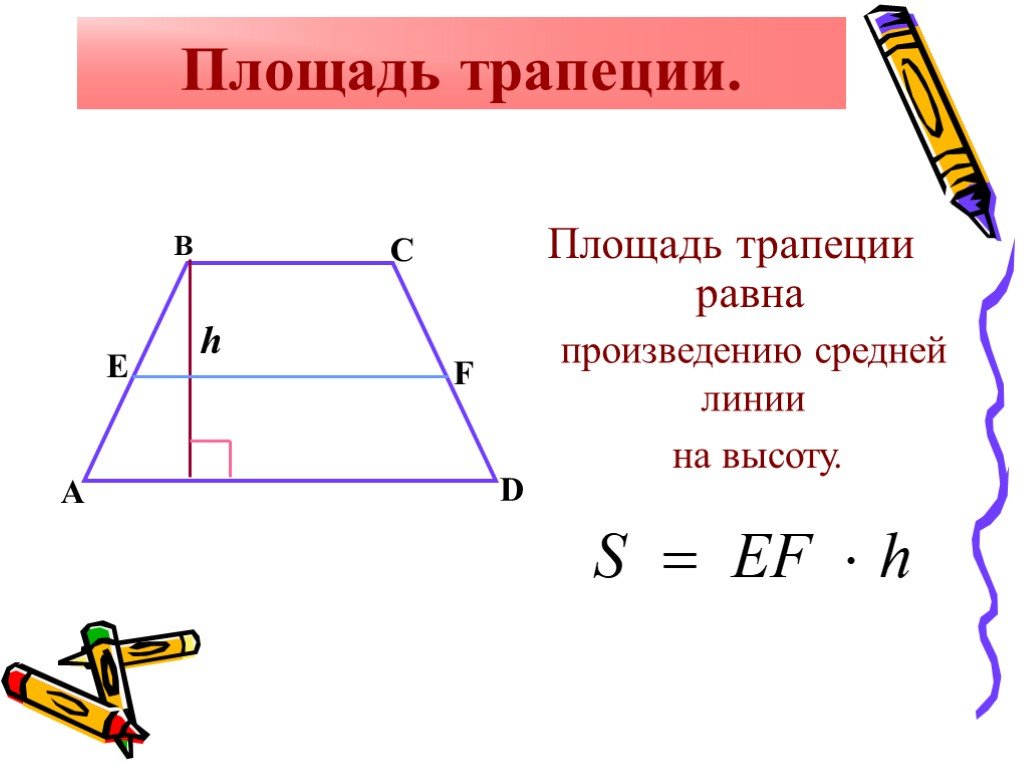
Таким образом, любая трапеция может быть достроена до треугольника. При этом:
- Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
- Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника
Свойства отрезка, соединяющего основания трапеции
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей (KO/ON) будет равно соотношению оснований трапеции (BC/AD).
KO / ON = BC / AD
Данное свойство следует из подобия соответствующих треугольников (см. выше).
Свойства отрезка, параллельного основаниям трапеции
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
- Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
- Длина отрезка , проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)
Формулы для нахождения диагоналей трапеции
a, b — основания трапеции
c, d — боковые стороны трапеции
d1 d2 — диагонали трапеции
α β — углы при большем основании трапеции
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:
1.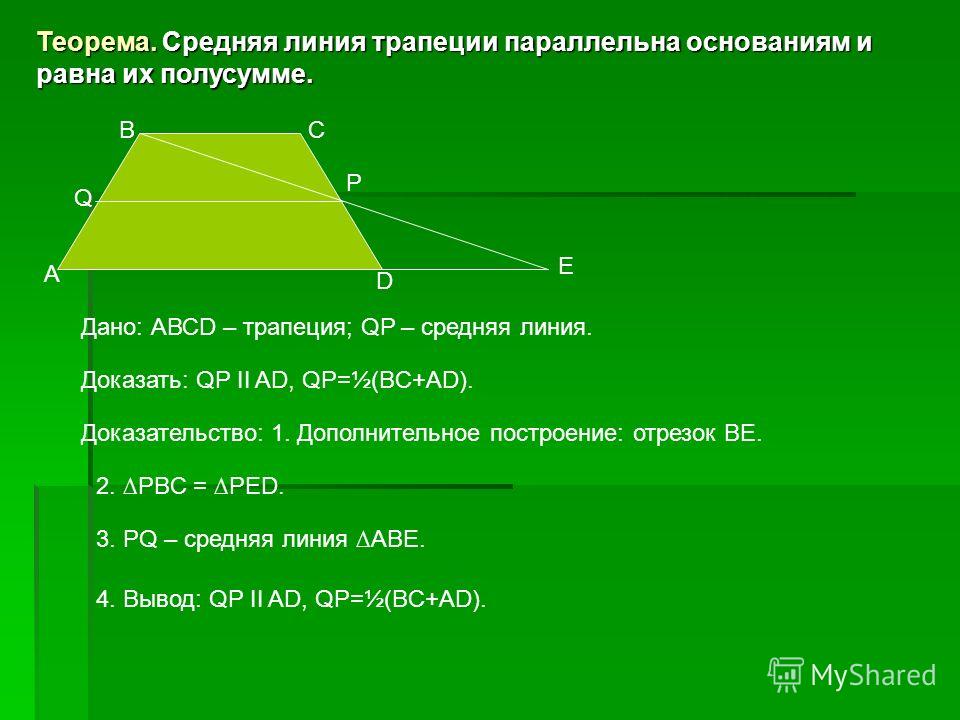 Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
2 . Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.
3 . Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ
Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.
Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.
Формулы нахождения диагоналей трапеции через высоту
Примечание . В данном уроке приведено решение задач по геометрии о трапециях.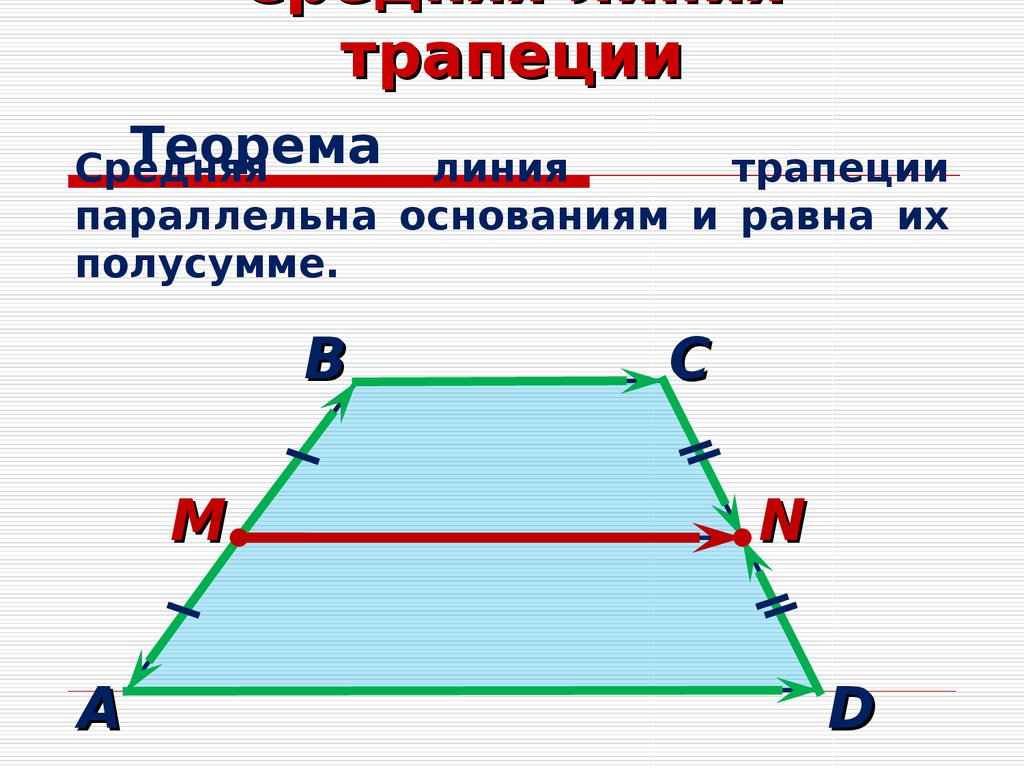 Если Вы не нашли решение задачи по геометрии, интересующего Вас типа — задайте вопрос на форуме .
Если Вы не нашли решение задачи по геометрии, интересующего Вас типа — задайте вопрос на форуме .
Задача .
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.
Решение .
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.
Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.
Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть
AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16
Ответ : 16 см
Задача
.
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.
Решение
.
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Значит
AD = AM+BC+KD
a + 8 + b = 24
a = 16 — b
Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора
H 2 + (24 — a) 2 = (5√17) 2
и
h 2 + (24 — b) 2 = 13 2
Учтем, что a = 16 — b , тогда в первом уравнении
h 2 + (24 — 16 + b) 2 = 425
h 2 = 425 — (8 + b) 2
Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:
425 — (8 + b) 2 + (24 — b) 2 = 169
-(64 + 16b + b) 2 + (24 — b) 2 = -256
-64 — 16b — b 2 + 576 — 48b + b 2 = -256
-64b = -768
b = 12
Таким образом, KD = 12
Откуда
h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25
h = 5
Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5 / 2 = 80 см 2
Ответ : площадь трапеции равна 80 см 2 .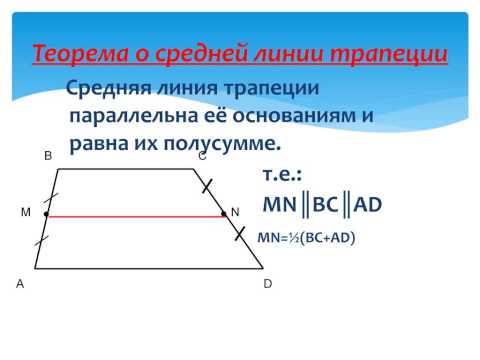
Четырёхугольник, у которого только две стороны параллельны называются трапецией .
Параллельные стороны трапеции называются её основаниями , а те стороны, которые не параллельны, называются боковыми сторонами . Если боковые стороны равны, то такая трапеция является равнобедренной. Расстояние между основаниями называется высотой трапеции.
Средняя Линия Трапеции
Средняя линия — это отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции параллельна её основаниям.
Теорема:
Если прямая, пересекающая середину одной боковой стороны, параллельна основаниям трапеции, то она делит пополам вторую боковую сторону трапеции.
Теорема:
Длина средней линии равна среднему арифметическому длин её оснований
MN || AB || DC
AM = MD; BN = NC
MN средняя линия, AB и CD — основания, AD и BC — боковые стороны
MN = (AB + DC)/2
Теорема:
Длина средней линии трапеции равна среднему арифметическому длин её оснований.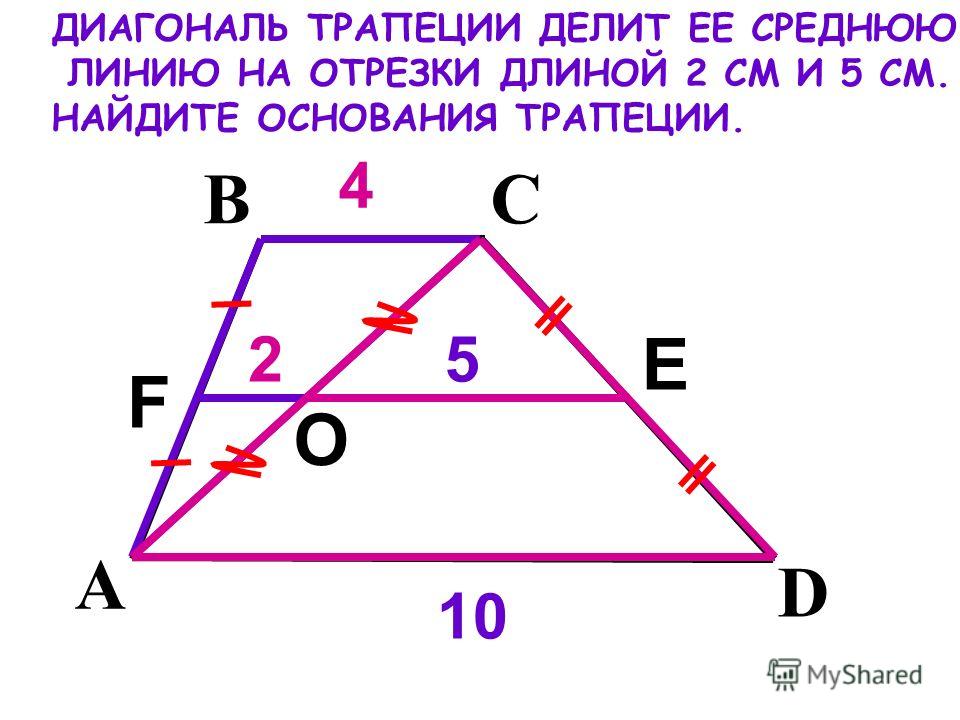
Основная задача : Доказать, что средняя линия трапеции делит пополам отрезок, концы которого лежат в середине оснований трапеции.
Средняя Линия Треугольника
Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника. Она параллельна третьей стороне и её длина равна половине длины третьей стороны.
Теорема : Если прямая, пересекающая середину одной стороны треугольника, параллельна другой стороне данного треугольника, то она делит третью сторону пополам.
AM = MC and BN = NC
=>
Применение свойств средней линии треугольника и трапеции
Деление отрезка на определённое количество равных частей.
Задача: Разделить отрезок AB на 5 равных частей.
Решение:
Пусть p это случайный луч, у которого начало это точка А, и который не лежит на прямой AB. Мы последовательно откладываем 5 равных сегментов на p AA 1 = A 1 A 2 = A 2 A 3 = A 3 A 4 = A 4 A 5
Мы соединяем A 5 с B и проводим такие прямые через A 4 , A 3 , A 2 и A 1 , которые параллельны A 5 B.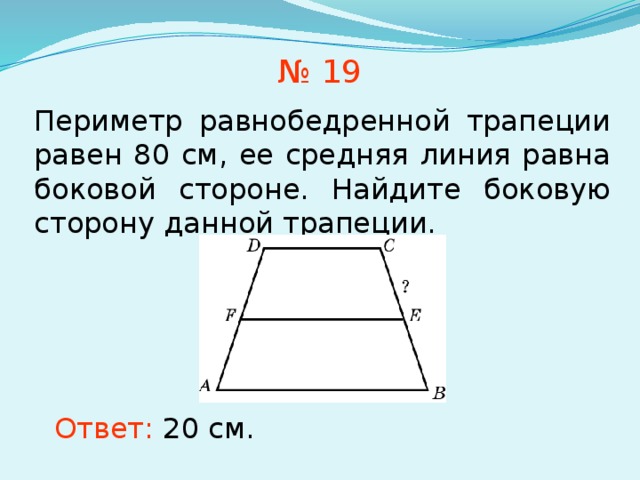 Они пересекают AB соответственно в точках B 4 , B 3 , B 2 и B 1 . Эти точки делят отрезок AB на 5 равных частей. Действительно, из трапеции BB 3 A 3 A 5 мы видим, что BB 4 = B 4 B 3 . Таким же образом, из трапеции B 4 B 2 A 2 A 4 получаем B 4 B 3 = B 3 B 2
Они пересекают AB соответственно в точках B 4 , B 3 , B 2 и B 1 . Эти точки делят отрезок AB на 5 равных частей. Действительно, из трапеции BB 3 A 3 A 5 мы видим, что BB 4 = B 4 B 3 . Таким же образом, из трапеции B 4 B 2 A 2 A 4 получаем B 4 B 3 = B 3 B 2
В то время как из трапеции B 3 B 1 A 1 A 3 , B 3 B 2 = B 2 B 1 .
Тогда из B 2 AA 2 следует, что B 2 B 1 = B 1 A. В заключении получаем:
AB 1 = B 1 B 2 = B 2 B 3 = B 3 B 4 = B 4 B
Ясно, что для разделения отрезка AB на другое количество равных частей, нам нужно проецировать то же самое количество равных сегментов на луч p. И далее продолжать вышеописанным способом.
Исследовательская работа «Сколько средних линий в трапеции?»
Слет научных обществ обучающихся
образовательных организаций общего и дополнительного образования
города Нижневартовска в 2019-2020 учебном году
Секция 5. «Прикладная математика»
Сколько средних линий в трапеции?
Автор: | Климачева Мария Константиновна, муниципальное бюджетное общеобразовательное учреждение «Средняя школа № 1», 8А класс |
Руководитель: | Якоби Зинаида Фёдоровна, учитель математики, муниципальное бюджетное общеобразовательное учреждение «Средняя школа № 1 имени Алексея Владимировича Войналовича» |
2020
Сколько средних линий в трапеции?
Климачева Мария Константиновна
Муниципальное бюджетное общеобразовательное учреждение
«Средняя школа № 1 имени Алексея Владимировича Войналовича»
8А класс
Аннотация
Цель: сколько трапеция имеет средних линий, определить особенные отличия про средние линии трапеции
Предмет исследования – средние линии трапеции
Объект исследования – трапеция
Основные методы исследования:
анализ
синтез
аналогии
сравнение
обобщение
Задачи исследования:
подобрать данные про средние линии трапеции
изучить особенные индивидуальности про средние линии в трапеции
исследовать задачи про средние линии трапеции, действующие в математической литературе
разобрать конкретные вопросы о средних линиях трапеции
Чтобы серьезно разобраться в текущем вопросе мы изучили соответствующую литературу и определили особенные индивидуальности средних линий трапеции, не изучаемые на уроках, нашли интересные заключения по проработанному материалу.
Наша работа имеет непосредственное большое использование на практике, а также теоретическую значимость.
Сколько средних линий в трапеции?
Климачева Мария Константиновна
Муниципальное бюджетное общеобразовательное учреждение
«Средняя школа № 1 имени Алексея Владимировича Войналовича»
8А класс
План исследований
№ | Элементы исследования | Дата |
1 | Определение проблемы исследования, ее темы. Обоснование актуальности исследования, формулирование гипотезы, цели, задач. | сентябрь |
2 | Объектная область: | |
3 | Выбор темы: | 30. |
4 | Формулирование гипотезы: Мы полагаем, что если непосредственно знать в совершенстве особенные индивидуальности средних линий трапеции, то их использование в свою очередь будет хорошим подспорьем ученикам в практическом направлении материала. | сентябрь |
5 | Задачи исследования: 1.Подобрать данные про средние линии трапеции 2. Изучить особенные индивидуальности про средние линии в трапеции 3. Исследовать задачи про средние линии, действующие в математической литературе 4. Разобрать конкретные вопросы о средних линиях трапеции | октябрь |
6 | Выбор методов исследования: анализ синтез аналогии сравнение обобщение | октябрь |
7 | Сбор и изучение материалов исследования: Л. Википедия.- ru.wikipedia.org/wiki /средняя линия И. А. Кушнир «Вторая средняя линия трапеции», журнал «Математика в школе» №2, 1993. В. В. Прасолов «Задачи по планиметрии» -М.: Наука, 2020 И. Х. Сивашинский «Задачник по элементарной математике», — М., Наука, 2015 – portfolio.1september.ru/work | сентябрь- ноябрь |
8 | Презентация результатов исследования | декабрь-февраль |
10 | Оформление исследовательского проекта | март |
Сколько средних линий в трапеции?
Климачева Мария Константиновна
Муниципальное бюджетное общеобразовательное учреждение
«Средняя школа № 1 имени Алексея Владимировича Войналовича»
8 А класс
Оглавление
Введение | 5 |
Научная статья | |
1. | 7 |
1.2. Особенные отличия средних линий трапеции, не изучаемые в школе | 7 |
1.3. Практическая направленность | 9 |
Заключение | 12 |
Литература | 13 |
«Геометрия полна приключений,
потому что за каждой задачей скрывается приключение мысли…»
В.Произволов
Введение
Сначала разберемся в простейшей задаче: В равнобокой трапеции диагонали при пересечении образуют угол 900. Высота трапеции равна а. Найти среднюю линию трапеции. Так как диагонали AC BD⇒ прямоугольные треугольники △АОЕ= △ВОЕ, △DFO=△CFO-равнобедренные. Из △АОЕ= △ВОЕ, △DFO=△CFO.⇒ FO=DF=FC, а OE=AE=EB. Так как FE =FO+OE= а.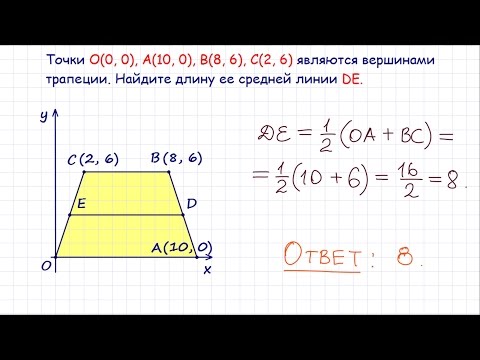 Равенство FO+OE=DF+AE, а DF+AE =½(AB+CD) позволяет сделать вывод, что средняя линия трапеции = а. Вывод задачи подтолкнул меня на раздумье: «А есть ли еще средние линии в трапеции?» В учебниках геометрии упоминается лишь только определение о единственной средней линии трапеции, ее отличиях. И, меня озарила идея сделать первые шаги информационного розыска о неизвестных средних линиях трапеции. В процессе собственных информационных поисков я нашла интересные факты, характеризующие средние линии трапеции. Полученные мною данные, как выяснилось практически не слишком известным фактом для школьников. За это время я приняла окончательное решение сконцентрировать сведения об данных неизвестных линиях, отыскать задачки, имеющие непосредственное отношение, и оформить изученный материал в виде исследовательской работы. Полагаю, собственно, что непосредственно приобретенный в процессе собственных информационных поисков мною материал станет увлекателен и может быть полезен всем тем, кто занимается занимательной наукой геометрией.
Равенство FO+OE=DF+AE, а DF+AE =½(AB+CD) позволяет сделать вывод, что средняя линия трапеции = а. Вывод задачи подтолкнул меня на раздумье: «А есть ли еще средние линии в трапеции?» В учебниках геометрии упоминается лишь только определение о единственной средней линии трапеции, ее отличиях. И, меня озарила идея сделать первые шаги информационного розыска о неизвестных средних линиях трапеции. В процессе собственных информационных поисков я нашла интересные факты, характеризующие средние линии трапеции. Полученные мною данные, как выяснилось практически не слишком известным фактом для школьников. За это время я приняла окончательное решение сконцентрировать сведения об данных неизвестных линиях, отыскать задачки, имеющие непосредственное отношение, и оформить изученный материал в виде исследовательской работы. Полагаю, собственно, что непосредственно приобретенный в процессе собственных информационных поисков мною материал станет увлекателен и может быть полезен всем тем, кто занимается занимательной наукой геометрией.
Актуальность работы:
Стоит отметить, непосредственно особенные индивидуальности средней линии трапеции были определены при решении проблемных задач. Стоит заметить, что решение некоторых задач было не всегда понятно. Вопросы, имеющие отношение ко второй средней линией трапеции смогла найти в публикациях следующих авторов: Лидского В. Б., Прасолова В. В., Сивашинского И. Х., Шахно К. У, ну и, конечно же, на страницах интернета. Было принято соображение по текущей теме написать исследовательскую работу. Наше исследование содержит непосредственно большое практическое использование, а также теоретическую значимость.
Гипотеза: Мы полагаем, что если непосредственно знать в совершенстве особенные индивидуальности средних линий трапеции, то их использование в свою очередь будет хорошим подспорьем ученикам в практическом направлении материала.
Новизна этого исследования состоит в том, что непосредственно данное направление не рассматривалось более глубоко и основательно.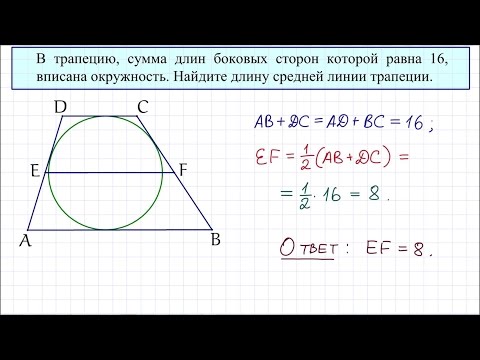 Важность этого исследования на практике заключена в том, что результатом будет заинтересованность школьников, что, непосредственно повысит их успешность в изучении.
Важность этого исследования на практике заключена в том, что результатом будет заинтересованность школьников, что, непосредственно повысит их успешность в изучении.
Цель: сколько средних линий имеет трапеция, определить особенные отличия средних линий трапеции
Задачи исследования:
подобрать данные про средние линии трапеции
изучить особенные индивидуальности про средние линии в трапеции
исследовать задачи про средние линии, действующие в математической литературе
разобрать конкретные вопросы про средние линии трапеции
Предмет исследования – трапеция
Объект исследования – средние линии трапеции
Основные методы исследования:
анализ
синтез
аналогии
сравнение
обобщение
1.1. вторая средняя линия трапеции.
Бесспорно, общеизвестна школьная трактовка: средняя линия трапеции это отрезок, который соединяет середины боковых сторон данной трапеции.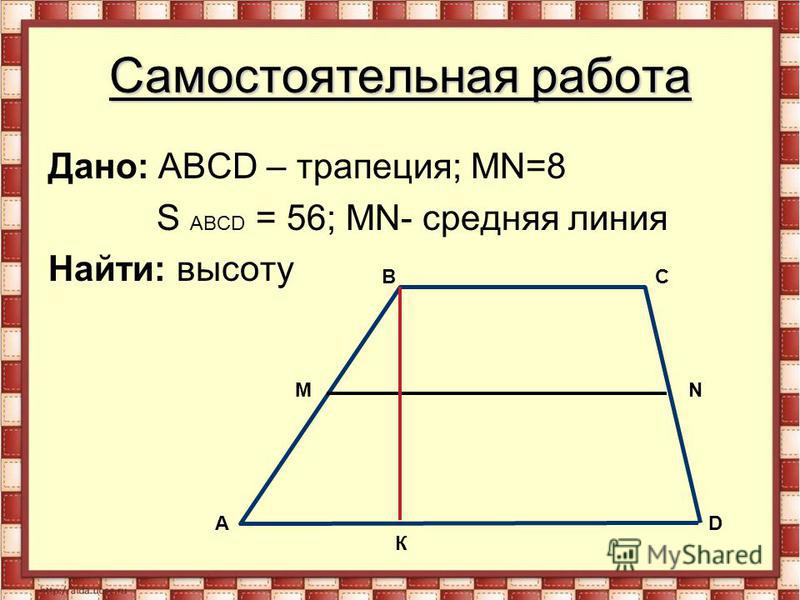 Давайте соединим середины оснований, и у нас непосредственно, получится вторая средняя линия т рапеции FE.
Давайте соединим середины оснований, и у нас непосредственно, получится вторая средняя линия т рапеции FE.
Общеизвестная формула средней линии трапеции ½ (AB+CD). Зарождается проблема: есть ли какая-либо взаимосвязь между боковыми сторонами и второй средней линией трапеции? Совершенно объяснимо, что вторая средняя линия трапеции не может быть равна полусумме оснований трапеции. Если нижнее основание растянуть, то длина FE не преобразится, а сумма боковых сторон трапеции останется без изменений.
р ис.1
B1
A1
П утем доказательства мы установили в трапеции ABCD DС||АB, FE и есть вторая средняя линия (рис.1)
F E = FD + AD +AE или FE = FC + BC + BE. Найдем сумму этих равенств: 2FE = (DF + FC) +(AE+DE)+(AD+BC).FE=1/2(AD+BC).
1.2. Особенные отличия средних линий трапеции, не изучаемые на уроках геометрии.
Разберем более детально несколько интересных свойств второй средней линии трапеции.
1 . В точке, в которой пересекаются две средние линии, они делятся пополам
Доказательство: В △ВСD и △ABD: KN — средняя линия △BCD⇒KN || BD и KN=½ BD. MS – также средняя линия △ABD, MS || BD, MS=½ BD (по свойству средней линии). Аналогично, МК || АС, MK=½ AC, NS || AC, NS=½ AC. ⇒MKNS – параллелограмм, a MN и FE –диагонали параллелограмма ⇒ KO = OS, MO = ON. ч. т. д.
2. Диагонали трапеции и вторая средняя линия пересекаются в одной точке
рис.4
B
K
C
A
Дано: ВК=КС
D
S
O
Доказать: AS=SD
Доказательство: (накрест лежащие углы) так как ВС||AD и секущей BD (вертикальные углы) ⇒ ~ , аналогично ~
⇒, BK =KC (по условию) ⇒ AS =SD ч. т. д.
3. Та прямая, частью которой эта линия является, пересекается в единой точке с теми прямыми, которые совпадают с боковыми сторонами
р ис.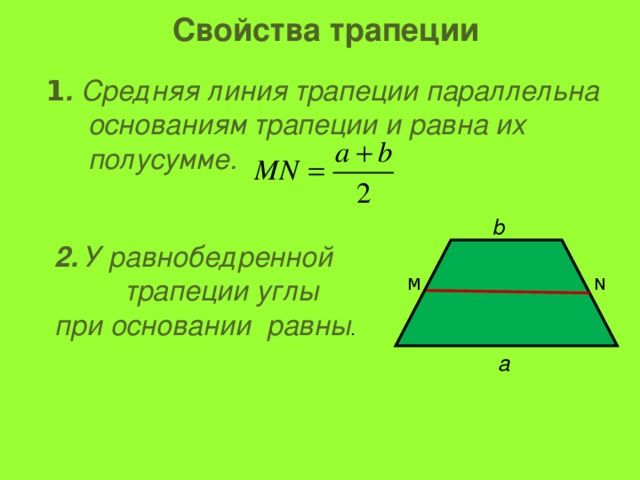 5
5
K
A
B
O
C
D
S
Доказательство: △ВОС~△AOD(по двум углам)
O DOC, OBOA, OA =k OB, OD = k OC.
Применим формулу вычисления середины отрезка:
O K=½ (ОВ+ОС), OS=½ (OA+OD), OS=½ (k∙OB + k∙OC)=½ k (OB+ OC)=k OK OK коллинеарен OS ОFE. ч. т. д
4. Средние линии равнобедренной трапеции перпендикулярны.
рис.6
5
Дано: ABCD — трапеция, АВ=CD, MN, FE – средние линии
Доказать: MN FE
Доказательство: Рассмотрим ∆АВС и ∆ADC: MK – средняя линия ∆АВС, МК||АС, МК=½ АС,NS – средняя линия ∆ADC, NS||AC, NS=½ АС.
По признаку параллелограмма противоположные стороны четырехугольника MKNS равны и параллельны ⇒MKNS – параллелограмм. Трапеция ABCD – равнобокая, AC = BD,MK=½ АС, KN=½ BD,MK=KN MKNS – ромб.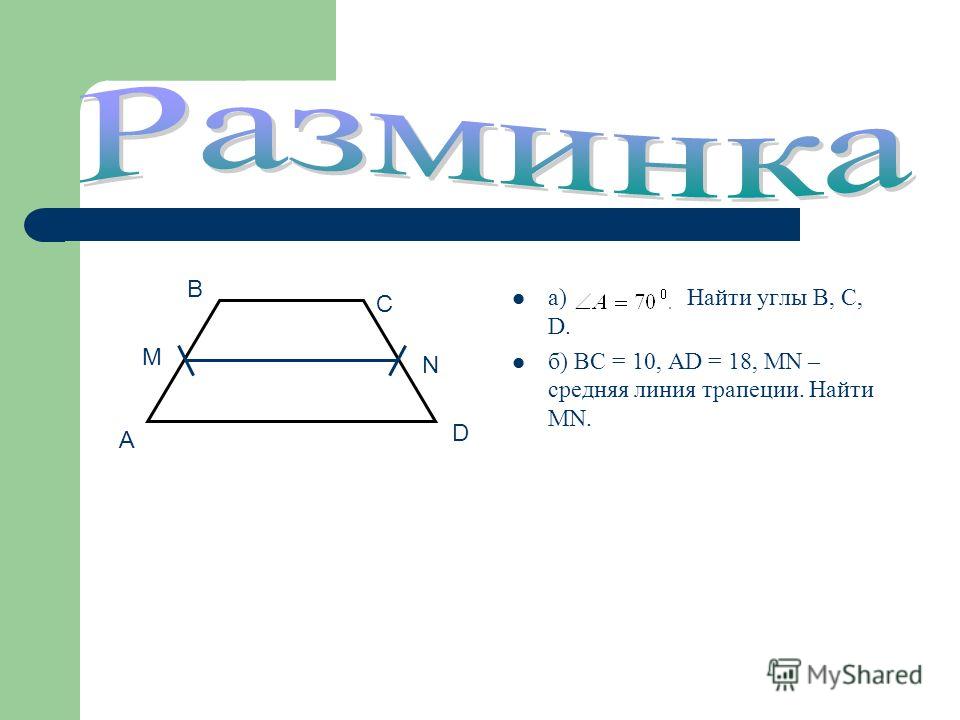 По свойству ромба MN FE. ч. т. д
По свойству ромба MN FE. ч. т. д
. В равнобокой трапеции (у которой боковые стороны идут под одним углом) средняя линия пересекает основания под углом в 90 градусов;
(см. доказательство предыдущего утверждения)
6. Если средние линии трапеции равны, то ее диагонали перпендикулярны
рис.7
1
Доказательство:
МKNS– параллелограмм, MN=KS (по условию). Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник, KN MK,т.к. KN||BD, MK||AC, то BD AC. ч. т. д
.3. Практическая направленность
Лично удалось встретить несколько задач, так или иначе имеющие связь со второй средней линией трапеции в публикациях Кушнир И. А. Рассмотрим решение некоторых задач:
Задача 1 (Кушнир И.А.)
В трапеции ABCD сумма углов при меньшем основании равна 270º.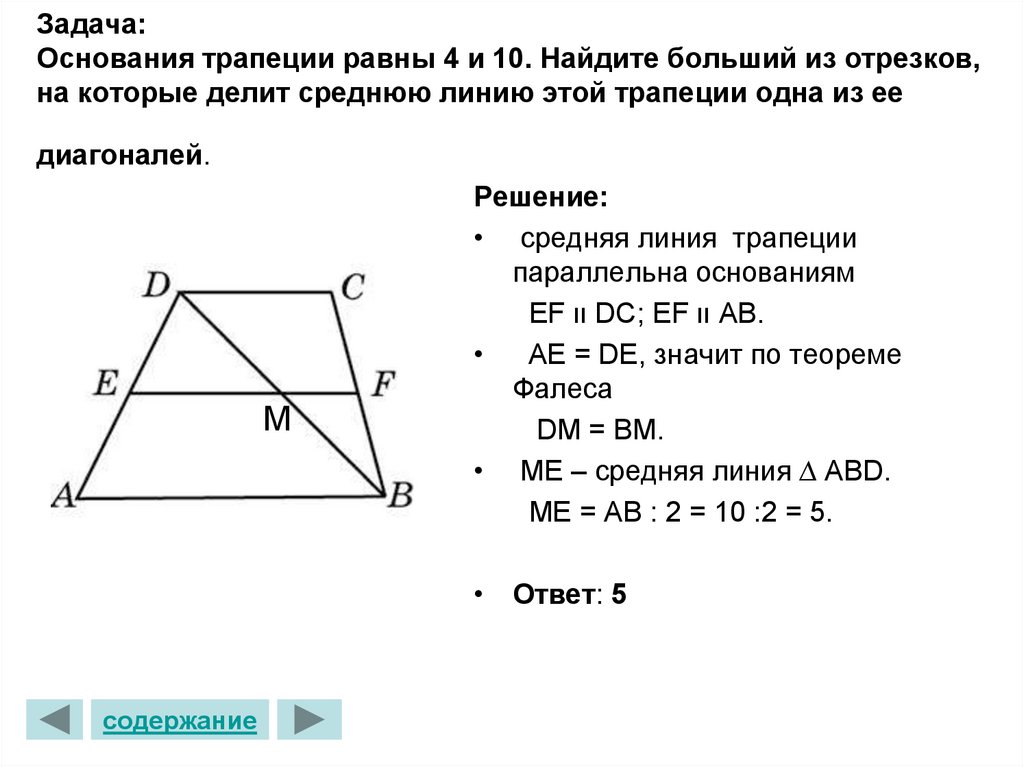 Найти длину второй средней линии, если основания равны а и в (а >в).
Найти длину второй средней линии, если основания равны а и в (а >в).
в треугольнике AMD
Поэтому, MN = , MF=
NF = MF – MN = (a – b)/2.
Ответ:(a-b)/2
M
C
N
B
A
D
F
Задача 2 (Кушнир И.А.)
Д
E
оказать, что площадь трапеции равна произведению второй средней линии на сумму перпендикуляров, проведенных к этой средней линии (или её продолжению) из двух противоположных вершин трапеции.
р
C
ис.9
B
N
M
A
F
D
Дано: ABCD – трапеция, EF – вторая средняя линия, СN EF, AM EF.
Доказать:
Доказательство: Рассмотрим △ AEF и△ ECF. , ⇒ . , то ч.т.д.
Задача 3 (Кушнир И. А.)
В трапеции ABCD сумма углов при основании AD равна 90º. Докажите, что отрезок, соединяющий середины оснований, равен ½ (AD – BC)
рис.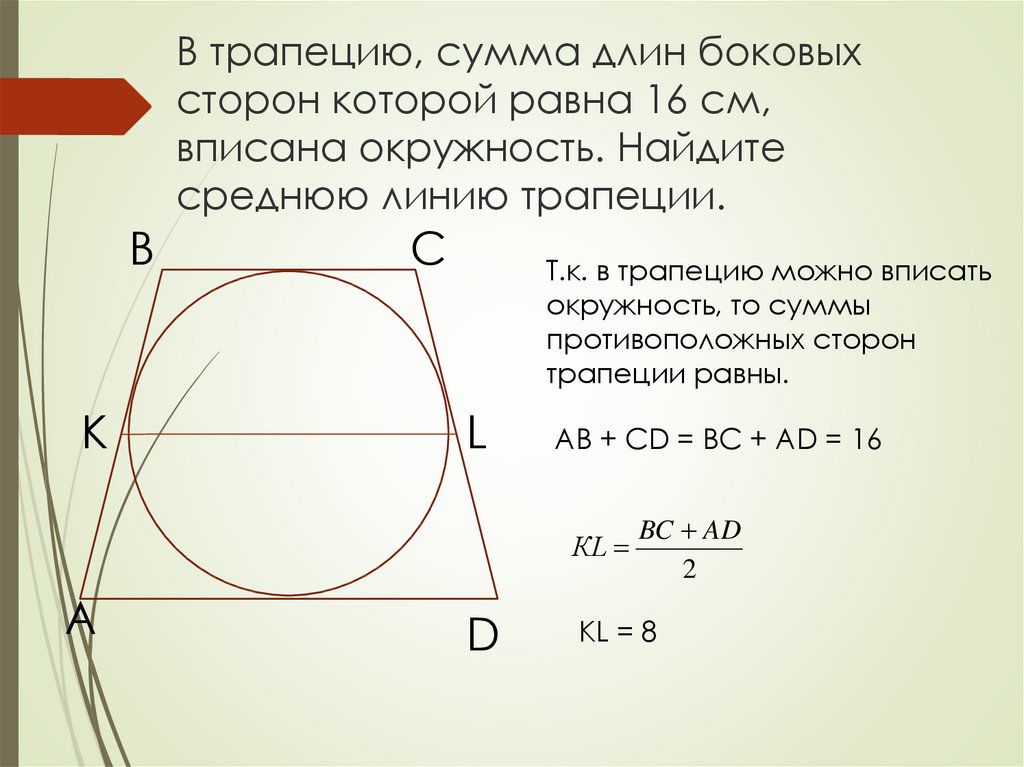 10 Р
10 Р
M
ешение: AF=FD, BN=NC
º, º,
AD – гипотенуза,
B
N
C
A
F
D
MF =AF=FD=½ AD
MN =½ BC
FN = MF – MN
FN =½ AD –½ BC =½ (AD – BC) ч. т. д.
Предлагаю задачи, составленные мной:
Задача 1
Верно ли утверждение: если прямая проходит через точку пересечения диагоналей и середину одного основания трапеции, то и второе основание она делит пополам?
Решение: Верно, см. свойство 2
Задача 2
В трапеции ABCD вторая средняя линия = 4 см, основания равны 12 см и 8 см, угол между средними линиями 30º. Найти площадь трапеции.
Р
B
K
C
A
H
S
D
ешение:
M O N
(соответственные), ,КН = 2 см. см².
Задача 3
Провести в трапеции вторую среднюю линию с помощью чертежной линейки.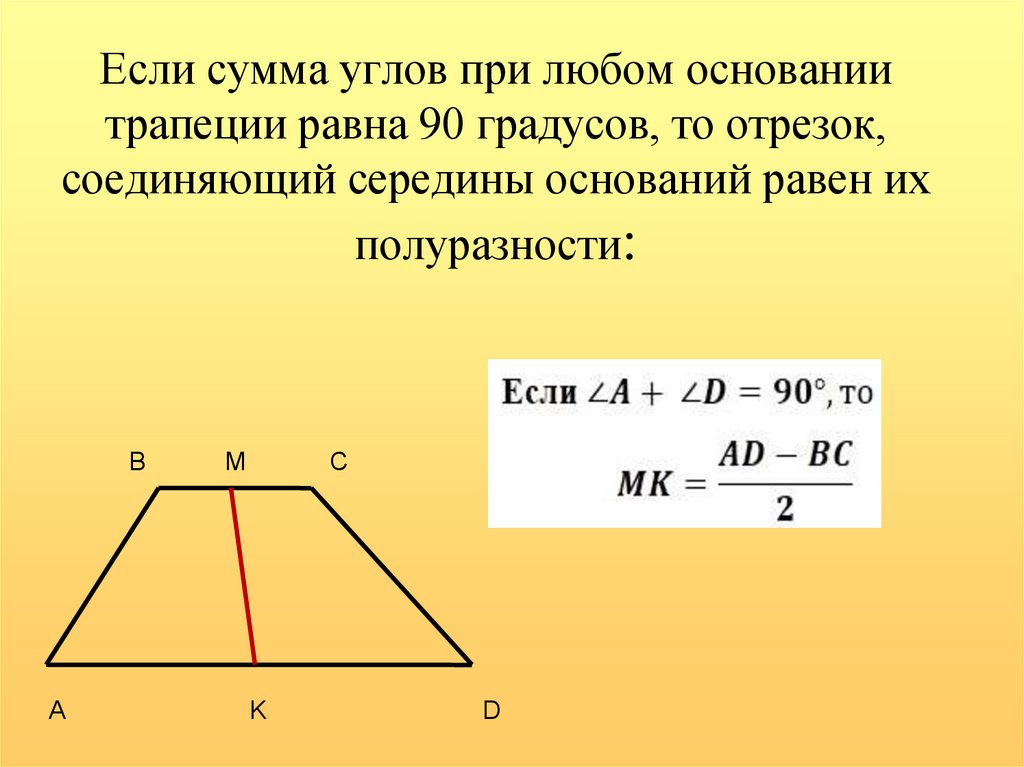
Решение:
соединим диагонали.
до пересечения продолжим боковые стороны.
проведем прямую через точку пересечения диагоналей и точку пересечения продолжений боковых сторон.
Получили искомую вторую среднюю линию трапеции.
K
O
S
D
A
B
C
Задача 4
В
Рассмотрим ∆КОС и ∆SOA. Они подобны по стороне и прилежащим углам. Значит, Так как точка К середина отрезка ВС, то КС= 8 см, а АS= 16cм. Следовательно, AD=32cм.
Средняя линия
трапеции АВСD ВС= 16 см, вторая средняя линия делится диагональю в отношении 1:2. Найдите среднюю линию трапеции АВСD
Решение:
В С
K
М О L
А S D
Задача 5
В торая средняя линяя равнобокой трапеции перпендикулярна её основаниям.
△АОD и △ВОС равнобедренные.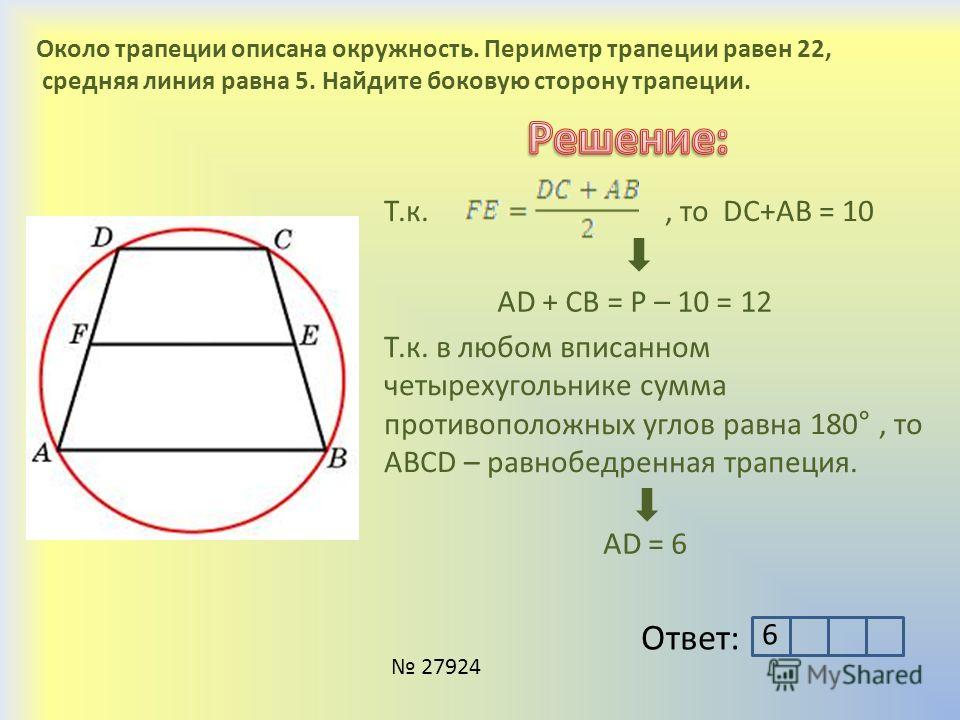 ОМ и ОК медианы этих треугольников. По свойству равнобедренного треугольника: медиана равнобедренного треугольника, опущенная на основание, является высотой треугольника. ⇒ КМ ┴ основаниям.
ОМ и ОК медианы этих треугольников. По свойству равнобедренного треугольника: медиана равнобедренного треугольника, опущенная на основание, является высотой треугольника. ⇒ КМ ┴ основаниям.
Заключение
Главной целью работы требовалось установить, сколько средних линий имеет трапеция, определить особенные индивидуальности средних линий трапеции.
Поставленные цели и задачи работы «Сколько средних линий в трапеции?» достигнуты.
В соответствии с результатами выполненной мною деятельности я выявила о существовании второй средней линии трапеции, о ее свойствах. Детально проанализировала решение отдельных задач, тем или иным образом имеющих отношение к средним линиям трапеции.
Стало понятно, почему вторая средняя линия трапеции применяется в решении задач достаточно редко, поэтому ее мало изучают во время школьного обучения. Но я не сожалею, что собственно затраченное время на постижение этой темы, позволило мне много нового выяснить о средних линиях трапеции, и некоторых ее интересных свойствах.
Мне представилась возможность сформировать исключительно несколько задач, связанных со второй средней линией трапеции, но я убеждена, что их количество прибавится.
Подводя итоги нашей работы с уверенностью можно сказать о том, что цель, определенная в процессе творения нашей работы, была достигнута, а задачи осуществлены.
Литература
Л. С. Атанасян. «Геометрия 7-9» Учебник для образовательных учреждений/- М., Просвещение, 2006
Википедия.- ru.wikipedia.org/wiki /средняя линия
И. А. Кушнир «Вторая средняя линия трапеции», журнал «Математика в школе» №2, 1993.
В. Б. Лидский, Л. В. Овсянников, А. Н. Тулайков, М. И. Шабунин «Задачи по элементарной математике» — М., Физматгиз, 2010
В. В. Прасолов «Задачи по планиметрии» -М.: Наука, 2020
И. Х. Сивашинский «Задачник по элементарной математике», — М., Наука, 2015
Фестиваль идей – portfolio.1september.ru/work
К. У. Шахно «Сборник задач по элементарной математике повышенной трудности», — Минск, Высшая школа, 2012.
https://ru.wikipedia.org/wiki/%D0%A1%D1%80%D0%B5%D0%B4%D0%BD%D1%8F%D1%8F_%D0%BB%D0%B8%D0%BD%D0%B8%D1%8F
Опубликовано в группе «УРОК.РФ: группа для участников конкурсов»
Середины трапеций — Криста Кинг Математика
Средняя часть трапеции соединяет ее непараллельные стороны
Средняя часть трапеции — это отрезок, соединяющий середины двух непараллельных сторон трапеции.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Если ???\overline{AB}\parallel\overline{DC}???, если ???F??? является серединой ???\overline{AD}???, и если ???E??? является серединой ???\overline{BC}???, затем ???\overline{FE}??? это середина трапеции.
Соотношение между длиной среднего отрезка и длинами параллельных сторон равно
???FE=\frac{1}{2}(AB+DC)???
Длина среднего сегмента трапеции всегда равна половине суммы длин параллельных сторон.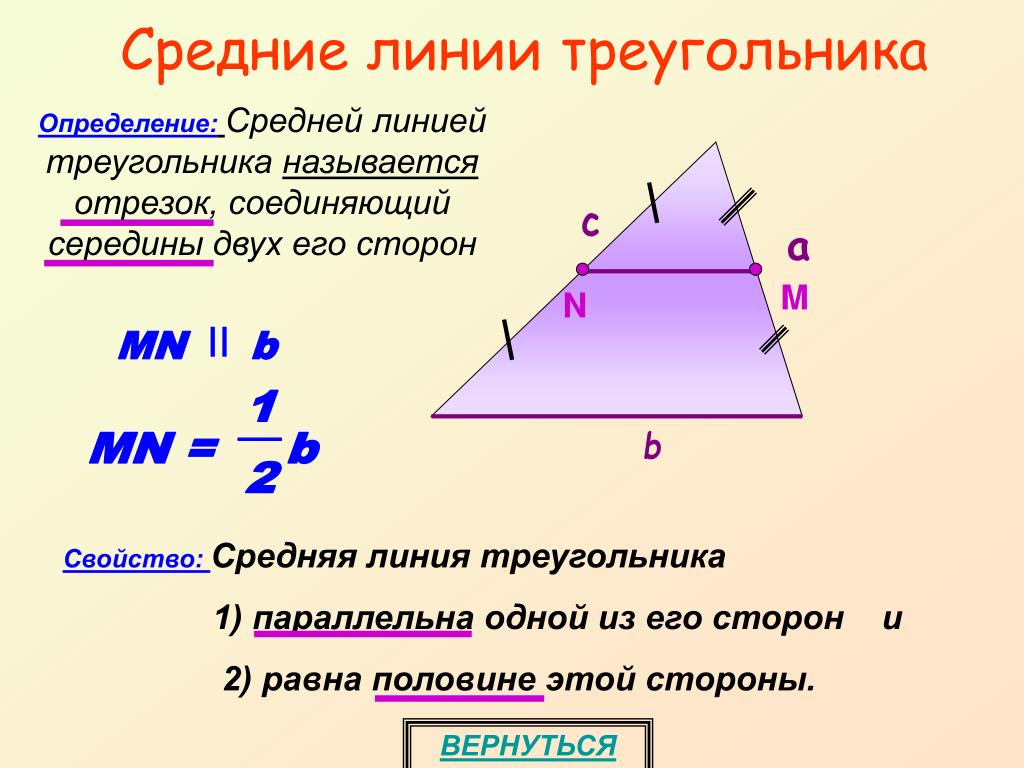
Как использовать среднюю часть трапеции для решения задач
Пройти курс
Хотите узнать больше о геометрии? У меня есть пошаговый курс для этого. 🙂
Учить больше
Нахождение длины стороны трапеции по длине ее середины
Пример
В изображенной трапеции ???\overline{TU}\parallel\overline{WV}???, ? ??ИКС??? является серединой ???\overline{TW}???, а ???Y??? является серединой ???\overline{UV}???. Какова длина ???\overline{WV}????
По определению ???\overline{XY}??? это середина трапеции. Следовательно, мы знаем, что
???XY=\frac{1}{2}(TU+WV)???
Давайте подставим то, что мы знаем, и найдем ???x???.
???29=\frac{1}{2}(23+2x+17)???
???29=\frac{1}{2}(40+2x)???
???29=20+х???
???9=х???
Тогда длина ???\overline{WV}???
???WV=2x+17???
???WV=2(9)+17???
???WV=35???
Средняя линия трапеции — это отрезок, соединяющий середины двух непараллельных сторон трапеции.
Пример
В координатной плоскости трапеция ???XYWZ??? имеет вершины в точках ???X=(-2,2)???, ???Y=(3,2)???, ???Z=(-3,-2)???, и ? ??W=(4,-2)???. Какова длина среднего отрезка вдоль оси ???x????
Вы можете построить трапецию и найти длины параллельных сторон.
Помните, что длина средней линии равна половине суммы параллельных сторон, поэтому длина средней линии равна
???\frac{1}{2}(XY+ZW)???
???\frac{1}{2}(5+7)???
???\frac{1}{2}(12)???
???6???
Получить доступ к полному курсу геометрии
Начать
Учим математикуКриста Кинг математика, учиться онлайн, онлайн курс, онлайн математика, геометрия, трапеции, средние сегменты, средние сегменты трапеций
0 лайковформул на все случаи жизни.
 Все варианты, как найти площадь трапеции
Все варианты, как найти площадь трапецииВ математике известно несколько видов четырехугольников: квадрат, прямоугольник, ромб, параллелограмм. Среди них трапеция — вид выпуклого четырехугольника, у которого две стороны параллельны, а две другие — нет. Параллельные противоположные стороны называются основаниями, а две другие – сторонами трапеции. Отрезок, соединяющий середины сторон, называется средней линией. Трапеции бывают нескольких видов: равнобедренные, прямоугольные, криволинейные. Для каждого типа трапеций существуют формулы нахождения площади.
Площадь трапеции
Чтобы найти площадь трапеции, нужно знать длину ее оснований и высоту. Высота трапеции — это отрезок, перпендикулярный основаниям. Пусть верхнее основание равно a, нижнее — b, а высота — h. Тогда можно вычислить площадь S по формуле:
S = ½ * (a + b) * h
т.е. возьмите половину суммы оснований, умноженных на высоту.
Вы также можете вычислить площадь трапеции, если знаете значение высоты и средней линии. Обозначим среднюю линию — m. Затем
Обозначим среднюю линию — m. Затем
Решим задачу посложнее: нам известны длины четырех сторон трапеции — a, b, c, d. Тогда площадь находится по формуле:
Если известны длины диагоналей и угол между ними, то площадь ищется так:
S = ½ * d1 * d2 * sinα
где d с индексы 1 и 2 — диагонали. В этой формуле при расчете дается синус угла.
При известных длинах основания a и b и двух углах у нижнего основания площадь рассчитывается следующим образом:
S = ½ * (b2 — a2) * (sin α * sin β / sin(α + β))
Площадь равнобедренной трапеции
Равнобедренная трапеция является частным случаем трапеции. Отличие ее в том, что такая трапеция представляет собой выпуклый четырехугольник с осью симметрии, проходящей через середины двух противоположных сторон. Его стороны равны.
Есть несколько способов найти площадь равнобедренной трапеции.
- По длине трех сторон. В этом случае длины сторон будут совпадать, поэтому они обозначаются одним значением — с, а и b — длины оснований:
- Если известны длина верхнего основания, боковой стороны и угол при нижнем основании, то площадь рассчитывается следующим образом:
S = c * sin α * (a + c * cos α)
где а — верхнее основание, с — сторона.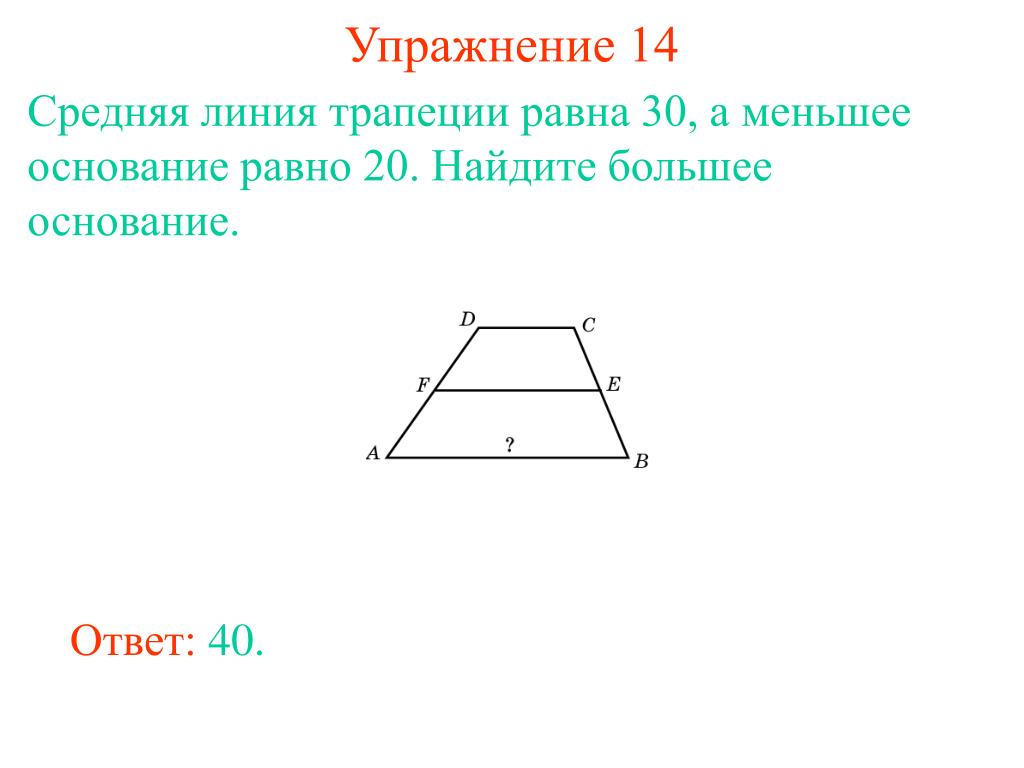
- Если вместо верхнего основания известна длина нижнего основания — b, то площадь рассчитывается по формуле:
S = c * sin α * (b — c * cos α)
- Если известны два основания и угол при нижнем основании, площадь вычисляется по тангенсу угла:
S = ½ * (b2 — a2) * tg α
- Также площадь вычисляется через диагонали и угол между ними. При этом диагонали равны по длине, поэтому каждая обозначается буквой d без индексов:
S = ½ * d2 * sinα
- Вычислите площадь трапеции, зная длину боковой стороны, среднюю линию и угол при нижнем основании.
Пусть сторона — с, средняя линия — м, угол — а, тогда:
S = m * c * sinα
Иногда в равностороннюю трапецию можно вписать окружность, радиус которой будет — r.
Известно, что в любую трапецию можно вписать окружность, если сумма длин оснований равна сумме длин ее сторон. Затем площадь находится через радиус вписанной окружности и угол при нижнем основании:
S = 4r2 / sinα
Такой же расчет производится через диаметр D вписанной окружности (кстати, он совпадает с высота трапеции):
Зная основания и угол, площадь равнобедренной трапеции вычисляется следующим образом:
S = a*b/sinα
(эта и последующие формулы справедливы только для трапеций с вписанной окружностью).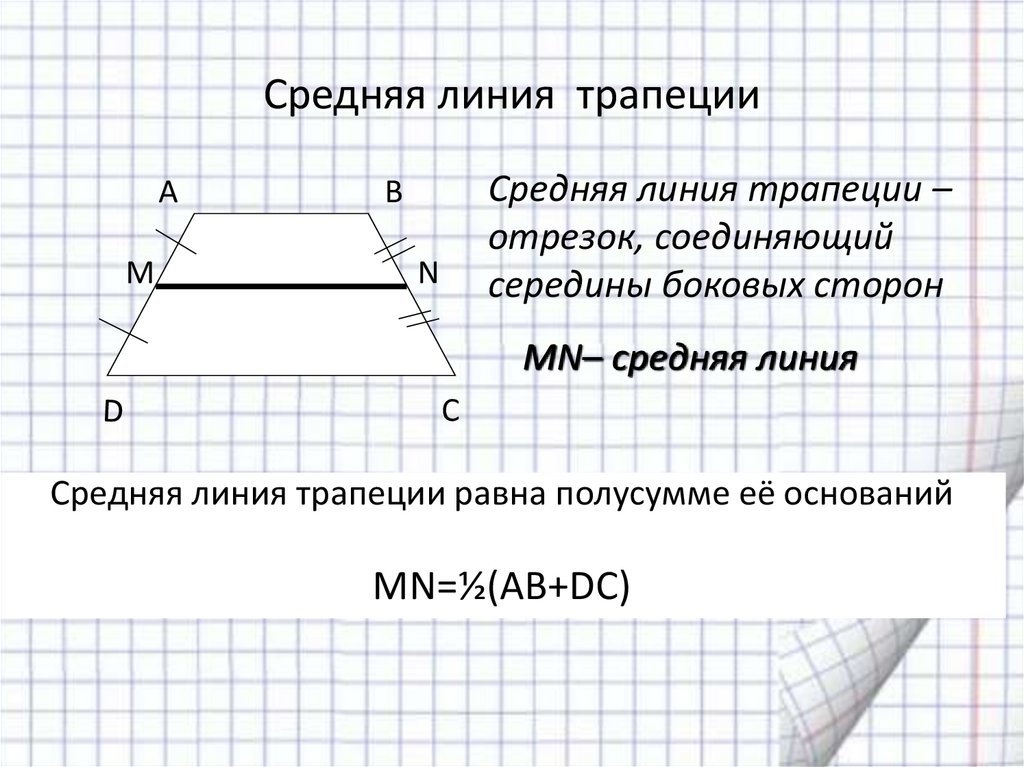
Через основания и радиус окружности площадь ищется следующим образом:
Если известны только основания, то площадь вычисляется по формуле:
Через основания и боковую линию, площадь трапеции с вписанной окружностью и через основания и среднюю линию — m вычисляется так:
Площадь прямоугольной трапеции
Прямоугольной называется трапеция, у которой одна из сторон перпендикулярна основаниям. В этом случае длина стороны совпадает с высотой трапеции.
Прямоугольная трапеция состоит из квадрата и треугольника. Найдя площадь каждой из фигур, сложите результаты и получите общую площадь фигуры.
Также общие формулы расчета площади трапеции подходят для расчета площади прямоугольной трапеции.
- Если длины оснований и высота (или перпендикулярная сторона) известны, то площадь рассчитывается по формуле:
S = (a + b) * h / 2
Поскольку h (высота) может быть стороной с. Тогда формула выглядит так:
S = (a + b) * c / 2
- Другой способ вычисления площади — умножить длину средней линии на высоту:
или по длине боковой перпендикулярной стороны:
- Следующий метод расчета — через половину произведения диагоналей на синус угла между ними:
S = ½ * d1 * d2 * sinα
Если диагонали перпендикулярны, то формула упрощается до:
S = ½ * d1 * d2
- сумма длин двух противоположных сторон) и радиус вписанной окружности.

Эта формула действительна для оснований. Если взять длины сторон, то одна из них будет равна удвоенному радиусу. Формула будет выглядеть так:
S = (2r + c) * r
- Если в трапецию вписана окружность, то площадь вычисляется так же:
где m — длина средней линии.
Площадь криволинейной трапеции
Криволинейная трапеция – плоская фигура, ограниченная графиком неотрицательной непрерывной функции y = f(x), определенной на отрезке , оси x и прямых линиях x = а, х = б. На самом деле две его стороны параллельны друг другу (основаниям), третья сторона перпендикулярна основаниям, а четвертая представляет собой кривую, соответствующую графику функции.
Площадь криволинейной трапеции ищется через интеграл по формуле Ньютона-Лейбница:
Так вычисляются площади различных видов трапеций. Но, помимо свойств сторон, трапеции обладают такими же свойствами углов. Как и у всех существующих четырехугольников, сумма внутренних углов трапеции равна 360 градусов.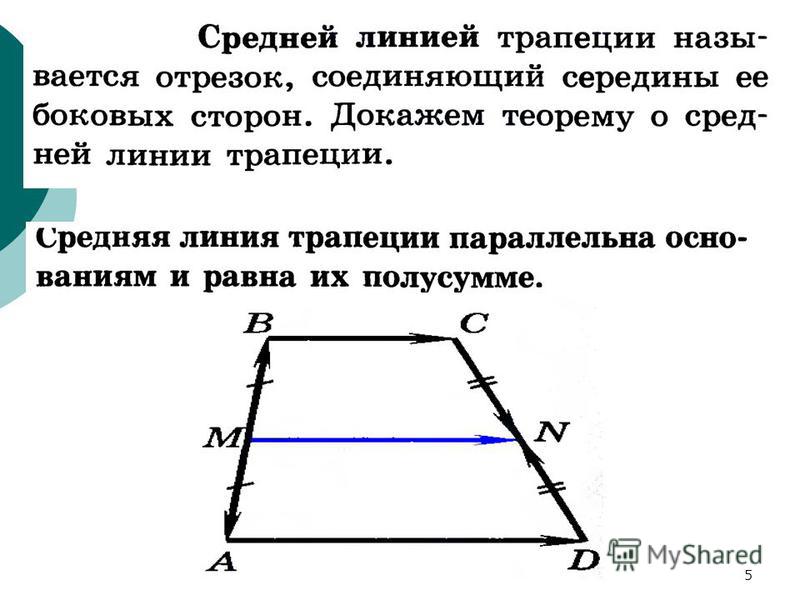 А сумма углов, прилежащих к стороне, равна 180 градусов.
А сумма углов, прилежащих к стороне, равна 180 градусов.
Геометрия – одна из наук, с применением которой на практике человек сталкивается практически ежедневно. Среди разнообразия геометрических фигур особого внимания заслуживает трапеция. Это выпуклая фигура с четырьмя сторонами, две из которых параллельны друг другу. Последние называются основаниями, а оставшиеся два — сторонами. Отрезок, перпендикулярный основаниям и определяющий величину зазора между ними, будет высотой трапеции. Как рассчитать его длину?
Нахождение высоты произвольной трапеции
По исходным данным определение высоты фигуры возможно несколькими способами.
Известная площадь
Если известны длины параллельных сторон, а также указана площадь фигуры, то для определения искомого перпендикуляра можно использовать следующее соотношение:
S=h* (a+b)/2, 90 106 h — искомое значение (высота), 90 106 S — площадь фигуры, 90 106 a и b — стороны, параллельные друг другу.
Из приведенной выше формулы следует, что h=2S/(a+b).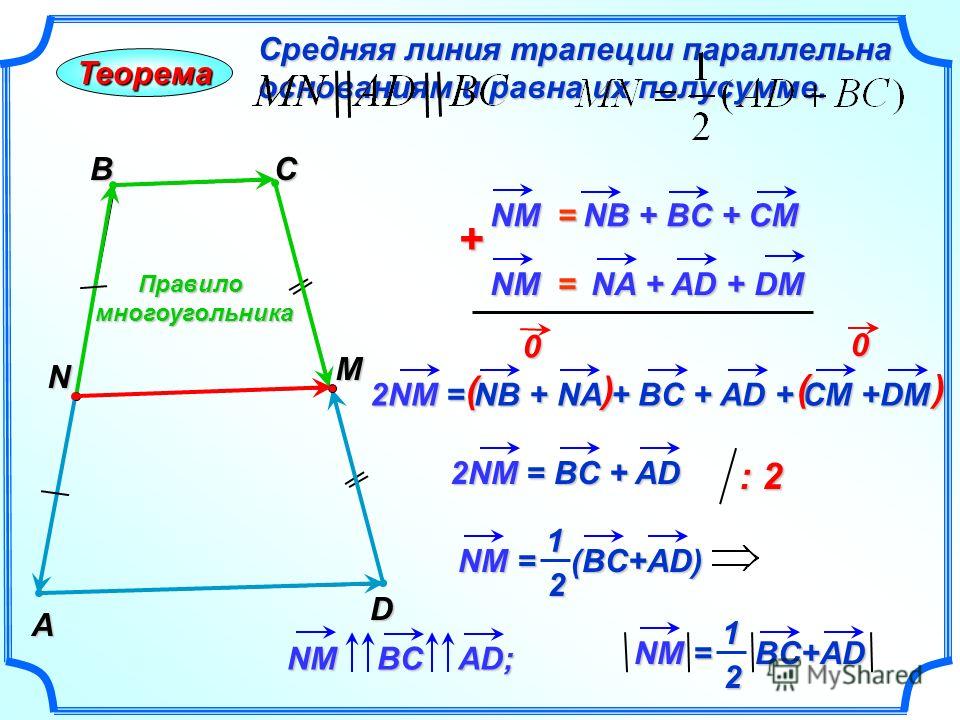
Известна величина средней линии
Если среди исходных данных кроме площади трапеции (S) известна также длина ее средней линии (l), то другая формула полезно для расчетов. Для начала стоит уточнить, что такое средняя линия для данного типа четырехугольника. Термин определяет часть прямой линии, соединяющей середины сторон фигуры.
На основании свойств трапеции l=(a+b)/2,
l — средняя линия,
a, b — стороны-основания четырехугольника.
Следовательно, h=2S/(a+b)=S/l.
Известны 4 стороны фигуры
В этом случае поможет теорема Пифагора. Опустив перпендикуляры на большую сторону-основание, используем ее для двух получившихся прямоугольных треугольников. Окончательное выражение будет выглядеть так:
h=√c 2 -(((a-b) 2 +c 2 -d 2)/2(a-b)) 2 ,
c и d — две другие стороны.
Углы у основания
Если у вас есть данные об основных углах, используйте тригонометрические функции.
h = c*sinα = d*sinβ,
α и β — углы при основании четырехугольника,
c и d — его стороны.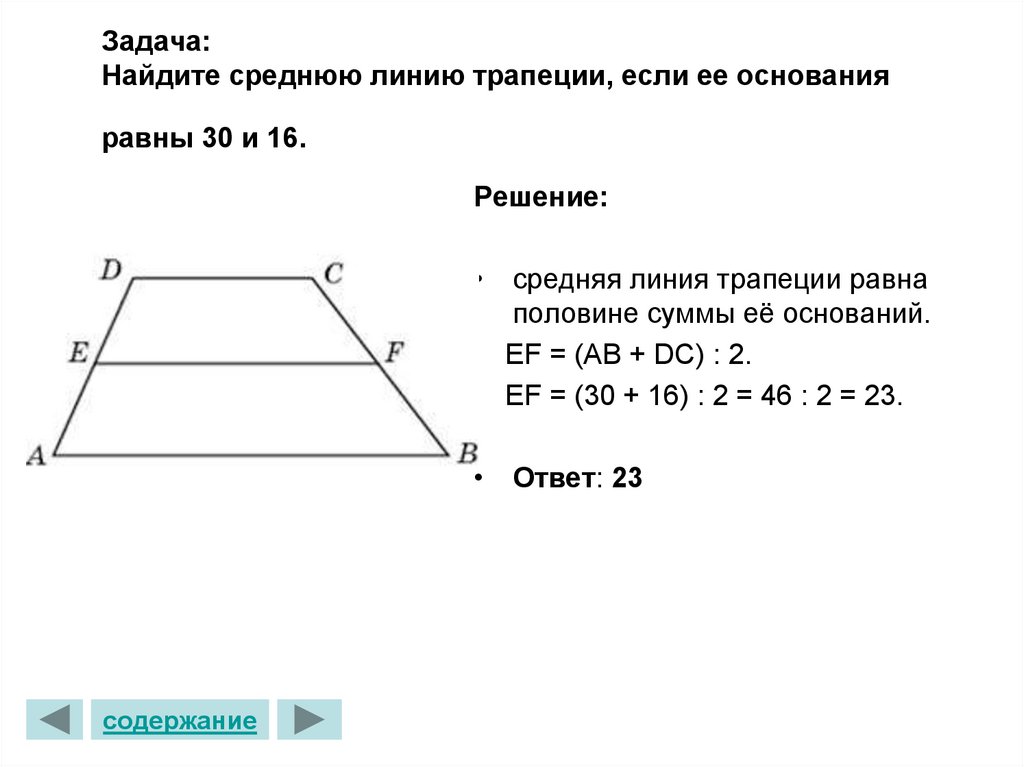
Диагонали фигуры и углы, которые они пересекают
Длиной диагонали называется длина отрезка, соединяющего противоположные вершины фигуры. Обозначим эти величины символами d1 и d2, а углы между ними γ и φ. Тогда:
h = (d1*d2)/(a+b) sin γ = (d1*d2)/(a+b) sinφ,
h = (d1*d2)/2l sin γ = (d1* d2)/2l sinφ,
a и b — стороны основания фигуры,
d1 и d2 — диагонали трапеции,
γ и φ — углы между диагоналями.
Высота фигуры и радиус вписанной в нее окружности
Как следует из определения этого вида окружности, она касается каждого основания в 1 точке, которые являются частью одной прямой. Следовательно, расстояние между ними — диаметр — нужная высота фигуры. А так как диаметр в два раза больше радиуса, то:
h = 2 * r,
r — радиус окружности, вписанной в данную трапецию.
Найдите высоту равнобедренной трапеции
- Как следует из формулировки, отличительной характеристикой равнобедренной трапеции является равенство ее сторон.
 Поэтому для нахождения высоты фигуры воспользуйтесь формулой определения этой величины в том случае, когда известны стороны трапеции.
Поэтому для нахождения высоты фигуры воспользуйтесь формулой определения этой величины в том случае, когда известны стороны трапеции.
Итак, если с = d, то h = √c 2 — (((а-b) 2 + c 2 -d 2) / 2 (а-b)) 2 = √c 2 — (а-b) 2 / 4 ,
а, b — основания четырехугольника,
c = d — его стороны.
- При наличии величины углов, образованных двумя сторонами (основанием и стороной), высота трапеции определяется следующим соотношением:
h = c*sinα,
h = с * tgα *cosα = с * tgα * (b — a)/2c = tgα * (b-a)/2,
α — угол при основании фигуры,
а, b (ас = d — его стороны.
- Если даны значения диагоналей фигуры, то выражение для нахождения высоты фигуры изменится, т.к. d1 = d2:
h = d1 2 /(a+b)*sinγ = d1 2 /(a+b)*sinφ,
h = d1 2 /2*l*sinγ = d1 2 /2*l*sinφ.
Есть много способов найти площадь трапеции. Обычно репетитор по математике знает несколько способов ее вычисления, остановимся на них подробнее:
1) , где AD и BC — основания, а BH — высота трапеции. Доказательство: проведите диагональ BD и выразите площади треугольников ABD и CDB через полупроизведение их оснований и высоты:
Доказательство: проведите диагональ BD и выразите площади треугольников ABD и CDB через полупроизведение их оснований и высоты:
, где DP – внешняя высота в
Складываем эти равенства почленно и, учитывая, что высоты BH и DP равны, получаем:
Выносим за скобки
К.Э.Д.
Следствие из формулы площади трапеции:
Так как полусумма оснований равна МН — средней линии трапеции, то
2) Применение общей формулы площади четырехугольника .
Площадь четырехугольника равна половине произведения диагоналей на синус угла между ними
Для доказательства достаточно разделить трапецию на 4 треугольника, площадь каждого выразить в термины «половина произведения диагоналей на синус угла между ними» (его принимают за угол, складывают получившиеся выражения, выносят за скобку и методом группировки разлагают эту скобку на множители, чтобы получить ее равенство выражению Отсюда
3) Метод диагонального сдвига
Это мой титул.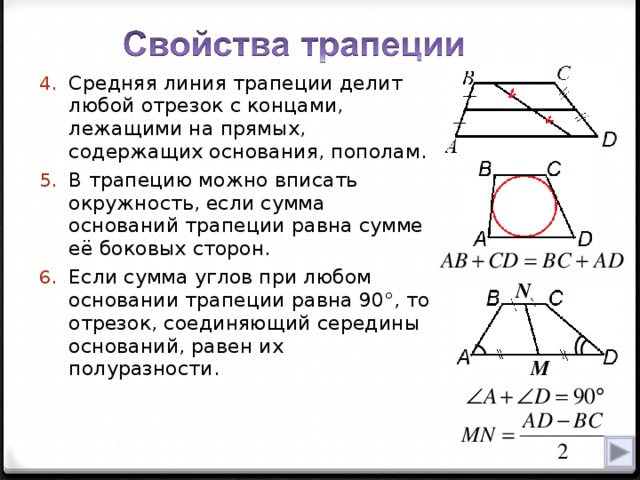 В школьных учебниках репетитор по математике не найдет такой рубрики. Описание техники можно найти только в дополнительных туториалах как пример решения задачи. Отмечу, что большинство интересных и полезных фактов планиметрии репетиторы по математике раскрывают учащимся в процессе выполнения практической работы. Это крайне неоптимально, потому что студенту нужно разделить их на отдельные теоремы и назвать «громкими именами». Одним из них является «диагональный сдвиг». О чем это? Проведем через вершину B прямую, параллельную AC, до пересечения с нижним основанием в точке E. В этом случае четырехугольник EBCA будет параллелограммом (по определению), а значит, BC=EA и EB=AC. Теперь нас интересует первое равенство. У нас есть:
В школьных учебниках репетитор по математике не найдет такой рубрики. Описание техники можно найти только в дополнительных туториалах как пример решения задачи. Отмечу, что большинство интересных и полезных фактов планиметрии репетиторы по математике раскрывают учащимся в процессе выполнения практической работы. Это крайне неоптимально, потому что студенту нужно разделить их на отдельные теоремы и назвать «громкими именами». Одним из них является «диагональный сдвиг». О чем это? Проведем через вершину B прямую, параллельную AC, до пересечения с нижним основанием в точке E. В этом случае четырехугольник EBCA будет параллелограммом (по определению), а значит, BC=EA и EB=AC. Теперь нас интересует первое равенство. У нас есть:
Обратите внимание, что треугольник BED, площадь которого равна площади трапеции, обладает рядом других замечательных свойств:
1) Его площадь равна площади трапеции
2) Его равнобедренность возникает одновременно с равнобедренная сторона самой трапеции
3) Ее верхний угол при вершине В равен углу между диагоналями трапеции (что очень часто используется в задачах)
4) Ее медиана ВК равна расстоянию QS между серединами оснований трапеции. Я недавно столкнулся с использованием этого свойства при подготовке студента на Мехмат МГУ по учебнику Ткачука, версия 1973 (задание дано внизу страницы).
Я недавно столкнулся с использованием этого свойства при подготовке студента на Мехмат МГУ по учебнику Ткачука, версия 1973 (задание дано внизу страницы).
Специальность репетитора по математике.
Иногда предлагаю задачи на очень хитрый способ нахождения квадрата трапеции. Я отношу это к специальным приемам, потому что на практике воспитатель редко их использует. Если вам нужно подготовиться к ЕГЭ по математике только по части Б, о них можно не читать. Для остальных скажу больше. Получается, что площадь трапеции вдвое больше площади треугольника с вершинами на концах одной стороны и середине другой, то есть треугольника ABS на рисунке:
Доказательство: начертите высоты SM и SN в треугольниках BCS и ADS и выразите сумму площадей этих треугольников:
Так как точка S является серединой CD, то (докажите сами). Найдем сумму площадей треугольников:
Так как эта сумма оказалась равной половине площади трапеции, то — второй ее половине. Ч.т.д.
В копилку специальных ходов воспитателя я бы включил форму вычисления площади равнобедренной трапеции по ее сторонам: где p — полупериметр трапеции.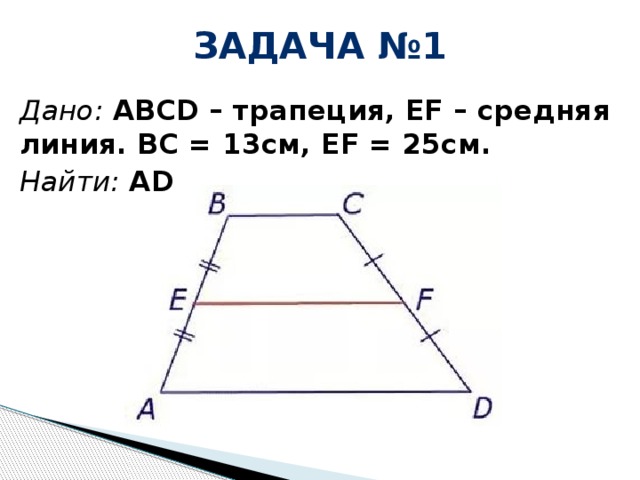 Я не буду приводить доказательства. Иначе ваш репетитор по математике останется без работы :). Приходи в класс!
Я не буду приводить доказательства. Иначе ваш репетитор по математике останется без работы :). Приходи в класс!
Задания на площадь трапеции:
Заметка репетитора по математике : Приведенный ниже список не является методическим пособием по теме, это лишь небольшая подборка интересных заданий по вышеуказанным методикам.
1) Нижнее основание равнобедренной трапеции равно 13, а верхнее 5. Найдите площадь трапеции, если ее диагональ перпендикулярна стороне.
2) Найдите площадь трапеции, если ее основания 2см и 5см, а стороны 2см и 3см.
3) У равнобедренной трапеции большее основание равно 11, сторона равна 5, а диагональ равна Найдите площадь трапеции.
4) Диагональ равнобедренной трапеции равна 5, а средняя линия равна 4. Найдите площадь.
5) У равнобедренной трапеции основания равны 12 и 20, а диагонали взаимно перпендикулярны. Вычислите площадь трапеции
6) Диагональ равнобедренной трапеции образует угол с ее нижним основанием. Найдите площадь трапеции, если ее высота равна 6 см.
7) Площадь трапеции 20, а одна из ее сторон 4см. Найдите расстояние до него от середины противоположной стороны.
8) Диагональ равнобедренной трапеции делит ее на треугольники с площадями 6 и 14. Найдите высоту, если сторона равна 4.
9) Диагонали трапеции равны 3 и 5, а отрезок, соединяющий середины треугольников оснований равно 2. Найдите площадь трапеции (Мехмат МГУ, 1970).
Я выбирал не самые сложные задачи (не бойтесь мехмата!) с расчетом на возможность их самостоятельного решения. Решайтесь на здоровье! Если вам нужно подготовиться к ЕГЭ по математике, то без участия в этом процессе формулы площади трапеции серьезные проблемы могут возникнуть даже с заданием В6, а тем более с С4. Не заводите тему и в случае каких-либо затруднений обращайтесь за помощью. Репетитор по математике всегда рад вам помочь.
Колпаков А.Н.
Репетитор по математике в Москве , подготовка к ЕГЭ в Строгино .
Практика прошлогодних ЕГЭ и ГИА показывает, что задачи по геометрии вызывают затруднения у многих школьников. Вы легко с ними справитесь, если запомните все необходимые формулы и потренируетесь в решении задач.
Вы легко с ними справитесь, если запомните все необходимые формулы и потренируетесь в решении задач.
В этой статье вы увидите формулы нахождения площади трапеции, а также примеры задач с решениями. Такие же могут попадаться вам в КИМах на сертификационных экзаменах или на олимпиадах. Поэтому относитесь к ним бережно.
Что нужно знать о трапеции?
Для начала вспомним, что трапецией называется четырехугольник, у которого две противоположные стороны, их еще называют основаниями, параллельны, а две другие нет.
В трапеции высоту (перпендикулярную основанию) также можно не указывать. Проводится средняя линия – это прямая, которая параллельна основаниям и равна половине их суммы. А также диагонали, которые могут пересекаться, образуя острые и тупые углы. Или, в некоторых случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность вокруг него.
Формулы площади трапеции
Сначала рассмотрим стандартные формулы нахождения площади трапеции. Способы расчета площади равнобедренных и криволинейных трапеций будут рассмотрены ниже.
Способы расчета площади равнобедренных и криволинейных трапеций будут рассмотрены ниже.
Итак, представьте, что у вас есть трапеция с основаниями a и b, у которой высота h опущена к большему основанию. Вычислить площадь фигуры в этом случае несложно. Нужно просто разделить на два сумму длин оснований и умножить полученное на высоту: S = 1/2(a + b)*h .
Возьмем другой случай: предположим, что помимо высоты у трапеции есть срединная линия m. Мы знаем формулу нахождения длины средней линии: m = 1/2(a + b). Поэтому мы с полным правом можем упростить формулу площади трапеции до следующего вида: S = m * h . Другими словами, чтобы найти площадь трапеции, нужно среднюю линию умножить на высоту.
Рассмотрим еще один вариант: в трапеции проведены диагонали d 1 и d 2 , которые пересекаются не под прямым углом α. Чтобы вычислить площадь такой трапеции, нужно произведение диагоналей разделить пополам и умножить полученное на грех угла между ними: S= 1/2d 1 d 2 *sinα .
Теперь рассмотрим формулу нахождения площади трапеции, если о ней ничего не известно, кроме длин всех ее сторон: a, b, c и d. Это громоздкая и сложная формула, но вам будет полезно запомнить ее на всякий случай: S = 1/2 (a + b) * √c 2 — ((1/2 (b — a)) * ((b — a) 2 + c 2 — d 2)) 2 .
Кстати, вышеприведенные примеры справедливы и для случая, когда нужна формула площади прямоугольной трапеции. Это трапеция, сторона которой примыкает к основаниям под прямым углом.
Равнобедренная трапеция
Трапеция, стороны которой равны, называется равнобедренной. Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.
Первый вариант: для случая, когда окружность радиуса r вписана внутрь равнобедренной трапеции, а боковая сторона и большее основание образуют острый угол α. В трапецию можно вписать окружность, если сумма длин ее оснований равна сумме длин сторон.
Площадь равнобедренной трапеции вычисляется следующим образом: квадрат радиуса вписанной окружности умножить на четыре и разделить все это на sinα: S = 4r 2 /sinα . Другая формула площади — это частный случай варианта, когда угол между большим основанием и стороной равен 30 0: S = 8r2 .
Другая формула площади — это частный случай варианта, когда угол между большим основанием и стороной равен 30 0: S = 8r2 .
Второй вариант: на этот раз берем равнобедренную трапецию, у которой, кроме того, проведены диагонали d 1 и d 2 , а также высота h. Если диагонали трапеции взаимно перпендикулярны, высота равна половине суммы оснований: h = 1/2 (a + b). Зная это, несложно преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h3 .
Формула площади криволинейной трапеции
Начнем с понимания: что такое криволинейная трапеция. Представьте ось координат и график непрерывной и неотрицательной функции f, которая не меняет знак в пределах заданного отрезка по оси x. Криволинейная трапеция образована графиком функции у = f(x) — вверху, ось х — внизу (отрезок), а по бокам — прямыми линиями, проведенными между точками а и b и графиком функции.
Вычислить площадь такой нестандартной фигуры вышеуказанными методами невозможно. Здесь нужно применить математический анализ и использовать интеграл. А именно, формула Ньютона-Лейбница — S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a) . В этой формуле F — первообразная нашей функции на выбранном интервале. А площадь криволинейной трапеции соответствует приращению первообразной на данном отрезке.
Здесь нужно применить математический анализ и использовать интеграл. А именно, формула Ньютона-Лейбница — S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a) . В этой формуле F — первообразная нашей функции на выбранном интервале. А площадь криволинейной трапеции соответствует приращению первообразной на данном отрезке.
Примеры задач
Чтобы все эти формулы лучше укладывались в голове, вот несколько примеров задач на нахождение площади трапеции. Будет лучше, если вы сначала сами попробуете решить задачи, а уже потом сверите полученный ответ с готовым решением.
Задание №1: Дана трапеция. Его большее основание 11 см, меньшее 4 см. У трапеции есть диагонали, одна длиной 12 см, другая 9 см.
Решение: Построить трапециевидную АМРС. Проведите прямую RX через вершину P так, чтобы она была параллельна диагонали MC и пересекала прямую AC в точке X. Получился треугольник APX.
Рассмотрим две фигуры, полученные в результате этих манипуляций: треугольник APX и параллелограмм CMPX.
Благодаря параллелограмму узнаем, что РХ = МС = 12 см и СХ = MP = 4 см. Где можно вычислить сторону АХ треугольника АРКА: АХ = АС + СХ = 11 + 4 = 15 см.
Мы также можем доказать, что треугольник ARCH прямоугольный (для этого применим теорему Пифагора — AX 2 = AP 2 + PX 2). И вычислить его площадь: S APX = 1/2 (AP * PX) = 1/2 (9* 12) = 54 см 2 .
Далее нужно доказать, что треугольники AMP и PCX равны по площади. Основой будет равенство сторон MP и CX (уже доказано выше). А также высоты, которые вы опускаете по этим сторонам — они равны высоте трапеции АМРС.
Все это позволит Вам утверждать, что S AMPC = S APX = 54 см 2 .
Задача №2: Дана трапеция КРМС. Точки О и Е расположены на его боковых сторонах, а ОЕ и КС параллельны. Также известно, что площади трапеций ORME и OXE находятся в соотношении 1:5. ПМ = а и КС = b. Вам нужно найти ОЭ.
Решение: Проведите через точку М прямую, параллельную РК, и обозначьте точку ее пересечения с ОЕ как Т. А — точка пересечения прямой, проведенной через точку Е, параллельной РК, с основанием КС.
А — точка пересечения прямой, проведенной через точку Е, параллельной РК, с основанием КС.
Введем еще одно обозначение — ОЕ = х. А также высоту h 1 для треугольника TME и высоту h 2 для треугольника AEC (можно самостоятельно доказать подобие этих треугольников).
Предположим, что b > a. Площади трапеций ORME и OXE связаны как 1:5, что дает нам право составить следующее уравнение: (x + a) * h 1 = 1/5 (b + x) * h 2 . преобразуем и получаем: h 1 / h 2 = 1/5 * ((b + x) / (x + a)).
Так как треугольники TME и AEC подобны, то h 1 / h 2 = (x — a) / (b — x). Объедините обе записи и получите: (х — а) / (b — х) = 1/5 * ((b + х) / (х + а)) ↔ 5 (х — а) (х + а) = (b + x) (b — x) ↔ 5 (x 2 — a 2) = (b 2 — x 2) ↔ 6x 2 = b 2 + 5a 2 ↔ x = √ (5a 2 + b 2) / 6.
Таким образом, ОЕ = x = √ (5a 2 + b 2) / 6.
Заключение
Геометрия не самая легкая из наук, но с экзаменационными заданиями вы наверняка справитесь. Просто нужно немного терпения при подготовке. И, конечно же, запомнить все необходимые формулы.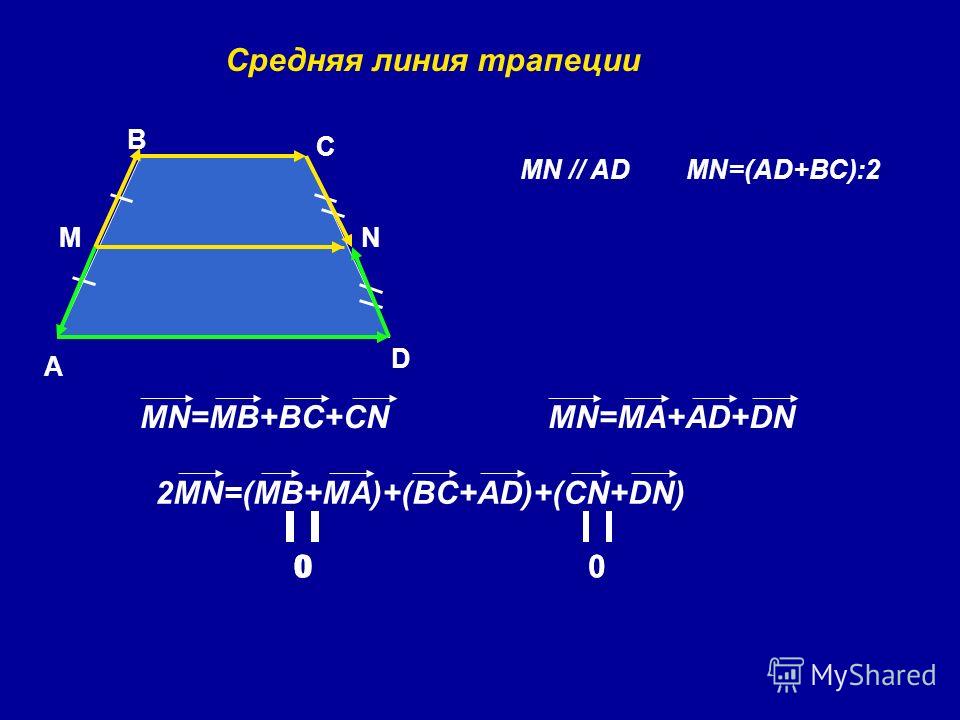
Мы постарались собрать в одном месте все формулы расчета площади трапеции, чтобы вы могли использовать их при подготовке к экзаменам и повторении материала.
Обязательно поделитесь этой статьей со своими одноклассниками и друзьями в социальных сетях. Пусть хороших оценок за ЕГЭ и ГИА будет больше!
сайта, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Трапецией называется выпуклый четырехугольник, у которого две противоположные стороны параллельны, а две другие непараллельны. Если все противоположные стороны четырехугольника попарно параллельны, то это параллелограмм.
Вам понадобится
- — все стороны трапеции (AB, BC, CD, DA).
Инструкция
- Непараллельные стороны трапеции называются боковыми сторонами, а параллельные – основаниями. Линия между основаниями, перпендикулярная им — высота трапеции . Если стороны трапеции равны, то она называется равнобедренной.
 Сначала рассмотрим решение для трапеции , которая не является равнобедренной.
Сначала рассмотрим решение для трапеции , которая не является равнобедренной. - Проведите линию BE от точки B до нижнего основания AD параллельно стороне трапеция CD. Так как BE и CD параллельны и проведены между параллельными основаниями трапеций BC и DA, то BCDE — параллелограмм, а его противоположные стороны BE и CD равны. БЫТЬ = КД.
- Рассмотрим треугольник ABE. Вычислите сторону AE. АЭ=АД-ЭД. Основания трапеции ВС и AD известны, а в параллелограмме BCDE противоположные стороны ED и ВС равны. ED=BC, поэтому AE=AD-BC.
- Теперь найдите площадь треугольника АВЕ по формуле Герона, вычислив полупериметр. S=корень(p*(p-AB)*(p-BE)*(p-AE)). В этой формуле p — полупериметр треугольника ABE. р=1/2*(АВ+ВЕ+АЭ). Для расчета площади вам известны все необходимые данные: AB, BE=CD, AE=AD-BC.
- Далее запишите площадь треугольника АВЕ другим способом — она равна половине произведения высоты треугольника ВН на сторону АЕ, к которой он проведен.


 д.
д.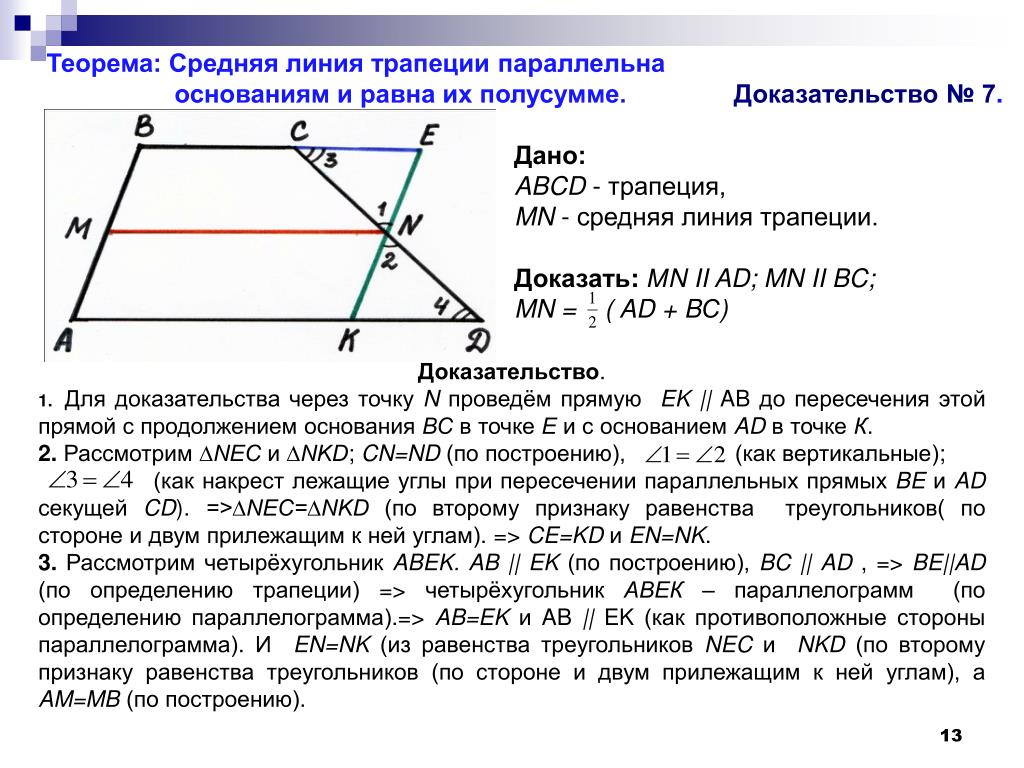 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. 09.2017
09.2017 С. Атанасян. «Геометрия 7-9» Учебник для образовательных учреждений/- М., Просвещение, 2006
С. Атанасян. «Геометрия 7-9» Учебник для образовательных учреждений/- М., Просвещение, 2006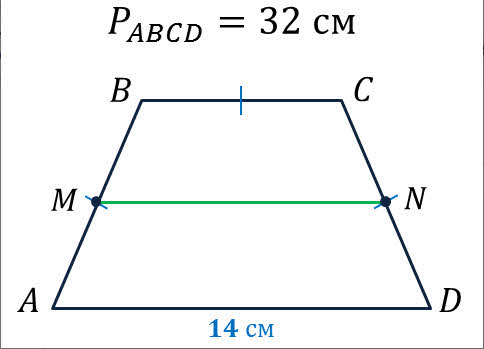 1.Вторая средняя линия трапеции
1.Вторая средняя линия трапеции
 Поэтому для нахождения высоты фигуры воспользуйтесь формулой определения этой величины в том случае, когда известны стороны трапеции.
Поэтому для нахождения высоты фигуры воспользуйтесь формулой определения этой величины в том случае, когда известны стороны трапеции.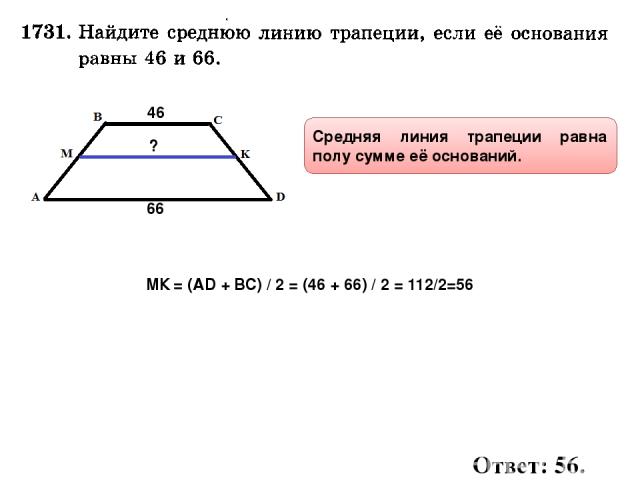 Сначала рассмотрим решение для трапеции , которая не является равнобедренной.
Сначала рассмотрим решение для трапеции , которая не является равнобедренной.