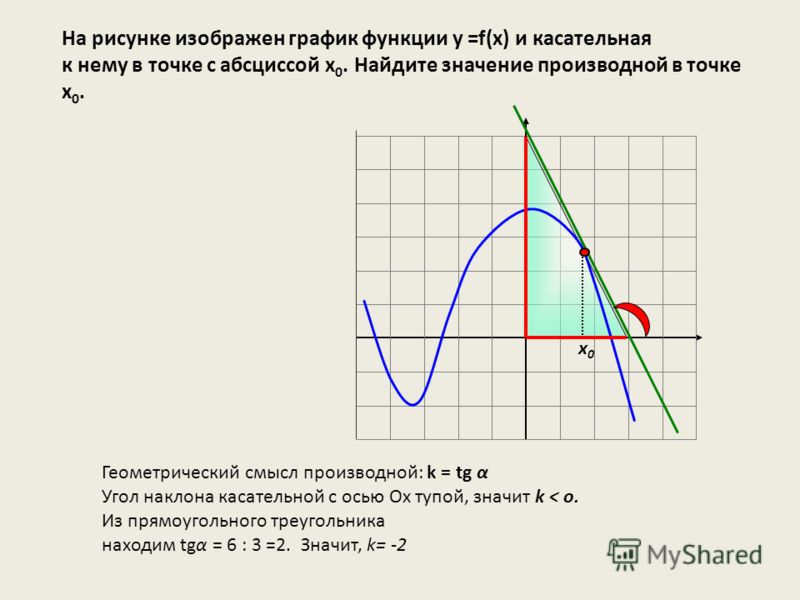
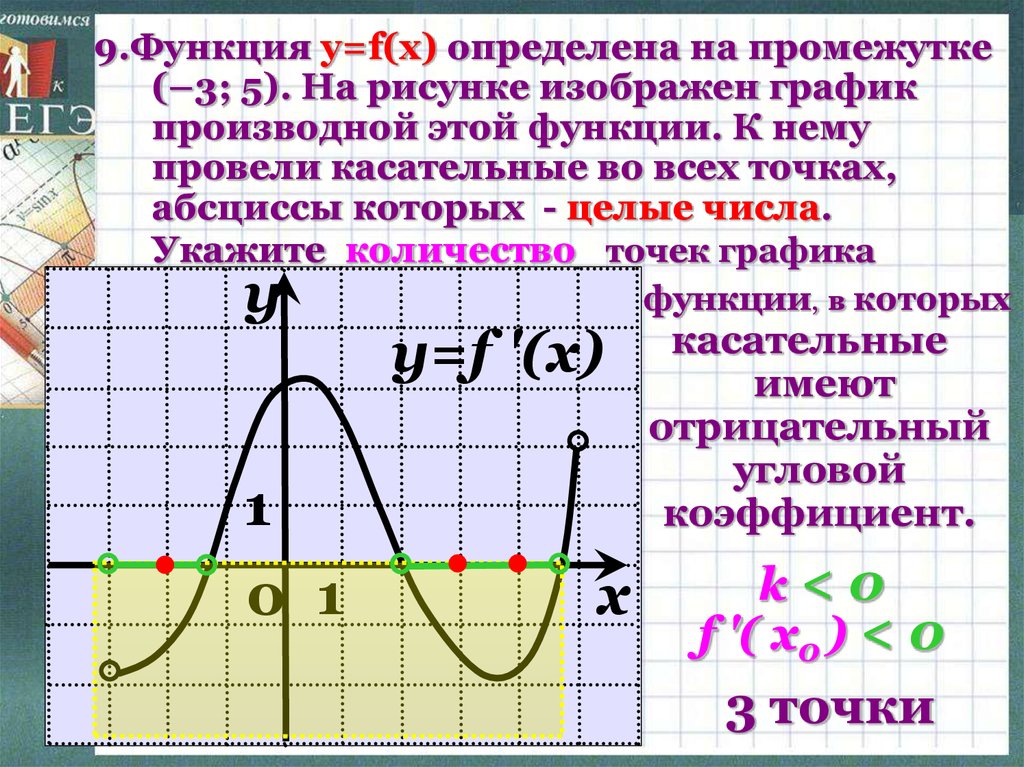
Как найти производную функции по графику и касательной: Уравнение касательной к графику функции

Содержание

На рисунке изображены график функции и касательная

Не откладывайте! ЗАГОВОРИТЕ на Английском!

ЗАМУЧИЛИ БОЛИ В СПИНЕ?

Александр | 2012-10-15

Данная статья является продолжением двух предыдущих. В статье «Геометрический смысл производной. Часть 1!» была изложена теория и рассмотрен один из способов нахождения производной по данному графику функции и касательной, проведенной в определённой точке графика.

Там же я обещал вам рассмотреть ещё один способ решения подобных задач. Напомню, что задания такого типа входят в состав экзамена по математике. В статье «Уравнение прямой, проведённой через две заданные точки» мы рассмотрели формулу, благодаря которой находится уравнение прямой.

Представленная в указанных статьях теория необходима, так как тот способ, который представлен ниже, непосредственно с ней связан. Итак, кратко:

Из курса алгебры известно, что уравнение прямой имеет вид:

где k – угловой коэффициент прямой.

То есть производная функции y = f(x) в точке x₀ равна угловому коэффициенту касательной:

2. Уравнение прямой, проходящей через две заданные точки имеет вид:

После подстановки координат в данное уравнение оно приводится к виду:

Таким образом, в случае, когда даны две точки, через которые проходит касательная (прямая) к графику функции, необходимо найти уравнение этой прямой. Решением задачи будет являться коэффициент k (он равен производной).

На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x_о. Найдите значение производной функции f(x) в точке x_о.

Как уже сказано, значение производной функции f(x) в точке x_о равно коэффициенту k из уравнения прямой y=kx+b.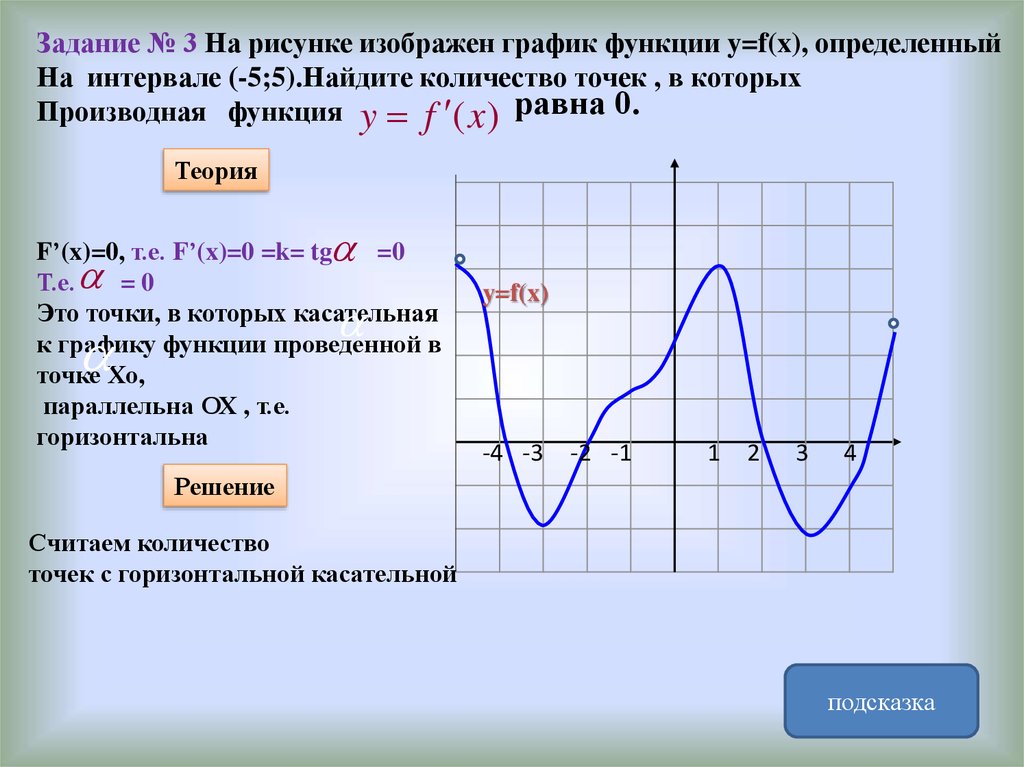

Во всех подобных задачах будут даны две точки, через которые проходит касательная, в данном случае это (–6;–2) и (–1; 8). Подставляем координаты в формулу уравнения прямой:

Настоятельно рекомендую вам сделать проверку (подставьте координаты обеих точек в уравнение). Цена ошибки как вы знаете – это потерянный бал на ЕГЭ.

Проверка:

– 2 = 2 (–6) + 10 → – 2 = – 2 Верно

8 = 2 (–1) + 10 → 8 = 8 Верно

Уравнение прямой найдено верно. Если вы знаете другие способы нахождения уравнения прямой, то используйте (их, кстати, около шести).

Таким образом, f ′(x) = k = 2.

Как видите, вычисления просты.

Ответ: 2

Вывод: если вы видите перед собой подобную задачу, где на координатной плоскости обозначены две точки, через которые проведена касательная, то:

1. Определите координаты точек. Точки могут быть и не обозначены (не выделены), но на координатной сетке будет отчётливо видно, как (через какие точки) проходит прямая.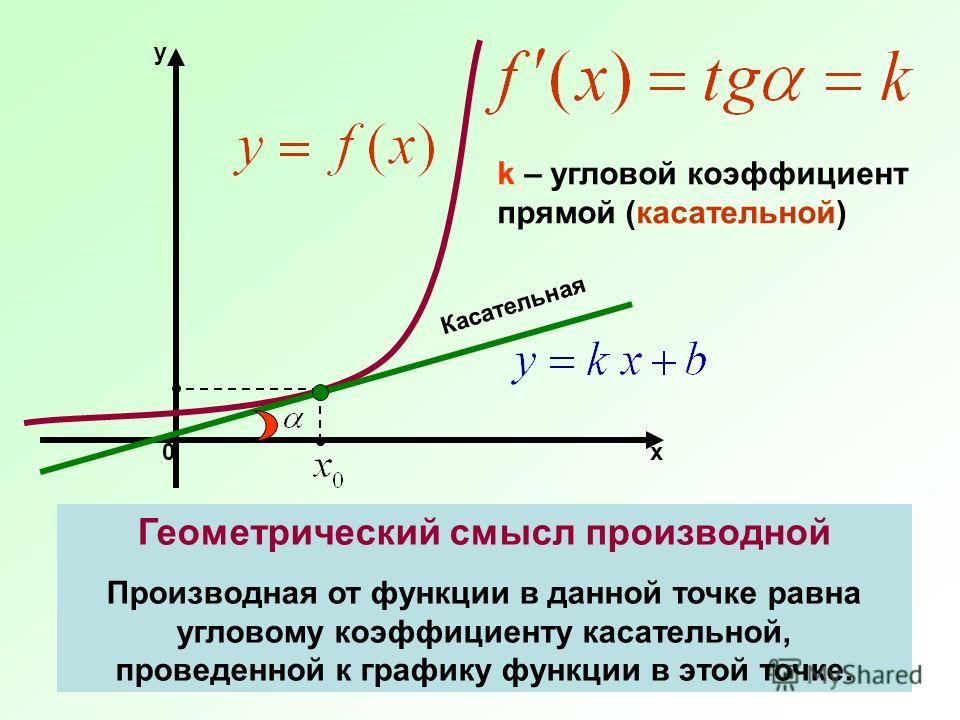

2. Найдите уравнение прямой (касательной) по представленной формуле или другим способом.

3. Проверьте полученное уравнение, подставив в него координаты точек.

4. Запишите ответ (коэффициент k).

На этом всё. Будет полезный материал в следующей статье!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Категория: Производная Графики | ЕГЭ-№7Производная

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Замучили боль и скованность в мышцах спины?

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

121. Геометрический и физический смысл производной

Рассмотрим график функции в декартовой системе координат (рис. 10.2). Возьмем на графике точку и точку . Проведем через эти точки прямую . Эта прямая называется Секущей.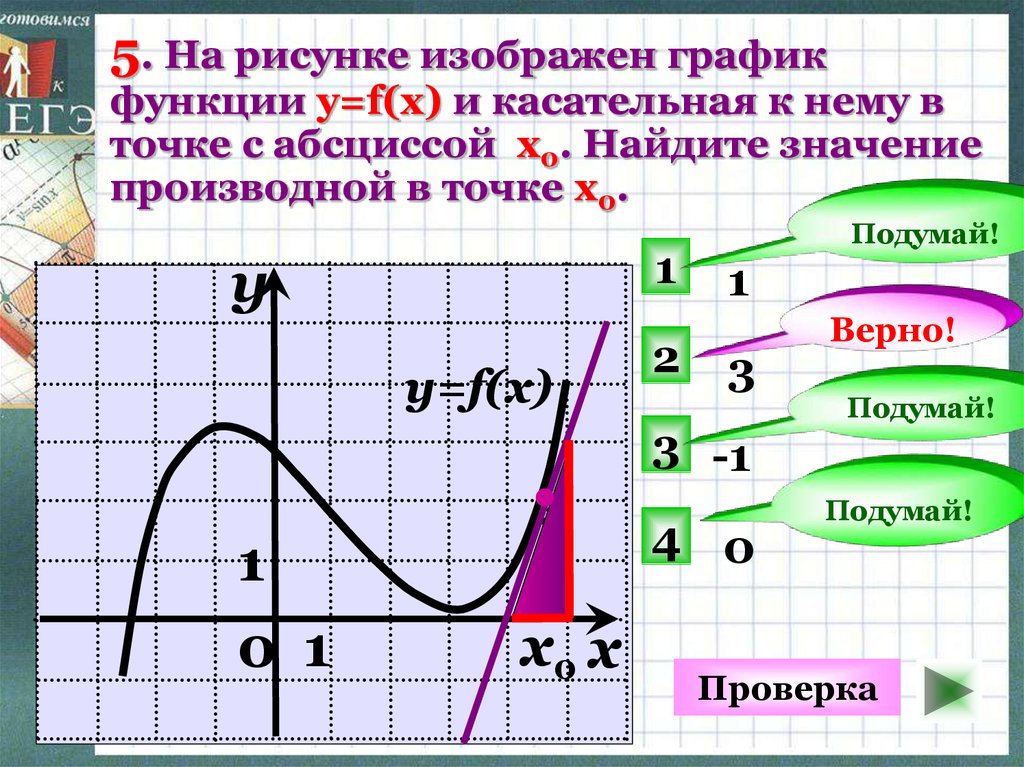 Ее уравнением будет , а угловой коэффициент этой прямой равен тангенсу угла наклона секущей:

Если то секущая MN поворачивается вокруг точки и переходит в касательную с угловым коэффициентом

Если , то секущая MN поворачивается вокруг точки М и в пределе переходит в касательную с угловым коэффициентом .

Угловой коэффициент касательной к графику функции в данной точке равен значению производной функции в этой
точке: .

Геометрический смысл производной состоит в том, что производная равна угловому коэффициенту касательной к графику функции в данной точке.

Значение производной в точке равно тангенсу угла наклона касательной (рис. 10.3).

Нормаль – это прямая, перпендикулярная к касательной в точке касания (рис. 10.3).

Уравнение касательной к кривой в точке запишем как уравнение прямой, которая проходит через заданную точку: .

Уравнение нормали к кривой в точке запишем так: .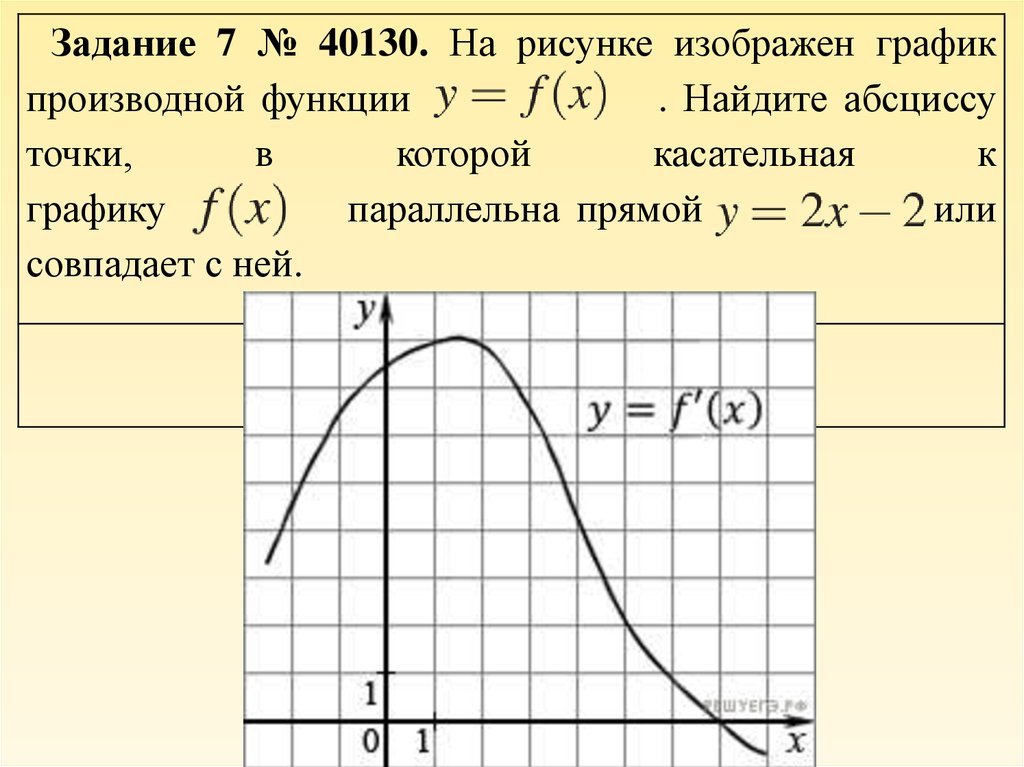

Пример 1. Напишите уравнение касательной к графику функции в точке с абсциссой .

Решение. 1) Найдем значение функции, если : .

2) Найдем первую производную функции: .

3) Найдем значение производной, если : .

4) Запишем уравнение касательной, которая проходит через данную точку : или .

Ответ. Уравнение касательной: .

Пример 2. Напишите уравнение нормали к графику функции в точке с абсциссой .

Решение. 1) Найдем значение функции, если : .

2) Найдем первую производную функции: .

3) Найдем значение производной, если : .

4) Запишем уравнение нормали, которая проходит через данную точку : или .

Ответ. Уравнение нормали: .

Рассмотрим задачу о свободном падении тела и найдем мгновенную скорость его движения.

Из физики мы знаем, что , где H – высота падения, G – ускорение свободного падения, T – время падения.

За время тело проходит расстояние , а за время – расстояние .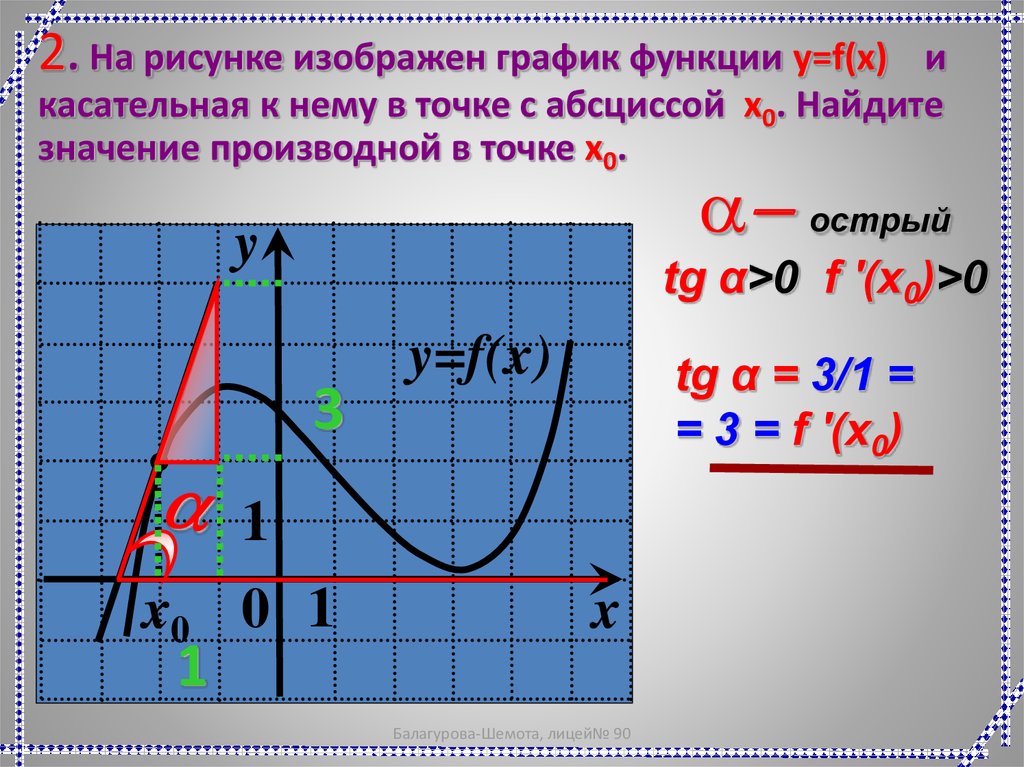 Приращение аргумента (времени T) будет равно , откуда .

Приращение функции будет равно:

Найдем предел отношения приращения функции к приращению ее аргумента T , если ΔT Стремится к нулю:

В левой части равенства мы получили значение производной функции , а в правой части значение мгновенной скорости тела в момент времени

T0.

Физический смысл производной. Производная функции в точке есть мгновенная скорость изменения функции в точке , т. е. скорость протекания процесса, который описывается зависимостью .

Например, если дана функция , то ее производная будет , тогда значение производной в точке будет , а значение производной в точке будет . Это значит, что в точке функция изменяется в 4 раза быстрее аргумента , а в точке изменяется в 6 раз быстрее (т. е. различная скорость изменения функции или протекания процесса). В этом и состоит физический смысл производной.

Операция нахождения (взятия) производной функции называется Дифференцированием функции.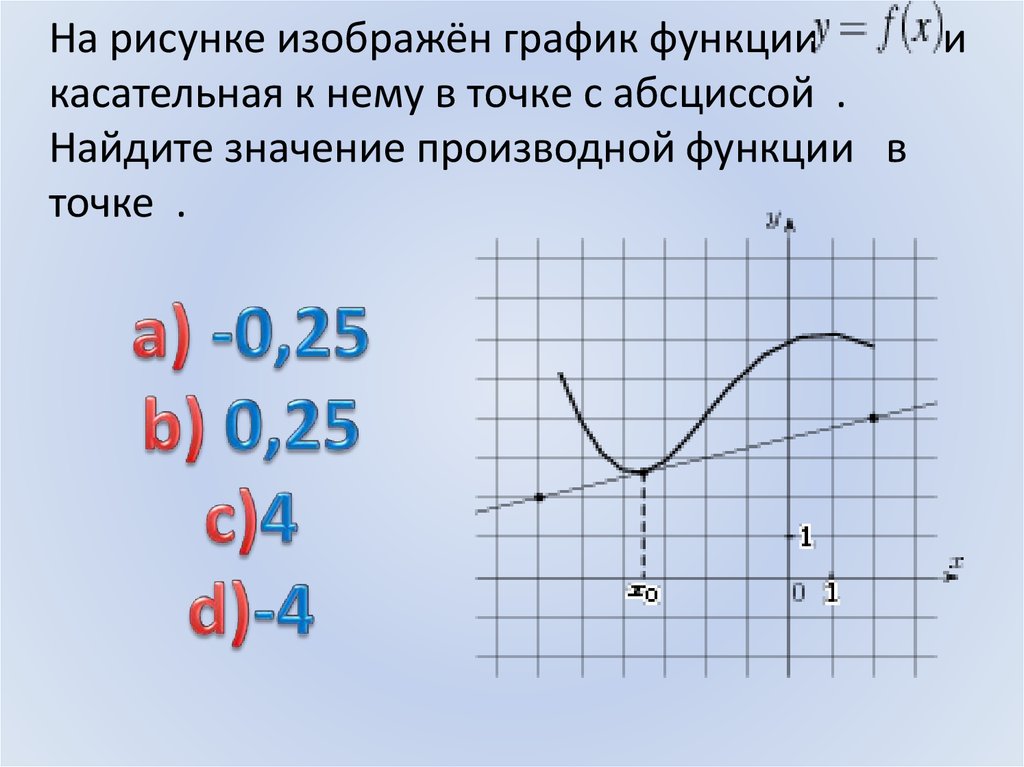

Ответьте на вопросы

1. Что показывает угловой коэффициент K в уравнении прямой ?

2. Чему равен угловой коэффициент касательной к кривой в точке ?

3. Как найти угловой коэффициент нормали к кривой в точке ?

4. В чем состоит геометрический смысл производной?

5. В чем состоит физический смысл производной?

< Предыдущая		Следующая >

Вертикальная касательная: определение, как найти

Возможно, вы захотите сначала прочитать эту статью: Что такое касательная?

Посмотрите видео или прочитайте ниже:

Определение вертикальной касательной и пример

Посмотрите это видео на YouTube.

Видео не видно? Кликните сюда.

Касательная кривой — это линия, которая касается кривой в одной точке. Он имеет тот же наклон, что и кривая в этой точке. A

вертикальная касательная касается кривой в точке, где градиент (наклон) кривой бесконечен и не определен. На графике он проходит параллельно оси Y.

Как найти вертикальную касательную

Общие шаги для нахождения вертикальной касательной в исчислении и градиента кривой:

Найдите производную функции . Производная (dy/dx) даст вам градиент (наклон) кривой.
Найти значение x, при котором dy/dx становится бесконечным ; вы ищете бесконечный наклон, поэтому вертикальная касательная кривой представляет собой вертикальную линию при этом значении x.

Вертикальная касательная в исчислении Пример

Пример задачи: Найдите вертикальную касательную кривой y = √(x – 2).

Шаг 1: Дифференцируйте y = √(x – 2). Вы можете использовать свой графический калькулятор или выполнить дифференцирование вручную (используя степенное правило и цепное правило). Я дифференцировал функцию с помощью этого онлайн-калькулятора (который также показывает вам шаги!):

Шаг 2: Найдите значения x , которые сделали бы dy/dx бесконечными.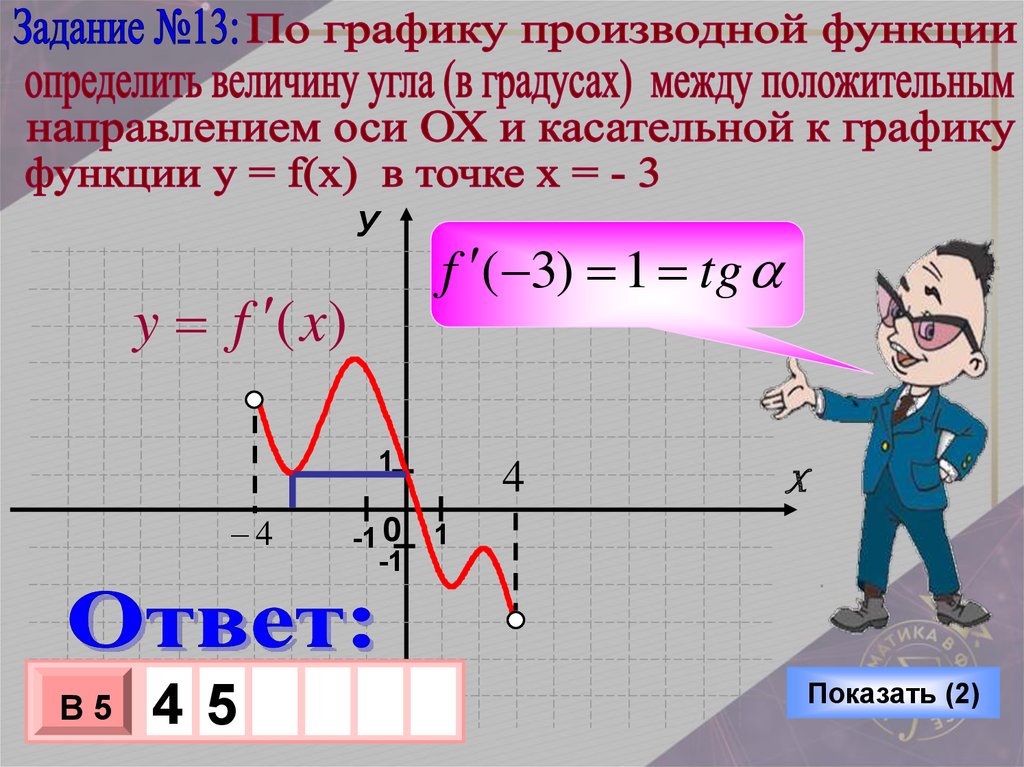 Здесь действительно пригодятся сильные навыки алгебры, хотя для этого примера задачи все, что вам нужно понять, что произойдет, если вы подставите «2» в уравнение производной:

Деление на ноль не определено. Это означает, что градиент кривой бесконечен (то есть вертикальен), когда x = 2.

Вертикальный тангенс кривой равен x = 2.
Вот и все!

Графики и таблицы

Если вы не можете сразу увидеть, где ваша функция может вернуть ноль, у вас есть два варианта:
Графики иногда могут помочь вам увидеть, где может быть вертикальная касательная линия.

Нарисуйте график функции — чтобы увидеть, где на графике может быть вертикальная касательная. я использовал этот удобный калькулятор HRW
, чтобы получить приведенный выше график y = √(x – 2). Совершенно очевидно, что в точке x = 2 существует касательная по вертикали, хотя вы все равно можете пройти через математические вычисления/алгебру, чтобы доказать это.
Составьте таблицу значений и проверьте несколько значений x.

Второй вариант может занять очень много времени; Сильные навыки алгебры (например, знание того, когда уравнение может привести к делению на ноль) помогут вам избежать необходимости составлять таблицу.

Советы:

Некоторые кривые могут иметь более одной вертикальной касательной . Всегда убедитесь, что вы нашли все значения x, которые делают градиент бесконечным. Вы можете использовать программное обеспечение для построения графиков, чтобы проверить на глаз места, где градиент становится вертикальным.

Дополнительные советы о том, где функции могут возвращать ноль, см. в разделе «Угадай и проверь» статьи домена и диапазона .

УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Вертикальная касательная: определение, как найти» От StatisticsHowTo.com : Элементарная статистика для всех нас! https://www. statisticshowto.com/calculus-definitions/vertical-tangent-definition-find/

————————————————— ————————-

Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!

Комментарии? Нужно опубликовать исправление?

Пожалуйста, Свяжитесь с нами .
Задание 2, запись
Задание 2, запись Задание 2 Запись
Проблема:
Исследуйте взаимосвязь между графиком функции и графиком производной функции. Учитывая функцию f (x), каково уравнение касательной в любой заданной точке. С использованием Графический калькулятор 2.2, график f(x) и касательная.
Стратегия:
Мы собираемся исследовать функцию f(x) = x ² .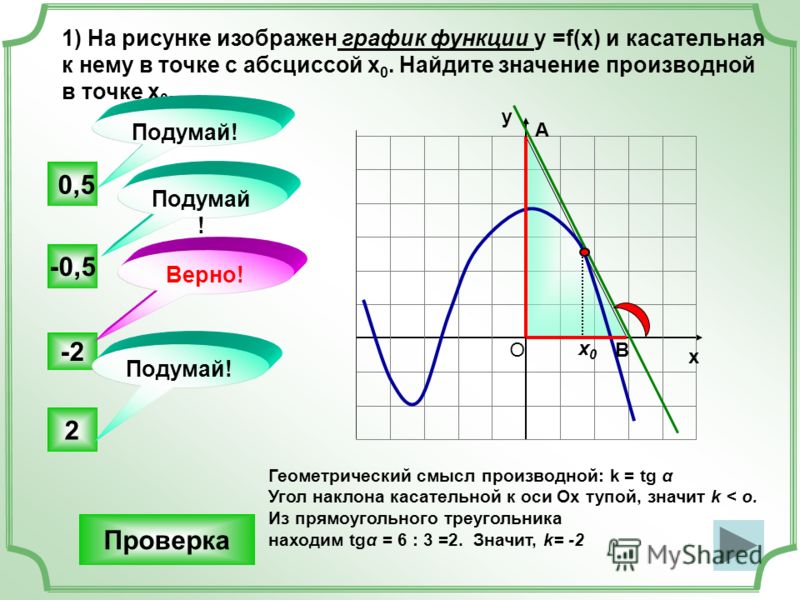 Мы довольно много знаем о производной функции из исчисления, поэтому мы начнем с него и перейдем к более общему случаю.
Основание:
Начнем с построения графика f(x) = x ² , просто чтобы посмотреть, как это выглядит.
График: f(x) = x
2
Мы знаем, что производная функции (f’) дает наклон прямой, касательной к функции в точке любая заданная точка х. (Тогда наклон равен f'(x).) Производная от f(x) = x ² равна f'(x) = 2x . Следовательно, наклон касательной в точке x = 1 равен м = 2(1) или м = 2 . Так как мы знаем наклона касательной, мы можем изобразить касательную, используя наклон и точку на касательной. Проще всего использовать точку касания. Поэтому воспользуемся точкой (1,1 ² ) или (1,1) . Точечно-наклонная форма уравнения линии имеет вид y — y ₁ = m(x — x ₁ ) .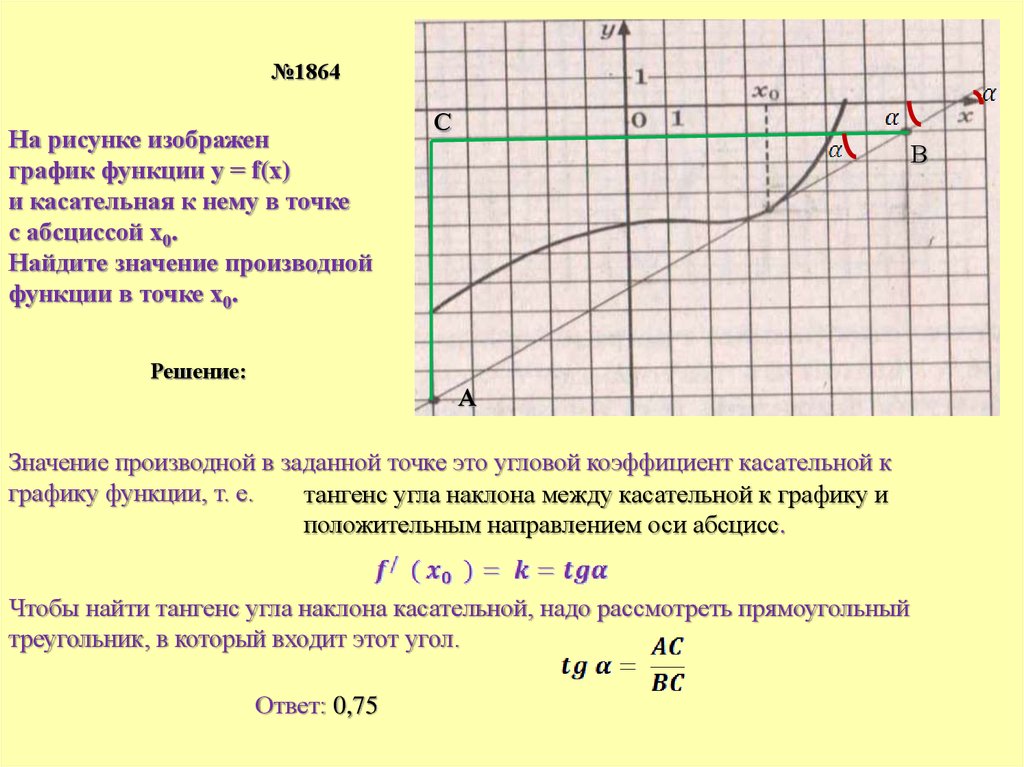 Подставляя в это уравнение, мы получаем у — 1 = 2(х — 1) . Упрощая, получаем y = x — 1 . Итак, давайте изобразим эту линию на тех же осях, что и наша оригинальная функция….

График: f(x) = x ² и y = x — 1
Разведка:
Теперь нам нужно обобщить это. Для этого разберем, что мы сделали, чтобы найти график касательной линии в х = 1 . Мы начали с нахождения производной f(x) при x = 1 . Помните, что с тех пор f(x) = x ² , f'(x) = 2x . Таким образом, чтобы взять производную при любом числе n, мы возьмем f'(n) = 2n . Это дает нам наклон m в любой точке n. Теперь, когда у нас есть наклон, нам нужно найти точку на нем. произвольная касательная. Сделать это просто. Все, что нам нужно сделать, это подключить наш n непосредственно к исходному функция. Это дает нам f(n) = n ² . Таким образом, наша точка будет (n,n ² ) .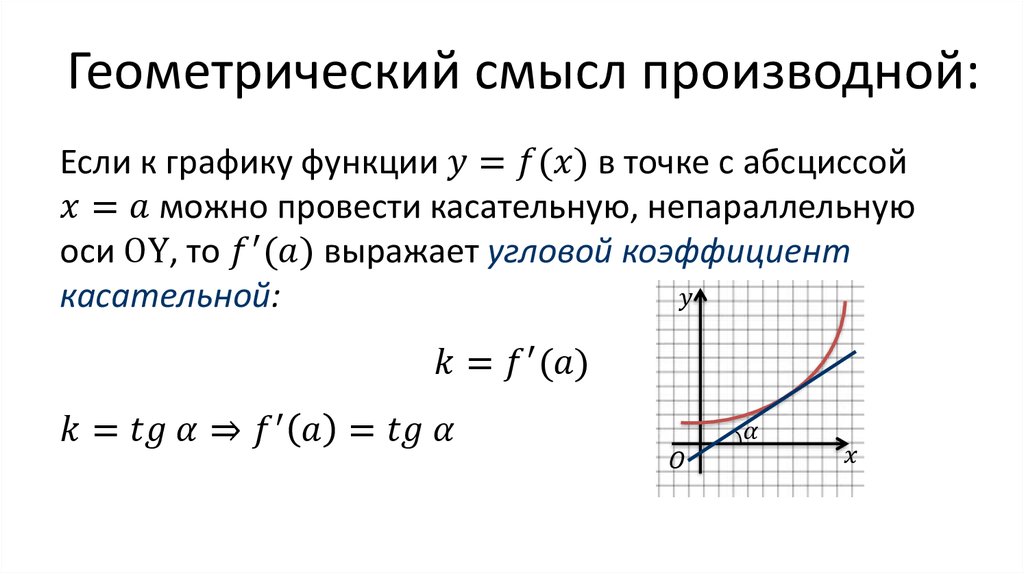 Теперь мы можем подключиться к точечно-наклонная форма уравнения прямой, чтобы найти нашу произвольную касательную к
f(x) = x ² . У нас есть m = 2n , x ₁ = n и y ₁ = n ² . Подставляя в уравнение y — y ₁ = m(x — x ₁ ) получаем у — n ² = 2n(x — n) . Упрощение дает нам y = (2n)(x — n) + n ² , а затем y = (2n)x — n ² . Теперь мы можем отобразить это и использовать Graphing Calculator для изменения значения n.
График: f(x) = x ² и y = (2n)x — n ² , значение n меняется
Выводы:
Мы показали, как можно найти касательную в любой точке графика f(x) = x ² . Это приводит На вопрос: как насчет нахождения касательной в любой точке любой -функции? Отслеживая наши шаги из этого исследования, это действие легко обобщить для любой функции f(x).
No related posts.