Теорема косинусов является обобщением теоремы Пифагора. Утверждения, обобщающие теорему Пифагора и эквивалентные теореме косинусов, были сформулированы отдельно для случаев острого и тупого угла в 12 и 13 предложениях II книги «Начал» древнегреческого математика Евклида (ок. 300 г. до н. э.). Утверждения, эквивалентные теореме косинусов для сферического треугольника, применялись в сочинениях математиков стран Средней Азии. Теорему косинусов для сферического треугольника в привычном нам виде сформулировал выдающийся немецкий астролог, астроном и математик Региомонтан (1436 — 1476), назвав её «теоремой Альбатегния» (по имени выдающегося средневекового астронома и математика Абу Абдаллах Мухаммад ибн Джабир ибн Синан ал-Баттани (858 — 929).
В Европе теорему косинусов популяризовал французский математик Франсуа Виет (1540 — 1603) в 16 столетии. В начале 19 века её стали записывать в принятых по сей день алгебраических обозначениях.
Следствие из теоремы косинусов
Теорема косинусов может быть использована для нахождения косинуса угла треугольника (рис.
 {\circ}=289+196-238=24$$
{\circ}=289+196-238=24$$Тогда
$$A B=\sqrt{247}$$
Ответ. $A B=\sqrt{247}$
Теорема косинусов: формулировка, следствия, доказательство и примеры
Теорема косинусов — в любом треугольнике квадрат одной стороны равен сумме квадратов двух других сторон минус удвоенное произведение этих двух сторон на косинус угла между ними.
Формула косинуса:
- a² = b² + c² – 2b.c.cosα
- b² = a² + c² – 2a.c.cosβ
- c² = a² + b² – 2a.b.cosγ
Например:
Одна сторона треугольника равна 12 см, другая — 8 см, между ними образовался угол 120º. Найдите длину третьей стороны.
Решение по формуле a² = b² + c² – 2b.c.cosα:
b = 12 см
c = 8 см
cos α = cos 120º = — 1/2 (это значение можно найти в таблицах)
a² = 12² + 8² – 2×12×8×(- 1/2)
a² = 144 + 64 – (–96)
a² = 304
a = √304
a ≈ 17,436
Длина третьей стороны — примерно 17,436 см.

Следствия
Следствие косинуса угла треугольника
При помощи теоремы косинусов можно найти косинус угла треугольника.
Формула:
Либо
Либо
Например:
сторона c = 6
сторона b = 7
сторона a = 8
Используйте теорему косинусов, чтобы найти угол β.
Решение:
Будем использовать эту версию формулы:
cos β = (6² + 8² − 7²) / 2×6×8
= (36 + 64 − 49) / 96
= 51 / 96
= 0,53125
= cos¯¹(0,53125)
≈ 57,9°
Следствие верхней части формулы cos α
Чтобы узнать, если угол α острый, прямой или тупой, нужно вычислить b²+c²−a² (это верхняя часть формулы для cos α):
- b²+c²−a²<0, значит угол α — тупой;
- b²+c²−a²=0, значит угол α — прямой;
- b²+c²−a²>0, значит угол α — острый.
Доказательство теоремы косинусов
Нужно доказать, что c² = a² + b² − 2a.b.cos C
1. Из определения косинуса известно, что в прямоугольном треугольнике BCD: cos C = CD/a <=> CD = a.
 cos C.
cos C.2. Вычитаем это из стороны b, так мы получим DA:
DA = b − a.cosC
3. Мы знаем из определения синуса, что в том же треугольнике BCD:
sin C = BD/a <=> BD = a.sinC.
4. Применяем теорему Пифагора в треугольнике ADB: c² = BD² + DA²
5. Заменим BD и DA из пунктов 2) и 3), получится выражение: c²= (a. sin C)²+(b−a.cos C)²
6. Раскрываем скобки: c² = a² sin ²C + b² − 2a.b.cosC + a².cos²C
6.1. Поменяем их местами (a²cos²C поставим на второе место): c² = a² sin ²C + a²cos²C + b² − 2a.b.cosC
7. Выносим за скобки «a²»: c² = a² (sin²C+cos²C) + b² − 2a.b.cosC
8. В скобках получилось основное тригонометрическим тождество (sin²α + cos²α = 1), значит его можно сократить т. к. умножение на единицу ничего не меняет, получилось: c² = a² + b² − 2a.b.cos C
Q.E.D.
Теорема косинусов для равнобедренного треугольника
В равнобедренном треугольнике:
- две его стороны равны;
- углы при основании равны.
Рассмотрим пример:
Используем формулу теоремы косинусов
a² = b² + c² – 2b.
 c.cosα
c.cosαПодставляем все известные:
x² = 8² + 8² – 2×8×8×cos140º
x² = 64 + 64 – 128 × (-0,766)
x² ≈ √226,048
x ≈ 15,035.
Теорема синусов
Теорема синусов гласит, что отношение стороны треугольника к синусу угла, противолежащего данной стороне, одинаково для всех сторон и углов в данном треугольнике:
Узнайте также, что такое Теорема Пифагора и Теорема Менелая.
Дата обновления 01/10/2020.
Другие значения и понятия, которые могут вас заинтересовать
- Аксиома
- Теорема Пифагора
- Гипотенуза
- Теорема Менелая
- Теорема Ферма
- Теорема Виета
- Гипотеза Пуанкаре
- Уравнения Максвелла
- Тангенс
- Квадратное уравнение
Узнай Что Такое: узнайте значения, понятия и определения.

ПоследниеПопулярныеКонтактыПолитика КонфиденциальностиО нас
2018 — 2023 © 7Graus
косинусов
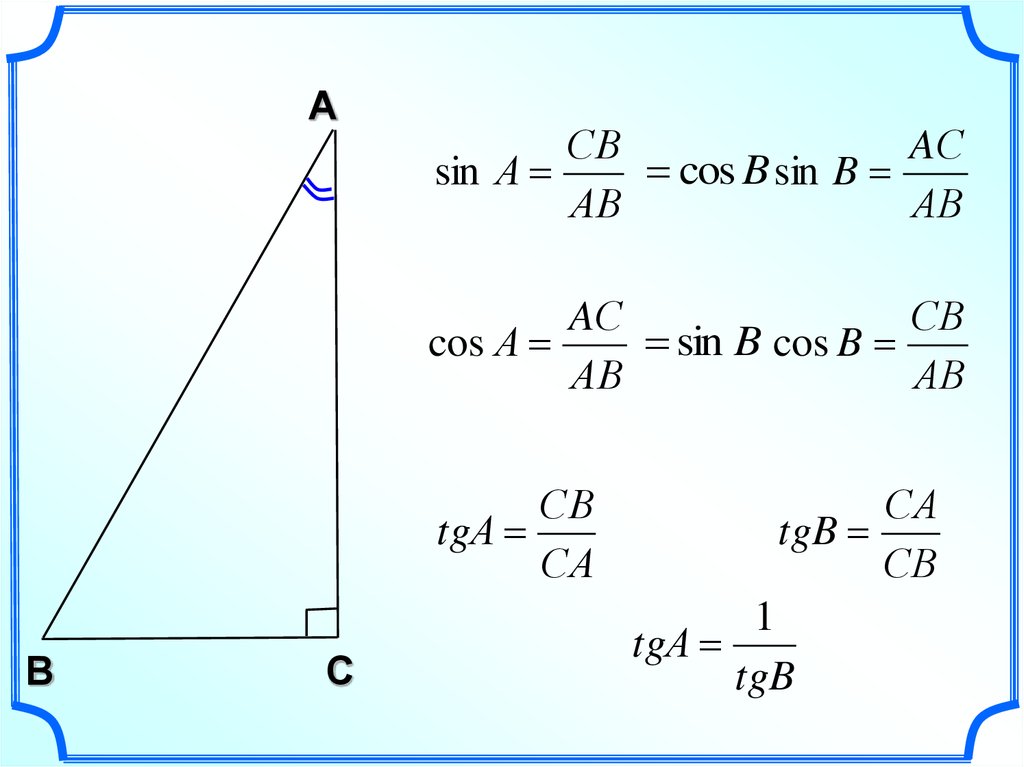
Как упоминалось ранее, мы обычно используем букву a для обозначения стороны, противоположной углу A, букву b для обозначения стороны, противоположной углу B, и букву c для обозначения стороны. противоположный угол C. Так как сумма углов в треугольнике равна 180°, а угол C равен 90°, то углы A и
Кроме того, cos A = sin B = b/c.

Тождество Пифагора для синусов и косинусов
Вспомним теорему Пифагора для прямоугольных треугольников. Он говорит, что
a 2 + b 2 = c 2 где c — гипотенуза. Это очень легко переводится в пифагорейское тождество синусов и косинусов. Разделите обе части на c 2 и вы получите
а 2 / в 2 + b 2 / c 2 = 1. Но a 2 / c 2 = (sin A ) 2 и b 2 / 2 = (cos A ) 2 . Чтобы уменьшить количество круглых скобок, которые необходимо написать, принято соглашение, что обозначение sin 2 A является аббревиатурой для (sin A ) 2 , и аналогично для степеней другого триггера.
 функции. Таким образом, мы доказали, что
функции. Таким образом, мы доказали, чтоsin 2 A + cos 2 A = 1 когда А острый угол. Мы еще не видели, какими должны быть синусы и косинусы других углов, но когда мы это увидим, мы получим для любого угла θ одно из важнейших тригонометрических тождеств, тождество Пифагора для синусов и косинусов:
Синусы и косинусы для особых общих углов
Мы можем легко вычислить синусы и косинусы для некоторых общих углов. Рассмотрим сначала 45° угол. Он находится в равнобедренном прямоугольном треугольнике, то есть 45°-45°-9треугольник 0°. В любой прямоугольный треугольник c 2 = a 2 + b 2 , но в этом один a = b, so c 2 = 2 a 2 . Следовательно c = a √2. Следовательно, и синус, и косинус 45° равно 1/√2, что также может быть записано как √2 / 2.

Далее рассмотрим углы 30° и 60°. В диапазоне 30°-60°-90° прямоугольный треугольник, отношения сторон равны 1 : √3 : 2. Отсюда следует, что sin 30° = cos 60° = 1/2 и sin 60° = cos 30° = √3 / 2.
Эти данные заносятся в эту таблицу.
Угол Градусы Радианы Косинус Синус 0003 π /2 0 1 60° π /3 1/2 √3 / 2 45° 929 /4 /4 2 √2 / 2 30° π /6 √3 / 2 1/2 0° 3 10Упражнения
Эти упражнения все относятся к прямоугольным треугольникам со стандартной маркировкой.

30. b = 2,25 метра и cos
33. b = 12 футов и cos B = 1/3. Найдите c и a.
35. б = 6,4, в = 7,8. Найдите А и А.
36. A = 23° 15′, c = 12,15. Найти а и б.
Советы
30. Косинус числа A связывает b с гипотенузой c, , так что вы можете сначала вычислить c. Зная b и c, , вы можете найти a по теореме Пифагора.
33. Вы знаете b и cos B. К сожалению, cos B — это отношение двух неизвестных вам сторон, а именно а/к. Тем не менее, это дает вам уравнение для работы: 1/3 = a/c. Тогда c = 3 a. Из теоремы Пифагора следует, что а 2 + 144 = 9 а 2 .
Вы можете решить это последнее уравнение для a , а затем найти c.
35. b и c дают A по косинусам и a по теореме Пифагора.
36. A и c дают a по синусам и b по косинусам.
Ответы
30. c = b /cos A = 2,25/0,15 = 15 метров; a = 14,83 метра.
33. 8 a 2 = 144, поэтому a 2 = 18. Следовательно, a равно 4,24 дюйма, или 4’3′.
c = 3 и , что составляет 12,73 фута или 12 футов 9 дюймов.35. cos A = b/c = 6,4/7,8 = 0,82. Следовательно, A = 34,86° = 34°52′, или около 35°.
a 2 = 7,8 2 – 6,4 2 = 19,9, поэтому a равно примерно 4,5.36. a = c

b = c cos A = 12,15 cos 23°15′ = 11,17.Cos (a + b) — формула, доказательство, примеры
В тригонометрии cos(a + b) является одним из важных тригонометрических тождеств, включающих составной угол. Это одна из формул тригонометрии, используемая для нахождения значения тригонометрической функции косинуса суммы углов. Расширение cos (a + b) помогает представить значение тригонометрической функции cos составного угла в терминах тригонометрических функций синуса и косинуса. Давайте подробно разберемся в тождестве cos (a + b) и его доказательстве в следующих разделах.
1. Что такое тождество Cos(a + b) в тригонометрии? 2. Cos(a + b) Формула составного угла 3. Доказательство формулы Cos(a + b) 4. Как применить Cos(a + b)? 5. 
Часто задаваемые вопросы по Cos(a + b) Что такое тождество Cos(a + b) в тригонометрии?
Cos(a+b) — тригонометрическое тождество для составных углов, представленное в виде суммы двух углов. Поэтому он применяется, когда угол, для которого должно быть вычислено значение функции косинуса, задан в виде суммы углов. Угол (a+b) здесь представляет собой составной угол.
Cos(a + b) Формула составного угла
Формула Cos(a + b) обычно называется формулой сложения косинуса в тригонометрии. Формула cos(a+b) для составного угла (a+b) может быть представлена как
cos (a + b) = cos a cos b — sin a sin b
где a и b — заданные углы.
Доказательство формулы Cos(a + b)
Проверка разложения формулы cos(a+b) может быть выполнена геометрически. Рассмотрим пошаговый вывод формулы косинуса тригонометрической функции суммы двух углов в этом разделе. При геометрическом доказательстве формулы cos(a+b) сначала предположим, что a, b и (a+b) — положительные острые углы, такие, что (a+b) < 90.
 Но эта формула, вообще говоря, верна для любых положительных или отрицательных значений a и b.
Но эта формула, вообще говоря, верна для любых положительных или отрицательных значений a и b.Чтобы доказать: cos (a + b) = cos a cos b — sin a sin b
Построение: Предположим, что вращающаяся линия OX вращается вокруг O против часовой стрелки до тех пор, пока она не достигнет Y. OX образует острый угол с Y, заданным как ∠XOY = a, от начального положения до его конечного положения. Опять же, эта линия вращается дальше в том же направлении и, начиная с положения OY, пока не достигнет Z, таким образом образуя острый угол, равный ∠YOZ = b. ∠XOZ = а + b < 90°.
На граничной линии составного угла (a + b) возьмем точку P на OZ и проведем перпендикуляры PQ и PR к OX и OY соответственно. Опять же, из R провести перпендикуляры RS и RT на OX и PQ соответственно.
Теперь из прямоугольного треугольника PQO получаем
cos (a + b) = OQ/OP
= (ОС — СК)/OP
= ОС/ОП — СК/ОП
= ОС/ОП — ТР/ОП
= ОС/ИЛИ ∙ ИЛИ/ОП + ТР/ПР ∙ ПР/ОП
= cos a cos b — sin ∠TPR sin b
= cos a cos b — sin a sin b, (так как мы знаем, ∠TPR = a)Следовательно, cos ( a + b) = cos a cos b — sin a sin б.

Как применить Cos(a + b)?
Разложение cos(a + b) можно использовать для нахождения значения тригонометрической функции косинуса для углов, которые можно представить как сумму стандартных углов в тригонометрии. Мы можем выполнить шаги, указанные ниже, чтобы научиться применять идентичность cos (a + b). Давайте оценим cos(30º + 60º), чтобы лучше понять это.
- Шаг 1: Сравните выражение cos(a + b) с данным выражением, чтобы определить углы ‘a’ и ‘b’. Здесь a = 30º и b = 60º.
- Шаг 2: Мы знаем, cos (a + b) = cos a cos b — sin a sin b.
⇒ cos(30° + 60°) = cos 30°cos 60° — sin 30°sin 60°
поскольку sin 60º = √3/2, sin 30º = 1/2, cos 60º = 1/2, cos 30º = √3/2
⇒ cos(30° + 60°) = (√3/2)(1/2) — (1/2)(√3/2) = √3/4 — √3/4 = 0
Кроме того, мы знаем, что cos 90º = 0. Следовательно, результат проверен.
☛ Связанные темы по Cos (a + b):
Вот некоторые темы, которые могут вас заинтересовать при чтении о cos(a+b).

- Закон синусов
- грех кост загар
- Тригонометрическая таблица
- Тригонометрические функции
Давайте рассмотрим несколько решенных примеров, чтобы лучше понять формулу cos(a+b).
Часто задаваемые вопросы по Cos(a + b)
Что такое Cos(a + b)?
Cos(a+b) — одно из важных тригонометрических тождеств, также называемое в тригонометрии формулой сложения косинусов. Cos(a+b) можно представить как cos(a + b) = cos a cos b — sin a sin b, где ‘a’ и ‘b’ — углы.
Что такое формула Cos(a + b)?
Формула cos(a+b) используется для выражения формулы составного угла cos через синус и косинус отдельных углов. Формула cos(a+b) в тригонометрии может быть представлена как cos(a + b) = cos a cos b — sin a sin b.
Что такое расширение cos(a + b)
Расширение cos(a+b) задается как cos (a + b) = cos a cos b — sin a sin b. Здесь a и b — меры углов.
Как доказать формулу Cos (a + b)?
Доказательство формулы cos(a + b) может быть дано методом геометрического построения.
 Первоначально мы предполагаем, что ‘a’, ‘b’ и (a+b) являются положительными острыми углами, так что (a+b) < 90. Щелкните здесь, чтобы понять пошаговый метод получения формулы cos(a+b).
Первоначально мы предполагаем, что ‘a’, ‘b’ и (a+b) являются положительными острыми углами, так что (a+b) < 90. Щелкните здесь, чтобы понять пошаговый метод получения формулы cos(a+b).Каковы применения формулы Cos (a + b)?
Cos(a+b) можно использовать для нахождения значения функции косинуса для углов, которые могут быть представлены в виде суммы стандартных или более простых углов. Таким образом, упрощается вывод при вычислении значений триггерных функций. Его также можно использовать для нахождения расширения других формул двойного и кратного угла.
Как найти значение Cos 15º, используя тождество Cos (a + b).
Значение cos 15° с использованием тождества (a + b) можно вычислить, сначала записав его как cos[(45°+(-30°)] и затем применив тождество cos(a+b) и используя тригонометрическую таблицу.
⇒ cos[(45°+(-30°)] = cos 45°cos(-30)° — sin(-30)°sin 45° = (1/√2)(√3/2) — (-1/2)(1/ √2) = (√3/2√2) + (1/2√2) = (√3+1)/2√2 = (√6+√2)/4Как найти Cos(a + b + c) используя Cos (a + b)?
Мы можем выразить cos(a+b+c) как cos((a+b)+c) и расширить, используя cos(a+b) и sin(a+ б) формула как, cos(a+b+c) = cos(a+b).


 {\circ}=289+196-238=24$$
{\circ}=289+196-238=24$$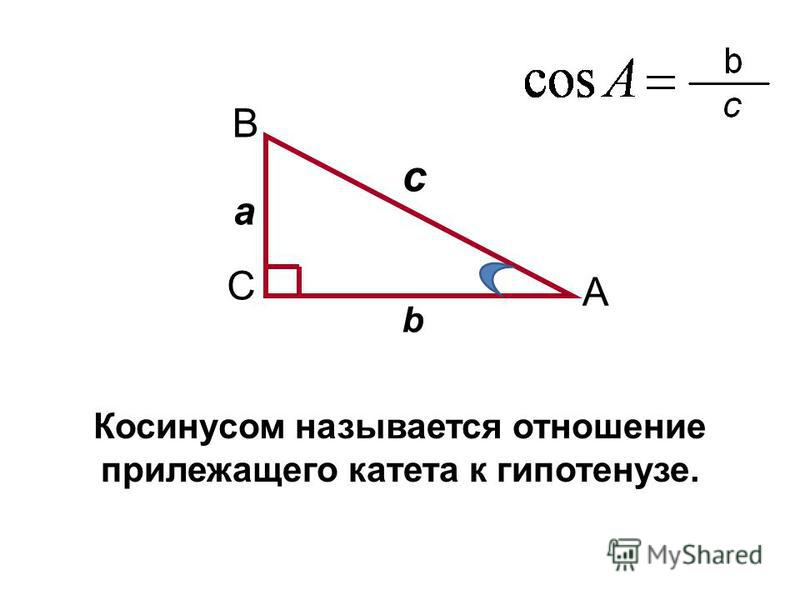
 cos C.
cos C. c.cosα
c.cosα

 функции. Таким образом, мы доказали, что
функции. Таким образом, мы доказали, что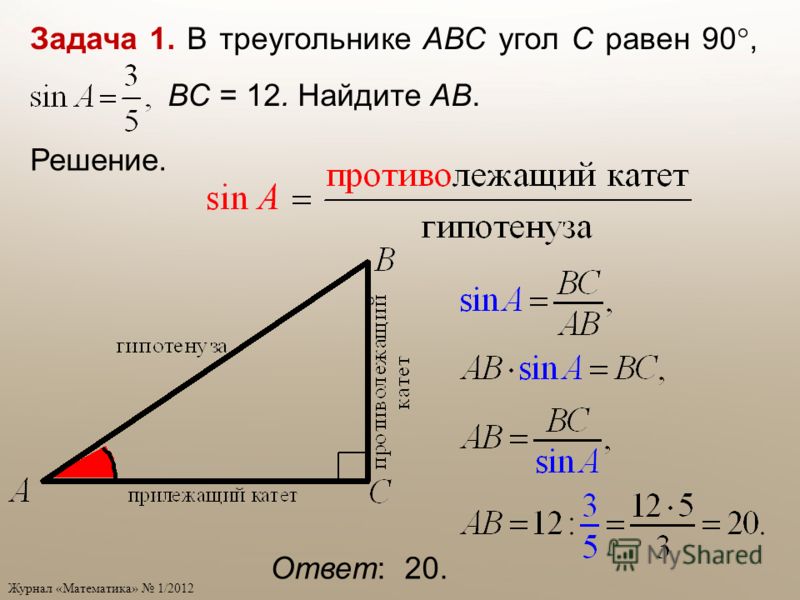


 Но эта формула, вообще говоря, верна для любых положительных или отрицательных значений a и b.
Но эта формула, вообще говоря, верна для любых положительных или отрицательных значений a и b.
 Первоначально мы предполагаем, что ‘a’, ‘b’ и (a+b) являются положительными острыми углами, так что (a+b) < 90. Щелкните здесь, чтобы понять пошаговый метод получения формулы cos(a+b).
Первоначально мы предполагаем, что ‘a’, ‘b’ и (a+b) являются положительными острыми углами, так что (a+b) < 90. Щелкните здесь, чтобы понять пошаговый метод получения формулы cos(a+b).