Как найти миноры матрицы 4х4: Определитель матрицы 4х4 – онлайн калькулятор с подробным решением.

Минор и алгебраическое дополнение матрицы.

Минор и алгебраическое дополнение матрицы.

Навигация по странице:

• Минор матрицы
• Алгебраическое дополнение матрицы
• Свойства алгебраического дополнения матрицы

Определение.

Минором M_ij к элементу a_ij определителя n-го порядка называется определитель (n — 1)-го порядка, полученный из исходного определителя вычеркиванием i-той строки и j-того столбца.

Пример 1.

Найти миноры матрицы A

A = 571-410203

Решение:

M11 =

5 7 1 -4 1 0 2 0 3

=

1 0 0 3

M11 =

1 0 0 3

= 1·3 — 0·0 = 3 — 0 = 3

M12 =

-4 0 2 3

= -4·3 — 0·2 = -12 -0 = -12

M13 =

-4 1 2 0

= -4·0 — 1·2 = 0 — 2 = -2

M21 =

7 1 0 3

= 7·3 — 1·0 = 21 — 0 = 21

M22 =

5 1 2 3

= 5·3 — 1·2 = 15 — 2 = 13

M23 =

5 7 2 0

= 5·0 — 7·2 = 0 — 14 = -14

M31 =

7 1 1 0

= 7·0 — 1·1 = 0 — 1 = -1

M32 =

5 1 -4 0

= 5·0 — 1·(-4) = 0 + 4 = 4

M33 =

5 7 -4 1

= 5·1 — 7·(-4) = 5 + 28 = 33

Определение.

Алгебраическим дополнением A_ij к элементу a_ij определителя n-го порядка называется число

A_ij = (-1)^{i + j} · M_ij

• Сумма произведений элементов строки (столбца) определителя на алгебраические дополнения к элементам этой строки (столбца) равна определителю матрицы:

  n
  Σ	aij·Aij = det(A)
  j = 1

• Сумма произведений элементов строки (столбца) определителя на алгебраические дополнения к элементам другой строки (столбца) равна нулю:

  n
  Σ	akj·Aij = 0           (i ≠ k)
  j = 1

• Сумма произведений элементов «произвольной» строки на алгебраические дополнения к элементам i-той строки определителя равна определителю, в котором вместо i-той строки записана «произвольная» строка.

Пример 2.

Найти алгебраические дополнения матрицы A

A₁₁ = 571-410203

Решение:

A₁₁ = (-1)^{1 + 1}·M₁₁ = (-1)²·1003 = 1·3 — 0·0 = 3 — 0 = 3

A₁₂ = (-1)^{1 + 2}·M₁₂ = (-1)³·-4023 = -(-4·3 — 0·2) = -(-12 -0) = 12

A₁₃ = (-1)^{1 + 3}·M₁₃ = (-1)⁴·-4120 = -4·0 — 1·2 = 0 — 2 = -2

A₂₁ = (-1)^{2 + 1}·M₂₁ = (-1)³·7103 = -(7·3 — 1·0) = -(21 — 0) = -21

A₂₂ = (-1)^{2 + 2}·M₂₂ = (-1)⁴·5123 = 5·3 — 1·2 = 15 — 2 = 13

A₂₃ = (-1)^{2 + 3}·M₂₃ = (-1)⁵·5720 = -(5·0 — 7·2) = -(0 — 14) = 14

A₃₁ = (-1)^{3 + 1}·M₃₁ = (-1)⁴·7110 = 7·0 — 1·1 = 0 — 1 = -1

A₃₂ = (-1)^{3 + 2}·M₃₂ = (-1)⁵·51-40 = -(5·0 — 1·(-4)) = -(0 + 4) = -4

A₃₃ = (-1)^{3 + 3}·M₃₃ = (-1)⁶·57-41 = 5·1 — 7·(-4) = 5 + 28 = 33

Онлайн калькуляторы с матрицами.

Упражнения с матрицами.

Алгебраические дополнения онлайн

Определение. Если в определителе n-го порядка вычеркнуть i строку и j столбец, то оставшийся определитель (n-1)-го порядка называется минором данного элемента a_i^j и обозначается M_i^j. Минором некоторого элемента определителя называется определитель, полученный из исходного вычеркиванием строки и столбца, на пересечении которых стоит данный элемент.
Главным минором k-го порядка матрицы А называется определитель, составленный из элементов, расположенных на пересечении ее k строк и k столбцов с одинаковыми номерами.
Угловым минором k-го порядка матрицы А называется определитель, составленный из элементов, расположенных на пересечении ее первых k строк и первых k столбцов.

Определение. Алгебраическим дополнением элемента a_i^j определителя D называется его минор, взятый со знаком (-1)^i+j.
Алгебраическое дополнение элемента a_i^j обозначается через A_i^j. Следовательно, A_i^j = (-1)^i+jM_i^j.

• Ввод данных
• Видеоинструкция

Размерность матрицы 2345678910

Пример №1. Дан определитель . Найти минор и алгебраическое дополнение элемента a₂¹ (выделен пунктиром).
Решение. Вычеркивая в определителе первую строку и второй столбец, на пересечении которых находится элемент a₂¹, получим . Тогда A₂¹ = (-1)¹⁺²M₂¹ = -14.
Теорема. Определитель равен сумме произведений элементов какой-нибудь строки или столбца на их алгебраические дополнения, т.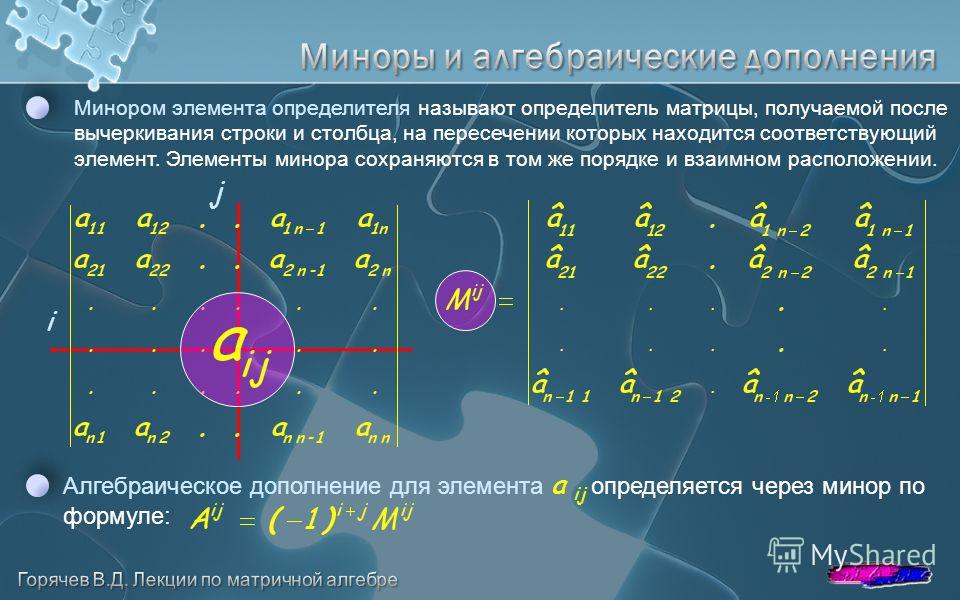 е.
D=ai01·Ai01+ai02·Ai02+ ... + ai0n·Ai0n  (*)
где i

0 – фиксировано.
Выражение (*) называют разложением определителя D по элементам строки с номером i₀.
Вычисление определителя n-го порядка сводится к вычислению одного определителя (n-1)-го порядка, для чего в какой–либо строке (или столбце) получают (n-1) нулей, а затем разлагают определитель по этой строке, пользуясь формулой (*).

Пример №2. Покажем нахождение алгебраических дополнений на примере определения обратной матрицы:

Решение находим с помощью калькулятора. Найдем главный определитель.
∆ = 0.73 ∙(0.72  ∙0.92 -(-0.17 ∙(-0.15  )))-(-0.19  ∙(-0.07  ∙0.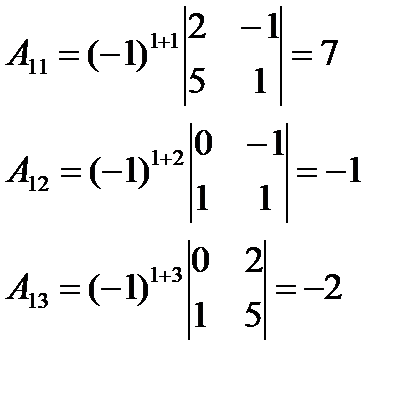 92 -(-0.17 ∙(-0.12  ))))+(-0.12 ∙(-0.07  ∙(-0.15 )-0.72  ∙(-0.12  ))) = 0.437197
Транспонированная матрица

Алгебраические дополнения

∆_1,1 = (0.72  ∙0.92 -(-0.15  ∙(-0.17 ))) = 0.6369

∆_1,2 = -(-0.07  ∙0.92 -(-0.12  ∙(-0.17 ))) = 0.0848

∆_1,3 = (-0.07  ∙(-0.15  )-(-0.12  ∙0.72  )) = 0.0969

∆_2,1 = -(-0.19  ∙0.92 -(-0.15  ∙(-0.12 ))) = 0.1928

∆_2,2 = (0.73 ∙0.92 -(-0.12  ∙(-0.12 ))) = 0.6572

∆_2,3 = -(0.73 ∙(-0.15  )-(-0.12  ∙(-0.19  ))) = 0.1323

∆_3,1 = (-0.19  ∙(-0.17 )-0.72  ∙(-0.12 )) = 0.1187

∆_3,2 = -(0.73 ∙(-0.17 )-(-0.07  ∙(-0.12 ))) = 0.1325

∆_3,3 = (0.73 ∙0.72  -(-0.07  ∙(-0.19  ))) = 0.5123
Обратная матрица

Пример №3. Алгебраическое дополнение также используется при определении количества остовных деревьев в графе.

Что такое миноры и кофакторы? Как они работают?

Примеры

Purplemath

Найти определитель матрицы 2×2 очень просто: вы просто выполняете перекрестное умножение и вычитаете: матриц 3×3, хотя и немного сложнее, но все же довольно просто: вы добавляете повторы первого и второго столбцов в конец определителя, умножаете по всем диагоналям, а также складываете и вычитаете в соответствии с правилом:

Но для детерминантов 4×4 и больших вам придется вернуться к меньшим детерминантам 2×2 и 3×3, используя так называемые «младшие» и «кофакторы».

Что такое минор определителя матрицы?

Минор определителя – это определитель, образованный удалением одной строки и одного столбца из исходного определителя. А поскольку в исходном определителе много строк и столбцов, из него можно составить множество миноров.

Как обозначаются или именуются отдельные несовершеннолетние?

Второстепенные элементы помечаются в соответствии со строкой и столбцом, которые были удалены из исходного определителя. Таким образом, если вы должны были перейти, скажем, к элементу a _2,4 из определителя некоторой матрицы A и вычеркнуть строку и столбец, которые проходят через этот элемент (то есть, если вы удалите второй строку и четвертый столбец от определителя), новый (и меньший) определитель называется младшим M _2,4 .

Ниже приведен пример этого:

определитель А :

вычеркнуть все записи, находящиеся в одной строке или столбце с записью а _2,4 :

меньший 0003

Один раз вы нашли минор M _{i, j} , пришло время найти кофактор.

Что такое кофактор определителя матрицы?

Кофактор соответствует минору для определенного элемента определителя матрицы. Чтобы найти кофактор определенной записи в этом определителе, выполните следующие действия:

1. Возьмите значения i и j из нижнего индекса минора, M _i,j , и сложите их.
2. Возьмите значение i  +  j и возложите его как степень на -1; другими словами, оцените (−1) ^{i + j} .
3. Умножить минор M _{i , j} на результат шага 2.

Результат (−1) ^i+j M _{i , j} является кофактором, C _j .

Но ты еще не закончил. Да, есть еще.

Как найти определитель с помощью миноров и кофакторов?

Чтобы найти определитель матрицы A с помощью миноров и кофакторов, вы должны выбрать строку или столбец матрицы, найти все кофакторы для этой строки или столбца, умножить каждый кофактор на соответствующий элемент матрицы, а затем добавьте все значения, которые вы получили.

Хорошо, да; это, вероятно, не имело особого смысла. Это можно сказать по-другому:

• У вас есть матрица A . Вам нужно найти его определитель.
• Он слишком велик, чтобы его можно было найти более простыми методами, поэтому вам придется найти его, «расширив строку или столбец».
• Первым шагом в этом «расширении» будет выбор строки или столбца. Допустим, вы выбираете третий ряд.
• Для каждой записи в третьей строке вы найдете кофактор этой записи и умножите запись на ее кофактор. То есть для элемента a _3,1 матрицы A вы найдете сомножитель C _3,1 , а затем умножите сомножитель на a _{3 ,1} запись: ( a _3,1 )( C _3,1 ). Для записи a _3,2 вы найдете кофактор C _3,2 и умножить: ( a _3,2 )( A _3,2 ). И так далее.
• Затем вы сложите все эти продукты: ( a _3,1 )( C _3,1 ) + ( a _3,2 )( 3,2 C
• ) + ( а _3,3 )( С _3,3 ) + . …

Полученная сумма есть значение определителя матрицы А .

(Вышеупомянутая запутанная путаница является причиной того, что никто не делает детерминанты вручную, если этого можно избежать: есть только , поэтому требуется много подверженной ошибкам бессмысленной рутинной работы.)

---

Неважно, какую строку или столбец вы используете. для вашего расширения; вы получите то же значение независимо. Но эта гибкость может быть полезной, потому что она позволяет вам стремиться к нулям.

• Найдите определитель следующей матрицы, разложив (а) по первой строке и (б) по третьему столбцу. (c) Сравните результаты каждого расширения.
  

(a) Чтобы расширить первую строку, мне нужно найти миноры, а затем кофакторы элементов первой строки; то есть мне нужно найти миноры для матричных элементов a _1,1 , a _1,2 , a _1,3 и a 2,009 _{а затем умножьте их на -1 или +1, чтобы получить кофакторы.}

Итак, определитель этой матрицы, найденный путем разложения по первой строке, равен:

(а) дет( А ) = а _1,1 С _1,1 + а _1,2 + и _1,3 С _1,3 + а _1,4 С _1,4

 () += 3 0                 )(3) + 1(0) = −6

(b) Чтобы разложить по третьему столбцу, мне нужно найти миноры, а затем кофакторы элементов третьего столбца: a _1,3 , a _2,3 , a _3,3 и a _4,3 .

Секундочку… a _2,3 — запись исходной матрицы равна нулю. Это означает, что я получу ноль для этого термина, когда я буду расширять столбец вниз, независимо от того, каким окажется значение минора M _2,3 . Так что мне на самом деле все равно, что такое кофактор C _2,3 ; Я могу просто поставить 0 для этой записи, потому что:

a _2,3 C _2,3 = (0)( C _2,3 ) = 0

На самом деле, я могу игнорировать *каждый* из последних трех членов в расширении вниз по третьему столбцу, потому что все записи третьего столбца (кроме первой записи, которую я уже сделал) будут равны нулю.

Таким образом, единственное вычисление, которое меня волнует, это то, которое я уже сделал:

(b) det( A ) = a _1,3 C _1,3

                 = (−2)(3) = −6

В части (c) этого упражнения я должен сравнить два значения определителя.

(c) Сравнение: Каждое расширение дает одно и то же значение.

Смысл этого упражнения в том, чтобы показать, что не имеет значения, по какой строке или по какому столбцу вы выполняете развертывание; полученное значение (при условии отсутствия арифметических ошибок) всегда будет одинаковым. Это означает, что вы можете выбрать строку или столбец, которые считаете самыми простыми, и это не повлияет на ваш окончательный ответ.

---

URL: https://www.purplemath.com/modules/minors.htm

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в поиске кофакторов. Попробуйте введенное упражнение или введите свое собственное упражнение. (Или пропустите виджет и перейдите на следующую страницу. ) Затем нажмите кнопку и выберите «Найти матрицу кофакторов», которая показывает *все* кофакторы, чтобы сравнить свой ответ с ответом Mathway. (Возможно, сначала вам придется нажать «Дополнительно…», чтобы увидеть параметр матрицы кофакторов. Матрица кофакторов показывает кофакторы для каждой записи в исходной матрице.)

Пожалуйста, примите файлы cookie «предпочтения», чтобы включить этот виджет.

(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)

Page 2

Как найти миноры матрицы nxn?

Найти минор матрицы \(n \times n\) легко, и шаги почти такие же, как поиск определителя. Это первый шаг, чтобы найти матрицу кофакторов. Мы начнем в этой статье с общей формы нахождения минора, как найти минор матрицы \(2\times 2\), \(3\times 3\) и \(4\times 4\) , где каждый раздел заканчивается примером.

Каковы миноры матрицы

Пусть \(A\) будет \(n \times n\) матрицей. В частности:

\(A = \begin{bmatrix}\begin{array}{cccc} a_{1,1} & a_{1,2} & \cdots & a_{1,n} \\ a_{2, 1} & a_{2,2} & \cdots & a_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n,1} & a_{n,2} & \cdots & a_{n,n} \end{array}\end{bmatrix}\)

Минор \(M_{i,j}\) матрицы \(A\) является определителем \(n-1 \times n-1\) подматрица \(A\), где удаляются \(i\)-я строка и \(j\)-й столбец. В математической записи мы получим

\(M_{i,j} = \begin{vmatrix} a_{1,1} & a_{1,2} & \cdots & a_{1,j-1} & a_{1,j+1} & \cdots & a_{1,n} \\ a_{2,1} & a_{2,2} & \cdots & a_{2,j-1} & a_{2,j+1} & \cdots & a_{2,n} \\ \vdots & \vdots & \ddots & \vdots & \vdots & \cdots & \vdots \\ a_{i-1,1} & a_{i-1,2} & \cdots & a_{i-1,j-1} & a_{i-1,j+1} & \cdots & a_{i-1,n} \\ a_{i+1,1} & a_{i+1 ,2} & \cdots & a_{i+1,j-1} & a_{i+1,j+1} & \cdots & a_{i+1,n} \\ \vdots & \vdots & \cdots & \vdots & \vdots & \ddots & \vdots \\ a_{n,1} & a_{n,2} & \cdots & a_{n,j-1} & a_{n,j+1} & \ cdots & a_{n,n} \end{vmatrix} \)

Нахождение всех миноров матрицы \(A\) и объединение их в новую матрицу называется матрицей миноров , которую мы будем обозначать как \(M\):

\( M = \begin {bmatrix}\begin{array}{cccc} M_{1,1} & M_{1,2} & \cdots & M_{1,n} \\ M_{2,1} & M_{2,2} & \cdots & M_{2,n} \\ \vdots & \vdots & \ddots & \vdots \\ M_{n,1} & M_{n,2} & \cdots & M_{n,n} \end{ array}\end{bmatrix} \)

В конце концов, это почти то же самое, что вычисление определителя. Разница лишь в том, что нам нужно удалить одну строку и один столбец. Мы сделаем несколько примеров в следующих разделах для большей ясности.

Как найти миноры матрицы 2×2?

Мы начнем с поиска миноров матрицы \(2\times 2\). Итак, пусть \(A\) будет матрицей \(2\times 2\). В частности:

\(A = \begin{bmatrix}\begin{array}{cc} a_{1,1} & a_{1,2} \\ a_{2,1} & a_{2,2} \ end{array}\end{bmatrix}\)

Для каждого минора \(M_{1,1}\), \(M_{1,2}\), \(M_{2,1}\) и \ (M_{2,2}\), нам нужно найти его определитель подматрицы \(1\times 1\) матрицы \(A\). Но матрица \(1\times 1\) — это один элемент. Следовательно, мы можем переписать миноры как:

\begin{equation*} M_{1,1} = a_{2,2}, \quad M_{1,2} = a_{2,1}, \quad M_{2,1} = a_{1 ,2}, \quad \text{and} \quad M_{2,2} = a_{1,1} \end{equation*} и это приводит к следующей матрице миноров \(M\)

\( M = \begin{bmatrix}\begin{array}{cc} M_{1,1} & M_{1,2} \\ M_{2,1} & M_{2,2} \end{массив}\end {bmatrix} = \begin{bmatrix}\begin{array}{cc} a_{2,2} & a_{2,1} \\ a_{1,2} & a_{1,1} \end{array} \end{bmatrix} \)

Пример.

\(A = \begin{bmatrix}\begin{array}{cc} 5 & -2 \\ 7 & 3 \end{array}\end{bmatrix} \ \Rightarrow \ M = \begin{bmatrix} \begin{массив}{cc} 3 и 7 \\ -2 и 5 \end{массив}\end{bmatrix} \)

Как найти миноры матрицы 3×3?

Теперь нам нужно произвести дополнительные вычисления, так как у нас есть 9 определителей. А именно, пусть \(A\) будет матрицей

\(A = \begin{bmatrix}\begin{array}{ccc} a_{1,1} & a_{1,2} & a_{1,3} \\ a_{2,1} & a_{2,2} & a_{2,3} \\ a_{3,1} & a_{3,2} & a_{3,3} \end{массив}\ end{bmatrix}\)

Тогда матрица миноров \(A\) равна

\[ M = \begin{bmatrix}\begin{array}{ccc} M_{1,1} & M_{1, 2} & M_{1,3} \\ M_{2,1} & M_{2,2} & M_{2,3} \\ M_{3,1} & M_{3,2} & M_{3 ,3} \end{массив} \end{bmatrix} \] \[ \quad = \begin{bmatrix}\begin{array}{ccc} \begin{vmatrix} a_{2,2} & a_{2,3 }\\ a_{3,2} & a_{3,3}\\ \end{vmatrix} & \begin{vmatrix} a_{2,1} & a_{2,3}\\ a_{3,1} & a_{3,3}\\ \end{vmatrix} & \begin{vmatrix} a_{2,1} & a_{2,2}\\ a_{3,1} & a_{3,2}\\ \end{vmatrix} \\\\ \begin{vmatrix} a_{1,2} & a_{1,3}\\ a_{3,2}& a_{3,3}\\ \end{vmatrix} & \begin{vmatrix} a_{1,1} & a_{1,3}\\ a_{3,1}& a_{3,3}\\ \end{vmatrix} & \begin{vmatrix} a_{1, 1} & a_{1,2}\\ a_{3,1}& a_{3,2}\\ \end{vmatrix} \\\\ \begin{vmatrix} a_{1,2} & a_{1 ,3}\\ a_{2,2}& a_{2,3}\\ \end{vmatrix} & \begin{vmatrix} a_{1,1} & a_{1,3}\\ a_{2, 1}& a_{2,3}\\ \end{vmatrix} & \begin{vmatrix} a_{1,1} & a_{1,2}\\ a_{2,1} & a_{2,2} \\ \end{vmatrix} \end{массив} \end{bmatrix} \]

Пример.

\[ A = \begin{bmatrix}\begin{array}{ccc} 3 & -1 & 6 \\ 2 & 5 & 7 \\ 1 & -3 & 1 \end{массив} \end{bmatrix } \\Rightarrow \ M = \begin{bmatrix}\begin{array}{ccc} 26 & -5 & -11 \\ 17 & -3 & -8 \\ -37 & 9 & 17 \end{array}\ end{bmatrix} \]

Как найти миноры матрицы 4×4?

В предыдущих разделах мы видели, что найти минор — это довольно простое и прямолинейное вычисление. Чтобы решить матрицу \(4\times 4\), нам нужно вычислить 16 определителей подматриц \(3\times 3\). Это очень много вычислений! Обычно это делают компьютеры, но здесь мы дадим несколько вычислений, как найти миноры матрицы \(4 \times 4\).

\[ A = \begin{bmatrix}\begin{array}{cccc} 3 & -1 & 6 & 2 \\ 2 & 5 & 7 & 4 \\ 1 & -3 & 1 & 9 \\ 4 & 1 & 3 & 7 \end{array}\end{bmatrix} \] Приведем пример для вычисления миноров \(M_{1,1}\) и \(M_{4,2}\). \[ M_{1,1} = \begin{vmatrix} 5 & 7 & 4\\ -3 & 1 & 9\\ 1 & 3 & 7 \end{vmatrix} = 5 \cdot \begin{vmatrix} 1 & 9\\ 3 и 7 \end{vmatrix} + 3 \cdot \begin{vmatrix} 7 и 4\\ 3 и 7 \end{vmatrix} + 1 \cdot \begin{vmatrix} 7 и 4\\ 1 и 9\end{vmatrix} \] \[= 5 \cdot (-20) + 3 \cdot 37 + 1 \cdot 59 = 70\] \[ M_{4,2} = \begin{vmatrix} 3 & 6 & 2 \\ 2 & 7 & 4 \\ 1 & 1 & 9 \\ \end{vmatrix} = 3 \cdot \begin{vmatrix} 7 & 4 \\ 1 & 9 \\ \end{vmatrix} – 2 \cdot \ begin{vmatrix} 6 & 2 \\ 1 & 9 \\ \end{vmatrix} + 1 \cdot \begin{vmatrix} 6 & 2 \\ 7 & 4 \\ \end{vmatrix} \] \[= 3\ cdot 59 – 2 \cdot 52 + 1 \cdot 14 = 83 \]

Заключение

Нахождение миноров матрицы может быть сделано легко и быстро для матриц \(2 \times 2\) и \(3 \times 3 \), но большее значение увеличит сложность вычислений.