Наклонная асимптота параметрической функции : Анализ-I
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
| Desman |
| ||
16/12/13 |
| ||
| |||
12.2013, 23:30 | ewert |
| |||
11/05/08 |
| |||
| ||||
12.2013, 23:40 | provincialka |
| |||
18/01/13 |
| |||
| ||||
12.2013, 23:42 | |
| ||
14/03/10 | |||
| |||
12.2013, 00:03 | provincialka |
| |||
18/01/13 |
| |||
| ||||
Поправлю.| Desman |
| ||
16/12/13 |
| ||
| |||
| provincialka |
| |||
18/01/13 |
| |||
| ||||
12.2013, 19:14 | Desman |
| |
16/12/13 | ||
| ||
12.2013, 21:05 | Aritaborian |
| ||
11/06/12 |
| ||
| |||
| Desman |
| ||
16/12/13 |
| ||
| |||
| provincialka |
| |||
18/01/13 |
| |||
| ||||
12.2013, 21:29 | Aritaborian |
| ||
11/06/12 |
| ||
| |||
12.2013, 23:20 | provincialka |
| |||
18/01/13 |
| |||
| ||||
12.2013, 23:47 | Desman |
| ||
16/12/13 |
| ||
| |||
12.2013, 01:39 | Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 14 ] |
Модераторы: Модераторы Математики, Супермодераторы
Наклонные (наклонные) асимптоты | Purplemath
VerticalHorizontalExamples
Purplemath
В предыдущем разделе, посвященном горизонтальным асимптотам, мы научились работать с рациональными функциями, где степень числителя равна или меньше степени знаменателя.
Но что произойдет, если степень на больше в числителе, чем в знаменателе?
Вспомним, что, когда степень знаменателя была больше степени числителя, мы видели, что значение в знаменателе становилось настолько больше, так быстро, что оно было настолько «сильнее», что «вытягивало» функционал значение до нуля, что дает нам горизонтальную асимптоту x — ось.
Содержание продолжается ниже
MathHelp.com
Разумно, если числитель имеет степень, которая больше, чем у знаменателя, тогда значение числителя должно быть «сильнее» и должно «тянуть» график вдали от оси x (то есть линия y = 0) или любое другое фиксированное значение y .
Чтобы исследовать это, давайте рассмотрим следующую функцию:
По причинам, которые вскоре станут ясны, я собираюсь применить к этому рациональному выражению длинное полиномиальное деление. Моя работа выглядит так:
Вверху находится частное, являющееся выражением линейного полинома −3 x − 3.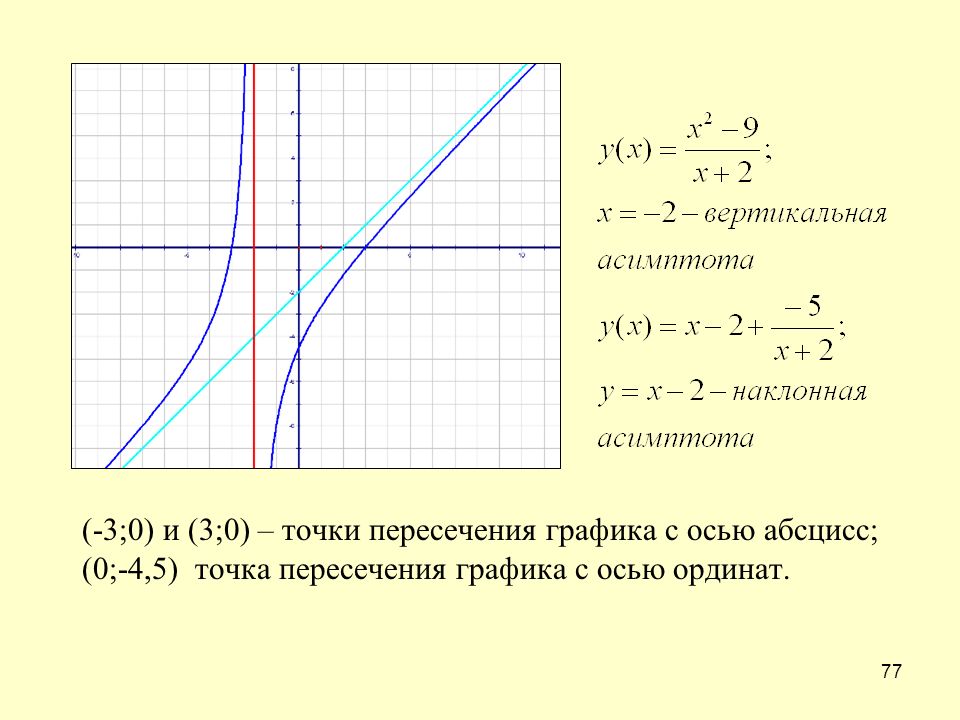
Внизу — остаток. Это означает, что с помощью деления в длинное число я могу преобразовать исходную рациональную функцию, которую они мне дали, в нечто похожее на формат смешанных чисел:
Это точно такая же функция. Все, что я сделал, это немного переставил его. Почему? Вы собираетесь увидеть.
Во-первых, взгляните на график рациональной функции, который они нам дали:
Вспоминая результаты моего деления в длину, вы знаете, что такое график0007 y = −3 x − 3 похоже; это убывающая прямая, пересекающая ось y в точке -3 и имеющая наклон м = -3.
Теперь взгляните на этот второй график той же рациональной функции, но с наложенной на него линией y = −3 x − 3:
Как видите, кроме середины графика рядом начало координат, график охватывает линию y = −3 x − 3. Из-за такого поведения графика как «тощего вдоль линии» линия y = −3 x − 3 является асимптотой.
Ясно, что это не горизонтальная асимптота. Вместо этого, поскольку его линия наклонена или, в причудливой терминологии, «наклонна», это называется «наклонной» (или «наклонной») асимптотой.
Графики показывают, что если степень числителя ровно на одну больше, чем степень знаменателя на (так что полиномиальная дробь «неправильная»), то график рациональной функции будет, грубо говоря, наклонная прямая линия с некоторыми неудобными кусочками посередине. Поскольку график будет почти равен этому наклонному прямолинейному эквиваленту, асимптота для такого рода рациональной функции называется «наклонной» (или «наклонной») асимптотой. Уравнение для наклонной асимптоты — это полиномиальная часть рационального числа, которое вы получите после выполнения длинного деления.
Между прочим, это соотношение — между неправильной рациональной функцией, ассоциированным с ней полиномом и графиком — выполняется независимо от разницы в степенях числителя и знаменателя. Однако в большинстве учебников вы работаете только с разницей в одну степень.
Чтобы найти наклонную асимптоту, я произведу деление в большую сторону: деление), а не остаток (то есть не последнее значение внизу). Тогда мой ответ:
Наклонная асимптота: y = x + 5
Здесь меня пытались подставить! Они опустили линейный член в многочлене вверху, а внизу расположили члены в неправильном порядке. Итак, когда я выполняю деление в длинное, мне нужно быть осторожным с отсутствующим линейным членом в числителе и со знаками, когда я переворачиваю члены в знаменателе.
Наклонная асимптота представляет собой полиномиальную часть ответа, поэтому:
Наклонная асимптота: y = −2 x − 4
Если вам не нравится часть этих упражнений с делением в длину, вернитесь и просмотрите прямо сейчас!
Примечание для любознательных о правилах горизонтальной и наклонной асимптот.
В противном случае перейдите к проработанным примерам.
URL: https://www.purplemath.com/modules/asymtote3.htm
Страница 1Страница 2Страница 4
Наклонные асимптоты — макеты
BY: Мэри Джейн Стерлинг и
Обновлено: 03-26-2016
Линейная алгебра для Dummies
Исследуйте книгу на Amazon
AN oblet или SLATE ASMANS AMAZON
AN . вертикальные и горизонтальные асимптоты. Другими словами, это помогает вам определить окончательное направление или форму графика рациональной функции. Наклонная асимптота иногда возникает, когда у вас нет горизонтальной асимптоты. Наклонные асимптоты требуют особых обстоятельств, но уравнения этих асимптот относительно легко найти, когда они встречаются.
Правило для наклонных асимптот состоит в том, что если самая высокая переменная степень рациональной функции встречается в числителе — и если эта степень ровно на больше, чем самая высокая степень в знаменателе, — тогда функция имеет наклонную асимптоту.
Вы можете найти уравнение наклонной асимптоты, разделив числитель правила функции на знаменатель и используя первые два члена в частном в уравнении прямой, которая является асимптотой.
Пример вопроса
Найти уравнение наклонной асимптоты в функции
y = x + 2. Чтобы найти это уравнение, вы должны разделить знаменатель правила функции на числитель. Этот шаг требует длинного деления . Вы не можете использовать синтетическое деление, потому что делитель не является двучленом в форме x – a . Вот как выглядит длинное деление:
Не обращайте внимания на остаток и используйте только первые два члена в частном в уравнении прямой.
Практические вопросы
Найти уравнение наклонной асимптоты в функции
Найти уравнение наклонной асимптоты в функции
Найти уравнение наклонной асимптоты в функции
Найти уравнение наклонной асимптоты в функции
Ниже приведены ответы на практические вопросы:
Ответ: y = x – 2.
