Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Решено
В прямоугольном треугольнике АВС угол С равен 90 градусов, AB = 4, tg А=0.
Решено
На полке было 12 книг. Несколько книг взяли с полки. После этого осталось на 4 книги больше, чем взяли. Сколько книг взяли с полки?
Решено
Ледокол 3 дня пробивал себе путь во льдах.В первый день он проплыл 2/5всего пути,во второй день 5/8 оставшегося пути, а в третий день оставшиеся 90км.Чему равен путь, который проплыл ледокол за 3 дня
Дано: геометрическая прогрессия (bn) задана условиями: b1=-2 , bn+1=3bn. Найдите b6. Объясните пожалуйста, как это решить?
Решено
дана арифмитическая прогрессия (аn)в которой a9=-22,2,a23=-41,8 найдите разность прогрессии
Пользуйтесь нашим приложением
«Функции y = sinx, y = cosx, их свойства и графики». 10-й класс
- org/Person»>
Шутова Любовь Михайловна
Разделы: Математика
Класс: 10
“Именно функция является тем средством
математического
языка, которое позволяет описывать процессы
движения,
присущие природе.”
Г.Галилей.
Цели и задачи:
Образовательные: отработать навыки построения и чтения графиков функций и проверить знания по данной теме.
Развивающие: развивать умения, анализировать, применять имеющие знания у учащихся в изменённой ситуации.
Воспитательные: воспитывать у учащихся аккуратность, любознательность, бережное отношение к окружающему миру, нравственные качества.
Тип урока: комбинированный.
Оборудование: доска, тетради, таблицы, раздаточный материал.
Ход урока:
I. Оргмомент. Объявление цели урока.
II. Проверка домашнего задания
(На доске заготовлены системы координат; №18.7а,18.9а,18.18а.)
III. Работа с классом:
1. Повторение теоретического материала:
а) дать определение функции;
б) дать определение графика функции;
в) какая функция называется возрастающей,
убывающей;
г) какая функция называется чётной, нечётной;
д) чему равен наименьший положительный период
функции;
е) каким свойством обладает график чётной
функции, нечётной функции;
ж) какая функция называется периодической.
IV. Работа с классом
V.
Историческая справкаФункция выражает зависимость между
переменными величинами. Каждая область знаний
химия, физика, биология, социология и др. имеет
свои объекты изучения, устанавливает свойства и
взаимосвязи между этими объектами в реальном
мире. Впервые функция вошла в математику под
именем “переменная величина”, в труде
французского математика и философа Рене Декарта
в 1637 году. Сам термин “функция” впервые
встречается в рукописи немецкого математика и
философа Г.Лейбница. Леонард Эйлер ввёл принятые
сейчас обозначения для функций. Сложный, очень
длительный путь развития понятия функции. С ним
связаны имена Н.И.Лобаческого, Л.Дерихле, Г.
Кантора. Сейчас многие науки берут на вооружение
математический аппарат.
 Летом солнце
приближается к зениту, лучи его падают почти
отвесно. Поток солнечной энергии одинаков во все
времена. Он зависит от угла падения лучей.
Меняется угол падения и меняется доля солнечной
энергии. Зависимость солнечной энергии от угла
падения лучей и выражает график y = sinx.
Летом солнце
приближается к зениту, лучи его падают почти
отвесно. Поток солнечной энергии одинаков во все
времена. Он зависит от угла падения лучей.
Меняется угол падения и меняется доля солнечной
энергии. Зависимость солнечной энергии от угла
падения лучей и выражает график y = sinx.
Vi. Устный счёт.
- Чему равно произведение tg1·tg89;
- Какая из функций принимает наибольшее значение y = sin2x или y = 2sinx;
- Представьте единицу в виде тригонометрических формул (1 = sin).
VII. Контрольный тест на два варианта.
Тест “Тригонометрические функции”
Вариант 1.
- 1. Какая из функций является обратной для
функции ?
а); б); в) ; г). - Вычислите: .

а) 1; б) 0; в) ; г) –1. - Найдите , если
.
а) ; б) ; в); г) . - Найдите область значений функции: .
а) ; б) ; в) ; г) . - Найти наименьшее значение функции .
а) ; б); в) –1; г) 0. - Какая из точек принадлежит графику функции .
а) ; б); в); г)
. Вариант 2.
- Какая из функций является обратной для функции ?
а); б) ; в) ; г) . - Вычислите: .
а) 1; б) ; в) ; г) . - Найдите , если
.
а) ; б) ; в); г) . - Найдите область значений функции: .
а) ; б) ; в) ; г) . - Найти наибольшее значение функции .
а) ; б); в) –1; г) 0. - Какая из точек принадлежит графику функции .
а) ; б); в); г).
Решите дифференциальное уравнение: $ y’ + y\cos x = \frac{1}{2} \sin2x$
Задай вопрос
спросил
Изменено 5 лет, 2 месяца назад
Просмотрено 2к раз
$\begingroup$ 9{\int R(x)\,dx}$.
Редактировать: Извините, я не знал, что кто-то другой ответил на вопрос прямо передо мной.
$\endgroup$
$\begingroup$
Вот подход «reductio in absurdum»:
$$y’ + y\cos(x)= \sin(x)\cos(x)$$
$$y’ = \cos(x) (\sin(x)-y)$$
теперь положим $\sin(x)-y = z$, получим $\cos(x)-y’ = z’$
$$\cos(x )-z’ = \cos(x)z$$
$$z’ = \cos(x)(1-z)$$
теперь пусть $1-z=a, -z’=a’$, $-a’ = \cos(x)a$
$а’ = -\cos(x)a$
Теперь помните о цепном правиле и предположите, что $-\cos(x)$ является внутренним производным к $a$.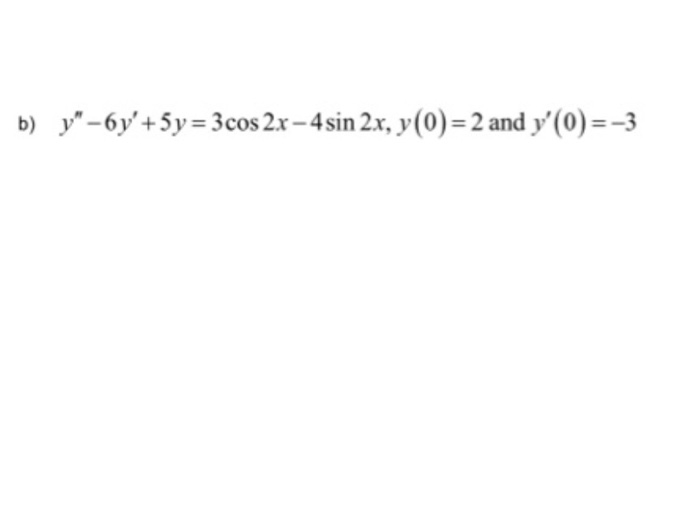

 02.17
02.17