Видеоурок по алгебре 9 класс тема Нули функции
Квадратичная функция
Уравнения и неравенства с одной переменной
Уравнения и неравенства с двумя переменными
Арифметическая и геометрическая прогрессии
Элементы комбинаторики и теории вероятностей
Показать все темы
Алгебра
Поделиться
0
0
03:29
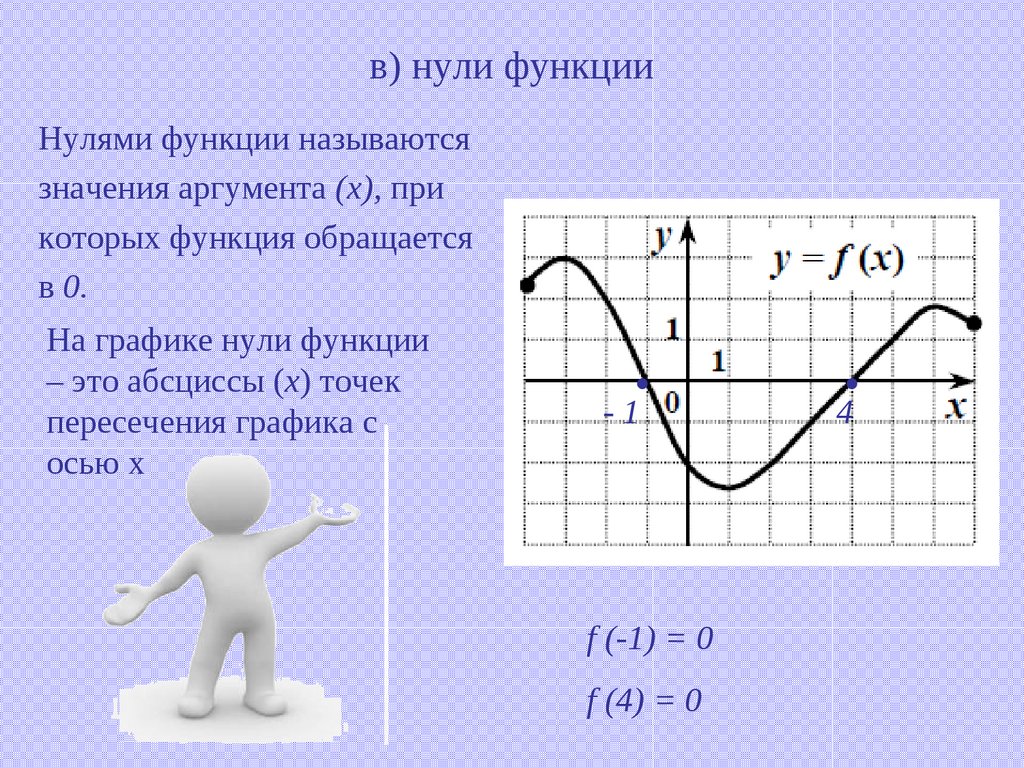
Нулями функции называются значение абсциссы, при котором значение функции равно нулю.
Чтобы найти нули функции, заданной формулой y=f(x), надо решить уравнение f(x)=0.
Если уравнение не имеет корней, нулей у функции нет.
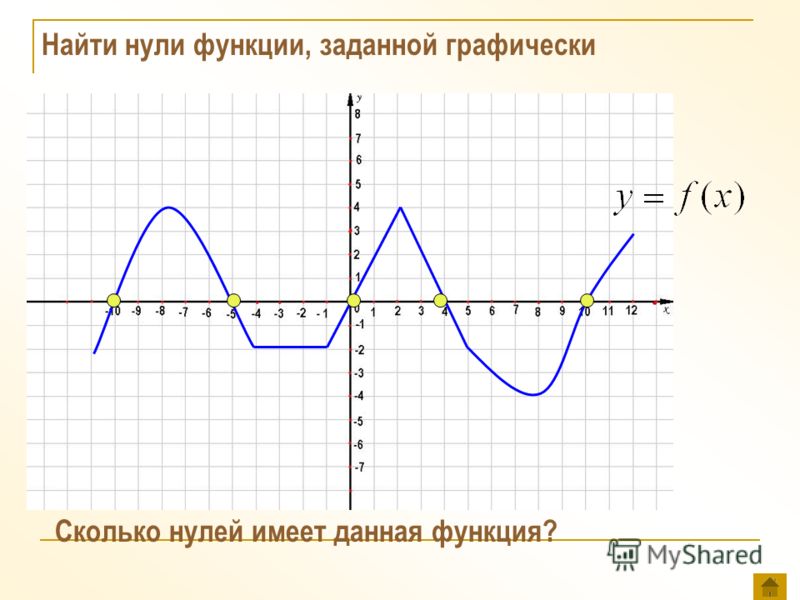
Чтобы найти нули функции, заданной графически, надо найти точки пересечения графика функции с осью абсцисс.
Математика. Нули функции + примеры + инструкция
Чтобы найти нули функции, заданной формулой y=f(x), надо решить уравнение f(x)=0.
Если уравнение не имеет корней, нулей у функции нет.
Примеры.
1) Найти нули линейной функции y=3x+15.
Решение:
Чтобы найти нули функции, решим уравнение 3x+15=0.
3x=-15; x= -5.
Таким образом, нуль функции y=3x+15 — x= -5.
Ответ:x= -5.
2) Найти нули квадратичной функции f(x)=x²-7x+12.
Решение:
Для нахождения нулей функции решим квадратное уравнение
x²-7x+12=0.
Его корни x1=3 и x2=4 являются нулями данной функции.
Ответ: x=3; x=4.
Инструкция
1. Нуль функции – это такое значение довода х, при котором значение функции равно нулю. Впрочем нулями могут быть лишь те доводы, которые входят в область определения исследуемой функции. То есть в такое уйма значений, для которых функция f(x) имеет толк. 2. Запишите заданную функцию и приравняйте ее к нулю, скажем f(x) = 2х?+5х+2 = 0. Решите получившееся уравнение и обнаружьте его действительные корни. Корни квадратного уравнения вычисляются с поддержкой нахождения дискриминанта. 2х?+5х+2 = 0;D = b?-4ac = 5?-4*2*2 = 9;х1 = (-b+?D)/2*а = (-5+3)/2*2 = -0,5;х2 = (-b-?D)/2*а = (-5-3)/2*2 = -2.Таким образом, в данном случае получены два корня квадратного уравнения, соответствующих доводам начальной функции f(x). 3. Все обнаруженные значения х проверьте на принадлежность к области определения заданной функции. Обнаружьте ООФ, для этого проверьте начальное выражение на наличие корней четной степени вида ?f (х), на присутствие дробей в функции с доводом в знаменателе, на наличие логарифмических либо тригонометрических выражений.
Примером этому может служить уравнение окружности.Нулями функции называются значение абсциссы, при котором значение функции равно нулю.
Если функция задана своим уравнением, то нулями функции будут решения уравнения . Если задан график функции , то нули функции — это значения , в которых график пересекает ось абсцисс.
Примеры нахождения нулей функции
ПРИМЕР 1
| Задание | Найти нули функции, график которой изображен на рисунке 1. Рис. 1
|
| Решение | Нули функции — это значения , в которых график пересекает ось абсцисс. График заданной функции пересекает ось при . |
| Ответ |
Как найти нули многочлена?
Нули полинома – это точки, в которых полином равен нулю. Здесь вы научитесь находить нули многочлена.
Нули полинома также известны как корни уравнения и часто обозначаются символами \(α\), \(β\) и \(γ\) соответственно.
Некоторые из методов, используемых для нахождения полиномиальных нулей, включают группировку, факторизацию и использование алгебраических выражений.
Пошаговое руководство по нулям многочлена
Нули многочлена — это значения \(x\), которые удовлетворяют уравнению \(y = f(x)\). Где \(f(x)\) — функция \(x\), а нули полинома — значения \(x\), для которых значение \(y\) равно нулю. Количество нулей полинома зависит от степени уравнения \(y = f (x)\). Все такие значения области определения функции, область значений которых равна нулю, называются нулями полинома.
Примечание: Графически нули многочлена представляют собой точки, в которых график \(y = f(x)\) пересекает ось \(x\).
Как найти нули многочлена?Существуют следующие типы уравнений и методы нахождения их полиномиальных нулей:
Линейное уравнение:
Линейное уравнение имеет вид \(y=ax+b\). Ноль этого уравнения можно вычислить, подставив \(y = 0\), и при упрощении мы получим \(ax+b=0\) или \(x=-\frac{b}{a}\).
Квадратное уравнение:
Существует два способа факторизации квадратного уравнения: 92+cx+d\) можно разложить на множители, применяя теорему об остатках. Согласно теореме об остатках, мы можем подставить любое меньшее значение для переменной \(x = α\), и если значение y достигает нуля, \(y = 0\), то \((x — α)\) равно один корень уравнения. Кроме того, мы можем разделить кубическое уравнение на \((x – α)\), используя деление в длину, чтобы получить квадратное уравнение. Наконец, квадратное уравнение можно решить факторизацией или методом формул, чтобы получить два требуемых корня уравнения.
9n-2+…px+q\). Эти многочлены более высокой степени можно разложить на множители, используя оставшуюся теорему, чтобы получить квадратное уравнение. И квадратное уравнение можно разложить на множители, чтобы получить два необходимых окончательных множителя.Представление нулей полинома на графике
Полиномиальное выражение в виде \(y = f (x)\) может быть представлено на графике по оси координат.
Значение \(x\) отображается на оси \(x\), а значение \(f(x)\) или значение \(y\) отображается на \(y\)- ось. Полиномиальное выражение может быть линейным выражением, квадратным выражением, кубическим выражением, основанным на степени полинома. Линейное выражение представляет собой линию, квадратное уравнение представляет собой кривую, а полином более высокой степени представляет собой кривую с неровными изгибами. 92-32x}\)
- \(\color{blue}{x=3 , x=\frac{1}{3}}\)
- \(\color{blue}{x=5}\ )
- \(\color{синий}{x=-2, x=-5, x=5}\)
- \(\color{синий}{x=0, x=-2, x=-4 , x=4}\)
3.4: Графики полиномиальных функций
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 34892
Цели обучения
- Определение нулей и их кратностей.
- Используйте факторинг для нахождения нулей полиномиальных функций.
- Поймите взаимосвязь между степенью и точками поворота.
- Граф полиномиальных функций.
Мы уже исследовали локальное поведение (расположение \(x\)- и \(y\)-перехватов) для квадратичных уравнений, частного случая многочленов. В этом разделе мы исследуем локальное поведение многочленов в целом. 93 \nonumber\]
Примечание на рисунке справа показывает, что поведение этой функции на каждом из \(x\)-отрезков отличается.
Пересечение \(x\) −3 является решением уравнения \((x+3)=0\). Граф проходит непосредственно через точку пересечения \(x\) в точке \(x=−3\). Фактор является линейным (имеет степень 1), поэтому поведение вблизи точки пересечения похоже на поведение прямой — она проходит непосредственно через точку пересечения. Мы называем это одиночным нулем, потому что ноль соответствует одному фактору функции. 9p\), поведение вблизи \(x\)-перехвата определяется степенью \(p\).
Мы говорим, что \(x=h\) есть нуль кратности \(p\).
- График полиномиальной функции будет касаться оси \(x\) в нулях с четными кратностями.
- График пересечет ось \(x\) в нулях с нечетной кратностью.
- Чем выше кратность, тем более пологая кривая у нуля.
- Сумма кратностей есть степень полиномиальной функции.
Для нулей с четной кратностью графики касаются или касаются оси \(x\). Для нулей с нечетной кратностью графики пересекают или пересекают ось \(x\). На рисунке ниже приведены примеры графиков полиномиальных функций с кратностью нуля 1, 2 и 3. Графики ясно показывают, что чем выше кратность, тем более плоский график у нуля.
Для более высоких четных степеней, таких как 4, 6 и 8, график по-прежнему будет касаться и отскакивать от горизонтальной оси, но для каждого увеличения четной степени график будет казаться более плоским по мере приближения и выхода из \ (х\)-ось.
Для более высоких нечетных степеней, таких как 5, 7 и 9, график по-прежнему будет пересекать горизонтальную ось, но с каждым увеличением нечетной степени график будет казаться более плоским по мере приближения и удаления от оси \(x\).
Как: Имея график полиномиальной функции, определить нули и их кратности
- Если график пересекает ось \(x\) в нуле, это ноль с нечетной кратностью.
- Если график касается и отскакивает от оси \(x\), это нуль с четной кратностью.
- Чем выше кратность нуля, тем более плоским становится график у нуля.
Пример \(\PageIndex{1}\): поиск нулей и их кратностей на графике
Используйте график функции степени 6 на рисунке ниже , чтобы определить нули функции и их возможные кратности.
| График полиномиальной функции степени 6. | Раствор Начиная слева, первый нуль находится в точке \(x=−3\).
Следующий ноль находится в точке \(x=−1\). В этот момент график выглядит почти линейным. Это один ноль кратности 1.
Последний нуль находится в точке \(x=4\). График пересекает ось \(x\), поэтому кратность нуля должна быть нечетной. Поскольку вокруг этого нуля график плоский, кратность, скорее всего, равна 3 (а не 1).
Полиномиальная функция имеет степень \(6\), поэтому сумма кратностей должна быть не меньше \(2+1+3\) или \(6\). |
Попробуйте \(\PageIndex{2}\)
Используйте график функции на рисунке ниже , чтобы определить нули функции и их возможные кратности.
График полиномиальной функции.
- Ответить
Ноль в -5 нечетный.
Поскольку кривая при -5 несколько плоская, кратность нуля, скорее всего, равна 3, а не 1.
Ноль при -1 имеет четную кратность 2.
Ноль при 3 имеет четную кратность. Поскольку кривая более пологая при 3, чем при -1, ноль, скорее всего, имеет кратность 4, а не 2.
Поскольку кривая при -5 несколько плоская, кратность нуля, скорее всего, равна 3, а не 1. Нахождение нулей и их кратностей из полиномиального уравнения
Напомним, что если \(f\) является полиномиальной функцией, значения \(x\), для которых \(f(x)=0\), называются 92+bx+c).\) Когда неприводимые квадратичные множители обнуляются и решаются относительно \(x\), получаются мнимые решения. Запишите каждый повторяющийся множитель в экспоненциальной форме.
92-7)\) при установке в ноль дает два иррациональных решения, \(x= \pm \sqrt{7}\)Теперь нам нужно подсчитать количество вхождений каждого нуля, тем самым определив кратность каждого действительного числа ноль.
- Решение \(x= 0\) встречается \(3\) раз, поэтому ноль \(0\) имеет кратность \(3\) или нечетную кратность.
- Решение \(x= 3\) встречается \(2\) раз, поэтому ноль \(3\) имеет кратность \(2\) или даже кратность.
- Решения действительных чисел \(x= -2\), \(x= \sqrt{7}\) и \(x= -\sqrt{7}\) встречаются \(1\) раз , поэтому эти нули имеют кратность \(1\) или нечетная кратность. 92+х\).
- Ответить
Нули \(-1\) и \(0\) имеют нечетную кратность \(1\). Ноль \(1\) имеет четную кратность \(2\)
График полиномиальных функций
Мы можем использовать то, что мы узнали о кратностях, поведении концов и точках пересечения, для построения графиков полиномиальных функций.
Давайте соберем все это вместе и посмотрим на шаги, необходимые для построения графика полиномиальных функций.Как: по заданной полиномиальной функции нарисовать график
- Определите конечное поведение, изучив ведущий член.
- Найдите точки пересечения и используйте кратность нулей, чтобы определить поведение многочлена на точках пересечения \(x\).
- Используйте конечное поведение и поведение на точках пересечения, чтобы нарисовать график.
- Опционально…
- Проверить симметрию. Если функция четная, ее график симметричен относительно оси \(y\), то есть \(f(−x)=f(x)\). Если функция является нечетной функцией, ее график симметричен относительно начала координат, то есть \(f(-x)=-f(x)\). 93\), так что конечным результатом является поведение вертикально отраженного кубика, при этом график падает вправо и движется в противоположном направлении (вверх) влево: \(\nwarrow \dots \searrow \) См. рисунок \ (\PageIndex{5a}\).
Рисунок \(\PageIndex{5a}\): Иллюстрация конечного поведения многочлена.
Шаг 2.
Этот граф имеет два \(x\)-перехвата. В точке \(x=−3\) множитель возводится в квадрат, что указывает на кратность 2. График будет отскакивать от точки пересечения \(x\). В точке \(x=5\) функция имеет кратность, равную единице, что указывает на то, что график пересечет ось на этом пересечении.
Перехват \(y\) находится путем вычисления \(f(0)\).
Рисунок \(\PageIndex{5b}\): график пересекается в точке пересечения \(x\) \((5, 0)\) и отскакивает в точке \((-3, 0)\). \(y\)-перехват равен \((0, 90)\).
Шаг 3. Соедините конечные линии поведения с точками пересечения.
92&=2 \\ x&=0, \:x=0 &&& x&={\pm}1 &&& x&={\pm}\sqrt{2} \end{align*}\] .
Это дает нам пять \(x\)-отрезков: \( (0,0)\), \((1,0)\), \((−1,0)\), \((\sqrt {2},0)\) и \((−\sqrt{2},0)\).
\(x\)-отрезки \((1,0)\), \((−1,0)\), \((\sqrt{2},0)\) и \((−\ sqrt{2},0)\) имеют нечетную кратность 1, поэтому график будет пересекать ось \(x\) в этих точках пересечения.
\(x\)-пересечение \((0,0)\) имеет четную кратность 2, поэтому график останется на той же стороне оси \(x\) в точке 2. (Говорят, что график касаться оси x в точке 2 или «отскакивать» от оси \(x\) в точке 2). 92+5=0 \\
x=3 & \text{or} & x=−3 &\text{or} &\text{(нет действительного решения)}
\end{массив} \)(x\)-отрезки \((3,0)\) и \((–3,0)\) имеют нечетную кратность 1, поэтому график будет пересекать ось \(x\) в этих точках пересечения.
Шаг 3. Многочлен является четной функцией, поскольку \(f(-x)=f(x)\), поэтому график симметричен относительно оси y. График появится ниже.
Мнимые нули не являются \(x\)-отрезками, но приведенный ниже график показывает, что они вносят свой вклад в «покачивания» (точки усечения) на графике функции. 93(х+3)(х+2)\)Поворотные точки
Определение: Поворотные точки
Поворотная точка — это точка графика, в которой график меняется от возрастания к убывающему (от подъема к падению) или от убывания к возрастанию (от падения к росту).
Многочлен степени \(n\) будет иметь не более \(n\) \(x\)-пересечений и \(n−1\) точек поворота.
Степень полиномиальной функции помогает нам определить количество \(x\)-перехватов и количество точек поворота. Полиномиальная функция от \(n\) 93\)
- Ответ
Имеется не более 12 \(x\)-перехватов и не более 11 поворотных точек.
Пример \(\PageIndex{12}\): получение выводов о полиномиальной функции на основе факторов
Учитывая функцию \(f(x)=−4x(x+3)(x−4)\), определить \(y\)-перехват и количество, расположение и кратность \(x\)-перехватов, и максимальное количество точек поворота.
Раствор
Перехват \(y\) находится путем вычисления \(f(0)\).
\[\begin{align*} f(0)&=−4(0)(0+3)(0−4)=0 \end{align*}\]
\(y\)- перехват равен \((0,0)\).
\(x\)-перехваты находятся путем нахождения нулей функции.
\( \begin{array}{ccc}
&0=-4x(x+3)(x-4) \\
x=0 & \text{или} \quad x+3=0 \quad\text {or} & x-4=0 \\
x=0 & \text{or} \quad x=−3 \quad\text{or} & x=4
\end{массив} \)Три \(x\)-перехваты \((0,0)\),\((–3,0)\) и \((4,0)\) имеют нечетную кратность 1,
Степень равна 3, поэтому граф имеет не более 2 поворотных точек.
Попробуйте \(\PageIndex{13}\)
Учитывая функцию \(f(x)=0,2(x−2)(x+1)(x−5)\), определите локальное поведение.
- Ответить
Функция представляет собой многочлен 3-й степени с тремя точками пересечения \(x\) \((2,0)\), \((−1,0)\) и \((5,0)\), все из которых имеют кратность 1, \(y\)-отрезок равен \((0,2)\), а граф имеет не более 2 точек поворота.
Пример \(\PageIndex{14}\): вывод полиномиальной функции из графика
Какой вывод мы можем сделать о степени полинома и старшем коэффициенте, представленном на графике, показанном ниже, на основе его пересечений и точек поворота?
График многочлена.Раствор
- Поведение графика на конце говорит нам о том, что это график полинома четной степени (концы идут в одном направлении) с положительным старшим коэффициентом (растет вправо).
- Граф имеет 2 \(x\)-перехвата, каждый с нечетной кратностью, что предполагает степень 2 или выше.
- На графике есть 3 поворотные точки, что предполагает степень 4 или выше.
Вывод: степень многочлена четная и не меньше 4.
Попробуйте \(\PageIndex{15}\)
Какой вывод мы можем сделать о полиноме, представленном на графике, показанном ниже, на основе его точек пересечения и точек поворота?
Полиномиальная функция
- Ответ
Поведение в конце указывает на полиномиальную функцию нечетной степени (заканчивается в противоположном направлении) с отрицательным старшим коэффициентом (падает вправо).
Имеется 3 \(x\)-перехвата с нечетной кратностью и 2 точки поворота, поэтому степень нечетна и не меньше 3.
Напишите формулу для многочлена, учитывая его график
Теперь, когда мы знаем, как находить нули полиномиальных функций, мы можем использовать их для написания формул на основе графиков. Поскольку полиномиальная функция , записанная в факторизованной форме, будет иметь отрезок \(x\), где каждый множитель равен нулю, мы можем сформировать функцию, которая будет проходить через множество отрезков \(x\), введя соответствующий набор факторов.
Примечание: факторизованная форма полиномов 9{p_n}\), где степени \(p_i\) каждого фактора могут быть определены поведением графика на соответствующем пересечении, а коэффициент растяжения \(a\) может быть определен при заданном значении функции, отличном от \(x\)-перехват.
Как: Имея график полиномиальной функции, напишите формулу для этой функции.
- Определите точки пересечения \(x\) на графике, чтобы найти множители многочлена.
- Изучите поведение графика на пересечениях \(x\), чтобы определить кратность каждого фактора.
- Найдите полином наименьшей степени, содержащий все множители, найденные на предыдущем шаге.
- Используйте любую другую точку на графике (может быть, проще всего пересечь \(y\)), чтобы определить коэффициент растяжения.
Пример \(\PageIndex{16}\): запись формулы для полиномиальной функции на основе графика
Постройте факторизованную форму возможного уравнения для каждого приведенного ниже графика.
(а) Рисунок \(\PageIndex{16a}\): График \(h(x)\). Раствор
Глядя на график этой функции, как показано на рисунке \(\PageIndex{16}\), видно, что есть \(x\)-перехваты в точках \(x=−3,−2, \text{ и }1\).
Каждый отрезок \(x\) соответствует нулю полиномиальной функции, а каждый нуль дает множитель, так что теперь мы можем записать полином в факторизованной форме.
\(ч(х)=а(х+3)(х+2)(х-1) \)
Коэффициент растяжения \(a\) можно найти, используя другую точку на графике, например точку пересечения \(y\), \((0,-6)\).
\[\begin{align*} f(0)&=a(0+3)(0+2)(0−1) \\ −6&=a(-6) \\ a&=1 \end{align *}\]
Таким образом \( h(x)=(x+3)(x+2)(x−1). \)
(б)
Рисунок \(\PageIndex{16b}\).Решение 92 (х + 3)\)
Основные понятия
- Полиномиальные функции степени 2 и выше являются гладкими непрерывными функциями.
- Чтобы найти нули полиномиальной функции, если ее можно разложить на множители, разложите функцию на множители и приравняйте каждый множитель к нулю.
- Другой способ найти точку пересечения \(x\) полиномиальной функции состоит в том, чтобы построить график функции и определить точки, в которых график пересекает ось \(x\).
- Проверить симметрию. Если функция четная, ее график симметричен относительно оси \(y\), то есть \(f(−x)=f(x)\). Если функция является нечетной функцией, ее график симметричен относительно начала координат, то есть \(f(-x)=-f(x)\). 93\), так что конечным результатом является поведение вертикально отраженного кубика, при этом график падает вправо и движется в противоположном направлении (вверх) влево: \(\nwarrow \dots \searrow \) См. рисунок \ (\PageIndex{5a}\).
Давайте соберем все это вместе и посмотрим на шаги, необходимые для построения графика полиномиальных функций.
Мнимые нули не являются \(x\)-отрезками, но приведенный ниже график показывает, что они вносят свой вклад в «покачивания» (точки усечения) на графике функции. 93(х+3)(х+2)\)
Имеется 3 \(x\)-перехвата с нечетной кратностью и 2 точки поворота, поэтому степень нечетна и не меньше 3.
