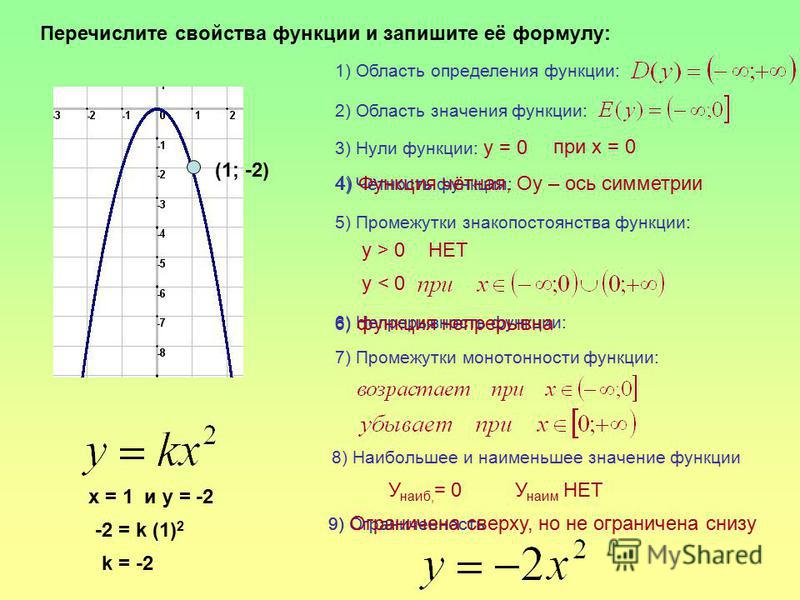
Урок 10. Нахождение области определения и области значения функции с помощью графика
Если функция задана графически, то для нахождения области определения её график надо спроектировать на ось Ох. А если график функции спроектировать на ось Оу, получим область изменения (значения) функции.
Нахождение области значений функции по её графику.
Постройте график функции. Во многих случаях проще найти область значений функции, построив её график.
Областью значений многих квадратичных функций является
(–∞, 0] или [0, ∞),
так как вершина
параболы, направленной вправо или влево, лежит на оси Х. В этом случае область значений включает все
положительные значения у,
если парабола возрастает, или все отрицательные значения у, если парабола убывает.
Вершины графиков некоторых функций лежат выше или ниже оси
ПРИМЕР:
Если координата у вершины параболы равна –4, а парабола возрастает, то область значений равна
[–4, ∞).
Построив график функции, вы увидите на нём точку, в которой функция имеет минимальное значение. Если наглядного минимума нет, он не существует, а график функции уходит в бесконечность.
Построив график функции, вы увидите на нём точку, в которой функция имеет максимальное значение. Если наглядного максимума нет, он не существует, а график функции уходит в бесконечность.
Самый простой
способ построить график функции – это воспользоваться графическим калькулятором
или специальным программным обеспечением.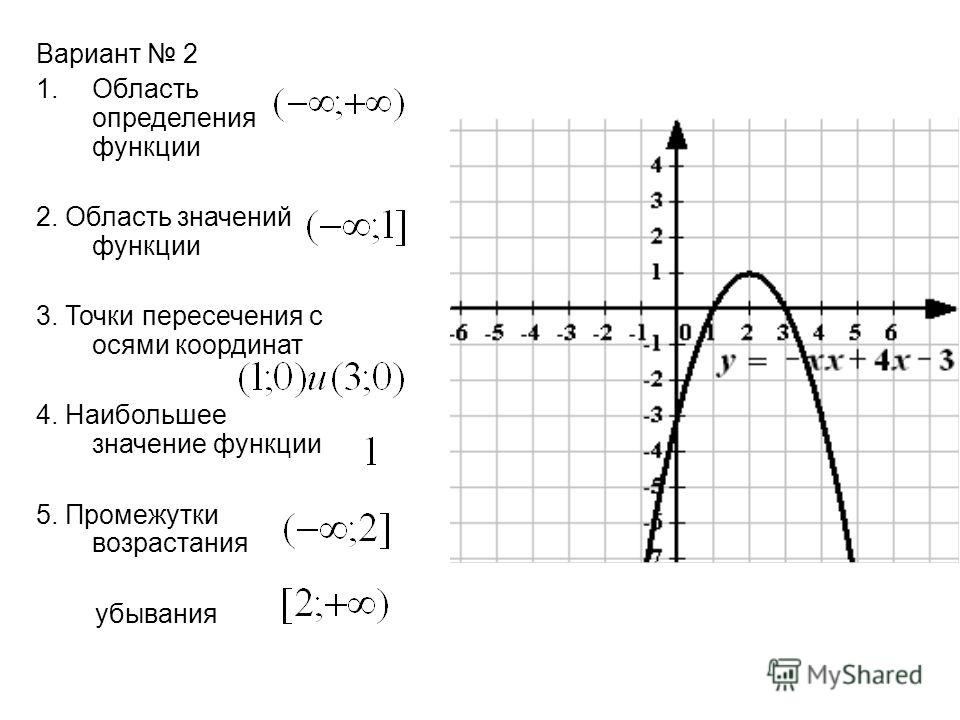
ПРИМЕР:
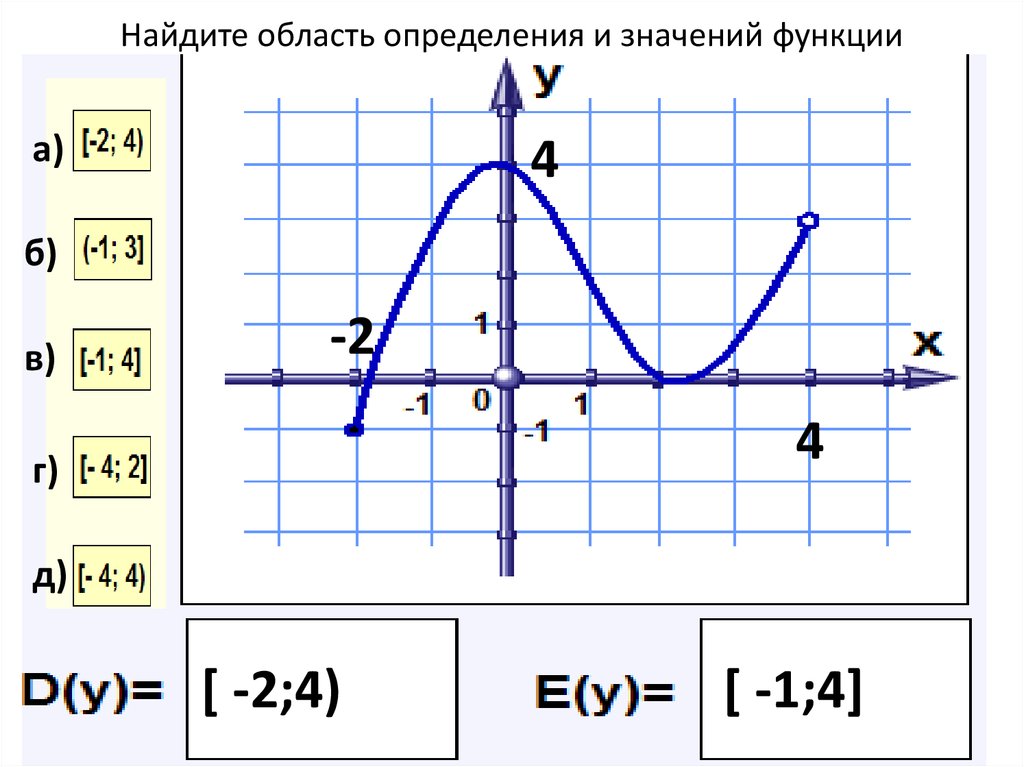
Найдите область определения и область значения функции по графику.
РЕШЕНИЕ:
Из графика видно, что функция стремится в бесконечность и вправо и влево вдоль оси х, не пересекая её (на графике белая точка), а также пересекает ось у в точке у = 9 (на графике тёмная точка), значит область определения будет
(–∞, –∞).
(0, 9].
Ноль не входит в область значений, а девять входит.
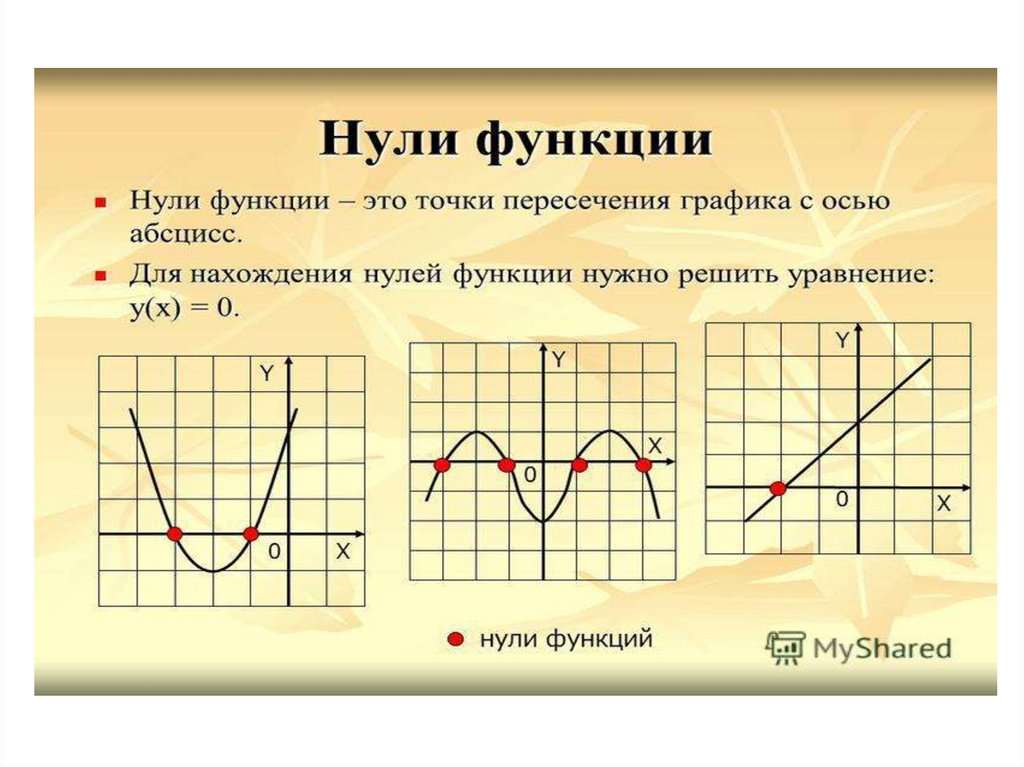
алгоритм нахождения области значения функции
Что такое функции, области определения и значений функции
Определение 1Функция — вид зависимости, при котором каждому элементу одного множества ставится в соответствие элемент другого множества.
В общем виде функцию в алгебре обозначают как y=f(x). Переменную x называют независимой переменной или аргументом функции, переменную y — зависимой переменной или значением функции.
Основными характеристиками функции являются:
- область определения;
- область значений.
Область определения — множество значений, которые может принимать аргумент функции, то есть переменная x. Область определения иногда называют областью допустимых значений. Обозначение области допустимых значений функции f: D (f).
Также область определения можно трактовать как проекцию графика функции на ось абсцисс.
Областью значений называется множество всех значений функции (переменной y), полученных при переборе всех значений переменной x из области определения. Принято следующее обозначение области значений: E (f).
В графическом изображении область значений — проекция графика функции на ось ординат.
Нахождение области значений осуществляется одним из следующих способов:
- графически;
- аналитически (по уравнению).
Способы нахождения области значений некоторых функций по графику
Чаще всего графический способ используют для функций с достаточно простой зависимостью. В этом случае построение графика не вызывает трудностей.
Приведем алгоритм нахождения области значений функции по графику:
- Ищем область определения функции. Например, у показательной функции или параболы аргумент может принимать любое значение из множества действительных чисел R, то есть E(f)=R. Если выражение f(x) является дробным, область определения находится из условия неравенства нулю знаменателя.
 Если выражение f(x) находится под квадратным корнем, область определения можно узнать из неравенства f(x)≥0.
Если выражение f(x) находится под квадратным корнем, область определения можно узнать из неравенства f(x)≥0. - Строим график функции по точкам.
- По графику функции находим ее минимум. Значение y_{min} будет являться нижней границей области значений. В том случае, когда минимум невозможно определить визуально, то есть функция не имеет минимума, границей будет -∞.
- Аналогично определяем максимум y_{max} и, соответственно, верхнюю границу области значений. Если максимум не определяется, границей области значения является +∞.
- Записываем область значений функции, при этом необходимо учесть точки разрыва, если они есть. Точки разрыва возникают, например, при исключении из области определения таких значений аргументов, при которых знаменатель обращается в ноль. Область значений записывают в виде числового промежутка. Границы, входящие в область, заключают в квадратные скобки, не входящие — в круглые. Если область значений включает в себя несколько числовых промежутков, их объединяют знаком «U», например: (-∞; 4]U[6; +∞).

Как найти область значений функции по уравнению
Нахождение области значений функции по заданному уравнению также сводится к вычислению экстремумов.
Рассмотрим два случая:
- Нахождение области значений функции, непрерывной на некотором заданном отрезке.
- Нахождение области значений функции, непрерывной на некотором интервале. Сюда же отнесем случаи, когда функция не существует в какой-либо точке. Например, точка нуля знаменателя, в которой функция не существует, а область определения терпит разрыв.
Алгоритм поиска области значений для первого случая:
- Находим производную функции.
- Приравниваем производную к нулю, находим корни уравнения f′(x)=0 и точки, в которых производная не существует — критические точки.
- Отмечаем корни, критические точки и границы заданного интервала на прямой и определяем знаки производной на каждом получившемся промежутке.
- Находим минимумы и максимумы функции. Если в некоторой точке x1 производная меняет знак с «+» на «-», то точка x1 — максимум, если с «-» на «+» — минимум.

- Подставляя значения аргументов для минимума и максимума функции в выражение f(x), находим минимальное и максимальное значения функции. В том случае, если имеются точки, в которых производная не существует, значение функции вычисляем через пределы по формулам: limx→x1-0f(x) и limx→x1+0f(x).
- Записываем область значений функции.
Для второго случая:
- Находим производную, приравниваем ее к нулю и определяем знаки производной на каждом промежутке.
- Определяем значение функции в каждой из точек. Для определения значения функции в граничных точках, а также в точках разрыва или точках, в которых производная не существует, вычисляем пределы функции аналогично указанным в пункте 5 для первого случая.
- Определяем и записываем область значений.
Примеры решений
Рассмотрим несколько примеров на нахождение области значений функции и приведем их решения.
Задача 1Найти область значений функции y=x по графику.
Решение:
Найдем область определения функции. Выражение под знаком квадратного корня всегда положительно, то есть x≥0, и область определения D(f(x))=[0; +∞). Теперь построим график функции.
Выражение под знаком квадратного корня всегда положительно, то есть x≥0, и область определения D(f(x))=[0; +∞). Теперь построим график функции.
Из графика видно, что минимальное значение переменная y принимает при x=0. Максимальное значение не определяется, при этом видно, что при возрастании x значении y также растет. Получили, что ymin=0, а область значений E(f(x))=[0; +∞).
Ответ: E(f(x))=[0; +∞).
Задача 2Найти область значений функции y=4xx2+2 на отрезке [-2; 2].
Решение:
Найдем область определения функции. Функция представляет собой дробь, однако, ее знаменатель не будет равен нулю при любых значениях x. Действительно, квадрат любого числа есть положительное число, получили в знаменателе сумму положительных чисел. Тогда D=R, где R — множество действительных чисел.
Найдем производную функции: y'(x)=4xx2+2’=4(2-x2)(x2+2)2.
Приравняем числитель производной к нулю и найдем корни получившегося уравнения: 8-4×2=0;x1=-2иx2=2.
Отметим корни на координатной оси и, поочередно подставляя значения x=-4,-2,2,4, определим знаки производной на каждом промежутке.
Из рисунка видно, что функция имеет один минимум и максимум. Вычислим значения ymin и ymax:
ymin=y(-2)=4·(-2)(-2)2+2=-2;
ymax=y(2)=4·(2)(2)2+2=2.
Экстремумы функции входят в заданный интервал и не являются точками разрыва области определения функции, то есть минимальные и максимальные значения должны быть включены в область значений.
Ответ:E(f(x))=[-2;2].
Задача 3Найти область значений функции y=5x+1 на области действительных чисел.
Решение:
Найдем область определения функции. Знаменатель не может быть равным нулю, значит, D(f(x))=(-∞; -1)U(-1;+∞).
Найдем производную: y'(x)=-5(x+1)2.
Получили, что производная не равна нулю при любых x. При x=-1 знаменатель производной обращается в ноль, то есть в данной точке производная не существует.
Отметим точку x=-1 и рассмотрим два промежутка: (-∞;-1) и (-1;+∞).
Определим знаки производной на каждом промежутке.
Из рисунка видно, что функция убывает на обоих интервалах и не имеет максимума или минимума.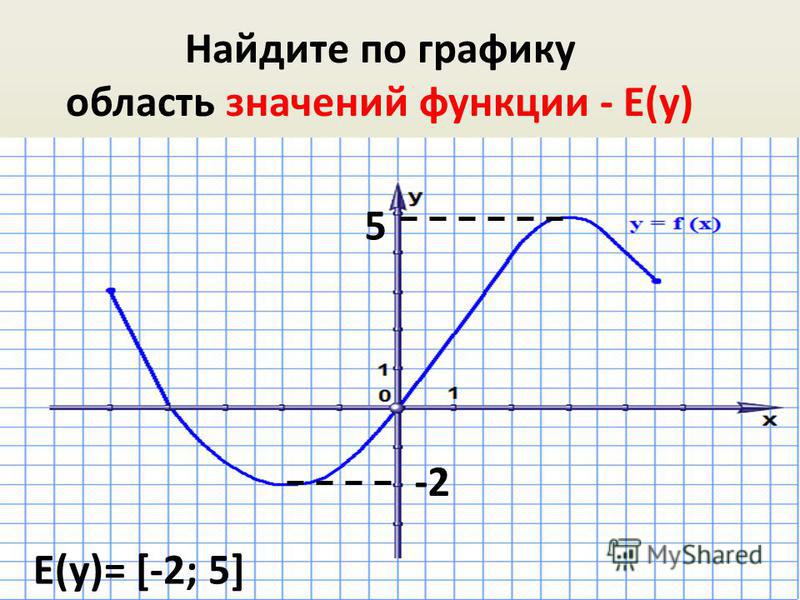
Теперь определим значение функции в точке x=-1, для чего вычислим пределы функции при x→-1-0 и x→-1+0.
limx→(-1-0)5x+1=5-1-0+1=5-0=-∞;
limx→(-1+0)5x+1=5-1+0+1=5+0=+∞.
Итак, точка x=-1 — это точка разрыва второго рода.
Значение функции на границах заданного интервала -∞ и +∞ также вычисляется с помощью пределов:
limx→-∞5x+1=5-∞+1=0;
limx→+∞5x+1=5+∞+1=0.
Данная функция является гиперболой с асимптотами x=-1 и y=0.
Область значений E(f(x))=(-∞; 0)U(0;+∞).
Ответ: E(f(x))=(-∞; 0)U(0;+∞).
Домен и диапазон — из графика
Функции в математике можно сравнить с работой автомата по продаже газированных напитков. Когда вы вкладываете определенную сумму денег, вы можете выбрать разные типы газированных напитков. Точно так же для функций мы вводим разные числа и в результате получаем новые числа. Домен и диапазон являются основными аспектами функций.
- Вы можете использовать четвертаки и однодолларовые купюры, чтобы купить содовую.
 Машина не даст вам никакого вкуса газировки, если вы введете пенни. Следовательно, домен представляет входные данные, которые мы можем здесь иметь, то есть монеты в четвертаке и однодолларовые купюры.
Машина не даст вам никакого вкуса газировки, если вы введете пенни. Следовательно, домен представляет входные данные, которые мы можем здесь иметь, то есть монеты в четвертаке и однодолларовые купюры. - Сколько бы вы ни заплатили, вы не получите чизбургер из автомата с газировкой. Таким образом, диапазон — это возможные выходы, которые мы можем здесь получить, то есть вкус газированных напитков в машине.
Давайте научимся находить область определения и область значений функции, а также отображать их.
| 1. | Что такое домен и диапазон? |
| 2. | Домен и диапазон функции |
| 3. | Домен функции |
| 4. | Диапазон функции |
| 5. | Как рассчитать домен и диапазон? |
| 6. | Домен и диапазон экспоненциальных функций |
| 7. | Область и диапазон тригонометрических функций |
8. | Домен и диапазон функции абсолютного значения |
| 9. | Домен и диапазон функции квадратного корня |
| 10. | Домен и диапазон из графика |
| 11. | Часто задаваемые вопросы о домене и диапазоне |
Что такое домен и диапазон?
Домен и диапазон отношения представляют собой наборы всех координат x и всех координат y упорядоченных пар соответственно. Например, если соотношение R = {(1, 2), (2, 2), (3, 3), (4, 3)}, то:
- Домен = набор всех x-координат = {1, 2, 3, 4}
- Диапазон = набор всех координат y = {2, 3}
Мы можем визуализировать это здесь:
Концепция домена и диапазона дополнительно реализована и для функций.
Домен и диапазон функции
Домен и диапазон функции являются компонентами функции. Домен — это набор всех входных значений функции, а диапазон — это возможный результат, заданный функцией.
Область определения и область значений этой функции f(x) = 2x задаются как область определения D = {x ∈ N}, область значений R = {y ∈ N: y = 2x}
Домен функции
Домен функции относится ко «всем значениям», которые могут быть введены в функцию без получения неопределенных значений. т. е. предметная область в математике — это набор всех возможных входных данных для функции. Рассмотрим приведенный выше блок как функцию f(x) = 2x
 При вводе значений x = {1,2,3,4,…} область определения представляет собой просто набор натуральных чисел. Но в общем случае (если область определения не указана как натуральные числа), f (x) = 2x определено для всех действительных значений x, и, следовательно, его областью определения является множество всех действительных чисел, которое обозначается (-∞, ∞) . Вот общие формулы, используемые для нахождения области определения различных типов функций. Здесь R — множество всех действительных чисел.
При вводе значений x = {1,2,3,4,…} область определения представляет собой просто набор натуральных чисел. Но в общем случае (если область определения не указана как натуральные числа), f (x) = 2x определено для всех действительных значений x, и, следовательно, его областью определения является множество всех действительных чисел, которое обозначается (-∞, ∞) . Вот общие формулы, используемые для нахождения области определения различных типов функций. Здесь R — множество всех действительных чисел.Правила нахождения области определения функции
- Область определения любой полиномиальной (линейной, квадратичной, кубической и т. д.) функции равна ℝ (все действительные числа).
- Область определения функции квадратного корня √x равна x ≥ 0.
- Область определения экспоненциальной функции ℝ.
- Область определения логарифмической функции x>0.
- Чтобы найти область определения рациональной функции y = f(x), установите знаменатель ≠ 0.

Как найти домен функции?
Чтобы найти область определения функции, мы просто применяем одно из вышеупомянутых правил определения области определения в зависимости от типа функции. Вот несколько примеров:
Пример 1: Чтобы найти область определения функции f(x) = √(x + 3), мы применяем упомянутое выше правило 2. Тогда получаем: x + 2 ≥ 0. Решая это неравенство, получаем x ≥ -2. Таким образом, область определения функции f(x) равна [-2, ∞).
Пример 2: Чтобы вычислить область определения функции g(x) = (2x + 1) / (x — 2), мы применяем упомянутое выше правило 5. Тогда мы получаем x — 2 ≠ 0. Решая это, мы получаем x ≠ 2. Таким образом, его областью определения является множество всех действительных чисел, кроме 2, которое в интервальной записи может быть записано как (-∞, 2) ∪ (2, ∞ ).
Диапазон функции
Диапазон функции — это набор всех ее выходов. Пример. Рассмотрим функцию f: A → B, где f(x) = 2x и каждое из A и B = {множество натуральных чисел}.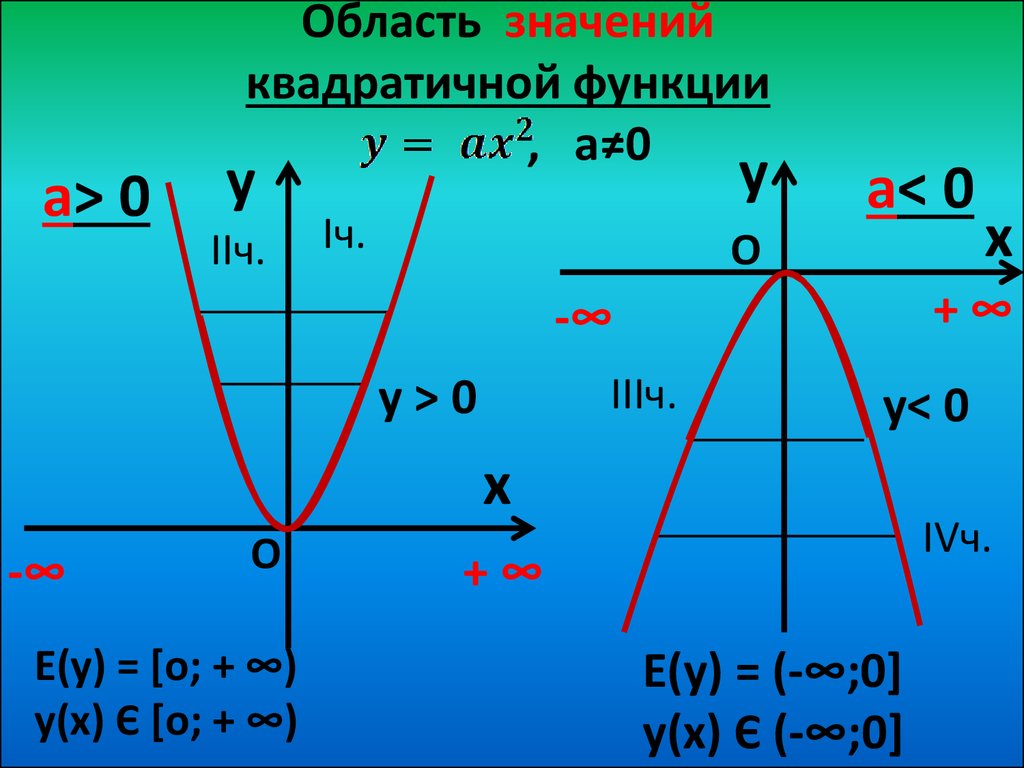 Здесь мы говорим, что А — домен, а В — содомен. Затем выход этой функции становится диапазоном. Диапазон = {множество четных натуральных чисел}. Элементы домена называются прообразами, а отображаемые элементы содомена называются изображениями. Здесь областью значений функции f является множество всех изображений элементов области (или) множество всех выходов функции.
Здесь мы говорим, что А — домен, а В — содомен. Затем выход этой функции становится диапазоном. Диапазон = {множество четных натуральных чисел}. Элементы домена называются прообразами, а отображаемые элементы содомена называются изображениями. Здесь областью значений функции f является множество всех изображений элементов области (или) множество всех выходов функции.
Правила нахождения диапазона функции
Лучший способ определить диапазон функции — построить ее график и посмотреть на значение y, которое охватывает график. Но вот общие правила, используемые для поиска диапазона некоторых популярных функций. Обратите внимание, что здесь ℝ представляет собой набор всех действительных чисел.
- Диапазон линейной функции ℝ.
- Диапазон квадратичной функции y = a(x — h) 2 + k равен:
y ≥ k, если a > 0 и
y ≤ k, если a < 0 - Диапазон функции извлечения квадратного корня: y ≥ 0.
- Диапазон экспоненциальной функции: y > 0.

- Диапазон логарифмической функции ℝ.
- Чтобы найти диапазон рациональной функции y = f(x), решите ее относительно x и установите знаменатель ≠ 0.
Как найти диапазон функции?
Если функция присутствует в одной из функций, упомянутых в приведенных выше правилах, мы можем сразу же применить правила и найти ее диапазон. В противном случае мы можем построить график и посмотреть на значения y, которые покрывает график, чтобы вычислить диапазон. Вот несколько примеров:
Пример 1: Чтобы вычислить диапазон функции f(x) = 2 (x — 3) 2 — 5, примените упомянутое выше правило 1. Тогда его диапазон равен y ≥ -5 (или) [-5, ∞).
Пример 2: Чтобы найти область значений функции g(x) = ln (2x — 3) + 4, мы применяем правило 4. Тогда мы получаем, что область значений представляет собой множество всех действительных чисел (ℝ) .
Как рассчитать домен и диапазон?
Предположим, X = {1, 2, 3, 4, 5} и Y = {1, 2, 3, 4, 5, 6}.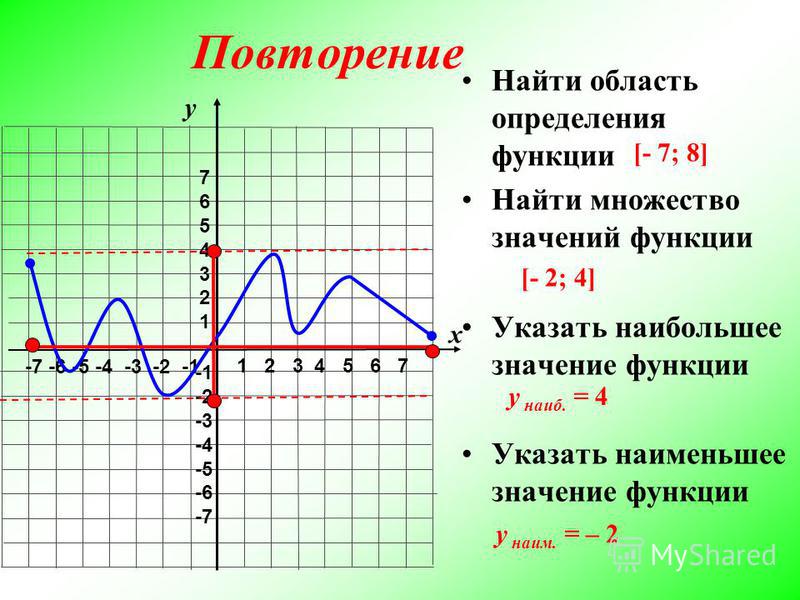 Рассмотрим функцию f: X → Y, где R = {(x,y) : y = x+1}.
Рассмотрим функцию f: X → Y, где R = {(x,y) : y = x+1}.
- Домен = входные значения. Таким образом, Домен = X = {1, 2, 3, 4, 5}
- Диапазон = выходные значения функции = {1 + 1, 2 + 1, 3 + 1, 4 + 1, 5 + 1} = {2, 3, 4, 5, 6}
Обратите внимание, что Y здесь кодовый домен, а НЕ диапазон.
Давайте разберемся в предметной области и диапазоне некоторых специальных функций, принимая во внимание различные типы функций.
Домен и диапазон экспоненциальных функций
Функция у = x , a ≥ 0 определяется для всех действительных чисел. Следовательно, областью определения экспоненциальной функции является вся вещественная прямая. Экспоненциальная функция всегда дает положительное значение. Таким образом, диапазон экспоненциальной функции имеет вид y= a x is {y ∈ ℝ: y > 0}. Следовательно, домен = ℝ, диапазон = (0, ∞)
Пример: Посмотрите на график этой функции f: 2 x
Обратите внимание, что значение функции ближе к 0, когда x стремится к ∞ но она никогда не достигнет значения 0.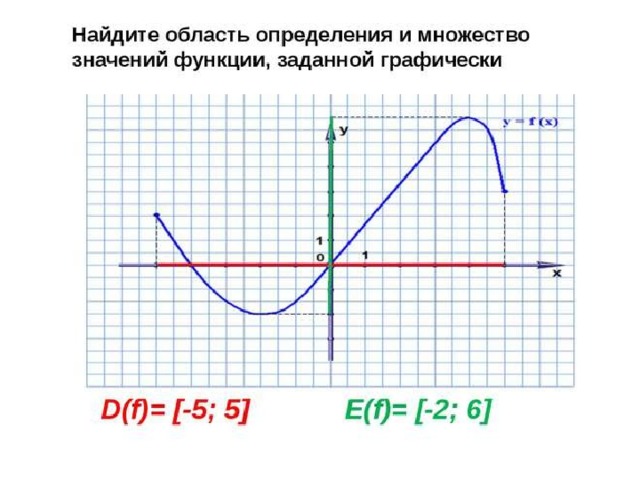 Область определения и диапазон экспоненциальных функций задаются следующим образом:
Область определения и диапазон экспоненциальных функций задаются следующим образом:
- Домен: Домен функции — множество ℝ.
- Диапазон: Экспоненциальная функция всегда приводит к положительным действительным значениям.
Область и диапазон тригонометрических функций
Посмотрите на график функций синуса и косинуса. Обратите внимание, что значение функций колеблется между -1 и 1 и определено для всех действительных чисел.
Таким образом, для каждой из функций синуса и косинуса:
- Домен: Областью определения функций является множество ℝ (или) (-∞, + ∞).
- Диапазон: Диапазон функций [-1, 1]
Область определения и диапазон всех тригонометрических функций показаны ниже:
| Тригонометрические функции | Домен | Диапазон |
|---|---|---|
| sin θ | (-∞, + ∞) | [-1, +1] |
| потому что θ | (-∞ +∞) | [-1, +1] |
| тан θ | ℝ — (2n + 1)π/2 | (-∞, +∞) |
| кроватка θ | ℝ — № | (-∞, +∞) |
| сек θ | ℝ — (2n + 1)π/2 | (-∞, -1] U [+1, +∞) |
| косек θ | ℝ — № | (-∞, -1] U [+1, +∞) |
Домен и диапазон функции абсолютного значения
Функция y = |ax + b| определено для всех действительных чисел.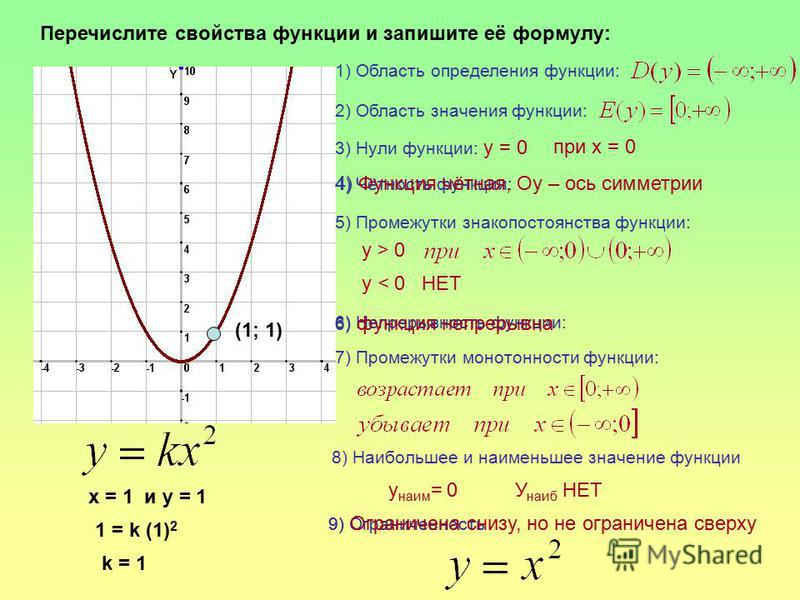 Итак, область определения функции абсолютного значения — это множество всех действительных чисел. Абсолютное значение числа всегда дает неотрицательное значение. Таким образом, диапазон функции абсолютного значения вида y= |ax+b| есть {y ∈ ℝ | у ≥ 0}. Область определения и диапазон функции абсолютного значения задаются следующим образом
Итак, область определения функции абсолютного значения — это множество всех действительных чисел. Абсолютное значение числа всегда дает неотрицательное значение. Таким образом, диапазон функции абсолютного значения вида y= |ax+b| есть {y ∈ ℝ | у ≥ 0}. Область определения и диапазон функции абсолютного значения задаются следующим образом
- Домен = ℝ
- Диапазон = [0, ∞)
Пример: Найдите область определения и область значений функции f(x) = |6 — x|.
- Домен: Домен функции — множество ℝ.
- Диапазон: Диапазон: [0, ∞)
Домен и диапазон функции квадратного корня
Функция квадратного корня имеет вид f(x) = √(ax+b). Мы знаем, что квадратный корень из отрицательного числа не определен. Таким образом, функция y= √(ax+b) определена только тогда, когда ax + b ≥ 0. Когда мы решим это для x, мы получим x ≥ -b/a.
Итак, область определения функции извлечения квадратного корня — это множество всех действительных чисел, больших или равных -b/a. Мы знаем, что квадратный корень всегда дает неотрицательное значение. Таким образом, областью действия функции квадратного корня является множество всех неотрицательных действительных чисел. Следовательно, область определения и область значений функции квадратного корня задаются следующим образом: Область определения = [-b/a, ∞), Область значений = [0, ∞)
Мы знаем, что квадратный корень всегда дает неотрицательное значение. Таким образом, областью действия функции квадратного корня является множество всех неотрицательных действительных чисел. Следовательно, область определения и область значений функции квадратного корня задаются следующим образом: Область определения = [-b/a, ∞), Область значений = [0, ∞)
Пример. Вычислите область определения и область значений функции h(x) = 2- √(-3x+2).
Домен: Функция извлечения квадратного корня определяется только тогда, когда значение внутри нее является неотрицательным числом. Итак, для домена
-3x+2 ≥ 0
-3x ≥ -2
x ≤ 2/3
Диапазон: Мы уже знаем, что функция квадратного корня всегда дает неотрицательное значение.
√(-3x+2) ≥ 0
Умножение -1 с обеих сторон
-√(-3x+2) ≤ 0
Добавление 2 с обеих сторон
2-√(-3x+2) ≤ 2
y≤ 2
Таким образом, область определения h(x) = (-∞, 2/3] и область значений h(x) = (-∞, 2].
Домен и диапазон из графика
Очень легко найти домен и диапазон графа. Набор значений x, покрываемых графиком, дает домен, а набор значений y, покрываемых графиком, дает диапазон. Но обратите внимание на следующие вещи, записывая домен и диапазон на графике.
- Посмотрите, проходит ли график тест вертикальной линии. В противном случае это не функция, и мы обычно не определяем область и диапазон для таких кривых.
- Если на графике есть какая-то дыра, то ее координаты не должны быть в домене и диапазоне.
- Если есть вертикальная асимптота, то соответствующего значения x не должно быть в области.
- Если есть горизонтальная асимптота, то соответствующее значение x не должно быть в диапазоне.
- Если граф разбит на части, то мы получаем несколько наборов/интервалов в домене и диапазоне и объединяем все такие наборы/интервалы символом «объединения» (∪).
- Если на конце кривой есть стрелка, то это означает, что кривая должна бесконечно продолжаться в этом конкретном направлении.

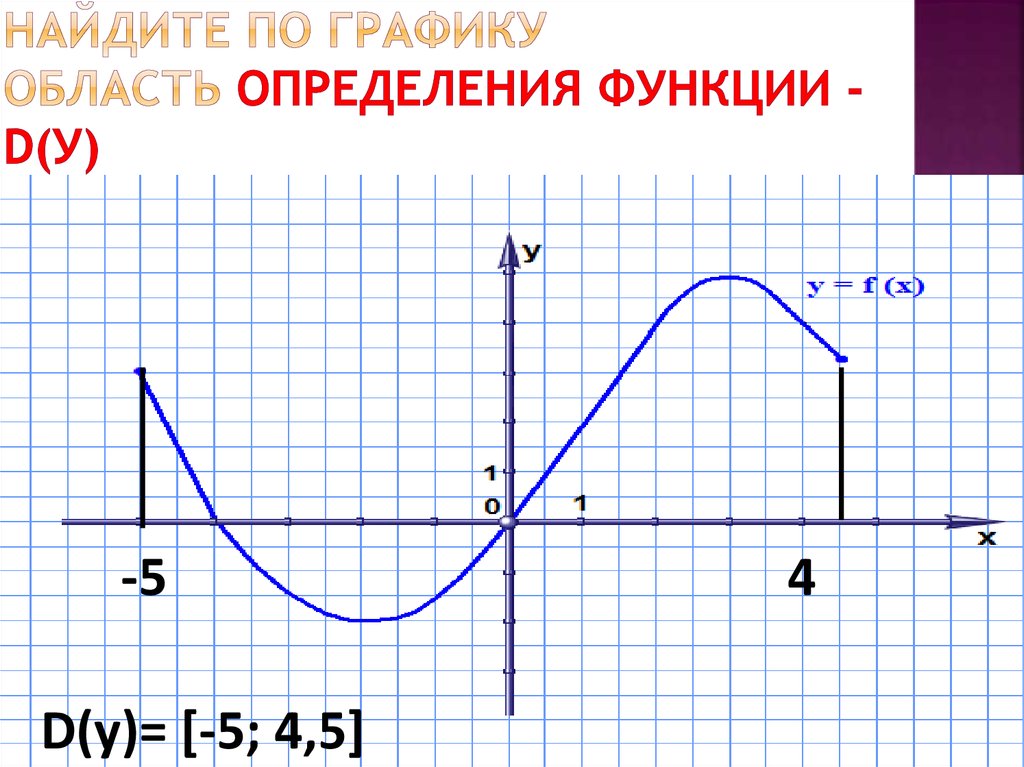
Пример 1:
Вот пример графика, и мы найдем домен и диапазон графика.
На приведенном выше графике:
- Все значения x от -∞ до ∞ покрываются графиком (из-за стрелок две кривые продолжаются бесконечно в заданных направлениях). Следовательно, область определения = (-∞, ∞).
- Все значения y, большие или равные или равные 0, покрываются графиком (см., что нет части кривой, которая находится ниже оси y). Следовательно, диапазон = [0, ∞).
Пример 2: Используя тот же процесс, упомянутый выше, домен графика ниже [-5, ∞), а его диапазон от графика равен (-∞, 5].
Диапазон:
- Область определения и диапазон функции — это набор всех возможных входов и выходов функции соответственно.0006
- Чтобы найти область определения функции f(x), подумайте, для каких значений x она определена.
- Чтобы вычислить диапазон функции f(x), подумайте, какие значения y она будет давать.
 Самый простой способ найти область значений функции — построить ее график.
Самый простой способ найти область значений функции — построить ее график.
☛ Связанные темы:
- Графические функции
- Кубические функции
- Обратные тригонометрические функции
Часто задаваемые вопросы о домене и диапазоне
Что такое домен и диапазон функции?
Домен и диапазон функции представляют собой набор всех входных и выходных данных, которые функция может дать соответственно. т. е. для любой функции y = f(x):
- областью определения является множество всех значений x, для которых f(x) определено.
- диапазон — это набор всех значений y, которые производит функция f(x).
Как записать домен и диапазон?
Мы пишем домен и диапазон функции как набор всех входов, которые функция может принимать, и выходов функций соответственно. Поскольку это не что иное, как наборы, мы можем записать их либо в форме обжарщика, либо в нотации построителя наборов.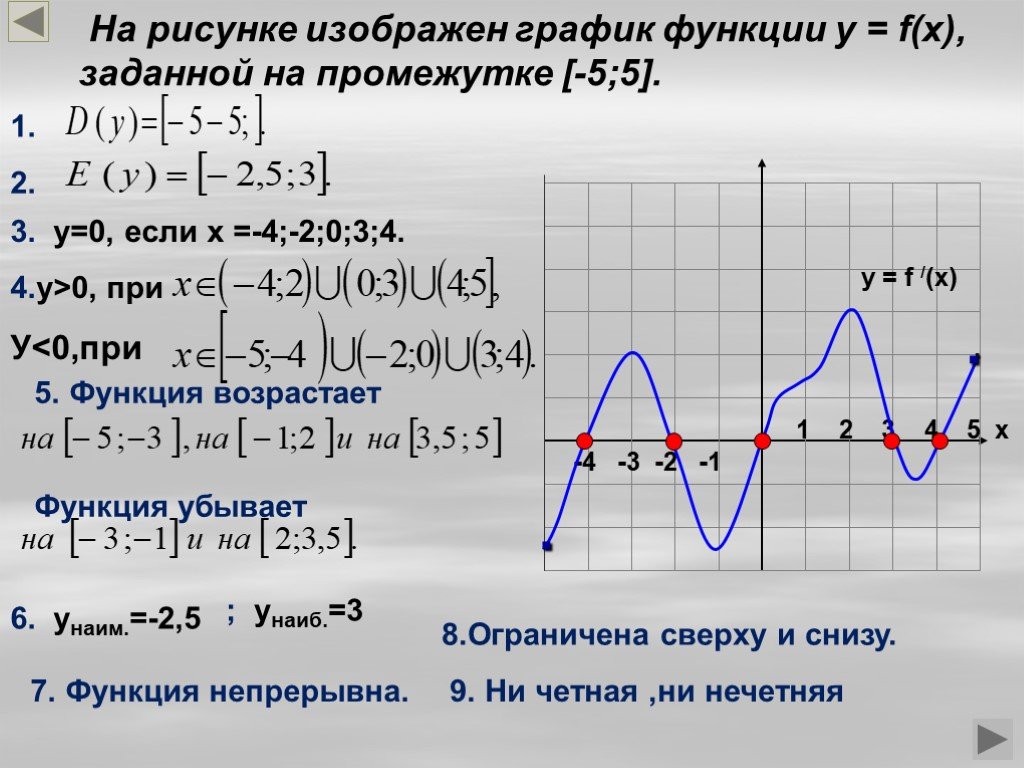 Домен и диапазон в обозначении интервала включают в себя открытые и квадратные скобки.
Домен и диапазон в обозначении интервала включают в себя открытые и квадратные скобки.
Как найти домен и диапазон графа?
Домен из графика — это набор всех значений x, которые охватывает график, а диапазон графика — это набор всех значений y, которые он охватывает.
Что такое область определения и диапазон постоянной функции?
Пусть постоянная функция равна f(x) = k. Область определения постоянной функции задается ℝ, то есть набором действительных чисел. Диапазон постоянной функции задается одноэлементным набором {k}. Домен и диапазон постоянной функции задаются как домен = ℝ и диапазон = {k}, который является одноэлементным набором.
Что такое определение предметной области в математике?
Область математики обычно определяется для отношений/функций. Область определения функции — это множество всех значений, которые можно в нее ввести. Например, для функции f(x) = √x в нее можно вводить только неотрицательные значения. Таким образом, его областью определения является множество всех неотрицательных действительных чисел.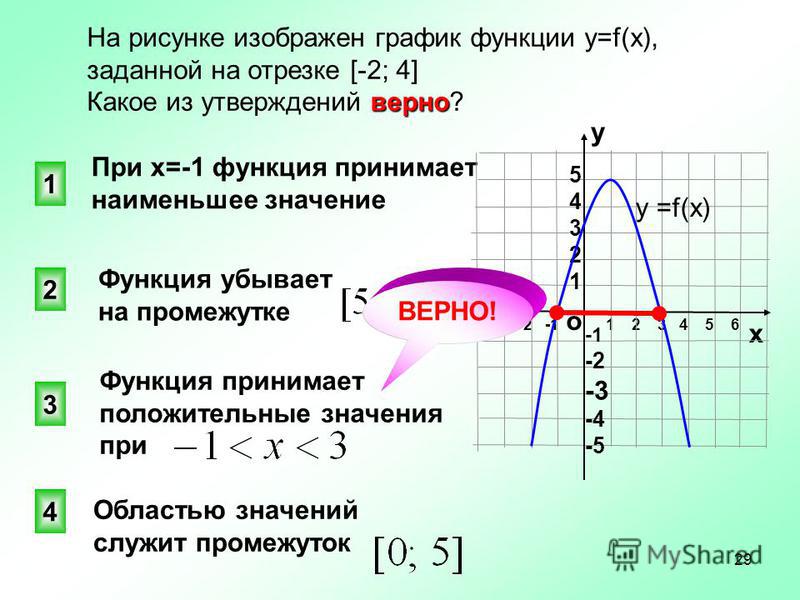
Как найти область определения рациональной функции?
Чтобы найти область определения рациональной функции, мы просто устанавливаем знаменатель не равным нулю. Например, чтобы найти область определения f(x) = 2/(x-3), мы устанавливаем x-3 ≠ 0, решая это, мы получаем x≠3. Таким образом, областью определения является множество всех рациональных чисел, кроме 3. В интервальной записи это можно записать как (-∞, 3) U (3, ∞).
Каковы правила определения области определения функции?
Вот несколько общих правил, используемых для нахождения области определения различных типов функций:
- f(x) = многочлен, областью определения является множество всех действительных чисел.
- f(x) = 1/x, домен, если множество всех действительных чисел, кроме x≠0.
- f(x) = √x, домен, если множество всех действительных чисел, таких что x ≥ 0.
- f(x) = ln x, областью определения является множество всех действительных чисел, для которых x > 0.

Как найти домен и диапазон функций?
Чтобы найти область определения функции y = f(x), нам нужно найти множество всех возможных значений x, которые не делают функцию неопределенной. Общие примеры включают деление на 0, извлечение квадратного корня из отрицательных чисел и т. д. Чтобы вычислить диапазон функции, представьте, какие значения y выдает функция. Когда воображение невозможно, нарисуйте график функции и посмотрите на значения y, которые покрывает график.
Как найти диапазон рациональной функции?
Чтобы найти диапазон рациональной функции, мы просто решаем уравнение относительно x и устанавливаем знаменатель не равным нулю. Например, чтобы найти диапазон y=2/(x-3), сначала решите его для x. Тогда мы получаем x-3 = 2/y и отсюда x = (2/y) + 3. Тогда его диапазон равен y≠0 (или) в интервальной записи, (-∞, 0) U (0, ∞ ).
Как найти область определения и область значений уравнения?
Чтобы найти область определения и область значений уравнения y = f(x), определите значения независимой переменной x, для которой определена функция.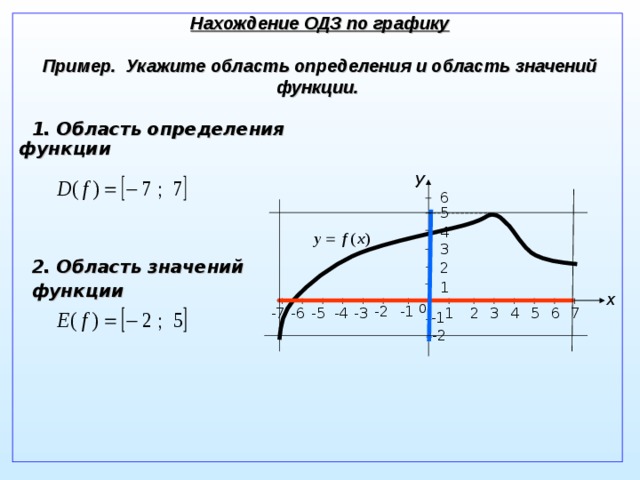 Чтобы вычислить диапазон функции, мы просто выражаем уравнение как x = g (y), а затем находим область определения g (y).
Чтобы вычислить диапазон функции, мы просто выражаем уравнение как x = g (y), а затем находим область определения g (y).
Как рассчитать домен и диапазон по графику функции?
Набор всех координат x всех точек кривой дает домен, а набор всех координат y всех точек кривой дает диапазон. Каждый из домена и диапазона может быть записан как набор или интервал.
В чем разница между доменом и диапазоном функции?
Домен и Диапазон функции являются компонентами функции. Область определения функции — это набор всех возможных входных данных для функции, тогда как диапазон функции — это набор всех выходных данных, которые может дать функция.
Что такое домен и диапазон отношения?
Домен и диапазон отношения находятся следующим образом. Пусть R — отношение непустого множества A к непустому множеству B. Область определения и диапазон отношения — это множество первых элементов и вторых элементов соответственно в упорядоченных парах в отношении R, называемое доменом.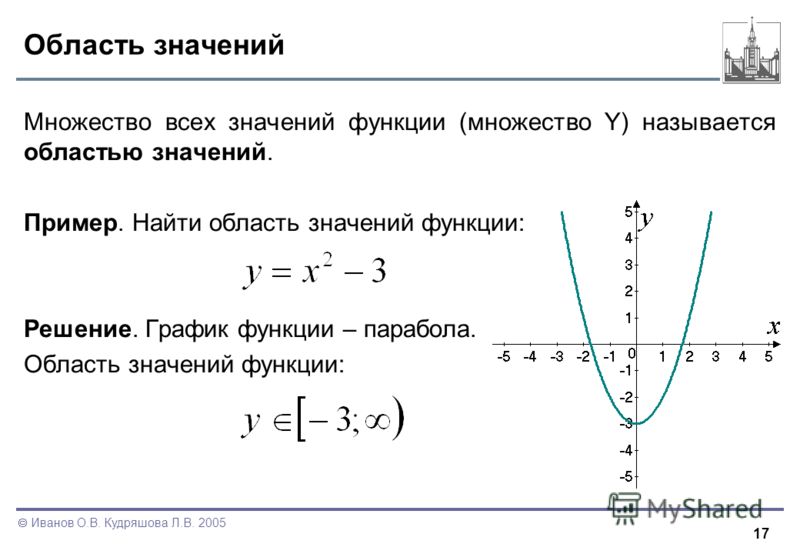
Что такое домен и диапазон составных функций?
Пусть составная функция равна h(x) = (f ∘ g)(x). Область определения и диапазон значений h определяются следующим образом. Область определения h либо совпадает с областью определения f, либо лежит в пределах области определения f. Диапазон h должен лежать в диапазоне g. Пусть f(x) = x 2 и g(x) = x+ 3. Мы знаем, что g: X → Y и f: Y → Z. Затем туман: X → Z. f(g(x)) = (x+3) 2 . Таким образом, домен и диапазон: domain= {Все элементы множества X}, range= {все элементы множества Z}
Что такое домен и диапазон квадратичной функции?
Область определения и область значений квадратичной функции y = a(x — h) 2 + k определяют характер параболы: направлена она вверх или вниз.
- y ≥ k, если функция имеет минимальное значение, т. е. когда a > 0 (парабола раскрывается)
- y ≤ k, если функция имеет максимальное значение, то есть когда a < 0 (парабола раскрывается вниз)
Как найти диапазон графика?
Ось Y отвечает за диапазон.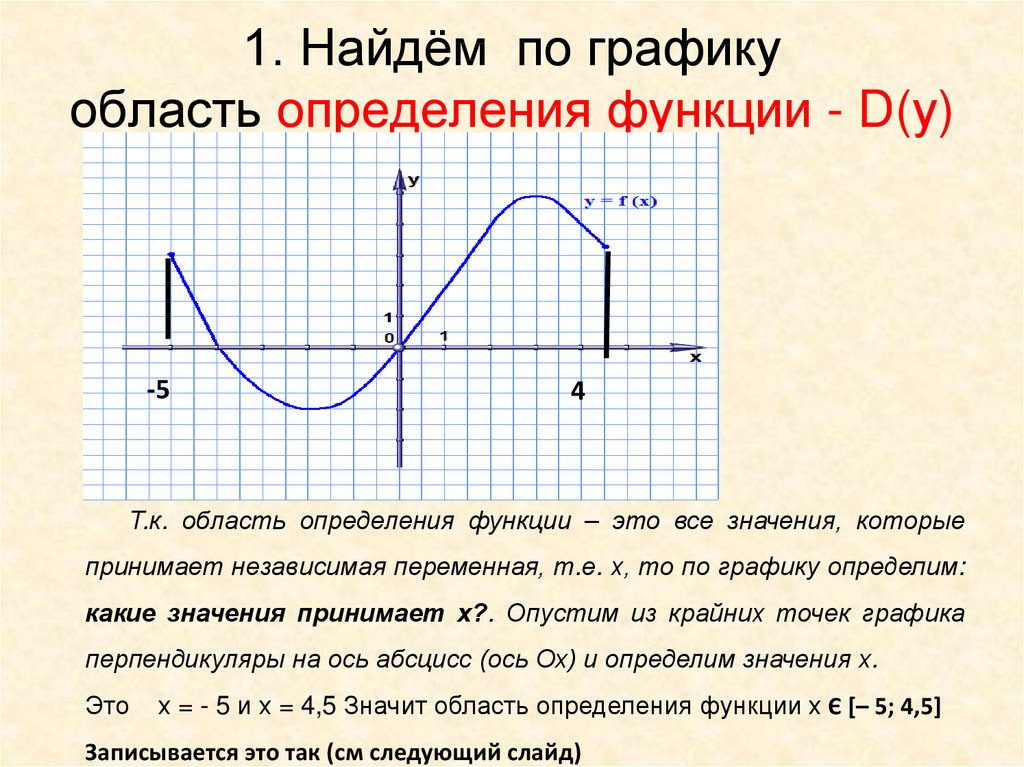 Таким образом, чтобы найти диапазон графика, посмотрите на значения y, охватываемые графиком. Самые высокие и самые низкие значения графиков полезны при записи диапазона графика.
Таким образом, чтобы найти диапазон графика, посмотрите на значения y, охватываемые графиком. Самые высокие и самые низкие значения графиков полезны при записи диапазона графика.
Поиск домена и диапазона по графикам | Колледж Алгебра |
Домен и диапазон
Другим способом определения области и диапазона функций является использование графиков. Поскольку домен относится к набору возможных входных значений, домен графика состоит из всех входных значений, показанных на оси 90 563 x 90 564. Диапазон представляет собой набор возможных выходных значений, которые показаны на оси и . Имейте в виду, что если график выходит за пределы видимой части графика, домен и диапазон могут быть больше, чем видимые значения. См. рис. 6.
Рисунок 6
Мы можем заметить, что граф простирается по горизонтали от
−5-5−5
вправо без границ, поэтому домен равен
[−5,∞)\left[-5,\ infty \right)[−5,∞)
. Вертикальный экстент графика — это все значения диапазона
Вертикальный экстент графика — это все значения диапазона
555
и ниже, поэтому диапазон равен
(−∞,5]\left(\mathrm{-\infty },5\right](−∞,5 ]
. Обратите внимание, что домен и диапазон всегда записываются от меньших значений к большим или слева направо для домена и от нижней части графика к верхней части графика для диапазона.
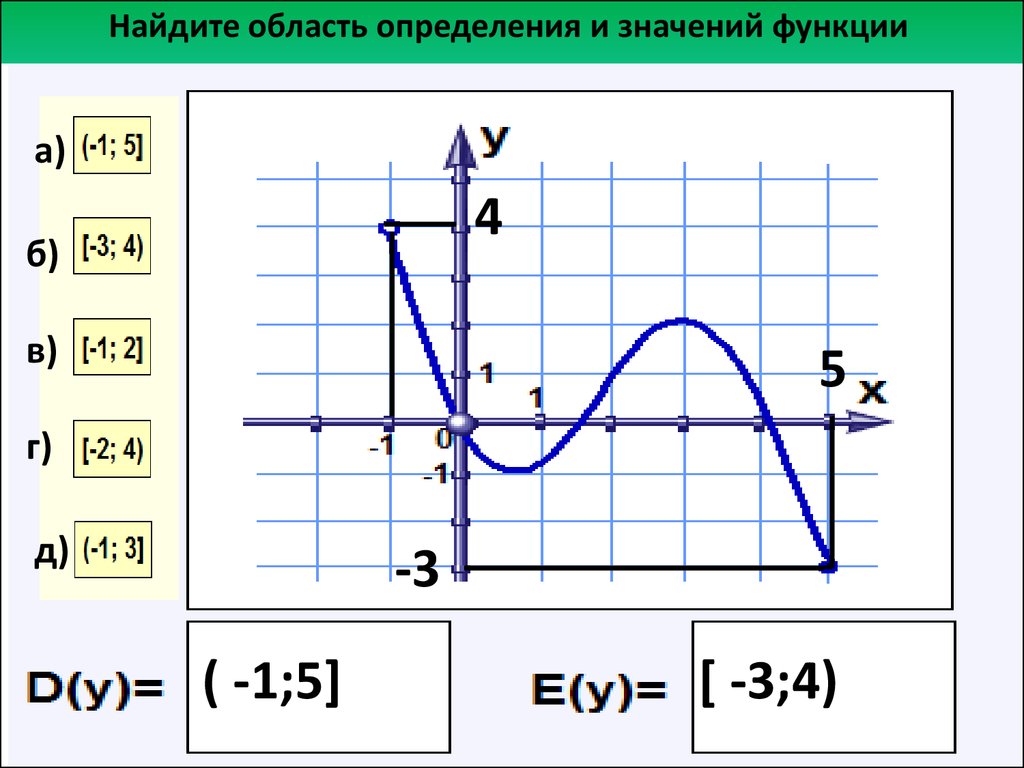
Пример 6. Поиск домена и диапазона на графике
Найдите область определения и область значений функции
fff
, график которой показан на рис. 7.
рис. домен
fff
составляет
(−3,1]\left(-3,1\right](−3,1]
.
Рисунок 8
Протяженность графика по вертикали от 0 до –4, поэтому диапазон равен
[−4,0)\влево[-4,0\вправо)[−4,0)
.
Пример 7. Определение области и диапазона по графику добычи нефти
Найдите область определения и диапазон функции
fff
, график которой показан на рисунке 9.
Рисунок 9. (кредит: модификация работы Управления энергетической информации США) горизонтальная ось — это «годы», которые мы представляем с помощью переменной
ttt
для времени. Выходное количество — «тысячи баррелей нефти в день», которое мы представляем с помощью переменной
bbb
для баррелей. Граф может продолжаться влево и вправо за пределами того, что просматривается, но на основе видимой части графа мы можем определить домен как
1973≤t≤20081973\le t\le 20081973≤t≤t≤2008
и диапазон приблизительно равен
180≤b≤2010180\le b\le 2010180≤b≤2010
.
В интервальных обозначениях домен равен [1973, 2008], а диапазон равен примерно [180, 2010]. Для домена и диапазона мы аппроксимируем наименьшее и наибольшее значения, поскольку они не попадают точно на линии сетки.
Попробуйте 6
Учитывая график на рисунке 10, определите домен и диапазон, используя обозначение интервала.
Рисунок 10
Решение
Вопросы и ответы
Могут ли домен и диапазон функции совпадать?
Да. Например, область определения и диапазон функции кубического корня — это множество всех действительных чисел.
Лицензии и атрибуции
Контент с лицензией CC, совместно используемый ранее
- Precalculus. Автор : Джей Абрамсон и др. Предоставлено : OpenStax. Расположен по адресу : https://openstax.


 Если выражение f(x) находится под квадратным корнем, область определения можно узнать из неравенства f(x)≥0.
Если выражение f(x) находится под квадратным корнем, область определения можно узнать из неравенства f(x)≥0.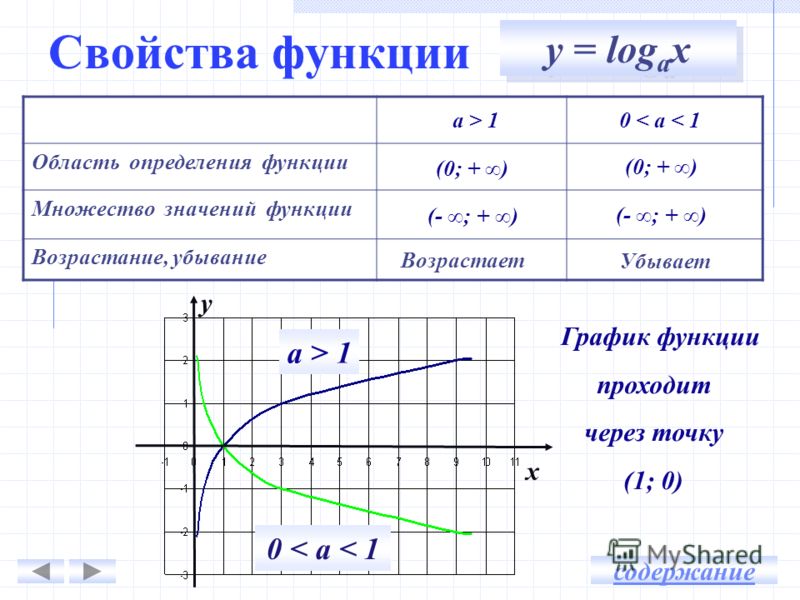
 Машина не даст вам никакого вкуса газировки, если вы введете пенни. Следовательно, домен представляет входные данные, которые мы можем здесь иметь, то есть монеты в четвертаке и однодолларовые купюры.
Машина не даст вам никакого вкуса газировки, если вы введете пенни. Следовательно, домен представляет входные данные, которые мы можем здесь иметь, то есть монеты в четвертаке и однодолларовые купюры.


 Самый простой способ найти область значений функции — построить ее график.
Самый простой способ найти область значений функции — построить ее график.