Как найти определенный интеграл: Как вычислить определенный интеграл, примеры решений

Определение определенного интеграла. Объем конуса интеграл. Объем тела вращения интеграл. Определение определенного интеграла римана.

• Альфашкола
• Статьи
• Определенный интеграл

Функция определенного интеграла  тесно связана с первообразной и неопределенным интегралом функции. Основное отличие состоит в том, что неопределенный интеграл, если он существует, то есть входит в область определения подынтегральной функции, является вещественным числовым значением, в то время как первообразная и неопределенный интеграл представляют собой бесконечное число функций, отличающихся только константой. Развитие определенного  интеграла начинается с функции \(f( x) \) на замкнутом интервале \([ a, b]\). 2}d\theta\)

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Анастасия Александровна Белая

Репетитор по математике

Стаж (лет)

Образование:

Могилёвский государственный университет имени А.А.Кулешова

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Наталья Николаевна Шарапова

Репетитор по математике

Стаж (лет)

Образование:

Челябинский государственный университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Тамара Анатольевна Меркулова

Репетитор по математике

Стаж (лет)

Образование:

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Предметы

• Математика
• Репетитор по физике
• Репетитор по химии
• Репетитор по русскому языку
• Репетитор по английскому языку
• Репетитор по обществознанию
• Репетитор по истории России
• Репетитор по биологии
• Репетитор по географии
• Репетитор по информатике

Специализации

• Подготовка к ОГЭ по математике
• Репетитор по геометрии
• Подготовка к олимпиадам по химии
• Репетитор по русскому языку для подготовки к ОГЭ
• ВПР по математике
• Репетитор для подготовки к ОГЭ по обществознанию
• Репетитор по биологии для подготовки к ЕГЭ
• Репетитор по информатике для подготовки к ОГЭ
• Репетитор по информатике для подготовки к ЕГЭ
• Подготовка к ОГЭ по литературе

Похожие статьи

• Порядок выполнения арифметических операций
• Скорость сближения и скорость удаления
• Расстояние между точками на координатной прямой
• Учимся решать текстовые задачи
• ЕГЭ по математике, базовый уровень. Планиметрия. Прямоугольный треугольник (вариант 5)
• Работа по математике
• ЕГЭ по математике, базовый уровень. Задачи на прогрессии
• Комплексы из-за внешности: учимся любить себя на примере звезд

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Текст с ошибкой:

Расскажите, что не так

Вычислить определенный интеграл. — примеры, решения

Пример 1:

Вычислить определенный интеграл.

Решение от преподавателя:

Пример 2:

Вычислить определенный интеграл.

Решение от преподавателя:

Пример 3:

Найти определенный интеграл:

Решение от преподавателя:

Пример 4:

Вычислить определенный интеграл:

Решение от преподавателя:

Делаем замену переменных: 
4x+2=t² 
Следовательно: 
x=t²/4-1/2 

Пример 5:

Вычислить определенный интеграл.

Решение от преподавателя:

Пример 6:

Вычислить определенный интеграл:

Решение от преподавателя:

Пример 7:

Найти определенный интеграл:

Решение от преподавателя:

Рассмотрим интегрирование правильной дроби. Для этого ее надо представить в виде суммы простейших дробей.

Пример 8:

Вычислить определенный интеграл:

Решение от преподавателя:

Пример 9:

Вычислить определенный интеграл.

Решение от преподавателя:

Пример 10:

Вычислить определенный интеграл.

Решение от преподавателя:

Пример 11:

Вычислить определенный интеграл.

Решение от преподавателя:

Пример 12:

Вычислить определенный интеграл:

Решение от преподавателя:

Пример 13:

Найти определенный интеграл:

Решение от преподавателя:

Пример 14:

Вычислить определенный интеграл:

Решение от преподавателя:

Пример 15:

Найти определенный интеграл:

Решение от преподавателя:

Пример 16:

Вычислить определенный интеграл:

Решение от преподавателя:

Пример 17:

Найти определенный интеграл:

Решение от преподавателя:

Пример 18:

Вычислить определенный интеграл.

Решение от преподавателя:

Пример 19:

Найти определенный интеграл:

Решение от преподавателя:

Пример 20:

Вычислить определенный интеграл:

Решение от преподавателя:

Пример 21:

Найти определенный интеграл:

Решение от преподавателя:

Пример 22:

Вычислить определенный интеграл:

Решение от преподавателя:

Пример 23:

Вычислить:

Решение от преподавателя:

Пример 24:

Вычислить определенный интеграл:

Решение от преподавателя:

Пример 25:

Вычислить определенный интеграл:

Решение от преподавателя:

Применяем универсальную тригонометрическую подстановку:

 = 
Представим выражение в виде простых дробей:

Интегрируя, получаем:

Возвращаясь к замене переменных, получаем:

Вычислим наш интеграл.

Пример 26:

Вычислить определенный интеграл.

Решение от преподавателя:

Пример 27:

Вычислить определенный интеграл:

Решение от преподавателя:

Пример 28:

Вычислить определенный интеграл:

Решение от преподавателя:

Пример 29:

Вычислить интеграл:

Решение от преподавателя:

Пример 30:

Вычислить определенный интеграл:

Решение от преподавателя:

Пример 31:

Найти определенный интеграл.

Решение от преподавателя:

Пример 32:

Вычислить определенный интеграл:

Решение от преподавателя:

Пример 33:

Вычислить определенный интеграл:

Решение от преподавателя:

Пример 34:

Вычислить определенный интеграл методом замены переменных:

Решение от преподавателя:

Пример 35:

Вычислить определенный интеграл:

Решение от преподавателя:

Пример 36:

Вычислить определенный интеграл методом замены переменных:

Решение от преподавателя:

Пример 37:

Вычислить определенный интеграл:

Решение от преподавателя:

Пример 38:

Вычислить определенный интеграл:

Решение от преподавателя:

Пример 39:

Вычислить определенный интеграл:

Решение от преподавателя:

Пример 40:

Вычислить определенный интеграл:

Решение от преподавателя:

Пример 41:

Вычислить определенные интегралы:

Решение от преподавателя:

Пример 42:

Вычислить определенный интеграл:

Решение от преподавателя:

Пример 43:

Вычислить определенный интеграл:

Решение от преподавателя:

Пример 44:

Вычислить определенный интеграл:

Решение от преподавателя:

Пример 45:

Вычислить интеграл:

Решение от преподавателя:

Пример 46:

Вычислить определенный интеграл:

Решение от преподавателя:

Пример 47:

Вычислить определенный интеграл или показать расходимость:

Решение от преподавателя:

Пример 48:

Вычислить определенные интегралы:

Решение от преподавателя:

Пример 49:

Вычислить определенный интеграл:

 

Решение от преподавателя:

Пример 50:

Вычислить определенный интеграл:

Решение от преподавателя:

Пример 51:

Вычислить определенный интеграл:

Решение от преподавателя:

Работа вам нужна срочно.

Не волнуйтесь, уложимся!

Заполните, пожалуйста, данные для автора:

• 22423 авторов готовы помочь тебе.
• 2402 онлайн

b f(x) \, dx$ находится между $(b — a) \text{max}_{x \in [a, b]} |f(x)|$ и $(b — a) \text{min }_{x \in [a, b]} -|f(x)|$) и проверить, удовлетворяет ли ему ваш ответ?

Можно ли выполнить интеграл совершенно по-другому и получить тот же ответ? (Это универсальный способ проверить свой ответ на задачу.)

Как и в комментарии Ландуроса, можете ли вы решить неопределенный интеграл, а затем продифференцировать его?

Другая общая, но менее простая стратегия, которая приходит на ум, состоит в том, чтобы посмотреть, может ли тот метод, который вы использовали для вычисления интеграла, также вычислить интеграл с дополнительным параметром в подынтегральном выражении; затем вы можете проверить, имеет ли ответ смысл как функцию параметра или, по крайней мере, разумно ли ваш метод обрабатывает параметр. 92} \, dx = \frac{\pi}{\sqrt{t}}$$

(которое мы также можем получить, подставив $x \mapsto \sqrt{t} x$, но снова притворимся на минуту, что не заметить это), и мы можем спросить себя, ведут ли себя обе стороны одинаково как функция $t$. Что ж, в левой части более высокие значения $t$ заставляют подынтегральную функцию убывать быстрее, поэтому интеграл должен быть убывающей функцией $t$, как это имеет место в правой части. Кроме того, интеграл должен стремиться к $0$ при $t \to \infty$ и должен стремиться к $\infty$ при $t \to 0$, что также имеет место на правой стороне. Вы можете попытаться адаптировать грубые верхнюю и нижнюю границы сверху и к этому случаю, и они продолжат совпадать. Это не проверка правильности числового ответа, а проверка того, что то, как вы используете метод контурной интеграции, дает ответы, которые ведут себя разумно. 9{1/2}$ имел правильное качественное поведение в зависимости от $t$; конечно, нет, и я нашел свою ошибку!)

Вычисление определенного интеграла: смысл

Вы, наверное, видели, как аппроксимировать площадь под кривыми, используя различные методы.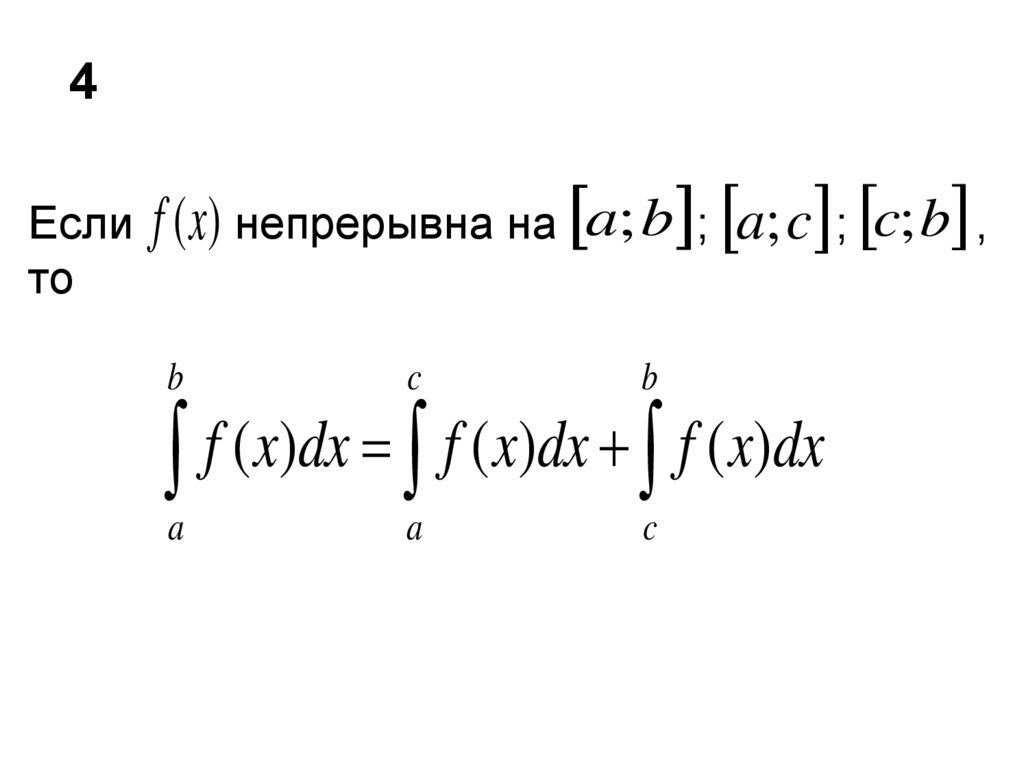 Наиболее распространенный способ аппроксимации площадей — использование прямоугольников. Это то, что мы знаем как сумма Римана .

Рис. 1. Аппроксимация площади под кривой с помощью прямоугольников.

А как насчет точно область ниже кривой?

Рис. 2. Область под кривой.

.

Определенные интегралы тесно связаны с площадью под кривой, поэтому в этой статье мы рассмотрим, как вычислять определенные интегралы.

Дополнительные сведения о площади между кривыми и о том, как ее найти, см. в статье Площадь между двумя кривыми.

Вычисление определенного интеграла Значение и пример

Вычислить определенный интеграл означает найти его 92 \mathrm{d}x = \frac{26}{3}\]

Но как вычислить определенный интеграл? Есть много способов. Наиболее распространенными являются:

• Взяв предел суммы Римана.

• Путем замены значений с использованием основной теоремы исчисления.

• Из графика с использованием геометрической формулы.

Давайте обратимся к каждому за раз.

Вычисление определенного интеграла как предела

Начнем с определения определения определенного интеграла. 9* \) — любая точка в регулярном разделе интервала.

Значения \( a \) и \( b \) известны как пределы интегрирования .

Дополнительные сведения и примеры по настройке интегралов см. в статье Определенные интегралы.

Это означает, что определенный интеграл определяется как предел суммы Римана при стремлении числа подынтервалов к бесконечности. Пожалуйста, ознакомьтесь с нашей статьей «Формирование сумм Римана», если вам нужно освежить в памяти эту тему! 92\) в интервале \( [0,5] \) равно \( \frac{125}{3}.\)

Вы могли заметить, что описанный выше метод не самый практичный. К счастью, есть более простой способ.

Вычисление определенного интеграла путем подстановки значений

Другой способ вычисления определенных интегралов заключается в использовании оценочной части Основополагающей теоремы исчисления.

Пусть \(f(x)\) — функция, интегрируемая на отрезке \([a,b], \), и пусть \(F(x) \) — первообразная функции \(f(x) .\) Оценочная часть основной теоремы исчисления утверждает, что 94 2x\,\mathrm{d}x.\]

Ответ:

В этом случае вы пытаетесь найти площадь под линейной функцией \( f(x)=2x.\) Начните с посмотрите на его график.

Рис. 3. График линейной функции.

Обратите внимание, что область под функцией представляет собой треугольник с основанием 4 и высотой 8.

Рис. 4. Область под функцией образует прямоугольный треугольник.

Следовательно, вы можете использовать формулу площади треугольника, чтобы найти эту площадь, поэтому 92} \, \mathrm{d}x = \frac{9}{2}\pi. \]

Вычисление определенных интегралов по графику

Как правило, функции имеют интервалы, на которых они положительны, и интервалы, на которых они отрицательны. Что происходит с площадью функции, если ее график находится ниже оси абсцисс? Вы все еще можете присвоить ему значение! Однако области, естественно, не могут быть отрицательными.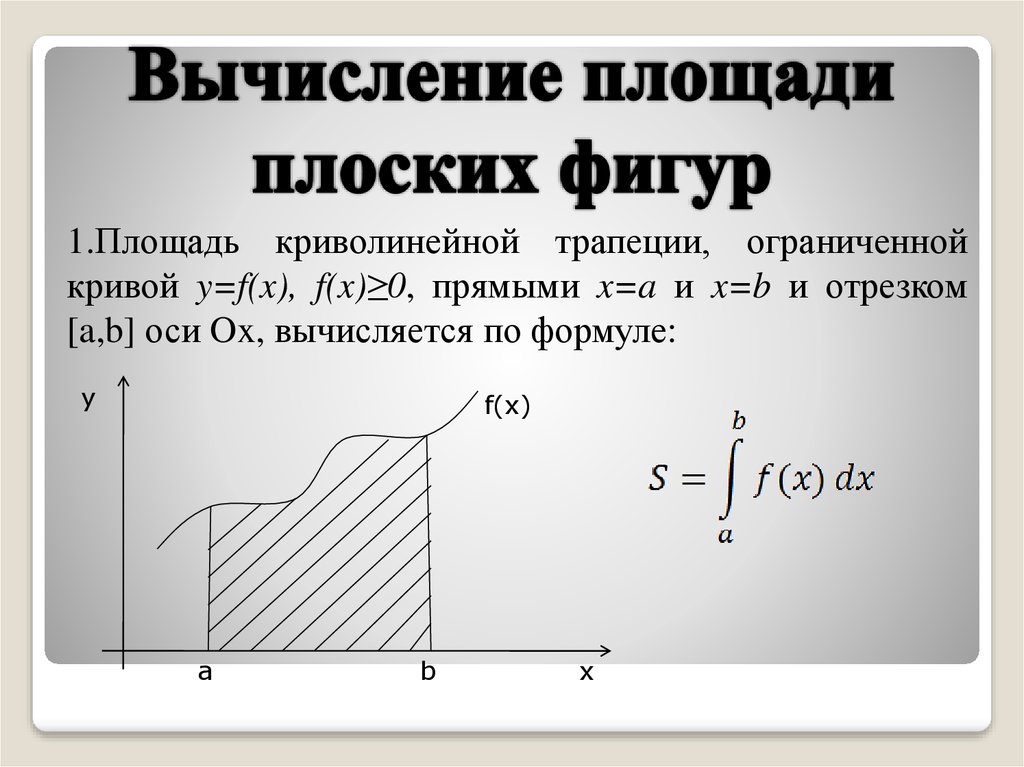

Чтобы обойти это, принято соглашение, определяющее область со знаком .

Область со знаком графа такова, что:

• Если график находится выше оси X, площадь определяется как положительная.
• Если график находится ниже оси X, площадь определяется как отрицательная.

Определенный интеграл, включающий эти два типа интервалов, также имеет связанную с ним площадь! Вы можете найти его, вычитая площадь под осью x из площади над осью x.

Рис. 6. Площадь между осью x и функцией с положительными и отрицательными интервалами.

Вы можете использовать метод по вашему выбору, чтобы найти площадь каждой части графика. 9b f(x)\,\mathrm{d}x \) интегрируемой и неотрицательной функции дает площадь между \( f(x)\) и осью x.

• Если функция отрицательная, площадь определяется как отрицательная
  .

Вы можете вычислить определенный интеграл , взяв предел суммы Римана при стремлении числа подынтервалов к бесконечности.

No related posts.