Как найти периметр и площадь формулы: Вычислите периметр и площадь прямоугольника со сторонами a и b если a=15 см b=100 см

Конспект урока: «Формулы периметра и площади прямоугольника» | План-конспект урока по математике (3 класс) на тему:

Урок математики 3 класс.

Тема: Формулы периметра и площади прямоугольника.

Цели: сформировать у детей понятие о формуле, учить записывать с помощью формул правила нахождения периметра, площади, выражать зависимость между величинами; продолжить формирование навыков решения составных уравнений; решения задач на нахождение площади и периметра; вычислительных навыков.

 Оборудование: мультимедийный проектор, тетрадь, учебник.

Ход урока.

I Организационный момент.

Слайд 1

 — Как вы понимаете пословицу: «Краткость – сестра таланта»? ( мнения детей).

 Как связана эта пословица с уроком математики?( мнения ребят)

 Попробуем разобраться?

II Мобилизирующий этап.

Слайд 2

 Составь уравнения к задачам и реши их.

 а) В гараже стояло 460 машин. Когда из гаража выехало несколько машин, то осталось 5 рядов по 44 машины в каждом. Сколько машин выехало из гаража? (460 – Х = 44 х 5)

б) В парке высадили несколько рядов лип по 25 деревьев в каждом ряду и еще 43 березы. Всего высадили 93 дерева. Сколько рядов лип было посажено? (25 х Х + 43 = 93)

 Слайд 3.

На какие группы можно разбить данные записи?

10 х 20                            30 + Х = 60

96 >90                             а х в

(а + в) х 2 = Р                 У х 9=72

а х в = S                         17 х а >а

Выслушиваются все мнения детей. ( уравнения, выражения, неравенства, формулы)

Что мы называем уравнением? (равенство, содержащее переменную, значение которой нужно найти).

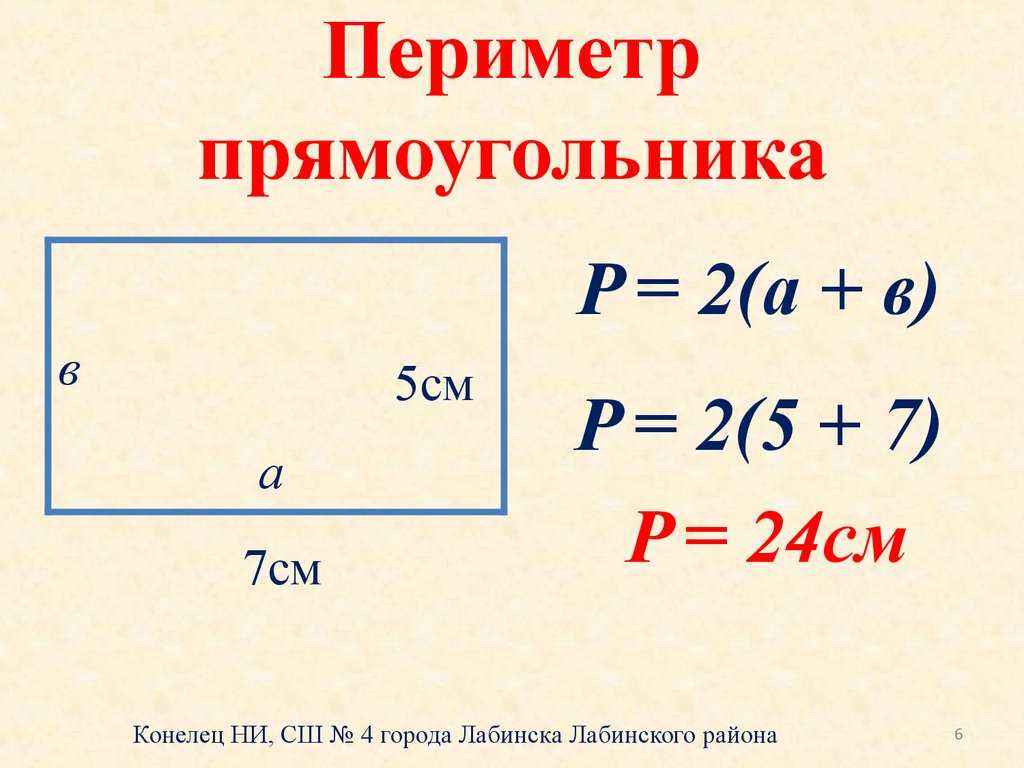
Что означает запись: (а + в) х 2 = Р      (Периметр)

Что означает запись:     а х в = S (Площадь)

Кто помнит, как мы иногда называли такие записи? ( Формулы)

В чем заключается отличие формулы от уравнения? (Формула – это равенство, которое помогает нам установить зависимость между величинами.) 

III.  Постановка учебной задачи урока. Фиксация проблемы

Попробуйте по формуле  периметра найти одну сторону прямоугольника?

Это задание вызывает затруднение у детей. Р= (а + в) х 2   — Проблема?  

Слайд 4.

Чему нам нужно научиться на сегодняшнем уроке?

(научиться, используя формулы, находить стороны прямоугольника по известным площади и периметру и одной стороны)

 Как же будет звучать тема нашего урока. «Формулы периметра и площади прямоугольника»  (тема и цели появляются на слайде № 6)

IV Ситуация успеха.  

Слайд 5.

            а  

      в

а х в =S

(а+в) х 2 = Р

Назовите первую формулу? ( формула площади)

Назовите  вторую формулу? ( формула периметра)

Давайте поработаем с первой формулой. Используя формулу, определите, как найти длину. Дети объясняют.

а = S : в

в = S : а

Что можно сказать о новых равенствах? ( В них длина и ширина выражены через площадь и другую сторону)

Давайте их прочитаем.

 S =а х в – Площадь прямоугольника равна произведению длин его сторон.

а = S :в – длина стороны прямоугольника равна частому площади и

в = S : а    известной     стороны.

 Запишите эти формулы в тетрадь. Выделите их рамкой.

Слайд 6

 Теперь посмотрим, как связаны между собой периметр и  строны прямоугольника. Напомните,  что такое периметр? (Сумма всех сторон прямоугольника)

Какую формулу можно записать?  Р= а +в +а +в  или Р =а х 2 + в х 2, или

Р= (а+в) х 2

Любой из этих формул можно пользоваться для нахождения периметра.

А какая формула удобнее всего? ( последняя).

Почему? (В ней всего 2 действия).

Физминутка для глаз

 Прочитайте последнюю формулу.

Р = (а+в) х 2  — Периметр прямоугольника равен сумvе  сторон, умноженной на два.

V «Открытие детьми нового»

Слайд 7

Опираясь на эту формулу, мы попробуем вывести формулу стороны прямоугольника по его периметру и известной стороне.

С чего начнем?

1. Выделим неизвестную сторону  Р = (а+в) х 2  .

Что вам напоминает эта запись? (Составное уравнение)

Решите его!

(а + в) 2=Р;

а + в = Р : 2;

а = Р : 2 — в 

 Все действия решения уравнения показываются поэтапно на слайде. Последнее равенство выделяется рамкой и фиксируется как формула нахождения стороны через известные периметр и сторону.

Теперь самостоятельно так же выведите формулу другой стороны.

Все выведенные формулы дети записывают в тетрадь, называя их значение.

 V Первичное закрепление

 Слайд 8

 а) Работа по учебнику.

№ 1  стр. 86 по рядам (с использованием формул, с проговариванием вслух)

№ 2  с комментированием (используя формулы)

 № 3  самостоятельно с самопроверкой по эталону.

Ф и з м и н у т к а .

  VI Повторение  изученного.

Слайд 9

№7 (г, д, е, ) по рядам

№8 с 88  частные случаи действий с числами 1 и 0

VII Подведение итогов.

Какая проблема возникла у нас в начале урока?

Можно ли, зная формулу периметра, вывести формулу нахождения  стороны по известным периметру и известной стороны.

Назовите её.

Справились мы с проблемой?

 Слайд 10

Ребята, и все же  зачем нам нужны формулы? (Используя формулы, мы легко можем найти неизвестное)

Что такое формула? (равенство, которое помогает установить зависимость между величинами).

Кто помнит пословицу в начале урока? ( Краткость —  сестра таланта.)

 Как она связана с нашим сегодняшним уроком?

Какой вывод можно сделать? (Зная формулы,  можно, экономя время, быстро найти значение.)

 Кому было трудно на уроке?

 Кто преодолел все трудности?

VIII  Задание на дом.

Слайд 11.

Найти где еще используется слово «формула», помимо  урока математики.

Стр. 87 № 6, стр.88 №10 (г).

Что такое периметр? Как найти периметр? Периметр квадрата и прямоугольника. Способы определения и примеры решения Как посчитать периметр фигуры

Сегодня у нас речь пойдет о том, как вычислить периметр многоугольника . Но сначала поговорим о многообразии фигур.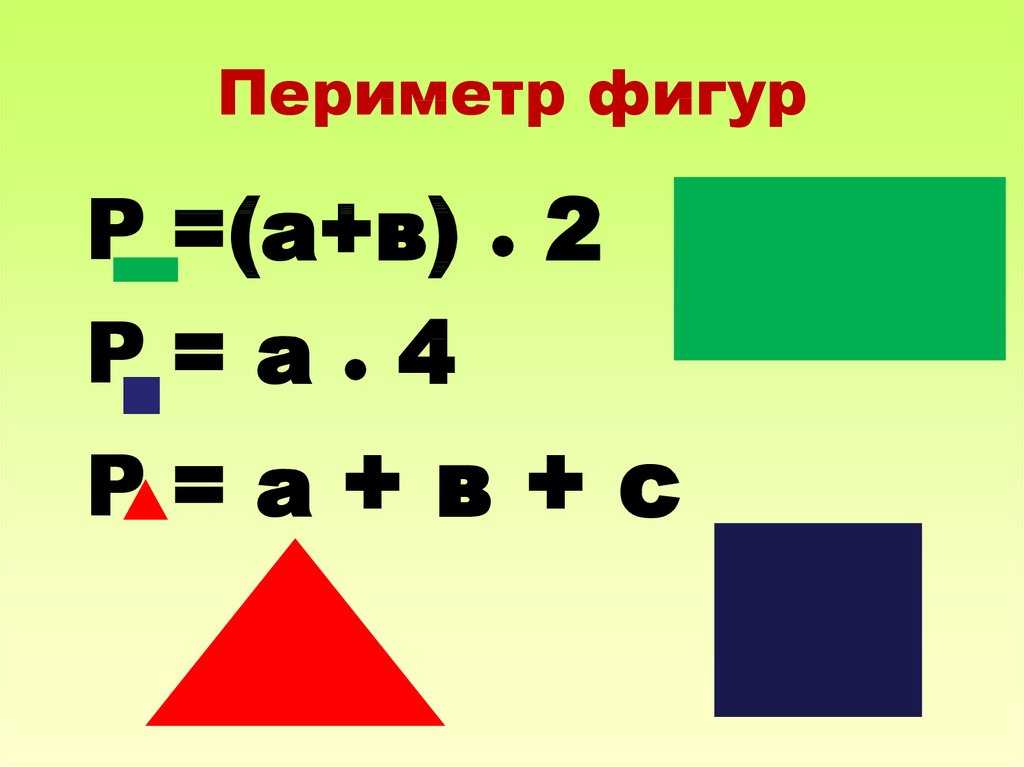 Посмотрите на рисунок. Какие фигуры мы здесь видим? Это прямоугольник и квадрат – многоугольники, которые имеют по четыре стороны, а также треугольник, имеющий три стороны, и пятиугольник с пятью сторонами.

И как же найти периметр этих фигур?

Для того, чтобы найти периметр многоугольника надо сложить длины всех его сторон .

Периметр обозначается заглавной латинской буквой Р .

Давайте рассмотрим несколько примеров.

Вычислим периметр многоугольника О. Как мы говорили ранее, периметр многоугольника – это сумма длин всех его сторон. Сложим все стороны нашего многоугольника:

Р = 15 + 17 + 10 + 10 + 20 + 15 = 87

Но можно вычислить периметр и другим способом, используя умножение. Мы видим, что некоторые стороны многоугольника одинаковы. У нас две стороны по 15 условных единиц и еще две по 10. Запишем выражение:

Р = 15 × 2 + 10 × 2 + 17 + 20 = 87

Теперь поговорим об особенностях вычисления периметра некоторых многоугольников.

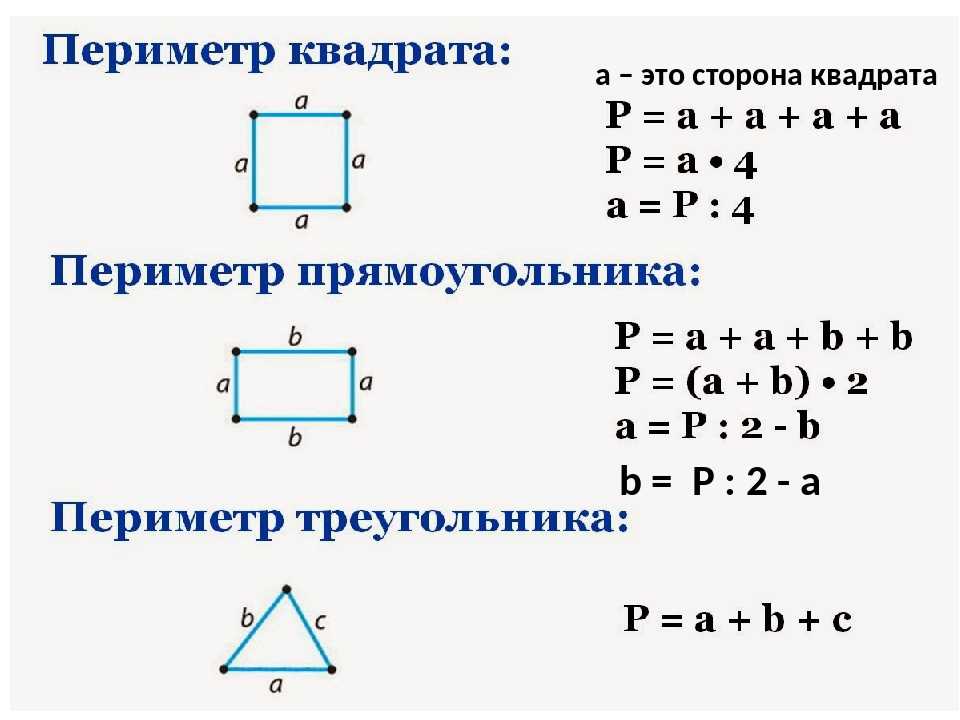
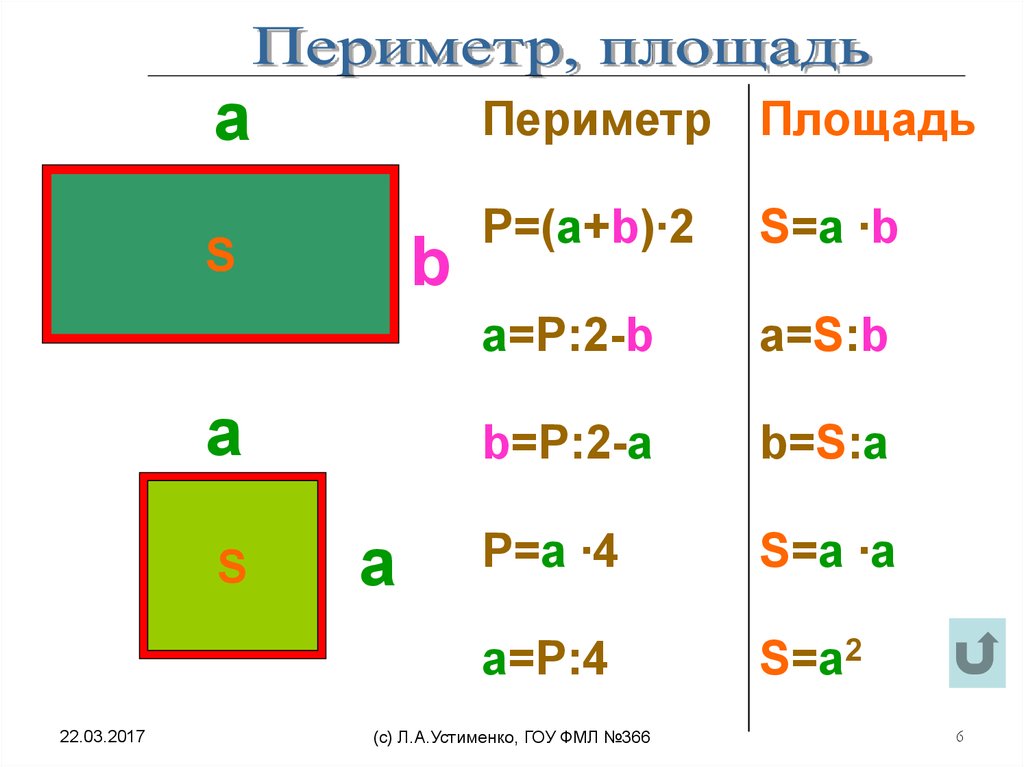
Прямоугольник – это такой четырехугольник, у которого противоположные стороны равны. Например, чтобы вычислить А со сторонами а и б , надо сложить эти стороны и умножить полученный результат на 2 :

Р(прямоугольника) = (а + б) × 2

То есть, если сторона прямоугольника а = 5 см , а сторона прямоугольника б = 3 см , то периметр прямоугольника будет:

Р = (5 + 3) × 2 = 16 см

А как найти неизвестные стороны прямоугольника, если известен его периметр и только одна из сторон?

Р(прямоугольника) = 2 × а + 2 × б

а = (Р – 2 × б) ÷ 2 или б = (Р – 2 × а) ÷ 2

Пример: Периметр прямоугольника 16 см, сторона а = 5 см. Чему равны остальные стороны прямоугольника?

Если мы знаем одну сторону прямоугольника, значит длины двух, из четырех сторон нам известны. Найдем остальные две стороны. То есть найдем одну, а вторая будет ей равна.

сторона б = (16 – 2 × 5) ÷ 2 = 3 см

Ответ: у прямоугольника две стороны по 5 см и две по 3 см.

Квадрат – это прямоугольник, у которого все стороны равны. Чтобы вычислить надо длину одной стороны умножить на 4:

Р(квадрата) = а × 4

Например, у квадрата В сторона а = 5 см. Чтобы найти его периметр:

Р(В) = 5 × 4 = 20 см

А если известен периметр квадрата, как найти длины его сторон? Очень просто, надо его периметр разделить на четыре:

а = Р ÷ 4

Пример: Периметр квадрата 24 см. Чему равны его стороны?

а = 24 ÷ 4 = 6

Ответ: Стороны квадрата равны 6 см.

По подобию вычисления периметра квадрата вычисляется периметр всех равносторонних многоугольников . То есть равен длине одной его стороны умноженной на количество сторон.

Если длина одной стороны многоугольника равна а , а число его сторон равно n , то его периметр будет равен:

Р(равностороннего многоугольника) = а × n

Например, у пятиугольника Д сторона а = 6 см . Найдем его периметр:

Р(Д) = 6 × 5 = 30 см

Ну а если известен периметр равностороннего многоугольника, то вычислить длины его сторон очень просто, надо разделить его периметр на количество сторон.

Периметр — это сумма длин всех сторон многоугольника.

• Для вычисления периметра геометрических фигур используются специальные формулы, где периметр обозначается буквой «P». Название фигуры рекомендуется писать маленькими буквами под знаком «P», чтобы знать чей периметр ты находишь.
• Периметр измеряется в единицах длины: мм, см, м, км и т.д.

Отличительные особенности прямоугольника

• Прямоугольник – это четырехугольник.
• Все параллельные стороны равны
• Все углы = 90º.
• Например в повседневной жизни прямоугольник может встречаться в виде — книги, монитора, крышки от стола или двери.

Как вычислить периметр прямоугольника

Существует 2 способа его нахождения:

• 1 способ. Складываем все стороны. P = a + а + b + b
• 2 способ. Сложить ширину и длину, и умножить на 2. P = (a + b) · 2. ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.

«a» — длина прямоугольника, более длинная пара его сторон.

«b» — ширина прямоугольника, более короткая пара его сторон.

Пример задачи на подсчет периметра прямоугольника:

Вычислите периметр прямоугольника, есть его ширина равна 3 см., а длина — 6.

Запомни формулы вычисления периметра прямоугольника!

Полупериметр — это сумма одной длины и одной ширины.

• Полупериметр прямоугольника — когда выполняешь первое действие в скобках – (a+b) .
• Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, т.е. умножить на 2.

Как найти площадь прямоугольника

Формула площади прямоугольника S= a*b

Если в условии известна длина одной стороны и длина диагонали, то площадь найти можно, используя в таких задачах, теорему Пифагора, она позволяет найти длину стороны прямоугольного треугольника если известны длины двух других сторон.

• : a 2 + b 2 = c 2 , где a и b – стороны треугольника, а с – гипотенуза, самая длинная сторона.

Помни!

1. Все квадраты – прямоугольники, но не все прямоугольники – квадраты. Так как:
   • Прямоугольник — это четырехугольник со всеми прямыми углами.
   • Квадрат — прямоугольник, у которого все стороны равны.
2. Если ты находишь площадь, ответ всегда будет в квадратных единицах (мм 2 , см 2 , м 2 , км 2 и т.д.)

Класс: 2

Цель: ознакомить с приёмом нахождения периметра прямоугольника.

Задачи: формировать умение решать задачи, связанные с нахождением периметра фигур, вырабатывать умения чертить геометрические фигуры, закрепить умение вычислять, применяя с переместительное свойство сложения, развивать навык устного счёта, логическое мышление, воспитывать познавательную активность и умение работать в коллективе.

Оборудование: ИКТ (мультимедийный проектор, презентация к уроку), картинки с геометрическими фигурами для физминутки, модель магического квадрата, у учеников – модели геометрических фигур, маркерные доски, линейки, учебники, тетради.

ХОД УРОКА

1. Организационный момент

Проверка готовности к уроку. Приветствие.

Начинается урок,
Он пойдёт ребятам впрок.
Постарайтесь всё понять –
И внимательно считать.

2. Устный счёт

а) Использование магических фигур. (Приложение 1 )

– Заполним клетки магического квадрата, назовите его особенности (сумма чисел по горизонталям, вертикалям и диагоналям равны) и определите волшебное число. (39)

По цепочке дети заполняют квадрат на доске и в тетрадях .

б) Знакомство со свойствами магических треугольников. (Приложение 2 )

– Суммы чисел в углах, образующие треугольник равны. Найдём волшебные числа у треугольника. Определи пропущенное число. Отметь его на маркерной доске.

3. Подготовка к изучению нового материала

– Перед Вами геометрические фигуры. Назовите их одним словом. (Четырёхугольники).
– Разделите их на 2 группы. (Приложение 3 )
– Что такое прямоугольники. (Прямоугольники – четырехугольники, у которых все углы прямые.)
– Что можно узнать, зная длины сторон четырёхугольников? Периметр – сумма длин сторон фигур.
– Найдите периметр белой фигуры, жёлтой.
– Почему у прямоугольников известны не все стороны?
– Какие свойства у противолежащих сторон прямоугольников? (У прямоугольника противоположные стороны равны).
– Если противоположные стороны равны, надо ли измерять все стороны? (Нет.)
– Правильно, достаточно измерить длину и ширину.
– Как вычислить удобным способом?

(Учащиеся работают устно с комментированием.)

4. Изучение новой темы

– Прочитайте тему нашего урока: «Периметр прямоугольника». (Приложение 4 )
– Помогите найти периметр данной фигуры, если её длина равна – а , а ширина – в .

Желающие находят Р у доски. Учащиеся в тетрадях записывают решение.

– Как записать это по-другому?

Р = а + а + в + в ,
Р = а х 2 + в х 2,
Р = (а + в ) х 2.

– Мы получили формулу нахождения периметра прямоугольника. (Приложение 5 )

5. Закрепление

Стр. 44 № 2.

Дети читают и записывают условие, вопрос, чертят фигуру, находят Р разными способами, записывают ответ.

6. Физминутка. Сигнальные карточки

Сколько клеточек зелёных,
Столько выполним наклонов.
Столько раз руками хлопнем.
Столько раз ногами топнем.
Сколько здесь у нас кружков,
Столько сделаем прыжков.
Мы присядем столько раз,
Столь подтянемся сейчас.

7. Практическая работа

– У Вас на партах лежат в конвертах геометрические фигуры. Как мы их назовём?
– Что такое прямоугольники?
– Что вы знаете о противолежащих сторонах прямоугольников?
– Измерьте стороны фигур по вариантам, найдите периметр разными способами.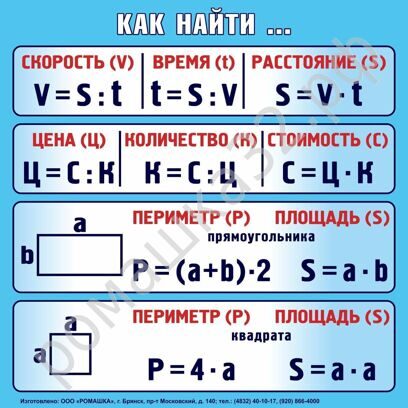
– Проверяем у соседа.

Взаимопроверка тетрадей .

– Прочитайте: Как нашли периметр? Что можно сказать о периметрах данных фигур? (Они равны) .
– Начертите прямоугольник с таким же Р, но другими сторонами.

Р 1 = (2 + 6) х 2 = 16 Р 1 = 2 х 2 + 6 х 2 = 16

Р 1 = 2 + 2 + 6 + 6 = 16
Р 2 = 3 + 3 + 5 + 5 = 16 Р 2 = (3 + 5) х 2 = 16
Р 3 = 4 + 4 + 4 + 4 = 16 Р 4 = 1 + 1 + 7 + 7 = 16

8. Графический диктант

Слева 6 клеток. Поставили точку. Начинаем движение. 2 – вправо, 4 – вправо вниз, 10 – влево, 4 – вправо вверх. Какая фигура? Преврати её в прямоугольник. Дострой. Найди Р разными способами.

Р = (5 + 2) х 2 = 14.
Р = 5 + 5 + 2 + 2 = 14.
Р = 5 х 2 + 2 х 2 = 14.

9. Пальчиковая гимнастика

Умножали, умножали.
Очень, очень мы устали.
Наши пальчики сплетём и соединим ладошки.
А потом, как только можем, крепко накрепко сожмём.
На дверях висит замок.
Кто его открыть не смог?
Мы замочком постучали,
Мы замочек повертели,
Мы замочек покрутили и открыли.

(Слова сопровождаются движениями)

10. Составление и решение задачи по условию (Приложение 8 )

Длина прямоугольника – 12 дм
Ширина – на 3 дм м.
Р – ?
В первом действии найдём ширину: 12 – 3 = 9 (дм) – ширина
Зная длину и ширину, узнаем Р одним из способов.
Р = (12 + 9) х 2 = 42 дм

11. Самостоятельная работа

12. Итог урока

– Чему учились. Как находили Р прямоугольника?

13.Оценивание

Оцениваются ответы учащихся у доски и выборочно в процессе самостоятельной работы.

14.Домашнее задание

С. 44 № 5 (с пояснениями).

Умение находить периметр прямоугольника очень важно для решения многих геометрических задач. Ниже приведена подробная инструкция по нахождению периметра разных прямоугольников.

Как найти периметр обычного прямоугольника

Обычный прямоугольник – четырехугольник, у которого параллельные стороны равны и все углы = 90º. Для нахождения его периметра существует 2 способа:

Складываем все стороны.

Вычислите периметр прямоугольника, есть его ширина равна 3 см., а длина – 6.

Решение (последовательность действий и рассуждения):

• Так как нам известны ширина и длина прямоугольника, найти его периметр не составит труда. Ширина параллельна ширине, а длина длине. Таким образом, в обычном прямоугольнике 2 ширины и 2 длины.
• Складываем все стороны (3 + 3 + 6 + 6) = 18 см.

Ответ: P = 18 см.

Второй способ заключается в следующем:

Нужно сложить ширину и длину, и умножить на 2. Формула этого способа имеет следующий вид: 2×(a + b), где a – ширина, b – длина.

В рамках данной задачи получим такое решение:

2×(3 + 6) = 2×9 = 18.

Ответ: P = 18.

Как найти периметр прямоугольника – квадрат

Квадрат является правильным четырехугольником. Правильным потому, что все его стороны и углы равны. Для нахождения его периметра так же существует два способа:

• Сложить все его стороны.
• Умножить его сторону на 4.

Пример: Найти периметр квадрата, если его сторона = 5 см.

Так как нам известна сторона квадрата, мы сможем найти его периметр.

Складываем все стороны: 5 + 5 + 5 + 5 = 20.

Ответ: P = 20 см.

Умножаем сторону квадрата на 4 (потому что все равны): 4×5 = 20.

Ответ: P = 20 см.

Как найти периметр прямоугольника – онлайн-ресурсы

Несмотря на то, что вышеупомянутые действия легки для понимания и освоения, вам может пригодиться несколько онлайн-калькуляторов, которые помогут вам вычислить периметры (площадь, объем) разных фигур. Просто вбейте необходимые значения и мини-программа рассчитает периметр нужной вам фигуры. Ниже приведен небольшой список.

Урок и презентация на тему: «Периметр и площадь прямоугольника»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 3 класса
Тренажер для 3 класса «Правила и упражнения по математике»
Электронное учебное пособие для 3 класса «Математика за 10 минут»

Что такое прямоугольник и квадрат

Прямоугольник – это четырёхугольник, у которого все углы прямые. Значит, противоположные стороны равны друг другу.

Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.

Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D …

Пример.

Читается так: четырёхугольник ABCD; квадрат EFGH.

Что такое периметр прямоугольника? Формула расчета периметра

Периметр прямоугольника – это сумма длин всех сторон прямоугольника или сумма длины и ширины, умноженная на 2.

Периметр обозначается латинской буквой P . Так как периметр — это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.

Например, периметр прямоугольника АВСD обозначается как P ABCD , где А, В, С, D — это вершины прямоугольника.

Запишем формулу периметра четырехугольника ABCD:

P ABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)

Пример.
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см.
Определим P ABCD .

Решение:
1. Нарисуем прямоугольник ABCD с исходными данными.
2. Напишем формулу для расчета периметра данного прямоугольника:

P ABCD = 2 * (AB + BС)

P ABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см

Ответ: P ABCD = 16 см.

Формула расчета периметра квадрата

У нас есть формула для определения периметра прямоугольника.

P ABCD = 2 * (AB + BC)

Применим её для определения периметра квадрата. Учитывая, что все стороны квадрата равны, получаем:

P ABCD = 4 * AB

Пример.
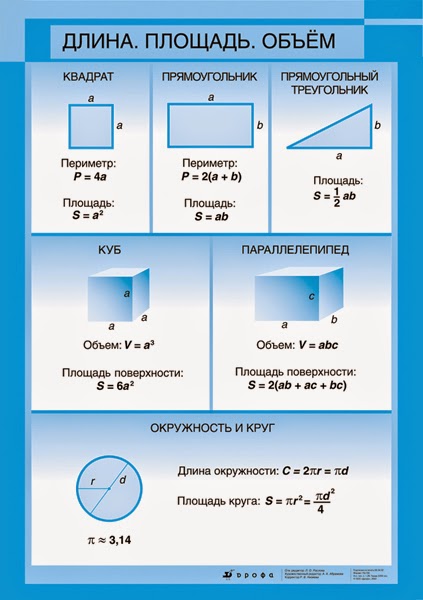
Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата.

Решение.
1. Нарисуем квадрат ABCD с исходными данными.

2. Вспомним формулу расчета периметра квадрата:

P ABCD = 4 * AB

3. Подставим в формулу наши данные:

P ABCD = 4 * 6 см = 24 см

Ответ: P ABCD = 24 см.

Задачи на нахождение периметра прямоугольника

1. Измерь ширину и длину прямоугольников. Определи их периметр.

2. Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника.

3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.

Где используется расчет периметра прямоугольника?

1. Задан участок земли, его нужно обнести забором. Какой длины будет забор?

В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора.

2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев.
Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.

Что такое площадь прямоугольника?

Площадь – это числовая характеристика фигуры. Площадь измеряется квадратными единицами длины: см 2 , м 2 , дм 2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.)
В вычислениях обозначается латинской буквой S .

Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Площадь прямоугольника вычисляется умножением длины АК на ширину КМ. Запишем это в виде формулы.

S AKMO = AK * KM

Пример.
Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?

S AKMO = AK * KM = 7 см * 2 см = 14 см 2 .

Ответ: 14 см 2 .

Формула вычисления площади квадрата

Площадь квадрата можно определить, умножив сторону саму на себя.

Пример.
В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.

S AВСО = AB * BC = AB * AB

Пример.
Определи площадь квадрата AKMO со стороной 8 см.

S AKMО = AK * KM = 8 см * 8 см = 64 см 2

Ответ: 64 см 2 .

Задачи на нахождение площади прямоугольника и квадрата

1.Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.

2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.

Периметр и площадь | Математика для гуманитарных наук |

Периметр

Периметр — это одномерное измерение, которое проводится по внешней стороне замкнутой геометрической формы. Давайте начнем обсуждение концепции периметра с примера.

Пошаговый пример

Рисунок 1.

Рисунок 2.

У Джозефа нет машины, поэтому ему приходится ездить на автобусе или ходить пешком, куда бы он ни пошел.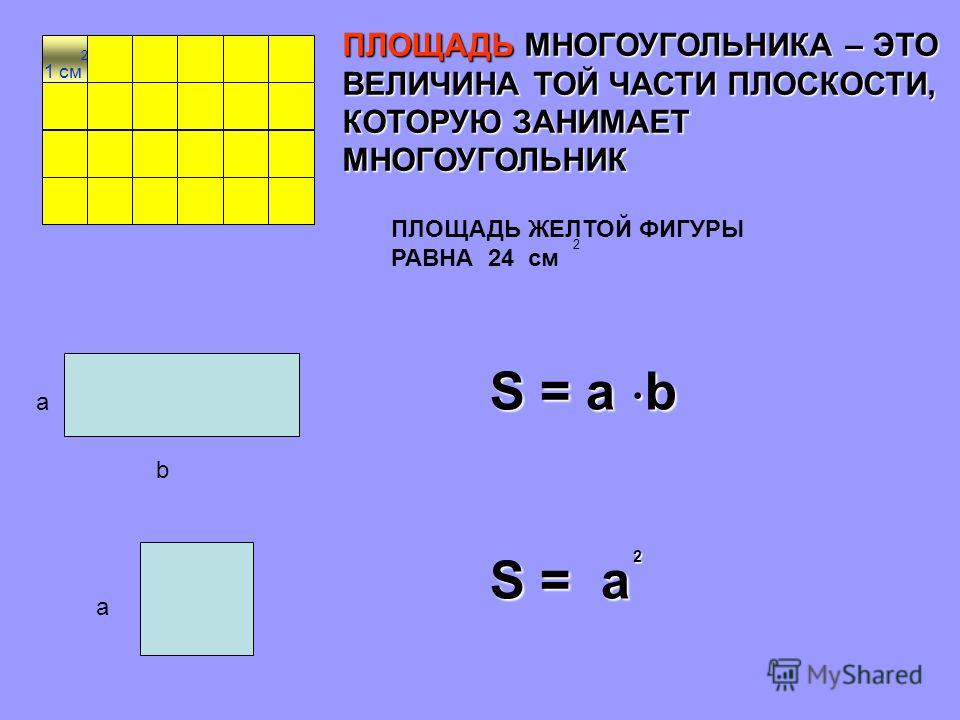 По понедельникам он должен ходить в школу, на работу и снова домой. Его маршрут изображен на рис. 1.

Очевидный вопрос, который следует задать в этой ситуации: «Сколько миль Джозеф проезжает по понедельникам»? Чтобы рассчитать каждое расстояние: 3 + 6 + 6 = 15.

Джозеф проходит 15 миль по понедельникам.

Еще один способ справиться с этой ситуацией — нарисовать фигуру, представляющую маршрут путешествия Джозефа и отмеченную расстоянием от одного места до другого.

Обратите внимание, что форма, созданная маршрутом Джозефа, представляет собой замкнутую геометрическую фигуру с тремя сторонами (треугольник) (см. рис. 2). Что мы можем спросить об этой форме: «Что такое периметр треугольника»?

Периметр означает «расстояние вокруг замкнутой фигуры или формы», и для вычисления мы добавляем каждую длину: 3 + 6 + 6 = 15

Наш вывод такой же, как и выше: Джозеф проходит 15 миль по понедельникам.

Однако мы смоделировали ситуацию с помощью геометрической формы, а затем применили определенную геометрическую концепцию ( периметр ) к вычислению расстояния, пройденного Джозефом.

Примечания по периметру

• Периметр — это одномерное измерение, которое представляет собой расстояние вокруг замкнутой геометрической фигуры или формы (без зазоров).
• Чтобы найти периметр, сложите длины каждой стороны фигуры.
• Если есть единицы, включите их в окончательный результат. Единицы измерения всегда будут одномерными (например, футы, дюймы, ярды, сантиметры и т. д.)

Чтобы вычислить периметр, наши фигуры должны быть замкнуты. На рис. 3 показана разница между закрытой и открытой фигурой.

Рисунок 3.

Пример 1

Найдите периметр каждой из фигур ниже.

1. Добавьте длины каждой стороны.

2. Иногда приходится делать предположения, если длины не помечены.

Решения

1. 12 шт.
2. 40 футов

Пример 2

Как найти периметр этой более сложной формы?

Раствор

Просто продолжайте добавлять длины сторон. 6 + 7 + 4 + 4 + 5 + 6 + 2 = 34 шт.

Если вы внимательно посмотрите на фигуры в предыдущих примерах, вы можете заметить некоторые способы записи каждого периметра в виде более явной формулы. Посмотрите, соответствуют ли результаты того, что мы сделали до сих пор, приведенным ниже формулам.

Форма		Периметр
Треугольник с длинами сторон, a , b , c :		P=a+b+cP=a+b+c\\P=a+b+c
Квадрат с длиной стороны a :		P=a+a+a+aP=a+a+a+a\\P=a+a+a+a P=4aP=4a\\P=4a
Прямоугольник с длинами сторон a , b :		P=a+b+a+bP=a+b+a+b\\P=a+b+a+b P=a+a+b+bP=a+a+b+b\ \P=a+a+b+b P=2a+2b P=2a+2b\\P=2a+2b

Окружность

Вы можете заметить, что мы еще не обсуждали расстояние вокруг очень важной геометрической формы: круга! Расстояние по окружности имеет специальное название, называемое окружности . Чтобы найти длину окружности, мы используем следующую формулу: C = 2πr

Рисунок 4.

В этой формуле π произносится как «пи» и определяется как длина окружности, деленная на ее диаметр:

π=Cd\displaystyle\pi=\frac{C}{d}\\π=dC​

. Обычно мы заменяем π приближением 3.14. Буква r представляет радиус круга.

Давайте посмотрим, откуда взялась формула длины окружности. На рисунке 4 показана общая окружность с радиусом 90 023 r.

Примечания о

C = 2π r

Помните, что в формуле при вычислении длины окружности C = 2π r мы умножаем следующим образом , обычно , подставляя 3,14 вместо π:

С = 2 × 3,14 × г

Часто использование ( ) помогает облегчить просмотр различных частей формулы:

C = (2)×(3,14)×( r )

Происхождение

C = 2π r

Как упоминалось ранее, специальное число π определяется как отношение длины окружности к ее диаметру. Мы можем записать это в виде уравнения:

Cd=π\displaystyle\frac{C}{d}=\pi\\dC​=π

Из нашей предыдущей работы мы знаем, что для определения неизвестного C мы можем переместить d в другую часть уравнения, написав C = π d. Диаметр полностью проходит через середину круга, поэтому диаметр в два раза больше радиуса. Мы можем обновить C с точки зрения радиуса как C = π(2 r ). Немного изменив порядок написания наших частей, мы можем сказать, что C = 2π r.

Воспользуемся формулой, чтобы найти длину окружности нескольких кругов.

Пример 3

Найдите длину окружности каждого из следующих кругов. Оставляйте свои ответы сначала в точной форме, а затем в округленной форме (с точностью до сотых). (Обратите внимание, что при указании радиуса его значение центрируется над сегментом радиуса. Когда указывается диаметр, его значение центрируется над сегментом диаметра. )

Решения

1. Точно 8π дюймов; округлено от точного ответа 25,13 дюйма; округлено с использованием 3,14 для π 25,12 в
2. Точно 12,44π м; округлено от точного ответа 39,08 м; округлено с помощью 3,14 для π 39,06 м

Точная форма и округленная форма

• π — число в точной форме. Он не округлый.
• 3.14 — приближение округленной формы для π

Почему так важно, какую форму мы используем? Это важно, потому что, когда мы округляем, мы вносим ошибку в наш окончательный результат. Для этого класса эта ошибка обычно приемлема. Однако вы обнаружите, что в других предметах, таких как физика или химия, этот уровень точности имеет большое значение. Давайте посмотрим на пример разницы в формах.

Пример 4

Радиус Луны составляет около 1079 миль. Что такое окружность? Давайте решим это, используя как точную форму, так и округленную форму:

Точное решение

C=2πr=2π(1079)=2158πC=2\pi{r}= 2\pi(1079)=2158\pi\\C =2πr=2π(1079)=2158π

Чтобы округлить из точного решения, используйте кнопку π на калькуляторе, чтобы получить

2158π≈6779,562158\pi\приблизительно6779,56\\2158π≈6779,56

7

С=2πr=2(3,14)(1079)≈6776,12C=2\pi{r}= 2(3,14)(1079)\приблизительно6776,12\\C=2πr=2(3,14)(1079)≈6776,12

Обратите внимание, что наши окончательные результаты отличаются. Эта разница является ошибкой, возникающей при использовании 3.14 в качестве начального приближения для π. Выполняя домашнее задание и тесты, внимательно читайте указания по каждой задаче, чтобы понять, какую форму использовать.

Пример 5

Найдите длину окружности или периметра в каждой описанной ниже ситуации. Включите чертеж формы с включенной информацией. Используйте примеры, чтобы определить, какие фигуры нужно рисовать. Показать все работы. Как и в примерах, если единицы включены, единицы должны присутствовать в конечном результате. Округлите до десятых, если не указано иное.

1. Найдите периметр квадрата со стороной 2,17 фута.
2. Найдите периметр прямоугольника со сторонами 4,2 и 3,8.
3. Найдите периметр треугольника со сторонами 2, 5, 7.
4. Найдите длину окружности радиусом 6 дюймов. Представьте ответ в точной форме, а также вычислите число π по формуле 3.14. Присутствует округлая форма с точностью до десятых.
5. Найдите длину окружности круга диаметром 14,8 дюйма. Представьте ответ в точной форме, а также вычислите, используя 3.14 для π. Присутствует округлая форма с точностью до десятых.

Решения

1. 8,68 футов
2. 16
3. 14
4. Точные 12π дюймов, округленные 37,7 дюймов
5. Точное 14,8π дюйма, округленное 46,5 дюйма

Пример 6

Определение расстояния вокруг нестандартных форм

Основные формулы для периметра прямолинейных фигур и длины окружности помогут нам найти расстояние вокруг более сложных фигур. Найдите расстояние вокруг следующей фигуры. Округлите окончательный ответ до десятых и используйте 3,14 для π.

Решение

34,7 дюйма

Пример 7

Применение периметра и окружности

Наши знания об основных геометрических фигурах можно применить для решения «реальных» задач.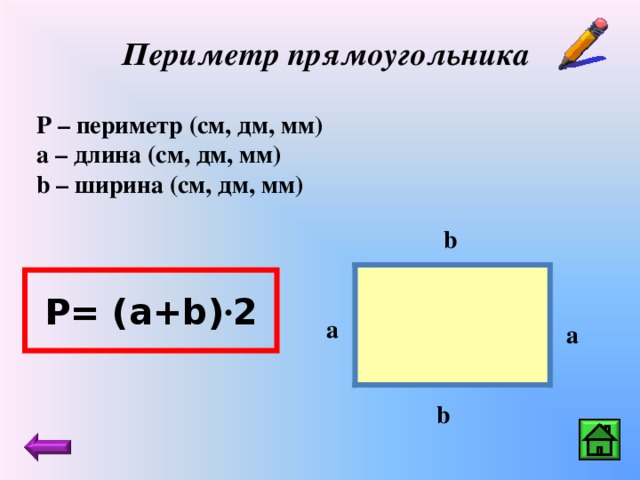

Уолли хочет добавить забор к задней части своего дома, чтобы его дети могли безопасно играть (см. схему ниже). Он начал измерять свой двор, но отвлекся и забыл закончить измерение перед тем, как пойти в магазин. Если он помнит, что задняя стена его дома имеет длину 15 ярдов, достаточно ли у него информации, чтобы купить необходимое ему ограждение? Если да, то сколько футов он должен купить?

Решение

81 фут

Площадь

Давайте еще раз взглянем на задний двор Уолли из примера 7, чтобы ввести следующее понятие: площадь.

Пошаговый пример

Уолли успешно огородил свой двор, но теперь хочет немного озеленить его и создать лужайку, как показано ниже.

Он направляется в местный магазин газонов и узнает, что для того, чтобы определить, сколько дерна ему нужно, он должен вычислить площадь участка, на который он хочет добавить траву.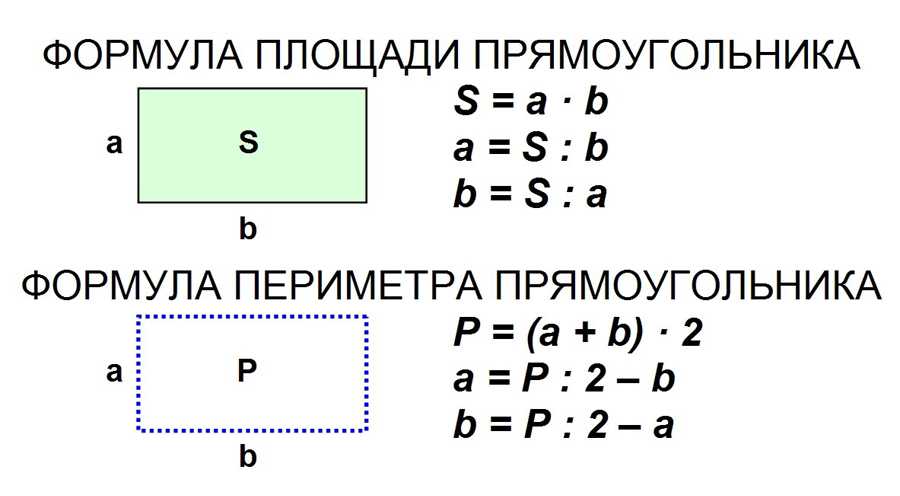 По пути домой он понимает, что если он разделит травяной участок на участки размером 1 фут на 1 фут, а затем посчитает их, то сможет определить площадь участка в квадратных футах. Вот информация, которую Уолли нарисовал, когда вернулся домой.

Уолли правильно определил, что площадь прямоугольной травянистой секции составляет 30 квадратных футов.

Примечания к площади

• Площадь — это двумерное измерение, представляющее объем пространства внутри двумерной формы.
• Чтобы найти площадь, подсчитайте количество единичных квадратов внутри фигуры.
• Если есть единицы, включите их в окончательный результат. Единицы измерения всегда будут двумерными (например, квадратные футы, квадратные ярды, квадратные мили и т. д.)

Пример 8

Найдите площадь каждой из фигур ниже.

1. Не забудьте подсчитать единицы квадратов внутри фигуры.

2. Есть ли здесь закономерность, которая облегчила бы нам работу?

Пример 9

Как найти площадь более сложных фигур? Разбейте области на формы, которые мы узнаем, и сложите значения площади вместе.

Если вы внимательно посмотрите на фигуры в предыдущих примерах, вы можете заметить некоторые способы записи каждой области в виде более явной формулы. Посмотрите, соответствуют ли результаты того, что мы сделали до сих пор, приведенным ниже формулам. 92\\А=а2

Прямоугольник с длинами сторон a , b

A=a⋅bA=a\cdot{b}\\A=a⋅b

(Вы также увидите это как

A=length⋅widthA=\text{длина}\cdot\text{ширина}\ \A=длина⋅ширина

)

Формулы площади для приведенных ниже фигур вывести сложнее, поэтому формулы приведены в таблице.

Форма	Форма
Треугольник с высотой h и основанием b A=12bh=bh3\displaystyle{A}=\frac{1}{2}bh=\frac{bh}{2}\\A=21​bh=2bh​ Читается как «половина основания, умноженная на высоту». Обратите внимание, что h — это расстояние по прямой линии от вершины треугольника непосредственно до другой стороны. На это указывает маленькое поле рядом с h . С точки зрения математики прямоугольник обозначает угол 90º (прямой).	Круг радиусом r 92\\A=πr2 Читается как «пи умножить на квадрат радиуса»
	Если ваш треугольник такой, как на рисунке слева, то высота нарисована и измерена за пределами треугольника. Формула площади такая же.

Пример 10

Найдите площадь для каждой описанной ситуации. Создайте рисунок формы с включенной информацией. Показать все работы. Как и в примерах, если включены единицы измерения, они должны присутствовать и в конечном результате. Используйте 3.14 для π и при необходимости округлите ответы до десятых.

1. Найдите площадь прямоугольника, длина которого равна 12,9 метра, а высота составляет одну треть этой суммы.
2. Найдите площадь треугольника с основанием

   2412\displaystyle{24}\frac{1}{2}\\2421​

   дюймов и высотой 7 дюймов.
3. Найдите площадь круга с радиусом

   213\displaystyle{2}\frac{1}{3}\\231​

   дюймов. Представьте ответ в точной форме, а также вычислите округленную форму, используя 3.14 для π. Присутствует округлая форма с точностью до десятых.

Решения

1. 55,5 м ² или 55,5 квадратных метров (округлено)
2. 85,8 дюйма ² или 85,8 квадратных дюйма (округленные)
3. Точное 49/9 π в ² , округленное 17,1 в ²

Пример 11

Найдите площадь для каждой описанной ситуации. Включите рисунок формы с включенной информацией. Показать все работы. Как и в примерах, если включены единицы, то единицы должны присутствовать в конечном результате. Округлите ответы до десятых, если не указано иное.

1. Найдите площадь квадрата со стороной 4,2 фута.
2. Найдите площадь прямоугольника со сторонами 4,2 и 3,8.
3. Найдите площадь треугольника с высотой 7 дм и основанием 12 дм.
4. Найдите площадь круга радиусом 6 дюймов. Представьте ответ в точной форме, а также вычислите, используя 3.14 для π. Присутствует округлая форма с точностью до десятых.

Решения

1. 17,64 фута ² или 17,64 кв. фута
2. 16,0
3. 42 дюйма ² или 42 квадратных дюйма
4. Точное число 36π в ² или 36π квадратных дюймов, округление до 3,14 для π 113,0 в ² или 113,0 квадратных дюймов

Пример 12

Нахождение площади нестандартных фигур

Основные формулы площади помогут нам найти площадь более сложных фигур. Это та же проблема, для которой мы нашли периметр ранее. Найдите площадь заданной фигуры. Вычислить, используя 3,14 для π и округлить до ближайшей десятой.

Решение

Округлено с использованием 3,14 для π 25,9 дюйма ²

Пример 13

Применение площади и периметра

Мы можем объединить наши знания о площади/периметре для решения таких задач, как эта.

Уолли все еще ремонтирует свой дом и должен закончить проект пола. Он хочет купить достаточное количество бамбукового паркета, чтобы покрыть площадь пола в комнатах A, C и коридоре B, а также достаточное количество бамбуковой кромки для плинтусов во всех помещениях. Сколько квадратных футов полов и сколько футов плинтусов он должен купить?

Решение

256 футов ² настил, 108 футов окантовка

Лицензии и атрибуты

Лицензионный контент CC, совместно используемый ранее

• Учебник по основам арифметики. Авторы : Донна Годе, Эми Вольпе и Дженифер Бохарт. Предоставлено : Общественный колледж Скоттсдейла. Расположен по адресу : https://sccmath.wordpress.com/. Лицензия : CC BY-SA: Attribution-ShareAlike

периметр, площадь

периметр, площадь

Периметр и площадь

Измерение снаружи и внутри

Твой папа только что закончил сооружение террасы на заднем дворе и хочет поставить вокруг нее перила, оставив 2-футовое пространство для входа. Ему также нужен большой кусок желтого холста, чтобы покрыть квадратный угол прямоугольной колоды, так что там будет теневое пятно. Он просит вас помочь ему рассчитать, какой длины перила и сколько холста нужно купить для проекта. Итак, вы рисуете эту диаграмму и вставляете показанные меры:

Длина перил составляет 2 фута меньше периметра или расстояния вокруг настила.
2 стороны размер 10 футов , одна сторона 15 футов а другая 13 футов (промежуток 2 фута).

10 + 10 + 15 + 13 = 48 футов перил.

Желтое полотно представляет собой квадрат со стороной = 5 футов 9 дюймов.0588 , поэтому мы можем « возвести в квадрат » в
25 квадратов , которые измеряют 1 фут на 1 фут .

Площадь холста для абажура составляет 5 футов × 5 футов = 25 квадратных футов (ft²).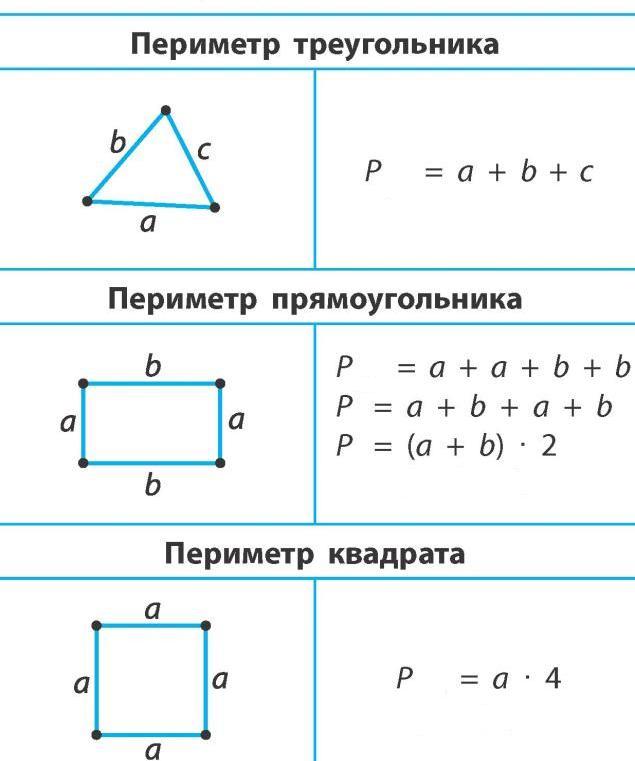

Периметр: измерение снаружи

Префикс пери- означает « вокруг или вокруг » — как в пери прицел — устройство, которое капитан подводной лодки использует для проверки того, что происходит на поверхности, когда субмарина находится под водой. . А «метр» означает «мера» — так что периметр означает меру или расстояние вокруг снаружи чего-то.

Когда нам нужно найти периметр неправильной фигуры , у которой нет равных сторон, мы просто добавляем длины всех сторон . Если у нас есть квадрат или прямоугольник , мы можем сократить путь, потому что — с квадратом все стороны равны той же длины , а с прямоугольник , у нас есть 2 пары сторон которые имеют одинаковую длину . Для этих фигур разрабатываем формул .

Поскольку прямоугольник имеет 2 пары равных сторон , вместо сложения их длин по отдельности для нахождения периметра мы используем формулу. Мы видим, что если мы удвоим сумму длины и ширины , мы получим периметр. Итак, «называем» длину и ширину л и ш — тогда пишем формулу.

P = 2 l + 2 w = 2 ( l + w )
а для квадрата или ромба это P = 4 s , где длина стороны = s .

длина и ширина прямоугольника также называются это основание и высота .

Примеры:

1) Найдите Периметр :

a) Параллелограмм (//gm) с верхом/низом = 7 сантиметров и сторонами = 9 сантиметров
Периметр = 2 (7 + 9) = 2 (16) = 32 сантиметра .

b) Прямоугольник с длиной ( l ) = 14 сантиметров и шириной ( w ) = 10 сантиметров
Периметр = 2 (14 + 10) = 2 (24) = 48 сантиметров.

c) A Квадрат со стороной ( s ) = 12 метров .
Периметр = 4 (12) = 48 метров .

ОСТОРОЖНО!! из смешанных единиц!! Если одна мера равна сантиметров , а другая метров , мы должны преобразовать , чтобы иметь единиц одинакового размера складывать и умножать. Ответы должны включать единицы!!

Пример:
Найдите периметр параллелограмма (//gm) с верхом/низом = 2 метров , сторона = 9 сантиметров .
Решение: Если мы заменим метров на сантиметров : 2 метра = 2 × 100 = 200 сантиметров
, то Периметр = 9 (20) = 418 сантиметров .
Или мы можем изменить 9 сантиметров на 0,09 метров ,
и Периметр = 2 (2 + 0,09) = 4,18 метра .

Область: покрытие поверхности

Вещи, которые мы используем, например, краски, обои и ковры, для покрытия таких поверхностей, как стены и полы, всегда измеряются и оцениваются по цене в квадратных единицах . Информация на каждой банке с краской этикетка включает количество квадратных футов или квадратных метров площади стены, краска покроет .

Мера поверхности , покрытой замкнутой фигурой, называется ПЛОЩАДЬ .
Мы измеряем площадь в КВАДРАТНЫХ ЕДИНИЦАХ — квадратные дюймы, квадратные футы, квадратные мили —
потому что, чтобы измерить площадь фигуры, мы » возводим в квадрат », а затем посчитайте квадраты.

Видим, чтобы полностью закрыть розовый квадрат ( 5 × 5 ), серыми квадратами ( 1 × 1 ),
мы будем использовать 5 рядов по 5 квадратов в каждом, так что всего нам понадобится 25 квадратов.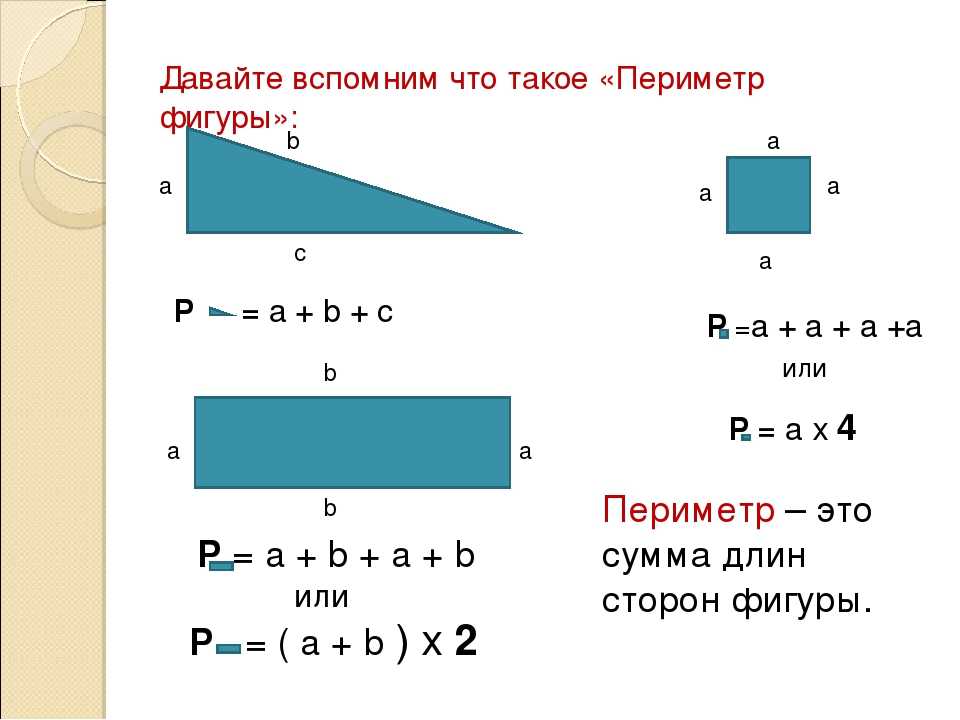
Площадь квадрата 5 на 5 = 25 единиц².
Площадь квадрата со стороной 9 дюймов = 81 дюйм² ( квадратных дюймов ).

Формулы площади
рисунок	Формула площади	Комментарии
Квадрат	А = с²	все стороны = с
Прямоугольник	А = Д × Ш	длина = l , ширина = w
треугольник	А = ½ ( ш × ч )	основание = b , высота перпендикуляра = h

.

Теперь возьмите карандаш, ластик и блокнот, скопируйте вопросы,
выполните практические упражнения, затем проверьте свою работу с решениями.
Если вы застряли, просмотрите примеры в уроке, а затем повторите попытку.

Практические упражнения

1) Для каждого изображения на диаграмме найдите периметр и площадь .
(убедитесь, что напишите формулу , используемую как для периметра, так и для площади)

2) Нарисуйте схему , затем решите каждый из этих вопросов:
а) Площадь прямоугольника = 36 дм². Длина l = 9 дюймов, найдите ширину w и периметр.
б) Периметр квадрата = 44 дюйма. Найдите длину стороны s и площадь.
в) Периметр прямоугольника равен 9.6 футов. Если основание равно дважды по длине высота ,
найти размеры и площадь.

3) Деревянная рамка вокруг фотографии размером 8 × 10 дюймов имеет ширину 2 дюйма со всех сторон.
Найдите а) периметр рамки; б) площадь деревянного каркаса.

Решения

1)

Периметр	Площадь
а) P = сумма сторон = 28,8 дюйма	Прямоугольник Область: A = B × H = 9 × 5 = 45 в² ТРИ -РАЙОН ( A = ½ ( A = ½ ( A = ½ ( A = ½ . × 2) = 9 дюймов² общая площадь = 45 кв. дюймов + 9 кв.0102	A = длина × ширина = 3,18 × 1,06 = 3,37 фут²
c) P = 4 с = 802 см 21	A = s² = 49 см²
d) P = сумма сторон = 29,3 ярда	Фигура представляет собой квадрат 4 на 4 и 2 треугольника: квадрат площадь: A = s² = 16 ярдов ² левый треугольник: a = ½bh = ½ (4²) = 8 ярдов ² Правой треугольник: A = ½BH = ½ (5,5 ² 4) = 98888 = ½ (5,5 × 4) = 11060998888 = ½ (5,5 × 4) = 98888 = ½ (5,5 × 4) = 8888 = ½ (5,5 × 4) = 88888889 гг. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт