3 класс, периметр и площадь прямоугольника
Дата публикации: .
Что такое прямоугольник и квадрат
Прямоугольник – это четырёхугольник, у которого все углы прямые. Значит, противоположные стороны равны друг другу.
Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.
Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D …
Пример.
Читается так: четырёхугольник ABCD; квадрат EFGH.
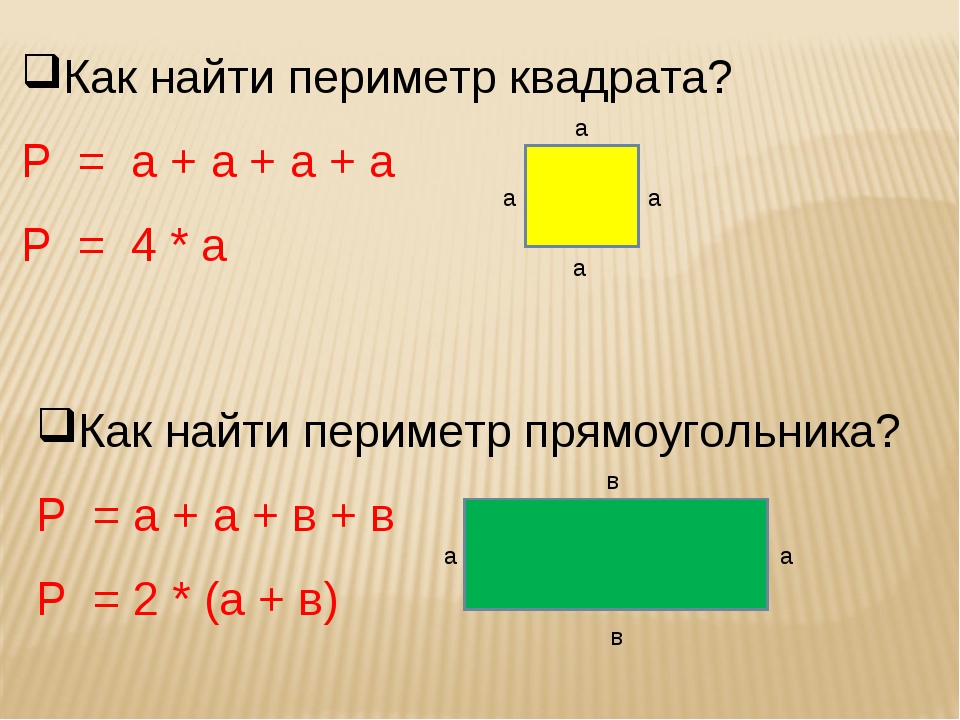
Что такое периметр прямоугольника? Формула расчета периметра
Периметр прямоугольника – это сумма длин всех сторон прямоугольника или сумма длины и ширины, умноженная на 2.
Периметр обозначается латинской буквой P. Так как периметр – это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.
Например, периметр прямоугольника АВСD обозначается как PABCD, где А, В, С, D – это вершины прямоугольника.
Запишем формулу периметра четырехугольника ABCD:
PABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)
Пример.
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см.
Определим PABCD.
Решение:
1. Нарисуем прямоугольник ABCD с исходными данными.
2. Напишем формулу для расчета периметра данного прямоугольника:
PABCD = 2 * (AB + BС)
3. Подставим в формулу наши данные:
PABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см
Ответ: PABCD = 16 см.
Формула расчета периметра квадрата
У нас есть формула для определения периметра прямоугольника.
PABCD = 2 * (AB + BC)
Применим её для определения периметра квадрата.
Учитывая, что все стороны квадрата равны, получаем:PABCD= 4 * AB
Пример.
Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата.
Решение.
1. Нарисуем квадрат ABCD с исходными данными.
2. Вспомним формулу расчета периметра квадрата:
PABCD = 4 * AB
3. Подставим в формулу наши данные:
PABCD = 4 * 6 см = 24 см
Ответ: PABCD = 24 см.Задачи на нахождение периметра прямоугольника
1. Измерь ширину и длину прямоугольников. Определи их периметр.
2. Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника.
3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.
Где используется расчет периметра прямоугольника?
1. Задан участок земли, его нужно обнести забором. Какой длины будет забор?
В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора.
2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев.
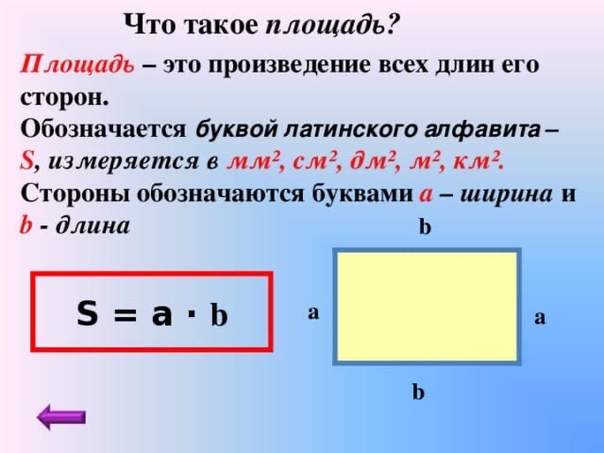
Что такое площадь прямоугольника?
Площадь – это числовая характеристика фигуры. Площадь измеряется квадратными единицами длины: см2, м2, дм2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.)
В вычислениях обозначается латинской буквой S.
Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Площадь прямоугольника вычисляется умножением длины АК на ширину КМ. Запишем это в виде формулы.
S AKMO = AK * KM
Пример.
Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?
S AKMO= AK * KM = 7 см * 2 см = 14 см2.
Формула вычисления площади квадрата
Площадь квадрата можно определить, умножив сторону саму на себя.
Пример.
В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.
S AВСО = AB * BC = AB * AB
Пример.
Определи площадь квадрата AKMO со стороной 8 см.
S AKMО = AK * KM = 8 см * 8 см = 64 см2
Ответ: 64 см2.Задачи на нахождение площади прямоугольника и квадрата
1.Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.
2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.
| 1. Организационный момент | – Ребята, наш урок мы сегодня начнем с
пословицы.
– Какой формулой мы воспользуемся для
нахождения площади? |
||||||||||||||
| 2. Самоопределение к деятельности Актуализация знаний |
– Ребята, вы выбрали верные формулы для
нахождения периметра и площади. Появляются
напротив каждой формулы слова.«Уменье –… найдет применение» – Вы заметили, что в пословице не хватает еще одного слова. Подумайте, за какой же формулой скрывается недостающее слово. Узнав его, мы сможем сказать девиз нашего урока. (Слайд 2) – Эти формулы будут нам сегодня помогать решать задачи на нахождение периметра и площади прямоугольника. На слайде представлены геометрические фигуры. (Слайд 3) Назовите номера фигур, которые являются прямоугольниками. Д: фигуры под номерами 1, 2, 3. Лишние фигуры исчезают по щелчку. Д: Высказывания под номерами 1, 4 являются ложными, а высказывания под номерами 2, 3, 5 – истинными. самостоятельно. (Слайд 5) – Молодцы, ребята.  Следующее задание решить
задачу. Найдите площадь прямоугольника со
сторонами 8см и 5см |
||||||||||||||
| Устные упражнения | 8 * 5 + 2 * 5 = 50 (см2) 8 * 5 = 40 (см2) 8 * 5 + 2 * 5 = 50 (см) 8 * 5 = 40 (см) 8 * 2 + 5 = 21 (см) (8 + 5) * 2 = 26 см – Найдите правильно
записанное решение задачи и запишите ответ в
тетрадь. Проверка решения. Д: Площадь измеряется квадратной меркой. |
||||||||||||||
| Ученики записывают величины в нужном порядке у себя в рабочих тетрадях | – Ребята, расположите величины в
порядке убывания . При верном составлении у вас
должно поучится слово. (Слайд 6)
|
||||||||||||||
3. Постановка учебной задачи |
Самопроверка записи – на слайде (клик
мышкой) Дети: 50м2, 15м2, 80 дм2, 7дм2, 70см2, 15см2 , 10см2– Какое слово у вас получилось? (Квадрат) |
||||||||||||||
| Исследование общих признаков геометрических фигур | – Определите содержание двух понятий
прямоугольника и квадрата:
Вывод: Чем больше содержание понятия,
тем меньше его объем. |
||||||||||||||
| Работа над построением графической модели | – Сравните объемы понятий
«прямоугольник» и «квадрат» (Слайд 7) Д: Объем понятия прямоугольник шире, чем объем понятия квадрат – Употребляя слова «все», «некоторый», «каждый», «ни один», установите отношения между понятиями квадрат и прямоугольник (Слайд 8) Д: Некоторые прямоугольники являются квадратами. Каждый квадрат является прямоугольником. – Как изобразить отношения между понятиями прямоугольник и квадрат? (Слайд 9) Д: С помощью кругов Эйлера-Венна. |
||||||||||||||
| Физпауза | Раз – согнуться, разогнуться, Два – нагнуться, потянуться, Три – в ладоши три хлопка, Головою три кивка, На четыре руки шире. 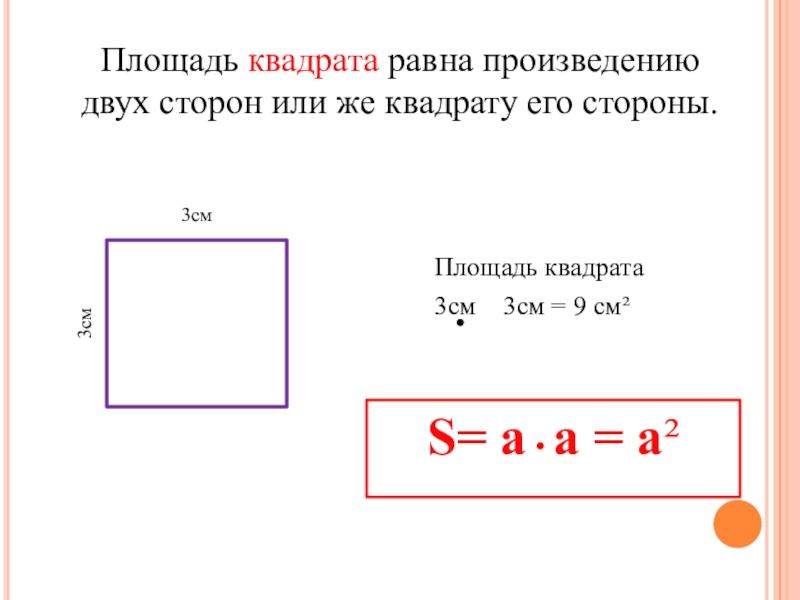 Пять, шесть – тихо сесть. |
||||||||||||||
| Использование проблемной ситуации. Своими вопросами учитель подводит учащихся к новым знаниям. | Можно ли вычислить периметр и площадь
квадрата, используя формулы? (Слайд 10)
Появляется формула: S = а * а. – Что это за формула? |
||||||||||||||
| 4. Закрепление (фронтальная работа) | – Сейчас, используя, формулы мы с вами
будем решать задачи. Учебник с.173 №590. – Прочитайте условие задачи. Длина школьного бассейна в 3раза больше его ширины. Чему равен P бассейна, если его ширина равна 9м. – О какой фигуре идет речь в задаче? (Прямоугольник) – Что известно в задаче? (Ширина прямоугольника, известно что длина в 3 раза больше его ширины). – Что мы можем узнать, используя эти данные? (Можем найти длину) – Как мы узнаем длину? а = 9 * 3 = 27 м – Можем ли мы зная длину и ширину прямоугольника, найти Р? (Можем, используя формулу Р = (а + в)* 2 Р б.  = (9 + 27) * 2 = 72 мВывод: Где в жизни можно применить полученные умения и навыки при решении задач на нахождение периметра и площади? Д: В строительстве, на дачном участке, в ремонтных работах. |
||||||||||||||
| Групповая работа (задания предложенные учащимся, имеют компетентностно-ориентированное содержание) Создание ситуации успеха. У группы ориентир на мыслительную деятельность « Мы группа, значит мы способны действовать. В ходе рассуждений при решении технического задания, предоставляется свобода для самовыражения. |
Класс делится на группы (бригады) по 4
человека. Каждой бригаде предлагается выполнить
техническое задание. (Слайд 11) Каждый участник представляет отдельный этап работы. Роли в группе показаны на магнитной доске: – организатор – спикер – секрет – контролер Группа, которая безошибочно справится с работой, выигрывает право принять участие в проведении ремонтных работ на территории школы во время осенних каникул.  Лучшая бригада награждается
путевкой в зимний пришкольный лагерь. (Слайд 12) |
||||||||||||||
| Использование метода моделирования.
Наиболее удобные способы записи. Ребята при выполнении работы используют материальную и математическую модели |
1 задание. На пришкольном
участке необходимо установить бордюр вокруг 2-х
детских площадок. Сколько потребуется материала,
если длина 1 бордюра 1 м? Д: Мы
воспользовались формулой для нахождения
периметра?
2 задание. Вычислите площади фигур,
если дана мерка. (Слайд 13) Д: Мы вычислили S фигур, используя мерку величиной 10м2. Путем переложения квадрата мерки на фигуры. Мы нашли а и b. Вторую фигуру, мы превратили в прямоугольник, пререложив квадраты, для быстроты вычисления. (Слайды 14, 15) 3 задание (Слайд 16). Часть покрытия на теннисном корте испортилась. Необходимо в ходе ремонтных работ заменить покрытие и установить ограждение вокруг корта. Сколько материала потребуется? Д: Чтобы найти площадь и периметр, надо
знать его длину. От данного прямоугольника
осталась часть, нам известна ширина 30 м2.
Слева мы добавляем до 20 м2 Длина 80 м2 и
вверху добавляем 60м2 . Используя, свойства
прямоугольника, у него противоположные стороны
равны.
– Молодцы, ребята вы отлично справились с техническим заданием! |
||||||||||||||
| 5. Домашнее задание | Составить задачу по вариантам. Составить 2 задачи на нахождение периметра и площади, используя числовые данные в пределах второго десятка. В будущем мы все должны научиться решать задачи на нахождение периметра и площади только на 5. |
||||||||||||||
| 6. Рефлексия | – Что удалось нам сегодня открыть на
уроке? Расскажите. (Решали практические задачи,
учились строить модели, взаимодействовать друг с
другом в группах, учились обосновывать свой
выбор, сравнивать, упорядочивать информацию) –
Какое задание показалось наиболее трудным? А
какое наиболее интересным. Д: Уроки математики учат нас знаниям, навыкам, что нам может пригодиться и найти применение в нашей жизни. – Девизом нашего урока были слова «Умение –
везде найдет применение». И мы это доказали,
применяя нужные формулы для решения задач.
Данное умение вам пригодится при выполнении
домашнего задания. |
Вычислите, сколько
материала уйдет на каждый участок?
Периметр и площадь треугольника | Геометрия
Периметр
Периметр любого треугольника равен сумме длин трёх его сторон. Общая формула для нахождения периметра треугольников:
P = a + b + c,
где P — это периметр треугольника, a, b и c — его стороны.
Периметр равнобедренного треугольника можно найти сложив последовательно длины его сторон или умножив длину боковой стороны на 2 и прибавив к произведению длину основания.
Общая формула для нахождения периметра равнобедренных треугольников будет выглядеть так:
P = 2a + b,
где P — это периметр равнобедренного треугольника, a — любая из боковых сторон, b — основание.
Периметр равностороннего треугольника можно найти сложив последовательно длины его сторон или умножив длину любой его стороны на 3. Общая формула для нахождения периметра равносторонних треугольников будет выглядеть так:
P = 3a,
где P — это периметр равностороннего треугольника, a — любая из его сторон.
Площадь
Для измерения площади треугольника можно сравнить его с параллелограммом. Рассмотрим треугольник ABC:
Если взять равный ему треугольник и приставить его так, чтобы получился параллелограмм, то получится параллелограмм с той же высотой и основанием, что и у данного треугольника:
В данном случае общая сторона сложенных вместе треугольников является диагональю образованного параллелограмма.
Из свойства параллелограммов известно, что диагональ всегда делит параллелограмм на два равных треугольника, значит площадь каждого треугольника равна половине площади параллелограмма.
Так как площадь параллелограмма равна произведению его основания на высоту, то площадь треугольника будет равна половине этого произведения. Значит для ΔABC площадь будет равна
Теперь рассмотрим прямоугольный треугольник:
Два равных прямоугольных треугольника можно сложить в прямоугольник, если прислонить их друг к другу гипотенузой. Так как площадь прямоугольника равна произведению его смежных сторон, то площадь данного треугольника равна:
Из это можно сделать вывод, что площадь любого прямоугольного треугольника равна произведению катетов, разделённому на 2.
Из данных примеров можно сделать вывод, что площадь любого треугольника равна произведению длин основания и высоты, опущенной на основание, разделённому на 2.
Общая формула площади треугольника:
где S — это площадь треугольника, a — его основание, ha — высота, опущенная на основание a.
Интернет-урок по математике «Задачи на нахождение площади и периметра
Прежде, чем решать задачи на нахождение периметра и площади геометрических фигур, напомню, что….
I уровень
1.Длина прямоугольника 8 дм, ширина 7 дм. Найди его площадь.
2.Длина стороны квадрата 6 см. Узнайте площадь и периметр квадрата.
3.У прямоугольника длина 7 см, ширина 5 см. Узнайте площадь и периметр прямоугольника.
4.Найдите периметр и площадь прямоугольника со сторонами 6 см и 8 см.
5.Длина прямоугольника 8 дм, ширина 5 дм. Найди его площадь.
6.Вычисли площадь прямоугольника, длины сторон которого равны 6 мм и 8 мм.
7.Ширина прямоугольника 7 дм, а длина 12 дм. Вычисли площадь.
8.Длина прямоугольника 9 дм, ширина 7 см. Найди его площадь.
9.Длина стороны квадрата 6 см. Узнай площадь.
10.Вычисли периметр квадрата со стороной 4 см.
11.Ширина прямоугольника равна 9 дм, а длина на 6 дм больше. Найдите его площадь.
12.Длина прямоугольника равна 5 дм, ширина — на 4 см меньше. Найдите Р и S этого прямоугольника.
13.Начерти прямоугольник, длина одной стороны которого 2 см, а длина другой в 3 раза больше. Найди его периметр и площадь.
14.Начерти прямоугольник, длина одной стороны которого 6 см, а длина другой в 2 раза больше. Найди его периметр и площадь.
15.Начерти прямоугольник, ширина которого равна 2 см, а длина на 3 см больше. Вычисли его периметр.
16.Сторона квадрата равна 3 см. Чему равен периметр?
17.Лист бумаги имеет квадратную форму. Его сторона равна 10 см. Чему равен периметр?
18.Начерти квадрат со стороной 6 см. Найдите его периметр. Периметр квадрата равен 28 см. Чему равна его сторона?
19.
Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычисли площадь окна.
20.Ширина прямоугольника 4 дм, а длина в 5 раз больше ширины. Найди площадь прямоугольника.
21.Площадь прямоугольника 36 см², его длина 9 см. Чему равна ширина прямоугольника?
II уровень
1.Начерти прямоугольник, длина одной стороны которого 2 см, а длина другой в 4 раза больше. Найди его периметр и площадь.
2.Длина прямоугольника равна 5 дм, ширина — на 4 см меньше. Найдите Р и S этого прямоугольника.
3.Дано: прямоугольник, а = 8 дм, в — на 2 см меньше. Найди Р и S.
4.Длина прямоугольника 12 см, а его ширина на 2 см меньше. Найдите площадь и периметр прямоугольника.
5.Сумма двух сторон квадрата 12 дм. Найдите периметр и площадь квадрата.
6.Найдите длину прямоугольника по его ширине – 8 дм и периметру–30 дм.
7.Периметр квадрата равен 32 см. Чему равна его сторона?
8.Периметр треугольника 21 см. Надите длину третьей стороны этого треугольника, если длины двух сторон 7 см и 8 см.
9.Периметр прямоугольника 20 см. Длина его стороны 6 см. Узнайте ширину прямоугольника и начертите его.
10.Площадь прямоугольника равна 270 кв.см, его длина 9 дм. Найдите периметр этого прямоугольника.
11.Периметр прямоугольника равен 54 м. Найдите площадь этого прямоугольника, если одна его сторона равна 18 м.
12.Найдите площадь квадрата, периметр которого равен 360 мм.
13. Периметр прямоугольника 40 см. Одна сторона 5 см.Чему равна его площадь?
14. Начерти квадрат, периметр которого равен периметру прямоугольника со сторонами 2 см и 6 см.
15. Дачный участок прямоугольной формы имеет длину 20 м и ширину 12 м. Какой длины забор надо поставить вокруг участка?
16. Периметр квадрата равен периметру треугольника со сторонами 6 см, 3 см и 7 см. Чему равна длина стороны квадрата?
17. У какой фигуры площадь больше и на сколько: у квадрата со стороной 4см или у прямоугольника со сторонами 2 см и 6 см?
18. Периметр прямоугольника равен 54 м.
Найди площадь этого прямоугольника, если одна его сторона равна 18 м.
19. Периметр квадратной песочницы 12 м. Найдите площадь этой песочницы.
20. Напишите все возможные варианты длины и ширины прямоугольника, если его периметр 24 см.
Составила Кислова Людмила Борисовна
Как решать задачи на нахождение периметра, площади и объёма фигур в 4-5 классе
ПЕРИМЕТР
Периметр – сумма длин всех сторон плоской геометрической фигуры. Чаще всего периметр измеряется в сантиметрах, метрах и километрах.
Чаще всего периметр обозначается буквой P.
Периметр прямоугольника – удвоенная сумма длины и высоты — 2∙(a+b)
Периметр квадрата – произведение любой его стороны на 4, так как стороны равны.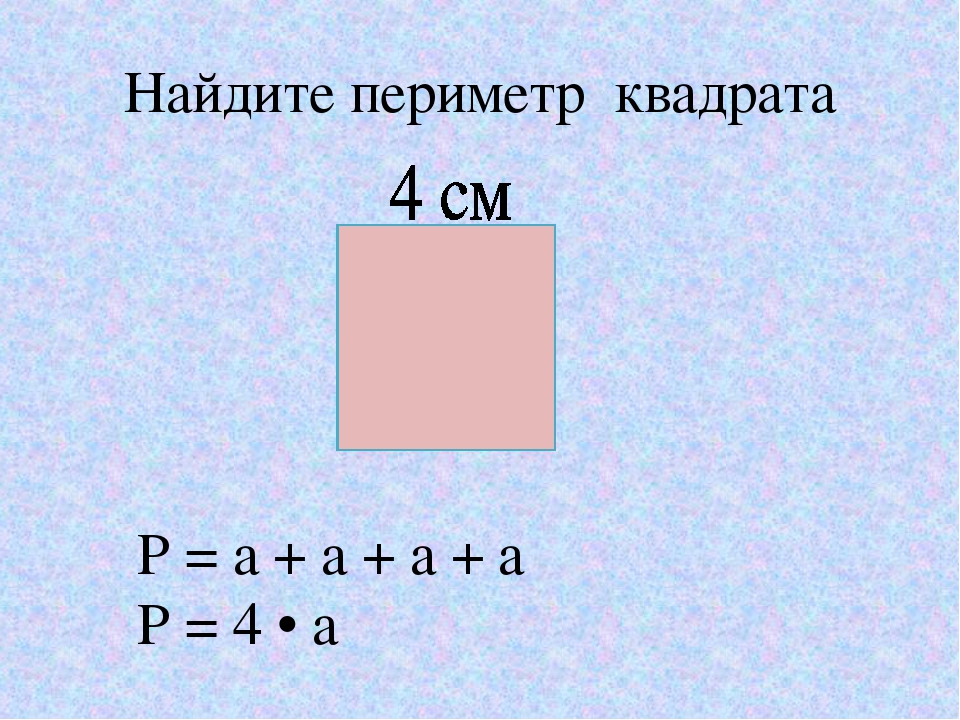
ПЛОЩАДЬ
Площадь – характеристика замкнутой геометрической фигуры, которая показывает ее размер. Чаще всего площадь измеряется в квадратных сантиметрах, квадратных метрах и квадратных километрах.
В отличие от периметра, не существует универсальной формулы площади. Для каждого типа фигур площадь вычисляется по своей особой формуле. Мы будем рассматривать только прямоугольники, квадраты и составные фигуры из прямоугольников и квадратов.
Чаще всего площадь обозначается буквой S.
Площадь прямоугольника – произведение длины на высоту.
Хотите, чтобы ваш ребёнок обучался самостоятельно?Вам поможет наш ВИДЕОКУРС
Разделим этот прямоугольник на квадраты
Мы получили 15 квадратов внутри этого прямоугольника – это и есть те самые 15 квадратных сантиметров, которые составляют площадь прямоугольника.
Площадь квадрата – произведение длины стороны на саму себя.
СОСТАВНЫЕ ФИГУРЫ
Разделим эту фигуру на прямоугольник и квадрат
Высота прямоугольника составит 5 – 3 = 2
СООТНОШЕНИЕ ПЛОЩАДИ И ПЕРИМЕТРА
Фигуры с одной и той же площадью могут иметь разный периметр
Почему у нас изменился периметр, хотя площадь, т.е. число квадратиков внутри фигуры, осталась прежней?
Потому что изменилось число граней квадратиков, которые участвуют в формировании сторон фигуры, т.е. перметра. В первой фигуре – большом квадрате, в формировании сторон участвовали по две внешних грани каждого маленького квадратика – общее число таких граней 8, и периметр равен 8.
Во второй фигуре у нас в формировании сторон участвуют по три грани у двух крайних квадратиков и по две грани внутренних квадратов. Общее число таких граней 10, и периметр равен 10.
ОБЪЁМ
Объём – количественная характеристика пространства, занимаемого телом или веществом.
Чаще всего объём измеряется в кубических сантиметрах, кубических дециметрах, кубических метрах и литрах.
1 л = 1 дм3
Не существует универсальной формулы объема. Для каждого типа фигур объём вычисляется по своей особой формуле. Мы будем рассматривать только прямоугольные параллелепипеды.
Чаще всего объём обозначается буквой V.
Прямоугольный параллелепипед – замкнутая фигура, у которой 6 прямоугольных граней (передняя, задняя, нижняя, верхняя и две боковые), и каждая из граней расположены под прямым углом к соседним.
Объём прямоугольного параллелепипеда – произведение его длины, ширины и высоты
Зная объём и две стороны, мы можем найти третью сторону:
c = (V:a):b = V:S
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.ЗАДАЧИ
Задача 1.
Найдите периметр и площадь прямоугольника, у которого ширина 10 см, и она меньше длины на 6 см.
x = 10 см – ширина
1. Найдём длину
y = 10 + 6 = 16 см
2. Найдём периметр
P = 2∙(10+16) = 52 см
3. Найдём площадь
S = 10∙16 = 160 см2
Ответ: P = 52 см, S = 160 см2
Задача 2. Какую ширину имеет прямоугольник, длина которого 50 см, а площадь совпадает с площадью квадрата периметром 80 см?
1. Вычислим сторону квадрата
4∙n = 80 — периметр
n = 20 см
2. Вычислим площадь квадрата
20∙20 = 400 см2
3. Вычислим ширину прямоугольника
50∙x = 400 см2
x = 8 см
Ответ: 8 см
Задача 3. Чему равна ширина прямоугольника, длина которого равна 15 м, а площадь 7500 дм2 ?
1 дм = 10 см, 1 м = 100 см, 1 м = 10 дм
1. Переведём длину прямоугольника в дм
x = 15∙10 = 150 дм
2.
Найдём ширину прямоугольника
150∙y = 7500
y = 7500:150 = 50 дм
Ответ: 50 дм
Задача 4. Длина прямоугольника равна 60 см, и она в 3 раза больше ширины стороны.
1. Найдите площадь этого прямоугольника.
2. Найдите площадь квадрата, который имеет такой же периметр, как и прямоугольник.
3. Найдите периметр квадрата, площадь которого в 12 раз меньше площади прямоугольника.
1. Найдём ширину прямоугольника
x = 60:3 = 20 см
2. Найдём площадь прямоугольника
S = 60∙20 = 1200 см
2. Найдём периметр прямоугольника
P = 2∙(60+20) = 160 см
3. Найдём сторону квадрата
y = 160:4 = 40 см
4. Найдём площадь квадрата
Sкв = 40∙40 = 1600 см2
5. Найдём площадь квадрата, которая в 12 раз меньше площади прямоугольника:
Sкв2 = 1200:12 = 100 см2
6. Найдём сторону такого квадрата
Площадь квадрата = 100 см2
Из таблицы умножения мы знаем, что 10∙10 = 100, значит сторона квадрата = 10 см
7.
Найдём периметр такого квадрата
P = 10∙4 = 40 см
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.Задача 5. В прямоугольнике АВСД сторона АВ 3 см, сторона ВС на 1 см длиннее, а диагональ ВД на 2 см длиннее АВ. Найдите периметр и площадь прямоугольника АВСД и треугольника АВД.
1. Найдём сторону ВС
ВС = 3+1 = 4
2. Найдём диагональ ВД
ВД = 3+2 = 5
3. Найдём периметр АВСД
P = 2∙(3+4) = 14 см
4. Найдём площадь АВСД
Sавсд = 3∙4 = 12 см2
5. Найдём периметр треугольника АВД
Pавд = 3 + 5 + 4 = 13 см
6. Найдём площадь треугольника АВД
Треугольник АВД занимает половину площади прямоугольника АВСД
Sавд = Sавсд:2
Sавд = 12:2 = 6 см2
Задача 6. В аквариум в форме прямоугольного параллелепипеда, основание которого имеет стороны 80 и 40 см, налили до краёв 160 л.
воды. Какова высота аквариума?
Решение
1. Переведём литры в кубические дециметры
1 л = 1 дм3, 160 л = 160 дм3
2. Переведём стороны аквариума в дециметры
1 дм = 10 см, 80 см = 8 дм, 40 см = 4 дм
3. Найдём высоту аквариума
V = a∙b∙c, a = 8, b = 4
c = (V:a):b
c = (160:8):4 = 5 дм
c = 5∙10 = 50 см
Ответ: 50 см
ПНШ 4 класс. Математика. Учебник № 1, с. 40
Зависимость между величинамиОтветы к с. 40112. Приведи пример двух величин, которые находятся в некоторой зависимости одна от другой, а также двух величин, которые не зависят друг от друга.
Зависят.
Количество тарелок на столе в столовой от количества обедающих учеников. Количество учебников в портфеле ученика от количества уроков в школе.
Не зависят.
Время начала уроков в школе от количества учеников в классе.
Количество дней в каникулах от погоды.
113. Заполни в тетради данную таблицу, если известно, что длина α на 3 см больше, чем длина b.
| α (см) | 12 | 65 | 50 | 187 | 4568 |
| b (см) | 9 | 62 | 47 | 184 | 4565 |
Будет ли в данном случае величина b однозначно зависеть от величины α?
Величина b однозначно зависит от величины α, так как при каждом значении α, можно найти единственное значение b.
114. Если известен периметр квадрата, то можно ли однозначно установить его площадь? Сделай это для квадрата, периметр которого равен 20 см.
Объясни, почему площадь квадрата однозначно зависит от его периметра.
Можно, поскольку по известному периметру можно вычислить сторону квадрата. А вычислив его сторону, можно потом вычислить площадь по этой найденной стороне.
1) 20 : 4 = 5 (см) – одна сторона
2) 5 • 5 = 25 (кв. см) – площадь
Площадь квадрата однозначно зависит от его периметра, поскольку каждому значению периметра квадрата соответствует единственное значение площади.
115. Начерти два прямоугольника, у одного из которых стороны имеют длину 6 см и 4 см, а у другого соответственно 8 см и 2 см. Вычисли периметр и площадь каждого из этих прямоугольников. Сравни получившиеся периметры между собой и получившиеся площади между собой.
Если известен периметр прямоугольника, то можно ли однозначно установить его площадь?
Объясни, почему площадь прямоугольника не будет однозначно зависеть от го периметра. А что можно сказать о зависимости площади квадрата от его периметра? Проиллюстрируй это на примере.
Первый прямоугольник: Р = (6 + 4) • 2 = 20 (см), S = 6 • 4 = 24 (кв. см).
Второй прямоугольник: Р = (8 + 2) • 2 = 20 (см), S = 8 • 2 = 16 (кв. см).
Периметры прямоугольников равны, а площадь первого прямоугольника больше площади второго прямоугольника: 24 кв. см > 16 кв. см.
По известному периметру прямоугольника нельзя однозначно установить его площадь.
Потому, что у прямоугольников с одинаковым периметром могут быть разные площади, как выяснилось выше.
Площадь квадрата однозначно зависит от его периметра. Это видно из предыдущего задания №114: каждому значению периметра квадрата соответствует единственное значение площади.
Ответы к заданиям. Математика. Учебник. Часть 1. Чекин А.Л. 2012 г.
Математика. 4 класс. Чекин А.Л.
4.7 / 5 ( 120 голосов )
Задачи на нахождение периметра и площади
1.
Длина прямоугольника 8 см, а ширина на 5 см короче. Чему равен его периметр?
2.На сколько периметр квадрата со стороной 1 дм 2 см больше, чем периметр квадрата со стороной 5 см?
3.Одна сторона треугольника 13 см, вторая на 9 см больше первой, а третья на 4 см меньше первой. Найди периметр треугольника АВС.
4. На сколько площадь прямоугольника со сторонами 3 см и 4 см, меньше, чем площадь прямоугольника со сторонами 4 см и 5 см?
5. На сколько площадь квадрата со стороной 5 см, больше, чем площадь квадрата со стороной 3 см?
1. Длина прямоугольника 8 см, а ширина на 5 см короче. Чему равен его периметр?
2.На сколько периметр квадрата со стороной 1 дм 2 см больше, чем периметр квадрата со стороной 5 см?
3.Одна сторона треугольника 13 см, вторая на 9 см больше первой, а третья на 4 см меньше первой. Найди периметр треугольника АВС.
4. На сколько площадь прямоугольника со сторонами 3 см и 4 см, меньше, чем площадь прямоугольника со сторонами 4 см и 5 см?
5.
На сколько площадь квадрата со стороной 5 см, больше, чем площадь квадрата со стороной 3 см?
1. Длина прямоугольника 8 см, а ширина на 5 см короче. Чему равен его периметр?
2.На сколько периметр квадрата со стороной 1 дм 2 см больше, чем периметр квадрата со стороной 5 см?
3.Одна сторона треугольника 13 см, вторая на 9 см больше первой, а третья на 4 см меньше первой. Найди периметр треугольника АВС.
4. На сколько площадь прямоугольника со сторонами 3 см и 4 см, меньше, чем площадь прямоугольника со сторонами 4 см и 5 см?
5. На сколько площадь квадрата со стороной 5 см, больше, чем площадь квадрата со стороной 3 см?
1. Длина прямоугольника 8 см, а ширина на 5 см короче. Чему равен его периметр?
2.На сколько периметр квадрата со стороной 1 дм 2 см больше, чем периметр квадрата со стороной 5 см?
3.Одна сторона треугольника 13 см, вторая на 9 см больше первой, а третья на 4 см меньше первой. Найди периметр треугольника АВС.
4.
На сколько площадь прямоугольника со сторонами 3 см и 4 см, меньше, чем площадь прямоугольника со сторонами 4 см и 5 см?
5. На сколько площадь квадрата со стороной 5 см, больше, чем площадь квадрата со стороной 3 см?
1. Длина прямоугольника 8 см, а ширина на 5 см короче. Чему равен его периметр?
2.На сколько периметр квадрата со стороной 1 дм 2 см больше, чем периметр квадрата со стороной 5 см?
3.Одна сторона треугольника 13 см, вторая на 9 см больше первой, а третья на 4 см меньше первой. Найди периметр треугольника АВС.
4. На сколько площадь прямоугольника со сторонами 3 см и 4 см, меньше, чем площадь прямоугольника со сторонами 4 см и 5 см?
5. На сколько площадь квадрата со стороной 5 см, больше, чем площадь квадрата со стороной 3 см?
1. Длина прямоугольника 8 см, а ширина на 5 см короче. Чему равен его периметр?
2.На сколько периметр квадрата со стороной 1 дм 2 см больше, чем периметр квадрата со стороной 5 см?
3.
Одна сторона треугольника 13 см, вторая на 9 см больше первой, а третья на 4 см меньше первой. Найди периметр треугольника АВС.
4. На сколько площадь прямоугольника со сторонами 3 см и 4 см, меньше, чем площадь прямоугольника со сторонами 4 см и 5 см?
5. На сколько площадь квадрата со стороной 5 см, больше, чем площадь квадрата со стороной 3 см?
Что такое периметр квадрата?
Периметр квадрата
Квадрат — это тип прямоугольника, в котором смежные стороны равны. Другими словами, все стороны квадрата равны.
Свойства квадрата:
(i) Все углы в квадрате одинаковы и равны 90º.
(ii) Все стороны квадрата равны.
Периметр квадрата
Периметр квадрата — это общая длина всех сторон квадрата.Следовательно, мы можем найти периметр квадрата, сложив все его четыре стороны.
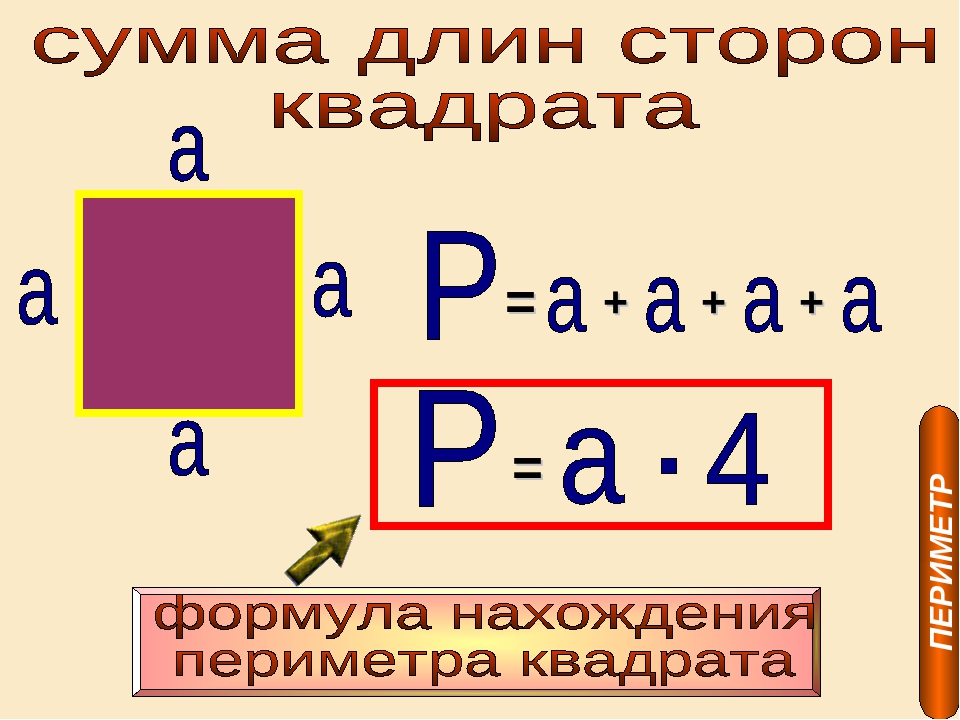
Периметр данного квадрата равен a + a + a + a.
Поскольку все стороны квадрата равны, нам нужна только одна сторона, чтобы найти его периметр.
Периметр данного квадрата:
а + а + а + а = 4 шт.
Следовательно, формула периметра квадрата = 4 × (длина любой одной стороны).
Сложные математические задачи с квадратами:Тип I: определение длины стороны, когда указан только периметр.
Пример 1 . Если периметр данного квадрата 12 см. Какова будет длина его стороны?
Решение : Учитывая, что периметр квадрата равен 12 см.
Пусть длина стороны будет ‘a’ см.
Мы знаем, что периметр квадрата = 4 × (длина стороны)
12 = 4 × (а)
a = 3 см
Тип II: Определение сторон с использованием свойств квадрата.
Пример 2 .Если a = 4 см в данном квадрате. Найдите b, c. и d.
Решение : Учитывая, что сторона a = 4 см.
Чтобы найти стороны b, c и d, мы используем свойство квадрата, которое гласит, что все стороны квадрата равны.
Следовательно, a = b = c = d = 4 см
Тип III: Определение периметра при заданной одной из сторон.
Пример 3 . Одна из сторон квадрата 5 см. Каков будет его периметр?
Решение : одна сторона квадрата равна 5 см.
Мы знаем, что периметр квадрата = 4 × (длина стороны)
= 4 × (5)
= 20 см
Пример 4 . Длина стороны квадратного деревянного каркаса 5 см. Найдите общую длину дерева, используемого в раме.
Решение: Учитывая, что длина стороны этого деревянного каркаса составляет 5 см.
Как известно, периметр квадрата = 4 × (длина стороны)
= 4 (5)
= 20 см
Таким образом, общая длина древесины составляет 20 см.
Интересные факты |
Площадь и периметр прямоугольников и квадратов
Возможно, вы слышали об измерении площади и периметра фигур.
Но что они собой представляют?
Периметр — это мера расстояния вокруг фигуры. Например, расстояние вокруг футбольного поля.
Площадь — это мера поверхности, которую что-то покрывает.Например, пространство, в которое вы выливаете тесто в форму для выпечки в духовке.
Расчет периметра прямоугольника или квадрата
Чтобы найти периметр прямоугольника или квадрата, вам нужно сложить длины всех четырех сторон. x в данном случае — длина прямоугольника, а y — ширина прямоугольника.
Периметр = x + x + y + y
Например, вы хотите найти периметр футбольного поля.
Чтобы рассчитать периметр футбольного поля, сначала измеряем:
Длина: 115 ярдов —
хШирина: 74 ярда —
у
Периметр = 115 + 115 + 74 + 74
По периметру 378 ярдов.
Расчет площади геометрической фигуры
Для вычисления площади квадратов и прямоугольников формула умножает длину на ширину.
Например, вы хотите узнать площадь вашего футбольного поля.
Чтобы рассчитать площадь футбольного поля, сначала измеряем:
Длина: 115 ярдов
Ширина: 74 ярда
Затем умножаем длину на ширину:
115 x 74 = 8 510 ярдов
Площадь футбольного поля составляет 8 510 квадратных ярдов.
Почему мы говорим о квадратных ярдах?
Чтобы ответить на этот вопрос, давайте начнем с квадрата.
Как видите, каждая сторона имеет длину 1 ярд. Таким образом, общая площадь квадрата равна 1×1, что составляет 1.
1 что?
Это не 1 ярд — это длина стороны, а не площадь квадрата. Площадь квадрата составляет «1 квадратный ярд».Квадратный ярд — это единица измерения площади, которую также можно записать как 1 ярд2.
Периметр квадрата — Веб-формулы
Квадрат — это правильный четырехугольник, у него четыре равные стороны и четыре равных угла (угол 90 градусов или прямые углы).
Квадратный четырехугольник с вершинами ABCD обозначим ABCD. Периметр квадрата (четырехугольника) определяется по формуле:
P = 4a
Где a — длина каждой стороны.
Свойства квадрата:
· Диагонали квадрата (четырехугольника) делят пополам
· Диагонали квадрата (четырехугольника) делят его углы пополам.
· Диагонали квадрата (четырехугольника) перпендикулярны.
· Противоположные стороны квадрата (четырехугольника) параллельны и равны.
· Все четыре угла квадрата (четырехугольника) равны. (Квадрат равен 360/4 = 90 градусов, поэтому каждый угол квадрата (четырехугольника) является прямым.)
· Диагонали квадрата (четырехугольника) равны.
Пример 1: Найдите площадь и периметр квадрата, длина стороны которого составляет 4 метра.
Решение:
Учитывая, что:
a = 4 м
Площадь квадрата = a 2 = 4 × 4 = 16 м 2
Периметр квадрата = 4 × 4 = 16 м
Пример 2 : Найдите периметр квадрата, длина сторон которого составляет 16 см.
Решение :
Периметр квадрата:
Пример 3: Каков периметр квадрата, если длина каждой стороны составляет 13 футов?
Решение :
Длина каждой стороны квадрата составляет 13 футов.
Периметр квадрата:
P = 4 ×
Р = 4 × 13
P = 52 футов
Периметр квадрата составляет 52 фута.
Пример 4: Периметр квадрата равен 24 см. Какой была бы длина его сторон, если бы периметр увеличился на 4 см?
Решение :
Новый периметр квадрата = 24 + 4 = 28 см.
Новый периметр квадрата = 4 × новая длина стороны квадрата
Пусть новая длина стороны квадрата = l см
a = 7 см
Пример 5: Площадь квадратного парка составляет 225 м 2 . Найдите его периметр.
Решение:
Дано:
Так как площадь составляет 225 м 2 , длину сторон можно легко определить:
A = s²
225 = s²
s = 15 м
Таким образом, периметр парка:
P = 4 × с.
P = 4 x 15 м.
P = 60 м.
Пример 6: Найдите периметр квадрата, длина стороны которого составляет 9,2 метра.
Решение :
Дано: Длина стороны (a) = 9,2 метра
Периметр квадрата = 4 ×
= 4 × 9,2
Периметр квадрата = 36,8 метра.
Периметр и площадь | Математика для гуманитарных наук
Периметр
Периметр — это одномерное измерение, которое проводится вокруг внешней стороны замкнутой геометрической формы.Давайте начнем обсуждение концепции периметра с примера.
Управляемый пример
Рисунок 1.
Рисунок 2.
У Джозефа нет машины, поэтому он должен ездить на автобусе или ходить пешком. По понедельникам он должен ехать в школу, на работу и снова домой. Его маршрут изображен на рисунке 1.
Очевидный вопрос, который следует задать в этой ситуации: «сколько миль проезжает Джозеф по понедельникам»? Для вычисления мы каждое расстояние: 3 + 6 + 6 = 15.
Джозеф проезжает 15 миль по понедельникам.
Другой способ справиться с этой ситуацией — нарисовать фигуру, представляющую маршрут путешествия Джозефа и помеченную расстоянием от одного места до другого.
Обратите внимание, что маршрут Джозефа представляет собой замкнутую геометрическую фигуру с тремя сторонами (треугольник) (см. Рисунок 2). Что мы можем спросить об этой форме: «каков периметр треугольника»?
Периметр означает «расстояние вокруг замкнутой фигуры или фигуры», и для вычисления мы складываем каждую длину: 3 + 6 + 6 = 15
Наш вывод тот же, что и выше: Джозеф проезжает 15 миль по понедельникам.
Однако мы смоделировали ситуацию с помощью геометрической формы, а затем применили конкретную геометрическую концепцию ( периметр ) к компьютеру, как далеко проехал Джозеф.
Примечания по периметру
- Периметр — это одномерное измерение, которое представляет собой расстояние вокруг замкнутой геометрической фигуры или фигуры (без промежутков).
- Чтобы найти периметр, сложите длины каждой стороны формы.
- Если есть единицы, включите единицы в окончательный результат.Единицы измерения всегда будут одномерными (например, футы, дюймы, ярды, сантиметры и т. Д.).
Чтобы вычислить периметр, наши фигуры должны быть замкнуты. На рисунке 3 показана разница между закрытой фигурой и открытой фигурой.
Рисунок 3.
Пример 1
Найдите периметр для каждой из фигур ниже.
- Сложите длину каждой стороны.
- Иногда приходится делать предположения, если длина не указана.
Решения
- 12 шт.
- 40 футов
Пример 2
Как найти периметр этой более сложной формы?
Решение
Просто продолжайте добавлять длины сторон.6 + 7 + 4 + 4 + 5 + 6 + 2 = 34 шт.
Если вы внимательно посмотрите на формы в предыдущих примерах, вы можете заметить некоторые способы записать каждый периметр в виде более явной формулы.
Посмотрите, соответствуют ли результаты того, что мы сделали, приведенным ниже формулам.
| Форма | Периметр | |
|---|---|---|
| Треугольник со сторонами, a , b , c : | [латекс] P = a + b + c \\ [/ латекс] | |
| Квадрат с длиной стороны a : | [латекс] P = a + a + a + a \\ [/ latex] [латекс] P = 4a \\ [/ latex] | |
| Прямоугольник со сторонами a , b : | [латекс] P = a + b + a + b \\ [/ латекс] [латекс] P = a + a + b + b \\ [/ латекс] [латекс] P = 2a + 2b \\ [ / латекс] | |
Окружность
Вы можете понять, что мы еще не обсуждали расстояние вокруг очень важной геометрической формы: круга! Расстояние по окружности имеет специальное название, называемое окружностью .Чтобы найти длину окружности, воспользуемся этой формулой: C = 2πr
Рисунок 4.
В этой формуле π произносится как «пи» и определяется как длина окружности круга, деленная на его диаметр: [latex] \ displaystyle \ pi = \ frac {C} {d} \\ [/ latex]. Обычно мы заменяем π приближением 3.14. Буква r представляет радиус круга.
Давайте посмотрим, откуда взялась формула для определения окружности. На рис. 4 показан общий круг с радиусом r.
Примечания о
C = 2π rПомните, что в формуле при вычислении длины окружности C = 2π r , мы умножаем , обычно , заменяя 3,14 вместо π:
C = 2 × 3,14 × r
Часто использование () помогает облегчить просмотр различных частей формулы:
С = (2) × (3,14) × ( r )
Происхождение
C = 2π rКак упоминалось ранее, специальное число π определяется как отношение длины окружности к ее диаметру.Мы можем записать это в форме уравнения как: [latex] \ displaystyle \ frac {C} {d} = \ pi \\ [/ latex]
Из нашей предыдущей работы мы знаем, что для определения неизвестного, C , мы можем переместить d на другую сторону уравнения, написав C = π d.
Диаметр полностью пересекает середину круга, поэтому диаметр в два раза больше радиуса. Мы можем обновить C с точки зрения радиуса как C = π (2 r ). После небольшого изменения порядка, в котором записаны наши детали, мы можем сказать, что C = 2π r.
Давайте воспользуемся формулой, чтобы найти длину окружности нескольких окружностей.
Пример 3
Найдите длину окружности каждого из следующих кругов. Свои ответы оставляйте сначала в точном виде, а затем в округленном (до сотых разрядов). (Обратите внимание, что когда указан радиус, его значение центрируется над сегментом радиуса. Когда указан диаметр, его значение центрируется над сегментом диаметра.)
Решения
- Точное значение 8π дюймов; округлено от точного ответа 25.13 дюймов; округлено с использованием 3,14 для π 25,12 из
- Точное 12,44π м; округлено от точного ответа 39,08 м; округлено с использованием 3,14 для π 39,06 м
Точная форма по сравнению с закругленной формой
- π — число в точной форме. Он не округлый.
- 3,14 — это приближение округленной формы для π
Он не округлый.Почему важно, какую форму мы используем? Это важно, потому что при округлении мы вносим ошибку в окончательный результат. Для этого класса такая ошибка обычно приемлема. Однако вы обнаружите, что в других предметах, таких как физика или химия, такой уровень точности имеет большое значение.Давайте посмотрим на примере разницы в формах.
Пример 4
Радиус Луны составляет около 1079 миль. Что такое окружность? Давайте решим это, используя как точную, так и округленную форму:
Точное решение
[латекс] C = 2 \ pi {r} = 2 \ pi (1079) = 2158 \ pi \\ [/ latex]
Чтобы округлить от до точного решения, используйте кнопку π на калькуляторе, чтобы получить
[латекс] 2158 \ pi \ ок. 6779,56 \ [/ латекс]
Округленное решение
[латекс] C = 2 \ pi {r} = 2 (3.14) (1079) \ приблизительно 6776,12 \ [/ латекс]
Обратите внимание, что наши окончательные результаты отличаются.
Эта разница — ошибка, созданная при использовании 3,14 в качестве начального приближения для π. Выполняя домашнее задание и тесты, внимательно читайте инструкции по каждой задаче, чтобы понять, какую форму использовать.
Пример 5
Найдите длину окружности или периметра для каждой описанной ниже ситуации. Включите рисунок формы с включенной информацией. Используйте примеры, чтобы определить, какие фигуры рисовать.Показать все работы. Как и в примерах, если включены единицы, то единицы должны присутствовать в вашем окончательном результате. Округлите до десятых, если не указано иное.
- Найдите периметр квадрата со стороной 2,17 фута.
- Найдите периметр прямоугольника со сторонами длиной 4,2 и 3,8.
- Найдите периметр треугольника со сторонами длиной 2, 5, 7.
- Найдите длину окружности радиуса 6 дюймов. Представьте ответ в точной форме, а также вычислите, используя 3.14 для π. Представьте округлую форму с точностью до десятых.
- Найдите длину окружности диаметром 14,8 дюйма. Представьте ответ в точной форме, а также вычислите, используя 3,14 для π. Представьте округлую форму с точностью до десятых.
Решения
- 8,68 футов
- 16
- 14
- Точное 12π дюйма, округленное 37,7 дюйма
- Точное 14,8π дюйма, Округленное 46,5 дюйма
Пример 6
Определение расстояния вокруг нестандартных форм
Основные формулы для периметра прямых фигур и окружности круга помогут нам найти расстояние вокруг более сложных фигур.Найдите расстояние вокруг следующей формы. Округлите окончательный ответ до десятых и используйте 3,14 вместо π.
Решение
34,7 дюйм
Пример 7
Аппликации периметра и окружности
Наши знания основных геометрических фигур могут быть применены для решения «реальных» задач.
Уолли хочет добавить забор позади своего дома, чтобы дети могли безопасно играть (см.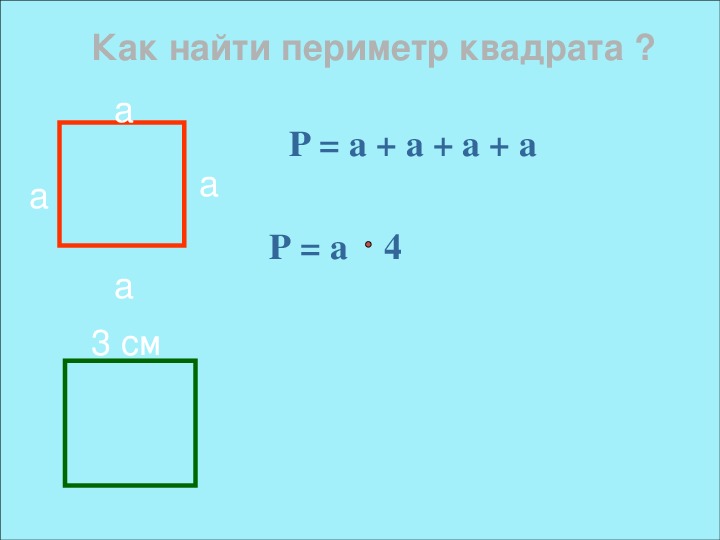
Диаграмму ниже). Он начал измерять свой двор, но отвлекся и забыл закончить измерения перед тем, как пойти в магазин.Если он помнит, что длина задней стены его дома составляет 15 ярдов, достаточно ли у него информации, чтобы купить необходимое ему ограждение? Если да, то сколько футов ему следует купить?
Решение
81 фут
Площадь
Давайте еще раз посмотрим на задний двор Уолли из примера 7, чтобы представить следующую концепцию: площадь.
Управляемый пример
Уолли успешно огородил свой двор, но теперь хочет добавить немного ландшафта и создать лужайку, как показано ниже.
Он направляется в местный магазин по продаже газонов и обнаруживает, что для того, чтобы определить, сколько дерна ему нужно, он должен вычислить квадратные метры площади, на которой он хочет добавить траву. По пути домой он понимает, что если разделит травянистую территорию на участки размером 1 фут на 1 фут, а затем пересчитает их, он сможет определить площадь в квадратных футах.
Вот информация, которую Уолли собрал, когда вернулся домой.
Уолли правильно определил, что площадь прямоугольного травянистого участка составляет 30 квадратных футов.
Заметки о зоне
- Площадь — это двумерное измерение, которое представляет собой объем пространства внутри двухмерной фигуры.
- Чтобы найти площадь, посчитайте количество единичных квадратов внутри фигуры.
- Если есть единицы, включите единицы в окончательный результат. Единицы измерения всегда будут двухмерными (например, квадратные футы, квадратные ярды, квадратные мили и т. Д.).
Пример 8
Найдите область для каждой из фигур ниже.
- Не забудьте посчитать единичные квадраты внутри фигуры.
- Есть здесь шаблон, который облегчил бы нашу работу?
Пример 9
Как найти область для более сложных фигур? Разбейте области на формы, которые мы узнаем, и сложите значения областей вместе.
Если вы внимательно посмотрите на формы в предыдущих примерах, вы можете заметить некоторые способы записать каждую область в виде более явной формулы.2 \ [/ латекс]
[латекс] A = a \ cdot {b} \\ [/ latex]
(Вы также увидите это как [latex] A = \ text {length} \ cdot \ text {width} \\ [/ latex])
Формулы площади для фигур ниже сложнее получить, поэтому формулы перечислены в таблице.
| Форма | Форма |
|---|---|
Треугольник высотой h и основанием b [латекс] \ displaystyle {A} = \ frac {1} {2} bh = \ frac {bh} {2} \\ [/ latex] Читается как «половина основания, умноженная на высоту» Обратите внимание, что h — это расстояние по прямой от вершины треугольника до другой стороны.2 \ [/ латекс] Читается как «пи, умноженный на радиус в квадрате» | |
Если ваш треугольник такой, как показано на рисунке слева, то высота нарисована и измерена за пределами треугольника. Формула площади такая же. |
Пример 10
Найдите область для каждой описанной ситуации. Создайте рисунок формы с включенной информацией. Показать все работы. Как и в примерах, если включены единицы, то единицы должны присутствовать в вашем окончательном результате.Используйте 3,14 для π и округлите ответы до десятых, если необходимо.
- Найдите площадь прямоугольника, длина которого составляет 12,9 метра, а высота — треть этой величины.
- Найдите площадь треугольника с основанием [latex] \ displaystyle {24} \ frac {1} {2} \\ [/ latex] дюймов и высотой 7 дюймов.
- Найдите площадь круга с радиусом [latex] \ displaystyle {2} \ frac {1} {3} \\ [/ latex] дюймов. Представьте ответ в точной форме, а также вычислите округленную форму, используя 3,14 для π. Представьте округлую форму с точностью до десятых.
Решения
- 55,5 м 2 или 55,5 кв.м (округлено)
- 85,8 дюйма 2 или 85,8 квадратных дюйма (округлено)
- Точное 49/9 π дюйма 2 , Округленное 17,1 дюйма 2
Пример 11
Найдите область в каждой описанной ситуации.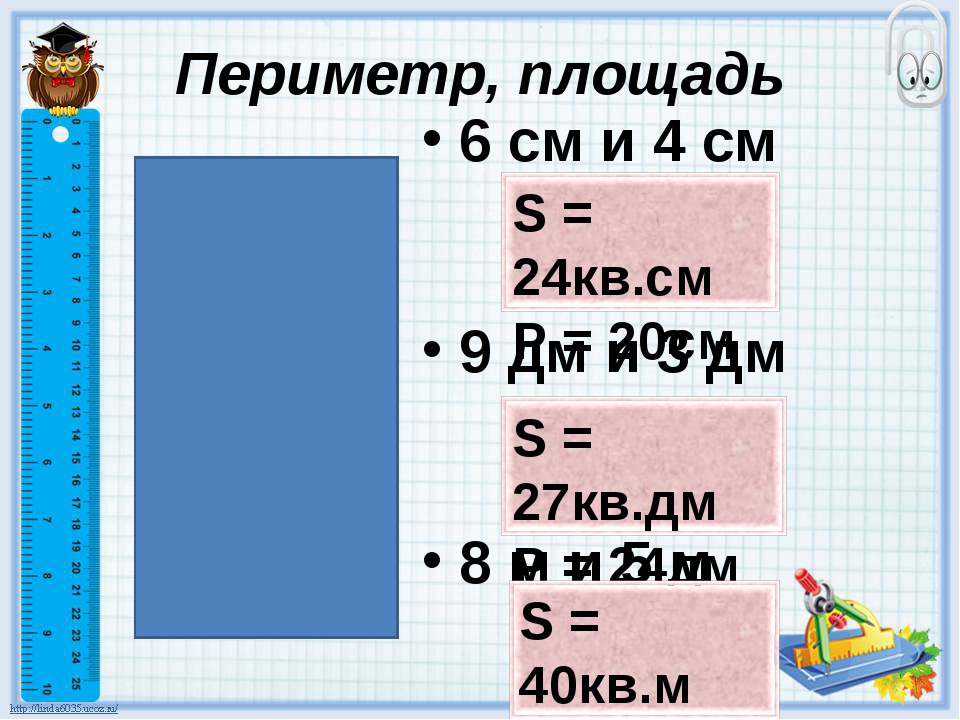
Включите рисунок формы с включенной информацией. Показать все работы. Как и в примерах, если включены единицы, то единицы должны присутствовать в вашем окончательном результате.Округляйте ответы до десятых, если не указано иное.
- Найдите площадь квадрата со стороной 4,2 фута.
- Найдите площадь прямоугольника со сторонами длиной 4,2 и 3,8.
- Найдите площадь треугольника высотой 7 дюймов и основанием 12 дюймов.
- Найдите площадь круга радиусом 6 дюймов. Представьте ответ в точной форме, а также вычислите, используя 3,14 для π. Представьте округлую форму с точностью до десятых.
Решения
- 17.64 фута 2 или 17,64 квадратных футов
- 16,0
- 42 дюйма 2 или 42 квадратных дюйма
- Точное 36π в 2 или 36π квадратных дюймов, округленное с использованием 3,14 для π 113,0 в 2 или 113,0 квадратных дюймов
Пример 12
Определение области нестандартных форм
Основные формулы площади помогут нам найти площадь более сложных фигур.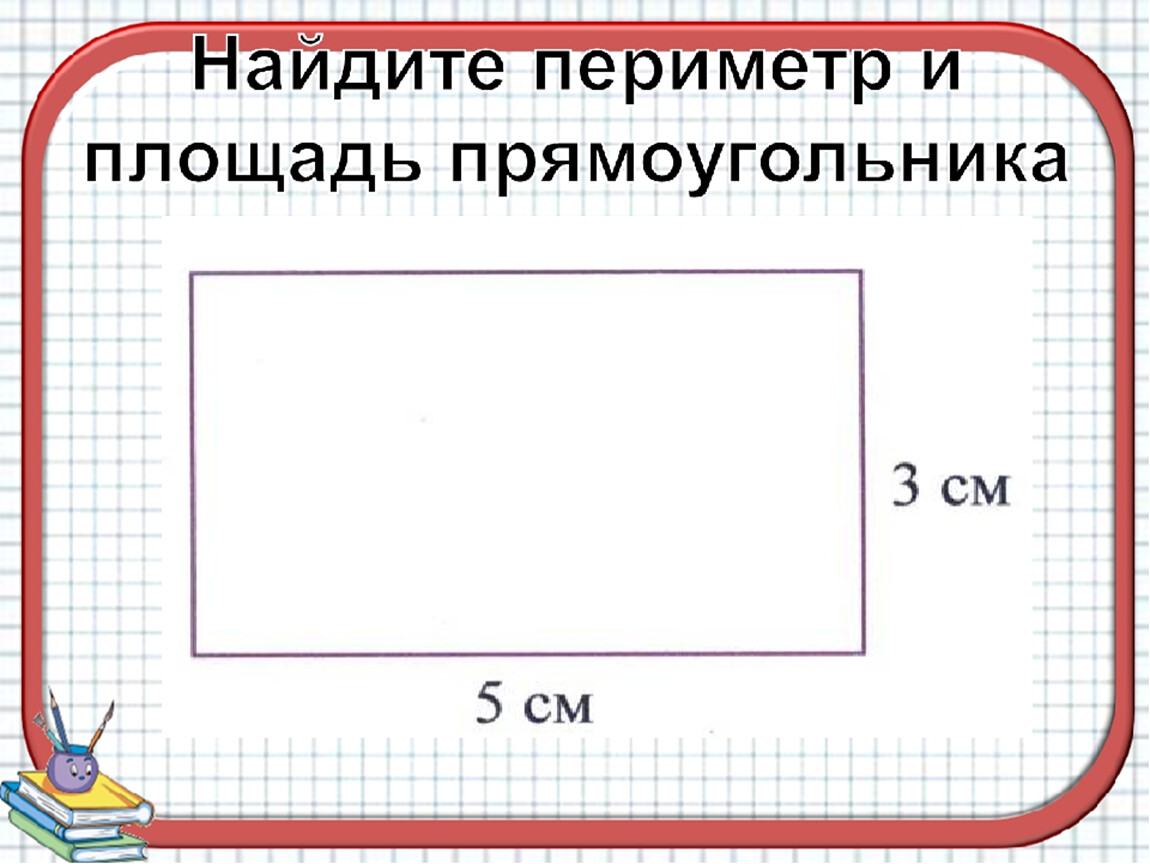
Это та же проблема, для которой мы нашли периметр ранее. Найдите площадь данной формы.Вычислить, используя 3,14 для π и округлить до ближайшей десятой.
Решение
Округлено с использованием 3,14 для π 25,9 дюйма 2
Пример 13
Применение площади и периметра
Мы можем объединить наши знания о площади / периметре для решения таких проблем, как эта.
Уолли все еще ремонтирует свой дом, и ему нужно завершить проект полов. Он хочет купить достаточно бамбукового пола, чтобы покрыть пространство в комнатах A, C и коридоре B, а также достаточно бамбуковой кромки для плинтусов во всех помещениях.Сколько квадратных футов пола и сколько футов плинтусов ему следует купить?
Решение
256 футов 2 настил, 108 футов окантовка
Связать площадь и периметр — по математике для 3-го класса
Как связаны площадь и периметр?
Периметр и площадь — разные вещи.
Но оба они связаны с длиной (или высотой) прямоугольника и шириной . Понимание того, что действительно может быть полезно в жизни.
Давайте рассмотрим
Что такое периметр?
Периметр — это длина или расстояние вокруг формы или пространства.
К найдите периметр фигуры или пространства, просто прибавьте длины всех сторон.
Есть ли 3 стороны, 4 стороны, 5 сторон … или больше. Просто сложите их все.
Что такое площадь?
Площадь — это пространство, занимаемое плоской формой.
Чтобы найти площадь прямоугольника, умножьте его ширины на высоту.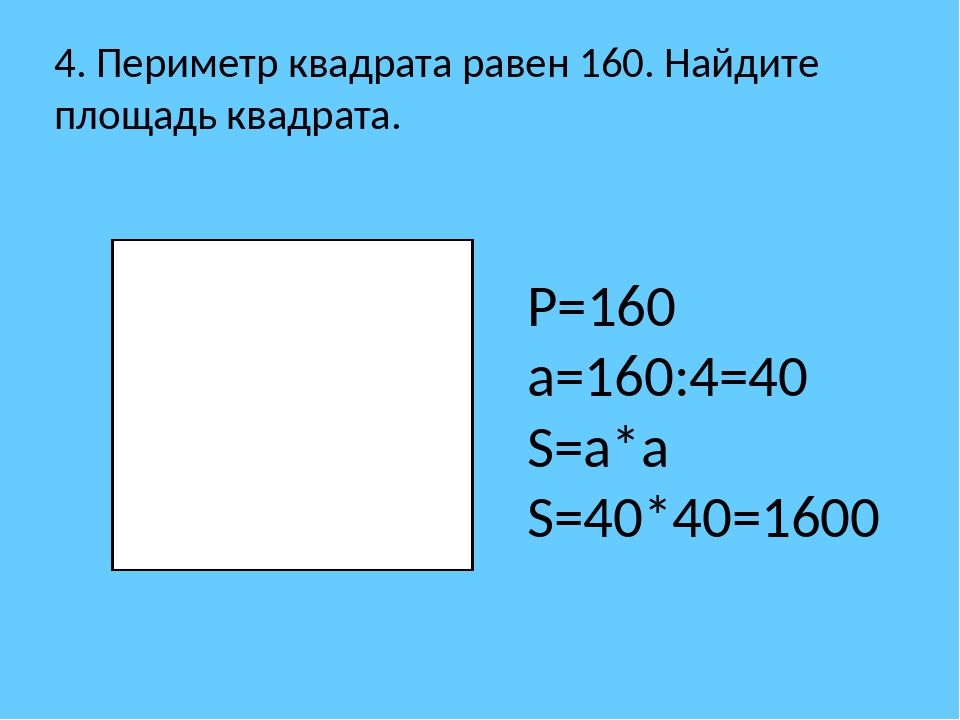
Отличный обзор работы! 🎊
Теперь попрактикуемся в решении задач по площади и периметру.
Пример 1: одинаковый периметр, разная площадь
Фигуры ниже имеют одинаковый периметр , но разную площадь .
Какова площадь прямоугольника B?
👉 Запустите , используя уже известную информацию.
У нас есть высота и ширина прямоугольника A. Мы можем использовать их, чтобы найти его периметр.
Мы делаем это, прибавляя к длине всех его сторон.
4 + 4 + 3 + 3 = 14 метров
Это означает, что периметр прямоугольника B также составляет 14 метров.
Мы пока не можем определить площадь B, потому что длина одной стороны все еще отсутствует. 😐
Как найти недостающую сторону? 🤔
👉 Мы работаем с той стороной, которую знаем.
— Мы знаем, что ширина 2 метра.
Поскольку противоположных сторон равны , удваиваем , чтобы получить сумму двух сторон.
2 + 2 = 4
Теперь мы вычтем полученную сумму из общего периметра.
14 — 4 = 10
Это означает, что сумма двух неизвестных сторон равна 10 м.
Мы делим на 2, чтобы получить длину каждой неизвестной стороны.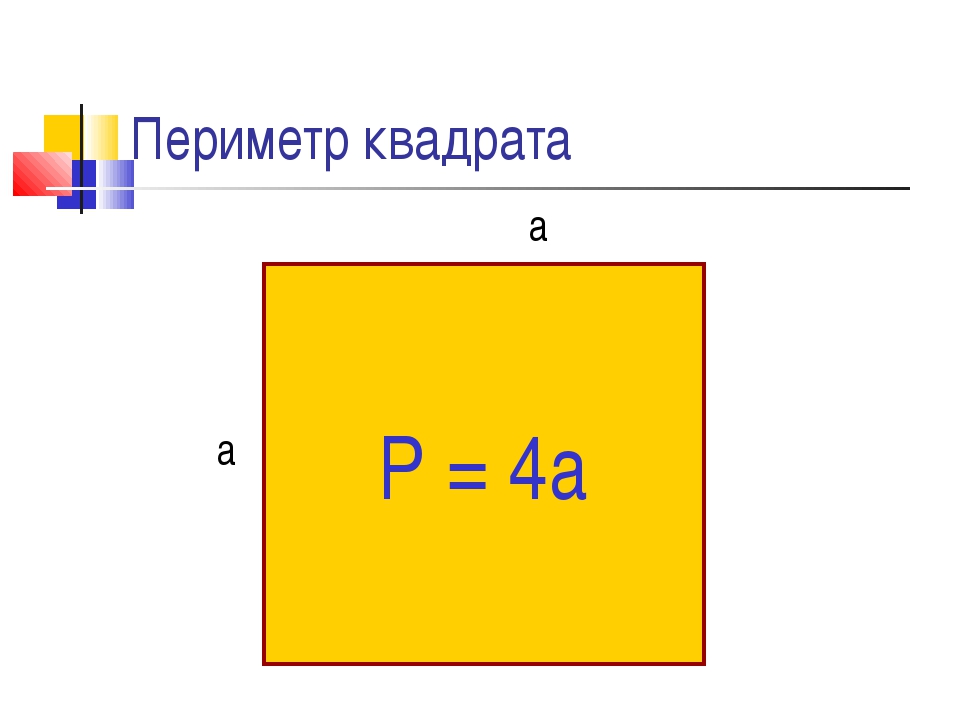
10 ÷ 2 = 5
👍 Теперь мы знаем, что высота прямоугольника B составляет 5 метров !
Давайте посмотрим, правильно ли это, сравнив его периметр с периметром прямоугольника A.
5 + 2 + 5 + 2 = 14 метров
😃 Это соответствует периметру прямоугольника A.Мы получили недостающую сторону прямоугольника B правильно!
Теперь, когда мы знаем высоту и ширину прямоугольника B, давайте найдем его площадь .
Это просто, мы просто умножаем на :
2 x 5 = 10 м²
✅ Площадь прямоугольника B составляет 10 квадратных метров (или 10 квадратных метров ).
Пример 2: Та же площадь, другой периметр
Прямоугольники ниже имеют одинаковую площадь , но разный периметр .
👆Что такое периметр прямоугольника A ?
👉 Чтобы найти периметр прямоугольника , нам нужно знать его высоту и ширину .
Нам известна только ширина прямоугольника A — его высота отсутствует !
Как определить его высоту? 🤔
Используя информацию, полученную из прямоугольника B.
Мы знаем, что площади двух прямоугольников равны. Если мы вычислим площадь прямоугольника B, то мы уже знаем площадь прямоугольника A.
Формула для площади — высота x ширина.
Давайте использовать это сейчас:
5 x 6 = 30 дюймов²
Площадь прямоугольника B составляет 30 кв.
👍 Это означает, что площадь прямоугольника A также составляет 30 дюймов² .
👉 Наш следующий шаг — найти недостающую сторону прямоугольника A. Мы делаем это, используя уже имеющуюся информацию.
Мы знаем, что ширина прямоугольника A составляет 3 дюйма, а его площадь составляет 30 дюймов².
Наша формула:
H x W = Площадь
Итак, давайте заполним нашу формулу числами:
H x 3 = 30
Вы помните, как решать уравнение с переменной? Это просто так.
Наша переменная — H (для высоты). Нам нужно получить его в одиночку с левой стороны.
Для этого нам нужно отменить умножение слева на , используя деление .
Мы делим с обеих сторон на 3!
Помните, что то, что вы делаете с одной стороны, должно выполняться и с другой стороны. Это сохранит уравнение сбалансированным .
H x 3 ÷ 3 = 30 ÷ 3
H = 10 дюймов
Отсутствующая сторона 10 дюймов .
Мы знаем, что это правильно, потому что когда мы умножаем на две стороны, чтобы получить его площадь, мы получаем 30 кв.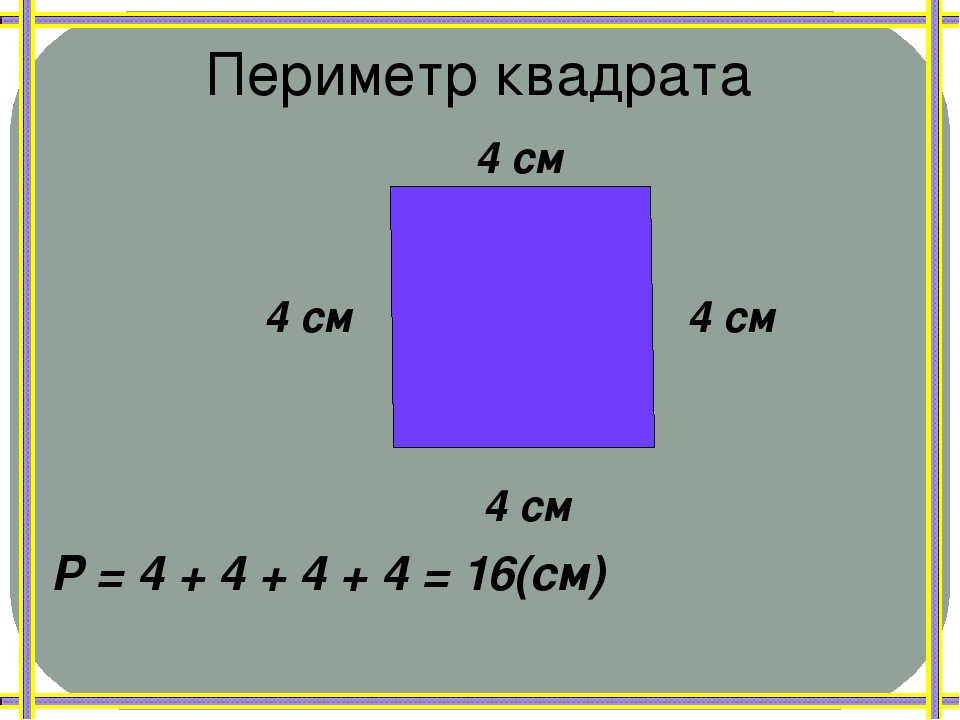
Дюймов.👍 Это соответствует области прямоугольника B!
👉 Теперь находим его периметр .
Это просто. Мы просто добавляем со всех сторон .
Помните, противоположные стороны прямоугольника всегда равны.
Это означает, что мы удваиваем высоту, а также ширину.
3 + 3 + 10 + 10 = 26 дюймов
✅ Периметр прямоугольника A составляет 26 дюймов .
Смотри и учись
Отличная работа! Теперь попробуйте выполнить практические упражнения.
💪
Применение площади и периметра Урок
Периметр
Периметр — это расстояние вокруг объекта снаружи. Периметр находится путем сложения длин всех сторон объекта вместе.
Например, периметр заданной формы вычисляется путем сложения всех длин объекта.
Периметр составит:
3 + 3 + 3 + 3 + 3 + 3 = 18
Итак, периметр 18 см.
Давайте посмотрим на несколько примеров:
Пример 1
При изготовлении открытки для родителей вы хотите обмотать ее пряжей. Измерьте стороны, чтобы узнать, сколько пряжи требуется.
Длина и ширина карты 6 дюймов и 4 дюйма соответственно.
Периметр карты:
6 + 4 + 4 + 6 = 20
Итак, для открытки требуется 20 дюймов пряжи.
Площадь
Площадь — это размер поверхности объекта или общий объем пространства, которое занимает объект.
Давайте посмотрим, как узнать площадь данного листа.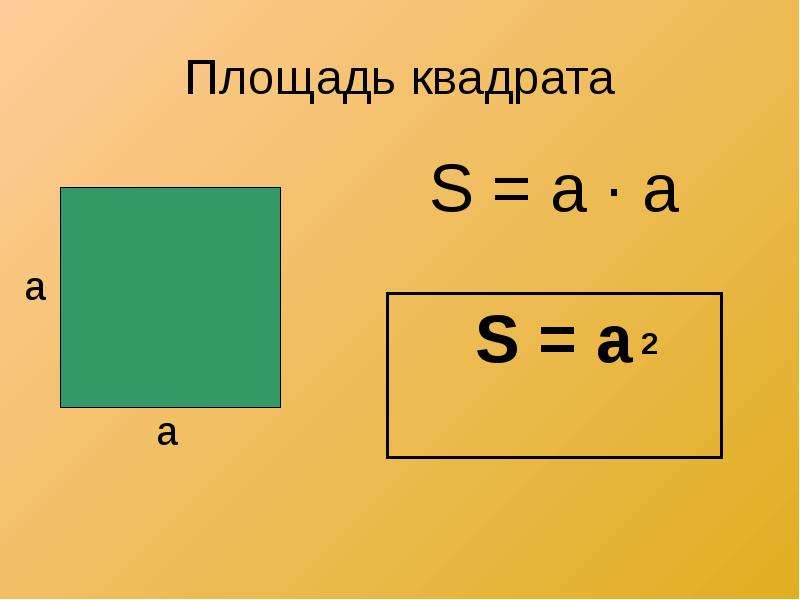
Чтобы определить площадь таких фигур, нам нужно использовать сетку.
Сначала нам нужно нарисовать фигуру на миллиметровой бумаге и нарисовать на ней фигуру.
Здесь мы можем заметить, что квадраты не совсем соответствуют форме, поэтому мы можем получить «приблизительный» ответ.
Здесь нам нужно это запомнить,
- более половины квадрата считается 1.
- меньше половины квадрата считается как 0.
Теперь посчитайте количество квадратов:
Вот как мы можем вычислить площадь неправильной формы.
Чтобы найти площадь правильных форм, таких как квадрат и прямоугольник, можно рассчитать по специальной формуле.
Площадь = Длина x Ширина
Давайте попробуем вопрос, чтобы найти площадь и периметр фигур.
Пример 1
Поле Дальтона прямоугольной формы имеет длину 10 м и ширину 6 м.
Он хочет обвести поле забором, чтобы защитить свое поле от животных. Какая длина провода требуется для завершения границы поля? Он также хочет знать, сколько площади требуется для орошения его поля. Вы можете ему помочь?
Поскольку мы хорошо знакомы с понятиями площади и периметра, мы легко можем ему помочь. Чтобы найти длину забора, необходимую для завершения границы поля, мы должны найти периметр.
Сложите длины всех сторон прямоугольного поля.
10 + 6 + 10 + 6 = 32
Итак, Далтону нужно 32 м проволоки, чтобы поставить забор вокруг поля.
Теперь давайте посчитаем площадь поля, чтобы найти часть для орошения.
Так как, площадь прямоугольника = длина x ширина
Итак, площадь орошаемой части = 10 x 6
= 60 м 2 .
Четвертый класс Урок Периметр и площадь (они одинаковые?)
Я призываю учеников к ковру.Розетка питания отображается на смарт-плате. Я начинаю с того, что сообщаю студентам, что в нашем сегодняшнем уроке используются формулы для определения площади и периметра фигур.
Я начинаю с повторения важной лексики для этого урока. Студентам необходимо знать эти термины, чтобы понять урок.
Словарь:
площадь — количество пространства внутри границы плоского (двухмерного) объекта, такого как прямоугольник или круг.
периметр — Расстояние вокруг двухмерной фигуры.
Формула— числа и символы, показывающие, как что-то придумать.
Затем я показываю на доске модель квадрата 10 x 10. Это то же самое, что и блок сотен, который я держал в начале урока. Я снова возвращаюсь к вопросу, который задавал ранее: «Имеет ли эта форма такую же площадь и периметр?» Я говорю студентам, что мы можем это выяснить. На смарт-доске отображается формула A = L x W. Я сообщил ученикам, что «L» означает длину, а «W» — ширину.Я указываю на длину и ширину на смарт-доске. Я спрашиваю: «Какова длина этой формы?» Вместе мы считаем, что 10 — это длина. «Какова ширина этой формы?» Вместе мы считаем, что 10 — это ширина.
На следующем слайде мы обсуждаем периметр формы.
Я сообщаю студентам, что, поскольку это квадрат, мы можем использовать формулу p = 4s. Я продолжаю говорить им, что они могут использовать эту формулу, только если это квадрат. Прошу студентов помочь мне найти периметр этой формы.
Это возвращает нас к вопросу. У этой формы одинаковая площадь и периметр? Ученики знают, что у этой формы разные площадь и периметр. (Я действительно подчеркиваю разницу в площади и периметре, потому что я хочу, чтобы ученики знали, что им нужно быть осторожными при вычислении площади и периметра. В прошлом я обнаружил, что некоторые ученики не перестают думать о том, какое измерение они просят дать. Они умеют делать площадь и периметр, но могут рассчитать площадь по периметру.)
Прежде чем ученики вернутся на свои места для работы в парах, я даю им другую формулу для периметра. Я сообщаю студентам, что они могут использовать p = 2L + 2W, чтобы найти периметр прямоугольника. Я рисую на доске прямоугольник длиной 3 дюйма и шириной 2 дюйма.