| 1 | Оценить с использованием заданного значения | квадратный корень из 50 | |
| 2 | Оценить с использованием заданного значения | квадратный корень из 45 | |
| 3 | Вычислить | 5+5 | |
| 4 | Вычислить | 7*7 | |
| 5 | Разложить на простые множители | 24 | |
| 6 | Преобразовать в смешанную дробь | 52/6 | |
| 7 | Преобразовать в смешанную дробь | 93/8 | |
| 8 | Преобразовать в смешанную дробь | 34/5 | |
| 9 | График | y=x+1 | |
| 10 | Оценить с использованием заданного значения | квадратный корень из 128 | |
| 11 | Найти площадь поверхности | сфера (3) | |
| 12 | Вычислить | 54-6÷2+6 | |
| 13 | График | y=-2x | |
| 14 | Вычислить | 8*8 | |
| 15 | Преобразовать в десятичную форму | 5/9 | |
| 16 | Оценить с использованием заданного значения | квадратный корень из 180 | |
| 17 | График | y=2 | |
| 18 | Преобразовать в смешанную дробь | 7/8 | |
| 19 | Вычислить | 9*9 | |
| 20 | Risolvere per C | C=5/9*(F-32) | |
| 21 | Упростить | 1/3+1 1/12 | |
| 22 | График | y=x+4 | |
| 23 | График | y=-3 | |
| 24 | График | x+y=3 | |
| 25 | График | x=5 | |
| 26 | Вычислить | 6*6 | |
| 27 | Вычислить | 2*2 | |
| 28 | Вычислить | 4*4 | |
| 29 | Вычислить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | |
| 30 | Вычислить | 1/3+13/12 | |
| 31 | Вычислить | 5*5 | |
| 32 | Risolvere per d | 2d=5v(o)-vr | |
| 33 | Преобразовать в смешанную дробь | 3/7 | |
| 34 | График | y=-2 | |
| 35 | Определить наклон | y=6 | |
| 36 | Перевести в процентное соотношение | 9 | |
| 37 | График | y=2x+2 | |
| 38 | График | y=2x-4 | |
| 39 | График | x=-3 | |
| 40 | Решить, используя свойство квадратного корня | x^2+5x+6=0 | |
| 41 | Преобразовать в смешанную дробь | 1/6 | |
| 42 | Преобразовать в десятичную форму | 9% | |
| 43 | Risolvere per n | 12n-24=14n+28 | |
| 44 | Вычислить | 16*4 | |
| 45 | Упростить | кубический корень из 125 | |
| 46 | Преобразовать в упрощенную дробь | 43% | |
| 47 | График | x=1 | |
| 48 | График | y=6 | |
| 49 | График | y=-7 | |
| 50 | График | y=4x+2 | |
| 51 | Определить наклон | y=7 | |
| 52 | График | y=3x+4 | |
| 53 | График | y=x+5 | |
| 54 | График | 3x+2y=6 | |
| 55 | Решить, используя свойство квадратного корня | x^2-5x+6=0 | |
| 56 | Решить, используя свойство квадратного корня | x^2-6x+5=0 | |
| 57 | Решить, используя свойство квадратного корня | x^2-9=0 | |
| 58 | Оценить с использованием заданного значения | квадратный корень из 192 | |
| 59 | Оценить с использованием заданного значения | квадратный корень из 25/36 | |
| 60 | Разложить на простые множители | 14 | |
| 61 | Преобразовать в смешанную дробь | 7/10 | |
| 62 | Risolvere per a | (-5a)/2=75 | |
| 63 | Упростить | x | |
| 64 | Вычислить | 6*4 | |
| 65 | Вычислить | 6+6 | |
| 66 | Вычислить | -3-5 | |
| 67 | Вычислить | -2-2 | |
| 68 | Упростить | квадратный корень из 1 | |
| 69 | Упростить | квадратный корень из 4 | |
| 70 | Найти обратную величину | 1/3 | |
| 71 | Преобразовать в смешанную дробь | 11/20 | |
| 72 | Преобразовать в смешанную дробь | 7/9 | |
| 73 | Найти НОК | 11 , 13 , 5 , 15 , 14 | , , , , |
| 74 | Решить, используя свойство квадратного корня | x^2-3x-10=0 | |
| 75 | Решить, используя свойство квадратного корня | x^2+2x-8=0 | |
| 76 | График | 3x+4y=12 | |
| 77 | График | 3x-2y=6 | |
| 78 | График | y=-x-2 | |
| 79 | График | y=3x+7 | |
| 80 | Определить, является ли полиномом | 2x+2 | |
| 81 | График | y=2x-6 | |
| 82 | График | y=2x-7 | |
| 83 | График | y=2x-2 | |
| 84 | График | y=-2x+1 | |
| 85 | График | y=-3x+4 | |
| 86 | График | y=-3x+2 | |
| 87 | График | y=x-4 | |
| 88 | Вычислить | (4/3)÷(7/2) | |
| 89 | График | 2x-3y=6 | |
| 90 | График | x+2y=4 | |
| 91 | График | x=7 | |
| 92 | График | x-y=5 | |
| 93 | Решить, используя свойство квадратного корня | x^2+3x-10=0 | |
| 94 | Решить, используя свойство квадратного корня | x^2-2x-3=0 | |
| 95 | Найти площадь поверхности | конус (12)(9) | |
| 96 | Преобразовать в смешанную дробь | 3/10 | |
| 97 | Преобразовать в смешанную дробь | 7/20 | |
| 98 | Преобразовать в смешанную дробь | 2/8 | |
| 99 | Risolvere per w | V=lwh | |
| 100 | Упростить | 6/(5m)+3/(7m^2) |
Что такое периметр? Как найти периметр? Периметр квадрата и прямоугольника.
 Способы определения и примеры решения Как посчитать периметр фигуры
Способы определения и примеры решения Как посчитать периметр фигурыСегодня у нас речь пойдет о том, как вычислить периметр многоугольника . Но сначала поговорим о многообразии фигур. Посмотрите на рисунок. Какие фигуры мы здесь видим? Это прямоугольник и квадрат – многоугольники, которые имеют по четыре стороны, а также треугольник, имеющий три стороны, и пятиугольник с пятью сторонами.
И как же найти периметр этих фигур?
Для того, чтобы найти периметр многоугольника надо сложить длины всех его сторон .
Периметр обозначается заглавной латинской буквой Р .
Давайте рассмотрим несколько примеров.
Вычислим периметр многоугольника О. Как мы говорили ранее, периметр многоугольника – это сумма длин всех его сторон. Сложим все стороны нашего многоугольника:
Р = 15 + 17 + 10 + 10 + 20 + 15 = 87
Но можно вычислить периметр и другим способом, используя умножение. Мы видим, что некоторые стороны многоугольника одинаковы. У нас две стороны по 15 условных единиц и еще две по 10. Запишем выражение:
У нас две стороны по 15 условных единиц и еще две по 10. Запишем выражение:
Р = 15 × 2 + 10 × 2 + 17 + 20 = 87
Теперь поговорим об особенностях вычисления периметра некоторых многоугольников.
Прямоугольник – это такой четырехугольник, у которого противоположные стороны равны. Например, чтобы вычислить А со сторонами а и б , надо сложить эти стороны и умножить полученный результат на 2 :
Р(прямоугольника) = (а + б) × 2
То есть, если сторона прямоугольника а = 5 см , а сторона прямоугольника б = 3 см , то периметр прямоугольника будет:
Р = (5 + 3) × 2 = 16 см
А как найти неизвестные стороны прямоугольника, если известен его периметр и только одна из сторон?
Р(прямоугольника) = 2 × а + 2 × б
а = (Р – 2 × б) ÷ 2 или б = (Р – 2 × а) ÷ 2
Пример: Периметр прямоугольника 16 см, сторона а = 5 см. Чему равны остальные стороны прямоугольника?
Если мы знаем одну сторону прямоугольника, значит длины двух, из четырех сторон нам известны. Найдем остальные две стороны. То есть найдем одну, а вторая будет ей равна.
Найдем остальные две стороны. То есть найдем одну, а вторая будет ей равна.
сторона б = (16 – 2 × 5) ÷ 2 = 3 см
Ответ: у прямоугольника две стороны по 5 см и две по 3 см.
Квадрат – это прямоугольник, у которого все стороны равны. Чтобы вычислить надо длину одной стороны умножить на 4:
Р(квадрата) = а × 4
Например, у квадрата В сторона а = 5 см. Чтобы найти его периметр:
Р(В) = 5 × 4 = 20 см
А если известен периметр квадрата, как найти длины его сторон? Очень просто, надо его периметр разделить на четыре:
а = Р ÷ 4
Пример: Периметр квадрата 24 см. Чему равны его стороны?
а = 24 ÷ 4 = 6
Ответ: Стороны квадрата равны 6 см.
По подобию вычисления периметра квадрата вычисляется периметр всех равносторонних многоугольников . То есть равен длине одной его стороны умноженной на количество сторон.
Если длина одной стороны многоугольника равна а , а число его сторон равно n , то его периметр будет равен:
Р(равностороннего многоугольника) = а × n
Например, у пятиугольника Д сторона а = 6 см
. Найдем его периметр:
Найдем его периметр:
Р(Д) = 6 × 5 = 30 см
Ну а если известен периметр равностороннего многоугольника, то вычислить длины его сторон очень просто, надо разделить его периметр на количество сторон.
Периметр — это сумма длин всех сторон многоугольника.
- Для вычисления периметра геометрических фигур используются специальные формулы, где периметр обозначается буквой «P». Название фигуры рекомендуется писать маленькими буквами под знаком «P», чтобы знать чей периметр ты находишь.
- Периметр измеряется в единицах длины: мм, см, м, км и т.д.
- Прямоугольник – это четырехугольник.
- Все параллельные стороны равны
- Все углы = 90º.
- Например в повседневной жизни прямоугольник может встречаться в виде — книги, монитора, крышки от стола или двери.
Существует 2 способа его нахождения:
- 1 способ.
 Складываем все стороны. P = a + а + b + b
Складываем все стороны. P = a + а + b + b - 2 способ. Сложить ширину и длину, и умножить на 2. P = (a + b) · 2. ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.
«a» — длина прямоугольника, более длинная пара его сторон.
«b» — ширина прямоугольника, более короткая пара его сторон.
Пример задачи на подсчет периметра прямоугольника:
Вычислите периметр прямоугольника, есть его ширина равна 3 см., а длина — 6.
Запомни формулы вычисления периметра прямоугольника!
Полупериметр — это сумма одной длины и одной ширины.
- Полупериметр прямоугольника — когда выполняешь первое действие в скобках – (a+b) .
- Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, т.е. умножить на 2.
Как найти площадь прямоугольника
Формула площади прямоугольника S= a*b
Если в условии известна длина одной стороны и длина диагонали, то площадь найти можно, используя в таких задачах, теорему Пифагора, она позволяет найти длину стороны прямоугольного треугольника если известны длины двух других сторон.
- : a 2 + b 2 = c 2 , где a и b – стороны треугольника, а с – гипотенуза, самая длинная сторона.
Помни!
- Все квадраты – прямоугольники, но не все прямоугольники – квадраты. Так как:
- Прямоугольник — это четырехугольник со всеми прямыми углами.
- Квадрат — прямоугольник, у которого все стороны равны.
- Если ты находишь площадь, ответ всегда будет в квадратных единицах (мм 2 , см 2 , м 2 , км 2 и т.д.)
Класс: 2
Цель: ознакомить с приёмом нахождения периметра прямоугольника.
Задачи: формировать умение решать задачи, связанные с нахождением периметра фигур, вырабатывать умения чертить геометрические фигуры, закрепить умение вычислять, применяя с переместительное свойство сложения, развивать навык устного счёта, логическое мышление, воспитывать познавательную активность и умение работать в коллективе.
Оборудование: ИКТ (мультимедийный
проектор, презентация к уроку), картинки с
геометрическими фигурами для физминутки, модель
магического квадрата, у учеников – модели
геометрических фигур, маркерные доски, линейки,
учебники, тетради.
ХОД УРОКА
1. Организационный момент
Проверка готовности к уроку. Приветствие.
Начинается урок,
Он пойдёт ребятам впрок.
Постарайтесь всё понять –
И внимательно считать.
2. Устный счёт
а) Использование магических фигур. (Приложение 1 )
– Заполним клетки магического квадрата, назовите его особенности (сумма чисел по горизонталям, вертикалям и диагоналям равны) и определите волшебное число. (39)
По цепочке дети заполняют квадрат на доске и в тетрадях .
б) Знакомство со свойствами магических треугольников. (Приложение 2 )
– Суммы чисел в углах, образующие треугольник равны. Найдём волшебные числа у треугольника. Определи пропущенное число. Отметь его на маркерной доске.
3. Подготовка к изучению нового материала
– Перед Вами геометрические фигуры. Назовите
их одним словом. (Четырёхугольники).
– Разделите их на 2 группы. (Приложение
3 )
(Приложение
3 )
– Что такое прямоугольники. (Прямоугольники –
четырехугольники, у которых все углы прямые.)
– Что можно узнать, зная длины сторон
четырёхугольников? Периметр – сумма длин сторон
фигур.
– Найдите периметр белой фигуры, жёлтой.
– Почему у прямоугольников известны не все
стороны?
– Какие свойства у противолежащих сторон
прямоугольников? (У прямоугольника
противоположные стороны равны).
– Если противоположные стороны равны, надо ли
измерять все стороны? (Нет.)
– Правильно, достаточно измерить длину и ширину.
– Как вычислить удобным способом? (Учащиеся
работают устно с комментированием.)
4. Изучение новой темы
– Прочитайте тему нашего урока: «Периметр
прямоугольника». (Приложение 4 )
– Помогите найти периметр данной фигуры, если её
длина равна – а , а ширина – в .
Желающие находят Р у доски. Учащиеся в
тетрадях записывают решение.
– Как записать это по-другому?
Р = а + а + в + в ,
Р = а х 2 + в х 2,
Р = (а + в ) х 2.
– Мы получили формулу нахождения периметра прямоугольника. (Приложение 5 )
5. Закрепление
Стр. 44 № 2.
Дети читают и записывают условие, вопрос, чертят фигуру, находят Р разными способами, записывают ответ.
6. Физминутка. Сигнальные карточки
Сколько клеточек зелёных,
Столько выполним наклонов.
Столько раз руками хлопнем.
Столько раз ногами топнем.
Сколько здесь у нас кружков,
Столько сделаем прыжков.
Мы присядем столько раз,
Столь подтянемся сейчас.
7. Практическая работа
– У Вас на партах лежат в конвертах
геометрические фигуры. Как мы их назовём?
– Что такое прямоугольники?
– Что вы знаете о противолежащих сторонах
прямоугольников?
– Измерьте стороны фигур по вариантам,
найдите периметр разными способами.
– Проверяем у соседа.
Взаимопроверка тетрадей .
– Прочитайте: Как нашли периметр? Что можно
сказать о периметрах данных фигур? (Они равны) .
– Начертите прямоугольник с таким же Р, но
другими сторонами.
Р 1 = (2 + 6) х 2 = 16 Р 1 = 2 х 2 + 6 х 2 = 16
Р 1 = 2 + 2 + 6 + 6 = 16
Р 2 = 3 + 3 + 5 + 5 = 16 Р 2 = (3 + 5) х 2 = 16
Р 3 = 4 + 4 + 4 + 4 = 16 Р 4 = 1 + 1 + 7 + 7 = 16
8. Графический диктант
Слева 6 клеток. Поставили точку. Начинаем движение. 2 – вправо, 4 – вправо вниз, 10 – влево, 4 – вправо вверх. Какая фигура? Преврати её в прямоугольник. Дострой. Найди Р разными способами.
Р = (5 + 2) х 2 = 14.
Р = 5 + 5 + 2 + 2 = 14.
Р = 5 х 2 + 2 х 2 = 14.
9. Пальчиковая гимнастика
Умножали, умножали.
Очень, очень мы устали.
Наши пальчики сплетём и соединим ладошки.
А потом, как только можем, крепко накрепко сожмём.
На дверях висит замок.
Кто его открыть не смог?
Мы замочком постучали,
Мы замочек повертели,
Мы замочек покрутили и открыли.
(Слова сопровождаются движениями)
10. Составление и решение задачи по условию (Приложение 8 )
Длина прямоугольника – 12 дм
Ширина – на 3 дм м.
Р – ?
В первом действии найдём ширину: 12 – 3 = 9 (дм) –
ширина
Зная длину и ширину, узнаем Р одним из способов.
Р = (12 + 9) х 2 = 42 дм
11. Самостоятельная работа
12. Итог урока
– Чему учились. Как находили Р прямоугольника?
13.Оценивание
Оцениваются ответы учащихся у доски и выборочно в процессе самостоятельной работы.
14.Домашнее задание
С. 44 № 5 (с пояснениями).
Умение находить периметр прямоугольника очень важно для решения многих геометрических задач. Ниже приведена подробная инструкция по нахождению периметра разных прямоугольников.
Как найти периметр обычного прямоугольника
Обычный прямоугольник – четырехугольник, у которого параллельные стороны равны и все углы = 90º. Для нахождения его периметра существует 2 способа:
Складываем все стороны.
Вычислите периметр прямоугольника, есть его ширина равна 3 см., а длина – 6.
Решение (последовательность действий и рассуждения):
- Так как нам известны ширина и длина прямоугольника, найти его периметр не составит труда. Ширина параллельна ширине, а длина длине. Таким образом, в обычном прямоугольнике 2 ширины и 2 длины.
- Складываем все стороны (3 + 3 + 6 + 6) = 18 см.
Ответ: P = 18 см.
Второй способ заключается в следующем:
Нужно сложить ширину и длину, и умножить на 2. Формула этого способа имеет следующий вид: 2×(a + b), где a – ширина, b – длина.
В рамках данной задачи получим такое решение:
2×(3 + 6) = 2×9 = 18.
Ответ: P = 18.
Как найти периметр прямоугольника – квадрат
Квадрат является правильным четырехугольником. Правильным потому, что все его стороны и углы равны. Для нахождения его периметра так же существует два способа:
Правильным потому, что все его стороны и углы равны. Для нахождения его периметра так же существует два способа:
- Сложить все его стороны.
- Умножить его сторону на 4.
Пример: Найти периметр квадрата, если его сторона = 5 см.
Так как нам известна сторона квадрата, мы сможем найти его периметр.
Складываем все стороны: 5 + 5 + 5 + 5 = 20.
Ответ: P = 20 см.
Умножаем сторону квадрата на 4 (потому что все равны): 4×5 = 20.
Ответ: P = 20 см.
Как найти периметр прямоугольника – онлайн-ресурсы
Несмотря на то, что вышеупомянутые действия легки для понимания и освоения, вам может пригодиться несколько онлайн-калькуляторов, которые помогут вам вычислить периметры (площадь, объем) разных фигур. Просто вбейте необходимые значения и мини-программа рассчитает периметр нужной вам фигуры. Ниже приведен небольшой список.
Урок и презентация на тему: «Периметр и площадь прямоугольника»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 3 класса
Тренажер для 3 класса «Правила и упражнения по математике»
Электронное учебное пособие для 3 класса «Математика за 10 минут»
Что такое прямоугольник и квадрат
Прямоугольник – это четырёхугольник, у которого все углы прямые. Значит, противоположные стороны равны друг другу.
Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.
Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D …
Пример.
Читается так: четырёхугольник ABCD; квадрат EFGH.
Что такое периметр прямоугольника? Формула расчета периметра
Периметр прямоугольника – это сумма длин всех сторон прямоугольника или сумма длины и ширины, умноженная на 2.Периметр обозначается латинской буквой P . Так как периметр — это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.
Так как периметр — это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.
Например, периметр прямоугольника АВСD обозначается как P ABCD , где А, В, С, D — это вершины прямоугольника.
Запишем формулу периметра четырехугольника ABCD:
P ABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)
Пример.
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см.
Определим P ABCD .
Решение:
1. Нарисуем прямоугольник ABCD с исходными данными.
2. Напишем формулу для расчета периметра данного прямоугольника:
P ABCD = 2 * (AB + BС)
P ABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см
Ответ: P ABCD = 16 см.
Формула расчета периметра квадрата
У нас есть формула для определения периметра прямоугольника.P ABCD = 2 * (AB + BC)
Применим её для определения периметра квадрата. Учитывая, что все стороны квадрата равны, получаем:
P ABCD = 4 * AB
Пример.

Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата.
Решение.
1. Нарисуем квадрат ABCD с исходными данными.
2. Вспомним формулу расчета периметра квадрата:
P ABCD = 4 * AB
3. Подставим в формулу наши данные:
P ABCD = 4 * 6 см = 24 см
Ответ: P ABCD = 24 см.
Задачи на нахождение периметра прямоугольника
1. Измерь ширину и длину прямоугольников. Определи их периметр.
2. Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника.
3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.
Где используется расчет периметра прямоугольника?
1. Задан участок земли, его нужно обнести забором. Какой длины будет забор?
В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора.
2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев.
Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.
Что такое площадь прямоугольника?
Площадь – это числовая характеристика фигуры. Площадь измеряется квадратными единицами длины: см 2 , м 2 , дм 2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.)В вычислениях обозначается латинской буквой S .
Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Площадь прямоугольника вычисляется умножением длины АК на ширину КМ. Запишем это в виде формулы.
S AKMO = AK * KM
Пример.
Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?
S AKMO = AK * KM = 7 см * 2 см = 14 см 2 .
Ответ: 14 см 2 .
Формула вычисления площади квадрата
Площадь квадрата можно определить, умножив сторону саму на себя.Пример.
В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.
S AВСО = AB * BC = AB * AB
Пример.
Определи площадь квадрата AKMO со стороной 8 см.
S AKMО = AK * KM = 8 см * 8 см = 64 см 2
Ответ: 64 см 2 .
Задачи на нахождение площади прямоугольника и квадрата
1.Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.
| 1 | Найти том | сфера (5) | | |
| 2 | Найти площадь | круг (5) | | |
| 3 | Найдите площадь поверхности | сфера (5) | | |
| 4 | Найти площадь | круг (7) | | |
| 5 | Найти площадь | круг (2) | | |
| 6 | Найти площадь | круг (4) | | |
| 7 | Найти площадь | круг (6) | | |
| 8 | Найти том | сфера (4) | | |
| 9 | Найти площадь | круг (3) | | |
| 10 9(1/2) | ||||
| 11 | Найти простую факторизацию | 741 | ||
| 12 | Найти том | сфера (3) | | |
| 13 | Оценить | 3 квадратный корень из 8*3 квадратный корень из 10 | ||
| 14 | Найти площадь | круг (10) | | |
| 15 | Найти площадь | круг (8) | | |
| 16 | Найдите площадь поверхности | сфера (6) | | |
| 17 | Найти простую факторизацию | 1162 | ||
| 18 | Найти площадь | круг (1) | | |
| 19 | Найдите окружность | круг (5) | | |
| 20 | Найти том | сфера (2) | | |
| 21 | Найти том | сфера (6) | | |
| 22 | Найдите площадь поверхности | сфера (4) | | |
| 23 | Найти том | сфера (7) | | |
| 24 | Оценить | квадратный корень из -121 | ||
| 25 | Найти простую факторизацию | 513 | ||
| 26 | Оценка | квадратный корень из 3/16* квадратный корень из 3/9 | ||
| 27 | Найти том | коробка (2)(2)(2) | | |
| 28 | Найдите окружность | круг (6) | | |
| 29 | Найдите окружность | круг (3) | | |
| 30 | Найдите площадь поверхности | сфера (2) | | |
| 31 | Оценить | 2 1/2÷22000000 | ||
| 32 | Найдите Том | коробка (5)(5)(5) | | |
| 33 | Найти том | коробка (10)(10)(10) | | |
| 34 | Найдите окружность | круг (4) | | |
| 35 | Преобразование в проценты | 1,7 | ||
| 36 | Оценить | (5/6)÷(4/1) | ||
| 37 | Оценить | 3/5+3/5 | ||
| 38 | Оценить | ф(-2) | 92 | |
| 40 | Найти площадь | круг (12) | | |
| 41 | Найти том | коробка (3)(3)(3) | | |
| 42 | Найти том | коробка (4)(4)(4) | 92-4*-1+2||
| 45 | Найти простую факторизацию | 228 | ||
| 46 | Оценить | 0+0 | ||
| 47 | Найти площадь | круг (9) | | |
| 48 | Найдите окружность | круг (8) | | |
| 49 | Найдите окружность | круг (7) | | |
| 50 | Найти том | сфера (10) | | |
| 51 | Найдите площадь поверхности | сфера (10) | | |
| 52 | Найдите площадь поверхности | сфера (7) | | |
| 53 | Определить, является простым или составным | 5 | ||
| 60 | Преобразование в упрощенную дробь | 2 1/4 | ||
| 61 | Найдите площадь поверхности | сфера (12) | | |
| 62 | Найти том | сфера (1) | | |
| 63 | Найдите окружность | круг (2) | | |
| 64 | Найти том | коробка (12)(12)(12) | | |
| 65 | Добавить | 2+2= | ||
| 66 | Найдите площадь поверхности | коробка (3)(3)(3) | | |
| 67 | Оценить | корень пятой степени из 6* корень шестой из 7 | ||
| 68 | Оценить | 7/40+17/50 | ||
| 69 | Найти простую факторизацию | 1617 | ||
| 70 | Оценить | 27-(квадратный корень из 89)/32 | ||
| 71 | Оценить | 9÷4 | ||
| 72 | Оценка 92 | |||
| 74 | Оценить | 1-(1-15/16) | ||
| 75 | Преобразование в упрощенную дробь | 8 | ||
| 76 | Оценка | 656-521 | 9-2 | |
| 79 | Оценить | 4-(6)/-5 | ||
| 80 | Оценить | 3-3*6+2 | ||
| 81 | Найдите площадь поверхности | коробка (5)(5)(5) | | |
| 82 | Найдите площадь поверхности | сфера (8) | | |
| 83 | Найти площадь | круг (14) | | |
| 84 | Преобразование в десятичное число | 5 ноября | ||
| 85 9-2 | ||||
| 88 | Оценить | 1/2*3*9 | ||
| 89 | Оценить | 4/4-17/-4 | ||
| 90 | Оценить | 11.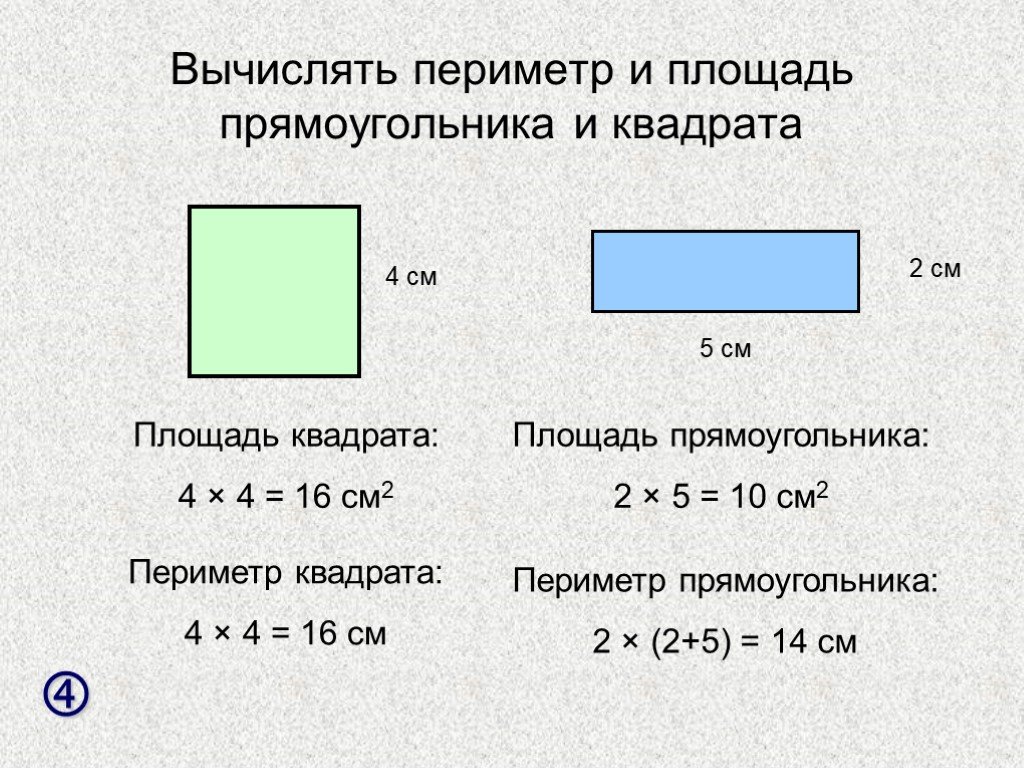 02+17.19 02+17.19 | ||
| 91 | Оценить | 3/5+3/10 | ||
| 92 | Оценить | 4/5*3/8 | ||
| 93 | Оценить | 6/(2(2+1)) | ||
| 94 | Упростить | квадратный корень из 144 | ||
| 95 | Преобразование в упрощенную дробь | 725% | ||
| 96 | Преобразование в упрощенную дробь | 6 1/4 | ||
| 97 | Оценить | 7/10-2/5 | ||
| 98 | Оценить | 6÷3 | ||
| 99 | Оценить | 5+4 | ||
| 100 | Оценить | квадратный корень из 12- квадратный корень из 192 |
Как найти периметр прямоугольника и квадрата
Как найти периметр прямоугольника и квадрата ПримерВидеоВопросыУрокПоделиться в Google Классе
ПримерВидеоВопросыУрокПоделиться в Google Классе
90 952- Периметр — это общее расстояние вокруг внешней стороны фигуры.

- Чтобы найти периметр фигуры, мы складываем стороны.
- Противоположные стороны прямоугольника имеют одинаковую длину.
- Складывая все четыре стороны, получаем 2 + 3 + 2 + 3 = 10 см.
- Периметр прямоугольника равен 10 см.
- Мы также можем найти периметр прямоугольника, сложив две смежные стороны и удвоив результат.
- 2 + 3 = 5см.
- Удвоение дает нам периметр 10 см.
- Общее расстояние по внешней стороне прямоугольника равно 10 см.
Сложите все четыре стороны прямоугольника, чтобы найти его периметр.
Как найти периметр прямоугольника
Чтобы найти периметр прямоугольника, сложите длины всех четырех сторон. Либо сложите вместе длину и ширину прямоугольника, а затем удвойте результат.
Периметр — это общее расстояние вокруг внешней стороны фигуры. Он находится путем сложения всех внешних длин фигуры.
Единицами периметра являются длины. Вот некоторые из наиболее распространенных единиц, в которых измеряется периметр.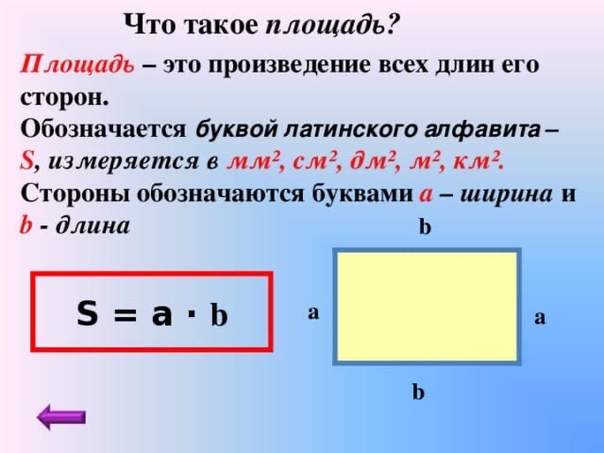
Вот пример нахождения периметра прямоугольника по двум его сторонам. Нам сообщают длину и ширину этого прямоугольника.
Длина 3 см, ширина 2 см.
Противоположные стороны прямоугольника имеют одинаковую длину.
Следовательно, если левая сторона прямоугольника равна 2 см, то и правая сторона равна 2 см.
Если верхняя сторона прямоугольника равна 3 см, то и нижняя сторона равна 3 см.
После того, как длины всех сторон фигуры отмечены, периметр можно найти, сложив эти длины вместе.
2 + 3 + 2 + 3 = 10
Следовательно, периметр этого прямоугольника равен 10 см. Это означает, что общее расстояние вокруг внешней стороны формы составляет 10 см.
Существует более быстрый метод определения периметра прямоугольника, если известны длина и ширина. Чтобы найти периметр прямоугольника, просто сложите длину и ширину, а затем умножьте результат на 2.
Это потому, что есть две ширины, которые отмечены ниже.
И две длины, которые отмечены ниже.
У прямоугольника две длины и две ширины. Мы можем сложить длину и ширину, а затем удвоить результат, потому что их два.
Складывая длину и ширину, получаем 2 + 3 = 5 см.
Так как есть две длины и две ширины, мы удваиваем это, чтобы получить 10 см.
Формула периметра прямоугольника: Периметр = 2 × (длина + ширина). Это можно записать как P = 2(l + w). Просто сложите длину и ширину, а затем умножьте результат на 2.
Формула для периметра прямоугольника может быть записана как P = 2l + 2w или P = l + l + w + w.
Вот еще один пример нахождения периметра прямоугольника. Воспользуемся формулой, чтобы найти периметр этого прямоугольника.
Р = 2(1 + ш). Мы добавляем длину и ширину, а затем удваиваем их.
20 + 15 = 35 мм. Мы удваиваем это, чтобы получить периметр 70 мм.
Общее расстояние вокруг внешней стороны этого прямоугольника равно 70 мм.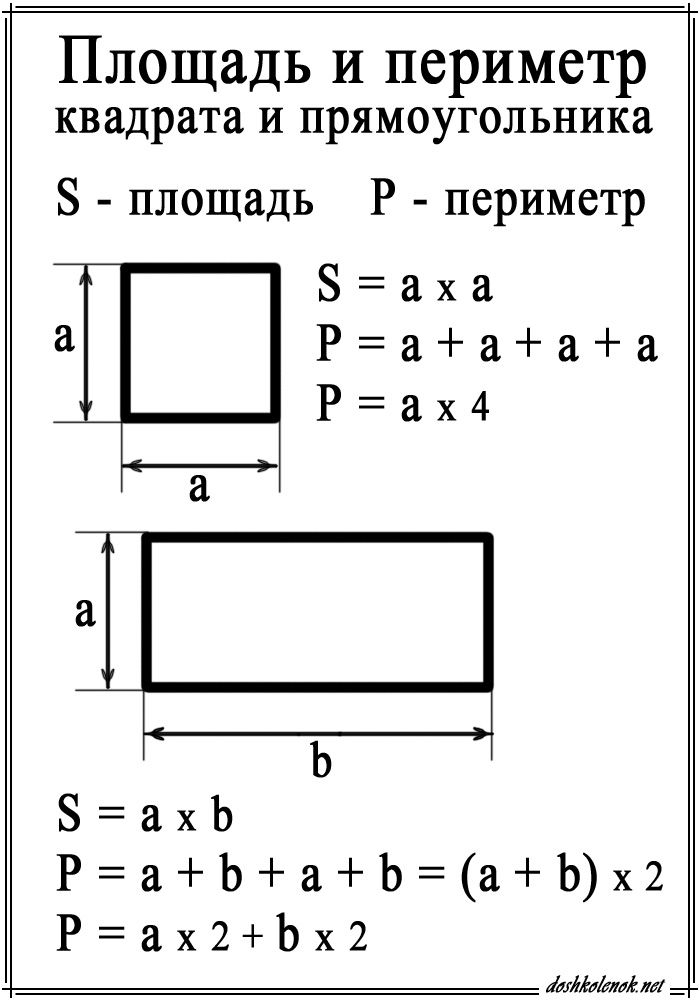
Периметр прямоугольников Словесные задачи
Чтобы решить текстовые задачи с периметром, сначала нарисуйте задачу, чтобы лучше ее представить. Затем отметьте длину всех сторон, прежде чем складывать их вместе.
Вот пример текстовой задачи на периметр прямоугольника.
Мы рисуем диаграмму ситуации, чтобы помочь нам визуализировать ее и отметить длины. Ширина показана ниже как две более короткие стороны.
Это длина. Длина всегда самая длинная сторона.
Найдя периметр прямоугольника, складываем все четыре стороны вместе. У нас есть 4 + 4 + 9 + 9.
Мы можем сложить две четверки, чтобы получить восемь, и мы можем сложить две девятки, чтобы получить 18.
8 + 18 = 26 см, значит, периметр прямоугольника равен 26 см.
Опять же, мы можем использовать формулу для более быстрого вычисления периметра прямоугольника.
P = 2(l + w) и, следовательно, P = 2(4 + 9).
Р = 2 × 13
Р = 26 см
Как найти периметр квадрата
Чтобы найти периметр квадрата, умножьте длину одной стороны на 4.

 Складываем все стороны. P = a + а + b + b
Складываем все стороны. P = a + а + b + b 
