Радиус шара формула: Калькулятор расчета радиуса шара через объем

формула поиска объема через диаметр, через радиус

Понятие объема геометрических фигур

Определение 1

Объем геометрической фигуры — количественная характеристика пространства, занимаемого телом или веществом, определяемая его формой и линейными размерами.

Представим себе два сосуда: один в форме куба, а второй произвольной формы, доверху наполненных жидкостью. Предположим, что для наполнения первого сосуда потребовалось m кг жидкости, а для наполнения второго сосуда n кг жидкости. Таким образом, второй сосуд в n/m раз больше первого. Величину, указывающую, во сколько раз второй сосуд больше первого, называют объемом второго сосуда, если первый сосуд при этом является единицей измерения. 

Источник: urok.1sept.ru

Из этого определения вытекают следующие свойства:

Следствие 1

Поскольку для заполнения каждого сосуда требуется определенное количество жидкости, то каждый сосуд имеет определенный положительный объем.

Следствие 2

Для заполнения равных сосудов требуется одно и то же количество жидкости, поэтому равные сосуды имеют равные объемы.

Следствие 3

Если данный сосуд разделить на две части, то количество жидкости, необходимое для заполнения всего сосуда, состоит из количества жидкости, необходимого для заполнения его частей. Поэтому объем всего сосуда равен сумме объемов его частей.

Общая формула для объемов тел вращения

Определение 2

Телом вращения в простейшем случае называется такое тело, которое плоскостями, перпендикулярными некоторой прямой (оси вращения), пересекается по кругам с центрами на этой прямой. Круговой цилиндр, конус, шар в геометрии являются примерами тел вращения. 

Источник: studfile.net

Для доказательства существования общей формулы вычисления объема тел вращения необходимо выполнить следующие построения. Введем декартовы координаты x, y, z, приняв ось тела за ось x. Плоскость xy пересекает поверхность тела по линии, для которой ось x является осью симметрии. Пусть  — уравнение той части линии, которая расположена над осью. Проведем через точку x оси абсцисс плоскость, перпендикулярную к ней, и обозначим через V(x) объем части тела, лежащей слева от этой плоскости, тогда V(x) является функцией от x. Найдем ее производную:

.

Разность  представляет собой объем слоя тела толщиной h между двумя плоскостями, перпендикулярными оси x, проходящими через точки с абсциссами x и x+h. Пусть M — наибольшее, а m — наименьшее значение функции f(x) на отрезке [x, x+h] . Тогда рассматриваемый слой тела содержит цилиндр с радиусом m, высотой h и содержится в цилиндре с радиусом M и той же высотой h. Поэтому:

.

Если f(x) — непрерывная функция, то при  левая и правая части последнего неравенства стремятся к одному и тому же пределу . К тому же пределу стремится и отношение, заключенное между ними, т.е. производная . 

Формула 1

Объем части тела, заключенной между параллельными плоскостями x = a и x = b будет вычисляться по формуле: .

Формула объема шара через диаметр

Основные понятия

Определение 3

Шаром называется множество всех точек пространства, находящихся от данной точки на расстоянии, не больше данного R.

Определение 4

Радиусом шара называют всякий отрезок, соединяющий центр шара с точкой шаровой поверхности.

Определение 5

Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром шара.

Определение 6

Концы любого диаметра шара называются диаметрально противоположными точками шара. Отрезок, соединяющий две любые точки шаровой поверхности и не являющийся диаметром шара, называют хордой шара.

Определение 7

Шаровым сегментом называется часть шара, отсекаемая от него плоскостью.

Определение 8

Шаровым слоем называется часть шара, расположенная между двумя параллельными плоскостями, пересекающими шар.

Определение 9

Шаровым сектором называется тело, которое получается из шарового сегмента и конуса следующим образом. Если шаровой сегмент меньше полушара, то шаровой сегмент дополняется конусом, у которого вершина в центре шара, а основанием является основание сегмента. Если же сегмент больше полушара, то указанный конус из него удаляется. 

Для иллюстрации определений можно нарисовать следующие эскизы.

Источник: demo.videouroki.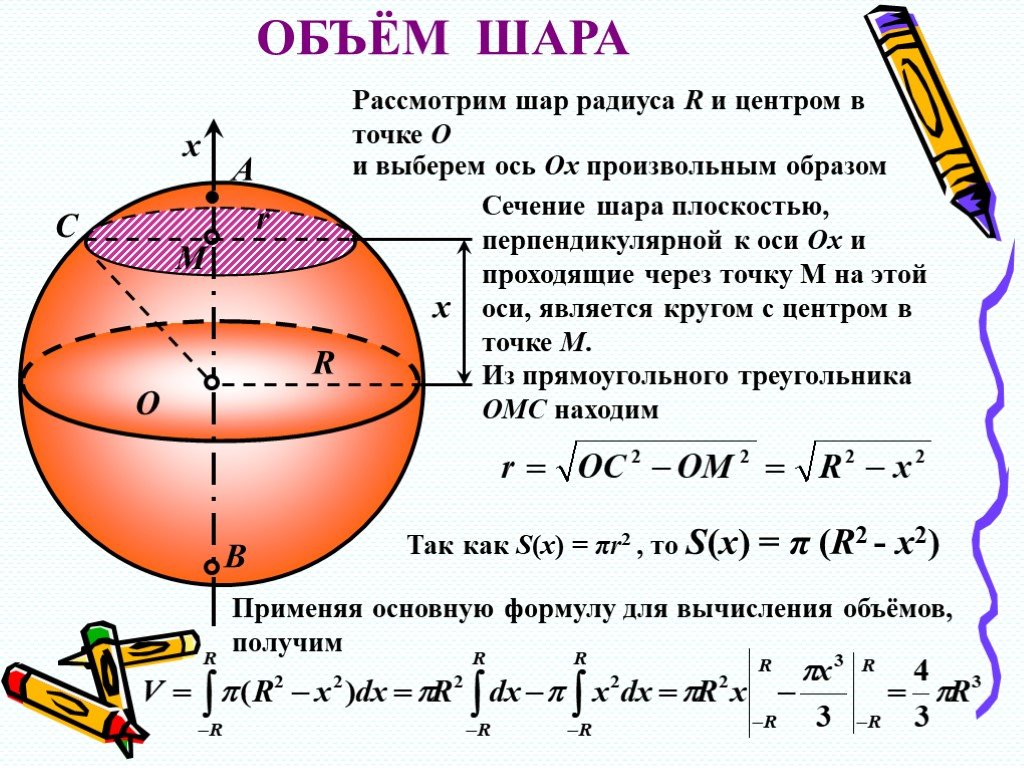 net

Формула объема шара через радиус и диаметр

Введем декартовы координаты, приняв центр шара за начало координат. Плоскость xy пересекает шар радиуса R по окружности, которая задается уравнением . Полуокружность, расположенная над осью x, задается уравнением .

Поэтому объем шарового слоя между плоскостями x = a и x = b определяется по формуле 

Для объема всего шара надо взять , из чего делаем следующий вывод:

Формула 2

Формула объема шара через радиус:

Формула 3

Зная, что радиус равен половине диаметра , получаем формулу объема шара через диаметр: 

Формулы объемов частей шара

Формула 4

Для получения объема шарового сегмента высотой H надо взять a = R-H,b = R. Получим объем шарового сегмента: 

Формула 5

Объем шарового сектора:  где R — радиус шара, а H — высота соответствующего шарового сегмента.

Формула объема шара через длину окружности

Длина окружности L определяется по формуле . Поставив ее в формулу 2 получим формулу для вычисления объема шара через длину окружности.

Формула 6

Формула объема шара через длину окружности: .

Пример 1

Решим задачу по математике для 11 класса. По разные стороны от центра шара проведены два параллельных сечения с площадью . Расстояние между сечениями равно 7 см. Определить объем шарового поля.

Чтобы решать задачу, необходимо сделать эскиз и записать формулу для вычисления объема шарового слоя: .

Чтобы найти объем шарового слоя необходимо знать его высоту и радиус оснований. Высота — это и есть расстояние между сечениями. Радиусы оснований найдем из площади сечений: .

Подставим радиусы оснований в формулу для вычисления объема шарового слоя: .

Формула объёма шара

Шар это геометрическое тело, образованное в результате вращения полукруга на оси своего диаметра.

Вычислить объем шара

Формула расчёта объёма шара

 

Объем шара можно вычислить по формуле:

 

V

=

4 3

π R3

 

R – радиус шара

V – объем шара

π – 3. 14

Пример нахождения объёма шара

 

Задача:

Найти объем шара радиусом 10 сантиметров.

Решение:

Для того чтобы вычислить объем шара формула используется следующая:

V

=

4 3

π R3

где V – искомый объем шара, π – 3,14, R – радиус.

Таким образом, при радиусе 10 сантиметров

объем шара равен:

V

=

4 3

3,14 × 103

= 4186,7

кубических сантиметров.

В геометрии шар определяется как некое тело, представляющее собой совокупность всех точек пространства, которые располагаются от центра на расстоянии, не более заданного, называемого радиусом шара. Поверхность шара именуется сферой, а сам он образуется путем вращения полукруга около его диаметра, остающегося неподвижным.

С этим геометрическим телом очень часто сталкиваются инженеры-конструкторы и архитекторы, которым часто приходится вычислять объем шара. Скажем, в конструкции передней подвески подавляющего большинства современных автомобилей используются так называемые шаровые опоры, в которых, как нетрудно догадаться из самого названия, одними из основных элементов являются именно шары. С их помощью происходит соединение ступиц управляемых колес и рычагов. От того, насколько правильно будет

вычислен их объем, во многом зависит не только долговечность этих узлов и правильность их работы, но и безопасность движения.

В технике широчайшее распространение получили такие детали, как шариковые подшипники, с помощью которых происходит крепление осей в неподвижных частях различных узлов и агрегатов и обеспечивается их вращение. Следует заметить, что при их расчете конструкторам требуется найти объем шара (а точнее – шаров, помещаемых в обойму) с высокой степенью точности. Что касается изготовления металлических шариков для подшипников, то они производятся из металлической проволоки при помощи сложного технологического процесса, включающего в себя стадии формовки, закалки, грубой шлифовки, чистовой притирки и очистки. Кстати говоря, те шарики, которые входят в конструкцию всех шариковых ручек, изготавливаются по точно такой же технологии.

Достаточно часто шары используются и в архитектуре, причем там они чаще всего являются декоративными элементами зданий и других сооружений. В большинстве случаев они изготавливаются из гранита, что зачастую требует больших затрат ручного труда. Конечно, соблюдать столь высокую точность изготовления этих шаров, как тех, которые применяются в различных агрегатах и механизмах, не требуется.

Без шаров немыслима такая интересная и популярная игра, как бильярд. Для их производства используются различные материалы (кость, камень, металл, пластмассы) и используются различные технологические процессы. Одним из основных требований, предъявляемых к бильярдным шарам, является их высокая прочность и способность выдерживать высокие механические нагрузки (прежде всего, ударные).

Кроме того, их поверхность должна представлять собой точную сферу для того, чтобы обеспечивалось плавное и ровное качение по поверхности бильярдных столов.

Наконец, без таких геометрических тел, как шары, не обходится ни одна новогодняя или рождественская елка. Изготавливаются эти украшения в большинстве случаев из стекла методом выдувания, и при их производстве наибольшее внимание уделяется не точности размеров, а эстетичности изделий. Технологический процесс при этом практически полностью автоматизирован и вручную елочные шары только упаковываются.

2}???

где ???D??? длина радиуса, ???(x_1,y_1,z_1)??? является одной точкой на поверхности сферы и ???(x_2,y_2,z_2)??? является центром сферы.

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

Как использовать две точки на сфере, чтобы найти уравнение сферы

Пройти курс

Хотите узнать больше об исчислении 3? У меня есть пошаговый курс для этого.

🙂

Узнать больше

Давайте попробуем пример, где нам даны точка на поверхности и центр сферы.

Пример

Найти уравнение сферы с центром ???(1,1,2)??? которая проходит через точку ???(2,4,6)???.

 

Поскольку в вопросе нам дан центр сферы, мы можем сразу же подставить его в уравнение сферы. 92??? в уравнение, или

решить для ???r???, заменить ???r??? в уравнение, затем возведите его в квадрат, чтобы упростить.

Любой способ будет работать, поэтому выполняйте шаги в любом порядке.

Давайте попробуем другой пример, когда нам дана развернутая форма уравнения и нам нужно найти центр и радиус.

Как найти центр и радиус из уравнения сферы

Пример

Найти центр и радиус сферы. 92???

Для этого нам нужно заполнить квадрат по каждой переменной. Помните, что процесс заполнения квадрата требует от нас использования коэффициента при члене первой степени. За ???х??? это ???2x??? поэтому коэффициент равен ???2???; для тебя??? это ???-2г??? так что коэффициент ???-2???; для ???z??? это ???-6z??? так что коэффициент ???-6???. Завершение квадрата говорит нам, что мы разделим каждый из этих коэффициентов на ???2???, а затем возьмем полученный результат и возведем его в квадрат. Эти окончательные значения будут тем, что мы добавляем (и вычитаем из) уравнения сферы. 92=25???

???r=5???

Подводя итог нашим выводам, можно сказать, что у сферы есть центр ???(-1,1,3)??? и радиусом ???r=5???.

Получите доступ к полному курсу Calculus 3

Начать

Учим математикуКриста Кинг 24 апреля 2018 г. центр, радиус, уравнение сферы

0 лайков

Какова площадь поверхности шара? Определение, формула, примеры

Какова площадь поверхности сферы?

Площадь поверхности сферы — это область или область, покрытая внешней изогнутой поверхностью сферы. {2}$ квадратных единиц

Связанные рабочие листы

Вывод площади поверхности сферы

Теперь, когда вы поняли площадь поверхности сферы, пришло время вывести формулу.

Греческий математик Архимед открыл, что площадь поверхности сферы равна площади боковой поверхности цилиндра, так что радиус сферы равен радиусу цилиндра, а высота цилиндра равна как диаметр сферы. Согласно Архимеду, сфера может вписаться в цилиндр так, что высота цилиндра станет диаметром сферы.

Итак, если радиус сферы и цилиндра равен «r», то

Площадь поверхности сферы $=$ Площадь боковой поверхности цилиндра

Мы знаем, что площадь боковой поверхности цилиндра $= 2\pi r h $, 

, где «r» — радиус, а «h» — высота цилиндра.

Теперь высота цилиндра = диаметру сферы.

Таким образом, $h = 2r$

Подставив значение «h» вместо «2r», получим уравнение площади поверхности сферы 9{2}$

Существует три типа площади поверхности твердых тел: площадь боковой поверхности (LSA), площадь криволинейной поверхности (CSA) и общая площадь поверхности (TSA).

Площадь криволинейной поверхности сферы

Площадь криволинейной поверхности представляет собой сумму площадей всех криволинейных областей твердого тела.

Площадь изогнутой поверхности сферы равна общей площади поверхности сферы, поскольку сфера имеет полностью изогнутую форму. Таким образом, формула площади криволинейной поверхности сферы равна 9{2}$ квадратных единиц

Как найти площадь поверхности сферы

Давайте разберемся, как рассчитать площадь поверхности сферы на примере. Если радиус шара 8 см. Какова будет площадь его поверхности?

Шаги для определения площади поверхности сферы приведены ниже:

• Шаг 1: 

Обратите внимание на радиус сферы. В приведенном выше примере радиус сферы равен 8 см. Если указан диаметр, разделите диаметр на 2, чтобы получить радиус. 9{2}_{2}}$

$\Rightarrow \frac{A_{1}}{A_{2}} = \frac{16}{9}$

Таким образом, отношение между суммой двух сфер площадь поверхности 16:9.