Площади фигур / Этюды // Математические этюды
Площади фигур / Этюды // Математические этюдыМатематические этюды
К списку
Площадь квадрата равна квадрату длины его стороны. Легко посчитать площадь фигуры, разбивающейся на несколько квадратов. А чему равна площадь фигуры, ограниченной произвольной кривой?
Наложим на изучаемую фигуру квадратную сетку.
Покрасим в жёлтый цвет квадраты, которые хотя бы частично пересекаются с фигурой. Чтобы зрительно увидеть и подсчитать площадь, занимаемую жёлтыми квадратами, сложим из них прямоугольник. Очевидно, что величина, которую мы хотим назвать площадью изучаемой фигуры, меньше площади этого жёлтого прямоугольника.
В синий цвет покрасим те квадраты, которые полностью лежат внутри нашей фигуры. Таких квадратов набралось, конечно, меньше, чем жёлтых. Выложим и из них прямоугольник.
Площадь нашей фигуры больше площади этого синего прямоугольника.
Для того чтобы получить более точные нижнюю и верхнюю границы искомой величины, рассмотрим сеточку из более маленьких квадратов. Повторим предыдущие действия. В жёлтый покрасим те квадраты, которые хотя бы частью пересекаются с фигурой. В синий — те, которые полностью лежат внутри фигуры. Снова площадь фигуры больше площади синего прямоугольника и меньше площади жёлтого. Но в этот раз, взяв более мелкую сетку, мы получили более точные границы.
Рассматривая ещё более мелкую сетку, мы получим еще более точные верхнюю и нижнюю границы площади изучаемой фигуры.
Будем продолжать уменьшать ячейки сетки, делая их всё мельче и мельче так, чтобы сторона квадратиков, из которых она составлена, стремилась к нулю.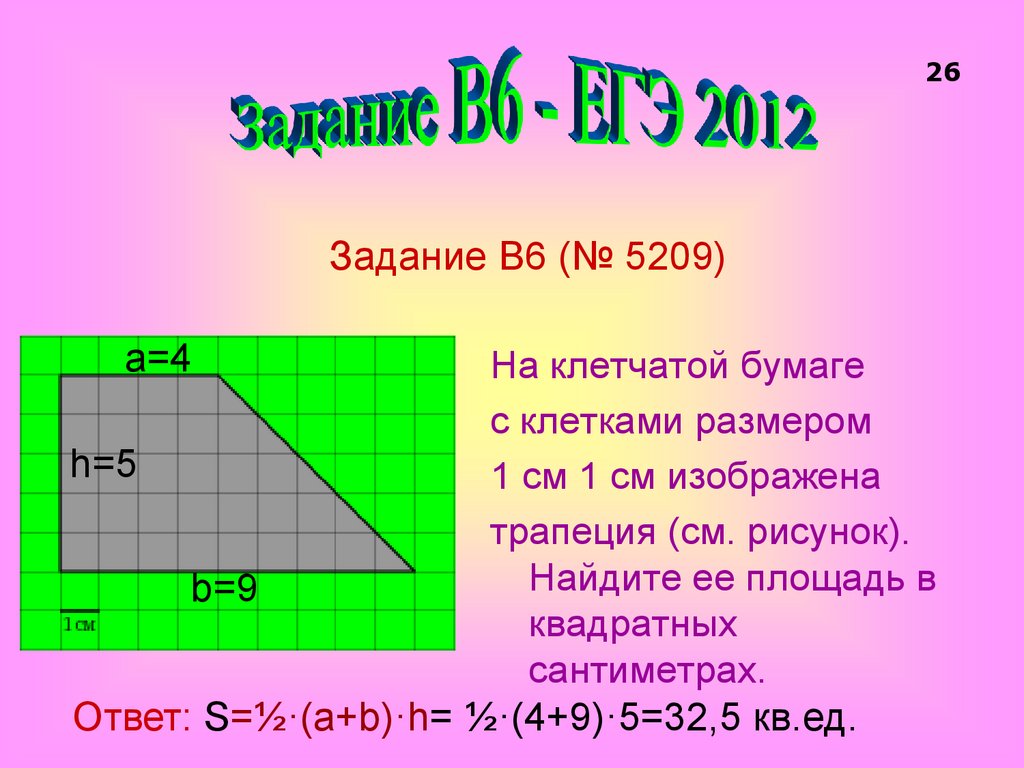
Площадью изучаемой фигуры по определению называется площадь двуцветного прямоугольника.
В жизни бывают случаи, когда необходимо приближённо определить площадь фигуры. При этом посчитанная площадь должна отличаться от настоящей не больше чем на некоторую заданную величину. Для решения этой задачи
необходимо взять сетку из таких квадратиков, чтобы разница между площадями жёлтого и синего прямоугольников не превосходила удвоенной заданной величины погрешности. Тогда за площадь изучаемой фигуры нужно взять
число, равное сумме площадей жёлтого и синего прямоугольников, поделённой пополам.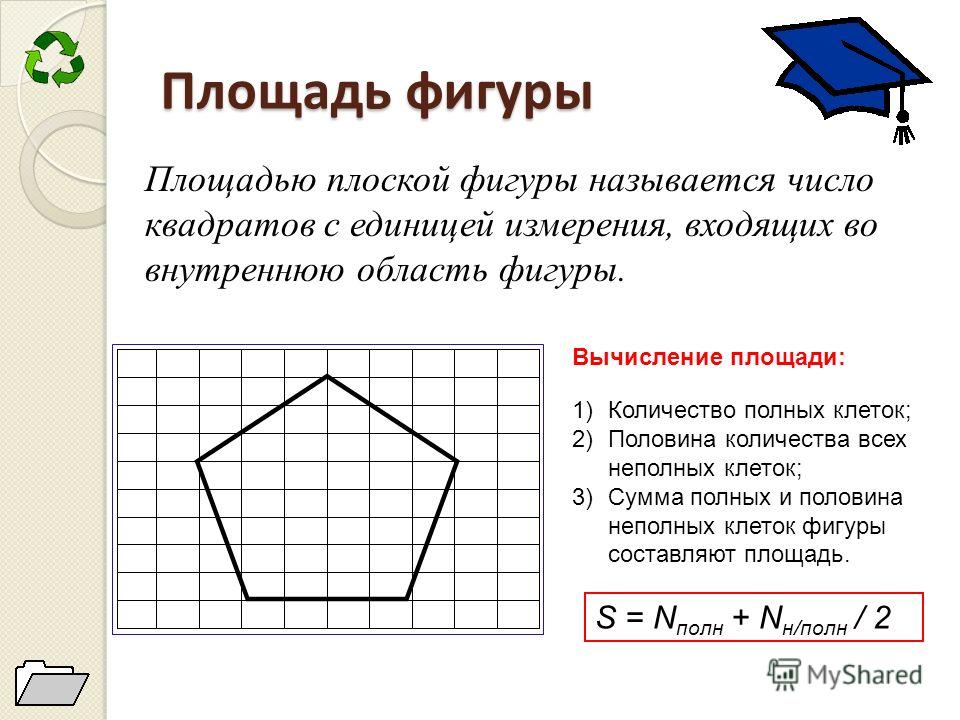
Другие этюды раздела «Площади и объёмы»
Обновлено Формула ПикаТеорема Пифагора: доказательство ЕвклидаОбновлено Теорема Пифагора: интерактивная головоломка Объём шара: весы Архимеда Объём шара Площадь на сфере: сферы, шапочки, кольца Теорема о косточке Сапог ШварцаМатематические этюды
Задачи на нахождение площади сложных фигур
Давайте вспомним, как найти площадь прямоугольника. Чтобы найти площадь прямоугольника, надо длину умножить на ширину.
Вот формула для нахождения площади прямоугольника:
S = a · b
В этой формуле латинской буквой S обозначается площадь, буквами a и b – стороны прямоугольника.
Выполним задание, в котором надо найти площадь прямоугольника со сторонами 5 см и 3 см.
Решение. Итак, чтобы найти площадь прямоугольника, надо его длину умножить на ширину.
Произведение чисел 5 и 3 равно 15. Значит, площадь прямоугольника
равна 15 квадратным сантиметрам.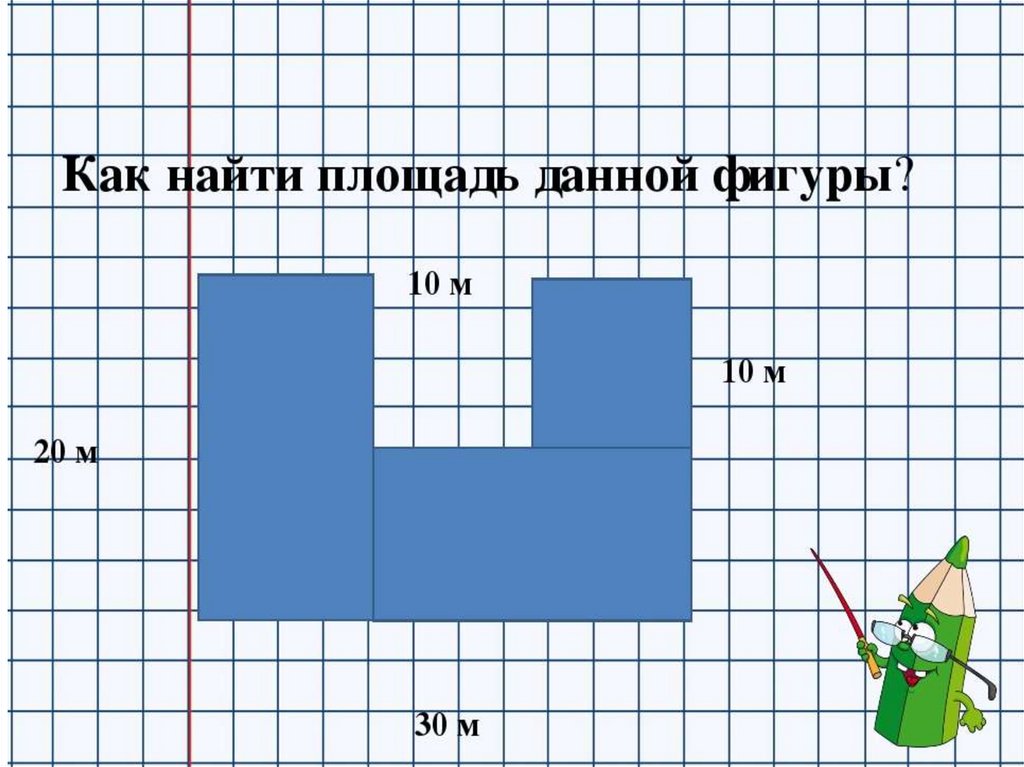
3 · 5 = 15 (см2)
Ответ: площадь прямоугольника равна 15 см2.
Теперь давайте найдём площадь квадрата со стороной 4 см.
Решение. У этого квадрата каждая сторона равна 4 см, поэтому умножим 4 на 4 и получится, что площадь квадрата равна 16 квадратным сантиметрам.
4 · 4 = 16 (см2)
Ответ: площадь квадрата равна 16 см2.
Ну а сейчас перейдём к решению задач, в которых нам надо будет найти площадь сложных фигур.
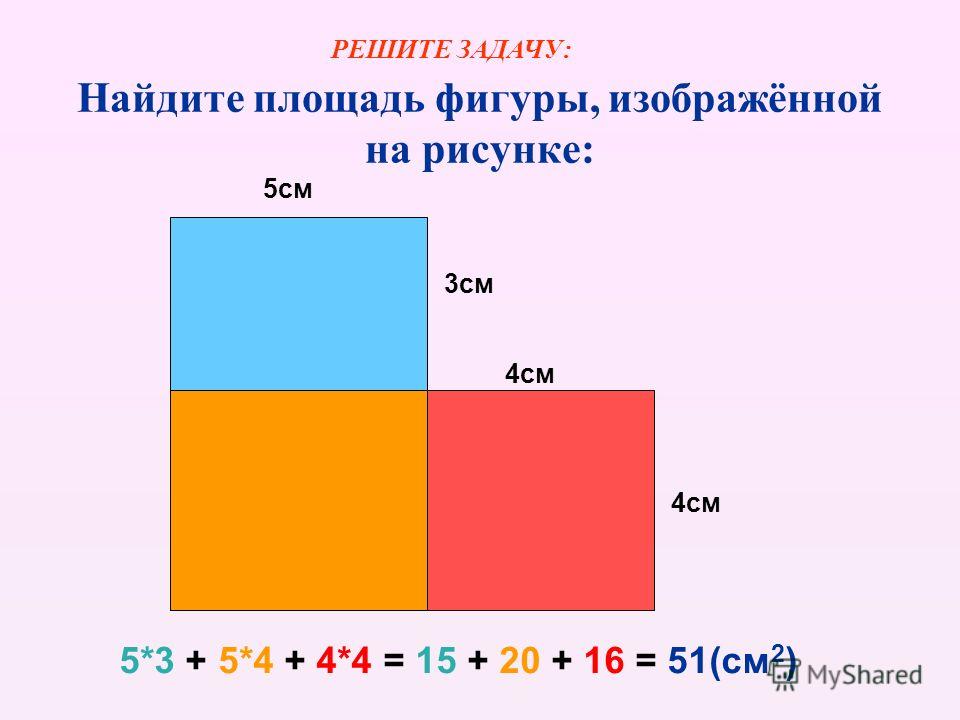
Найдите площадь фигуры, изображённой на рисунке.
Эта фигура не является ни прямоугольником, ни квадратом. Но мы можем разделить эту фигуру на два прямоугольника, например, вот таким образом.
А площади прямоугольников мы легко можем найти с помощью известной формулы.
Напомним, что противоположные стороны прямоугольника равны.
Итак, стороны первого прямоугольника равны 5 см и 4 см.
5 · 4 = 20 (см2) – площадь первого прямоугольника
Найдём площадь второго прямоугольника.
Ширина этого прямоугольника равна 2 см.
7 – 4 = 3 (см) – длина второго прямоугольника
3 · 2 = 6 (см2) – площадь второго прямоугольника
Мы нашли площади прямоугольников, из которых состоит сложная фигура. Чтобы найти площадь этой фигуры, надо сложить найденные площади.
20 + 6 = 26 (см2) – площадь сложной фигуры
Ответ: площадь фигуры, изображённой на рисунке, равна 26 см2.
Площадь этой сложной фигуры найти другим способом. Можно разделить её на два прямоугольника вот таким образом.
Найдём площадь первого прямоугольника.
Одна его сторона равна 4 см.
5 – 2 = 3 (см) – длина стороны первого прямоугольника
4 · 3 = 12 (см2) – площадь первого прямоугольника
Теперь найдём площадь второго прямоугольника.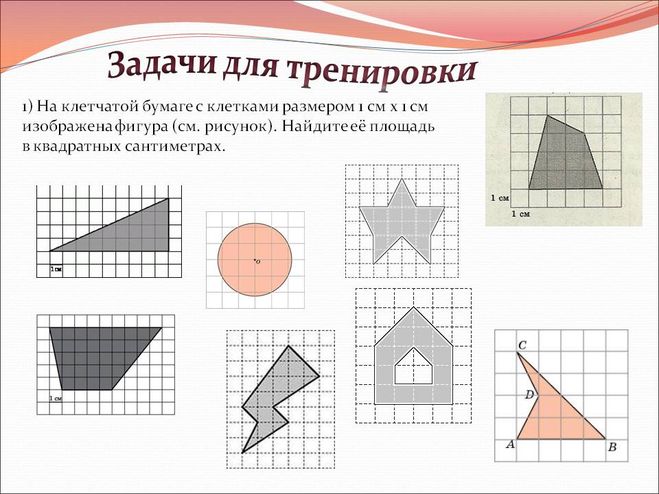
7 · 2 = 14 (см2) – площадь второго прямоугольника
12 + 14 = 26 (см2) – площадь сложной фигуры
Ответ: площадь фигуры, изображённой на рисунке, равна 26 см2.
Решим следующую задачу.
Найдём площадь ещё одной фигуры, изображённой на рисунке.
Чтобы найти площадь этой фигуры, тоже разделим её на простые фигуры. Сделаем это вот таким образом.
Получилось 3 прямоугольника.
Найдём площадь первого прямоугольника.
7 · 2 = 14 (см2) – площадь первого прямоугольника
Найдём площадь второго прямоугольника.
7 – 4 = 3 (см) – длина одной стороны второго прямоугольника
8 – 2 – 3 = 3 (см) – длина другой стороны второго прямоугольника
Получается, что это квадрат, так как длина всех его сторон равна 3 см.
3 · 3 = 9 (см2) – площадь квадрата
И найдём площадь последнего прямоугольника.
Его ширина равна 3 см. Длина равна 7 см.
3 · 7 = 21 (см2) – площадь третьего прямоугольника
Таким образом, мы нашли площади всех трёх фигур, на которые разделили данную сложную фигуру. Площадь этой сложной фигуры найдём как сумму площадей трёх фигур.
14 + 9 + 21 = 44 (см2) – площадь сложной фигуры
Ответ: площадь фигуры, изображённой на рисунке, равна 44 см2
Отметим, что площадь этой фигуры можно было бы найти, разделив её на простые фигуры и вот таким образом:
И решим ещё одну задачу.
Найдите площадь незаштрихованной фигуры.
На рисунке изображён прямоугольник со сторонами 9 см и 5 см. Внутри этого прямоугольника расположен ещё один прямоугольник со сторонами 5 см и 3 см. Давайте найдём площадь каждого из них.
9 · 5 = 45 (см2) – площадь большего прямоугольника
5 · 3 = 15 (см2) – площадь меньшего прямоугольника
А как найти площадь незаштрихованной фигуры? Площадь этой фигуры
найдём, если из площади большего прямоугольника вычтем площадь меньшего
прямоугольника.
45 – 15 = 30 (см2) – площадь незаштрихованной фигуры
Ответ: площадь незаштрихованной фигуры равна 30 см2.
Площади сложных фигур — Математика 3 класса
На последних уроках вы научились находить площади прямоугольников и квадратов.
В этом уроке вы научитесь находить площадь сложных фигур .
Комплекс Фигуры — это формы, которые не являются ни квадратами, ни прямоугольниками.
Их также называют неправильными формами. 🤓
Площадь сложных фигур
Как узнать площадь этого парка?
Чтобы найти площадь сложной формы , начните с разбиения на меньших, квадратных и обычных фигур.
Как мы можем разделить это?
Ты понял! Мы можем разделить эту фигуру на прямоугольник и квадрат. 😁
👆 7 км и 2 км пройдено из потому что они не больше не применяется к новым формам.
👉 Сначала найдем площадь вершины прямоугольника .
2 x 7 = 14
Прямоугольник имеет площадь 14 км² (квадратных километров).
👉 Затем находим площадь из квадрата.
5 х 5 = 25
Площадь квадрата 25 км² (квадратных километров).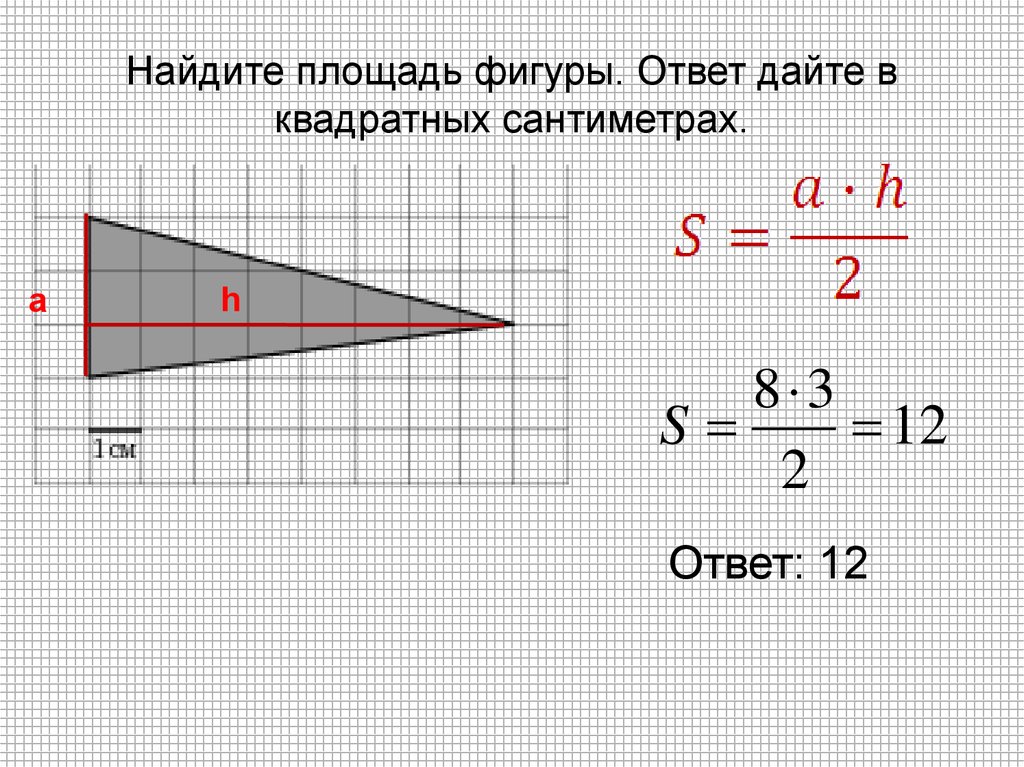
👉 Теперь мы добавляем две области, , чтобы получить площадь всего парка.
14 + 25 = 39
Площадь парка составляет 39 кв. ✅
Пример 2: Площадь бассейна
Какова площадь этого бассейна? 🤔
Сначала , вы должны выяснить, как разделить на на .
— Один из способов — разделить его на 3 прямоугольника.
— Другой способ — разделить его на 2 прямоугольника.
Как проще? 🤔
Да, второй! Потому что нам нужно иметь дело только с двумя формами.
Таким образом найдем площадь бассейна. 👇
Взгляните на размеры двух прямоугольников:
Совет : Мы не знали длину большей стороны второго прямоугольника, поэтому нам пришлось добавить длины сторон, которые мы знали.
Чтобы найти площадь первого прямоугольника , умножьте 8 м на 9 м:
8 x 9 = 72 м² :6 x 16 = 96 м²Теперь складываем две площади вместе:
72 + 96 = 168 м²youtube.com/embed/hqqtumES-rQ» frameborder=»0″>
Теперь попробуйте попрактиковаться. 😃
Площадь составных фигур — формула, примеры, определение
LearnPracticeDownload
Площадь составных фигур — это площадь, покрываемая любой составной фигурой. Составная форма — это форма, в которой несколько полигонов соединяются вместе, чтобы сформировать требуемую форму. Эти формы или фигуры могут состоять из комбинации треугольников, квадратов, четырехугольников и т. д. Разделите составную фигуру на основные формы, такие как квадрат, треугольник, прямоугольник, шестиугольник и т. д., чтобы определить площадь составных фигур.
В основном составная фигура состоит из основных фигур, соединенных вместе. Его также называют «составной» или «сложной» формой. Область составной формы объясняется в этом мини-уроке вместе с решенными примерами и практическими вопросами.
1. Какова площадь составных фигур? 2. Как найти площадь составных фигур? 3. Часто задаваемые вопросы по области составных форм Какова площадь составных фигур?
Площадь составных фигур — это площадь объединенных фигур одного или нескольких простых многоугольников и кругов. Чтобы вычислить площадь составных фигур, мы можем сложить площади всех основных фигур вместе. Чтобы найти площадь составных фигур, просто найдите площадь каждой фигуры и сложите их вместе. Следующий рисунок даст представление о том, как найти площадь составной фигуры. Единица площади составных фигур выражается в м 2 , см 2 , дюймы 2 или футы 2 и т. д.
Как найти площадь составных фигур?
Область составных фигур представляет собой комбинацию основных форм. С помощью следующих шагов, упомянутых ниже, мы можем вычислить площадь составных фигур.
- Шаг 1 : Разбейте составную фигуру на основные формы.
- Шаг 2 : Найдите площадь каждой базовой фигуры.
Шаг 3 : Сложите все области основных фигур вместе. - Шаг 4 : Представьте ответ в квадратных единицах.
Чтобы разложить любую составную фигуру, мы должны уметь вычислять площадь некоторых основных фигур, таких как квадраты, треугольники, прямоугольники и т. д. Проверьте таблицу ниже, содержащую площадь основных фигур.
Наименование базовой формы Площадь базовой формы Треугольник Площадь треугольника = (1/2) × основание × высота.
Также можно найти площадь треугольника, если известны длины его сторон, используя формулу Герона. Согласно формуле, площадь = \(\sqrt{s(s-a)(s-b)(s-c)}\), где s = периметр/2 = (a + b + c)/2, a, b и c равны длина его сторон.Квадрат Площадь квадрата = (длина) 2 Прямоугольник Площадь прямоугольника = длина × ширина Параллелограмм Площадь параллелограмма = основание × высота Трапеция Площадь трапеции = (1/2) × (сумма длин параллельных сторон) × высота Ромб Площадь ромба = (1/2) × (произведение диагоналей) Пример: Найдите площадь составной фигуры, которая образована соединением квадрата и треугольника. Длина стороны квадрата равна 5 единицам. Основание и высота треугольника равны 6 единицам и 7 единицам соответственно.
Решение: Длина стороны квадрата = 5 единиц, основание треугольника = 6 единиц и высота треугольника = 7 единиц
Площадь составной фигуры = площадь квадрата + площадь треугольник
⇒ А = (5) 2 + [(1/2) × 6 × 7]
⇒ A = 25 + 21 = 46 квадратных единицПлощадь составной фигуры составляет 46 квадратных единиц.
Решенные примеры на площади составных фигур
Пример 1: Вычислите площадь этой составной формы, показанной на рисунке ниже.
Решение : Длина и ширина прямоугольника ABCD равны 2 дюймам и 7 дюймам.
Длина стороны квадрата DEFG равна 3 дюймам.Используя формулу площади составной фигуры,
Площадь составной фигуры = площадь прямоугольника + площадь квадрата.
⇒ Площадь составной формы = длина × ширина + сторона 2
⇒ Площадь составной формы = BC × AB + DE 2
⇒ Площадь составной фигуры = 2 × 7 + 3 2
⇒ Площадь составной фигуры = 14+9 = 23 квадратных дюйма.Следовательно, площадь данной составной фигуры составляет 23 квадратных дюйма.
Пример 2: Составная фигура имеет площадь 500 квадратных единиц. Фигура состоит из круга и треугольника, а площадь треугольника составляет 350 квадратных единиц.
Какова площадь круга?
Решение: Учитывая площадь составной фигуры = 500 квадратных единиц и площадь треугольника = 350 квадратных единиц
Используя формулу площади составной фигуры, площадь составной фигуры = площадь треугольника + площадь круг.
⇒ 500 = 350 + площадь круга
⇒ Площадь круга = 500 — 350
⇒ Площадь круга = 150 квадратных единиц.Следовательно, площадь круга равна 150 квадратных единиц.
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по области составных фигур
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по области составных форм
Какова площадь составных фигур?
Площадь составных фигур определяется как площадь, покрываемая любой составной фигурой.
Что такое Формула площади составных фигур?
Не существует фиксированной формулы для определения площади составных фигур. Площадь составных фигур можно рассчитать, разделив составную фигуру на основные формы, такие как квадрат, треугольник, круг, прямоугольник, многоугольник и т. д., и сложив их площади.
Какова единица площади составных фигур?
Площадь составных фигур можно узнать, сложив площади всех фигур вместе. Единица площади составных фигур выражается в квадратных единицах, таких как м 2 , см 2 , дюймы 2 или футы 2 и т. д.
Как найти площадь составных фигур?
Шаги для нахождения площади составных фигур:
- Шаг 1 : Разделите составную фигуру на основные формы.
- Шаг 2 : Найдите площадь каждой базовой формы отдельно.
Какова площадь круга?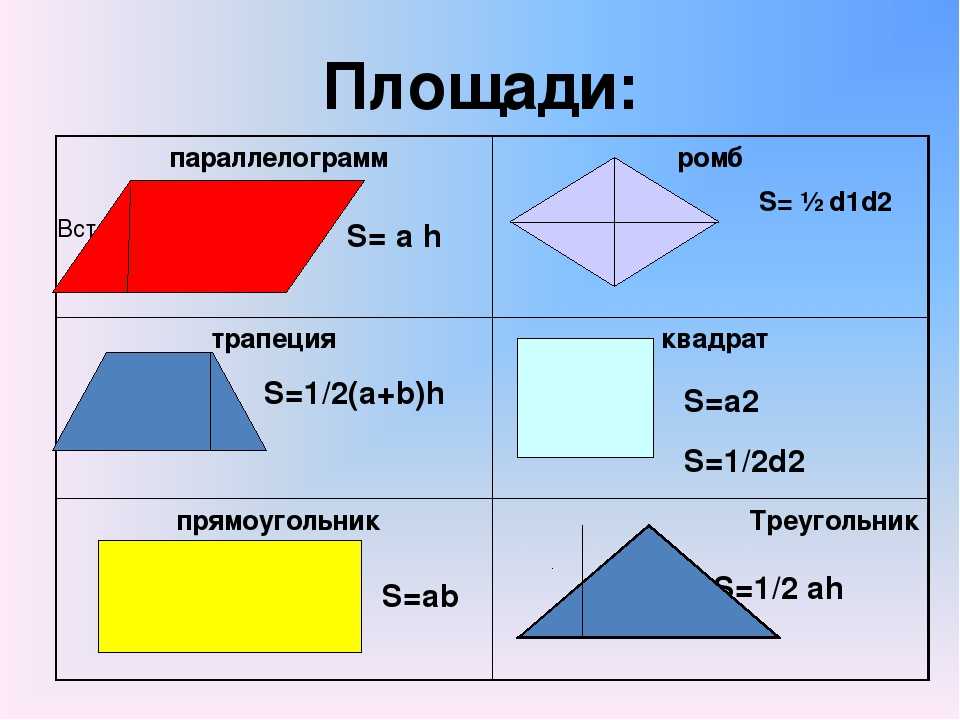
Составная форма состоит из основных фигур, соединенных вместе. Таким образом, площадь составной фигуры находится путем сложения по отдельности всех основных фигур.