Как найти площадь фигуры 4 класс формула пример: Как найти площадь фигуры, формула

Как найти площадь фигуры

Площадь прямоугольника равна произведению длины и ширины смежных сторон. Площадь параллелограмма равна произведению основания и высоты. Площадь ромба равна половине произведения его диагоналей. Площадь треугольника равна половине произведения основания и высоты. Для нахождения площади фигуры, у которой разные стороны, можно использовать формулу S = a × h, где a — сторона, h — высота, или формулу S = a × b × sinα, где a и b — две стороны, sinα — синус угла между ними.

Некоторые свойства площади фигур

Содержание:

• Как найти площадь в 4 классе?
• Как найти площадь квадрата или прямоугольника?
• Что такое площадь математика 5 класс?
• Что такое площадь 2 класс?

Как найти площадь кривой фигуры 4 класс

Палетку используют для измерения площади фигур, ограниченных кривой линией.

Чтобы найти площадь данной фигуры, нужно:

1. На данную фигуру наложить палетку.
2. Сосчитать, сколько целых клеток- квадратных единиц — содержится в фигуре.
3. Сосчитать, сколько нецелых квадратных единиц содержится в фигуре.

Как найти площадь 4 класс

S = a × b, где S — площадь; a, b — длина и ширина.

Как найти площадь многоугольника

Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников. Площадь первой фигуры равна сумме площадей двух маленьких фигур, из которых состоит эта фигура. Площадь второй фигуры равна сумме площадей трех маленьких фигур, из которых состоит эта фигура.

Как найти площадь и периметр фигур

Площадь прямоугольника равна произведению его длины и ширины. S = · b, где S — площадь, — длина, b — ширина прямоугольника. Периметр прямоугольника равен удвоенной сумме его длины и ширины. P = ( b) · 2, где P — периметр, — длина, b — ширина прямоугольника.

Как найти площадь в 4 классе

Чтобы найти площадь прямоугольника, надо длину умножить на ширину S = a× b .

Как найти площадь треугольника 4 класс пример

S пр = a ⋅ b . Поэтому для определения площади прямоугольного треугольника необходимо это произведение a ⋅ b разделить на 2. Чтобы найти площадь прямоугольного треугольника, нужно произведение его катетов разделить на 2.

Как найти площадь и периметр 4 класс

Площадь прямоугольника равна произведению его длины и ширины. S = · b, где S — площадь, — длина, b — ширина прямоугольника. Периметр прямоугольника равен удвоенной сумме его длины и ширины. P = ( b) · 2, где P — периметр, — длина, b — ширина прямоугольника.

Как найти площадь квадрата или прямоугольника

Площадь прямоугольника равна произведению его длины и ширины: ・ . Площадь квадрата равна произведению двух его соседних сторон: ・ .

Как найти площадь прямоугольника

2) Для вычисления площади прямоугольника нужно умножить его длину на ширину. Формула для вычисления площади прямоугольника имеет следующий вид : S = a*b.

Как найти площадь квадрата в третьем классе

Если известна длина стороны

Умножаем ее на то же число или возводим в квадрат. S = a × a = a2, где S — площадь, a — сторона. Эту формулу проходят в 3 классе.

Как найти Как найти площадь квадрата

Возведите длину стороны в квадрат.

Это все, что от вас требуется. Если длина сторон квадрата равна 3 см, то для вычисления площади квадрата нужно просто возвести ее в квадрат: 3 см x 3 см = 9 см2.

Как найти площадь прямоугольника 2 класс формула

Площадь прямоугольника равна произведению его длины и ширины. S = · b, где S — площадь, — длина, b — ширина прямоугольника.

Как найти площадь прямоугольника 3 класс примеры

Чтобы найти площадь прямоугольника, надо найти произведение длин его сторон. 2 см ⋅ 4 см = 8 см 2 . Длина и ширина прямоугольника должны быть выражены (записаны) в одинаковых единицах длины.

Что такое площадь математика 5 класс

Площадь указывает на размер плоскости, которую занимает фигура. Если вырезать любую фигуру из листа бумаги, положить на поверхность, а потом обвести карандашом, мы получим визуальное воплощение характеристики площади. Площади двух абсолютно разных фигур могут быть одинаковыми.

Что такое площадь в математике пятый класс

Площадь — это плоскость внутри замкнутой геометрической фигуры.

Что такое площадь для детей

Когда мы говорим о площади, мы говорим о «части плоскости, заключённой внутри замкнутой геометрической фигуры», о том, сколько места занимает фигура на плоскости. Площадь находят мерками, квадратиками (поэтому и единицы площади квадратные — так детям понятнее).

Что такое площадь в математике формула

S = a × b, где a, b — длина и ширина прямоугольника. S = a × √(d2 — а2), где а — известная сторона, d — диагональ. Диагональ — это отрезок, который соединяет вершины противоположных углов. Она есть во всех фигурах, число вершин которых больше трех.

Что такое площадь первый класс

Площадь – это место, которое занимает фигура, периметр – длина границы фигуры. Периметр определяется числом отрезков – сторон клеток, ограничивающий квадрат и прямоугольник.

Что такое площадь для 2 класса

Площадь – свойство фигуры, занимать место на плоскости. Площадь – это внутренняя часть фигуры.

Что такое площадь 2 класс

Площадь – свойство фигуры, занимать место на плоскости. Площадь – это внутренняя часть фигуры.

Что такое площадь объяснение

Площадь — это плоскость внутри замкнутой геометрической фигуры.

Что такое площадь квадрата 2 класс

Площадь квадрата равна квадрату его стороны. Периметр квадрата равен сумме его четырех сторон.

Что такое площадь и что такое периметр

Периметр квадрата равен сумме длин всех его сторон. Площадь квадрата равна произведению длин двух его сторон. Периметр фигуры обозначают большой латинской буквой P, площадь — большой латинской буквой S, а стороны фигур — маленькими латинскими буквами , b и др.

Что такое площадь в математике 4 класс

Площадь-это свойство фигур занимать место на плоскости. Квадратный километр-единица измерения площади, равная площади квадрата со стороной 1м.

Что такое площадь в математике 3 класс

Площадь – внутренняя часть любой плоской геометрической фигуры. Квадрат – это прямоугольник, у которого все стороны равны. Прямоугольник – это четырёхугольник, у которого все углы прямые. Квадратный сантиметр – квадрат со стороной 1 сантиметр.

Задачи на нахождение площади сложных фигур

Давайте вспомним, как найти площадь прямоугольника. Чтобы найти площадь прямоугольника, надо длину умножить на ширину.

Вот формула для нахождения площади прямоугольника:

S = a · b

В этой формуле латинской буквой S обозначается площадь, буквами a и b  – стороны прямоугольника.

Выполним задание, в котором надо найти площадь прямоугольника со сторонами 5 см и 3 см.

Решение. Итак, чтобы найти площадь прямоугольника, надо его длину умножить на ширину.

Произведение чисел 5 и 3 равно 15. Значит, площадь прямоугольника равна 15 квадратным сантиметрам. Не забудьте, что площадь измеряется именно в квадратных единицах.

В данной задаче это квадратные сантиметры. Также важно помнить, что длина и ширина должны быть выражены в одинаковых единицах длины.

3 · 5 = 15 (см²)

Ответ: площадь прямоугольника равна 15 см².

Теперь давайте найдём площадь квадрата со стороной 4 см.

Решение. У этого квадрата каждая сторона равна 4 см, поэтому умножим 4 на 4 и получится, что площадь квадрата равна 16 квадратным сантиметрам.

4 · 4 = 16 (см²)

Ответ: площадь квадрата равна 16 см².

Ну а сейчас перейдём к решению задач, в которых нам надо будет найти площадь сложных фигур.

Найдите площадь фигуры, изображённой на рисунке.

Эта фигура не является ни прямоугольником, ни квадратом. Но мы можем разделить эту фигуру на два прямоугольника, например, вот таким образом.

 А площади прямоугольников мы легко можем найти с помощью известной формулы.

Напомним, что противоположные стороны прямоугольника равны.

Итак, стороны первого прямоугольника равны 5 см и 4 см.

5 · 4 = 20 (см²) – площадь первого прямоугольника

Найдём площадь второго прямоугольника.

Ширина этого прямоугольника равна 2 см.

7 – 4 = 3 (см) – длина второго прямоугольника

3 · 2 = 6 (см²) – площадь второго прямоугольника

Мы нашли площади прямоугольников, из которых состоит сложная фигура. Чтобы найти площадь этой фигуры, надо сложить найденные площади.

20 + 6 = 26 (см²) – площадь сложной фигуры

Ответ: площадь фигуры, изображённой на рисунке, равна 26 см².

Площадь этой сложной фигуры найти другим способом. Можно разделить её на два прямоугольника вот таким образом.

Найдём площадь первого прямоугольника.

Одна его сторона равна 4 см.

5 – 2 = 3 (см) – длина стороны первого прямоугольника

4 · 3 = 12 (см²) – площадь первого прямоугольника

Теперь найдём площадь второго прямоугольника.

7 · 2 = 14 (см²) – площадь второго прямоугольника

12 + 14 = 26 (см²) – площадь сложной фигуры

Ответ: площадь фигуры, изображённой на рисунке, равна 26 см².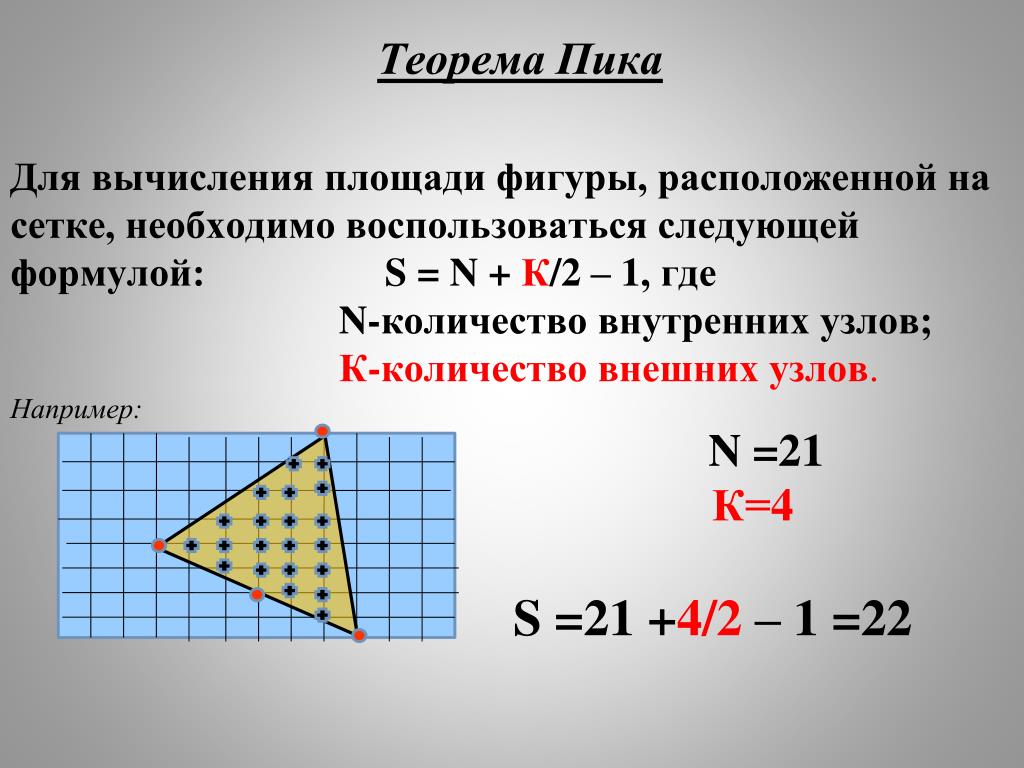

Решим следующую задачу.

Найдём площадь ещё одной фигуры, изображённой на рисунке.

Чтобы найти площадь этой фигуры, тоже разделим её на простые фигуры. Сделаем это вот таким образом.

Получилось 3 прямоугольника.

Найдём площадь первого прямоугольника.

7 · 2 = 14 (см²) – площадь первого прямоугольника

Найдём площадь второго прямоугольника.

7 – 4 = 3 (см) – длина одной стороны второго прямоугольника

8 – 2 – 3 = 3 (см) – длина другой стороны второго прямоугольника

Получается, что это квадрат, так как длина всех его сторон равна 3 см.

3 · 3 = 9 (см²) – площадь квадрата

И найдём площадь последнего прямоугольника.

Его ширина равна 3 см. Длина равна 7 см.

3 · 7 = 21 (см²) – площадь третьего прямоугольника

Таким образом, мы нашли площади всех трёх фигур, на которые разделили данную сложную фигуру. Площадь этой сложной фигуры найдём как сумму площадей трёх фигур.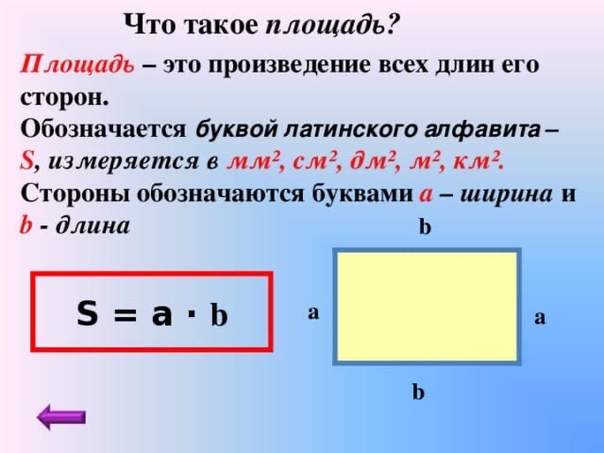

14 + 9 + 21 = 44 (см²) – площадь сложной фигуры

Ответ: площадь фигуры, изображённой на рисунке, равна 44 см

2

Отметим, что площадь этой фигуры можно было бы найти, разделив её на простые фигуры и вот таким образом:

И решим ещё одну задачу.

Найдите площадь незаштрихованной фигуры.

На рисунке изображён прямоугольник со сторонами 9 см и 5 см. Внутри этого прямоугольника расположен ещё один прямоугольник со сторонами 5 см и 3 см. Давайте найдём площадь каждого из них.

9 · 5 = 45 (см²) – площадь большего прямоугольника

5 · 3 = 15 (см²) – площадь меньшего прямоугольника

А как найти площадь незаштрихованной фигуры? Площадь этой фигуры найдём, если из площади большего прямоугольника вычтем площадь меньшего прямоугольника.

45 – 15 = 30 (см²) – площадь незаштрихованной фигуры

Ответ: площадь незаштрихованной фигуры равна 30 см².

Как найти площадь прямоугольника?

Площадь прямоугольника — один из самых важных и популярных параметров прямоугольника.

В этой статье мы рассмотрим основные теории и математические формулы, связанные с площадью прямоугольника, например, площадь прямоугольника, формулу площади прямоугольника и ее применение в повседневной жизни.


Все ли мы знаем, что такое прямоугольник? Во-первых, давайте разберемся с некоторыми фундаментальными понятиями, связанными с прямоугольником. Прямоугольник — это замкнутая фигура, состоящая из 4 сторон, как и квадрат. Но, в отличие от квадрата, у прямоугольника не все стороны равны. Прямоугольник – это четырехсторонняя фигура, у которой противоположные стороны равны и параллельны. Чтобы понять это, посмотрите на рисунок ниже:

Вы можете видеть, что сторона, отмеченная как A, противоположна стороне, отмеченной как C, и равна стороне, отмеченной как C. Точно так же сторона, отмеченная как B, равна и противоположна стороне, отмеченной как D. Следовательно, ABCD — прямоугольник.

«Вы также можете заметить, что квадрат — это частный случай прямоугольников, у которых все противоположные стороны равны».

В повседневной жизни мы можем встретить прямоугольники повсюду. Блокноты, на которых вы пишете книги, которые вы изучаете, представляют собой прямоугольники. Некоторыми прекрасными примерами прямоугольных форм являются плитка, установленная в вашем доме, школьная доска, которую учитель использует в школе, обеденный стол, форма вашего телевизионного экрана и многое другое.

Давайте теперь изучим некоторые математические термины и понятия, связанные с прямоугольником:

• У прямоугольника только противоположные стороны равны и параллельны. Две смежные стороны никогда не бывают равными в случае прямоугольника.
• Прямоугольник — это параллелограмм. Это означает, что противоположные стороны прямоугольника равны и параллельны друг другу, или противоположные стороны никогда не пересекаются.
• Диагональ прямоугольника делит его на два равновеликих треугольника.
• Периметр прямоугольника: Расстояние, пройденное границей прямоугольника, называется периметром прямоугольника. Это математически формулируется как

P (прямоугольник) = 2 (длина + ширина)

Теперь, когда мы хорошо разобрались с основами прямоугольника, давайте узнаем площадь прямоугольника и формулу площади прямоугольника.

Какова площадь прямоугольника?

Все ли мы знакомы с определением «площади», прежде чем углубляться в площадь прямоугольника? Пространство, заметаемое или покрываемое любой замкнутой фигурой, называется площадью. Площадь фигуры – это площадь, которая лежит внутри границ этой фигуры. Это приводит нас к выводу, что площадь прямоугольника относится к области, которую он заметает или покрывает. Другими словами, площадь прямоугольника — это двумерная область, расположенная внутри его периметра.

Ниже приведен рисунок. Площадь прямоугольника обозначена закрашенной желтой областью, а его граница обозначена красной линией.

Далее в этой статье мы увидим формулу площади прямоугольника. Используя эту формулу, вы даже можете определить площадь пола вашего дома, площадь экрана вашего компьютера или мобильного телефона и т.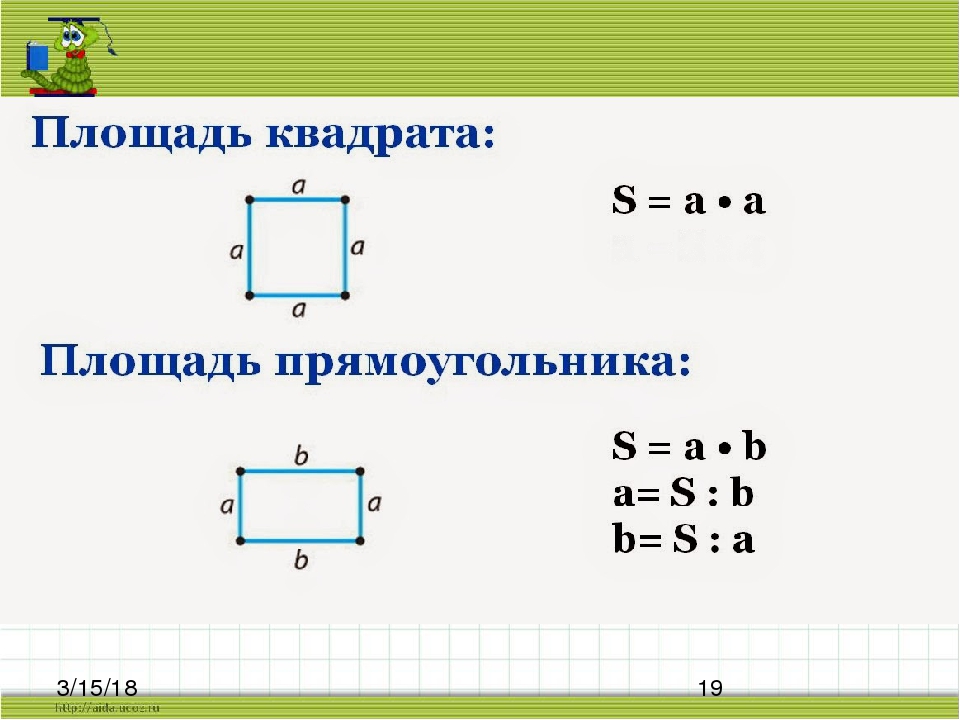 д.

Как найти площадь прямоугольника?

Количество единичных квадратов, которые идеально помещаются внутри прямоугольника, дает площадь этого прямоугольника. Вы могли запутаться с этим определением, не так ли? Не волнуйся; давайте проясним это для вас.

Например, давайте сделаем прямоугольник с длиной = 2 см и шириной = 3 см. Попробуем теперь поместить внутри этого прямоугольника квадраты длины 1 единица.

«Единичная длина: 1 известна как единичная длина. Единицами измерения могут быть см, дюймы, м, футы и т. д., но помните, что всякий раз, когда пишется единица измерения длины, всегда понимайте ее как 1».

Таким образом, квадраты единичной длины означают, что длина каждой стороны квадрата равна единице. Как мы видим на рисунке ниже, 6 квадратов единичной длины могут легко поместиться внутри этого прямоугольника, поэтому мы можем сказать, что площадь прямоугольника равна 6 единицам. Также мы знаем, что стороны прямоугольника в см; следовательно, площадь прямоугольника изменится с 6 единиц на 6 см.

Мы завершили все концептуальные занятия в области прямоугольника. Далее изучим и выведем формулу площади прямоугольника.

Формула площади прямоугольника

Формула, которую мы сейчас изучим, является одной из самых простых формул в математике. Несмотря на простоту, это одна из самых мощных формул. Площадь найдена по этой формуле только от изучаемой вами таблицы до жилой комнаты.

Площадь прямоугольной формулы определяется как:

Площадь = длина x ширина или длина x дыхание

Произведение длины и ширины прямоугольника дает нам формулу площади этого прямоугольника. Пусть размер прямоугольника будет «а», а дыхание — «b»; поэтому площадь «А» записывается как 

A = a x b (квадратные единицы)

Пример: Длина прямоугольной крыши 12 м, а ширина 7 м. Найдите площадь дерева, которой можно было бы покрыть всю крышу.

Решение: Заданная длина ‘a’ = 12

                          ширина ‘b’ = 7 

                Площадь дерева, необходимая для покрытия всей крыши = Площадь крыши  

                         A (крыша) = a x b

                                       = 12 x 7

                                        = 84 м ²

Теперь, когда мы узнали формулу площади прямоугольника, давайте научимся ее вычислять.

Как вычислить площадь прямоугольника?

Шаги по вычислению площади прямоугольника приведены ниже. Если вы правильно выполните эти шаги, вы никогда не получите ошибок в своих решениях.

Шаг 1: Запишите размеры данного прямоугольника из вопросов.

Шаг 2: Поместите значения в область формулы прямоугольника, т. е. длину x ширину.

Шаг 3: Умножьте значения и получите произведение.

Шаг 4: Запишите результат в квадратных единицах

Чтобы лучше понять, как вычислить площадь прямоугольника, рассмотрим следующий пример. Вычислим площадь прямоугольника длиной 20 единиц и шириной 5 единиц.

Шаг 1: Длина прямоугольника = 20 единиц, ширина прямоугольника = 5 единиц

Шаг 2: Формула площади прямоугольника = длина x ширина 100

Шаг 4: Площадь прямоугольника 100 квадратных единиц.

Доказательство площади прямоугольника?

На протяжении всей статьи мы вычисляли площадь прямоугольника как «длина × ширина».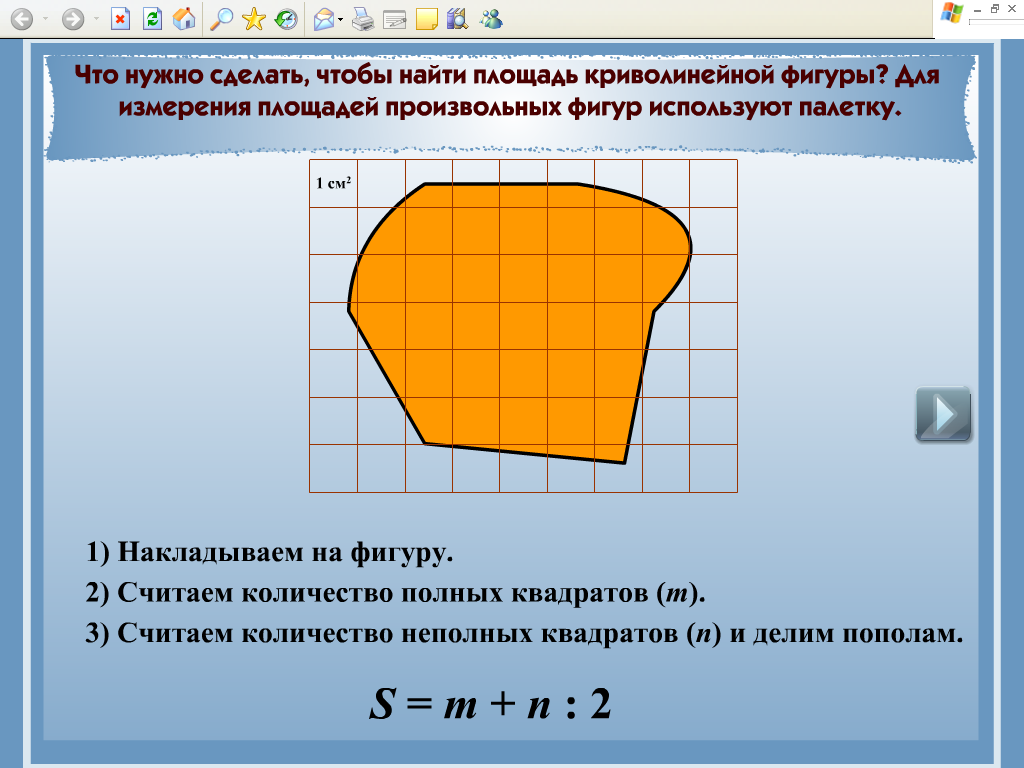 Но когда-нибудь задумывались, почему это формула? В этом разделе выведем формулу площади прямоугольника.

См. приведенный ниже рисунок. Мы видим прямоугольник KLMN с диагональю KM. Эта диагональ разделила прямоугольник на два равновеликих треугольника. Следовательно, площадь прямоугольника = 2 х площадь 1 треугольника.

Возьмем треугольник KMN. Основание KN треугольника — это длина прямоугольника, скажем, «а», а MN ширина прямоугольника — это высота треугольника, скажем, «b». Поскольку KMN является прямоугольным треугольником (поскольку смежные стороны прямоугольника перпендикулярны друг другу)

Мы знаем, что площадь треугольника равна ½ x основание x высота 

Следовательно, площадь KMN = ½ x a x b

Также , площадь прямоугольника = 2 x (площадь KMN)

                                                 = 2 x ½ x a x b

                                         = a x b 

Отсюда доказано, что площадь прямоугольника всегда равна его длине x ширине.

Предположим теперь, что нам не известны размеры длины какого-либо прямоугольника; вместо этого нам дана длина любой из диагоналей и ширина. Как узнать площадь? Узнаем в следующем разделе этой статьи.

Площадь прямоугольника по диагонали

Как упоминалось ранее, диагональ делит прямоугольник на два прямоугольных треугольника. Мы воспользуемся теоремой Пифагора, чтобы найти формулу для нахождения площади прямоугольника с помощью диагоналей.

Согласно теореме Пифагора:

(Гипотенуза) ² = (Основание) ² + (Перпендикулярная высота) ²

В этом случае:

9000 2 Пусть диагональ будет «d», длина — «l». а ширина будет ‘b’.

(Диагональ) ² = (Длина) ² + (Ширина) ²

(d) ² = (l) ² + (b) ²

(л) ² = (г) ² – (б) ²

л = √(г) ² – (b) ²

Подставив значение l в основную формулу

Площадь прямоугольника = l x b  = {(d) ² – (b) ² } x b 

Таким образом, площадь прямоугольника, если известны длина одной диагонали и размер ширины, равна {(d) ² – (b) ² } x b = {(Диагональ) ² – (Ширина) ² } x Ширина 

Таким образом, вы можете использовать любой из методов, чтобы найти площадь прямоугольника в зависимости от данных, которые вам даны.

Решенные примеры для площади прямоугольника 

Пример 1. Прямоугольная ферма имеет длину и ширину 80 ярдов и 60 ярдов соответственно. Найдите площадь фермы.

Решение: 

Ферма имеет длину 80 ярдов и ширину 60 ярдов.

Площадь фермы A: A = l w

= 60 ярдов x 80 ярдов

= 4800 квадратных ярдов

В результате площадь фермы составляет 4800 квадратных ярдов.

Пример 2: Прямоугольный экран имеет длину 15 см. Площадь его поверхности составляет 180 квадратных сантиметров. Найдите его ширину.

Решение:

180 квадратных сантиметров — это размер экрана.

15 см — длина экрана.

Площадь прямоугольника = длина x ширина.

Следовательно, площадь/длина=ширине

Следовательно, ширина экрана равна 180/15, или 12 см.

Часто задаваемые вопросы

1. Что такое площадь прямоугольника в геометрии?

Ответ. Площадь прямоугольника — это простая формула, с помощью которой можно найти площадь прямоугольника. Он использует длину и ширину прямоугольника, которые являются его сторонами.

2. Какая формула площади прямоугольника?

Ответ. Формула площади прямоугольника: A = l * w, где l — длина, а w — ширина.

3. Что такое единица площади прямоугольника?

Ответ. Единицей площади прямоугольника являются квадратные метры.

4. Почему мы вычисляем площадь прямоугольника?

Ответ. Площадь прямоугольника вычисляется путем умножения ширины прямоугольника на его длину.

5. Как найти площадь прямоугольника, используя его диагональ?

Ответ. Вы можете найти площадь прямоугольника, используя его диагональ. Просто разделите количество квадратных единиц на количество диагональных единиц. Например, 4×5 имеет площадь 20 и диагональ 10, поэтому мы разделим 20 на 10, чтобы получить 2, что и является нашим ответом.

Площадь прямоугольников: формулы, уравнения и примеры

Прямоугольник — это частный случай четырехугольника, представляющего собой четырехстороннюю плоскую фигуру. Все 4 внутренних угла прямоугольника прямые. Книга, футбольное поле, окно, дорожный чемодан — все это примеры прямоугольников.

Теперь предположим, что вы хотите вычислить общую площадь футбольного поля. Затем вам нужно знать, как вычислить площадь прямоугольника.

Прямоугольник – это четырехугольник, все внутренние углы которого прямые. Двумерное пространство, занимаемое прямоугольником, называется площадью прямоугольника.

Четырехугольник с двумя парами параллельных противоположных сторон называется параллелограммом. Так как все углы прямоугольника прямые, то и противоположные пары сторон прямоугольника всегда параллельны. Это делает каждый прямоугольник параллелограммом. На самом деле прямоугольник считается особым типом параллелограмма.

Площадь прямоугольников: Формула

Рассмотрим следующий прямоугольник.

Иллюстрация прямоугольника, Нилабхро Датта – StudySmarter Originals b — длина стороны АВ, которая здесь считается основанием. Условно одну из длинных сторон прямоугольника принимают за основание, а одну из сторон, перпендикулярных основанию, считают высотой. В этом прямоугольнике высота равна длине AD.

В некоторых соглашениях основание и высота называются длиной и шириной прямоугольника.

Частный случай: Формула площади квадрата

Квадрат – это частный случай прямоугольника. Кроме того, что все 4 внутренних угла прямые, все 4 стороны квадрата равны.

Квадратная иллюстрация, Нилабхро Датта, StudySmarter Originals

Посмотрите на приведенный выше квадрат и вспомните формулу площади прямоугольника: Площадь = основание × высота.

Так как все 4 стороны квадрата равны, то основание и высота равны. Достаточно знать длину стороны квадрата, чтобы вычислить его площадь. Таким образом, в случае квадрата формула может быть сокращена до:

Площадь=длинастороны×длинастороны=(длинастороны)2

Площадь прямоугольников: квадратные единицы

Рассматривая площадь фигуры, помните, что площадь измеряется в квадратных единицах , таких как квадратные сантиметры (см ² ), квадратные футы (футы ² ), квадратные дюймы (в ² ) и т.  д. . Подумайте, сколько квадратных единиц необходимо, чтобы точно и исчерпывающе покрыть всю поверхность замкнутой фигуры. Эта сумма и есть площадь фигуры.

Квадратные единицы, Jurgensen & Brown– Геометрия

Площадь прямоугольников: примеры задач

Прямоугольник площадью 60 м ² имеет длину основания 20 м. Какова высота прямоугольника?

Решение

Площадь = b × h

⇒ 60 м ² = 20 м × h

⇒ h = 60 м ² ÷ 2 0 м

⇒ h = 3 м

Если вы зная длину 1 из сторон (основание или высоту) прямоугольника и длину диагонали, вы можете вычислить неизвестную длину стороны (высоту или основание), используя теорему Пифагора. Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух других сторон.

На следующем рисунке показано, как диагональ прямоугольника делит его на 2 прямоугольных треугольника, что позволяет нам использовать теорему Пифагора. Затем, когда известны и основание, и высота прямоугольника, можно вычислить площадь.

Диагональ прямоугольника делит его на 2 прямоугольных треугольника, Nilabhro Datta — StudySmarter Originals

В следующем прямоугольнике ABCD, AB = 9, BD = 15. Найдите площадь прямоугольника.

Решение

Поскольку внутренние углы прямоугольника прямые, BD — это гипотенуза прямоугольного треугольника, ΔABD.

SO,

в соответствии с питагорской теоремой,

AD2+AB2 = BD2 порядка 2+92 = 152, Ад2 = 152-92thyt

= 12 футов × 9 футов

= 108 футов ²

Сторона квадрата равна 10 футам. Какова площадь квадрата?

Решение

Площадь = сторона × сторона

= 10 футов × 10 футов. четырехугольник, у которого все внутренние углы прямые .

1. Площадь прямоугольника определяется по формуле:

   Площадь = b × h

   где b = основание, h = высота.

2. Квадрат является частным случаем прямоугольника.

   No related posts.