Рассмотрим функцию, которая связывает координаты следующим соотношением: .
Чтобы построить график рассматриваемой функции, определим несколько значений этой функции для некоторых значений аргумента .
Составим таблицу значений функции для указанных выше значений аргумента .
Теперь отмечаем в прямоугольной системе координат точки с координатами (0; 0), (1; 1), (2; 4), (3; 9), (1; 1), (2; 4), (3; 9).
Далее соединяем отмеченные точки плавной линией.
Мы построили график функции и этот график называют параболой.
Можно вычислить координаты других точек, удовлетворяющих равенству , и отметить их на координатной плоскости. Все они попадут на эту параболу.
Точка с координатами (0; 0) делит параболу на две равные части, называемые ветвями параболы, эти ветви неограниченно уходят вверх. Саму точку с координатами (0; 0), называют  В вершине одна ветвь параболы плавно переходит в другую.
В вершине одна ветвь параболы плавно переходит в другую.
Свойства функции
- Областью определения функции являются все числа.
- Областью значений функции являются все неотрицательные числа, так квадрат любого числа положителен или равен нулю, то есть при любом выполняется неравенство .
- Если , то . Поэтому график функции проходит через начало координат. Также, запомните, значение аргумента, при котором значение функции равно нулю, называют нуль функции. Значит, — нуль функции .
- Если , то . Значит, все точки графика функции, кроме точки (0; 0), расположены выше оси .
- Противоположным значениям соответствует одно и то же значение . Это следует из того, что при любом . Значит, точки графика функции , имеющие противоположные абсциссы, симметричны относительно оси , поэтому ось ординат является осью симметрии параболы.
 Также функцию симметричную относительно оси ординат называют четной функцией, значит, функция является четной.
Также функцию симметричную относительно оси ординат называют четной функцией, значит, функция является четной.
Советуем посмотреть:
Квадратные корни. Арифметический квадратный корень
Свойства арифметического квадратного корня
Тождественные преобразования выражений, содержащих арифметические квадратные корни
Квадратные корни. Дейстительные числа
Правило встречается в следующих упражнениях:
8 класс
Номер 1, Мерзляк, Полонский, Якир, Учебник
Номер 2, Мерзляк, Полонский, Якир, Учебник
Номер 5, Мерзляк, Полонский, Якир, Учебник
Номер 350, Мерзляк, Полонский, Якир, Учебник
Номер 351, Мерзляк, Полонский, Якир, Учебник
Номер 352, Мерзляк, Полонский, Якир, Учебник
Номер 359, Мерзляк, Полонский, Якир, Учебник
Номер 360, Мерзляк, Полонский, Якир, Учебник
Номер 364, Мерзляк, Полонский, Якир, Учебник
Номер 427, Мерзляк, Полонский, Якир, Учебник
Что такое координаты x и y?
- Рахул Авати
Координаты X и y — это, соответственно, горизонтальный и вертикальный адреса точки в любом двумерном (2D) пространстве, таком как лист бумаги или экран дисплея компьютера. Вместе эти координаты помогают определить точное местоположение точки.
Вместе эти координаты помогают определить точное местоположение точки.
В декартовой системе координат координаты x и y являются частью осей x и y в 2D-пространстве. Для точки в пространстве координаты x и y записываются в виде упорядоченной пары (x, y). Первое число представляет положение точки на оси x, а второе число представляет ее положение на оси y. Координаты также могут быть записаны как (x,y) без пробела после запятой.
Координаты X и Y (оси) — это горизонтальные и вертикальные адреса в 2D-пространстве.Порядок координат x и y в упорядоченной паре важен. Координата x всегда идет первой, за ней следует координата y. Вот почему (3, 4) не то же самое, что (4, 3).
(3, 4) относится к точке на три единицы справа от нуля и на четыре единицы выше нуля.
(4, 3) относится к точке на четыре единицы справа от нуля и на три единицы выше нуля.
Две оси пересекаются перпендикулярно в исходной или нулевой точке. Координаты x и y этого местоположения записываются как (0, 0) или (0,0).
Оси x и y, на которых нанесены координаты x и y, образуют координатную плоскость. Система была изобретена французским математиком Рене Декартом и известна как декартова система координат.
Координатная плоскость необходима для представления любой точки в заданном 2D-пространстве. Плоскость, образованная пересечением двух осей, является двумерной, поскольку для определения положения любой точки на этой плоскости требуются две точки данных:
- его расстояние по оси x
- его расстояние по оси Y
Эти расстояния представлены координатой x и координатой y соответственно.
Значение x точки (x, y) известно как абсцисса . Он представляет собой расстояние точки от начала координат или вдоль горизонтальной оси X. Значение y точки (x, y) известно как ордината . Он представляет собой вертикальное или перпендикулярное расстояние точки от начала координат или от оси x.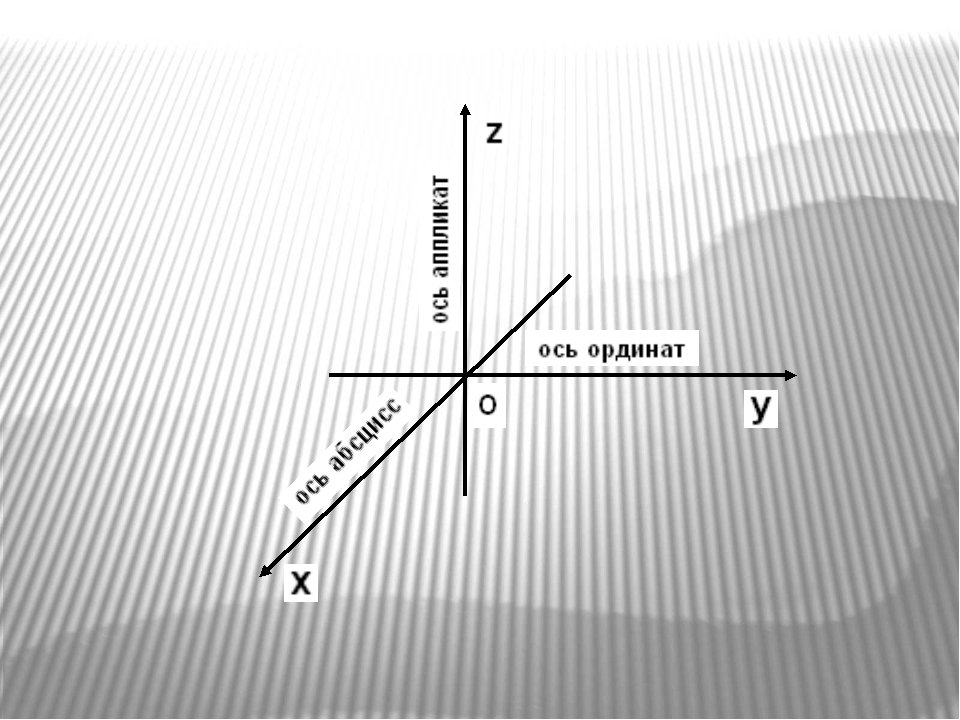
Точка, в которой линия пересекает ось x, называется x- точкой пересечения , а точка, в которой она пересекает ось y, называется точкой пересечения y . Координата y точки пересечения x равна 0, а координата x точки пересечения y равна 0. Если доступно уравнение прямой (y = mx + b), подстановка x = 0 в уравнение дает y -перехват. Точно так же подстановка y = 0 дает точку пересечения по оси x.
Координатная плоскость разделена на четыре квадранта:
- Квадрант 1 находится вверху справа.
- Квадрант 2 находится вверху слева.
- Квадрант 3 находится внизу слева.
- Квадрант 4 находится внизу справа.
Любая точка в двумерном пространстве представлена координатами x и y в виде упорядоченной пары, любая из которых может быть нулевой, положительной или отрицательной.
Если одно из значений равно нулю, точка представлена следующим образом:
- (0, y): координата x равна нулю, поэтому точка лежит на оси y.

- (0, 10): точка находится на оси Y и на 10 единиц выше .
- (0, -10): точка находится на оси Y и на 10 единиц ниже .
- (x, 0): координата y равна нулю, поэтому точка лежит на оси x.
- (10, 0): точка находится на оси X и на 10 единиц вправо от нуля.
- (-10, 0): точка находится на оси х и 10 единицах к осталось нулей.
Если обе координаты x и y равны нулю (0, 0), точка находится в начале координат, где оси x и y пересекаются.
Если обе координаты x и y отличны от нуля, точка находится где-то на двумерной координатной плоскости в одном из ее четырех квадрантов.
Пример 1
Здесь рассмотрим точку M в координатной плоскости.
М лежит на одну единицу правее нуля и на две единицы выше нуля. Таким образом, его координата x равна (1), а его координата y равна (2). Вместе его координаты (x, y) представлены на двухмерной координатной плоскости следующим образом:
М = (1, 2)
Точка M находится в квадранте 1.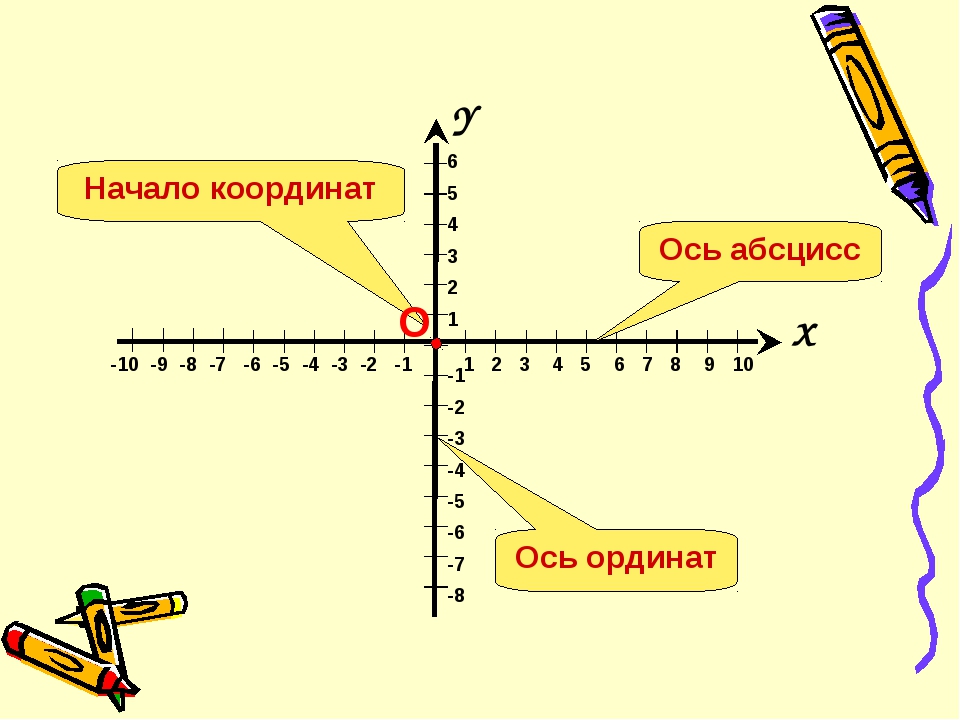
Пример 2
Здесь рассмотрим точку N в координатной плоскости.
N лежит на три единицы левее нуля и на четыре единицы ниже нуля. Итак, его координата x равна (-3), а координата y равна (-4). Вместе его координаты (x, y) представлены на двухмерной координатной плоскости следующим образом:
Н = (-3, -4)
Точка N находится в квадранте 3.
Положительные и отрицательные значения в 4 квадрантахВ зависимости от положения точки в одном из четырех квадрантов координатной плоскости координаты x и y будут иметь положительные или отрицательные значения. Если координата x находится в левой части плоскости, она имеет отрицательное значение, а если в правой, то ее значение положительное.
Аналогично, если координата y находится в верхней части плоскости, ее значение положительно. Если он находится в нижней плоскости, он имеет отрицательное значение. Левая, правая, верхняя и нижняя части плоскости определяются положением точки от начала координат или нулевого значения.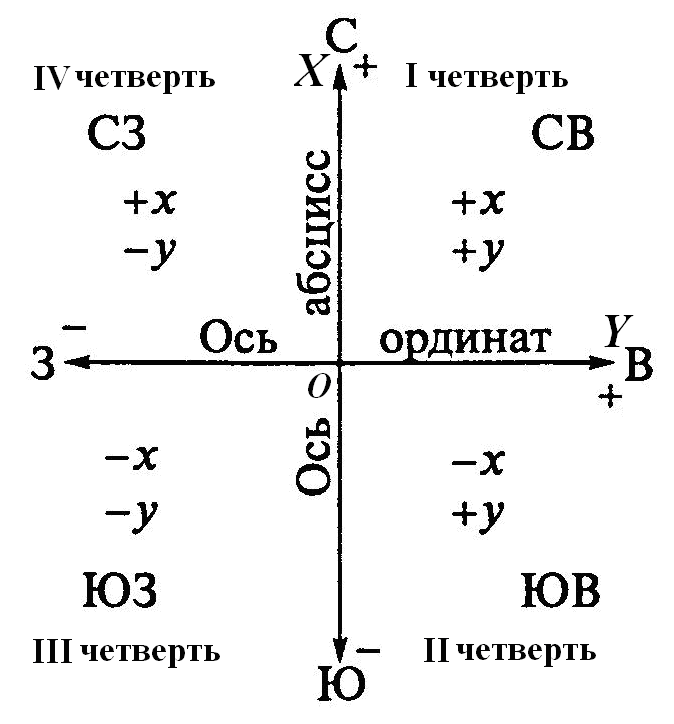
| Квадрант | Местоположение точки | Значение X (положительное/отрицательное) | Значение Y (положительное/отрицательное) | (х, у) |
Квадрант 1 | Вверху справа | Положительный | Положительный | (+, +) |
Квадрант 2 | Вверху слева | Отрицательный | Положительный | (-, +) |
Квадрант 3 | Внизу слева | Отрицательный | Отрицательный | (-, -) |
Квадрант 4 | Внизу справа | Положительный | Отрицательный | (+, -) |
Пример 1
(2, 5): точка находится в квадранте 1, на две единицы вправо от нуля и на пять единиц выше нуля.
Пример 2
(-2, 5): точка находится в квадранте 2, две единицы до осталось нуля и пять единиц выше нуля.
Пример 3
(-2, -5): точка находится в квадранте 3, две единицы до слева от нуля и пять единиц ниже нуля.
Пример 4
(2, -5): точка находится в квадранте 4, на две единицы правее нуля и на пять единиц ниже нуля.
Использование координат x и yКоординаты x и y точки необходимы для определения расстояния этой точки от заявленного начала координат 2D-пространства. Координаты также используются для нахождения середины и наклона линии, а также для определения ее линейного уравнения.
Линейное уравнение прямой представляется как y = mx + b:
- м = уклон = изменение по у / изменение по х
- х = координата х, «как далеко»
- y = координата y, «как далеко вверх»
- b = значение y, когда x = 0
Вот как выглядит пара координат (x, y), если значение x известно и уравнение выражается как y = 2x + 2:
| Координата X | Координата Y | Уклон (м) | у = 2х + 2 | (х, у) |
0 | 2 | 2 | 2 | (0, 2) |
1 | 4 | 2 | 4 | (1, 4) |
2 | 6 | 2 | 6 | (2, 6) |
3 | 8 | 2 | 8 | (3, 8) |
4 | 10 | 2 | 10 | (4, 10) |
Чтобы изобразить уравнение y = 2x + 2, каждая координата в каждой упорядоченной паре расположена на координатной сетке. Затем координаты x и y соединяются в прямую линию.
Затем координаты x и y соединяются в прямую линию.
См. также: математические символы .
Последнее обновление: август 2022 г.
Продолжить чтение О координатах x и y- Медицинская школа Kaiser Permanente для обучения студентов современным технологиям
- Как предприятия будут использовать еще не определенную метавселенную
- Чем CPU, GPU и DPU отличаются друг от друга?
- Как улучшение математических навыков может помочь в программировании
- Будущее науки о данных: карьерный рост и отраслевые тенденции
управление правами на информацию (IRM)
Управление правами на доступ к данным (IRM) — это дисциплина, которая включает в себя управление, контроль и защиту содержимого от нежелательного доступа.
Сеть- CSU/DSU (блок обслуживания канала/блок обслуживания данных)
CSU/DSU (Channel Service Unit/Data Service Unit) — аппаратное устройство размером примерно с модем.
 Он преобразует цифровые данные …
Он преобразует цифровые данные … - потоковая передача данных
Потоковая передача данных — это непрерывная передача данных из одного или нескольких источников с постоянной высокой скоростью для обработки в определенные …
- граница службы безопасного доступа (SASE)
Пограничный сервис безопасного доступа, также известный как SASE и произносится как «дерзкий», представляет собой модель облачной архитектуры, объединяющую сеть и …
- черный список приложений (занесение приложений в черный список)
Занесение приложений в черный список — все чаще называемое занесением в черный список — представляет собой практику сетевого или компьютерного администрирования, используемую …
- соковыжималка
Juice jacking — это эксплойт безопасности, в котором зараженная зарядная станция USB используется для компрометации устройств, которые к ней подключаются.

- безопасность гипервизора
Безопасность гипервизора — это процесс обеспечения безопасности гипервизора (программного обеспечения, обеспечивающего виртуализацию) на протяжении…
- Общепринятые принципы ведения учета (Принципы)
Общепринятые принципы ведения документации — это основа для управления записями таким образом, чтобы поддерживать …
- система управления обучением (LMS)
Система управления обучением представляет собой программное приложение или веб-технологию, используемую для планирования, реализации и оценки конкретных …
- Информационный век
Информационная эпоха — это идея о том, что доступ к информации и контроль над ней являются определяющими характеристиками нынешней эпохи …
- аутсорсинг процесса подбора персонала (RPO)
Аутсорсинг процесса найма (RPO) — это когда работодатель передает ответственность за поиск потенциальных кандидатов на работу .
 ..
.. - специалист по кадрам (HR)
Специалист по персоналу — это специалист по кадрам, который выполняет повседневные обязанности по управлению талантами, сотрудникам …
- жизненный цикл сотрудника
Жизненный цикл сотрудника — это модель человеческих ресурсов, которая определяет различные этапы, через которые работник проходит в …
- Платформа Adobe Experience
Adobe Experience Platform — это набор решений Adobe для управления качеством обслуживания клиентов (CXM).
- виртуальный помощник (помощник ИИ)
Виртуальный помощник, также называемый помощником ИИ или цифровым помощником, представляет собой прикладную программу, которая понимает естественные …
- входящий маркетинг
Входящий маркетинг — это стратегия, направленная на привлечение клиентов или лидов с помощью созданного компанией интернет-контента, тем самым .
 ..
..
Координаты X и Y — определение, примеры, как найти
30-DAY PROMIS | ПОЛУЧИТЕ 100% ВОЗВРАТ ДЕНЬГИ*
*T&C ApplyLearnPracticeDownload
Координаты X и Y помогают определить точку на осях координат и записываются в виде упорядоченной пары (x, y). Координаты точки обозначаются как (x, y), где x представляет положение точки относительно оси x, а y представляет положение точки относительно оси y.
Давайте узнаем больше о координатах x и y, их расположении и использовании.
| 1. | Что такое координаты X и Y? |
| 2. | Координаты X и Y в четырех квадрантах |
| 3. | Как найти координаты X и Y? |
| 4. | Использование координат X и Y |
| 5. | Примеры координат X и Y |
| 6. | Практические вопросы |
7. | Часто задаваемые вопросы о координатах X и Y |
Что такое координаты X и Y?
Координаты X и Y — это адрес, который помогает найти точку в двумерном пространстве. Любая точка на координатной плоскости определяется точкой (x, y), где значение x — это положение точки относительно оси x, а значение y — положение точки относительно оси y. -ось. Координаты x и y точки имеют положительные или отрицательные значения в зависимости от расположения точки в разных квадрантах.
Здесь давайте рассмотрим два важных термина, относящихся к координатам x и y.
- Абсцисса (координата x): это значение x в точке (x, y) и длина перпендикуляра, проведенного из точки к оси y. т. е. это горизонтальное расстояние от точки до оси Y.
- Ордината (координата y) : это значение y в точке (x, y) и длина перпендикуляра, проведенного из точки к оси x. т. е. это расстояние по вертикали от точки до оси x.

Координаты X и Y в четырех квадрантах
Свойства координат x и y точки, представленной в четырех квадрантах декартовой плоскости, следующие:
- Координаты x и y начала координат равны (0, 0), что является точка пересечения оси x и оси y.
- Координаты x и y точки на оси x имеют вид (a, 0), и здесь координата y точки равна нулю.
- Координаты x и y точки на оси y имеют форму (0, b), и здесь координата x точки равна нулю.
- Точка, представленная в первом квадранте (x, y), имеет оба положительных значения и построена относительно положительной оси x и положительной оси y.
- Точка, представленная во втором квадранте, равна (-x, y) и нанесена относительно отрицательной оси x и положительной оси y.
- Точка, представленная в третьем квадранте (-x, -y), нанесена относительно отрицательной оси x и отрицательной оси y.
- Точка, представленная в четвертом квадранте (x, -y), нанесена относительно положительной оси x и отрицательной оси y.

Как найти координаты X и Y?
Чтобы найти координаты x и y данной точки,
- Посмотрите, каково ее расстояние по перпендикуляру от оси y, и это ваша координата x (x).
- Посмотрите, каково его перпендикулярное расстояние от оси x и это ваша координата y (y).
- Запишите значения x и y в упорядоченной паре (x, y) и измените знаки x и y в соответствии с квадрантом, в котором они находятся.
Пример: Найдите координаты x и y показанной точки A.
Решение:
Проведите горизонтальную и вертикальную линии из точки A к осям y и x соответственно и посмотрите, что они измеряют.
Теперь, учитывая, что точка А лежит в квадранте 4, А = (2, -5).
Использование координат X и Y
Координаты x и y точки полезны для выполнения многочисленных операций по нахождению расстояния, средней точки, наклона линии, уравнения прямой и т. д. Кроме того, некоторые из других важных применений координат x и y суть в следующем.
д. Кроме того, некоторые из других важных применений координат x и y суть в следующем.
- Координаты x и y помогают найти точку на осях координат.
- Координаты x и y для двух заданных точек можно использовать для определения расстояния между двумя точками.
- Координаты x и y для двух точек помогают найти наклон линии.
- Координаты x и y для двух точек помогают найти уравнение прямой.
☛ Связанные темы:
- Калькулятор средней точки
- Калькулятор расстояний
- Калькулятор уклона
Примеры координат X и Y
Пример 1: Найдите координаты x и y середины линии, соединяющей точки (5, -3), (1, 7).
Решение:
Даны точки (x 1 , y 1 ) = (5, -3) и (x 2 , y 2 ) = (1, 7).
Середина прямой, соединяющей эти точки, равна MP = ((x 1 + x 2 )/2, (y 1 + y 2 )/2)
= ((5 + 1 )//2, (-3 + 7)/2)
= (6/2, 4/2)
= (3, 2)
Ответ: Следовательно, координаты x и y середины линии, соединяющей две точки, равны (3, 2).

Пример 2: Каковы координаты x и y центра тяжести треугольника с вершинами (2, 0), (5, 2), (-1, 4)?
Решение:
Тремя вершинами треугольника являются (x 1 , y 1 ) = (2, 0), (x 2 , y 2 ) = (5, 2), (х 3 , у 3 ) = (-1, 4).
Координаты центра тяжести треугольника C = ((x 1 + x 2 + x 3 )/3, (y 1 + y 2 + y 3 )/ 3).
= ((2 + 5 + (-1))/3, (0 + 2 + 4)/3)
= (6/3, 6/3)
= (2, 2)
Ответ: Следовательно, координаты x и y центра тяжести треугольника равны (2, 2).
Пример 3: Если |x| = 3 и |у| = 4 и точка (x, y) находится в квадранте II, то каковы координаты x и y?
Решение:
Абсолютные значения x и y задаются следующим образом:
|x| = 3 ⇒ х = ± 3
|у| = 4 ⇒ y = ± 4
Поскольку (x, y) находится в квадранте II, x отрицательно, а y положительно.
 Следовательно, x = -3 и y = 4.
Следовательно, x = -3 и y = 4.Ответ: Координаты x и y равны -3 и 4 соответственно.
перейти к слайду перейти к слайду перейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Записаться на бесплатный пробный урок
Практические вопросы по координатам X и Y
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о координатах X и Y
Как определить координаты X и Y?
Координаты x и y могут быть легко идентифицированы из заданной точки на осях координат. Для точки (a, b) первым значением всегда является координата x, а вторым значением всегда является координата y.
Как записать координаты X и Y?
Координаты x и y записываются как (x, y).

 Также функцию симметричную относительно оси ординат называют четной функцией, значит, функция является четной.
Также функцию симметричную относительно оси ординат называют четной функцией, значит, функция является четной.
 Он преобразует цифровые данные …
Он преобразует цифровые данные …
 ..
.. ..
..


 Следовательно, x = -3 и y = 4.
Следовательно, x = -3 и y = 4.