Как узнать площадь прямоугольника. Периметр и площадь прямоугольника
Для того, чтобы находить периметр и площадь прямоугольника, нужно знать формулы и главное — уметь применять их для решения задач — ведь они бывают разной сложности.
Очень часто при решении задач легкого уровня достаточно знать основные формулы и решить их просто подставляя нужные значения.
Если задачи посложнее и в их условии нет данных нужных для формулы, нужно их находить с помощью других алгебраических действий.
В этом случае можно навести следующий пример
нужно найти площадь прямоугольника, если его периметр равен 120 см, а стороны относятся как 2 к 3
сначала составляем уравнение , чтобы найти стороны используя при этом формулу периметра (P=2(а+b ):
2*(2х+3Х)=120 решаем его, х=12 значит стороны равны 24 см и 36 см и теперь уже подставляем значения в формулу площади S=ab и находим ее S=24*36=864 см.кв.
Площадь прямоугольника равна произведению длины и ширины и вычисляется по формуле a*b, где а и b -стороны прямоугольника.
Нахождение площади прямоугольника — умножим длину прямоугольника на его ширину.
Нахождение периметра прямоугольника (сумма длин всех сторон) — простым сложением длин всех сторон, либо к длине продольной стороны прямоугольника, прибавляем длину поперечной и полученную сумму умножаем на два.
Если представить, что ваш огород прямоугольной формы и вам необходимо участок обложить забором, то наверное перед вами возникнет вопрос, а какой длины будет забор, чтобы правильно рассчитать расход стройматериалов. Вы сложите длины сторон забора и найдете ПЕРИМЕТР. Если зададитесь вопросом, какое количество земли нужно перекопать на этом участке, то придется искать ПЛОЩАДЬ, а для этого нужно будет перемножить длину на ширину участка, ведь как известно у прямоугольника противоположные стороны попарно равны. Не стоит забывать, что квадрат тоже прямоугольник, чтобы найти периметр квадрата, нужно длину умножить на 4, а площадь — длину стороны умножить на себя.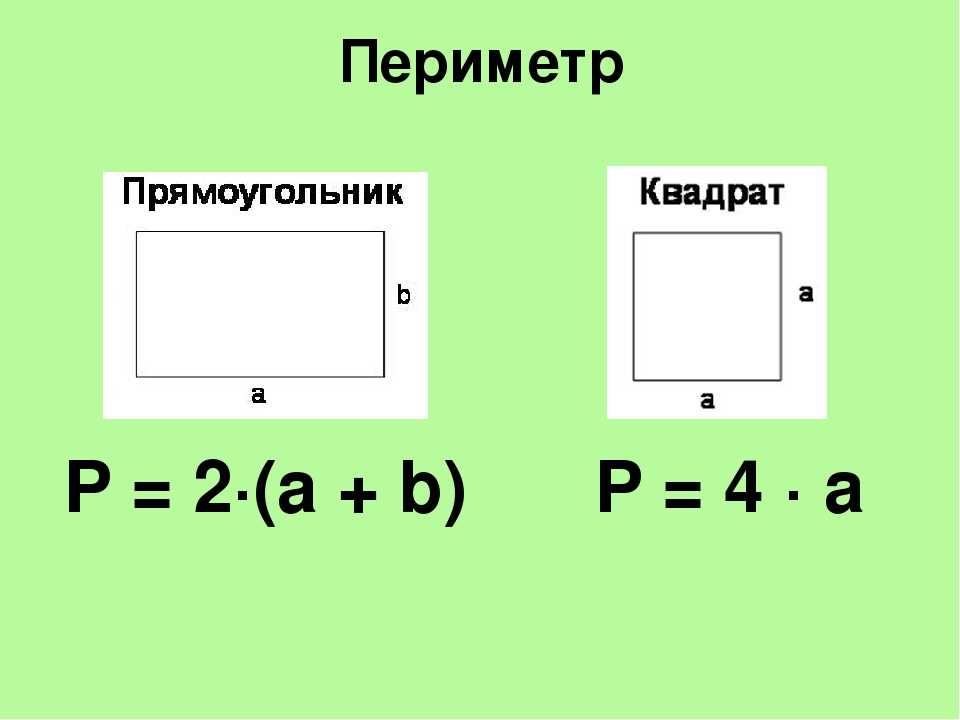
Вспомним школьный курс математики. Так периметр прямоугольника находится по формуле суммы двух его сторон умноженных на 2. То есть Р=2*(а+b), где а и b это стороны прямоугольника. Площадь, соответственно находится с помощью формулы S=a*b, где a и b также являются его сторонами.
Если не вдаваться в глубокие подробности, то найти площадь и периметр геометрической фигуры прямоугольник очень просто. Обозначим стороны такого прямоугольника латинскими буквами: a, b, c и d. Пусть a = c — это длина прямоугольника, а b и d — это ширина прямоугольника.
Площадь прямоугольника:
Периметр прямоугольника:
S = a + b + c + d
Периметр прямоугольника — это длины всех его сторон. Исходя из того, что у этой фигуры четыре стороны, или две пары, при этом противолежащие стороны равны друг другу, можно прийти к выводу, что уместно сложить значения двух разновеликих сторон и умножить полученное значение на два.
Площадь находится также просто: мы просто перемножаем разновеликие стороны.
Площадь вычисляется при умножении длинной стороны прямоугольника с короткой. А периметр-это (длин. сторона+ кор. сторона)*2
Можно пойти самым простым путем нахождения площади прямоугольника. А именно, умножить длину прямоугольника (как правило, это a) на ширину прямоугольника (как правило, это B). А вот периметр ищем при помощи сложения всех сторон, или, проще говоря: 2a+2b
Прямоугольник это геометрическая фигура, а именно четырехугольник, у которого все углы прямые. Получается, что противоположные стороны равны друг другу.
Периметр прямоугольника это сумма длин всех сторон прямоугольника, либо сумма длины и ширины, умноженная на 2.
Периметр это длина всех сторон прямоугольника, то он измеряется в единицах длины: см, мм, м, дм, км.
P=AB+CD+AD+BC или P=2*(AB+AD).
Площадь измеряется квадратными единицами длины: м2, см2, дм2 и обозначается латинской буквой S.
Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Площадь прямоугольника рассчитывается путем умножения его длины на ширину полученное произведение и будет площадь.
Периметр прямоугольника находится путем суммирования длины и ширины, полученную сумму нужно еще умножить на два, это и будет искомый периметр.
Если у прямоугольника заданы две противолежащие стороны, то все просто перемножаем их и получаем площадь, складываем и удваиваем и получаем периметр. Однако чаще в учебниках задают самый разнобой — сторону и периметр, сторону и площадь, сторону и диагональ. Как поступать в этих случаях.
Вот это идеальная задача.
Могут быть заданы сторона и диагональ. В этом случае находим вторую сторону по теореме Пифагора — как второй катет в треугольнике где гипотенуза диагональ прямоугольника.
В итоге мы имеем вот какие формулы для нахождения периметра прямоугольника:
А если по простому преобразовать эти же формулы, то получаются формулы для нахождения площади во всех вариантах задач:
Прямоугольник – это частный случай четырехугольника. Это значит, что у прямоугольника четыре стороны. Его противоположные стороны равны: так например, если одна из его сторон равна 10 см, то противоположная ей будет так же равны 10 см. Частным случаем прямоугольника является квадрат. Квадрат – это прямоугольник, у которого все стороны равны. Для вычисления площади квадрата можно пользоваться тем же алгоритмом, что и для вычисления площади прямоугольника.
Это значит, что у прямоугольника четыре стороны. Его противоположные стороны равны: так например, если одна из его сторон равна 10 см, то противоположная ей будет так же равны 10 см. Частным случаем прямоугольника является квадрат. Квадрат – это прямоугольник, у которого все стороны равны. Для вычисления площади квадрата можно пользоваться тем же алгоритмом, что и для вычисления площади прямоугольника.
Как узнать площадь прямоугольника по двум сторонам
Для того чтобы найти площадь прямоугольника, надо умножить его длину на ширину: Площадь = Длина × Ширина. В случае, указанном ниже: Площадь = AB × BC.
Как узнать площадь прямоугольника по стороне и длине диагонали
В некоторых задачах необходимо найти площадь прямоугольника, используя длину диагонали и одну из сторон. Диагональ прямоугольника делит его на два равных прямоугольных треугольника. Следовательно, можно определить вторую сторону прямоугольника, воспользовавшись теоремой Пифагора. После этого задача сводится к предыдущему пункту. 2 × sin(острого угла между диагоналями)/2.
2 × sin(острого угла между диагоналями)/2.
Урок и презентация на тему: «Периметр и площадь прямоугольника»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 3 класса
Тренажер для 3 класса «Правила и упражнения по математике»
Электронное учебное пособие для 3 класса «Математика за 10 минут»
Что такое прямоугольник и квадрат
Прямоугольник – это четырёхугольник, у которого все углы прямые. Значит, противоположные стороны равны друг другу.
Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.
Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы:  ..
..
Пример.
Читается так: четырёхугольник ABCD; квадрат EFGH.
Что такое периметр прямоугольника? Формула расчета периметра
Периметр прямоугольника – это сумма длин всех сторон прямоугольника или сумма длины и ширины, умноженная на 2.
Периметр обозначается латинской буквой P . Так как периметр — это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.
Например, периметр прямоугольника АВСD обозначается как P ABCD , где А, В, С, D — это вершины прямоугольника.
Запишем формулу периметра четырехугольника ABCD:
P ABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)
Пример.
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см.
Определим P ABCD .
Решение:
1. Нарисуем прямоугольник ABCD с исходными данными.
2. Напишем формулу для расчета периметра данного прямоугольника:
P ABCD = 2 * (AB + BС)
P ABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см
Ответ: P ABCD = 16 см.
Формула расчета периметра квадрата
У нас есть формула для определения периметра прямоугольника.
P ABCD = 2 * (AB + BC)
Применим её для определения периметра квадрата. Учитывая, что все стороны квадрата равны, получаем:
P ABCD = 4 * AB
Пример.
Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата.
Решение.
1. Нарисуем квадрат ABCD с исходными данными.
2. Вспомним формулу расчета периметра квадрата:
P ABCD = 4 * AB
3. Подставим в формулу наши данные:
P ABCD = 4 * 6 см = 24 см
Ответ: P ABCD = 24 см.
Задачи на нахождение периметра прямоугольника
1. Измерь ширину и длину прямоугольников. Определи их периметр.
2. Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника.
3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.
Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.
Где используется расчет периметра прямоугольника?
1. Задан участок земли, его нужно обнести забором. Какой длины будет забор?
В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора.
2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев.
Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.
Что такое площадь прямоугольника?
Площадь – это числовая характеристика фигуры.
Площадь измеряется квадратными единицами длины: см 2 , м 2 , дм 2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.)
В вычислениях обозначается латинской буквой S .
Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Площадь прямоугольника вычисляется умножением длины АК на ширину КМ. Запишем это в виде формулы.
S AKMO = AK * KM
Пример.
Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?
S AKMO = AK * KM = 7 см * 2 см = 14 см 2 .
Ответ: 14 см 2 .
Формула вычисления площади квадрата
Площадь квадрата можно определить, умножив сторону саму на себя.
Пример.
В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.
S AВСО = AB * BC = AB * AB
Пример.
Определи площадь квадрата AKMO со стороной 8 см.
S AKMО = AK * KM = 8 см * 8 см = 64 см 2
Ответ: 64 см 2 .
Задачи на нахождение площади прямоугольника и квадрата
 Вычисли его площадь. Запиши ответ в квадратных сантиметрах.
Вычисли его площадь. Запиши ответ в квадратных сантиметрах.2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.
Геометрия постигает свойства и колляции двумерных и пространственных фигур. Числовыми величинами, характеризующими такие конструкции, являются площадь и периметр, вычисление которых производится по знаменитым формулам либо выражается одно через другое.
Инструкция
1. Прямоугольник.Задача: вычислите площадь прямоугольника, если вестимо, что его периметр равен 40, а длина b в 1,5 раза огромнее ширины a.
2. Решение.Используйте знаменитую формулу периметра, он равен сумме всех сторон фигуры. В данном случае P = 2 a + 2 b. Из исходных данных задачи вы знаете, что b = 1,5 a, следственно, P = 2 a + 2 1,5 a = 5 a, откуда a = 8. Обнаружьте длину b = 1,5 8 = 12.
3. Запишите формулу для площади прямоугольника:S = a b,Подставьте вестимые величины:S = 8 *12 = 96.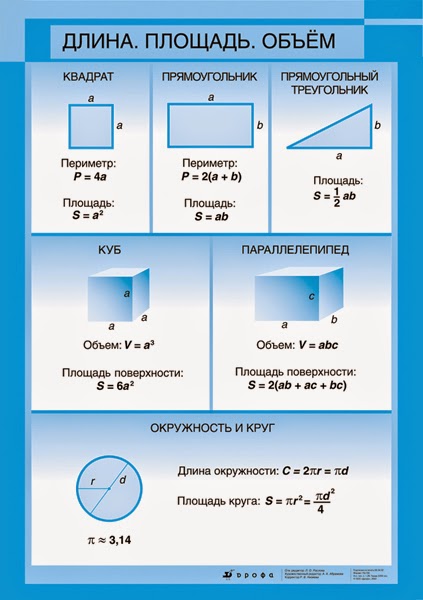
4. Квадрат.Задача: обнаружьте площадь квадрата, если периметр равен 36.
5. Решение.Квадрат – частный случай прямоугольника, где все стороны равны, следственно, его периметр равен 4 a, откуда a = 8. Площадь квадрата определите по формуле S = a? = 64.
6. Треугольник.Задача: пускай дан произвольный треугольник ABC, периметр которого равен 29. Узнайте величину его площади, если знаменито, что высота BH, опущенная на сторону AC, делит ее на отрезки с длинами 3 и 4 см.
7. Решение.Для начала припомните формулу площади для треугольника:S = 1/2 c h, где c – основание и h – высота фигуры. В нашем случае основанием будет сторона AC, которая знаменита по условию задачи: AC = 3+4 = 7, осталось обнаружить высоту BH.
8. Высота является перпендикуляром, проведенным к стороне из противоположной вершины, следственно, она разделять треугольник ABC на два прямоугольных треугольника. Зная это качество, разглядите треугольник ABH. Припомните формулу Пифагора, согласно которой:AB? = BH? + AH? = BH? + 9 ? AB = ?(h? + 9).В треугольнике BHC по тому же тезису запишите:BC? = BH? + HC? = BH? + 16 ? BC = ?(h? + 16).
Припомните формулу Пифагора, согласно которой:AB? = BH? + AH? = BH? + 9 ? AB = ?(h? + 9).В треугольнике BHC по тому же тезису запишите:BC? = BH? + HC? = BH? + 16 ? BC = ?(h? + 16).
9. Примените формулу периметра:P = AB + BC + ACПодставьте величины, выраженные через высоту:P = 29 = ?(h? + 9) + ?(h? + 16) + 7.
10. Решите уравнение:?(h? + 9) + ?(h? + 16) = 22 ? [замена t? = h? + 9]:?(t? + 7) = 22 – t, возведите обе стороны равенства в квадрат:t? + 7 = 484 – 44 t + t? ? t?10,84h? + 9 = 117,5 ? h ? 10,42
11. Обнаружьте площадь треугольника ABC:S = 1/2 7 10,42 = 36,47.
При решении, необходимо принять во внимание, что решить задачу о нахождении площади прямоугольника только из длины его сторон нельзя .
В этом несложно убедиться. Пусть периметр прямоугольника будет равен 20 см. Это будет верно, если его стороны 1 и 9, 2 и 8, 3 и 7 см. Все эти три прямоугольника будут иметь одинаковый периметр, равный двадцати сантиметрам. (1 + 9) * 2 = 20 точно также как и (2 + 8) * 2 = 20 см.
Как видно, мы можем подобрать бесконечное количество вариантов размеров сторон прямоугольника, периметр которого будет равен заданному значению.
Площадь прямоугольников с заданным периметром 20 см, но с различными сторонами будет различна. Для приведенного примера — 9, 16 и 21 квадратных сантиметров соответственно.
S 1 = 1 * 9 = 9 см 2
S 2 = 2 * 8 = 16 см 2
S 3 = 3 * 7 = 21 см 2
Как видим, вариантов площади фигуры при заданном периметре — бесконечное количество.
Замечание для любознательных . В случае с прямоугольником, у которого задан периметр, максимальную площадь будет иметь квадрат.
Таким образом, для того, чтобы вычислить площадь прямоугольника из его периметра, нужно обязательно знать либо соотношение его сторон, либо длину одной из них. Единственной фигурой, которая имеет однозначную зависимость своей площади от периметра, является круг. Только для круга и возможно решение.
В этом уроке:
- Задача 4.
 Изменение длины сторон при сохранении площади прямоугольника
Изменение длины сторон при сохранении площади прямоугольника
Задача 1. Найти стороны прямоугольника из площади
Периметр прямоугольника равен 32 сантиметрам, а сумма площадей квадратов, построенных на каждой из его сторон — 260 квадратных сантиметров. Найдите стороны прямоугольника.
Решение.
2(x+y)=32
Согласно условию задачи, сумма площадей квадратов построенных на каждой из его сторон (квадратов, соответственно, четыре) будет равна
2x 2 +2y 2 =260
x+y=16
x=16-y
2(16-y) 2 +2y 2 =260
2(256-32y+y 2)+2y 2 =260
512-64y+4y 2 -260=0
4y 2 -64y+252=0
D=4096-16×252=64
x 1 =9
x 2 =7
Теперь примем во внимание, что исходя из того, что x+y=16 (см. выше) при x=9, то y=7 и наоборот, если x=7, то y=9
Ответ : Стороны прямоугольника равны 7 и 9 сантиметров
Задача 2. Найти стороны прямоугольника из периметра
Периметр прямоугольника 26 см, а сумма площадей квадратов, построенных на двух его смежных сторонах, равна 89 кв. см. Найдите стороны прямоугольника.
см. Найдите стороны прямоугольника.
Решение.
Обозначим стороны прямоугольника как x и y.
Тогда периметр прямоугольника равен:
2(x+y)=26
Сумма площадей квадратов построенных на каждой из его сторон (квадратов, соответственно, два и это квадраты ширины и высоты, поскольку стороны смежные) будет равна
x 2 +y 2 =89
Решаем полученную систему уравнений. Из первого уравнения выводим, что
x+y=13
y=13-y
Теперь выполняем подстановку во второе уравнение, заменяя x его эквивалентом.
(13-y) 2 +y 2 =89
169-26y+y 2 +y 2 -89=0
2y 2 -26y+80=0
Решаем полученное квадратное уравнение.
D=676-640=36
x 1 =5
x 2 =8
Теперь примем во внимание, что исходя из того, что x+y=13 (см. выше) при x=5, то y=8 и наоборот, если x=8, то y=5
Ответ: 5 и 8 см
Задача 3. Найти площадь прямоугольника из пропорции его сторон
Найти площадь прямоугольника если его периметр равен 26 см а стороны пропорциональны как 2 к 3.
Решение.
Обозначим стороны прямоугольника через коэффициент пропорциональности x.
Откуда длина одной стороны будет равна 2x, другой — 3х.
Тогда:
2(2x+3x)=26
2x+3x=13
5x=13
x=13/5
Теперь, исходя из полученных данных, определим площадь прямоугольника:
2x*3x=2*13/5*3*13/5=40,56 см 2
Длина прямоугольника увеличена на 25%. На сколько процентов надо уменьшить ширину, чтобы его площадь не изменилась?
Решение .
Площадь прямоугольника равна
S = ab
В нашем случае один из множителей увеличился на 25%, что означает a 2 = 1,25a . Таким образом, новая площадь прямоугольника должна быть равна
S 2 = 1,25ab
Таким образом, для того, чтобы вернуть площадь прямоугольника к начальному значению, то
S 2 = S / 1.25
S 2 = 1,25ab / 1.25
Поскольку новый размер а изменять нельзя, то
S 2 = (1,25a) b / 1. 25
25
1 / 1,25 = 0,8
Таким образом, величину второй стороны нужно уменьшить на (1 — 0,8) * 100% = 20%
Ответ : ширину нужно уменьшить на 20%.
Как найти площадь и периметр дроби? – Обзоры Вики
Аналогично, что такое модель площади? В математике площадная модель прямоугольная диаграмма или модель, используемая для задач на умножение и деление, в котором множители или частное и делитель определяют длину и ширину прямоугольника. … Затем мы складываем, чтобы получить площадь целого, которая является произведением или частным.
Что такое формула площади? Для прямоугольника длиной l и шириной w формула для вычисления площади имеет следующий вид: A = lw (прямоугольник). То есть площадь прямоугольника — это длина, умноженная на ширину. В качестве особого случая, поскольку l = w в случае квадрата, площадь квадрата со стороной s определяется по формуле: A = s2 (площадь).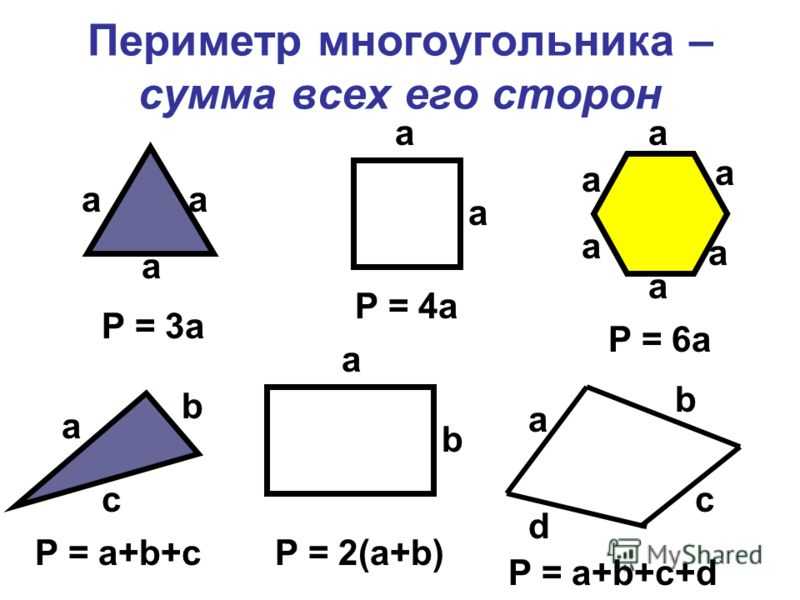
Как найти площадь? Площадь рассчитывается умножив длину фигуры на ее ширину.
Во-вторых, как вы решаете для области? Чтобы найти площадь прямоугольника, умножьте его ширину на высоту. Если мы знаем две стороны прямоугольника разной длины, то у нас есть и высота, и ширина.
Что такое область в математике?
Площадь по математике объем пространства, занимаемого двухмерной фигурой. Узнайте, как вычислить площадь для различных фигур, например площадь квадрата по формуле.
тогда что такое умножение площади? Умножение на 1-значное число с использованием площадных моделей
Покажите задачу в виде площади прямоугольника, а затем разбейте этот прямоугольник на более мелкие части для облегчения решения. Этот метод также известен как умножение на ящик.
Как вы делаете площадь в математике? Чтобы вычислить площадь квадрата или прямоугольника, умножьте его высоту на ширину. Если высота и ширина указаны в см, площадь отображается в см².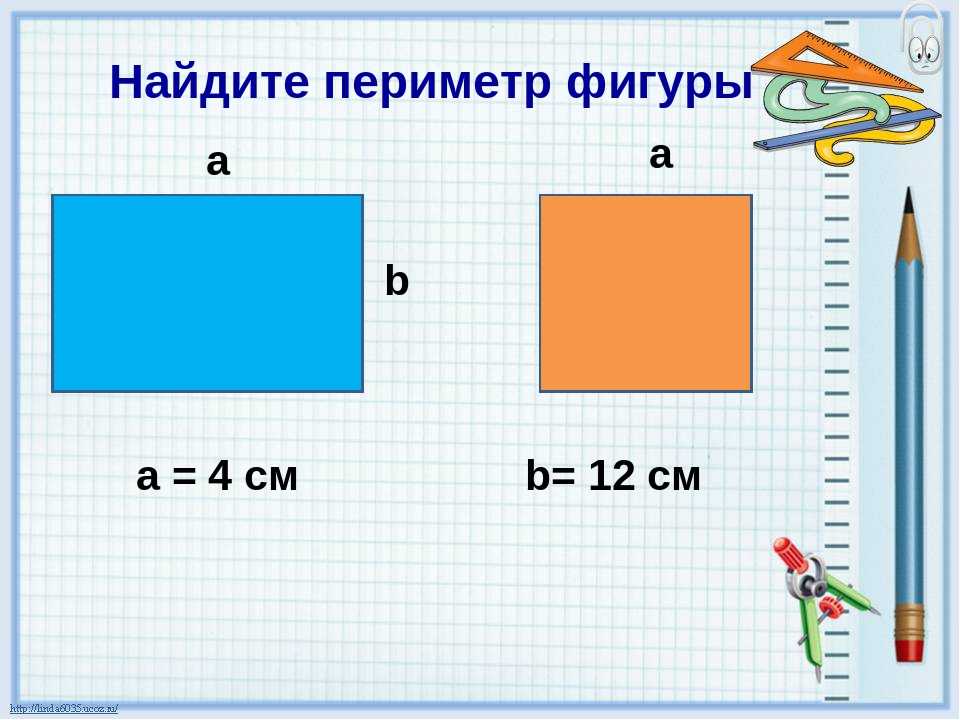 Если высота и ширина указаны в м, площадь отображается в м². Квадрат со стороной 5 м имеет площадь 25 м², потому что 5 × 5 = 25.
Если высота и ширина указаны в м, площадь отображается в м². Квадрат со стороной 5 м имеет площадь 25 м², потому что 5 × 5 = 25.
Какова формула площади и пример?
Каждая геометрическая фигура имеет свою площадь и периметр. Существуют разные формулы площади и периметра каждой формы, поскольку они имеют разные измерения.
…
Диаграмма формулы площади и периметра.
| цифры | Формула площади | Переменные |
|---|---|---|
| Площадь Квадрата | Площадь = а 2 | a = стороны квадрата |
| Площадь треугольника | Площадь = 1/2 ш × в | b = основание h = высота |
• 30 сентября 2020 г.
Как найти площадь всех форм? Как рассчитать площадь?
- Формула площади квадрата: A = a²
- Формула площади прямоугольника: A = a * b.
- Формулы площади треугольника: A = b * h / 2 или. …
- Формула площади круга: A = πr²
- Формула площади сектора круга: A = r² * угол / 2.

- Формула площади эллипса: A = a * b * π
- Формула площади трапеции: A = (a + b) * h / 2.
- Формулы площади параллелограмма:
Как вы измеряете площадь земли?
В случае жилой недвижимости площадь обычно указывается в квадратных футах (квадратных футах). Однако в случае сельскохозяйственных земель площадь собственности указывается в акрах или гектарах. Для того, чтобы измерить размер земельного участка, вам понадобится умножить длину и ширину имеющейся земли.
Пример площади? Площадь мера того, сколько места есть на плоской поверхности. … Например, в прямоугольнике мы находим площадь, умножая длину на ширину. В прямоугольнике выше площадь 2 × 4 или 8. Если вы посчитаете маленькие квадратики, то обнаружите, что их 8.
Как написать область?
Площадь измеряется в квадратных единицах, таких как квадратные дюймы, квадратные футы или квадратные метры. Чтобы найти площадь прямоугольника, умножьте длину на ширину. Формула: А = Д * Ш где A — площадь, L — длина, W — ширина, а * означает умножение.
Как найти площадь с тремя числами?
Как умножать дроби? Есть 3 простых шага для умножения дробей
- Умножьте верхние числа (числители).
- Умножьте нижние числа (знаменатели).
- При необходимости упростите дробь.
Что такое площадь в 4 классе по математике?
Определение: Площадь мера пространства внутри региона. Объекты разной формы могут иметь одинаковую площадь. Все следующие фигуры имеют площадь 5 квадратных единиц, хотя их формы различаются.
Что такое площадь Math ks2? Площадь измерение пространства внутри двумерной формы. Существует множество различных способов вычисления площади правильных фигур.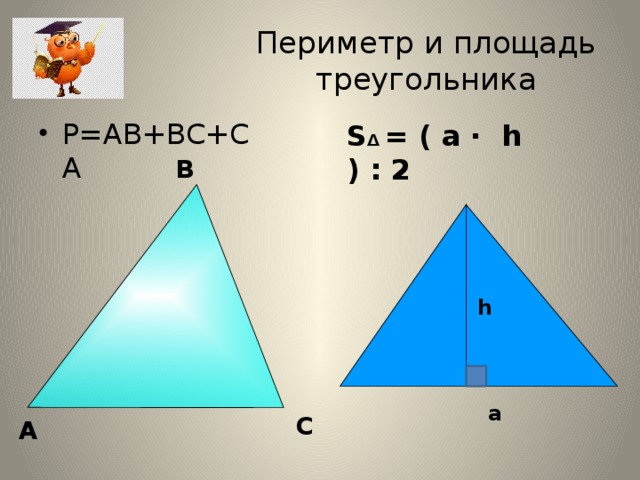
Что такое пример области?
Что такое Площадь?
| Название формы: | Формула площади: |
|---|---|
| Треугольник | Площадь = bh, где b — основание, а h — высота. |
| Квадратный | Площадь = l × l, где l — длина каждой стороны. |
| Прямоугольные | Площадь = l × w, где l — длина, а w — ширина. |
| Параллелограмм | Площадь = b × h, где b — основание, а h — высота по перпендикуляру. |
Что такое область 3-го класса?
Площадь количество места, которое занимает плоская форма или поверхность. Совет: только двумерные объекты имеют площадь. Трехмерные объекты имеют объем. Обложка книги плоская. Передняя часть двери шкафа плоская.
Как найти площадь фигуры с 4 разными сторонами? Используйте следующее уравнение: Площадь = сторона × сторона или A = s . Пример: если одна сторона квадрата имеет длину 4 фута (t = 4), то площадь этого квадрата равна просто t 2 , или 4 х 4 = 16 квадратных футов.
Пример: если одна сторона квадрата имеет длину 4 фута (t = 4), то площадь этого квадрата равна просто t 2 , или 4 х 4 = 16 квадратных футов.
…
Параллелограммы включают:
- Квадраты: Четыре стороны одинаковой длины. …
- Прямоугольники: четыре стороны; противоположные стороны имеют одинаковую длину.
Как найти площадь фигуры разной длины?
Как пользоваться калькулятором неровной площади?
- Шаг 1: Измерьте все стороны площади одной единицей (футы, метры, дюймы или любые другие).
- Шаг 2: Введите длину горизонтальных сторон в поля «Длина 1» и «Длина 2», а ширину вертикальных сторон в поля «Ширина 1» и «Ширина 2».
- Шаг 3: Нажмите кнопку расчета. …
- Наша формула: Площадь = b × h.
| |||||||
| |||||||
| |||||||
У нас есть два ответа для вас Привет, Бруклин, Предположим, у вас есть 4 фута материала для фоторамки, и вы хотите сделать рамку для одной из своих фотографий. или вы можете сделать рамку для фотографии вашего любимого жирафа или за фотографию, которую вы сделали во время поездки в горы. Каждый из этих прямоугольников имеет одинаковый периметр, 4 фута, но площади совершенно разные. Между периметром прямоугольника и его площадью нет прямой зависимости. Пенни
Привет, Бруклин, Вам нужно знать комбинацию любых двух из следующих: длина, ширина, периметр, площадь. Очевидно, если вы знаете длину и ширину, вы установили! Вы можете рассчитать периметр, используя P = 2L + 2W, и вы можете рассчитать площадь, используя A = LW . Если известна площадь, а также длина или ширина, можно использовать формулу площади для определения другого измерения: Если известен периметр, а также длина или ширина, можно использовать формулу периметра для определения другого измерения: Если вы знаете и площадь, и периметр, вы также можете определить размеры, но это требует немного больше усилий и требует либо угадывания и проверки (что может оказаться трудным или невозможным, если какое-либо измерение иррационально), либо решения квадратного уравнения. Дано A = 15, P = 16 15 = L(8 — L) Мы бы выбрали L = 5 (только потому, что по соглашению мы думаем, что длина — это более длинная сторона) и, подставив в одно из наших исходных уравнений, мы находим, что ширина равна 3,9.0055 Надеюсь, это поможет,
| |||||||
Площадь и периметр – определение, формула и примеры
Площадь и периметр в математике – это два важных свойства двумерных фигур.
Периметр определяет расстояние до границы формы, тогда как площадь объясняет занимаемую ею область. Площадь и периметр — важная тема математики, которая используется в повседневной жизни. Это применимо к любой форме и размеру, будь то правильные или неправильные.
Каждая фигура имеет свою площадь и формулу периметра.
Вы, должно быть, узнали о различных формах, таких как треугольник, квадрат, прямоугольник, круг, сфера и т. д.
Это применимо к любой форме и размеру, будь то правильные или неправильные.
Каждая фигура имеет свою площадь и формулу периметра.
Вы, должно быть, узнали о различных формах, таких как треугольник, квадрат, прямоугольник, круг, сфера и т. д.
Цифровой маркетингГрафический дизайнMS Excel (10 часов)Курс подготовки к собеседованиюПрограмма предпринимательстваНаписание контента Программа «Чемпион» (средний язык хинди) Группа биологии Программа чемпиона 12-го класса (средний английский язык) Группа математики Группа 12-го класса Программа чемпиона (средний английский язык) Группа биологии Программа чемпиона 10-го класса (средний язык хинди) Программа чемпиона 10-го класса (средний английский язык)
Бесплатные демонстрационные занятия
Зарегистрируйтесь здесь, чтобы получить бесплатные демонстрационные занятия
Выберите категориюНавыкиПравительствоАкадемические науки
Выберите курс
Пожалуйста, заполните имя
Пожалуйста, введите только 10-значный номер мобильного телефона
Пожалуйста, выберите курс
Пожалуйста, заполните адрес электронной почты
Что-то пошло не так!
Загрузите приложение и начните обучение
Источник: Safalta. com
com
Здесь объясняются площади и периметры всех фигур. Присоединяйтесь к онлайн-школе Safalta School и подготовьтесь к экзаменам на совет директоров под руководством наших опытных преподавателей. Наша онлайн-школа призвана помочь учащимся подготовиться к экзаменам на совет директоров, обеспечив учащимся концептуальную ясность по всем предметам и возможность набрать максимальные баллы на экзаменах.
Что такое площадь?
Площадь — это область, ограниченная формой объекта. Пространство, охватываемое фигурой или любой двумерной геометрической фигурой на плоскости, — это площадь фигуры. Площадь всех фигур зависит от их размеров и свойств. Разные формы имеют разную площадь. Площадь квадрата отличается от площади воздушного змея.
Если два объекта имеют одинаковую форму, то нет необходимости, чтобы площадь, покрываемая ими, была одинаковой до тех пор, пока размеры обеих фигур также не будут равны.
Предположим, есть два прямоугольника с длиной L1 и L2 и шириной B1 и B2. Таким образом, площади обоих прямоугольных блоков, скажем, A1 и A2, будут равны, только если L1=L2 и B1=B2.
Таким образом, площади обоих прямоугольных блоков, скажем, A1 и A2, будут равны, только если L1=L2 и B1=B2.
Что такое периметр?
Периметр фигуры определяется как общее расстояние вокруг фигуры. По сути, периметр — это длина любой фигуры, если она развернута в линейную форму. Периметр – это общее расстояние, охватывающее фигуру в двухмерной плоскости. Периметры различных форм могут совпадать по длине друг с другом в зависимости от их размеров.
Например, если из металлической проволоки длиной L сделать круг, то из этой же проволоки можно построить квадрат, стороны которого равны по длине.
Ссылки по теме-
- Объем сферы
- Конвертер см в дюймы (см в дюймы)
- Преобразование римских цифр
В чем разница между площадью и периметром?
Вот список различий между площадью и периметром:
Зона | Периметр |
| Площадь — это область, занимаемая фигурой | Периметр — это общее расстояние, пройденное границей формы |
Площадь измеряется в квадратных единицах (м2, см2, дюйм2 и т. д.) д.) | Периметр измеряется в единицах (м, см, дюймы, футы и т. д.) |
| Пример: Площадь прямоугольного участка равна произведению его длины на ширину. | Пример: Периметр прямоугольного участка равен сумме всех его четырех границ, т. е. 2 (длина + ширина). |
Площадь и периметр Для всех фигур
Существует множество типов фигур. Наиболее распространенными являются квадрат, треугольник, прямоугольник, круг и т. д. Чтобы узнать площадь и периметр всего этого, нам нужны разные формулы.
Периметр и площадь прямоугольника
Прямоугольник — это фигура/форма, у которой противоположные стороны равны, а все углы равны 90 градусам.
Площадь прямоугольника — это пространство, занимаемое им в плоскости XY.
|
где a и b — длина и ширина прямоугольника.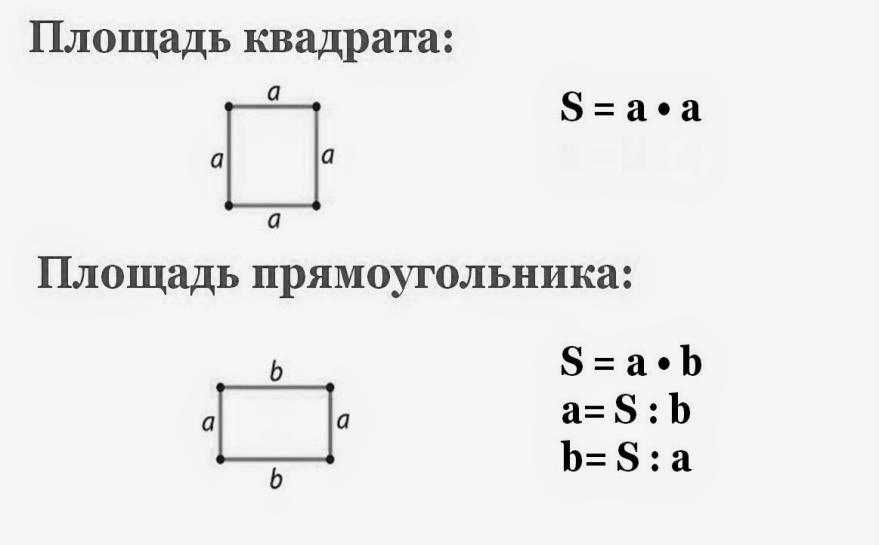
Периметр и площадь квадрата
Квадрат — это фигура/форма, у которой все четыре стороны равны, а все углы равны 90 градусам. Площадь квадрата — это пространство, занимаемое квадратом в 2D-плоскости, а его периметр — это расстояние, пройденное по внешней линии.
|
где а — длина стороны квадрата.
Вы также можете прочитать-
- Периметр прямоугольника
- Площадь квадрата
- Площадь прямоугольника
Периметр и площадь треугольника
Треугольник имеет три стороны.
Следовательно, периметр любого данного треугольника, будь то разносторонний, равнобедренный или равносторонний, будет равен сумме длин всех трех сторон. А площадь любого треугольника — это занимаемое им пространство на плоскости.
|
Площадь и длина окружности
Площадь окружности – это область, занимаемая ею на плоскости.
В случае круга расстояние от внешней линии круга называется окружностью.
|
Формулы площади и периметра
Вот список площадей и периметров для разных фигур в табличном виде. Учащиеся могут использовать эту таблицу для решения задач на основе приведенных здесь формул.
| Форма | Зона | Периметр | Условия |
| Круг | А = π × r2 | Окружность = 2πr | r = радиус окружности |
| Треугольник | А = ½ × Ш × В | С = а+б+с | б = база
ч = высота а, b и с — стороны треугольника |
| Квадрат | А = а2 | Р = 4а | а = длина стороны |
| Прямоугольник | А = Д × Ш | Р = 2(л + ш) | л = длина
ш = ширина |
| Параллелограмм | А = б × ч | Р = 2(а+б) | а = сторона
б = база h=высота по вертикали |
Применение площади и периметра
Мы знаем, что площадь — это в основном пространство, покрытое этими фигурами, а периметр — это расстояние вокруг фигуры. Если вы хотите покрасить стены своего нового дома, вам нужно знать площадь, чтобы рассчитать необходимое количество краски и ее стоимость.
Если вы хотите покрасить стены своего нового дома, вам нужно знать площадь, чтобы рассчитать необходимое количество краски и ее стоимость.
Например, чтобы оградить сад в вашем доме, необходимая длина материала для ограждения равна периметру сада. Если это квадратный сад, каждая сторона которого равна см, то периметр будет равен 4а см. Площадь — это пространство, содержащееся в фигуре или заданной фигуре. Он рассчитывается в квадратных единицах. Предположим, вы хотите починить плитку в своем новом доме, вам нужно знать площадь пола, чтобы знать нет. плитки, необходимой для покрытия всего пола. В этой статье давайте рассмотрим формулы площади и периметра некоторых основных фигур со схемами и примерами.
Примеры решения для площади и периметра
Вот несколько примеров решения, основанных на формулах площади и периметра различных форм.
Пример 1:
Если радиус окружности равен 21 см. Найдите его площадь и длину окружности.
Решение:
Дано, радиус = 21 см
Следовательно, площадь = π × r2
A = 22/7 × 21 × 21
A = 1386 кв.см.
Окружность, C = 2πr
C = 2 x 22/7 x 21 = 132 см
Пример 2:
Если длина стороны квадрата 11 см. Затем найдите его площадь, а также найдите общую длину его границы.
Решение:
Дано, длина стороны, a = 11 см
Площадь = a2 = 112 = 121 кв.см
Общая длина его границы, Периметр = 4a = 4 x 11 = 44 кв. см.
Площадь — это область, охватываемая фигурой или фигурой, тогда как периметр — это расстояние, покрываемое внешней границей фигуры.
Единицей площади является квадратная единица или единица2, а единица измерения периметра такая же, как и единица измерения.
Периметр любого многоугольника равен сумме его сторон.
Периметр = сумма всех сторон
Круг представляет собой изогнутую форму, и его площадь и периметр определяются радиусом.

 Изменение длины сторон при сохранении площади прямоугольника
Изменение длины сторон при сохранении площади прямоугольника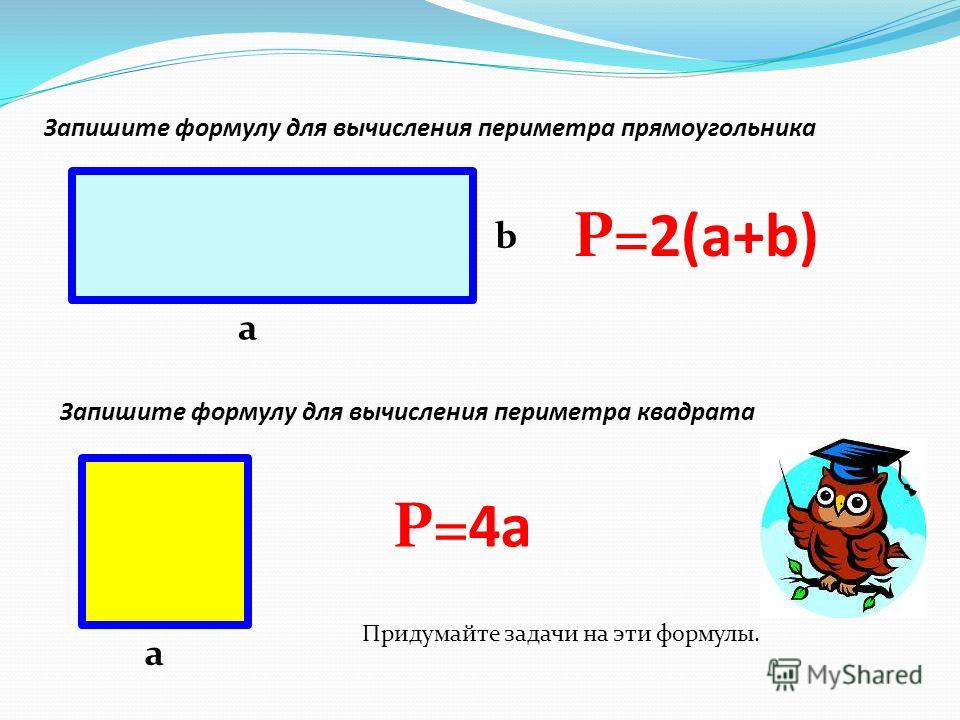
 Вы можете сделать рамку для своей фотографии новорожденного ребенка тети Марты и дяди Фреда.
Вы можете сделать рамку для своей фотографии новорожденного ребенка тети Марты и дяди Фреда.
