Как найти площадь овала формула: Площадь эллипса

Как найти площадь круга

Окружность — одна из самых  совершенных фигур в геометрии. Построить ее очень просто — нужен только циркуль. Но при своем совершенстве окружность создает одну из самых сложных проблем — определение площади круга. Почему это является проблемой? Дело в том, что площадь измеряется в квадратных единицах (метрах, дециметрах, миллиметрах…). Но превратить круг в прямоугольник или квадрат практически невозможно. Задача эта беспокоила умы математиков и философов на протяжении тысячелетий и даже получала собственное название — квадратура круга.

Чтобы разобраться в проблеме нужно разделить понятия окружности и круга.  Окружность — это замкнутая линия, все точки которой находятся на одинаковом расстоянии от центра. А круг — это часть плоскости, ограниченная этой окружностью. Для окружности мы ищем длину, а для круга — площадь. Какую бы часть круга, ограниченную окружностью, мы не выбрали, одна из сторон обязательно будет криволинейной. Это усложняет расчет площади, если не использовать интегрального исчисления.

Приблизительно, с высокой долей точности можно найти площадь окружности через диаметр по формуле:

Это самая простая формула, позволяющая найти площадь круга, когда известный радиус. Но может возникнуть вопрос, почему найденная площадь будет неточной?  Сложность связана с числом π — это отношение длины окружности к диаметру, не имеющая конечного значения. Такие числа называют иррациональными. Еще в 1761 году Иоганн Ламберт доказал, что эта постоянная трансцендентная, то есть, если возвести ее в квадрат, все равно получится иррациональное число.

Сложное доказательство этого утверждения создали Феликс Клейн и профессор Линдеманн. Практическое значение этого открытия состоит в том, что любая формула для определения площади круга, где используется число π дает приблизительный результат, то есть, квадратура круга невозможна в принципе. На данный момент известно число «Пи» с точностью до 31, 4 триллиона знаков после запятой. Для вычислений используют значение 3, 14, а для более точных — 3, 1415926.

Содержание

1. Способы вычисления площади круга
2. Вычисление площади по радиусу
3. Как найти площадь круга через длину окружности
4. Как вычислить площадь круга, описанного вокруг правильного многоугольника

Для решения повседневных и большинство технических задач вполне достаточно формулы S= π∙ D²/4. Но в геометрии есть свои подходы к решению. Не всегда дано радиус (диаметр), а измерить эту величину можно только косвенным путем при помощи построений описанных и вписанных многоугольников, дополнительных построений и т.д. Рассмотрим наиболее популярные методы, как узнать площадь круга, более подробно. Сразу же оговоримся, способ интегрального исчисления затрагивать не будем, хотя он и наиболее точный. Воспользуемся только геометрическими способами решения.

Вычисление площади по радиусу

S = π∙r² — формула для вычисления площади круга, если известный радиус. Как видно, это просто запись предыдущего выражения с учетом того, что r = D/2, отсюда r² = (D/2)² = D²/4, что и использовано в основной формуле.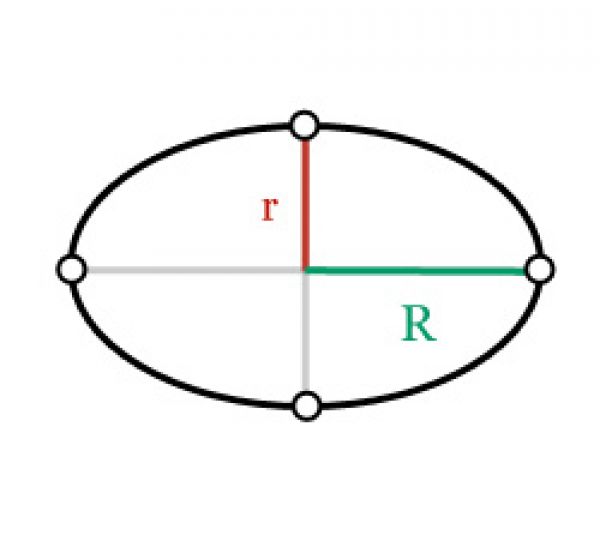

Как найти площадь круга через длину окружности

Для начала вспомним, как вычисляется длина окружности. Здесь, как и в других формулах для круга и окружности используется постоянная π. Нужно запомнить, что в математике и физике этот символ является непременным участником всех вычислений, связанных с кругом, окружностью, циклическими процессами, движением по дуге. В частности, длину окружности находим по формулам L=2 πR, или L= πD. Используя их, находим:

R=L/2 π; (1)

D=L/ π.  (2)

Используя запись 1 в формуле S = π∙r2 получаем:

S = π(L/2 π)² = L/4 π.

Аналогичный результат получим, используя формулу 2.

Как вычислить площадь круга, описанного вокруг правильного многоугольника

В каждый круг легко вписать любой правильный многоугольник. Рассмотрим случаи с самыми простыми фигурами. Если в круг вписан квадрат, то формула будет выглядеть так:

S=​2​​π⋅a​²​​​​/2, где а – сторона квадрата.

 

Если в круг вписан равносторонний (правильный) треугольник, то формула будет выглядеть так:

S=π⋅​​​a​²/3.

Если в равностороннем треугольнике неизвестна длина стороны, но известна высота, то используем формулу:

S=π⋅(​​​2⋅h​​/3)​^2​​.

Если треугольники неправильные, например, равнобедренные или разносторонние, то формулы получаются сложнее. Например, для вычисления площади по данным равнобедренного треугольника используется формула:

S=π⋅(​ a⁴/4⋅a​²​​−b​²​​​​)

В случае прямоугольного треугольника, мы используем формулу:

S=​π/4​​⋅(a​²​​+b​²)​​.

Если круг описан вокруг равнобедренной трапеции, то рассчитать площадь можно по более сложной формуле:

S=π⋅( a⋅d⋅c/​4⋅√​p⋅(p−a)⋅(p−d)⋅(p−c)​​​​​).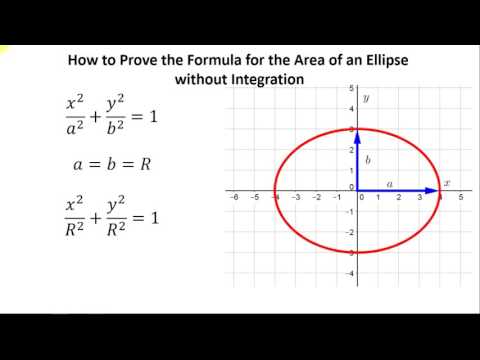

Как видим, задачу вычисления площади круга можно решить при помощи готовых формул, рассчитанных практически для любого случая, используя вписанные или описанные простые геометрические фигуры. Приведем еще несколько из готовых формул, на этот раз, для фигур, внутри которых находится круг неизвестного радиуса:

S=π⋅​​​a​^2​​/12 – для равностороннего треугольника;

S=π⋅​​​b​²/4^​​​​⋅(tg​α​/2​​​​)​²​​ — для равнобедренной трапеции;

 

S=π⋅(​а/2​​)​²​​=​π⋅а​²/4^​​ — для квадрата.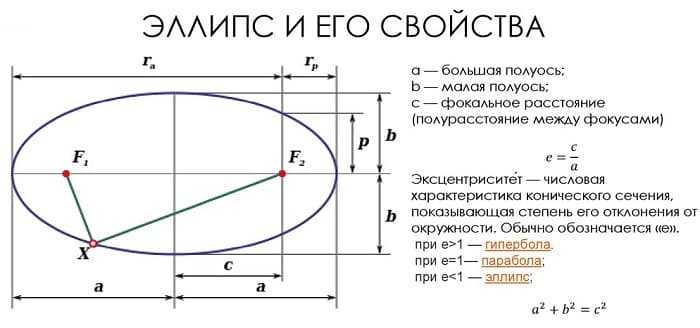

 

Учитывая небольшой объем статьи, все формулы приводим без доказательств, как руководство для практического использования при решении геометрических или технических задач.

Часто возникает проблема определения площади полукруга. Это можно сделать очень просто, вычислив площадь полного круга и разделив ее на 2. Если использовать формулу, то выглядеть это будет так:

S = π∙r²/2, или

S= π∙ D²/4/2 = S= π∙ D²/8.

Для решения практических задач сложно пользоваться формулами, да и времени для этого найти не всегда получается. Лучше всего воспользоваться онлайн-калькуляторами на специализированных сайтах. Здесь важно правильно замерить нужные параметры в требуемых единицах. Нот для учеников и студентов такие сервисы не подходят — легкое получение готового результата отучает мыслить самостоятельно и никак не углубляет знаний.

 

 

КАК НАЙТИ ПЛОЩАДЬ КРУГА??? | Ньютонов

Как найти площадь круга? У меня этот вопрос встал очень остро на экзамене по физике в университете, когда я решал одну из задач. Память человека вещь непредсказуемая, сегодня ты помнишь все до мелочей, а завтра это все уже выветрилось из головы. И благо если это была глупость какая, а если нет? Если это день рождения жены или тещи, пароль аккаунта в контакте, или площадь круга. Как это было в моем случае.

Здравствуйте дорогие друзья, меня зовут Валентин Анатольевич, и сегодня мы вычисляем площадь круга 3 способами. Точнее способ будет один, это формула , но вот варианты ее получения будут различны.

Честно говоря, я уже и не помню правильно или нет решил ту задачу, я даже не помню, что это была за задача. Но сам момент того, как выполняя промежуточные расчеты я интегрировал уравнение окружности, чтоб получить казалось бы, простейшую формулу из школьной программы… сильно врезался в память
Итак, первый способ у нас будет от студентов физико-математических факультетов.

Интегрирование.

1. Берем уравнение окружности. Для тех, кто не знает его легко получить из теоремы Пифагора, заменив там катеты на координаты x и y, а за гипотенузу приняв радиус R. Конечно, при условии, что центр окружности будет находится на пересечении координатных осей.

   

К счастью, это я помнил.
2. Выражаем y.

   

3. Если вычислить определенный интеграл для значений x от 0 до R, мы получим площадь одной четверти круга.

   

Соответственно, чтоб получить всю площадь, нам необходимо будет все это безобразие до множить на 4.

   

4. Давайте выполним замену переменной, и представим x как . Тогда: .
5. Найдем пределы интегрирования. Для этого необходимо в наше уравнение замены переменной подставить значения x и вычислить чему будет равно t при этих значениях. Получаем промежуток от 0 до .
6. Итак запишем нашу формулу:

   

7. Сделаем еще кое какие математические преобразования и вычислим определенный интеграл по формуле Ньютона -Лейбница.

   

   

   

Готово!!! В принципе, не так сложно если не впадать в ступор при виде синусов и косинусов, а также уметь интегрировать.

Но вот вопрос. Люди умели находить с большой точностью площадь круга и до интегрального исчисления. Поэтому давайте попробуем обойтись интегралов.

Площадь прямоугольника

Условно, можно сказать, что площадь — это количество квадратиков, со стороной в единицу помещающихся в данной фигуре. К примеру, кухня в хрущевке имеет размеры 2 на 3 метра. Перемножаем длину на ширину и получаем площадь 6 квадратных метров. То есть если у нас имеется 6 квадратных кусков линолеума, со стороной в 1 метр, мы ими полностью без остатка, покроем весь пол.

Прямоугольную кухню легко разбить на квадраты, но что делать если у нас круг? Скажем круглый кусок сыра.
Любой старший прапорщик, обладая не дюжей армейской смекалкой вам скажет, что нужно в таком случае из круга сделать прямоугольник. И он окажется прав. Почему? По тому что старший прапорщик всегда прав.
В общем метод номер два. Метод старших прапорщиков.

Перегруппировка

Делим круг на восемь равных секторов и совмещаем друг с другом.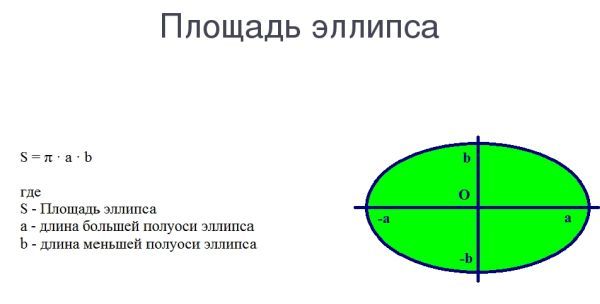

Отдаленно напоминает прямоугольник? Нет? Отжимаемся восемь раз, и делим еще.

Если секторов будет бесконечно много, то в таком случае, искривления их дуг будут незначительны. А это значит мы получим уже треугольники.
Опять совместим их друг с другом как и в первом случае. И у нас уже идеальный прямоугольник, с шириной равной радиусу , и длиной в половину длины окружности, то есть .
Перемножаем получаем:

   

Если внимательно посмотреть на полученную формулу мы увидим, что с её помощью можно найти площадь прямоугольного треугольника с основанием равным длине окружности и высотой равной ее радиусу.

Равенство площадей такого треугольника и круга доказывал Архимед, в своей работе о площадях круга.
Я не буду приводить здесь доказательство этой теоремы, скажу только, что Архимед использовал многоугольники. Один вписанный в окружность, а другой описанный вокруг нее. Площадь круга находилась где-то между площадями этих многоугольников, причем при увеличении сторон, их площади приближались друг к другу, а значит приближались и к площади круга.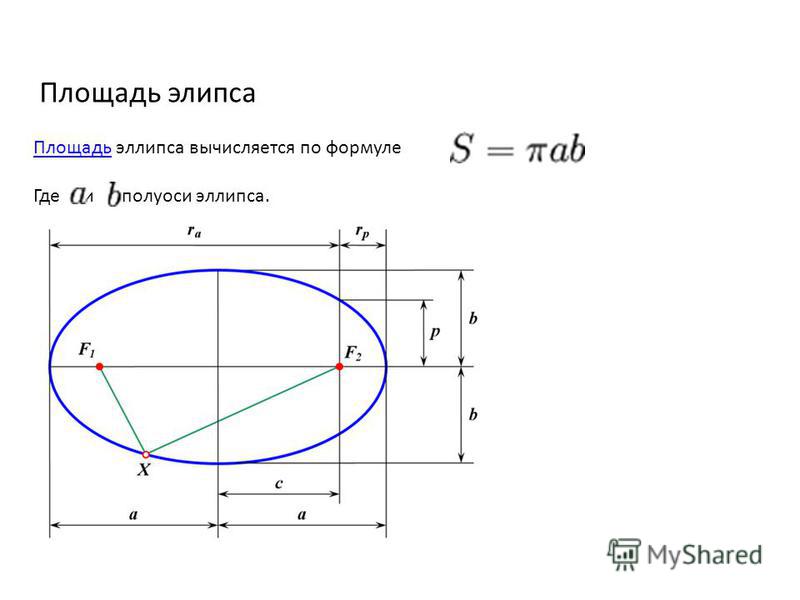
Но все же как получить из круга треугольник? Давайте воспользуемся методом неделимых Бонавентуры Кавальери.

Метод неделимых

Представим, что наш круг состоит из бесконечно большого числа окружностей, толщина линий которых стремится к нулю. Если развернуть эти окружности в отрезки и сложить друг на друга стопкой, мы получим треугольник с основанием равным длине большей окружности, то есть и высотой равной радиусу.
Площадь треугольника как известно это половина произведения основания на высоту.
Или в нашем случае .

Те, кто внимательно слушал, наверно помнят, что в теореме Архимеда говорится о прямоугольном треугольнике. Но его довольно легко получить сместив наши отрезки к левому или правому краю. К слову, так легким движением мы докажем еще одну теорему из школьной геометрии. Если знаете какую, пишите в комментариях.
Так же можете написать, как старшие прапорщики находят объем шара, или как бы с этой задачей справился Бонавентура Кавальери.
А я с вами прощаюсь, желаю счастья и до скорых встреч.

Площадь эллипса — веб-формулы

Эллипс выглядит как правильный овал, который получается, когда конус разрезается наклонной плоскостью таким образом, что получается замкнутая кривая, не пересекающая основание. Эллипс представляет собой замкнутую кривую и симметричен относительно центра. В эллипсе расстояние двух точек внутри эллипса от точки эллипса равно расстоянию любой другой точки эллипса от той же точки. Эти точки внутри эллипса называются очаги.

 

Площадь круга определяется по формуле A = π · r ² , что совпадает с A = π · r · r . Если окружность сплющить, она примет форму эллипса, а полуоси такого эллипса (например, ОА и ОВ на рисунке ниже) будут удлиненным и укороченным радиусами.

 

Если «a» обозначает OA, а «b» обозначает OB, можно доказать, что площадь эллипса можно найти, подставив «ab» вместо «rr» в формуле площади круга. , что дает следующую формулу площади эллипса:

 

 

А = π · а · б

Где а = большая полуось или ½ большой оси.
b = малая полуось или ½ малой оси.

 

 

Пример 1: Если a = 6,0 см и b = 7,0 см, найдите площадь эллипса.

Раствор :

 

А = π · а · б

А = π · 6,0 · 7,0 = 131,98 см ²

 

 

 

Пример 2: Вычислите площадь эллипса, где большой радиус равен 4 см, а малый радиус равен 3 см.

Раствор :

а = 4; б = 3

Площадь эллипса:

А = π · а · б

А = π · 4 · 3

А = 37,68 см ²

 

 

Пример 3: Вычислите площадь эллипса, радиусы которого равны 12,5 футов и 13 футов соответственно?

Раствор :

Учитывая, что: a = 12,5 футов и b = 13 футов

А = π · а · б

А = π · а · б

А = 3,14 × 12,5 × 13

А = 510,25 см ²

 

Следовательно, площадь эллипса = 510,25 см ²

 

 

Пример 4: Эллипс имеет горизонтальный радиус 8 см и вертикальный радиус 5 см. Найдите площадь эллипса.

 

Решение :

Учитывая, что:

Горизонтальный радиус (а) = 8 см

Вертикальный радиус (b)     = 5 см

 

А = π · а · б

А = π · 8 · 5

А = 125,6 см ²

 

Пример 5: Эллипс имеет горизонтальный радиус 90,5 см и вертикальный радиус 5,5 см. Найдите площадь эллипса.

Раствор :

Учитывая, что:

Горизонтальный радиус (а) = 9,5 см

Вертикальный радиус (b) = 5,5 см

А = π · а · б

А = π · 9,15 · 5,5

A = 164,065 см ²

исчисление — Найдите площадь эллипса

спросил 9\ гидроразрыва {\ pi} {2} $ $ Что соответствует: $$2ab[(\frac{\pi}{2}+0)-(0+0)]$$ Что в итоге переходит к: $$\pi ab$$

$\endgroup$

3

$\begingroup$

Метод 1 Площадь области $R$ в $2$D определяется выражением $$ A=\iint_R1\,dA.