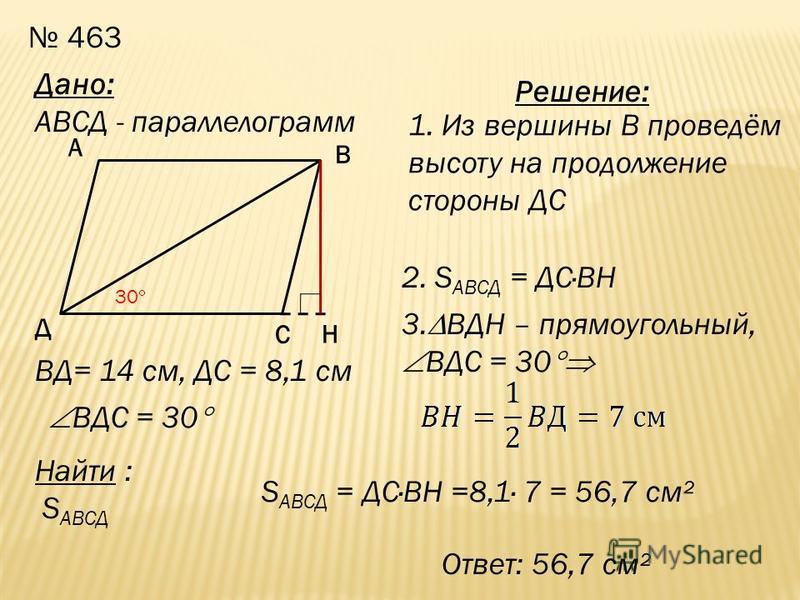
Задачи на площадь треугольника с решением 9 класс: Задачи по теме «Площадь треугольника» | Методическая разработка по геометрии (9 класс):

Содержание

Решение задач по теме «площади фигур». 9 класс (подготовка к ОГЭ)

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ
«ПЛОЩАДИ ФИГУР»
9 КЛАСС
(ПОДГОТОВКА К ОГЭ)
ЗАДАЧА №1.
На клетчатой бумаге с размером
клетки 1×1 изображён треугольник. Найдите
его площадь.
ЗАДАЧА №2.
На клетчатой бумаге с размером
клетки 1×1 изображена трапеция. Найдите её
площадь.
ЗАДАЧА №3.
На клетчатой бумаге с размером

клетки 1×1 изображён параллелограмм.
Найдите его площадь.
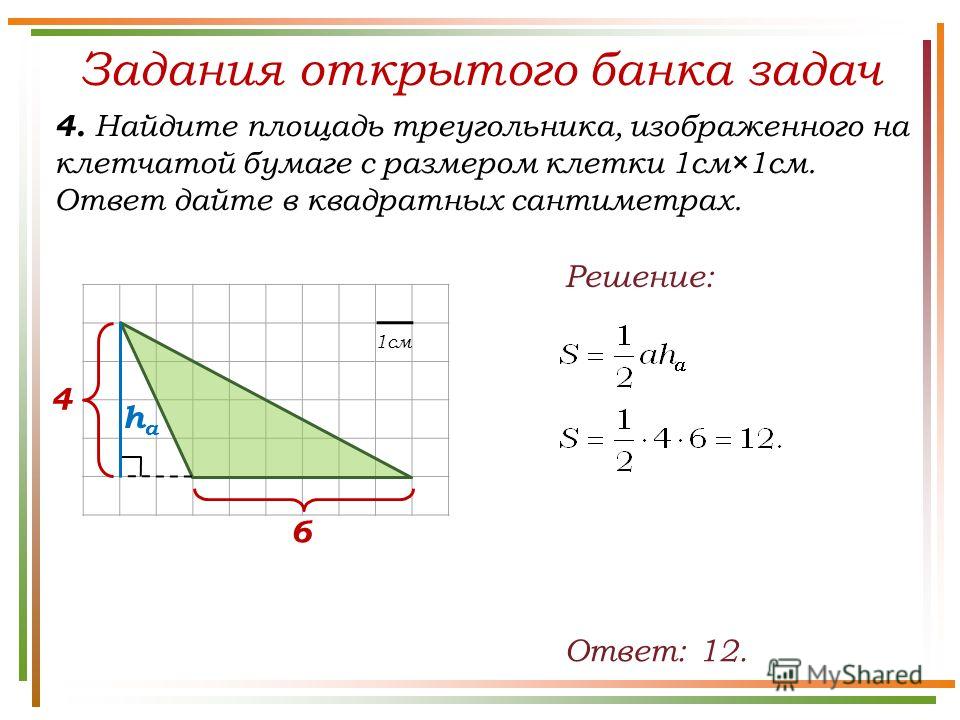
ЗАДАЧА №4.
На клетчатой бумаге с размером
клетки 1×1 изображён ромб.
Найдите площадь этого ромба.
ЗАДАЧА №5.
Периметр квадрата равен
160. Найдите площадь этого
квадрата.
ЗАДАЧА №6.
Найдите площадь квадрата,
описанного около окружности
радиуса 40.
ЗАДАЧА №7.
На клетчатой бумаге с размером
клетки 1×1 изображён треугольник. Найдите
его площадь.
ЗАДАЧА №8.
На клетчатой бумаге с размером
клетки 1×1 изображена трапеция. Найдите её
площадь.
ЗАДАЧА №9.
На клетчатой бумаге с размером
клетки 1×1 изображён параллелограмм.
Найдите его площадь.
ЗАДАЧА №10.
Найдите площадь параллелограмма,
изображённого на рисунке.
ЗАДАЧА №11.
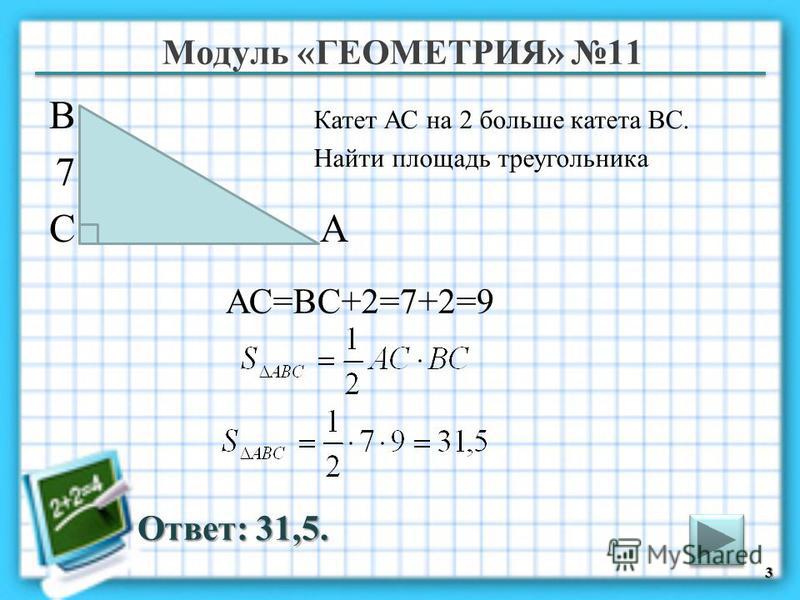
Два катета прямоугольного
треугольника равны 6 и 7.
Найдите площадь этого
треугольника.
ЗАДАЧА №12.
Найдите площадь ромба, если
его диагонали равны 14 и 6.

ЗАДАЧА №13.
Сторона треугольника равна 24, а
высота, проведённая к этой стороне,
равна 19. Найдите площадь этого
треугольника.
ЗАДАЧА №14.
Основания трапеции равны
4 и 10, а высота равна 5.
Найдите площадь этой трапеции.
ЗАДАЧА №15.
Найдите площадь параллелограмма,
изображённого на рисунке.
ЗАДАЧА №16.
Сторона квадрата равна 5√3.
Найдите площадь этого
квадрата.
ЗАДАЧА №17.
Сторона ромба равна 10, а
расстояние от точки пересечения
диагоналей ромба до неё равно 3.
Найдите площадь этого ромба.
ЗАДАЧА №19.
Периметр ромба равен 36, а один
из углов равен 30°. Найдите
площадь этого ромба.
ЗАДАЧА №20.
Площадь
параллелограмма ABCD равна 180.
Точка E — середина стороны AB.
Найдите площадь трапеции DAEC.
ЗАДАЧА №21.
В равнобедренной трапеции основания
равны 2 и 8, а один из углов между
боковой стороной и основанием
равен 45°. Найдите площадь этой
трапеции.

ЗАДАЧА №22.
На стороне AC треугольника ABC отмечена
точка D так, что AD=5, DC=7. Площадь
треугольника ABC равна 60. Найдите площадь
треугольника ABD.
ЗАДАЧА №23.
Площадь параллелограмма равна 40, а
две его стороны равны 5 и 10. Найдите
его высоты. В ответе укажите большую
высоту.
ЗАДАЧА №24.
НАЙДИТЕ ПЛОЩАДЬ ТРЕУГОЛЬНИКА
ЗАДАЧА №25.
НАЙДИТЕ ПЛОЩАДЬ ТРЕУГОЛЬНИКА
ЗАДАЧА №26.
ЗАДАЧА №27.
ЗАДАЧА №28.
ЗАДАЧА №29.
ЗАДАЧА №30.
ЗАДАЧА №31.
ЗАДАЧА №32.
85
?
40
ЗАДАЧА №33.
ЗАДАЧА № 34
ЗАДАЧА № 35
НА КЛЕТЧАТОЙ БУМАГЕ С
РАЗМЕРОМ КЛЕТКИ 1 СМ × 1 СМ ИЗОБРАЖЕНА
ФИГУРА. НАЙДИТЕ ЕЁ ПЛОЩАДЬ. ОТВЕТ ДАЙТЕ
В КВАДРАТНЫХ САНТИМЕТРАХ.

ЗАДАЧА № 35
НА КЛЕТЧАТОЙ БУМАГЕ С
РАЗМЕРОМ КЛЕТКИ 1 СМ × 1 СМ ИЗОБРАЖЕНА
ФИГУРА. НАЙДИТЕ ЕЁ ПЛОЩАДЬ. ОТВЕТ ДАЙТЕ
В КВАДРАТНЫХ САНТИМЕТРАХ.
ЗАДАЧА № 35
НА КЛЕТЧАТОЙ БУМАГЕ С
РАЗМЕРОМ КЛЕТКИ 1 СМ × 1 СМ ИЗОБРАЖЕНА
ФИГУРА. НАЙДИТЕ ЕЁ ПЛОЩАДЬ.

ОТВЕТ ДАЙТЕ
В КВАДРАТНЫХ САНТИМЕТРАХ.
ЗАДАЧА № 35
НА КЛЕТЧАТОЙ БУМАГЕ С
РАЗМЕРОМ КЛЕТКИ 1 СМ × 1 СМ ИЗОБРАЖЕНА
ФИГУРА. НАЙДИТЕ ЕЁ ПЛОЩАДЬ. ОТВЕТ ДАЙТЕ
В КВАДРАТНЫХ САНТИМЕТРАХ.

English Русский Правила

Конспект урока по геометрии «Площадь треугольника» 9 класс

Разработка урока по теме: «Площадь треугольника», 9 класс

учителя математики МОУ СОШ №1

п. Селижарово Андреевой Т.В.

Разработка урока по теме: «Площадь треугольника».

9 класс. Подготовка к ГИА.

Цель урока:

— Систематизировать знания учащихся по теме;

— Проверить уровень усвоения материала;

— Формировать познавательную активность, умение работать рационально, самостоятельно;

-Развивать культуру математической речи.

Задачи урока:

— Повторить формулы площади треугольника;

— Рассмотреть решение типовых задач;

— Закрепить навыки решения задач по данным формулам;

— Научить работать самостоятельно.

Оборудование:

интерактивная доска, раздаточный материал, листы самопроверки.

Ход урока:

1. Организационный момент: (объявление темы, цели, задачи урока).

— Здравствуйте, ребята. Сегодня на уроке мы продолжим подготовку к итоговой аттестации. Тема урока: «Площадь треугольника». С материалами по данной теме мы знакомились и работали в 7-9 классах. А как вы думаете, чем мы будем заниматься на уроке? (слайд 1-2).

2. Домашним заданием было повторить формулы площади треугольника. Возьмите листы самопроверки и в строке «формулы» запишите все формулы, которые вы знаете для нахождения площади треугольника. Проверьте результат (слайд 3).

В графе самооценки отметьте, сколько формул вы записали правильно.

Хочу вам напомнить еще несколько формул, встречающихся при решении задач на нахождение площади треугольника (слайд 4-5).

3. Одним из вопросов экзамена в разделе «Геометрия» надо установить истинность утверждений. Предлагаю соревнование по вариантам. Ученик 1 варианта выбирает вопрос на экране и ученика со 2 варианта, который будет отвечать на вопрос, а потом наоборот. Все остальные фиксируют свои ответы в листах самооценки (презентация «теоретический квадрат»). Отметьте сколько у вас правильных ответов. (Приложение1).

4. Более подготовленным учащимся предлагается решить задачи самостоятельно и записать их решение на доске (Приложение2).

5. Фронтальная работа. Решение задач (слайды7 -14). По выбору учителя.

Решения задач учащиеся записывают в листах самопроверки.

6. Проверяется решение задач на доске.

7. Самостоятельная работа (Приложение3).

Ответы учащиеся записывают в лист самопроверки.

8. Проверка самостоятельной работы (слайд 15).

9. Подведение итога урока (слайд 16).

10. Домашнее задание: решить не менее 4 задач (Приложение4).

Приложение 1.

Теоретический «квадрат».

Если гипотенуза одного прямоугольного треугольника равна гипотенузе другого прямоугольного треугольника, то треугольники равны (неверно).
Если сторона и два угла одного треугольника соответственно равны стороне и двум углам другого треугольника, то такие треугольники равны (неверно).
Если вписанный угол равен 60°, то центральный угол, опирающийся на ту же дугу окружности, равен 30°(неверно).
Любые два равнобедренных треугольника подобны (верно).
Любые два прямоугольных треугольника подобны (неверно).
Площадь треугольника равна произведению его сторон на высоту, проведенную к этой стороне (неверно).
Площадь треугольника равна половине произведению его стороны на высоту (неверно).
Сумма углов прямоугольного треугольника равна 180° (верно).
Треугольники со сторонами 1, 2, 3 не существует (верно).
Треугольник АВС, у которого АВ=5, ВС=6, АС=7, является прямоугольным (неверно).
В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета (верно).
Стороны равнобедренного треугольника равны 12 см и 5 см.

Основанием является сторона 12 см (неверно).

Приложение 2.

Карточки.

Задача №1.

В равностороннем треугольнике АВС проведена средняя линия DF. Вычислите площадь четырехугольника ADFC, если периметр ∆FDB равен 18 см.

Задача №2.

В треугольнике АВС стороны равны 5, 6 и 7.

Найдите радиус окружности, описанной около треугольника.

Задача №3.

В треугольнике АВС сторона ВС =34 см. Перпендикуляр MN, проведенный из середины ВС к прямой АС, делит сторону АС

на отрезки AN = 25 см и NC = 15 см.

Найдите площадь треугольника АВС.

Приложение 3.

Самостоятельная работа.

Вариант

Площадь прямоугольного треугольника равна 224. Один из его катетов равен 28.

Найдите другой катет.

Площадь треугольника АВС равна 168. DE – средняя линия. Найдите площадь треугольника CDE.
Боковая сторона равнобедренного треугольника равна 52, а основание равно 96. Найдите площадь этого треугольника.
В треугольнике АВС АВ=АС=4, а cos A= — . Найдите площадь треугольника.
В треугольнике АВС проведена высота СН. Известно, что АВ=3СН, СН=3. Найдите площадь треугольника.

2 вариант.

Найдите площадь треугольника, две стороны которого равны 44 и 8, а угол между ними равен 30°.
Площадь прямоугольного треугольника равна 105. Один из его катетов на 1 больше другого. Найдите меньший катет.
Угол при вершине, противолежащий основанию равнобедренного треугольника, равен 150°. Найдите боковую сторону треугольника, если его площадь равна 25.
Периметр треугольника равен 96, а радиус вписанной окружности равен 16. Найдите площадь этого треугольника.
В прямоугольном треугольнике высота, проведенная из вершины прямого угла, равна медиане, проведенной из того же угла. Гипотенуза этого треугольника равна 6. Найдите его площадь.

Приложение 4.

Домашнее задание:

Угол при вершине, противолежащий основанию равнобедренного треугольника, равен 150°. Боковая сторона треугольника равна 2. Найдите площадь треугольника.
Площадь прямоугольного треугольника равна 69. Один из его катетов равен 23. Найдите другой катет.
Найдите площадь треугольника, две стороны которого равны 16 и 12, а угол между ними равен 30°.
Площадь треугольника АВС равна 12, DE – средняя линия. Найдите площадь треугольника CDE.
Боковая сторона равнобедренного треугольника равна 85, а основание равно 150. Найдите площадь этого треугольника.
Угол при вершине, противолежащий основанию равнобедренного треугольника, равен 30°. Найдите боковую сторону треугольника, если его площадь равна 529.
Периметр треугольника равен 8, а радиус вписанной окружности равен 2. Найдите площадь этого треугольника.

Решения NCERT для математики класса 9, глава 9, области параллелограммов и треугольников

Решения NCERT для математики класса 9, глава 9, области параллелограммов и треугольников Ex 9.1 являются частью решений NCERT для математики класса 9. Здесь мы дали решения NCERT для математики класса 9, глава 9, области параллелограммов и треугольников, пример 9.1.

Решения NCERT для математики 9 класса Глава 9 Площади параллелограммов и треугольников Упр. 9.1

Упр. 9.1 Математика 9 класса Вопрос 1
Какие из следующих фигур лежат на одном основании и между одинаковыми параллелями. В таком случае запишите общее основание и две параллели.

Решение:
Фигуры (i), (iii) и (v) лежат на одном основании и между одними и теми же параллелями.

г.

	Общая база	Две параллели
Рис. (i)	DC	DC и AB
Рис. (iii)	QR	QR и PS
Рис. (v)	г. н.э.	AD и BQ

Решения NCERT для класса 9Математическая глава 9 Площадь параллелограммов и треугольников (समान्तर चतुर्भुज और त्ा

NCERT). 9 Математика Вопрос 1.

На рисунке ABCD — параллелограмм, AE ⊥ DC и CF ⊥ AD. Если AB = 16 см, AE = 8 см и CF = 10 см, найдите AD.

Решение:
BSOУ нас есть, AE ⊥ DC и AB = 16 см
∵ AB = CD [Противоположные стороны параллелограмма]
∴ CD = 16 см
Теперь, площадь параллелограмма ABCD = CD x AE
= (16 x 8) см ² = 128 см ² [∵ AE = 8 см]
Поскольку, CF ⊥ AD
∴ Площадь параллелограмма ABCD = AD x CF
⇒ AD x CF = 128 см
⇒ AD x 10 см = 128 см ² [∵ CF = 10 см]
⇒ AD = \(\frac { 128 }{ 10 }\) см = 12,8 см 10
Таким образом, требуемая длина AD составляет 12,8 см

Упражнение 9.2 Класс 9 Математика Вопрос 2. { gm }EBCG)\) … (1) 9{ gm }ABCD)\) …(2)
Из (1) и (2) имеем ar(∆APB) = ar(∆BQC).

Пример 9.2 Класс 9 Математика Вопрос 4.
На рисунке P — точка внутри параллелограмма ABCD. Покажите, что

(i) ar (APB) + ar (PCD) = \(\frac { 1 }{ 2 } ar(ABCD)\)
(ii) ar (APD) + ar(PBC) = ar (APB ) + ar (PCD)
Решение:
Имеем параллелограмм ABCD, т. е. AB || КД и БК || ОБЪЯВЛЕНИЕ. Нарисуем EF || АБ и ГГ || AD через P.

(i) ∆APB и || ^gm AEFB находятся на одном основании AB и между теми же параллелями AB и EF. 9{ gm }ABCD)\) …….(6)
Из (3) и (6) имеем
ar(∆APD) + ar(∆PBC) = ar(∆APB) + ar(∆PCD)

Пример 9.2 Класс 9 Математика Вопрос 5.
На рисунке PQRS и ABRS являются параллелограммами, а X – любая точка на стороне BR. Покажите, что
(i) ar (PQRS) = ar (ABRS)
(ii) ar (AXS) = \(\frac { 1 }{ 2 } ar(PQRS)\)

Решение:
(i) Параллелограмм PQRS и параллелограмм ABRS находятся на одном основании RS и между одними и теми же параллелями RS и PB.
∴ ar(PQRS) = ar(ABRS)
(ii) AAXS и || ^гм АБРС находятся на одной базе АС и между теми же параллелями АС и БР. *
∴ ar(AXS) = \(\frac { 1 }{ 2 } ar(ABRS)\) …(1)
Но ar(PQRS) = ar(ABRS) …(2) [Доказано в части (i) ]
Из (1) и (2) получаем
ar(AXS) = \(\frac { 1 }{ 2 } ar(PQRS)\)

Пример 9.2 Математика для 9 класса, вопрос 6.
У фермера было поле в виде параллелограмма PQRS. Она взяла любую точку А на RS и соединила ее с точками P и Q. На сколько частей разбито поле? Каковы формы этих частей? Фермер хочет посеять пшеницу и бобовые на равных участках поля по отдельности. Как она должна это сделать. 9{ gm }PQRS)\) …(2)
Из (1) и (2) имеем
ar(∆PAQ) = ar[(∆APS) + (∆QAR)]
Таким образом, фермер может сеять пшеницу в (∆PAQ) и бобовые в [(∆APS) + (∆QAR)] или пшеницу в [(∆APS) + (∆QAR)] и бобовые в (∆PAQ).

Решения NCERT для математики класса 9 Глава 9 Площади параллелограммов и треугольников Пример 9.3

Пример 9. 3 Математика класса 9 Вопрос 1.
На рисунке E — это любая точка на медиане AD ∆ABC. Покажите, что ar (ABE) = ar (ACE).

Решение:
У нас есть ∆ABC такое, что AD является медианой.
∴ ar(∆ABD) = ar(∆ACD) …(1)
[∵ Медиана делит треугольник на два равновеликих треугольника]
Аналогично, в ∆BEC имеем
ar(∆BED) = ar( ∆DEC) …(2)
Вычитая (2) из (1), получаем
ar(∆ABD) – ar(∆BED) = ar(∆ACD) – ar(∆DEC)
⇒ ar(∆ABE) = ар(∆ACE).

Упр. 9.3 Класс 9 Математика Вопрос 2.
В треугольнике ABC точка E является серединой медианы AD. Покажите, что ax (BED) = \(\frac { 1 }{ 2 } ar(ABC)\).
Решение:
У нас есть ∆ABC и его медиана AD.
Соединим B и E.

Так как медиана делит треугольник на два равновеликих треугольника.
ar (∆ABD) = \(\frac { 1 }{ 2 } ar(\Delta ABC)\) …….(1)
Теперь в ∆ABD BE является медианой.
[ ∵ E – середина AD]
∴ ar(∆BED) = \(\frac { 1 }{ 2 } ar(\Delta ABC)\) …(2)
Из (1) и (2 ), имеем
ar(∆BED) = \(\frac { 1 }{ 2 }\) [\(\frac { 1 }{ 2 } ar(\Delta ABC)\) ]
⇒ ar(∆BED) = \(\frac { 1 }{ 4 } ar(\Delta ABC)\)

Упр. 9.3 Класс 9 Математика Вопрос 3.
Покажите, что диагонали параллелограмма делят его на четыре треугольника одинаковой площади.
Решение:
У нас есть параллелограмм ABCD (скажем)
такой, что его диагонали пересекаются в точке O.
∵ Диагонали параллелограмма делят друг друга пополам.
∴ AO = OC и BO = OD
Построим CE ⊥ BD.
Теперь ar(∆BOC) = \(\frac { 1 }{ 2 }\)BO x CE и
ar(∆DOC) = \(\frac { 1 }{ 2 }\)OD x CE

Поскольку , BO = OD
∴ ar(∆BOC) = ar(∆DOC) …(1)
Аналогично, ar(∆AOD) = ar(∆DOC) …(2)
и ar(∆AOB) = ar(∆ BOC) …(3)
Из (1), (2) и (3) имеем
ar(∆AOB) = ar(∆BOC) = ar(∆COD) = ar(∆DOA)
Таким образом, диагонали параллелограмма делят его на четыре равновеликих треугольника.

Упражнение 9.3 Математика для 9 класса Вопрос 4.
На рисунке ABC и ABD — два треугольника с одним основанием AB. Если отрезок CD делится пополам отрезком AB в точке O, покажите, что ar(ABC) = ar(ABD)

Решение:
имеем, что ∆ABC и ∆ABD лежат на одном и том же основании AB.
∵ CD делится пополам в точке O. [Дано]
∴ CO = OD
Теперь в ∆ACD AO является медианой
∴ ar(∆OAC) = ar(∆OAD) …(1)
Опять же, в ∆BCD , BO — медиана
∴ ar(∆OBC) = ar(∆ODB) …(2)
Складывая (1) и (2), имеем
ar(∆OAQ + ar(∆OBQ) = ar(∆OAD) + ar(∆ ODB)
⇒ ar(∆ABC) = ar(∆ABD)

Пример 9.3 Класс 9 Математика Вопрос 5.
D, E и F являются соответственно серединами сторон BC, CA и AB ∆ABC. Покажите, что
(i) BDEF является параллелограммом
(ii) ar(DEF) = \(\frac { 1 }{ 4 } ar(ABC)\)
(iii) ar(BDEF) = \(\frac { 1 }{ 4 } ar(ABC)\)

Решение:
У нас есть ∆ABC такое
, что D,E и Fare являются серединами BC, CA и AB соответственно.

(i) В ∆ABC E и F являются серединами AC и B D C AB соответственно.
∴ КВ || BC [Теорема о средней точке]
⇒ EF || BD
Кроме того, EF = \(\frac { 1 }{ 2 } (BC)\)
⇒ EF = BD [D — середина BC]
Поскольку BDEF — четырехугольник, одна пара противоположных сторон которого параллельна и одинаковой длины.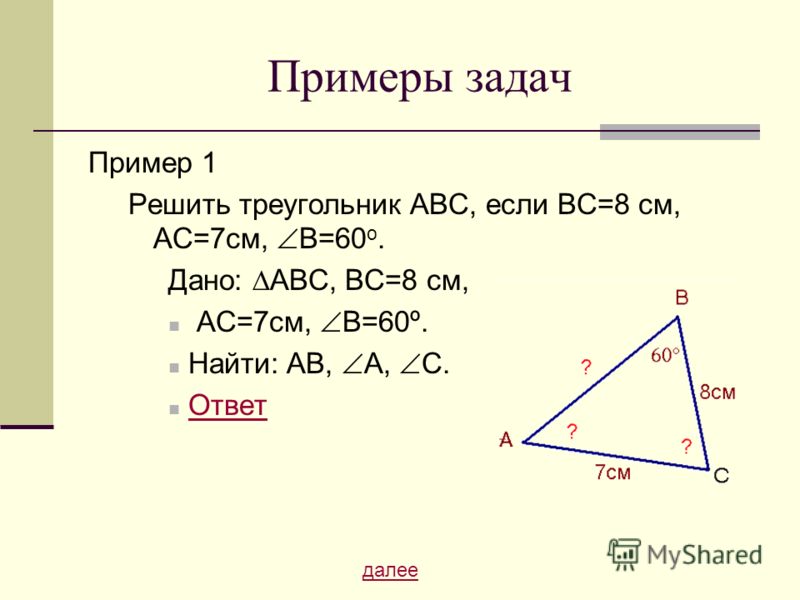
∴ BDEF — параллелограмм.

(ii) Мы доказали, что BDEF является параллелограммом.
Точно так же DCEF является параллелограммом, и DEAF также является параллелограммом.
Теперь параллелограмм BDEF и параллелограмм DCEF находятся на одном основании EF и между одними и теми же параллелями BC и EF.
∴ ar(|| ^гм BDEF) = ar(|| ^гм DCEF)
⇒ \(\frac { 1 }{ 2 }\)ar(|| ^гм BDEF) = \(\frac { 1 }{ 2 }\)ar(|| ^gm DCEF)
⇒ ar(∆BDF) = ar(∆CDE) …(1)
[Диагональ параллелограмма делит его на два равновеликих треугольника]
Аналогично , ar(∆CDE) = ar(∆DEF) …(2)
и ar(∆AEF) = ar(∆DEF) …(3)
Из (1), (2) и (3) имеем
ar(∆AEF) = ar(∆FBD) = ar(∆DEF) = ar(∆CDE)
Таким образом, ar(∆ABC) = ar(∆AEF) + ar(∆FBD) + ar(∆DEF) + ar(∆CDE) = 4 ar(∆DEF)
⇒ ar(∆DEF) = \(\frac { 1 }{ 4 }\)ar(∆ABC)

(iii) Имеем, ar (|| ^гм BDEF) = ar(∆BDF) + ar(∆DEF)
= ar(∆DEF) + ar(∆DEF) [∵ ar(∆DEF) = ar(∆BDF)]
2ar(∆DEF) = 2[\(\frac { 1 }{ 4 }\)ar(∆ABC)]
= \(\frac { 1 }{ 2 }\)ar(∆ABC)
Таким образом, ar (|| ^gm BDEF) = \(\frac { 1 }{ 2 }\)ar(∆ABC)

Упражнение 9. 3 Класс 9 Математика Вопрос 6.
На рисунке диагонали AC и BD четырехугольника ABCD пересекаются в точке 0 так, что OB = OD. Если AB = CD, то покажите, что
(i) ar(DOC) = ar(AOB)
(ii) ar (DCB) = ar (ACB)
(iii) DA || CB или ABCD — параллелограмм

Решение:
Имеем четырехугольник ABCD, диагонали которого AC и BD пересекаются в точке O.
Имеем также, что OB = OD, AB = CD Нарисуем DE ⊥ AC и BF ⊥ AC

(i) В ∆DEO и ∆BFO имеем
DO = BO [Дано]
∠DOE = ∠BOF [Вертикально противоположные углы]
∠DEO = ∠BFO [Каждый 90°]
∴ ∆DEO ≅ ∆BFO [По конгруэнтности A AS]
⇒ DE = BF [По C.P.C.T.]
и ar(∆DEO) = ar(∆BFO) …(1)
Теперь в ∆DEC и ∆BFA имеем
∠DEC = ∠BFA [Каждые 90°]
DE = BF [Доказано выше]
DC = BA [Дано]
∴ ∆DEC ≅ ∆BFA [По RHS-конгруэнтности]
⇒ ar(∆DEC) = ar(∆BFA) …(2)
и ∠1 = ∠2 …(3) [по C.P.C.T.]
Складывая (1) и (2), получаем
ar(∆DEO) + ar(∆DEC) = ar(∆BFO) + ar(∆BFA)
⇒ ar(∆DOC) = ar(∆AOB)

(ii) Поскольку ar(∆DOC) = ar(∆AOB) [ Доказано выше]
Добавляя ar(∆BOC) с обеих сторон, получаем
ar(∆DOC) + ar(∆BOC) = ar(∆AOB) + ar(∆BOC)
⇒ ar(∆DCB) = ar(∆ACB)

(iii) Так как ∆DCS и ∆ACB находятся на одном и том же основании CB и имеют равные площади.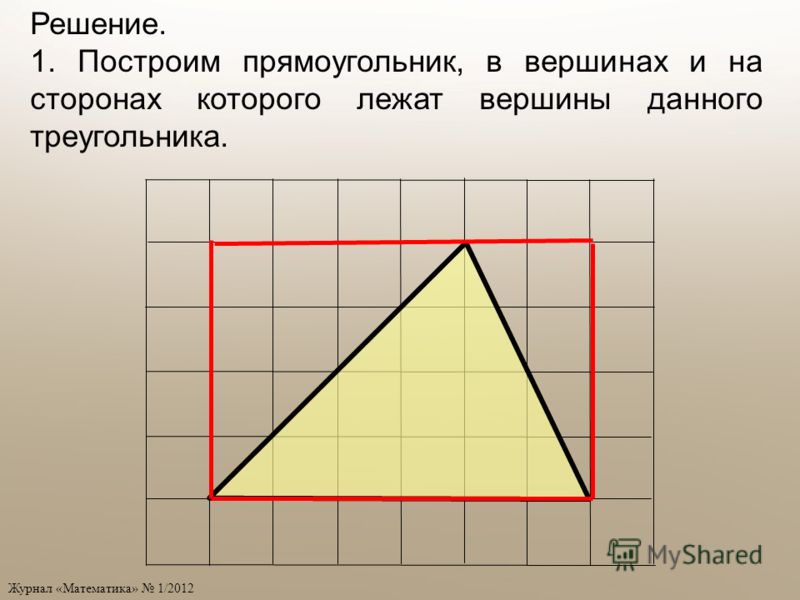
∴ Лежат между одинаковыми параллелями CB и DA.
⇒ КБ || DA
Также ∠1 = ∠2, [по (3)]
, которые являются альтернативными внутренними углами.
Итак, АБ || CD
Значит, ABCD — параллелограмм.

Пример 9.3 Класс 9 Математика Вопрос 7.
D и E — точки на сторонах AB и AC соответственно ∆ ABC, такие что ar (DBC) = ar (EBC). Докажите, что DE || ДО Н.Э.
Решение:
У нас есть ∆ABC, а точки D и E таковы, что ar(DBC) = ar{EBC)
Так как ∆DBC и ∆EBC лежат на одном основании BC и имеют одинаковую площадь.

∴ Они должны лежать между одними и теми же параллелями DE и BC.
Следовательно, DE || BC

Упражнение 9.3 Класс 9 Математика Вопрос 8.
XY – это прямая, параллельная стороне BC треугольника ∆ ABC. Если BE ||AC и CF || AB пересекаются с XY в точках E и F соответственно, покажите, что ar (ABE) = ar (ACF)
Решение:
У нас есть ∆ABC такое, что XY || до н.э.,
г. до н.э. || AC и CF || АБ. 9{ gm }BCFX)\) …(2)
Кроме того, параллелограмм BCFX и параллелограмм BCYE находятся на одном основании BC и между одними и теми же параллелями BC и EF.
∴ ar(|| ^гм BCFX) = ar(|| ^гм BCYE) ………(3)
Из (1), (2) и (3) получаем
ar(∆BE) = ar(∆ACF)

Пример 9.3 Класс 9 Математика Вопрос 9.
Сторона AB параллелограмма ABCD проведена в любую точку P. Прямая, проходящая через A и параллельная CP, пересекает CB, полученную в точке Q, и затем завершается параллелограмм PBQR. (см. рисунок). 9{ gm }PBQR)\)
⇒ ar( || ^gm ABCD) = ar(|| ^gm PBQR)

Упражнение 9.3 Класс 9 по математике Вопрос 10.
Диагонали AC и BD трапеции ABCD с AB | | DC пересекаются в точке O. Докажите, что ar (AOD) = ar (BOC)

Решение:
BBlliWWp имеют трапецию ABCD, имеющую AB || CD и его диагонали AC и BD пересекаются в точке O.
. Так как треугольники на одном основании и между одними и теми же параллелями имеют равные площади.
∆ABD и ∆ABC находятся на одном основании AB и между одними и теми же параллелями AB и DC
∴ ar(∆ABD) = ar(∆ABC)
Вычитая ar(∆AOB) с обеих сторон, получаем

ar(∆ABD) – ar(∆AOB) = ar(∆ABC) – ar(∆AOB) )
⇒ ar(∆AOD) = ar(∆BOC)

Пример 9. 3 Математика для 9 класса Вопрос 11.
На рисунке ABCDE представляет собой пятиугольник. Прямая через B, параллельная AC, пересекает DC, произведенный в точке F. Покажите, что
(i) ar (ACB) = ar (ACF)
(ii) ar (AEDF) = ar (ABCDE)

Решение:
У нас есть пятиугольник ABCDE, в котором BF || AC и DC получают по F.
(i) Так как треугольники между одними и теми же параллелями и на одном основании равны по площади.
∆ACB и ∆ACF находятся на одном основании AC и между одними и теми же параллелями AC и BF.
∴ ar(∆ACB) = ar(∆ACF)

(ii) Поскольку ar(∆ACB) = ar(∆ACF) [доказано выше]
Прибавив ar(quad. AEDC) к обеим частям, мы получим
⇒ ar(∆ACB) + ar(квадратный AEDC) = ar(∆ACF) + ar(квадратный AEDC)
∴ ar(ABCDE) = ar(AEDF)

Пример 9.3 Класс 9 Математика Вопрос 12.
Житель деревни У Итваари есть земельный участок в форме четырехугольника. Грам Панчаят из деревни решил занять часть своего участка в одном из углов для строительства Центра здоровья. Итваари соглашается с вышеуказанным предложением при условии, что ему будет предоставлено равное количество земли вместо его земли, примыкающей к его участку, с тем чтобы сформировать треугольный участок. Объясните, как это предложение будет реализовано.
Решение:
У нас есть участок в виде четырехугольника ABCD.
Нарисуем DF || AC и присоединиться к AF и CF.

Теперь ∆DAF и ∆DCF находятся на одном основании DF и между одними и теми же параллелями AC и DF.
∴ ar(ADAF) = ar(ADCF)
Вычитая ar(∆DEF) с обеих сторон, мы получаем
ar(∆DAF) – ar(∆DEF) = ar(∆DCF) – ar(∆DEF)
⇒ ar(∆ADE) = ar(∆CEF)
Часть ∆ADE может быть захвачена Грам Панчаятом путем добавления земли (∆CEF) к его (итваари) земле, чтобы сформировать треугольный участок,
т.е. ∆ABF.
Докажем, что ar(∆ABF) = ar(quad. ABCD), имеем
ar(ACEF) = ar(AADE) [Доказано выше]
Прибавив ar(quad. ABCE) к обеим сторонам, получим
ar (∆CEF) + ar(четверка ABCE) = ar(∆ADE) + ar (четверка ABCE)
⇒ ar(∆ABF) = ar (четверка ABCD)

Пример 9. 3 Класс 9 Математика Вопрос 13.
ABCD является трапецией с AB || ОКРУГ КОЛУМБИЯ. Прямая, параллельная AC, пересекает AB в точке X и BC в точке Y. Докажите, что ar(ADX) = ar(ACY). [Подсказка Join IX]
Решение:
У нас есть трапеция ABCD такая, что AB || ОКРУГ КОЛУМБИЯ.
ХУ || AC встречается с AB в X и BC в Y. Соединим CX.

∆ADX и ∆ACX находятся на одной базе AX и между одними и теми же параллелями AX и DC.
∴ ar(∆ADX) = ar(∆ACX) …(1)
∵∆ACX и ∆ACY находятся на одном основании AC и между одними и теми же параллелями AC и XY.
∴ ar(∆ACX) = ar(∆ACY) …(2)
Из (1) и (2) имеем
ar(∆ADX) = ar(∆ACY)

Пример 9.3 Класс 9 Математика Вопрос 14
На рисунке AP || БК || КР. Докажите, что ar(AQC) = ax(PBR).

Решение:
У нас есть, AP || БК || КР
∵ ∆BCQ и ∆BQR находятся на одном основании BQ и между одними и теми же параллелями BQ и CR.
∴ ar(∆BCQ) = ar(∆BQR) …(1)
∵ ∆ABQ и ∆PBQ находятся на одном основании BQ и между одними и теми же параллелями AP и BQ.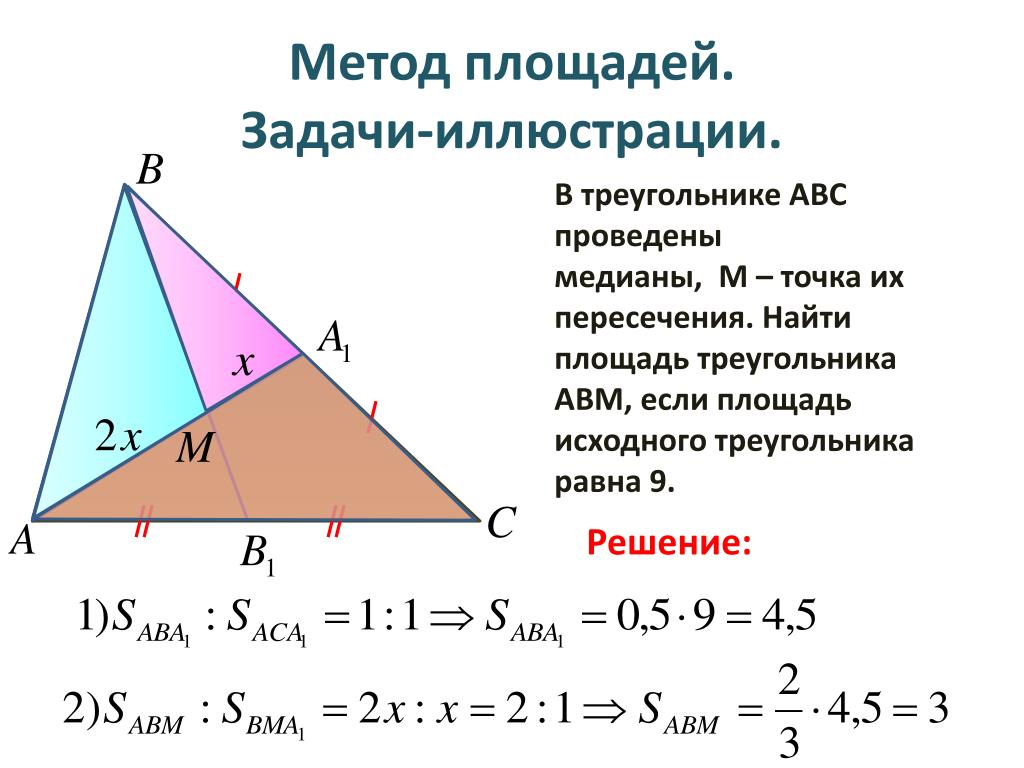
∴ ar(∆ABQ) = ar(∆PBQ) …(2)
Складывая (1) и (2), получаем
ar(∆BCQ) + ar(∆ABQ) = ar(∆BQR) + ar( ∆PBQ)
⇒ ar(∆AQC) = ar(∆PBR)

Пример 9.3 Математика 9 класса Вопрос 15.
Диагонали AC и BD четырехугольника ABCD пересекаются в 0 таким образом, что ax(AOD) = ar( БОК). Докажите, что ABCD — трапеция.
Решение:
У нас есть четырехугольник ABCD, диагонали которого AC и BD пересекаются в точке O так, что
ar(∆AOD) = ar(∆BOC) [Дано]

Прибавив ar(∆AOB) к обеим сторонам, мы получим
ar(∆AOD) + ar(∆AOB) = ar(∆BOC) + ar(∆AOB)
⇒ ar(∆ABD) = ar(∆ABC)
Кроме того, они находятся на одном и том же основании AB.
Так как треугольники лежат на одном основании и имеют одинаковую площадь.
∴ Они должны лежать между одними и теми же параллелями.
∴ АВ || DC
Итак, ABCD — четырехугольник, у которого пара противоположных сторон параллельна.
Итак, ABCD — трапеция.

Пример 9.3 Класс 9 Математика Вопрос 16.
На рисунке ax(DRC) = ar(DPC) и ai(BDP) = ar(ARC). Докажите, что оба четырехугольника ABCD и DCPR являются трапециями.

Решение:
tfclfiftУ нас есть ar(∆DRC) = ar(∆DPC) [Дано]
И они находятся на одной и той же базе DC.
∴ ∆DRC и ∆DPC должны располагаться между одними и теми же параллелями.
Итак, округ Колумбия || RP, т. е. пара противоположных сторон четырехугольника DCPR параллельна.
∴ Четырехугольник DCPR является трапецией.
Опять у нас
ar(∆BDP) = ar(∆ARC) [Дано] …(1)
Кроме того, ar(∆DPC) = ar(∆DRC) [Дано] …(2)
Вычитая (2) из (1), получаем
ar(∆BDP) – ar(∆DPC) = ar(∆ARQ – ar(∆DRQ
⇒ ar(∆BDC) = ar(∆ADC)
И они находятся на одной базе DC.
∴ ABDC и AADC должны лежать между одними и теми же параллелями
Итак, AB || DC т. е. пара противоположных сторон четырехугольника ABCD параллельна
∴ Четырехугольник ABCD является трапецией

NCERT Решения для математики 9 класса Глава 9 Площади параллелограммов и Треугольники Пр 9.

Упр. 9.4 Класс 9 Математика Вопрос 1.
Параллелограмм ABCD и прямоугольник ABEF лежат на одном основании AB и имеют равные площади. Докажите, что периметр параллелограмма больше периметра прямоугольника.
Решение:
Имеются параллелограмм ABCD и прямоугольник ABEF такие, что
ar(||gm ABCD) = ar(прямоугольник ABEF)

AB = CD [Противоположные стороны параллелограмма]
и AB = EF [Противоположные стороны прямоугольник]
⇒ CD = EF
⇒ AB + CD = AB + EF … (1)
BE < BC и AF < AD [В прямоугольном треугольнике гипотенуза — самая длинная сторона] ⇒ (BC + AD) > (BE + АФ) …(2)
Из (1) и (2) имеем
(AB + CD) + (BC+AD) > (AB + EF) + BE + AF)
⇒ (AB + BC + CD + DA) > (AB + BE + EF + FA)
⇒ Периметр параллелограмма ABCD > Периметр прямоугольника ABEF.

Пример 9.4 Математика для 9 класса Вопрос 2.
На рисунке D и E — две точки на BC, такие что BD = DE = EC. Покажите, что ar(ABD) = ar(ADE) = ar(AEC).

Решение:
Проведем AF перпендикулярно BC
так, чтобы AF была высотой ∆ABD, ∆ADE и ∆AEC.

Пример 9.4 Класс 9 Математика Вопрос 3.
На рисунке ABCD, DCFE и ABFE являются параллелограммами. Покажите, что ar(ADE) = ax(BCF).

Решение:
Так как ABCD является параллелограммом [Дано]
∴ Его противоположные стороны параллельны и равны.
т. е. AD = BC …(1)
Теперь ∆ADE и ∆BCF находятся на равных основаниях AD = BC [из (1)] и между одними и теми же параллелями AB и EF.
Итак, ar(∆ADE) = ar(∆BCF).

Упражнение 9.4 Класс 9 по математике Вопрос 4.
На рисунке ABCD представляет собой параллелограмм, а BC приводится в точку Q так, что AD = CQ. Если AQ пересекает DC в точке P, покажите, что ar(BPC) = ax(DPQ).[Подсказка Соедините AC.]

Решение:
У нас есть параллелограмм ABCD и AD = CQ. Присоединяемся к АС.
Мы знаем, что треугольники с одним и тем же основанием и между одними и теми же параллелями равны по площади.
Так как ∆QAC и ∆QDC находятся на одном основании QC и между одними и теми же параллелями AD и BQ.
∴ ar(∆QAC) = ar(∆QDC)
Вычитая ar(∆QPC) с обеих сторон, мы имеем
ar(∆QAQ – ar(∆QPC) = ar(∆QDC) – ar(∆QPC)
⇒ ar(∆PAQ = ar(∆QDP) …(1)
Так как ∆PAC и ∆PBC находятся на одной и той же базовой PC и между одними и теми же параллелями AB и CD.
∴ ar(∆PAC) = ar(∆PBC) …(2)
Из (1) и (2) получаем
ar(∆PBC) = ar(∆QDP)

Ex 9.4 Class 9 Maths Question 5
На рисунке ABC и BDE — два равносторонних треугольника, середина которых — D. Если AE пересекает BC в точке F, покажите, что

[Подсказка Соедините EC и AD. Покажите, что БЫТЬ || AC и DE || AB, etc.]
Решение:
Давайте объединим EC и AD. Нарисуйте ЕР ⊥ БК.
Пусть AB = BC = CA = a, тогда
BD = \(\frac { a }{ 2 }\) = DE = BE

(ii) Поскольку треугольники ∆ABC и ∆BED равносторонние.
⇒ ∠ACB = ∠DBE = 60°
⇒ BE || AC
∆BAE и ∆BEC находятся на одной базе BE и между одними и теми же параллелями BE и AC.
ar(∆BAE) = ar(∆BEC)
⇒ ar(∆BAE) = 2 ar(∆BDE) [ DE — медиана ∆EBC. ∴ ар(∆БЭК) = || ar(∆BDE)]
⇒ ar(ABDE) = \(\frac { 1 }{ 2 }\)ar(∆BAE)

(iii) ar(∆ABC) = 4 ar(∆BDE)[Доказано в (i) часть]
ar(∆BEC) = 2 ar(∆BDE)
[ ∵ DE медиана ∆BEC]
⇒ ar(∆ABC) = 2 ar(∆BEC)

(iv) Поскольку, ∆ ABC и ∆BDE — равносторонние треугольники.
⇒ ∠ABC = ∠BDE = 60°
⇒ АВ || DE
∆BED и ∆AED находятся на одном основании ED и между одними и теми же параллелями AB и DE.
∴ ar(∆BED) = ar(∆AED)
Вычитая ar(AEFD) с обеих сторон, получаем
⇒ ar(∆BED) – ar(∆EFD) = ar(∆AED) – ar(∆EFD)
⇒ ar(∆BEE) = ar(∆AFD)

(v) В прямоугольном ∆ABD получаем

Из (1) и (2) получаем
ar(∆AFD) = 2 ar( ∆EFD)
ar(∆AFD) = ar(∆BEF) [Из части (iv)]
⇒ ar(∆BFE) = 2 ar(∆EFD)

(vi) ar(∆AFC) = ar(∆ AFD) + ar(∆ADC)
= ar(∆BFE) + \(\frac { 1 }{ 2 }\) ar(∆ABC) [Из части (iv)]
= ar(∆BFE) + \(\frac { 1 }{ 2 } \) x 4 x ar(∆BDE) [Из части (i)]
= ar(∆BFE) + 2ar(∆BDE)
= 2ar(∆FED) + 2[ar(∆BFE) + ar(∆FED) )]
= 2ar(∆FED) + 2[2ar(∆FED) + ar(∆FED)] [Из части (v)]
= 2ar(∆FED) + 2[3ar(∆FED)]
= 2ar (∆FED) + 6ar(∆FED)
= 8ar(∆FED)
∴ ar(∆FED) = \(\frac { 1 }{ 8 }\) ar(∆AFC)

Ex 9. 4 Class 9 Math Question 6.
диагоналей AC и BD четырехугольника ABCD пересекаются в точке P. Докажите, что
ar(APB) x ar(CPD) = ar(APD) x ar(BPC).
[Подсказка. Из A и C проведите перпендикуляры к BD.]
Решение:
У нас есть четырехугольник ABCD, диагонали AC и BD которого пересекаются в точке P.
Проведем AM ⊥ BD и CN ⊥ BD.

Упражнение 9.4 Математика для 9 класса Вопрос 7.
P и Q — середины сторон AB и BC треугольника ABC, а R — середина AP. Покажите, что

Решение:
У нас есть ∆ABC такой, что P — середина AB, а Q — середина BC.
Кроме того, R является средней точкой AP. Давайте присоединимся к AQ, RQ, ПК и ПК.

(i) В ∆APQ R является средней точкой AP. [Дано] B

∴RQ является медианой ∆APQ.
⇒ ar(∆PRQ) = \(\frac { 1 }{ 2 }\)ar(∆APQ) …(1)
В ∆ABQ точка P является серединой AB.
∴ QP является медианой ∆ABQ.
∴ ar(∆APQ) = \(\frac { 1 }{ 2 }\)ar(∆ABQ) …(2)

Пример 9. 4 Класс 9 Математика Вопрос 8.
На рисунке ABC прямоугольный треугольник с прямым углом в точке A. BCED, ACFG и ABMN — квадраты со сторонами BC, CA и AB соответственно. Отрезок AX ⊥ DE пересекает BC в точке Y. Покажите, что

(i) ∆MBC = ∆ABD
(ii) ar(BYXD) = 2 ar(MBC)
(iii) ar(BYXD) = ax(ABMN)
(iv) ∆FCB ≅ ∆ACE
(v) ar(CYXE) = 2 ar(FCB)
(vi) ar(CYXE) = ax(ACFG)
(vii) ar(BCED) = ar(ABMN) + ar(ACFG)
Решение:
Имеем право ∆ ABC такой, что BCED, ACFG и ABMN являются квадратами со сторонами BC, CA и AB соответственно. Отрезок AX 1 DE также нарисован так, что он пересекает BC в точке Y. обе стороны)
или ∠ABD = ∠MBC
В ∆ABD и ∆MBC имеем
AB = MB [стороны квадрата]
BD = BC
∠ABD = ∠MBC [доказано выше]
∴ ∆ABD = ∆MBC [By конгруэнтность SAS]

(ii) Так как параллелограмм BYXD и ∆ABD лежат на одном основании BD и между одними и теми же параллелями BD и AX.
∴ ar(∆ABD) = \(\frac { 1 }{ 2 }\)ar(|| ^gm BYXD)
Но ∆ABD ≅ ∆MBC [Из части (i)]
Так как конгруэнтные треугольники равны
районов.
∴ ar(∆MBC) = \(\frac { 1 }{ 2 }\)ar(|| ^gm BYXD)
⇒ ar(|| ^гм BYXD) = 2ar(∆MBC)

(iii) Так как ar(|| ^гм BYXD) = 2ar(∆MBC) …(1) [Из (ii ) часть]
и или(квадрат АБМН) = 2или(∆MBC) …(2)
[АБМН и АМВС находятся на одном основании MB и между одними и теми же параллелями MB и NC]
Из (1) и (2), у нас есть
ar(BYXD) = ar(ABMN) .

(iv) ∠FCA = ∠BCE (каждый 90°)
или ∠FCA+ ∠ACB = ∠BCE+ ∠ACB
[путем добавления ∠ACB с обеих сторон]
⇒ ∠FCB = ∠ACE
В ∆ACEB и ∆FCB , у нас
FC = AC [Стороны квадрата]
CB = CE [Стороны квадрата]
∠FCB = ∠ACE [Доказано выше]
⇒ ∆FCB ≅ ∆ACE [По конгруэнтности SAS]

(v) Поскольку, | | ^г CYXE и ∆ACE находятся на одном основании CE и между одними и теми же параллелями CE и AX.
∴ ar(|| ^gm CYXE) = 2ar(∆ACE)
Но ∆ACE ≅ ∆FCB [Из части (iv)]
Так как конгруэнтные треугольники равны по площади.
∴ ар (||< ^гм CYXE) = 2ар(∆FCB)

(vi) Поскольку, ар(|| ^гмCYXE) = 2ar(∆FCB) …(3)
[Из части (v)]
Также (quad. ACFG) и ∆FCB находятся на одном основании FC и между одними и теми же параллелями FC и BG.
⇒ ar(четв. ACFG) = 2ar(∆FCB) …(4)
Из (3) и (4) получаем
ar(quad. CYXE) = ar(quad. ACFG) …(5)

(vii) Имеем ar(quad. BCED)
= ar(quad. CYXE) + ar(quad. BYXD)
= ar(quad. CYXE) + ar(quad. ABMN)
[Из части (iii)]
Таким образом, ar(quad.BCED)
=ar(quad.ABMN)+ar(quad.ACFG)
[Из (vi) части]

Мы надеемся, что решения NCERT для класса 9 по математике, глава 9, области параллелограммов и треугольников, пример 9.1, помогут вам. Если у вас есть какие-либо вопросы относительно решений NCERT для математики класса 9, глава 9, области параллелограммов и треугольников, пример 9.1, оставьте комментарий ниже, и мы свяжемся с вами в ближайшее время.

Площадь равнобедренного треугольника – формула, определение, примеры, часто задаваемые вопросы

Площадь равнобедренного треугольника – это пространство, ограниченное сторонами треугольника. Общая формула нахождения площади равнобедренного треугольника определяется как половина произведения основания и высоты треугольника. Помимо этого, для нахождения площади треугольников используются различные формулы. Треугольники классифицируются в зависимости от их сторон, различные типы треугольников в зависимости от сторон приведены ниже:

Равносторонний треугольник: Треугольник, у которого все три стороны равны.
Равнобедренный треугольник: Треугольник, у которого две стороны равны.
Разносторонний треугольник: Треугольник, все стороны которого не равны.

Что такое равнобедренный треугольник?

Равнобедренный треугольник — это треугольник с двумя равными сторонами. Два угла, противолежащие двум равным сторонам, также равны. Предположим, что в треугольнике △ABC, если стороны AB и AC равны, ABC является равнобедренным треугольником с ∠B = ∠C. Равнобедренный треугольник описывается теоремой «Если две стороны треугольника равны, то и угол, противолежащий им, также равен».

Какова площадь равнобедренного треугольника?

Полное пространство, занимаемое внутри границы равнобедренного треугольника, называется его площадью. В равнобедренном треугольнике площадь легко вычислить, если известны высота и основание треугольника. Произведение половины на основание и высоту равнобедренного треугольника дает площадь равнобедренного треугольника.

Isosceles Triangle Formula

Area of an isosceles triangle is given by the formula listed below:

Area = ½ × base × Height

Also,

Perimeter of isosceles triangle (P) = 2a + b
Высота равнобедренного треугольника (h) = √(a ² − b ²/4)
, где a, b — стороны равнобедренного треугольника.

Формулы площади равнобедренного треугольника

Для нахождения площади равнобедренного треугольника используются различные формулы.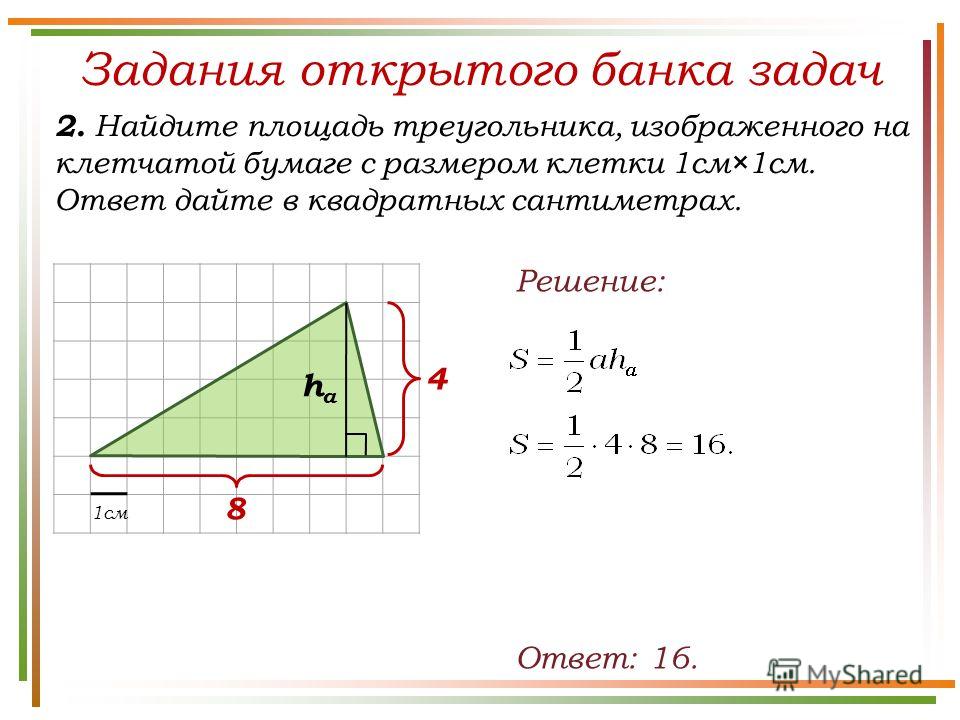 Некоторые из наиболее часто используемых формул для площади равнобедренного треугольника перечислены ниже:

Если даны основание и высота A = ½ × b × h
Если даны все три стороны A = ½[√( a ² − b ² ⁄4) × b]
Если даны длины двух сторон и угол между ними A = ½ × b × c × sin(α)
Если два угла а длина между ними равна A =
Для равнобедренного прямоугольного треугольника A = ½ × a ²

Формула площади равнобедренного треугольника со сторонами

треугольника, то высоту треугольника можно вычислить по следующей формуле:

Высота равнобедренного треугольника = √(a ² − b ² /4)

Площадь равнобедренного треугольника Треугольник (если даны все стороны) = ½[√(a ² − b ² /4) × b]
где,
b = основание равнобедренного треугольника
a = длина двух равных сторон

Как найти площадь треугольника Равнобедренный треугольник?

Чтобы найти площадь равнобедренного треугольника, выполните следующие действия:

Шаг 1: Отметьте длину (l) и ширину (b) данного треугольника.

Шаг 2: Умножьте значения, полученные на шаге 1, и разделите их на 2.

Шаг 3: Полученный результат представляет собой требуемую площадь, она измеряется в м ²

Вычисление площади равнобедренного треугольника высота треугольника или высота могут быть вычислены. Формула для вычисления площади равнобедренного треугольника со сторонами выглядит следующим образом:
Площадь равнобедренного треугольника = ½[√(a ² − b ²/4) × b]
где,
b = основание равнобедренного треугольника
a = длина двух равных сторон

= сторона 90 AC03 из приведенного выше рисунка, равной длины)
BD = DC = ½ BC = ½ b (Перпендикуляр от угла при вершине ∠A делит основание BC пополам)
Используя теорему Пифагора об ΔABD,
a ² = (b/2) ^{9
+ (AD) ²}
AD =
Высота равнобедренного треугольника =
Известно, что общая формула площади треугольника: Площадь = ½ × b × h
Подставляя значение высоты, получаем
Площадь равнобедренного треугольника = ½ [√ (A ² — B ² /4) × B]
Площадь правой угловой изоб «Треугольники
Площадь Изонлеров Правой треуголь Прямоугольный треугольник Площадь = ½ × a ²
Вывод:
Площадь равнобедренного треугольника (Площадь) = ½ × основание × высота
/ 8 × высота
/ 8 × 9 a0 2
Периметр равнобедренного прямоугольного треугольника P = (2+√2)a
Вывод:
Периметр равнобедренного прямоугольного треугольника равен сумме всех сторон равнобедренного прямоугольного треугольника.
Пусть две равные стороны равны и . По теореме Пифагора неравная сторона равна a√2.
Периметр Isockeles Правой треугольник = a+a+a√2
= 2a+a√2
= a (2+√2)
= a (2+√2)
Область Isosceles Triungle Использование Тригонометрия
Если известны длина двух сторон и угол между ними,
A = ½ × b × c × sin(α)
где,
b, c — стороны данного треугольника
α — угол между ними
Стороны между ними приведены,
A =
, где
C — стороны данного треугольника
α, β — это угол, связанный с ними
. Равнобедренный треугольник
Пример 1: Найдите площадь равнобедренного треугольника, сторона которого равна 13 см, а основание равно 24 см.
Решение:
У нас есть, A = 13 и B = 24.
Площадь Isockeles Triangle дается,
A =
=
= 1/2 × 5 24
. = 60 см ²
Пример 2: Найдите площадь равнобедренного треугольника с равна стороне 10 см и основанию 12 см.
Решение:
У нас есть, A = 10 и B = 12.
Площадь Isockeles Triangle дается,
A =
=
= 1/2 × 8
. = 48 см ²
Пример 3. Найдите площадь равнобедренного треугольника со стороной , равной , равной 5 см, и основанием , равным 6 см.
Решение:
У нас есть, A = 5 и B = 6.
Площадь Isockeles Triangle дается,
A =
=
= 1/2 × 4 ×
. = 12см ²

Решение:

Имеем a = 15 и b = 24,
Площадь равнобедренного треугольника определяется как равные стороны 17 см и основание 30 см.
Решение:
Имеем a = 17 и b = 30.0002 = 1/2 × 8 × 30
= 120 см ²
.
Решение:
У нас есть, A = 20 и B = 24.
Площадь Isockeles Triangle дается,
A =
=
= 1/2 × 16 × 24
. = 192 см ²
Пример 7: Найдите площадь равнобедренного треугольника с равна стороне 25 см и основанию 30 см.
Решение:
У нас есть, A = 25 и B = 30.
Площадь Isockeles Triangle дается,
A =
=
= 1/2 × 20 × 300003
= 300 см ²
Часто задаваемые вопросы о площади равнобедренного треугольника
Вопрос 1: Какова площадь равнобедренного треугольника?
Ответ:
Площадь фигуры – это пространство, ограниченное границами фигуры. Итак, площадь равнобедренного треугольника можно определить как пространство, занимаемое равнобедренным треугольником.
Вопрос 2: Что вы подразумеваете под равнобедренным треугольником?
Ответ:
Равнобедренный треугольник можно определить как треугольник, который имеет две равные стороны, также в равнобедренном треугольнике противоположные углы равны. Некоторые из свойств равнобедренного треугольника:

Две равные стороны равнобедренного треугольника равны, и угол между ними называется углом при вершине или углом при вершине.
Сторона, противоположная углу при вершине, называется основанием, и в равнобедренном треугольнике углы при основании также равны.
Вопрос 3: Напишите формулу для нахождения площади равнобедренного треугольника.
Ответ:
Для вычисления площади равнобедренного треугольника используется следующая формула:
A = ½ × b × h
где
b — основание треугольника,
h — высота треугольника.
Вопрос 4 : Напишите формулу для нахождения периметра равнобедренного треугольника.

Ответ:
Для вычисления периметра равнобедренного треугольника используется следующая формула:
P = 2a + b
где,
а, b — стороны равнобедренного треугольника.
Вопрос 5: Напишите формулу площади равнобедренного прямоугольного треугольника.
No related posts.