Как найти радиус трубы формула
Главная » Разное » Как найти радиус трубы формула
площади поверхности, толщины стенки, массы
При строительстве и обустройстве дома трубы не всегда используются для транспортировки жидкостей или газов. Часто они выступают как строительный материал — для создания каркаса различных построек, опор для навесов и т.д. При определении параметров систем и сооружений необходимо высчитать разные характеристики ее составляющих. В данном случае сам процесс называют расчет трубы, а включает он в себя как измерения, так и вычисления.
Для чего нужны расчеты параметров труб
Содержание статьи
В современном строительстве используются не только стальные или оцинкованные трубы. Выбор уже довольно широк — ПВХ, полиэтилен (ПНД и ПВД), полипропилен, металлопластк, гофрированная нержавейка. Они хороши тем, что имеют не такую большую массу, как стальные аналоги. Тем не менее, при транспортировке полимерных изделий в больших объемах знать их массу желательно — чтобы понять, какая машина нужна. Вес металлических труб еще важнее — доставку считают по тоннажу. Так что этот параметр желательно контролировать.
Вес металлических труб еще важнее — доставку считают по тоннажу. Так что этот параметр желательно контролировать.
То, что нельзя измерить, можно рассчитать
Знать площадь наружной поверхности трубы надо для закупки краски и теплоизоляционных материалов. Красят только стальные изделия, ведь они подвержены коррозии в отличие от полимерных. Вот и приходится защищать поверхность от воздействия агрессивных сред. Используют их чаще для строительства заборов, каркасов для хозпостроек (гаражей, сараев, беседок, бытовок), так что условия эксплуатации — тяжелы, защита необходима, потому все каркасы требуют окраски. Вот тут и потребуется площадь окрашиваемой поверхности — наружная площадь трубы.
При сооружении системы водоснабжения частного дома или дачи, трубы прокладывают от источника воды (колодца или скважины) до дома — под землей. И все равно, чтобы они не замерзли, требуется утепление. Рассчитать количество утеплителя можно зная площадь наружной поверхности трубопровода. Только в этом случае надо брать материал с солидным запасом — стыки должны перекрываться с солидным запасом.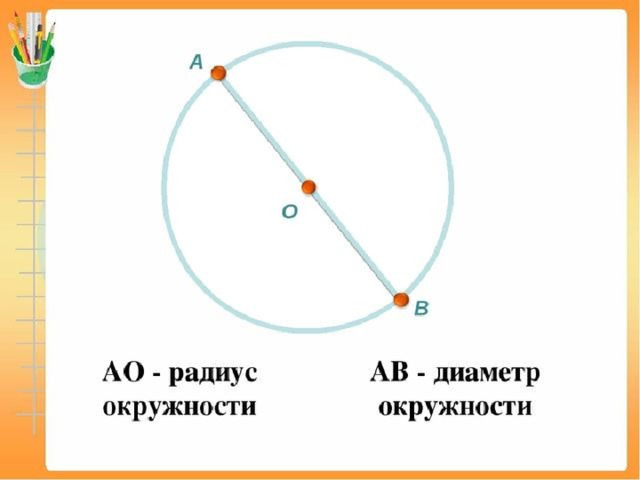
Сечение трубы необходимо для определения пропускной способности — сможет ли данное изделие провести требуемое количество жидкости или газа. Этот же параметр часто нужен при выборе диаметра труб для отопления и водопровода, расчета производительности насоса и т.д.
Внутренний и наружный диаметр, толщина стенки, радиус
Трубы — специфический продукт. Они имеют внутренний и наружный диаметр, так как стенка у них толстая, ее толщина зависит от типа трубы и материала из которого она изготовлена. В технических характеристиках чаще указывают наружный диаметр и толщину стенки.
Внутренний и наружный диаметр трубы, толщина стенки
Имея эти два значения, легко высчитать внутренний диаметр — от наружного отнять удвоенную толщину стенки: d = D — 2*S. Если у вас наружный диаметр 32 мм, толщина стенки 3 мм, то внутренний диаметр будет: 32 мм — 2 * 3 мм = 26 мм.
Если же наоборот, имеется внутренний диаметр и толщина стенки, а нужен наружный — к имеющемуся значению добавляем удвоенную толщину стеки.
С радиусами (обозначаются буквой R) еще проще — это половина от диаметра: R = 1/2 D. Например, найдем радиус трубы диаметром 32 мм. Просто 32 делим на два, получаем 16 мм.
Измерения штангенциркулем более точные
Что делать, если технических данных трубы нет? Измерять. Если особая точность не нужна, подойдет и обычная линейка, для более точных измерений лучше использовать штангенциркуль.
Расчет площади поверхности трубы
Труба представляет собой очень длинный цилиндр, и площадь поверхность трубы рассчитывается как площадь цилиндра. Для вычислений потребуется радиус (внутренний или наружный — зависит от того, какую поверхность вам надо рассчитать) и длина отрезка, который вам необходим.
Формула расчета боковой поверхности трубы
Чтобы найти боковую площадь цилиндра, перемножаем радиус и длину, полученное значение умножаем на два, а потом — на число «Пи», получаем искомую величину. При желании можно рассчитать поверхность одного метра, ее потом можно умножать на нужную длину.
Для примера рассчитаем наружную поверхность куска трубы длиной 5 метров, с диаметром 12 см. Для начала высчитаем диаметр: делим диаметр на 2, получаем 6 см. Теперь все величины надо привести к одним единицам измерения. Так как площадь считается в квадратных метрах, то сантиметры переводим в метры. 6 см = 0,06 м. Дальше подставляем все в формулу: S = 2 * 3,14 * 0,06 * 5 = 1,884 м2. Если округлить, получится 1,9 м2.
Расчет веса
С расчетом веса трубы все просто: надо знать, сколько весит погонный метр, затем эту величину умножить на длину в метрах. Вес круглых стальных труб есть в справочниках, так как этот вид металлопроката стандартизован. Масса одного погонного метра зависит от диаметра и толщины стенки. Один момент: стандартный вес дан для стали плотностью 7,85 г/см2 — это тот вид, который рекомендован ГОСТом.
Таблица веса круглых стальных труб
В таблице Д — наружный диаметр, условный проход — внутренний диаметр, И еще один важный момент: указана масса обычных стального проката, оцинкованные на 3% тяжелее.
Таблица веса профилированной трубы квадратного сечения
Как высчитать площадь поперечного сечения
Формула нахождения площади сечения круглой трубы
Если труба круглая, площадь сечения считать надо по формуле площади круга: S = π*R2. Где R — радиус (внутренний), π — 3,14. Итого, надо возвести радиус в квадрат и умножить его на 3,14.
Например, площадь сечения трубы диаметром 90 мм. Находим радиус — 90 мм / 2 = 45 мм. В сантиметрах это 4,5 см. Возводим в квадрат: 4,5 * 4,5 = 2,025 см2, подставляем в формулу S = 2 * 20,25 см2 = 40,5 см 2.
Площадь сечения профилированной трубы считается по формуле площади прямоугольника: S = a * b, где a и b — длины сторон прямоугольника. Если считать сечение профиля 40 х 50 мм, получим S = 40 мм * 50 мм = 2000 мм2 или 20 см2 или 0,002 м2.
Как рассчитать объем воды в трубопроводе
При организации системы отопления бывает нужен такой параметр, как объем воды, которая поместится в трубе. Это необходимо при расчете количества теплоносителя в системе. Для данного случая нужна формула объема цилиндра.
Это необходимо при расчете количества теплоносителя в системе. Для данного случая нужна формула объема цилиндра.
Формула расчета объема воды в трубе
Тут есть два пути: сначала высчитать площадь сечения (описано выше) и ее умножить на длину трубопровода. Если считать все по формуле, нужен будет внутренний радиус и общая длинна трубопровода. Рассчитаем сколько воды поместится в системе из 32 миллиметровых труб длиной 30 метров.
Сначала переведем миллиметры в метры: 32 мм = 0,032 м, находим радиус (делим пополам) — 0,016 м. Подставляем в формулу V = 3,14 * 0,0162 * 30 м = 0,0241 м3. Получилось = чуть больше двух сотых кубометра. Но мы привыкли объем системы измерять литрами. Чтобы кубометры перевести в литры, надо умножить полученную цифру на 1000. Получается 24,1 литра.
Калькулятор объема трубы
Как определить объем трубы?
Цилиндр — это трехмерное твердое тело с совпадающими основаниями в паре параллельных плоскостей. Эти основания представляют собой конгруэнтные круги. 2) \ frac {\ pi} {4} \ times h $$
2) \ frac {\ pi} {4} \ times h $$
где $ D $ и $ d $ — внешний и внутренний диаметр соответственно.3 $$ Работа с объемом трубы с шагом показывает полный пошаговый расчет для определения объема внутри трубы при длине ее внутреннего радиуса $ 10 \; in $ и высоте $ 8 \; in $ с использованием формулы объема. Для любых других значений базовых радиусов и высоты трубы просто введите три положительных вещественных числа и нажмите кнопку «Создать работу». Ученики начальной школы могут использовать этот калькулятор объема трубы для создания работы, проверки результатов измерения объема трехмерных тел или эффективного выполнения домашних заданий..
Как найти квадратный дюйм трубы
Подсказка
Если у вас нет доступа к отверстию трубы, но вы знаете толщину стенки трубы, оберните измерительную ленту вокруг трубы, чтобы определить длину окружности в дюймах. Затем разделите окружность на 3,1415, чтобы найти внешний диаметр. Разделите внешний диаметр на два, чтобы найти внешний радиус. Затем вычтите из полученного результата толщину стенки трубы в дюймах, чтобы найти внутренний радиус отверстия трубы.
Затем вычтите из полученного результата толщину стенки трубы в дюймах, чтобы найти внутренний радиус отверстия трубы.
Отверстие трубы может быть измерено в квадратных дюймах.
Определение площади отверстия трубы в квадратных дюймах может быть полезно при определении пропускной способности трубы. Труба с большим отверстием позволяет проходить большему количеству жидкости и требует более медленного потока, чем труба с меньшим отверстием. Вы также можете использовать квадратные дюймы трубы для других расчетов, таких как определение веса заполненной трубы и определение площади поверхности внутри трубы.
.
Определение радиуса круга и калькулятор
Определение радиуса круга и калькулятор — Math Open Reference
1. Линия от центра круга до точки на окружности.
2. Расстояние от центра круга до точки на окружности.
Попробуйте это Перетащите оранжевую точку. Синяя линия всегда остается радиусом круга.
Радиус круга — это длина линии от центра до любой точки на его крае.Форма множественного числа — радиусы (произносится как «луч-ди-глаз»). На рисунке выше перетащите оранжевую точку и убедитесь, что радиус всегда постоянен в любой точке круга.
Иногда слово «радиус» используется для обозначения самой линии. В этом смысле вы можете увидеть «нарисовать радиус круга». В более позднем смысле это длина линии, поэтому ее называют «радиус круга 1,7 сантиметра».
Если известен диаметр
Учитывая диаметр круга, радиус просто равен половине диаметра: где:
D — диаметр окружности
Если вы знаете окружность
Если вам известна длина окружности, радиус можно найти по формуле
, где:
C — длина окружности
π — Пи, приблизительно 3.142
Если известен район
Если вам известна площадь круга, радиус можно найти по формуле
, где:
A — площадь круга
π — Пи, примерно 3,142
Калькулятор
Воспользуйтесь калькулятором выше, чтобы вычислить свойства круга.
Введите любое одно значение, и остальные три будут рассчитаны. Например: введите радиус и нажмите «Рассчитать». Будут рассчитаны площадь, диаметр и окружность.
Точно так же, если вы войдете в область, будет вычислен радиус, необходимый для получения этой области, а также диаметр и окружность.
Сопутствующие товары
Диаметр Ширина круга. Диаметр в два раза больше радиуса. Увидеть диаметр круга
Окружность Окружность — это расстояние по краю круга. Видеть Окружность круга подробнее.
Что попробовать
- На рисунке выше нажмите «Сброс» и перетащите оранжевую точку.Обратите внимание, что радиус имеет одинаковую длину в любой точке круга.
- Щелкните «Показать диаметр». Перетащите любую оранжевую точку на концах линии диаметра. Обратите внимание на то, что радиус всегда равен половине диаметра.
- Снимите флажок «фиксированный размер». Повторите вышесказанное и обратите внимание на то, что радиус всегда равен половине диаметра, независимо от размера круга.

Другие темы кружка
Общие
Уравнения окружности
Углы по окружности
Дуги
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
.
Что такое гидравлический радиус? — Определение из Trenchlesspedia
Переключить навигацию Меню
- Статьи Земляные работы Обычное туннелирование Скучно Монтаж Разрыв трубы Оборудование
.
Как найти периметр круга зная диаметр.
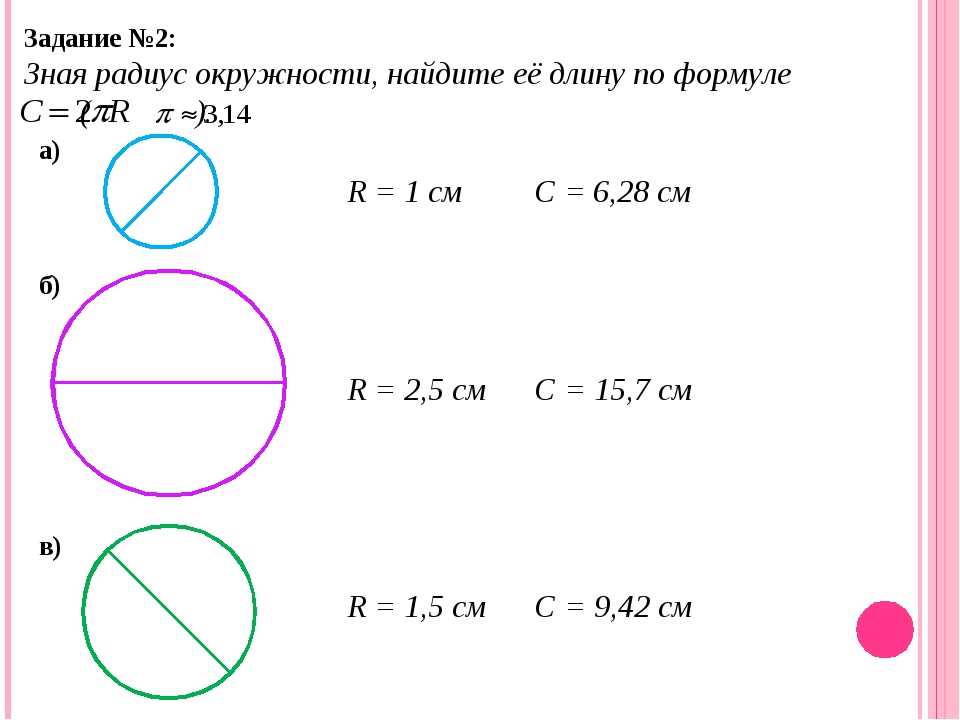
 Как найти длину окружности: через диаметр и радиус
Как найти длину окружности: через диаметр и радиусГлавная » Киевстар » Как найти периметр круга зная диаметр. Как найти длину окружности: через диаметр и радиус
Таким образом, длину окружности (C ) можно вычислить, умножив константу π на диаметр (D ), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:
C = πD = 2πR
где C — длина окружности, π — константа, D — диаметр окружности , R — радиус окружности.
Так как окружность является границей круга , то длину окружности можно также назвать длиной круга или периметром круга.
Задачи на длину окружности
Задача 1. Найти длину окружности, если её диаметр равен 5 см.
Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:
C ≈ 3,14 · 5 = 15,7 (см)
Задача 2. Найти длину окружности, радиус которой равен 3,5 м.
Найти длину окружности, радиус которой равен 3,5 м.
Сначала найдём диаметр окружности, умножив длину радиуса на 2:
D = 3,5 · 2 = 7 (м)
теперь найдём длину окружности, умножив π на диаметр:
C ≈ 3,14 · 7 = 21,98 (м)
Задача 3. Найти радиус окружности, длина которой равна 7,85 м.
Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2
Площадь круга
Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга :
S = πr 2
где S — площадь круга, а r — радиус круга.
Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:
Задачи на площадь круга
Задача 1. Найти площадь круга, если его радиус равен 2 см.
Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:
S ≈ 3,14 · 2 2 = 3,14 · 4 = 12,56 (см 2)
Задача 2. Найти площадь круга, если его диаметр равен 7 см.
Найти площадь круга, если его диаметр равен 7 см.
Сначала найдём радиус круга, разделив его диаметр на 2:
7: 2 = 3,5 (см)
теперь вычислим площадь круга по формуле:
S = πr 2 ≈ 3,14 · 3,5 2 = 3,14 · 12,25 = 38,465 (см 2)
Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
| S = π | D 2 | ≈ 3,14 | 7 2 | = 3,14 | 49 | = | 153,86 | = 38,465 (см 2) |
| 4 | 4 | 4 | 4 |
Задача 3. Найти радиус круга, если его площадь равна 12,56 м 2 .
Чтобы найти радиус круга по его площади, надо площадь круга разделить π , а затем из полученного результата извлечь квадратный корень:
r = √S : π
следовательно радиус будет равен:
r ≈ √12,56: 3,14 = √4 = 2 (м)
Число
πДлину окружности предметов, окружающих нас, можно измерить с помощью сантиметровой ленты или верёвки (нитки), длину которой потом можно померить отдельно.
Чтобы понять, как это можно сделать, возьмём несколько круглых предметов, у которых можно измерить и длину окружности и диаметр. Вычислим отношение длины к диаметру, в итоге получим следующий ряд чисел:
Из этого можно сделать вывод, что отношение длины окружности к её диаметру это постоянная величина для каждой отдельной окружности и для всех окружностей в целом. Это отношение и обозначается буквой π .
Используя эти знания, можно по радиусу или диаметру окружности находить её длину. Например, для вычисления длины окружности с радиусом 3 см нужно умножить радиус на 2 (так мы получим диаметр), а полученный диаметр умножить на π . В итоге, с помощью числа π мы узнали, что длина окружности с радиусом 3 см равна 18,84 см.
Инструкция
Сначала надо исходные данные к задаче. Дело в том, что ее условии не может быть явно сказано, какова радиуса окружности . Вместо этого в задаче может быть дана длина диаметра окружности . Диаметр окружности — отрезок, который объединяет между собой две противоположные точки окружности , проходя через ее центр. Проанализировав определения окружности , можно сказать, что длина диаметра удвоенной длине радиуса.
Теперь можно принять радиус окружности равным R. Тогда для длины окружности необходимо воспользоваться формулой:
L = 2πR = πD, где L — длина окружности , D — диаметр окружности
Обратите внимание
Окружность можно вписать в многоугольник, либо описать вокруг него. При этом, если окружность вписана, то она в точках касания со сторонами многоугольника будет делить их пополам. Чтобы узнать радиус вписанной окружности, нужно поделить площадь многоугольника на половину его периметра:
R = S/p.
Если окружность описана вокруг треугольника, то ее радиус находится по следующей формуле:
R = a*b*c/4S, где a, b, c — это стороны данного треугольника, S — площадь треугольника, вокруг которого описана окружность.
Если требуется описать окружность вокруг четырехугольника, то это можно будет сделать при соблюдении двух условий:
Четырехугольник должен быть выпуклым.
В сумме противоположные углы четырехугольника должны составлять 180°
Полезный совет
Помимо традиционного штангенциркуля, для начертания окружности можно применять и трафареты. В современных трафаретах включены окружность разных диаметров. Данные трафареты можно приобрести в любом магазине канцтоваров.
Источники:
- Как найти длину окружности?
Окружность — замкнутая кривая линия, все точки которой находятся на равном расстоянии от одной точки. Эта точка — центр окружности, а отрезок между точкой на кривой и ее центром называется радиусом окружности.
Инструкция
Если через центр окружности провести прямую линию, то ее отрезок между двумя точками пересечения этой прямой с окружностью называется диаметром данной окружности. Половина диаметра, от центра до точки пересечения диаметра с окружность — это радиус
Половина диаметра, от центра до точки пересечения диаметра с окружность — это радиус
окружности. Если окружность разрезать в произвольной точке, выпрямить и измерить, то полученная величина является длиной данной окружности.
Начертите несколько окружностей разным раствором циркуля. Визуальное сравнение позволяет сделать вывод, что больший диаметр очерчивает больший круг, ограниченный окружностью с большей длиной. Следовательно, между диаметром окружности и ее длиной существует прямо пропорциональная зависимость.
По физическому смыслу параметр «длина окружности» соответствует , ограниченного ломаной линией. Если вписать в окружность правильный n-угольник со стороной b, то периметр такой фигуры Р равен произведению стороны b на число сторон n: Р=b*n. Сторона b может быть определена по формуле: b=2R*Sin (π/n), где R — радиус окружности, в которую вписали n-угольник.
При увеличении числа сторон периметр вписанного многоугольника будет все больше приближаться к L. Р= b*n=2n*R*Sin (π/n)=n*D*Sin (π/n). Зависимость между длиной окружности L и ее диаметром D постоянна. Отношение L/D=n*Sin (π/n) при стремлении числа сторон вписанного многоугольника к бесконечности стремится к числу π, постоянной величине, называемой «число пи» и выраженной бесконечной десятичной дробью. Для расчетов без применения вычислительной техники принимается значение π=3,14. Длина окружности и ее диаметр связаны формулой: L= πD. Для окружности разделите ее длину на число π=3,14.
Зависимость между длиной окружности L и ее диаметром D постоянна. Отношение L/D=n*Sin (π/n) при стремлении числа сторон вписанного многоугольника к бесконечности стремится к числу π, постоянной величине, называемой «число пи» и выраженной бесконечной десятичной дробью. Для расчетов без применения вычислительной техники принимается значение π=3,14. Длина окружности и ее диаметр связаны формулой: L= πD. Для окружности разделите ее длину на число π=3,14.
И в чем ее отличие от круга. Возьмите ручку или цвета и нарисуйте на листке бумаги обычный круг. Закрасьте всю середину полученной фигуры синим карандашом. Красный контур, обозначающий границы фигуры, — это окружность. А вот синее содержимое внутри нее — и есть круг.
Размеры круга и окружности определяются диаметром. На красной линии, обозначающей окружность, отметьте две точки таким образом, чтобы они оказались зеркальным отражением друг друга. Соедините их линией. Отрезок обязательно пройдет через точку в центре окружности. Этот отрезок, соединяющий противоположные части окружности, и называется в геометрии диаметром.
Отрезок, который тянется не через центр окружности, но смыкается с ней противоположными концами, называется хордой. Следовательно, хорда, пролегающая через точку центра окружности, и является ее диаметром.
Обозначается диаметр латинской буквой D. Находить диаметр окружности можно по таким значениям, как площадь, длина и радиус круга.
Расстояние от центральной точки до точки, отложенной на окружности, называется радиусом и обозначается буквой R. Знание величины радиуса помогает вычислить диаметр окружности одним несложным действием:
К примеру, радиус — 7 см. Умножаем 7 см на 2 и получаем величину, равную 14 см. Ответ: D заданной фигуры равен 14 см.
Иногда приходится определять диаметр окружности лишь по ее длине. Здесь необходимо применить специальную формулу, помогающую определить Формула L = 2 Пи * R, где 2 — это неизменная величина (константа), а Пи = 3,14. А так как известно, что R = D * 2, то формулу можно представить и другим способом
Данное выражение применимо и как формула диаметра окружности. Подставив известные в задаче величины, решаем уравнение с одним неизвестным. Допустим, длина равна 7 м. Следовательно:
Подставив известные в задаче величины, решаем уравнение с одним неизвестным. Допустим, длина равна 7 м. Следовательно:
Ответ: диаметр равен 21,98 метрам.
Если известно значение площади, то также можно определить диаметр окружности. Формула, которая применяется в данном случае, выглядит так:
D = 2 * (S / Пи) * (1 / 2)
S — в данном случае Допустим, в задаче она равна 30 кв. м. Получаем:
D = 2 * (30 / 3, 14) * (1 / 2) D = 9, 55414
При обозначенной в задаче величине, равной объему (V) шара, применяется следующая формула нахождения диаметра: D = (6 V / Пи) * 1 / 3.
Иногда приходится находить диаметр окружности, вписанной в треугольник. Для этого по формуле находим радиус представленной окружности:
R = S / p (S — площадь заданного треугольника, а p — периметр, разделенный на 2).
Полученный результат увеличиваем вдвое, учитывая, что D = 2 * R.
Нередко находить диаметр окружности приходится и в быту. К примеру, при определении что равносильно его диаметру. Для этого необходимо обмотать палец потенциального обладателя кольца ниткой. Отметить точки соприкосновения двух концов. Измерить линейкой длину от точки до точки. Полученное значение умножаем на 3,14, следуя формуле определения диаметра при известной длине. Так что, утверждение о том, что познания в геометрии и алгебре в жизни не пригодятся, не всегда соответствует действительности. А это является серьезным поводом для того, чтобы более ответственно относиться к школьным предметам.
Для этого необходимо обмотать палец потенциального обладателя кольца ниткой. Отметить точки соприкосновения двух концов. Измерить линейкой длину от точки до точки. Полученное значение умножаем на 3,14, следуя формуле определения диаметра при известной длине. Так что, утверждение о том, что познания в геометрии и алгебре в жизни не пригодятся, не всегда соответствует действительности. А это является серьезным поводом для того, чтобы более ответственно относиться к школьным предметам.
Окружностью называют кривую линию, которая ограничивает собой круг. В геометрии фигуры плоские, поэтому определение относится к двухмерному изображению. Предполагается, что все точки этой кривой удалены от центра круга на равное расстояние.
У окружности есть несколько характеристик, на основе которых производят расчеты, связанные с этой геометрической фигурой. В их число входит: диаметр, радиус, площадь и длина окружности. Эти характеристики взаимосвязаны, то есть для их вычисления достаточно информации хотя бы об одной из составляющих.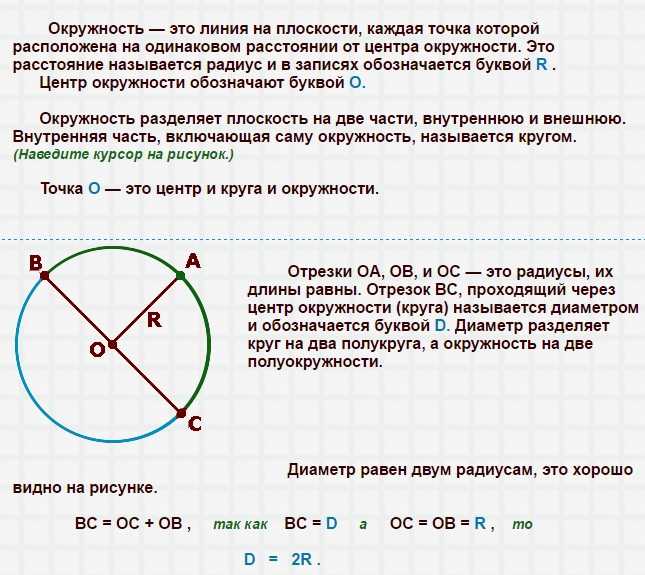 Например, зная только радиус геометрической фигуры по формуле можно найти длину окружности, диаметр, и ее площадь.
Например, зная только радиус геометрической фигуры по формуле можно найти длину окружности, диаметр, и ее площадь.
- Радиус окружности – это отрезок внутри окружности, соединённый с ее центром.
- Диаметр – это отрезок внутри окружности, соединяющий ее точки и проходящий через центр. По сути, диаметр – это два радиуса. Именно так выглядит формула для его вычисления: D=2r.
- Есть еще одна составляющая окружности – хорда. Эта прямая, которая соединяет две точки окружности, но не всегда проходит через центр. Так вот ту хорду, которая через него проходит, тоже называют диаметром.
Как узнать длину окружности? Сейчас выясним.
Длина окружности: формула
Для обозначения этой характеристики выбрана латинская буква p. Еще Архимед доказал, что отношение длины окружности к ее диаметру является одним и тем же числом для всех окружностей: это число π, которое приблизительно равно 3,14159. Формула для вычисления π выглядит так: π = p/d. Согласно этой формуле, величина p равна πd, то есть длина окружности: p= πd.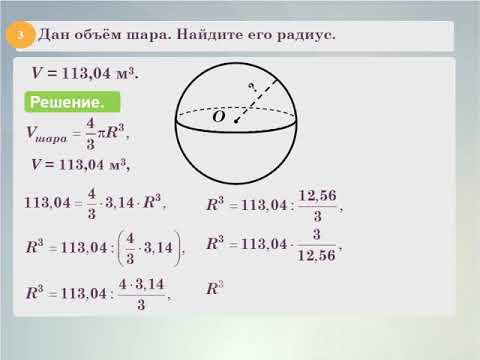 Поскольку d (диаметр) равен двум радиусам, то эту же формулу длины окружности можно записать как p=2πr.Рассмотрим применение формулы на примере простых задач:
Поскольку d (диаметр) равен двум радиусам, то эту же формулу длины окружности можно записать как p=2πr.Рассмотрим применение формулы на примере простых задач:
Задача 1
У основания царь-колокола диаметр равен 6,6 метров. Какова длина окружности основания колокола?
- Итак, формула для вычисления окружности — p= πd
- Подставляем имеющееся значение в формулу: p=3,14*6,6= 20,724
Ответ: длина окружности основания колокола 20,7 метра.
Задача 2
Искусственный спутник Земли вращается на расстоянии 320 км от планеты. Радиус Земли – 6370 км. Какова длина круговой орбиты спутника?
- 1.Вычислим радиус круговой орбиты спутника Земли: 6370+320=6690 (км)
- 2.Вычислим длину круговой орбиты спутника по формуле: P=2πr
- 3.P=2*3,14*6690=42013,2
Ответ: длина круговой орбиты спутника Земли 42013,2 км.
Способы измерения длины окружности
Вычисление длины окружности на практике используется не часто. Причиной тому приблизительное значение числа π. В быту для поиска длины круга используют специальный прибор – курвиметр. На окружности отмечают произвольную точку отсчета и ведут от нее прибор строго по линии, пока опять не дойдут до этой точки.
В быту для поиска длины круга используют специальный прибор – курвиметр. На окружности отмечают произвольную точку отсчета и ведут от нее прибор строго по линии, пока опять не дойдут до этой точки.
Как найти длину окружности? Нужно просто держать в голове незамысловатые формуля для вычислений.
1. Сложнее найти длину окружности через диаметр , по этому сначала разберём этот вариант.
Пример: Найдите длину окружности диаметр которой равен 6 см . Мы используем приведённую выше формулу длины окружности, только сначала нам необходимо найти радиус. Для этого мы делим диаметр 6 см на 2 и получаем радиус окружности 3 см.
После этого всё предельно просто: Умножаем число Пи на 2 и на полученный радиус в 3 см.
2 * 3,14 * 3 см = 6,28 * 3см = 18,84 см.
2. А теперь ещё раз разберём простой вариант найдите длину окружности радиус равен 5 см
Решение: Радиус 5 см умножаем на 2 и умножаем на 3,14. Не пугайтесь, ведь перестановка местами множителей не влияет на результат, и формулу длины окружности можно применять в любой последовательности.
5см * 2 * 3,14 = 10 см * 3,14 = 31.4 см — это найденная длина окружности для радиуса 5 см!
Онлайн калькулятор длины окружности
Наш калькулятор длины окружности произведёт все эти не хитрые вычисления мгновенно и распишет решение в строку и с комментариями. Мы рассчитаем длину окружности для радиуса 3, 5, 6, 8 или 1 см, или диаметр равен 4, 10, 15, 20 дм, нашему калькулятору без разницы для какого значения радиуса найти длину окружности.
Все вычисления будут точными, оттестированными специалистами математиками. Результаты можно использовать в решении школьных задач по геометрии или математике, а также при рабочих расчётах в строительстве или в ремонте и отделке помещений, когда требуются точные вычисления по этой формуле.
Радиус и диаметр — Математика с мамой
Радиус и диаметрExampleVideoQuestionsLesson
Share to Google Classroom
ExampleVideoQuestionsLesson
Share to Google Classroom
- Центр круга показан маленькой черной точкой.

- Радиусом называется любая линия, которая проходит между центром и краем круга.
- Радиус круга может идти в любом направлении.
- Все радиусы одной и той же окружности всегда будут иметь одинаковую длину.
- Это потому, что расстояние от центра до края всегда одинаково для каждого круга.
- Диаметром является любая линия, идущая от одной стороны круга к другой, и она должна проходить через центр круга.
- Диаметр вдвое больше радиуса.
- Мы говорим, что Диаметр = 2 × Радиус.
- Если мы знаем длину радиуса, мы можем удвоить ее, чтобы получить длину диаметра.
- Если мы знаем длину диаметра, мы можем разделить его пополам, чтобы получить длину радиуса.
Радиус — это любая линия от центра до края круга.
Диаметр — это любая линия от одной стороны круга до другой, проходящая через центр.
Что такое радиус круга?
Радиус круга — это любая линия, соединяющая центр круга с его краем.
Радиус равен половине расстояния от одной стороны круга до другой и, следовательно, равен половине диаметра.
Неважно, в каком направлении находится радиус. Это означает, что у каждого круга может быть много разных линий, которые являются радиусом.
Вот еще один пример радиуса, показанного на той же окружности.
Вот еще один пример радиуса, снова показанный на той же окружности.
Чтобы сказать более одного радиуса, мы говорим радиусов .
Мы видим, что все радиусы имеют одинаковую длину. Это потому, что каждый радиус — это просто расстояние от центра до внешнего края.
Каков диаметр круга?
Диаметром круга называется любая линия, проходящая от одной стороны круга к другой через центр круга.
Диаметр в два раза больше радиуса окружности.
Диаметр проходит прямо через окружность, но он должен проходить прямо через центральную точку.
Неважно, в каком направлении идет диаметр, однако диаметр должен представлять собой непрерывную прямую линию. Он не может изменить направление.
У круга может быть много разных диаметров. Вот еще один пример диаметра.
Диаметр наибольшая
хордаЛюбая линия, соединяющая две точки на краю круга.
круга, потому что он проходит прямо через центр круга.
Как получить диаметр из радиуса
Диаметр в два раза больше длины радиуса. Следовательно, если вы знаете радиус, умножьте его на 2, чтобы найти диаметр.
Можно сказать, что диаметр = 2 × радиус.
Например, если радиус равен 4 см, то мы можем умножить его на 2, чтобы найти диаметр.
2 × 4 см = 8 см, значит, диаметр этого круга равен 8 см.
Мы видим, что два радиуса по 4 см составляют диаметр, длина которого составляет 8 см.
Если нам говорят радиус круга, мы просто удваиваем его, чтобы найти диаметр.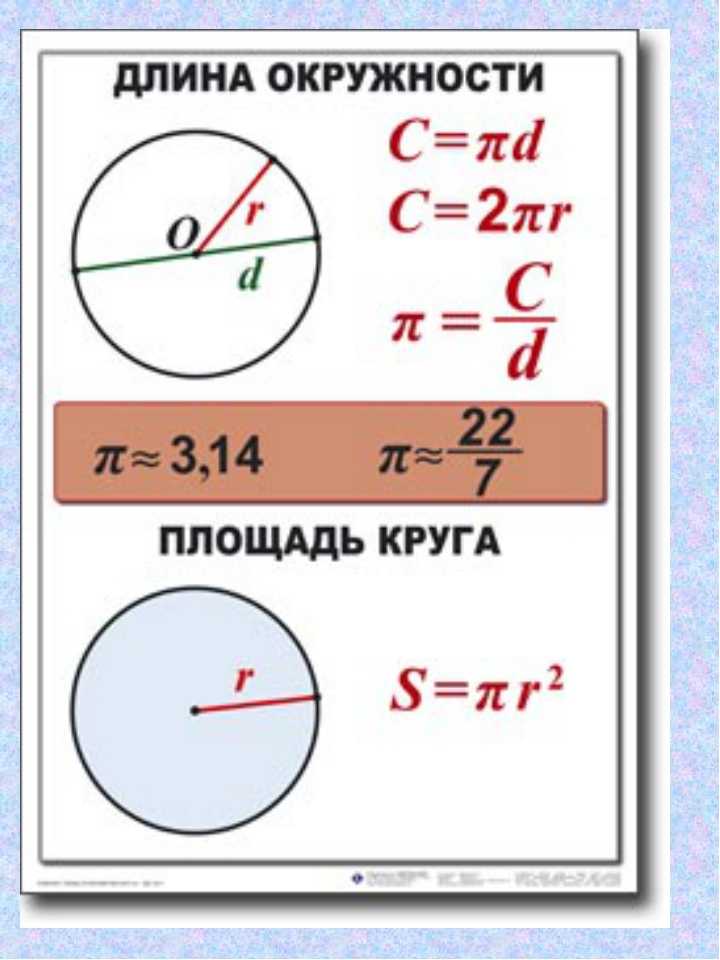
Это потому, что радиус находится на половине пути от центра круга, а диаметр — на всем пути через круг, проходящий через центр.
Как получить радиус из диаметра?
Радиус круга равен половине его диаметра. Если мы знаем диаметр, мы делим его пополам, чтобы найти радиус.
Можно сказать, что радиус = 1 / 2 × диаметр.
Например, в этом круге диаметр равен 10 м.
10 м — это расстояние от одной стороны до другой, проходящее через центр круга.
Радиус равен половине этого расстояния.
Радиус равен 1 / 2 × 10.
Половина 10 равна 5, значит, радиус равен 5 м.
Это потому, что диаметр составляет весь путь, а радиус — только половину пути.
Соотношение, что радиус равен половине диаметра, а диаметр в два раза больше радиуса, всегда верно для всех окружностей.
какова площадь круга радиусом 6 дюймов?
Вот ответ на вопросы типа: как найти площадь круга радиусом 6 дюймов?
| ||||||||||||
Площадь круга радиусом 6 это 113.1 | |
Изображение кружка = 6d = 12C = 37,7 | А = πr 2 = π(d2) 2 А = С 2 4π π = 3,1415A = площадь C = окружность или периметр r = радиус , d = диаметр |
Площадь круга в пересчете на
радиус :Площадь = π·r 2 = 3,14·6 2 = 113,1 квадратных дюймов (*)
Площадь круга относительно
диаметра :Площадь = π·(d2) 2 = 3,14·(122) 2 = 3,14·(6) 2 = 113,1 квадратных дюймов (*)
Площадь круга относительно
длины окружности :Площадь = С 2 4π = 37,7 2 4π = 1421,29(4·3,14) = 1421,2912,56 = 113,1 квадратных дюймов (*)
(*) 113,09733552923 дюймов, точно или ограничено точностью этого калькулятора (13 знаков после запятой).
Примечание: для простоты указанные выше операции были округлены до 2 знаков после запятой, а число π округлено до 3,14.
Окружность радиусом = 6 или диаметром = 12 или окружностью = 37,7 дюйма имеет площадь:
- 7.29676 × 10 -8 квадратных километров (км²)
- 0,0729676 квадратных метров (м²)
- 729,676 квадратных сантимеров (CM²)
- 72967,676 квадратных сантиметров (CM²)
- 72967,6,676 квадратных сантеров (CM²)
- 72967,6,67,676. (ми²)
- 0,0872685 квадратных ярдов (ярдов²)
- 0,785417 квадратных футов (фут²)
- 113,1 квадратных дюймов (дюйм²)
Используйте приведенный ниже калькулятор площади круга, чтобы найти площадь круга по заданному радиусу или другим параметрам. Для расчета площади вам достаточно ввести положительное числовое значение в одно из 3-х полей калькулятора. Вы также можете увидеть в нижней части калькулятора пошаговое решение.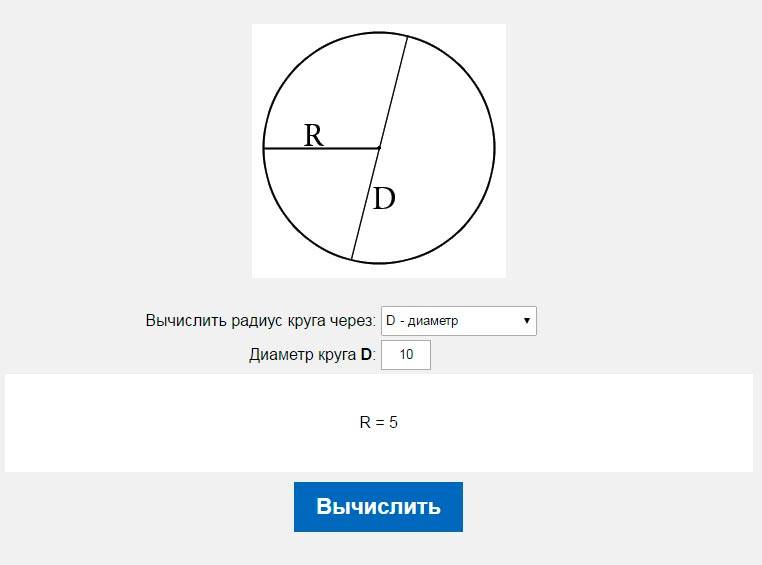
Формула площади круга
Вот три способа нахождения площади круга (формулы):
Формула площади круга в пересчете на радиус
A = πr 2
Формула площади круга в пересчете на радиус диаметр
A = π(d2) 2
Формула площади круга в пересчете на длину окружности
A = C 2 4π
См. ниже некоторые определения, относящиеся к формулам: расстояние вокруг края круга.
Радиус
Радиусом круга является любой из отрезков прямой от его центра до периметра. Радиус равен половине диаметра или r = d2.
Диаметр
Диаметром окружности называется любой отрезок прямой линии, проходящий через центр окружности и концы которого лежат на окружности. Диаметр в два раза больше радиуса или d = 2·r.
Греческая буква π
π обозначает число Пи, которое определяется как отношение длины окружности к ее диаметру или π = Cd
. Для простоты можно использовать Pi = 3,14 или Pi = 3,1415.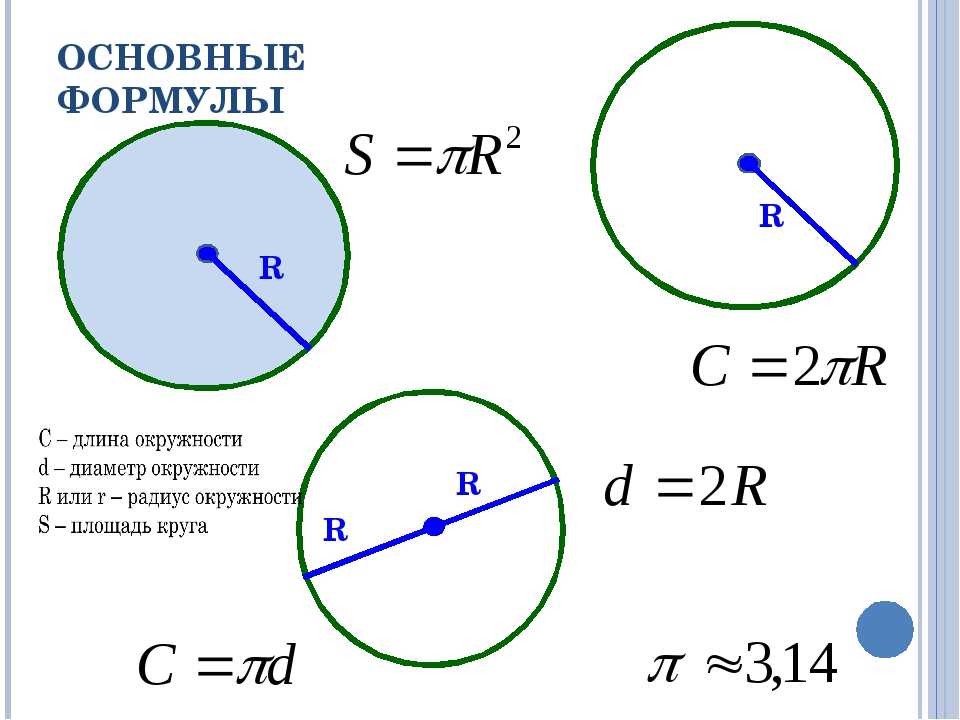



 изм:
изм: