№ 1097 Математика 6 класс Виленкин. Помогите найти расстояние между точками! – Рамблер/класс
№ 1097 Математика 6 класс Виленкин. Помогите найти расстояние между точками! – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Найдите расстояние между точками А(а) и В(b), если:
а) а = 2, b = 8; в) а = -1, b = 6; д) а = 3,2, b = -4,7;
ответы
а) 8 — 2 = 6;
б) -3 — (-5) = -3 + 5 = 3;
в) 6 — (-1) =6 + 1 = 7;
г) 5 — (-4)= = 5 + 4 = 9;
д) 3,2 — (-4,7) = 3,2 + 4,7 = 7,9;
е) -2,5 — (-8,1) = -2,5 + 8,1 = 5,6.
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Психология
3 класс
5 класс
Репетитор
похожие вопросы 5
Приветик! Кто решил? № 411 Математика 6 класс Виленкин.
Выполните вычисления с помощью микрокалькулятора и резуль-
тат округлите до тысячных:
3,281 ∙ 0,57 + 4,356 ∙ 0,278 — 13,758 (Подробнее…)
ГДЗМатематика6 классВиленкин Н.Я.
678. Изобразите этот круг, проведите диаметр, радиус и укажите их длины.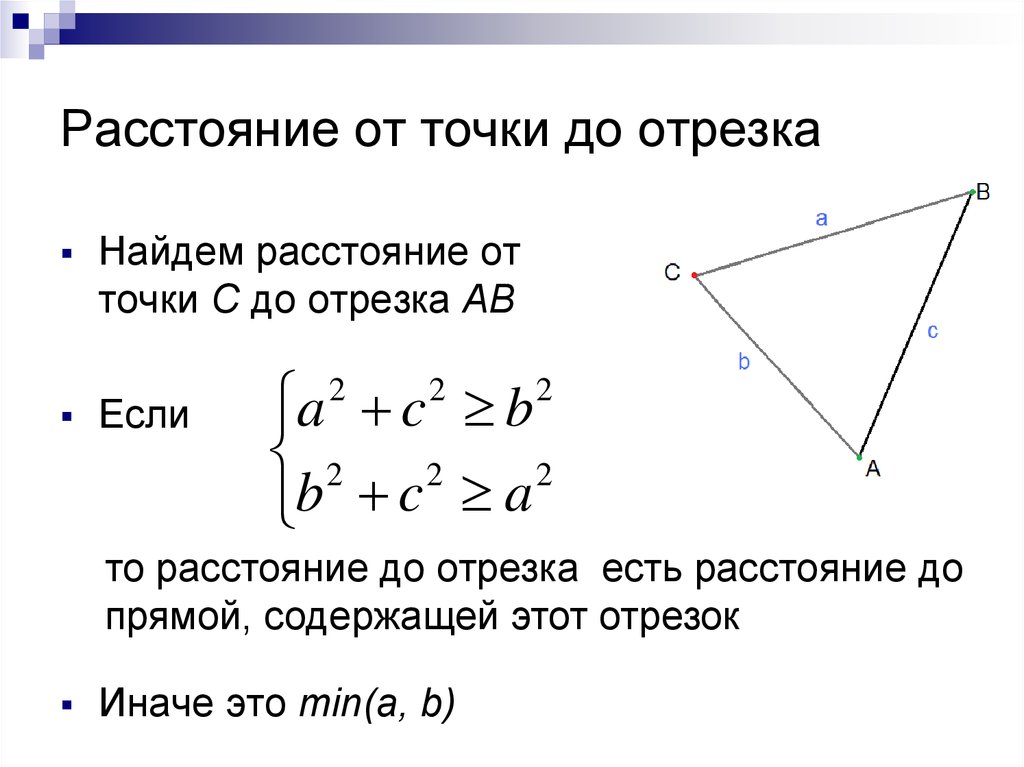
6 класс Мордкович математика ГДЗ
678. Площадь круга равна:
а) 28,26 см2; б) 113,04 см2; в) 0,5024 дм2; г) 78,5 см2.
Изобразите этот круг, (Подробнее…)
ГДЗМордкович А.Г.Алгебра6 класс
Помогите установить соответствие между неравенствами. Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№17. Под руководством Ященко И.В.
Здравствуйте! Помогите установить соответствие между неравенствами и их решениями: (Подробнее…)
ЕГЭЭкзаменыМатематикаЯщенко И.В.
Помогите выбрать утверждения. Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№18. Под руководством Ященко И.В.
ЕГЭЭкзаменыМатематикаЯщенко И.В.
11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И.
П. ГДЗ. Вариант 12.
11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
Как найти расстояние от точки до точки
На первый взгляд может показаться, что математика сложна и коварна, но это далеко не так. Если приложить усилия к её изучению, то можно удивиться тому, насколько быстро вы измените своё мнение о ней. Давайте же разберём одну из тем, которая поможет находить расстояние от точки до точки при различных условиях. После того как вы изучите данную статью, вы можете решить предоставленные задания, чтобы лучше закрепить пройденный материал.
Математические термины
Для начала введём некоторые определения.
Определения
Расстояние между точками – это измерение отрезка, находящегося между этими точками, составляющего длину расстояния.
Эти отрезки располагаются в определенном масштабе, потому как необходимо знать единицу длины для их измерения, без этого нельзя.
Функция – это связь величин, выражаемая в зависимости одной переменной Y, от второй переменной X.
Произвольная функция (точка) – это такая точка, которую можно расположить в любом месте.
Координатная прямая – это прямая, на которой изображают точку отсчёта 0 и единичные отрезки. Прямой также задают направление.
Действительные числа – это совокупность рациональных и иррациональных чисел.
Рациональное число – это такое число, которое может находиться в виде обыкновенной дроби, в отличие от иррационального числа.
Иррациональное число – это бесконечная непериодическая десятичная дробь. Такое число нельзя представить в виде обыкновенной дроби.
Модуль или же абсолютная величина – это обязательно неотрицательное число, которое является расстоянием определённых точек.
Как определить расстояние между точками, находящимися на координатной прямой
Важно
Чтобы найти расстояние от одной точки до другой, т.
е. длину этого отрезка, нужно сравнить его с другим таким отрезком в заданном масштабе.
Действительные числа
Рассмотрим этот способ на примере:
Здесь мы имеем координатную прямую OX, на которой отмечена точка A. Она произвольная, поэтому мы можем задать ей любое действительное число, пусть это будет 3.
Отрезок – это единица длины, поэтому все отрезки, что мы отложили от точки O нужно сложить, вследствие чего полученное количество единичных отрезков будет равняться длине отрезка OA. В данном случае здесь три отрезка, поэтому и ответ таков.
Ещё один пример, где точку отсчёта O и произвольную точку A соединяют 2 отрезка. Это значит, что расстояние длин всех единичных отрезков OA равно 2. Если же точка A будет иметь другое число, например: 6, то мы откладываем от точки O именно 6 единичных отрезков и получаем искомое расстояние.
Рациональные числа
С действительным числами всё понятно, а что делать с рациональными? Представим, что координаты точки A равны 5,5.
Из этого следует, что нам нужно отложить из точки O сначала 5 единичных отрезков, то есть, целое число, а после прибавить 0,5. Иногда это кажется невозможным, ведь некоторые числа трудно представить в виде отрезка, из-за чего приходится искать самое приближенное значение числа.
Иррациональные числа
Иррациональным числам данный метод не подходит, потому как такие числа нельзя поставить на координатной прямой OX. Для примера приведём числа √5, √8, √17. Здесь можно перейти к отвлечённому представлению и посмотреть на эти числа таким образом:
- 0>A – если 0 больше A, то A имеет отрицательное значение координат: |OA| = (–A).
- 0<A – если 0 меньше A, то A имеет положительное значение координат: |OA| = (A).
Также можно сказать, что это подходит и к действительным числами. Если точка A будет находиться на начальной точке O, то и расстояние между ними будет равно 0. Здесь нужно уметь хорошо работать с рисунком, тогда всё будет понятно.
- Модуль
Важно помнить, что расстояние между точками не может быть отрицательным.
В данном случае у нас есть модуль числа A, что является расстоянием OA и это число 3.
Если на координатной прямой будут точки A и B, то их расстояние нужно определить по модулю разности этих координат. Получается, чтобы найти длину отрезка AB, необходимо из числа точки B отнять число точки A:
4-2=2.
Как определить расстояние между двумя точками на плоскости
Представим прямоугольную систему координат и плоскость на ней, с находящимися там точками A и B. Далее проведём прямые от этих точек к осям Ox и Oy, как на изображении. В следствие этого образовались точки Ax и Ay, а также Bx и By.
Из этого можно вывести несколько вариантов:
- Ось Ox
В случае расположения точек A и B на прямой, которая в свою очередь перпендикулярна оси Ox – точки A и B совпадают, а модуль AB равен модулю AyBy. Как говорилось ранее, для нахождения длины промежутка (расстояния) между двумя точками, нужно найти разность модуля заданных координат, поэтому можно сказать, что:
|AB| = |AyBy| = |yB – yA|.
{2}\]
- Точки не лежат на прямой, которая перпендикулярна оси Ox и Oy
Теперь поговорим о прямоугольном треугольнике ABC. Чтобы найти расстояние на плоскости между точкой A и точкой B, необходимо воспользоваться формулой:
|AB| = √(xB – xA)² + (yB – yA)².
Эта формула доказывает правильность ранее написанных утверждений к тем заданиям, на графиках которых точки лежат на прямой, перпендикулярной Ox и Oy.
Если точки совпадают, к ним справедливо равенство:
|AB| = √(xB – xA)² + (yB – yA)² = √0² + 0² = 0.
По рисунку видно, что:
|AC| = |AxBx|, а также |BC|=|AyBy|. Далее вспомним теорему Пифагора и с её помощью запишем равенство:
|AB|² = |AC|² + |BC|²
|AB|² = |AxBx|² + |AyBy|²
√|AxBx|² + |AyBy|²
√|xB – xA|² + |yB – yA|²
√(xB – xA)² + (yB – yA)²
Пример
Найдите расстояние между двумя точками на плоскости, если известно, что они находятся на прямоугольной системе координат со значениями: A (3, –1), а также B (X + 3, 7).
Также надо найти значение действительного числа X, зная, что при них расстояние между точками будет равно 10.
Чтобы решить эту задачу, необходимо использовать формулу:
|AB| = √(xB – xA)² + (yB – yA)².
После этого действия подставляем вышеприведённые числа:
√(X + 3 – 3)² + (7 – ( – 1))² = √X² + 64.
Далее обратим внимание на то, что |AB| = 10 и составим равенство:
√X² + 64 = 10
X² + 64 = 100
X = ± 6
Ответ: |AB| = 10, при X = ±6.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Как определить расстояние между точками в пространстве
Более сложным заданием на нахождение расстояния является то, где точки расположены в пространстве, а не на плоскости.
Возьмём точки, имеющие свои координаты: A (xA, yA, zA), B (xB, yB, zB). Они размещены на прямоугольной системе координат Oxyz. Имея эти данные, мы можем приступить к поиску расстояния между этими точками.
{2}\]
После чего выполним такие действия:
|AxBx| = |xB – xA|
|AyBy| = |yB – yA|
|AzBz| = |zB – zA|
Теперь выполним преобразование получившегося выражения:
|AB|² = |AxBx|² + |AyBy|² + |AzBz|² = |xB – xA|² + |yB – yA|² + |zB – zA|² = (xB – xA)² + (yB – yA)² + (zB – zA)².
После всех этих действий мы можем выделить основную формулу, которая применяется для нахождения расстояния точек в пространстве:
=√(xB – xA)² + (yB – yA)² + (zB – zA)².
Её можно применять в тех случаях, когда точки располагаются на прямой, которая параллельна координатной оси или же они находятся на этой координатной оси. При совпадении точек эта формула также действительна.
Пример
Найдите расстояние между точками, которые лежат на прямоугольной системе координат в трёхмерном пространстве, координаты которых: A (2, 3, 4), а также B (-6, -1, 5).
Перейдём к решению, воспользовавшись формулой:
√(xB – xA)² + (yB – yA)² + (zB – zA)².
Подставляем имеющиеся значения:
√(–6 – 2)² + (–1 – 3)² + (5 – 4)² = √64 + 16 + 1 = √81 = 9.
Ответ: расстояние |AB| равно 9.
Задачи для самостоятельного решения
- Задача
Найдите расстояние между точками на плоскости, если известно, что они находятся на прямоугольной системе координат со значениями: A (2, 5), а также B (6, 4). - Задача
Найдите расстояние между точками на плоскости, если известно, что они находятся на прямоугольной системе координат со значениями: A (1, 6), а также B (1, 25).
- Задача
Найдите расстояние между точками, которые лежат на прямоугольной системе координат в трёхмерном пространстве, координаты которых: A (1, -3, 4), а также B (4, 1, 4). - Задача
Найдите расстояние между точками, которые лежат на прямоугольной системе координат в трёхмерном пространстве, координаты которых: A (2, -2, 7), а также B (6, 2, 5).
Ответы с решением:
- Решение первой задачи
Для решения понадобится формула:
|AB| = √(xB – xA)² + (yB – yA)².
Далее подставляем числа:
|AB| = √(6 – 2)² + (4 – 5)² = √4² + (–1)² = √16 + 1 = √17.
Ответ: |AB| равен √17. - Решение второй задачи
Формула для нахождения:
|AB| = √(xB – xA)² + (yB – yA)².
Подставляем:
Ответ: |AB| равен 19. - Решение третьей задачи
Запишем формулу:
√(xB – xA)² + (yB – yA)² + (zB – zA)².
Подставим числа:
√(4 – 1)² + (1 – (–3))² + (4 – 4)² = √(3)² + (4)² + (0)² = √9 + 16 + 0 = √25 = 5.
Ответ: |AB| равняется 5. - Решение четвертой задачи
Записываем формулу для решения:
√(xB – xA)² + (yB – yA)² + (zB – zA)²
Заменим на координаты точек:
√(6 – 2)² + (2 – (–2))² + (5 – 7)² = √(4)² + (4)² + (–2)² = √16 + 16 + 4= √36 = 6.
Ответ: |AB| равняется 6.
Видео-вопрос: Расчет расстояния между двумя точками по формуле расстояния
Стенограмма видео
Какая из следующих точек находится на расстоянии пяти корней два от начала координат? (А) Ноль, пять; (Б) пять, ноль; (C) пять корней два, пять корней два; или (Д) пять, пять.
Итак, нам дали координаты четырех точек и попросили определить, какая из этих точек находится на заданном расстоянии в пять корней две единицы от начала координат. Рассмотрим, как найти расстояние общей точки с координатами 𝑥, 𝑦 от начала координат. Мы обозначим это расстояние по прямой как 𝑑. Мы можем нарисовать прямоугольный треугольник, и расстояние от точки до начала координат будет равно длине гипотенузы этого треугольника. Если мы знаем координаты этой точки, мы можем вычислить значение 𝑑, применив теорему Пифагора, которая гласит, что в прямоугольном треугольнике сумма квадратов двух более коротких сторон равна квадрату гипотенузы.
Теперь длина горизонтальной стороны в этом конкретном треугольнике равна 𝑥, потому что это расстояние по оси 𝑥. А длина вертикальной стороны равна 𝑦; это расстояние по оси 𝑦. Таким образом, применяя теорему Пифагора, мы получаем, что 𝑑 в квадрате равно 𝑥 в квадрате плюс 𝑦 в квадрате. Извлекая квадратный корень из обеих частей этого уравнения, мы получаем, что 𝑑 равно квадратному корню из 𝑥 в квадрате плюс 𝑦 в квадрате.
Теперь предположим, что точка находится в другом квадранте. Предположим, например, что это было во втором квадранте, где 𝑥 отрицательно, а 𝑦 положительно. На этот раз длина горизонтальной стороны треугольника будет равна абсолютной величине 𝑥. Но когда мы возводим в квадрат абсолютное значение 𝑥, это то же самое, что 𝑥 в квадрате. Таким образом, формула, которую мы только что записали, будет работать независимо от того, в каком квадранте находится интересующая нас точка или даже если она находится на любой из осей координат.
По сути, эта формула является частным случаем более общей формулы для расчета расстояния между любыми двумя точками. Предположим, у нас есть две точки с координатами 𝑥 один, 𝑦 один и 𝑥 два, 𝑦 два. Если начертить прямоугольный треугольник ниже линии, соединяющей эти две точки, то длина горизонтальной стороны будет разницей между 𝑥-координатами. Это 𝑥 два минус 𝑥 один. А длина вертикальной стороны будет разностью 𝑦-координат. Это 𝑦 два минус 𝑦 один.
Квадратный корень с обеих сторон, мы имеем, что 𝑑 равно квадратному корню из 𝑥 двух минус 𝑥 один в квадрате плюс 𝑦 два минус 𝑦 один в квадрате. А это общая формула расстояния для нахождения расстояния между любыми двумя точками на координатной сетке, которую мы должны запомнить. Теперь в этой задаче мы конкретно находим расстояние между каждой точкой и началом координат, которое имеет нулевые координаты. Таким образом, заменив ноль на 𝑥 единицу и 𝑦 единицу и 𝑥, 𝑦 на координаты каждой точки, мы увидим, что формула расстояния упростится до формулы, которую мы записали ранее. Итак, все, что нам нужно сделать, это подставить координаты каждой точки в эту формулу и посмотреть, что дает нам ответ из пяти корней из двух.
Тогда начнем с варианта (А). И мы имеем, что расстояние между этой точкой и началом координат, 𝑑 sub 𝐴, равно квадратному корню из нуля в квадрате плюс пять в квадрате. Это квадратный корень из нуля плюс 25 или просто квадратный корень из 25, то есть пять. Таким образом, точка (A) не является правильным расстоянием от начала координат.
Рассмотрим точку (B). Для точки (B) расстояние равно квадратному корню из пяти в квадрате плюс ноль в квадрате. Опять же, это квадратный корень из 25, который равен пяти. На самом деле, для каждой из этих точек мы можем увидеть, что их расстояние от начала координат составляет пять единиц, просто нарисовав их на координатной сетке, так как каждая точка лежит на одной из координатных осей.
Далее рассмотрим точку (C). И на этот раз расстояние от начала координат равно квадратному корню из пяти корней из двух в квадрате плюс пять корней из двух в квадрате. Помните, пять корней два в квадрате означает пять корней два, умноженных на пять корней два, что мы можем записать как пять умножить на пять умножить на корень на два умножить на корень два.