Как найти синус и косинус и тангенс угла: Синус, косинус и тангенс угла — урок. Геометрия, 9 класс.

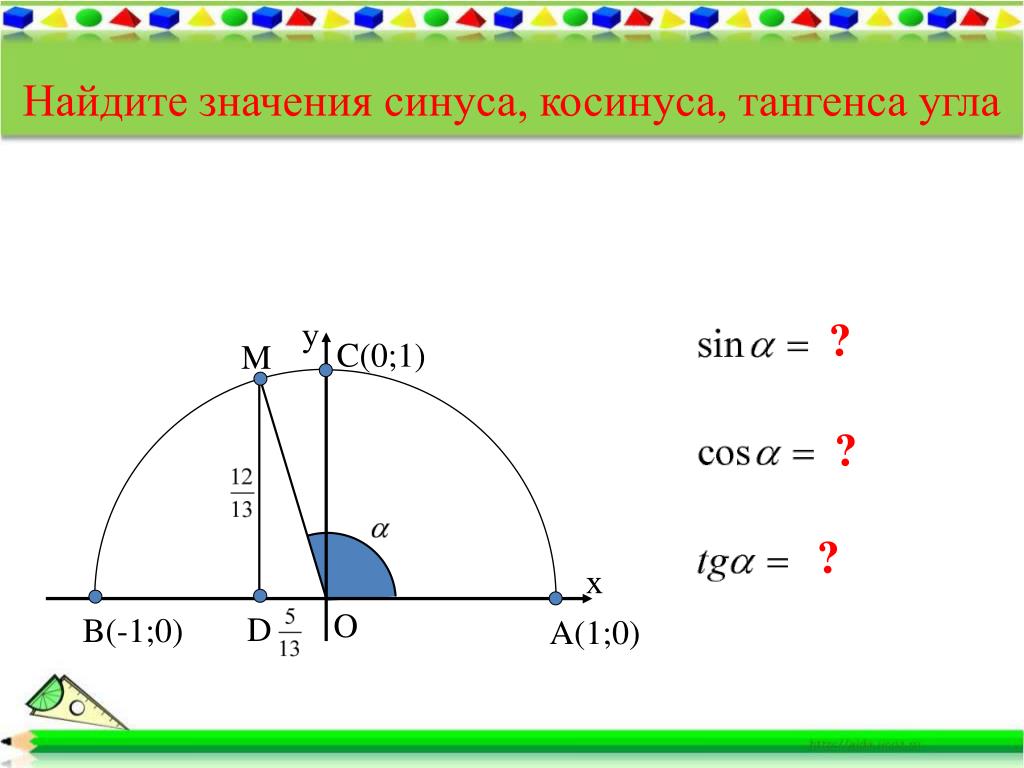
Найти синус, косинус и тангенс в таблицах Google

Тригонометрические функции —  синус ,  косинус и тангенс — основаны на прямоугольном треугольнике (треугольник, содержащий угол, равный 90 градусам).

В математическом классе эти тригонометрические функции находятся с использованием различных тригонометрических соотношений, сравнивающих длину соседних и противоположных сторон треугольника с длиной гипотенузы или друг с другом.

В  таблицах Google эти триггерные функции можно найти с помощью функций SIN, COS и TAN для углов, измеренных в  радианах .

01

из 03

Градусы против радианов

Использование вышеупомянутых тригонометрических функций в таблицах Google может быть проще, чем делать это вручную, но, как уже упоминалось, важно понимать, что при использовании этих функций угол должен измеряться в  радианах,  а не в  градусах,  что является наиболее с нами не знакомы.

Радианы связаны с радиусом круга, причем один радиан приблизительно равен 57 градусам.

Чтобы упростить работу с функциями триггера, используйте функцию РАДИАНЫ в Google Spreadsheets, чтобы преобразовать измеряемый угол из градусов в радианы, как показано в ячейке B2 на изображении выше, где угол 30 градусов преобразуется в 0,5235987756 радиан.

Другие варианты для преобразования из градусов в радианы включают в себя:

• вложение функции RADIANS внутрь функции SIN — как показано в строке 3 в примере;
• используя функцию PI Google Spreadsheets   в формуле:  угол (градусы) * PI () / 180,  как показано в строке 4 в примере.

 

02

из 03

Синтаксис триггерных функций и аргументы

Синтаксис функции   относится к макету функции и включает в себя имя  функции  , скобки и  аргументы .

Синтаксис для функции SIN:

= SIN (угол)

Синтаксис для функции COS:

= COS (угол)

Синтаксис для функции TAN:

= TAN (угол)

угол — вычисляемый угол — измеряется в радианах
— для этого аргумента можно ввести размер угла в радианах или, альтернативно,  ссылку ячейки  на местоположение этих данных в  рабочем листе .

Пример: использование функции SIN Google Spreadsheets

Этот пример охватывает шаги, используемые для ввода функции SIN в ячейку C2 на изображении выше, чтобы найти синус угла 30 градусов или 0,5235987756 радиан.

Те же шаги можно использовать для вычисления косинуса и тангенса для угла, как показано в строках 11 и 12 на изображении выше.

Google Spreadsheets не использует  диалоговые окна  для ввода аргументов функции, которые можно найти в Excel. Вместо этого у него есть поле 

автоматического предложения,  которое появляется при вводе имени функции в ячейку.

1. Нажмите на ячейку C2, чтобы сделать ее  активной ячейкой  — здесь будут отображаться результаты функции SIN;
2. Введите знак равенства (=), за которым следует имя функции  sin;
3. По мере ввода   появляется окно автоматического предложения с именами функций, которые начинаются с буквы S;
4. Когда в поле  появится имя  SIN , нажмите на имя указателем мыши, чтобы ввести имя функции и открыть круглые или круглые скобки в ячейке C2.

03

из 03

Ввод аргумента функции

Как видно на рисунке выше, аргумент для функции SIN вводится после открытой круглой скобки.

1. Нажмите на ячейку B2 на рабочем листе, чтобы ввести эту ссылку на ячейку в качестве   аргумента угла ;
2. Нажмите  клавишу Enter  на клавиатуре, чтобы ввести закрывающую скобку «  )  » после аргумента функции и завершить функцию;
3. Значение 0,5 должно появиться в ячейке C2 — это синус угла 30 градусов;
4. При нажатии на ячейку C2 полная функция  = SIN (B2)  появляется на  панели формул  над рабочим листом.

#СТОИМОСТЬ! Ошибки и пустые ячейки

Функция SIN отображает #  ЗНАЧЕНИЕ!  ошибка, если ссылка, используемая в качестве аргумента функции, указывает на ячейку, содержащую текст. В пятой строке приведенного выше примера вы можете увидеть это, когда ссылка на ячейку указывает на текстовую метку:  Угол (Радианы).

Если ячейка указывает на пустую ячейку, функция возвращает нулевое значение (см. Строку шесть выше). Тригонные функции Google Spreadsheets интерпретируют пустые ячейки как ноль, а синус нулевых радиан равен нулю.

 

Как калькулятор находит синус угла?

В этом уравнении следует отметить две вещи:

1. Чтобы найти синус, нам нужно работать с многочленом, и
2. Этот многочлен бесконечен. Калькулятор будет только оценивать ответ, поэтому, чем сложнее наш калькулятор, тем больше знаков после запятой он сможет отображать. (Для тех из нас, кто не знаком с восклицательным знаком, используемым в этом уравнении, у меня есть еще один блог о факториальной функции.)

Процесс преобразования синусоидальной функции в многочлен выше называется разложением в ряд Тейлора или Маклорена; это полезный инструмент, который преподается в углубленном исчислении (студенты, изучающие AP Исчисление BC или Анализ и подход более высокого уровня в IB, изучат его в ходе курса).

Давайте посмотрим, как теперь мы можем «вычислить» синус произвольного угла с помощью простого четырехфункционального калькулятора (который может только складывать, вычитать, умножать и делить).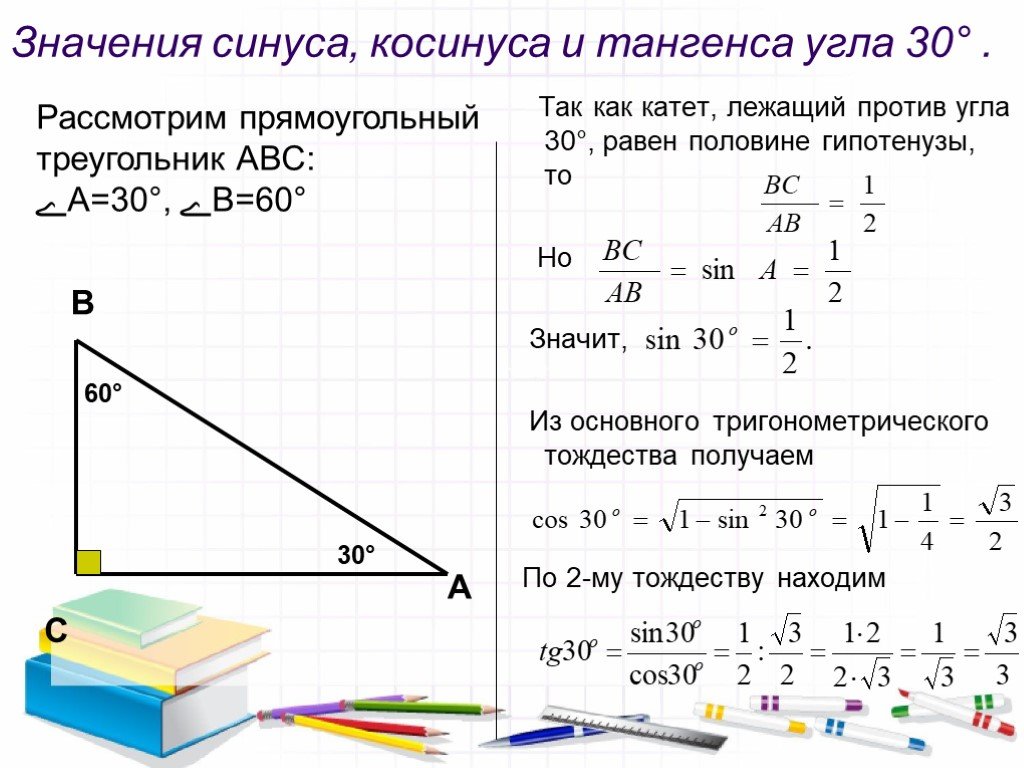

Сначала мы придумаем угол. Возьмем 53°. Для справки, результат синуса 53° равен 0,79663551005… Поскольку в большинстве вопросов нам потребуется округлить только до трех значащих цифр, давайте округлим его до 4 ст.ф. в качестве сравнения, что даст нам эталонное значение 0,7966.

Используя только стандартный калькулятор с четырьмя функциями, мы сначала переведем угол из градусов в радианы. Для этого нам нужно будет умножить 53 на π, а затем разделить на 180. Поскольку в большинстве четырехфункциональных калькуляторов нет числа π, мы оценим его, используя 3,14159.. Таким образом, угол в радианах следует оценивать как 0,925023722.

Далее применим расширение. Мы будем работать только с первыми тремя терминами, чтобы увидеть, насколько близко мы подходим.

Нахождение результата факториала должно быть довольно простым даже с помощью калькулятора с четырьмя функциями, так как нам просто нужно умножать по одному числу за раз. В данном случае 3! = 6 и 5! = 120.

Самая сложная часть — мощность. Опять же, большинство четырехфункциональных калькуляторов не имеют функции «степени». Тем не менее, большинство этих калькуляторов имеют встроенный короткий путь для нахождения результата степени положительного целого числа. Для этого вы дважды нажимаете кнопку умножения, а затем нажимаете знак равенства «n» минус один раз, где «n» — это степень, которую мы ищем. Например, чтобы найти 4

5 , мы начинаем с 4, затем дважды нажимаем кратное и четыре раза нажимаем равно. Таким образом, мы должны получить следующее:

x = 0,925023722

x ³ = 0,791514017

x ⁵ = 0,677273917

Наконец, мы рассчитываем результат второго и третьего срока:

2 ⁷⁷ term = 0,791514017 / 6 = 0,131919002

              3 ^rd term = 0,677273917 / 120 = 0,005643943

0003

0,925023722 – 0,131919002 + 0,005643943 = 0,798748664

По сравнению с округленным значением 0,7966 (4 ст.ф.), мы видим, что результат, скорее всего, будет считаться неверным. Это может быть связано с округлением при расчете каждого шага и с тем, что мы используем только три члена для оценки ответа.

В конце концов, никому из нас не будет смысла делать это вручную. Калькуляторы в настоящее время могут обрабатывать числа с молниеносной скоростью, поэтому мы должны просто позволить им выполнять тяжелую работу. Интересно то, что какой бы сложной или продвинутой ни была концепция в математике, по своей сути она все равно, скорее всего, является набором арифметических операций.

Тригонометрические соотношения

Мы повеселились с треугольниками и катетами, Пифагором и его изобретением, показателями и квадратными корнями. А если серьезно, то это не лежит в основе триггера.

Настоящие триггеры крутятся под звуки синуса, косинуса и тангенса.

Что сказать?

Три основных тригонометрических соотношения: синус , косинус и тангенс .

Оставайтесь с нами. Мы не говорим на другом языке (если вы не считаете латынь другим языком).

Их аббревиатуры/прозвища: sin, cos и tan. Хороший способ запомнить их определения — это странная аббревиатура:

SOHCAHTOA

Давайте посмотрим, как этот парень работает с прямоугольным треугольником:

SOH означает S posite 006 0 ine0s сторона над H ypotenuse:

 

CAH означает C осин равен A смежной стороне над ч ypotenuse:

TOH Стоимость T Angent Equals O PPOSIT треугольников. Если в вашем треугольнике нет прямого угла, все ставки сняты.

Пример задачи

Если a = 8 и b = 15 в следующем прямоугольном треугольнике, найдите синус, косинус и тангенс угла А .

Сначала используйте a ² + b ² = c ² , чтобы найти c , гипотенузу.

c ² = 8 ² + 15 ²

c ² = 64 + 225

c ² = 289

c = 17

Now давайте подставим c = 17 в наши отношения (о нет, не те же снова) для sin, cos и tan.

Пример задачи

В следующем треугольнике найдите синус, косинус и тангенс угла B .

Если B сбивает вас с толку, не волнуйтесь. Вы по-прежнему применяете коэффициенты таким же образом. Синус по-прежнему находится напротив гипотенузы и так далее.

Но сначала нам нужна недостающая нога. Мы знаем другой катет и гипотенузу, поэтому мы можем использовать Пифагора, чтобы найти и .

a ² = c ² – b ²
a ² = 29 ² – 20 ²
a ² = 841 – 400
a ²

= 441
a = 21

Относительно угла B 20 — противолежащая сторона, 21 — прилежащая сторона, а 29 — гипотенуза.