| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |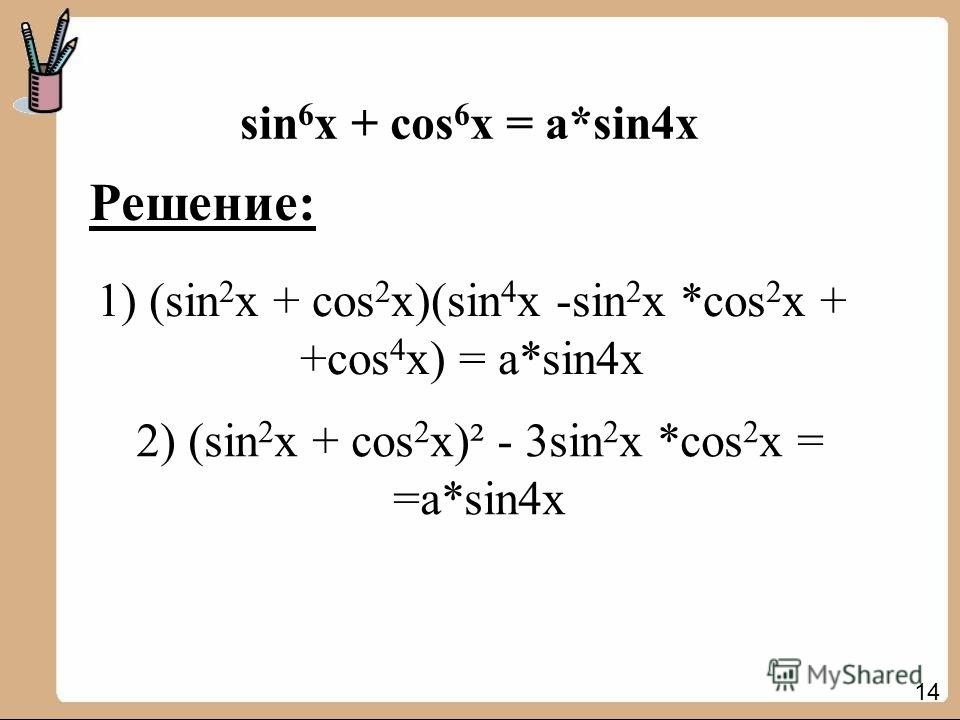
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |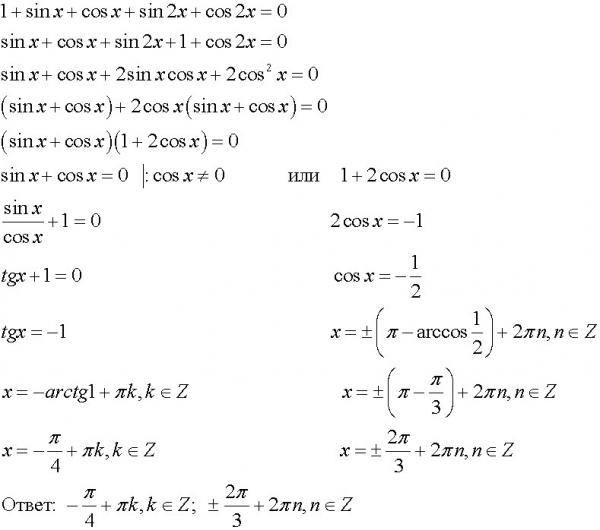
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |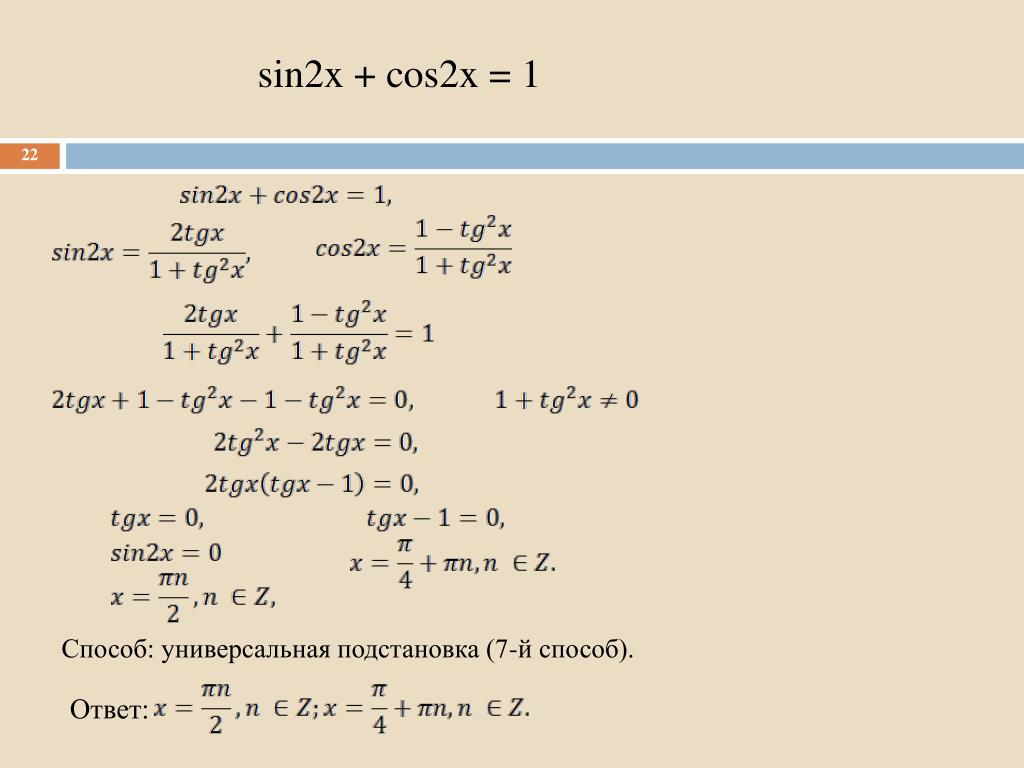
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | ||
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |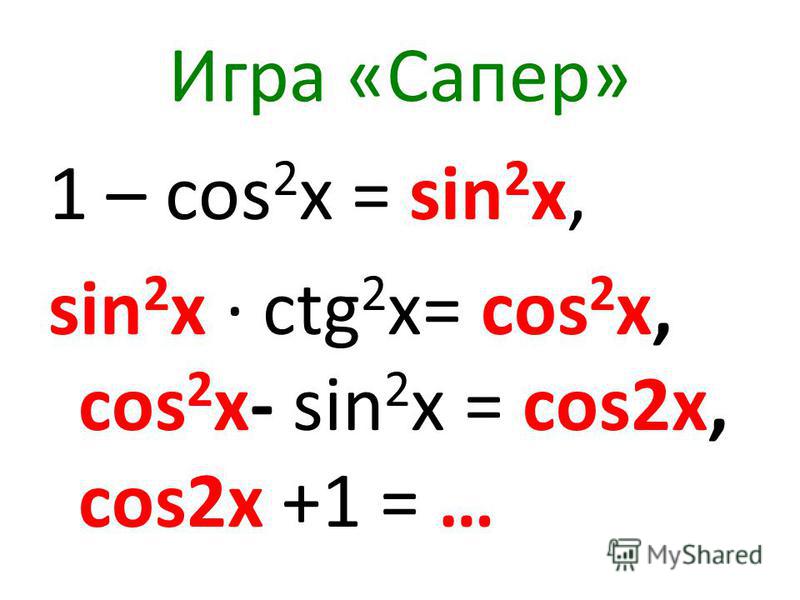
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | sin(120 град. ) | ||
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Разложение на множители. — Студопедия
Поделись
Пример. Решить уравнение: sinx+cosx=1sinx+cosx=1.
Решение. Перенесем влево все члены равенства: sinx+cosx−1=0sinx+cosx-1=0. Используя формулы двойного угла, преобразуем и разложим на множители левую часть:
sinx—2sin2 x2=0sinx—2sin2 x2=0,
2sin x2cos x2−2sin2 x2=02sin x2cos x2-2sin2 x2=0,
2sin x2(cos x2−sin x2)=02sin x2(cos x2-sin x2)=0,
1.
sin x2=0sin x2=0, x2=πnx2=πn, x1=2πnx1=2πn.
2. cos x2−sin x2=0cos x2-sin x2=0, tg x2=1tg x2=1, x2=arctg1+πnx2=arctg1+πn, x2=π4+πnx2=π4+πn, x2=π2+2πnx2=π2+2πn.
Ответ: x1=2πnx1=2πn, x2=π2+2πnx2=π2+2πn.
Приведение к однородному уравнению
Вначале нужно данное тригонометрическое уравнение привести к одному из двух видов:
asinx+bcosx=0asinx+bcosx=0 (однородное уравнение первой степени) или asin2x+bsinxcosx+ccos2x=0asin2x+bsinxcosx+ccos2x=0 (однородное уравнение второй степени).
Потом разделить обе части на cosx≠0cosx≠0 — для первого случая, и на cos2x≠0cos2x≠0 — для второго. Получим уравнения относительно tg xtg x: a tg x+b=0a tg x+b=0 и a tg2x+b tg x+c=0a tg2x+b tg x+c=0, которые нужно решить известными способами.
Пример. Решить уравнение: 2sin2x+sinxcosx—cos2x=12sin2x+sinxcosx—cos2x=1.
Решение. Запишем правую часть, как 1=sin2x+cos2x1=sin2x+cos2x:
2sin2x+sinxcosx—cos2x=2sin2x+sinxcosx—cos2x= sin2x+cos2xsin2x+cos2x,
2sin2x+sinxcosx—cos2x−2sin2x+sinxcosx—cos2x- sin2x—cos2x=0sin2x—cos2x=0
sin2x+sinxcosx—2cos2x=0sin2x+sinxcosx—2cos2x=0.
Это однородное тригонометрическое уравнение второй степени, разделим его левую и правую части на cos2x≠0cos2x≠0, получим:
sin2xcos2x+sinxcosxcos2x—2cos2xcos2x=0sin2xcos2x+sinxcosxcos2x—2cos2xcos2x=0
tg2x+tgx—2=0tg2x+tgx—2=0. Введем замену tgx=ttgx=t, в результате t2+t—2=0t2+t—2=0. Корни этого уравнения: t1=−2t1=-2 и t2=1t2=1. Тогда:
1. tgx=−2tgx=-2, x1=arctg(−2)+πnx1=arctg(-2)+πn, n∈Zn∈Z
2. tgx=1tgx=1, x=arctg1+πnx=arctg1+πn, x2=π4+πnx2=π4+πn, n∈Zn∈Z.
Ответ. x1=arctg(−2)+πnx1=arctg(-2)+πn, n∈Zn∈Z, x2=π4+πnx2=π4+πn, n∈Zn∈Z.
Переход к половинному углу
Пример. Решить уравнение: 11sinx—2cosx=1011sinx—2cosx=10.
Решение. Применим формулы двойного угла, в результате: 22sin(x2)cos(x2)−22sin(x2)cos(x2)- 2cos2x2+2sin2x2=2cos2x2+2sin2x2= 10sin2x2+10cos2x210sin2x2+10cos2x2
4tg2x2—11tgx2+6=04tg2x2—11tgx2+6=0
Применив описанный выше алгебраический метод, получим:
1. tgx2=2tgx2=2, x1=2arctg2+2πnx1=2arctg2+2πn, n∈Zn∈Z,
2.
tgx2=34tgx2=34, x2=arctg34+2πnx2=arctg34+2πn, n∈Zn∈Z.
Ответ. x1=2arctg2+2πn,n∈Zx1=2arctg2+2πn,n∈Z, x2=arctg34+2πnx2=arctg34+2πn, n∈Zn∈Z.
Введение вспомогательного угла
В тригонометрическом уравнении asinx+bcosx=casinx+bcosx=c, где a,b,c — коэффициенты, а x — переменная, разделим обе части на √a2+b2a2+b2:
a√a2+b2sinx+aa2+b2sinx+ b√a2+b2cosx=ba2+b2cosx= c√a2+b2ca2+b2.
Коэффициенты в левой части имеют свойства синуса и косинуса, а именно сумма их квадратов равна 1 и их модули не больше 1. Обозначим их следующим образом: a√a2+b2=cosφaa2+b2=cosφ, b√a2+b2=sinφba2+b2=sinφ, c√a2+b2=Cca2+b2=C, тогда:
cosφsinx+sinφcosx=Ccosφsinx+sinφcosx=C.
Подробнее рассмотрим на следующем примере:
Пример. Решить уравнение: 3sinx+4cosx=23sinx+4cosx=2.
Решение. Разделим обе части равенства на √32+4232+42, получим:
3sinx√32+42+3sinx32+42+ 4cosx√32+42=4cosx32+42= 2√32+42232+42
35sinx+45cosx=2535sinx+45cosx=25.
Обозначим 35=cosφ35=cosφ , 45=sinφ45=sinφ.
Так как sinφ>0sinφ>0, cosφ>0cosφ>0, то в качестве вспомогательного угла возьмем φ=arcsin 45φ=arcsin 45. Тогда наше равенство запишем в виде:
cosφsinx+sinφcosx=25cosφsinx+sinφcosx=25
Применив формулу суммы углов для синуса, запишем наше равенство в следующем виде:
sin(x+φ)=25sin(x+φ)=25,
x+φ=(−1)narcsin 25+πnx+φ=(-1)narcsin 25+πn, n∈Zn∈Z,
x=(−1)n arcsin 25−x=(-1)n arcsin 25- arcsin 45+πnarcsin 45+πn, n∈Zn∈Z.
Ответ. x=(−1)narcsin 25−x=(-1)narcsin 25- arcsin 45+πnarcsin 45+πn, n∈Zn∈Z.
Дробно-рациональные тригонометрические уравнения
Это равенства с дробями, в числителях и знаменателях которых есть тригонометрические функции.
Пример. Решить уравнение. sinx1+cosx=1−cosxsinx1+cosx=1-cosx.
Решение. Умножим и разделим правую часть равенства на (1+cosx)(1+cosx). В результате получим:
sinx1+cosx=sinx1+cosx= (1−cosx)(1+cosx)1+cosx(1-cosx)(1+cosx)1+cosx
sinx1+cosx=sinx1+cosx= 1−cos2x1+cosx1-cos2x1+cosx
sinx1+cosx=sinx1+cosx= sin2x1+cosxsin2x1+cosx
sinx1+cosx−sinx1+cosx- sin2x1+cosx=0sin2x1+cosx=0
sinx−sin2x1+cosx=0sinx-sin2x1+cosx=0
Учитывая, что знаменатель равным быть нулю не может, получим 1+cosx≠01+cosx≠0, cosx≠−1cosx≠-1, x≠π+2πn,n∈Zx≠π+2πn,n∈Z.
Приравняем к нулю числитель дроби: sinx−sin2x=0sinx-sin2x=0, sinx(1−sinx)=0sinx(1-sinx)=0. Тогда sinx=0sinx=0 или 1−sinx=01-sinx=0.
1. sinx=0sinx=0, x=πnx=πn, n∈Zn∈Z
2. 1−sinx=01-sinx=0, sinx=−1sinx=-1, x=π2+2πn,n∈Zx=π2+2πn,n∈Z.
Учитывая, что x≠π+2πn,n∈Zx≠π+2πn,n∈Z, решениями будут x=2πn,n∈Zx=2πn,n∈Z и x=π2+2πnx=π2+2πn, n∈Zn∈Z.
Ответ. x=2πnx=2πn, n∈Zn∈Z, x=π2+2πnx=π2+2πn, n∈Zn∈Z.
2x = 0`Чтобы найти x, рассмотрите приведенное выше выражение как квадратное уравнение. Тогда фактор.
`(2cosx — sinx) ( cosx + sinx) = 0`
Установите каждый коэффициент равным нулю и найдите x.
> `2cosx — sinx = 0`
Разделите обе части на cos…
См.
Этот ответ сейчас
Запустите 48-часовую бесплатную пробную версию , чтобы разблокировать этот и тысячи других ответов. Наслаждайтесь eNotes без рекламы и отмените подписку в любое время.
Получите 48 часов бесплатного доступа 92x = 0` Чтобы найти x, рассмотрите приведенное выше выражение как квадратное уравнение.
Тогда фактор.
`(2cosx — sinx) ( cosx + sinx) = 0`
Установите каждый коэффициент равным нулю и найдите x.
> `2cosx — sinx = 0`
Разделите обе части на cos x.
`2 — (sinx)/(cosx) = 0`
«tanx = 2`
Обратите внимание, что функция тангенса положительна в квадрантах I и III. Итак,
«x = 63,43` и `243,43` градусов
Другой множитель: 92x` are:
`x_1 = 63.43 + 360k`degrees
`x_2 = 135 + 360k` degrees
`x_3 = 243.43 + 360k` degrees and
`x_4 = 315 + 360 тыс. градусов
Утверждено редакцией eNotes
Математика
Последний ответ опубликован 07 сентября 2010 г. в 12:47:25.
Что означают буквы R, Q, N и Z в математике?
14 ответов воспитателя
математика
Последний ответ опубликован 07 октября 2013 г.
в 20:13:27.
Как определить, является ли это уравнение линейной или нелинейной функцией?
84 Ответы воспитателя
Математика
Последний ответ опубликован 14 ноября 2011 г. в 5:49:28.
Решите для b2:A= 1/2h (b1+b2)
1 Ответ учителя
Математика
Последний ответ опубликован 3 октября 2011 г. в 14:12:01.
Этот предел представляет собой производную некоторой функции f при некотором числе a. укажите это f и a. lim h->0 [(4-й корень из)(16+h)-2]/h a=? ф=?
1 Ответ учителя
Математика
Последний ответ опубликован 17 августа 2010 г. в 8:49.:11 утра
Учитывая f(x) и g(x), найдите (туман)(X) и (gof)(x) f(x) = 2x g(x) = x+3
8 ответов учителя
математика
Последний ответ опубликован 09 октября 2017 г.
в 00:54:39
Добавьте 1 плюс 2 плюс 3 плюс 4. . . вплоть до 100.
3 Ответа воспитателя
Математика
Последний ответ опубликован 25 февраля 2016 г. в 18:48:45.
Сколько времени (в часах) займет ваше путешествие, если вы проедете 350 км со средней скоростью 80 км/ч? Какова формула с данными: время, расстояние, скорость или скорость?
1 Ответ учителя
Математика
Последний ответ опубликован 15 мая 2012 г. в 7:13:43.
Как записать sin x через cos x?
1 Ответ учителя
Математика
Последний ответ опубликован 25 июня 2010 г. в 22:03:54.
Шестигранный кубик бросают четыре раза. Какова вероятность того, что на всех четырех бросках выпадет шестерка?
4 Ответа воспитателя
Математика
Последний ответ опубликован 24 апреля 2010 г.