| Поставить LIKE | и поделиться ссылкой |
На данном калькуляторе можно посчитать сложение вычитание деление или умножение дробей.
Рациональные уравнения онлайн калькуляторНаш калькулятор поможет вам решить рациональное уравнение или неравенство. Искусственный интеллект, который лежит в основе калькулятора, даст ответ с подробным решением и пояснениями. Калькулятор полезен старшеклассникам при подготовке к контрольным работам и экзаменам, для проверки знаний перед ЕГЭ, родителям школьников с целью контроля решения многих задач по математике и алгебре. Добро пожаловать на сайт Pocket TeacherНаш искусственный интеллект решает сложные математические задания за секундыМы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. начатьРациональные уравненияВ рациональных уравнениях обе части уравнения представляют собой рациональные выражения вида: s(x) = 0 или расширено: s(x) = b(x), где s(x), b(x) – рациональные выражения. Рациональное выражение является алгебраическим выражением, которое состоит из рациональных чисел и переменной величины, соединенных с помощью сложения, вычитания, умножения, деления и возведения в степень с натуральным показателем. Таким образом, это целые и дробные выражения без радикалов. Действия с рациональными числами обладают свойствами действий с целыми числами. К примеру, при умножении рациональных чисел есть дополнительное свойство – умножение взаимно обратных чисел. Для того чтобы умножить два рациональных числа, необходимо умножить модули этих чисел, а перед ответом поставить «плюс», если у множителей одинаковые знаки и «минус», если знаки разные. Умножение рационального числа на ноль. Когда в рациональном уравнении хоть один множитель – ноль, то и произведение будет равняться нолю. Умножение рациональных чисел с разными знаками. При умножении нескольких чисел с разными знаками, необходимо умножить модули каждого из этих чисел. Если количество множителей с отрицательными знаками – четное, то произведение всегда будет со знаком «плюс», если количество множителей с отрицательными знаками – нечетное, то и произведение будет со знаком «минус». Делить на ноль в рациональных уравнениях, как и в обычных нельзя. Чтобы решить рациональное уравнение, необходимо определить тип этого уравнения и применить некоторые математические хитрости, созданные для этого типа. Если Вы не помните этих хитростей, то можете воспользоваться калькулятором для решения рациональных уравнений, который быстро подберёт все корни данного уравнений. Решением рационального уравнения будут являться корень – конкретное число, при постановке которого в уравнение даст верное равенство. Корней рационального уравнения может быть много и важно в решении не упустить ни один корень. Бесплатный онлайн калькуляторНаш бесплатный решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Наш искусственный интеллект решает сложные математические задания за секунды. Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь! Калькулятор Уравнений. Решение Уравнений ОнлайнВвод распознает различные синонимы функций, как asin , arsin , arcsin Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x) Список математических функций и констант : • ln(x) — натуральный логарифм • sh(x) — гиперболический синус • ch(x) — гиперболический косинус • th(x) — гиперболический тангенс • cth(x) — гиперболический котангенс • sch(x) — гиперболический секанс • csch(x) — гиперболический косеканс • arsh(x) — обратный гиперболический синус • arch(x) — обратный гиперболический косинус • arth(x) — обратный гиперболический тангенс • arcth(x) — обратный гиперболический котангенс • arsch(x) — обратный гиперболический секанс • arcsch(x) — обратный гиперболический косеканс источники: http://www. http://mathdf.com/equ/ru/ |
Калькулятор дробей решение уравнений с дробями
Дробью в математике называется число, представляющее часть единицы или несколько её частей. Обыкновенная дробь записывается в виде двух чисел, разделенных обычно горизонтальной чертой, обозначающей знак деления. Число, располагающееся над чертой, называется числителем. Число, располагающееся под чертой, называется знаменателем. Знаменатель дроби показывает количество равных частей, на которое разделено целое, а числитель дроби — количество взятых этих частей целого.
Дроби бывают правильными и неправильными. Правильной называется дробь, у которой числитель меньше знаменателя. Если у дроби числитель больше знаменателя, то такая дробь называется неправильной. Смешанной называется дробь, записанная в виде целого числа и правильной дроби, и понимается как сумма этого числа и дробной части. Соответственно, дробь, не имеющая целую часть,называется простой дробью. Любая смешанная дробь может быть преобразована в неправильную простую дробь (см. пример ниже).
Соответственно, дробь, не имеющая целую часть,называется простой дробью. Любая смешанная дробь может быть преобразована в неправильную простую дробь (см. пример ниже).
Рациональные уравнения онлайн калькулятор
Наш калькулятор поможет вам решить рациональное уравнение или неравенство. Искусственный интеллект, который лежит в основе калькулятора, даст ответ с подробным решением и пояснениями.
Калькулятор полезен старшеклассникам при подготовке к контрольным работам и экзаменам, для проверки знаний перед ЕГЭ, родителям школьников с целью контроля решения многих задач по математике и алгебре.
Добро пожаловать на сайт Pocket Teacher
Наш искусственный интеллект решает сложные математические задания за секунды
Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!
начать
Рациональные уравнения
В рациональных уравнениях обе части уравнения представляют собой рациональные выражения вида: s(x) = 0 или расширено: s(x) = b(x), где s(x), b(x) – рациональные выражения.
Рациональное выражение является алгебраическим выражением, которое состоит из рациональных чисел и переменной величины, соединенных с помощью сложения, вычитания, умножения, деления и возведения в степень с натуральным показателем. Таким образом, это целые и дробные выражения без радикалов.
Действия с рациональными числами обладают свойствами действий с целыми числами.
К примеру, при умножении рациональных чисел есть дополнительное свойство – умножение взаимно обратных чисел. Для того чтобы умножить два рациональных числа, необходимо умножить модули этих чисел, а перед ответом поставить «плюс», если у множителей одинаковые знаки и «минус», если знаки разные.
Умножение рационального числа на ноль. Когда в рациональном уравнении хоть один множитель – ноль, то и произведение будет равняться нолю.
Умножение рациональных чисел с разными знаками. При умножении нескольких чисел с разными знаками, необходимо умножить модули каждого из этих чисел. Если количество множителей с отрицательными знаками – четное, то произведение всегда будет со знаком «плюс», если количество множителей с отрицательными знаками – нечетное, то и произведение будет со знаком «минус».
Делить на ноль в рациональных уравнениях, как и в обычных нельзя.
Чтобы решить рациональное уравнение, необходимо определить тип этого уравнения и применить некоторые математические хитрости, созданные для этого типа. Если Вы не помните этих хитростей, то можете воспользоваться калькулятором для решения рациональных уравнений, который быстро подберёт все корни данного уравнений.
Решением рационального уравнения будут являться корень – конкретное число, при постановке которого в уравнение даст верное равенство. Корней рационального уравнения может быть много и важно в решении не упустить ни один корень.
Бесплатный онлайн калькулятор
Наш бесплатный решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в калькуляторе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей группе ВКонтакте: pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
Вступайте в нашу группу, мы всегда рады помочь вам.
Наш искусственный интеллект решает сложные математические задания за секунды.
Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!
источники:
http://calc.by/math-calculators/fraction-calculator.html
http://pocketteacher.ru/calculator-rationalnih-uravneniy-ru
Калькулятор дробей — примеры, онлайн-калькулятор дробей
Калькулятор дробей выполняет сложение, вычитание, умножение и деление двух заданных дробей. Дроби — это числовые значения, представляющие часть целого. Простая дробь задается обозначением — числитель/знаменатель.
Что такое калькулятор дробей?
Калькулятор дробей — это онлайн-инструмент, который можно использовать для сложения, вычитания, умножения и деления дробей с одинаковыми или разными знаменателями. Это обеспечивает быстрый и простой способ решения сложных проблем, а также подсчет результатов в течение нескольких секунд. Чтобы использовать Калькулятор дробей , введите значения в поля ввода, указанные ниже.
Чтобы использовать Калькулятор дробей , введите значения в поля ввода, указанные ниже.
Калькулятор дробей
ПРИМЕЧАНИЕ. Вводите значения не более 4 цифр.
Как пользоваться калькулятором дробей?
Выполните следующие простые действия, чтобы сложить, умножить, вычесть или разделить любые две дроби с помощью онлайн-калькулятора дробей:
- Шаг 1: Перейдите к онлайн-калькулятору дробей Cuemath.
- Шаг 2: Введите значения в поля ввода калькулятора дробей и выберите операцию, которую хотите выполнить.
- Шаг 3: Нажмите кнопку «Рассчитать», чтобы сложить, вычесть, умножить и разделить две дроби.
- Шаг 4: Нажмите кнопку «Сброс», чтобы очистить поля и ввести новые значения.
Как работает калькулятор дробей?
Числитель дроби используется для описания количества равных частей целого, а знаменатель показывает полную часть или целое. Следует отметить, что для существования дроби знаменатель должен быть ненулевым.
- Сложение : Чтобы сложить дроби, первый шаг — иметь одинаковые знаменатели. Для определения общего знаменателя возьмите их НОК. Затем умножьте знаменатель на число, которое дает то же значение, что и НОК. На это число также будет умножаться числитель. Как только обе дроби будут иметь одинаковые знаменатели, сложите числители.
- Вычитание : Вычитание двух дробей можно выполнять только в том случае, если обе дроби имеют общие знаменатели. Используя метод НОК, дроби можно преобразовать так, чтобы они имели одинаковые знаменатели, а затем вычесть числители.
- Умножение : Умножение дробей намного проще, чем сложение или вычитание. Сначала умножьте числители, затем умножьте знаменатели. После этого сократите дробь до наименьшего значения, чтобы получить окончательный ответ.
- Деление : Деление дробей аналогично умножению. Здесь мы умножаем первую дробь на обратную (обратную) второй и упрощаем ее до наименьшей формы.

Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Запишитесь на бесплатный пробный урок
Решенные примеры на калькуляторе дробей
Пример 1:
Добавьте (2/3) + (5/6) и проверьте это с помощью калькулятора дробей.
Решение:
Поскольку знаменатели не совпадают, находим НОК.
НОК (3, 6) = 6
(2/3) + (5/6) = [(2 × 2)/(3 × 2)] + (5/6)
= 4/6 + 5/6
= (4 + 5)/6 = 9/6 = 3/2
Пример 2:
Вычтите (7/8) — (1/4) и проверьте это с помощью калькулятора дробей.
Решение:
НОК (8, 4) = 8
(7/8) — (1/4) = (7/8) — [(1 × 2)/(2 × 4)]
= 7/8 — 2/8
= (7 — 2)/8 = 5/8
Умножить (4/15) × (9/16) и проверьте его с помощью калькулятора дробей.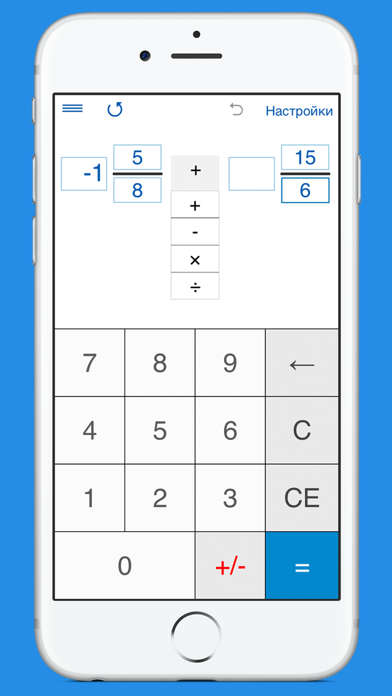 Пример 4:
Пример 4:
Разделите (2/3) ÷ (4/5) и проверьте это с помощью калькулятора дробей.
Решение:
Обратное число 4/5 равно 5/4.
(2/3) ÷ (4/5) = (2/3) × (5/4)
= 10/12
= 5/6
Точно так же вы можете попробовать калькулятор дробей для выполнения сложения , вычитание, умножение и деление двух дробей для следующего:
- (5/11) + (4/7)
- (14.11) — (2/3)
- (2/9) × (3/8)
- Дроби
- Смешанные фракции
Калькулятор дробей онлайн • Математический калькулятор
Калькулятор дробей – очень полезная вещь в математике. Это помогает легко работать с математическими дробями. Использование этого онлайн-калькулятора даст только правильный ответ. Существенная и главная цель состоит в том, чтобы в первую очередь прояснить, как рассчитывать результаты.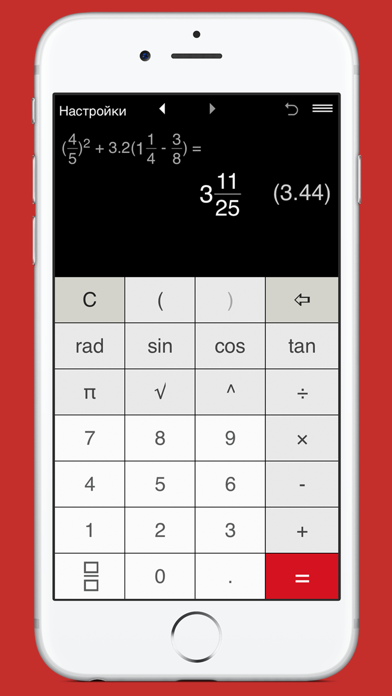
Калькулятор дробей может вычислять сложение, вычитание, умножение, деление, упрощение и преобразование между дробями и десятичными числами. Введите подходящие значения, в идеале целые числа, выберите нужную операцию и нажмите кнопку «Рассчитать», чтобы начать подсчет.
«Калькулятор упрощенных дробей» принимает смешанные числа. Для смешанных чисел не забудьте оставить пробел между целым числом и дробной частью. Детям важно научиться представлять действия сложения, вычитания, умножения и деления. Это идеально подходит для проверки работы.
мне нужен калькулятор Shet Yung May Fraction To Inge Sponsor
— Никки; (@nikeeewl) 1 февраля 2019 г.
Работаю над калькулятором мелких дробей для деревообработки. @warpling блестяще предложил назвать его «империалистическим»?
— Сэм Соффес (@soffes) 18 декабря 2017 г.
6÷2(3) = 6÷2×3 согласно калькулятору, т.
к. это не дробь. Не знаю, как объяснить это без бумаги, но я бы сказал, что это 1, только если это 6÷[2×(1+2)] и я инженер. Калькулятор будет думать, что это 1, только если вы поставите лишнюю скобку.
— медведь. ㅇㅅㅇ (@yooniesbear) 22 декабря 2018 г.
для всех на TL…. вот как вы получите оба ответа с помощью калькулятора. учитывая форматирование. похоже, что он просит 6 разделить на ВСЕ из 2 (1 + 2), а не просто 6 разделить на 2. если бы это было написано в виде дроби, не было бы споров pic.twitter.com/E1QL9y7zRZ
— Алекса (@cloudjmnie) 22 декабря 2018 г.
Ну, вы знаете, что меня пытали и заставляли учиться делить дроби, когда я был школьником без калькулятора, так что похоже, что нам всем приходится пережить немного страданий в жизни, Кайли. https://t.co/4eR1n9j4aU
— TR3YWAY (@TreyRisner) 27 ноября 2018 г.
Сегодня мне неожиданно пришлось делать дроби.

 (-2) +1.
(-2) +1.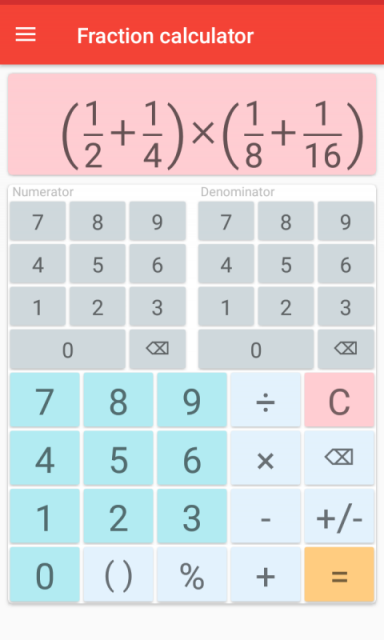 Останется только переписать в тетрадь!
Останется только переписать в тетрадь!
 Все, что вам необходимо сделать — это просто ввести свои данные в калькуляторе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей группе ВКонтакте: pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
Все, что вам необходимо сделать — это просто ввести свои данные в калькуляторе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей группе ВКонтакте: pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам. pocketteacher.ru/calculator-rationalnih-uravneniy-ru
pocketteacher.ru/calculator-rationalnih-uravneniy-ru
 к. это не дробь. Не знаю, как объяснить это без бумаги, но я бы сказал, что это 1, только если это 6÷[2×(1+2)] и я инженер. Калькулятор будет думать, что это 1, только если вы поставите лишнюю скобку.
к. это не дробь. Не знаю, как объяснить это без бумаги, но я бы сказал, что это 1, только если это 6÷[2×(1+2)] и я инженер. Калькулятор будет думать, что это 1, только если вы поставите лишнюю скобку.