Построить график y=log1/2(снизу)(x-4)… -reshimne.ru
Новые вопросы
Ответы
нужно составить таблицу: x 1/2 2 4 y 3 1 0 и по 3 этим точкам на координатной плоскости легко строится график.
Похожие вопросы
В магазине 798 кг.овощей. в 1 день продано 5/19 , а во 2 день 5/12 . Сколько осталось?…
Помогите решить с 185-189 (а, б)
Заранее спасибо)…
5целых2/9-4/9 плиз момогите…
Решите 9 целых 3/10 — 4 целых…
Если возможно замени в выражениях произведением в виде квадрата или куба числа :
. ..
..
В три школы привезли учебники В первую школу 360 книг ,во вторую на 110 книг меньше,чем в первую,а в третью на 120 книг меньше чем во вторую Сколько книг поступило в третью школу?…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
3-8| Перепишите экспоненциальную форму в ее эквивалентную логарифмическую форму, и перепишите логарифмическую форму в ее эквивалентную экспоненциальную форму. 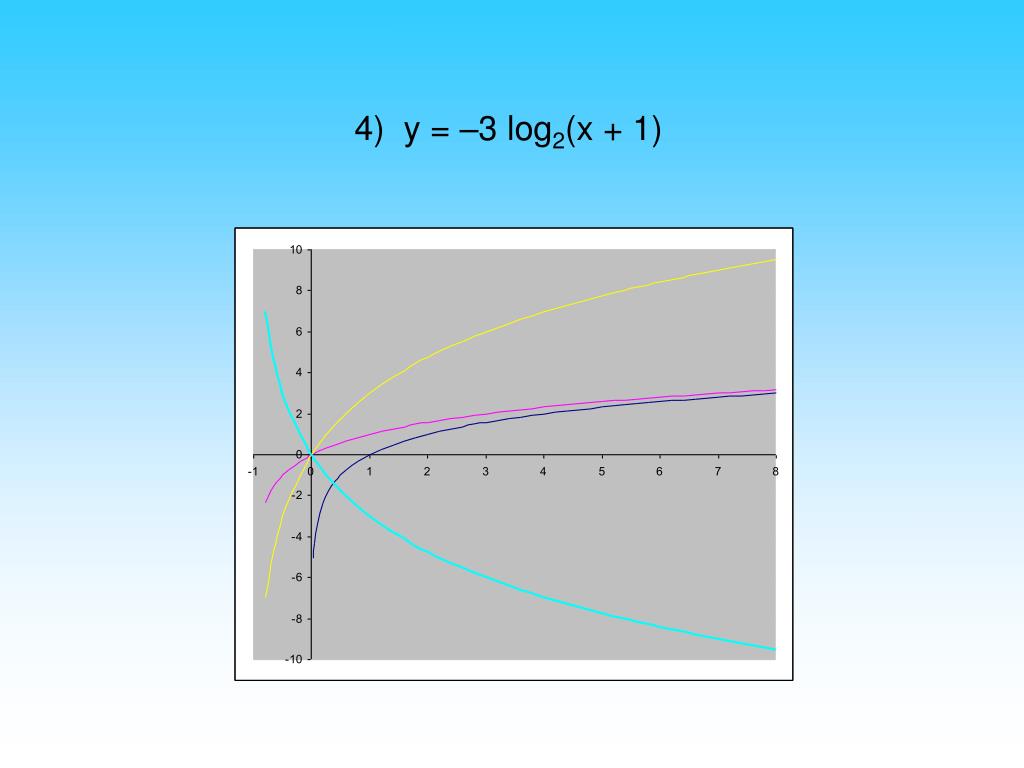 | |||||||||||||||
| 0 0 4] | 2 5 = 32 журнал 2 32 = 5 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 0 6] | 10 4 = 0,0001 log 10 0,0001 = 4 | ||||||||||||||
| 8] | журнал 5 5 = 1 5 1 = 5 | ||||||||||||||
| 0 0 10] | log 4 1 ⁄ 64 = 3 4 3 = 1 ⁄ 64 | ||||||||||||||
Решите следующие логарифмические уравнения. | |||||||||||||||
| 0 0 14] | x = log 3 1 ⁄ 81 3 x = 1 ⁄ 3 4 х = 4 | ||||||||||||||
| 0 0 16] | журнал x 27 ⁄ 64 = 3 x 3 = 3 3 ⁄ 4 3 х = 3 ⁄ 4 | ||||||||||||||
| 0 0 18] | 7 x = логарифм 7 5 √ 7 7 x = 5 √ 7 х = 1 ⁄ 5 | ||||||||||||||
| 0 0 20] | х = 12 log 12 5 журнал 12 х = журнал 12 5 х = 5 | ||||||||||||||
| 0 0 22] | х = 8 log 8 11 бревно 8 х = журнал 8 11 х = 11 | ||||||||||||||
| 24] | х 2 = 16 х = 4 1 = 1 ⁄ 4 | ||||||||||||||
| 26] | журнал 2 х = 3 х = 2 3 = 8 | ||||||||||||||
| 0 0 28] | x = log 5 4 √ 25 5 х = 25 1/4 х = 1 ⁄ 2 | ||||||||||||||
| 0 0 30] | log 4 х = 7 ⁄ 2х = 4 7/2 = (2 2 ) 7/2 = 2 7 = 128 | ||||||||||||||
| 32] | log 1/3 ( x + 6 ) = 2 х + 6 = ( 1 ⁄ 3 ) 2 х = 9 6 = 3 | ||||||||||||||
| 34] | журнал x4 19 = 1 ( х 4 ) 1 = 19 х = 19 +4 = 23 | ||||||||||||||
| 36] | 4 x 24 = log x 1 , где x > 0, x ≠ 1 4 х 24 = 0 х = 24 ⁄ 4 = 6 | ||||||||||||||
Учитывая график f (x) = log 2 x используйте этот график в качестве эталона при построении графика следующей функции. Дайте домен и диапазон. Дайте домен и диапазон. | |||||||||||||||
| 40] | f (x) = log 2 ( x + 3 ) График этой функции такой же, как график f (x) = log 2 x , переведенное влево на 3 единиц. Домен — ( 3, ∞) , а диапазон — ( ∞, ∞) . | ||||||||||||||
| Учитывая график f (x) = log 1/2 x используйте этот график в качестве эталона при построении графиков следующих функций. Дайте домен и диапазон. | |||||||||||||||
| 42] | f (x) = (log 1/2 x) 2 у = (логарифм 1/2 х) 2 у + 2 = логарифм 1/2 х х = ( 1 ⁄ 2 ) у+2 = 2 у2 График этой функции такой же, как график f (x) = log 1/2 x в переводе вниз на 2 единиц. Домен — (0, ∞) , а диапазон — ( ∞, ∞) . Линия x = 0 или ось Y является вертикальной асимптотой. | ||||||||||||||
| Нарисуйте график следующих функций. | |||||||||||||||
| 52] | f (x) = логарифм 10 x y = log 10 x x = 10 y
Линия x = 0 или ось Y является вертикальной асимптотой. | ||||||||||||||
| 54] | f (x) = log 1/3 ( 3 x ) y = log 1/3 ( 3 x ) 3 x = ( 1 ⁄ 3 ) y 7 х = 3 ( 1 ⁄ 3 ) у .
Линия x = 3 является вертикальной асимптотой. | ||||||||||||||
| 56] | f (x) = log 2 ( x + 2 ) 3 у = логарифм 2 ( х + 2 ) 3 у + 3 = log 2 ( х + 2 ) х + 2 = 2 у+3 х = 2 у+3 2
Линия x = 2 является вертикальной асимптотой. | ||||||||||||||
| Используйте свойства логарифмов, чтобы переписать следующие выражения. По возможности упрощайте результаты. Предположим, что все переменные представляют положительные действительные числа. | |||||||||||||||
| 0 0 64] | бревно 3 4p ⁄ q Использование правила частных, = лог 3 4п лог 3 п Использование правила произведения, = лог. 3 4 + лог. 3 п лог. 3 р | ||||||||||||||
| 66] |
Использование правила отношения, = логарифм 2 2 √ 3 логарифм 2 5 Использование правила произведения, = логарифм 2 2 + логарифм 2 √ 3 логарифм 3 5 Упрощение, = 1 + логарифм 2 3 1/2 логарифм 3 5 909:30 Использование правила мощности,= 1 + 1 ⁄ 2 логарифм 2 3 логарифм 3 5 | ||||||||||||||
| 68] | log 6 ( 7m + 3q ) К этой задаче нельзя применить правило. | ||||||||||||||
| 0 0 70] |
Упрощение = бревно р ( м 5 н 4 ⁄ т 2 ) 1/3 Использование правила мощности, = 1 ⁄ 3 логарифм p ( м 5 н 4 ⁄ т 2 ) Использование правила отношения, = 1 ⁄ 3 (логарифм р м 5 н 4 бревно р т 2 ) Использование правила произведения, = 1 ⁄ 3 ( бревно p м 5 + бревно p n 4 бревно p t 2 8) Использование правила мощности, = 1 ⁄ 3 ( 5 бревно п м + 4 бревна п н 2 бревна п т ) | ||||||||||||||
| 0 0 72] | log 2 xy ⁄ tqr Использование правила отношения, = log 2 xy log 2 tqr Использование правила продукта, = бревно 2 х + бревно 2 у бревно 2 t + бревно 2 q + бревно 2 r | ||||||||||||||
| 0 0 74] |
Упрощение,
Использование правила отношения, = журнал 4 a 1/3 · б 1/4 бревно 4 c 1/2 · d 2/3 Использование правила произведения, = бревно 4 а 1/3 + бревно 4 б 1/4 бревно 4 c 1/2 + бревно 4 d 2/3 Использование правила мощности, = 1 ⁄ 3 логарифм 4 а + 1 ⁄ 4 логарифм 4 б 1 ⁄ 2 бревно 4 c + 2 ⁄ 3 бревно 4 d | ||||||||||||||
Запишите каждое выражение в виде одинарного логарифма с коэффициентом 1 . Предположим, что все переменные представляют положительные действительные числа. | |||||||||||||||
| 76] | бревно b k + бревно b m бревно b a Использование правила произведения, = log b км log b a Использование правила отношения, = логарифм б км ⁄ а | ||||||||||||||
| 78] | лог б р лог б q лог б г Упрощение по ассоциативному закону = логарифм b p (логарифм b q + логарифм b r ) Использование правила произведения, = логарифм б п (лог б кв) Использование правила отношения, = логарифм б р ⁄ кв | ||||||||||||||
| 0 0 80] | 1 ⁄ 2 LOG Y P 3 Q 4 2 ⁄ 3 Log Y P 4 4 4 4 4 4 4 4 4 4 4 4 4 4 . Использование правила степени, = логарифм y (p 3 q 4 ) 1/2 логарифм y (p 4 q 3 97 ) 290 Использование правила отношения, = log y p 3/2 q 2 ⁄ p 8/3 q 2 | ||||||||||||||
| 82] | 5 log a ( z + 7 ) + log a ( 2z + 9 ) Использование степенного правила, = log a (z + 7) 5 + log a (2z + 9) Использование правила произведения, = логарифм a [(z + 7) 5 (2z + 9)] | ||||||||||||||
| 0 0 84] | ( 3 ⁄ 4 ) бревно 3 16п 4 ( 2 ⁄ 3 ) журнал 3 8p 3 Использование правила степени, = журнал 3 (16p 4 ) 3/4 бревно 3 ( 8п 3 ) 2/3 Использование правила отношения, = log 3 2 3 p 3 ⁄ 2 2 p 2 | ||||||||||||||
Учитывая приближения log 10 2 = 0,3010 log 10 3 = 0,4771 определяют значения следующих логарифмов. | |||||||||||||||
| 86] | бревно 10 12 = бревно 10 2 · 2 · 3 Использование правила произведения, = лог. 10 2 + лог. 10 2 + лог. 10 3 Подстановка данных значений, = 0,3010 + 0,3010 + 0,4771 | ||||||||||||||
| 0 0 88] | log 10 2 ⁄ 9 Использование правила отношения, = бревно 10 2 бревно 10 9 Использование правила произведения, = журнал 10 2 журнал 10 3 + журнал 10 3 Подстановка заданных значений, = 0,3010 0,4771 + 0,4771 | ||||||||||||||
| 0 0 90] | бревно 10 20 ⁄ 27 Использование правила отношения, = лог. Использование правила произведения, = log 10 2 + log 10 10 log 10 3 3 Используя правило силы, Подстановка заданных значений, = 0,3010 + 1 3 · 0,4771 | ||||||||||||||
| 0 0 92] | бревно 10 36 1/3 Использование степенного правила, = 1 ⁄ 3 [ логарифм 10 36 ] Использование правила произведения, = 1 ⁄ 3 [ логарифм 10 4 + журнал 10 9 ] Использование правила мощности, = 1 ⁄ 3 [ 2 log 10 2 + 2 log 10 3 ] Подстановка заданных значений, = 1 ⁄ 3 [2 (0,3010) + 2 (0,4771)] | ||||||||||||||
Используйте свойства логарифмов для вычисления следующих выражений.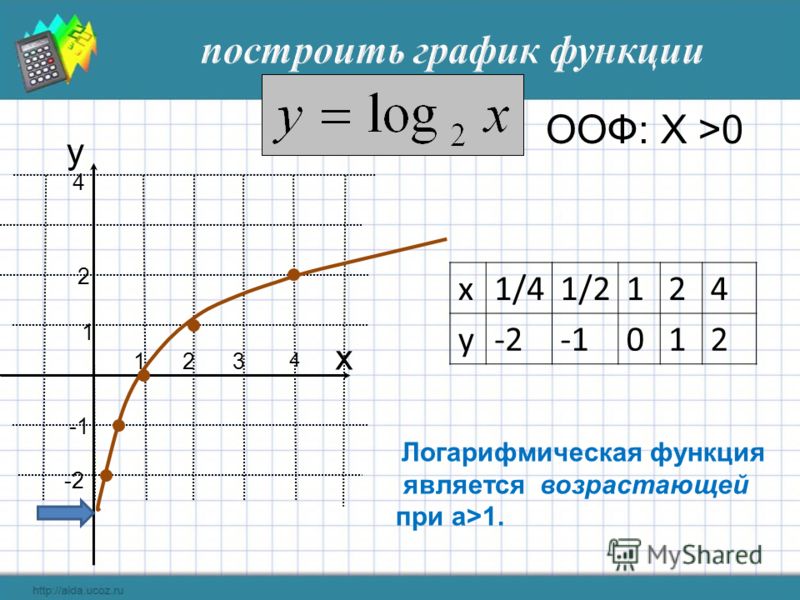 | |||||||||||||||
| 0 0 96б] | log 10 (0,01) 3 = log 10 (10 2 ) 3 Согласно теореме об обратных величинах, уравнение 7 = 6 | ||||||||||||||
| 0 0 96d] | 1000 бревно 10 5 = 10 3 log 10 5 Согласно теореме об обратных величинах, уравнение 6 = 125 | ||||||||||||||
Постройте график следующей функции.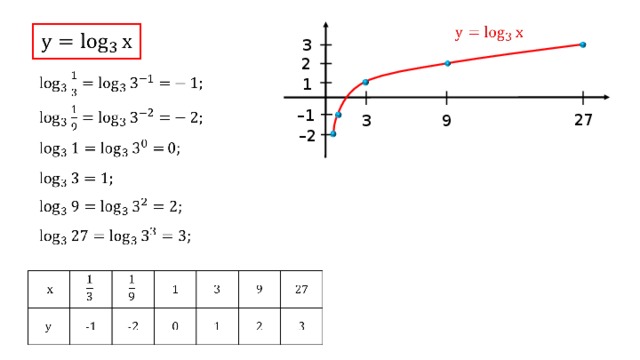 | |||||||||||||||

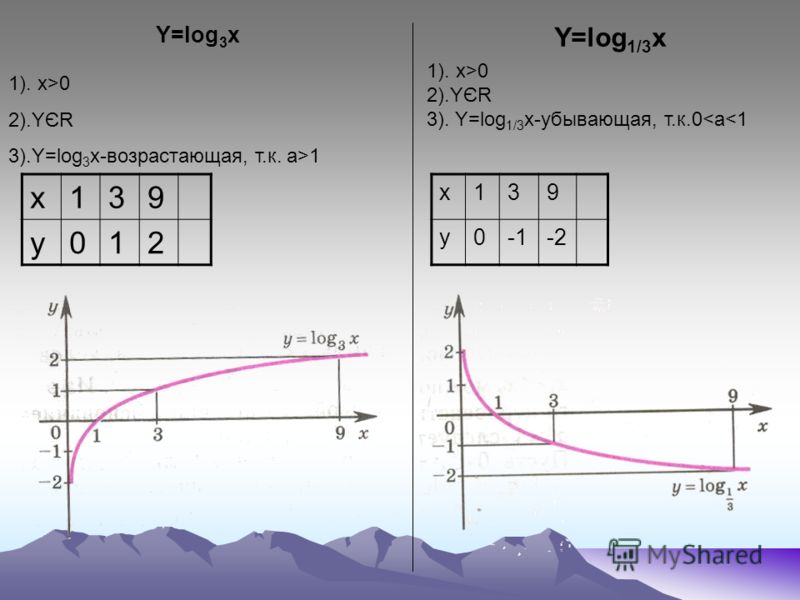
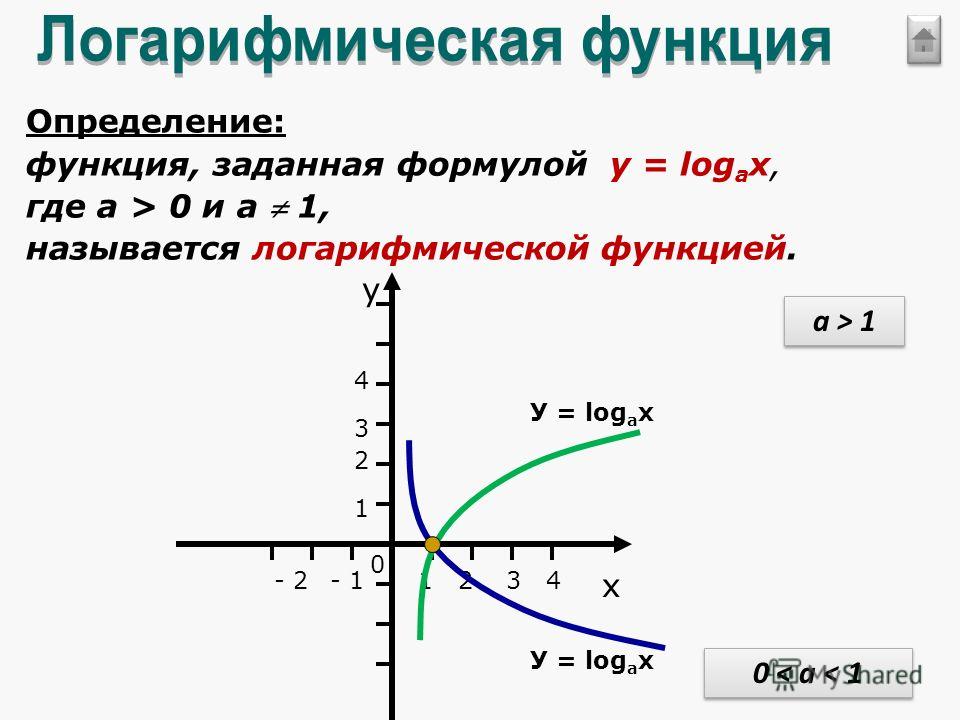
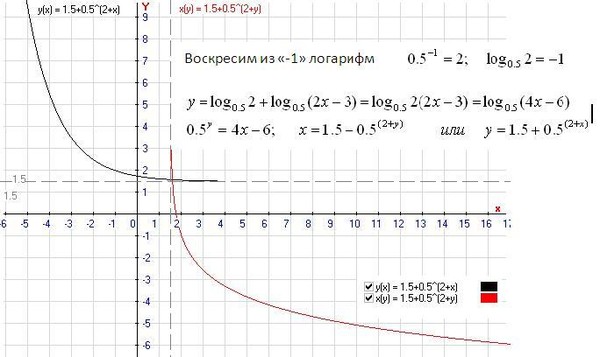
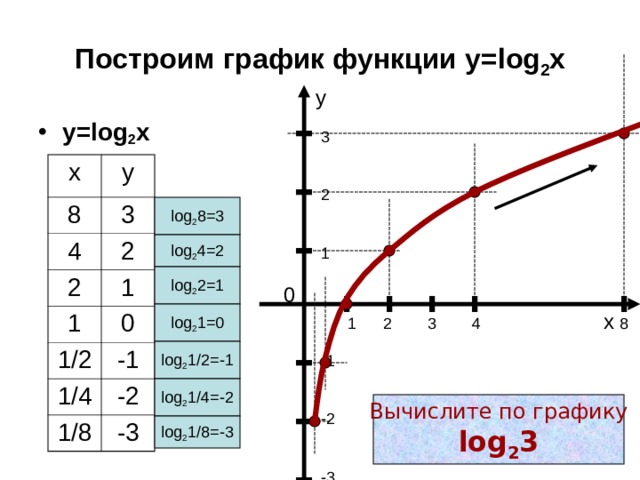

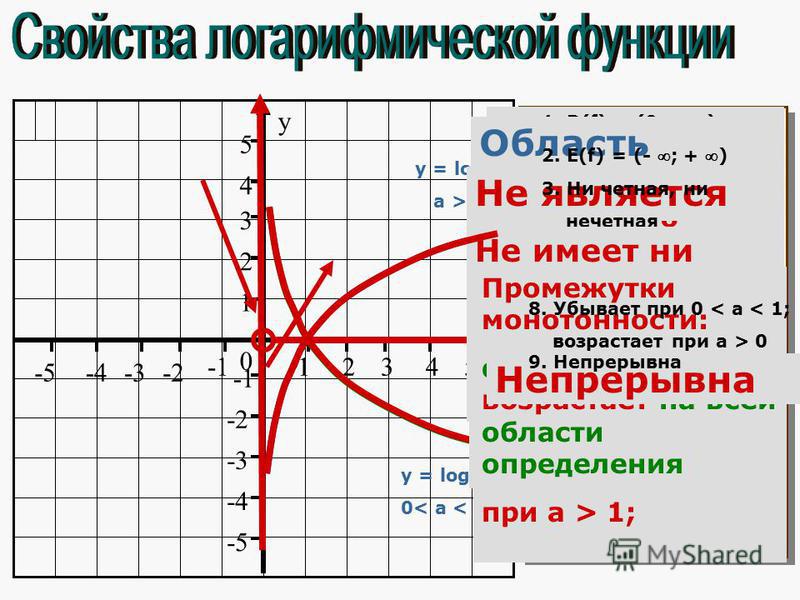
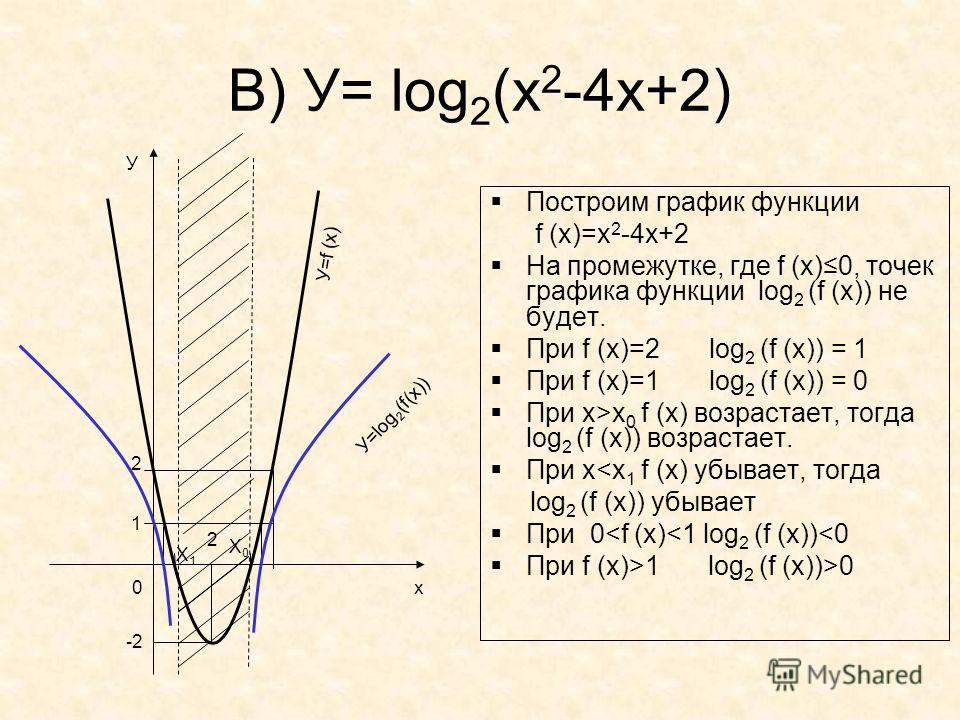
 10 20 лог. 10 27
10 20 лог. 10 27