Математика 6 класс. Тест на сложение и вычитание отрицательных чисел — Колпаков Александр Николаевич
Действия с отрицательными числами (наравне с линейными уравнениями) — наиболее важная тема из всех изучаемых в курсе математики за 6 класс. Более того, если ученик, штурмующий высоты ЕГЭ, путается в элементарных арифметических действиях на первом же занятии с репетитором — неудовлетворительный результат на экзамене можно исключить только при гигантском объеме занятий в течение года. Поэтому крайне важно не запускать математику на самых ранних этапах. Решайте с Вашим ребенком тематические тесты с моего сайта. Они позволят в некотором приближении распознать зарождающиеся проблемы.
Задача 1. Вычислите 5 + (-7)
Ответ:
Задача 2. Вычислите -5 +(- 7)
Ответ:
Задача 3. Вычислите -3 + 1,6
Ответ:
Задача 4.
Ответ:
Задача 5. Вычислите -1,8 — 1,17
Ответ:
Задача 6. Вычислите -1,8 -(- 0,187)
Ответ:
Задача 7. Вычислите 12,9 — 50
Ответ:
Задача 8. Вычислите -50,5 — 12,916
Ответ:
Задача 9. Вычислите -13 — ( -24,5)
Ответ:
Задача 10. Вычислите -1,2 — ( -(-(-0,8)))
Ответ:
Задача 11. Вычислите -1 -2 -3 -4 -5 -6 -7 -8 — 9 -10
Ответ:
Задача 12. Вычислить -1,22 — ( -3,22)
Ответ:
Задача 13.
Вычислить -5 — 2,71 -(-3,17)
Ответ:
Задача 14. Вычислите 10 -(-18,2) — 30,92
Ответ:
Задача 15. Вычислите -0,22 — 2,99 -(-17)
Ответ:
В приведенном тесте проверяются только навыки сложения и вычитания целых чисел и десятичных дробей. При необходимости репетитору по математике легко составить подобные упражнения с обыкновенными дробями, увеличив количество действий в одном примере до трёх — четырёх. Далее можно усложнять номера различными комбинациями видов дробей (обыкновенная с десятичной дробью в одном примере), а также вовлекая в процесс следующие действия: умножение и деление.
Хочу особо подчеркнуть, что без основных арифметических навыков изучение алгебры невозможно. Грамотный репетитор по математике не станет форсировать события материалами старшей школы, пока не приведет в порядок азы арифметики.
Если ко мне для подготовки к ЕГЭ в 10-11 классе приходит нулевой ученик, то чаще всего я начинаю работу с числовых операций, выражений. Этот процесс нельзя вести параллельно с изучением производных, логарифмов и синусов с косинусами. Такие попытки, как правило, обречены на неудачу. Более того, после стратегических ошибок репетитора дети перестают верить в свои способности и начинают еще больше ненавидеть математику.
С уважением, Колпаков Александр. Занятия в Строгино по авторским материалам.
Во втором классе учащиеся должны знать название компонентов действий сложения и вычитания — Мегаобучалка
МЕТОДИКА ОБУЧЕНИЯ АРИФМЕТИЧЕСКИМ ДЕЙСТВИЯМ И ФОРМИРОВАНИЯ ВЫЧИСЛИТЕЛЬНЫХ НАВЫКОВ
1. Сложение и вычитание в пределах двадцати.
2. Сложение, вычитание, умножение и деление в пределах 20.
3. Таблица умножения.
4. Арифметические действия в пределах 1000.
5. Арифметические действия над многозначными числами.
Обучение сложению и вычитанию в пределах 10.
С арифметическими действиями учащиеся знакомятся сразу же после изучения числа 2. Изучение каждого из чисел первого десятка (кроме 1), завершается изучением действий сложения и вычитания в пределах этого числа. Действие сложение и вычитание изучаются параллельно.
Учащиеся знакомятся со знаками сложения — плюсом (+), вычитания- минусом (-) и знаком равенства — равно (=).
При изучении данной темы учащиеся должны овладеть приемами вычисления, получить прочные вычислительные навыки, заучить результаты сложения и вычитания в пределах 10, а также состав чисел первого 10, узнавать и показывать компоненты и результаты двух арифметических действий и понимать их названия в речи учителя.
По мере овладения учащимися натуральной последовательностью чисел и свойством этого ряда нужно знакомить и с приемами сложения и вычитания, опирающимся на это свойство натурального ряда чисел. Дети учатся этим приемам прибавлять и вычитать единицу из числа, т.е. присчитывать и отсчитывать по 1.
Когда учащиеся научились прибавлять и вычитать по одному, надо учить их прибавлять по два.
Когда учащиеся овладели приемами присчитывания, учитель знакомит их с приемами отсчитывания.
Если приемами присчитывания ученики первого класса овладевают довольно быстро, то приемами отсчитывания — намного медленнее.
Трудность состоит в том, что прием отсчитывания основан на хорошем знании обратного счета, а обратный счет для многих учащихся первого класса труден. Кроме того, ученики плохо запоминают — сколько нужно отнять, сколько уже отняли, сколько ещё надо отнять.
При изучении каждого числа первого десятка учащиеся получают представление и о составе этих чисел.
В начале необходимо давать такие упражнения, в которых одно из слагаемых воспринимаются детьми наглядно, а второе они отыскивают по представлению.
При выполнении действий сложения и вычитания в пределах данного числа вводятся решение примеров с отсутствующим компонентом. Его обозначают точками, рамками, знаками вопросов и т.
д., например:
[] + I – 3, 4 +… = б, ? – 2 = 4. б — ? = 2.
Запишем 1-1=0 (отсутствие предметов обозначают цифры О) Решаются еще примеры, когда разность равна нулю.
Нуль сравнивается с единицей. Устанавливается, что ноль меньше единицы, единица больше нуля, поэтому ноль должен стоять перед единицей. Однако учитель должен помнить, что ноль не относится к натуральным числам. Поэтому ряд натуральных чисел должен начинаться с единицы.
Вводить число ноль в качестве вычитаемого, а потом и слагаемого следует на большом числе упражнений. Смысл действий с нулем будет лучше понять учащимся, если ноль в качестве вычитаемого и ноль в качестве слагаемого будет вводиться не одновременно. Затем проводятся упражнения на дифференциацию примеров, в которых ноль будет слагаемым и вычитаемым.
Полезно показать учащимся и зависимость изменения суммы от применения слагаемых, а также изменения остатка от изменения уменьшаемого.
Учитель первого класса должен обращать внимание учащихся на то, что сумма всегда больше каждого из слагаемых, а остаток всегда меньше уменьшаемых.
Уменьшаемое больше или равно вычитаемому, в противном случае вычитание произвести нельзя.
Уже с первого класса ученики должны быть приучены к проверке правильности решения примеров.
Овладение вычислительными приемами сложения и вычитания в пределах 20 основано на хорошем знании сложения и вычитания в пределах 10, знание нумерации и состава чисел в пределах 20.
При изучении действий сложения и вычитания в пределах 20, как и при изучении соответствующих действий в пределах 10, большое значение имеет наглядность и практическая деятельность с пособиями самих учащихся. Поэтому все виды наглядных пособий, используемых при изучении нумерации, найдут применение и при изучении арифметических действий.
Действия сложения и вычитания целесообразнее изучать параллельно после знакомства с определенным случаем сложения изучать соответствующий случай вычитания сопоставления со сложением.
Во втором классе учащиеся должны знать название компонентов действий сложения и вычитания.
1. Приемы сложения и вычитания, основанные на знаниях десятичного состава чисел.
2. Сложение и вычитание без перехода через десяток:
а) к двухзначному числу прибавляется однозначное число. Из двухзначного числа вычитается однозначное число;
б) получение суммы 20 и вычитание однозначного числа из 20;
в) вычитание из двухзначного числа двухзначного: 15-12, 20-15.
Решение примеров такого вида можно объяснить разными приемами:
1. Разложить уменьшаемое и вычитаемое на десятки и единицы и вычитать десятки из десятков, единицы из единиц.
2. Разложить вычитаемое на десяток и единицы. Вычитать из уменьшаемого десятки, а из полученного числа — единицы.
3. Сложение и вычитание с переходом через ряд представляет наибольшие трудности для учащихся, с психофизическими нарушениями. вычитание с переходом через десяток тоже требует ряд операций;
— уменьшаемое разложить на десяток и единицы
— вычитаемое разложить на два числа, одно из которых равно числу уменьшаемого единицы
— вычесть единицы
— вычесть из десятка оставшееся число единиц
Подготовительная работа должна заключаться в повторении:
а) таблица сложения и вычитания в пределах 10,
б) состава чисел первого десятка (всех возможных вариантов
из двух чисел)
в) дополнение чисел до 10
г) разложение двухзначного числа на десятки и единицы
д) вычитание из десяти однозначных чисел
е) рассмотрение случаев вида 17-7, 15-5.
Сложение и вычитание отрицательных чисел. Рабочие листы.
. Рабочие листы.
Основные математические листы
Фракционный рабочие листы
Проблемы с словами
Другие рабочие листы
Измерение и преобразования
Паттерны и зажимы
Цвет. По номеру
Holiday & Seasonal
.0032 Печатные формыКалькуляторы
Рабочие листы по математике по классам
Рабочие листы Новости
Рабочие листы для сложения и вычитания отрицательных чисел.
Отрицательные числа. Сложение и вычитание 1
Отрицательные числа. Сложение и вычитание 2
Отрицательные числа. Сложение и вычитание 3
Отрицательные числа. : Сложение и вычитание 5
Отрицательные числа: четыре условия: сложение и вычитание 6
Отрицательные числа: четыре условия: сложение и вычитание 7
Отрицательные числа: порядок операций Скобки: сложение и вычитание 8
Отрицательные числа: порядок операций Круглые скобки: сложение и вычитание 9
Приемы сложения и вычитания отрицательных чисел
Сложение и вычитание чисел поначалу может сбивать с толку, потому что представление об отрицательном количестве чего-либо может показаться странным даже шестикласснику.
Вместо этого введите понятие отрицательных чисел, используя измерения, которые могут убедительно давать отрицательные результаты. Хорошим примером является температура, значения которой могут опускаться ниже нуля (это особенно хорошо, если понимать температуру в градусах Цельсия, поскольку ноль имеет там очень четкое значение). Другим хорошим выбором может быть высота над или под уровнем моря.
Работа с числовой прямой — еще одна отличная стратегия для визуализации того, как вычитание может создавать отрицательные целые числа в более абстрактном контексте.
Отслеживание знаков
Часть проблемы сложения и вычитания отрицательных чисел заключается в том, чтобы выяснить, что делать со знаками. Мы изучаем наши факты вычитания и приучаемся к этому символу минус, который сразу же означает отнять второе число справа. С отрицательными числами это часто неверно.
Вот правила сложения и вычитания отрицательных чисел:
- Добавление положительного числа — это сложение (например, 4 + (+2) = 4 + 2 = 6
- Вычитание отрицательного числа является сложением (например, 4 — (-2) = 4 + 2 = 6
- Добавление отрицательного числа является вычитанием, (например, 4 + (-2) = 4 — 2 = 2
- Вычитание положительного числа является вычитанием (например, 4 — (+2) = 4 — 2 = 6
Обычно, конечно, мы не показываем знаки перед положительными числами, поэтому два приведенных выше правила выглядят точно так же, как стандартное сложение и вычитание!Два других правила являются ключевыми, которые следует помнить при объединении отрицательных чисел.
.. Вычитание отрицательного значения такое же, как сложение, а добавление отрицательного значения такое же, как вычитание.Если учащиеся смогут запомнить эти два новых поворота , сложение и вычитание с отрицательными числами станет проще простого!0003
Сложение и вычитание положительных и отрицательных чисел
Эта статья является расширенной версией статьи, опубликованной в NRICH в 2008 году. В этой версии содержится исходная статья.
Мы часто расстраиваемся, когда слышим, как студенты говорят: «Два минуса дают плюс», потому что это показывает заученную фразу, которая часто используется неправильно. Например, все мы слышали, как студенты говорят что-то вроде «минус четыре минус два равно шести, потому что два минуса дают плюс!»
Модели обучения сложению и вычитанию положительных и отрицательных чисел, которыми мы делимся в этой статье, предназначены для того, чтобы привести к пониманию. Мы сделаем предложения о том, как именно использовать язык, чтобы поддержать понимание различия между операциями и направленными числами.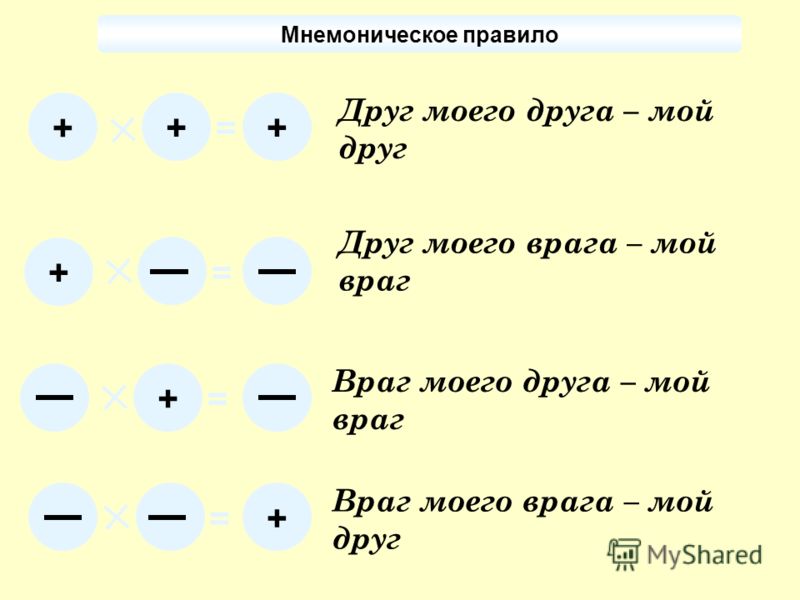
Есть четыре возможности, которые нам нужно понять с помощью наших моделей:
Добавление положительного числа
Добавление отрицательного числа
Вычитание положительного числа
Вычитание отрицательного числа
Воздушный шар
В этой модели мы представляем положительные числа как «дуновения» горячего воздуха, а отрицательные числа — как мешки с песком.
| Модель | Расчет | Результат |
| Добавление струй горячего воздуха | Добавление положительного числа | Увеличение (по высоте) |
| Добавление мешков с песком | Добавление отрицательного числа | Уменьшение (по высоте) |
| Вычитание струй горячего воздуха | Вычитание положительного числа | Уменьшение (по высоте) |
| Вычитание мешков с песком | Вычитание отрицательного числа | Увеличение (по высоте) |
Теперь мы можем описать вычисление, такое как 4 + (-2) — (+5) — (-1) + (+7) следующим образом:
Мой шар стартует на высоте +4.
Я добавляю два мешка с песком (два вниз), вычитаю пять струй горячего воздуха (пять вниз), вычитаю один мешок с песком (один вверх), затем добавляю семь струй горячего воздуха (семь вверх). Мой шар заканчивается на высоте +5.
В конце концов, мы хотим, чтобы учащиеся прочитали вычисление как «Четыре прибавьте минус два, вычтите плюс пять, вычтите минус один, прибавьте плюс семь» (или замените слова операции сложение/вычитание на плюс/минус, но всегда настаивайте на положительные и отрицательные для знаков, сопровождающих числа), и подумайте про себя «Четыре, два вниз, пять вниз, один вверх, вверх семь дюймов или аналогичный.
Спасибо Алану Месфину ( ), который предложил альтернативу завязывания гелиевых шаров (как в фильме «Вверх») вместо добавления струй горячего воздуха для обозначения добавления положительного числа.
Модель счастья
Мэри Клир использует аналогичный подход:
«Я считаю, что сложение и вычитание с отрицательными числами имеет смысл.
-10$ до $10$) вверху или вдоль верхней части доски. Вместе со студентами мы проводим мозговой штурм по ПОЗИТИВНЫМ и НЕГАТИВНЫМ вещам. Мы говорим о том, что вы чувствуете, если кто-то дарит вам что-то позитивное или если кто-то забирает его. Мы говорим о том, что вы чувствуете, если кто-то дает вам что-то негативное или если кто-то забирает его. 9-2$.
Что, если бы вы дали мне отработку на 3 доллара? И т.д.
В какой-то момент я обычно заставляю всех учеников указывать направление, в котором я должен двигаться по шкале, так что легко увидеть, кто еще не понял. Как только класс становится уверенным, я обычно начинаю записывать некоторые расчеты на доске или прошу ученика сделать это за меня! Обычно я позволяю им предлагать ходы, которые уменьшат мое счастье по шкале, которую я имею на своем счету. числовая строка.
В заключение, прежде чем я попрошу их ответить на множество стандартных + и — вопросов, мы придумываем задачу типа: 9-8) =$ ?
, чтобы сделать вместе».
Модель футбола
В этой модели мы представляем положительные числа как хороших футболистов, которые забивают много голов, а отрицательные числа — как плохих футболистов, забивающих голы в свои ворота.
Когда приходит время трансферов, мы можем добавить новых игроков в нашу команду или вывод игроков из команды
| Модель | Расчет | Результат |
| Покупайте хороших игроков | Добавление положительного числа | Повышение |
| Купить плохих игроков | Добавление отрицательного числа | Понижение (в лиге) |
| Продавать хороших игроков | Вычитание положительного числа | Понижение (в лиге) |
| Продать плохих игроков | Вычитание отрицательного числа | Повышение (в лиге) |
Итак, представьте, что мы купили 5 хороших игроков, продали 2 хороших, купили 3 плохих и продали 7 плохих. Мы можем написать следующий расчет, чтобы узнать общий эффект: 9-7)$
Таким образом, в целом мы улучшаем нашу позицию на 7.
Во всех этих моделях мы используем аналогию, где добавление чего-то положительного или вычитание чего-то отрицательного улучшает ситуацию (более счастливая, более высокая позиция в лиге, воздушный шар поднимается вверх).
Проблема Странный банковский счет использует контекст внесения и снятия денег, но не имеет такой строгой аналогии, чтобы объяснить все четыре возможности, отраженные в таблицах выше. Однако его можно использовать для введения понятия направленного числа, а затем использовать в сочетании с другой моделью.
Наконец, мы предлагаем более абстрактный взгляд на сложение и вычитание положительных и отрицательных чисел, не полагаясь на аналогию:
Счетчики Модель 9-2$?
Это $3$
Когда мы разделим это, мы можем получить разные суммы:
2$ + 1 = 3 $$3 — 2 = 1$ $3 — 1 = 2$ | Верх + Низ = Целиком Весь — Верх = Низ Весь — Низ = Верх |
Если мы разделим его по-разному, мы можем получить разные суммы:
| 9-1$ | Верх + Низ = Целиком Весь — Верх = Низ Весь — Низ = Верх
|
Учеников можно попросить составить три разные суммы на основе их разбиений на другие наборы плюсов и минусов.