Как найти угол фи
Что такое косинус фи в электрике
Допустим, вы купили компрессор для полива растений или электродвигатель для циркулярной пилы. В инструкции по эксплуатации помимо основных технических характеристик (таких, как потребляемый ток, рабочее напряжение, частота вращения) вы можете обнаружить такой непонятный показатель, как косинус фи (cos ϕ). Данная информация может быть указана и на пластинке (шильдике), закрепленной на корпусе прибора. В нашей статье мы постараемся объяснить простым и доступным языком всем, даже пользователям далеким от электротехнических тонкостей, как тригонометрическая функция (знакомая нам со школьной скамьи) влияет на работу всем нам привычных электробытовых приборов, и почему ее называют коэффициентом мощности.
Важно! Все нижесказанное касается только сетей переменного тока.
Далекий от электротехники, но весьма наглядный пример
Чтобы объяснить, каким образом угол ϕ (а точнее его косинус) влияет на мощность, рассмотрим пример, не имеющий никакого отношения к электротехнике. Допустим нам необходимо передвинуть тележку, стоящую на рельсах. Чтобы удобнее было производить данную операцию, к ее передней части прикрепляем канат.
Допустим нам необходимо передвинуть тележку, стоящую на рельсах. Чтобы удобнее было производить данную операцию, к ее передней части прикрепляем канат.
Если мы будем тянуть за веревку прямо вперед по направлению движения, то для перемещения тележки нам понадобится приложить достаточно небольшое усилие. Однако если находиться сбоку от рельсов и тянуть за канат в сторону, то для движения тележки с такой же скоростью необходимо будет приложить значительно большее усилие. Причем чем больше угол (ϕ) между направлением движения и прикладываемым усилием, тем больше «мощности» потребуется от нас.
Вывод! То есть, увеличение угла ϕ ведет к увеличению расходуемой нами энергии (при одной и той же выполненной работе).
Сдвиг фаз между напряжением и током
При использовании энергии переменного тока происходит приблизительно то же самое. При активной нагрузке (например, при включении электрочайника или лампы накаливания) переменные напряжение (U) и ток (I) полностью совпадают по фазе и одновременно достигают своих максимальных значений. В данном случае мощность потребителя электроэнергии можно рассчитать по формуле P=U•I.
В данном случае мощность потребителя электроэнергии можно рассчитать по формуле P=U•I.
Для сети переменного тока работающий электродвигатель, имеющийся, например, в стиральной машине, является комплексной нагрузкой, включающей в себя активную и индуктивную составляющие. При подаче напряжения на такой прибор оно появляется на обмотках, практически, мгновенно. А вот ток (из-за влияния индуктивности) запаздывает. То есть между ними образуется так называемый сдвиг фаз, который мы и называем ϕ.
При активно-емкостной нагрузке, наоборот, переменный ток сразу начинает течь через конденсатор, а напряжение отстает от него по фазе на величину ϕ.
Треугольник мощностей
Коэффициент мощности (PF) – это отношение мощностей: активной полезной (P) к полной (S). Чтобы показать, каким образом сдвиг фаз влияет на PF, используем так называемый треугольник мощностей. И вот тут-то нам и потребуются минимальные знания школьной тригонометрии.
Из теории о прямоугольных треугольниках всем нам известно, что cos ϕ=P/S. То есть, косинус фи — это и есть коэффициент мощности (PF), который показывает, какая часть от полной мощности (S= U•I) фактически необходима для конкретной нагрузки. Чем больше реактивная составляющая Q, тем меньше полезная P. Чтобы вычислить активную мощность необходимо полную S умножить на косинус фи: P= S•cos ϕ.
То есть, косинус фи — это и есть коэффициент мощности (PF), который показывает, какая часть от полной мощности (S= U•I) фактически необходима для конкретной нагрузки. Чем больше реактивная составляющая Q, тем меньше полезная P. Чтобы вычислить активную мощность необходимо полную S умножить на косинус фи: P= S•cos ϕ.
На заметку! Считать косинус фи абсолютным аналогом коэффициента мощности можно только при том условии, что мы имеем в электрической сети идеальную синусоиду. Для более точного расчета необходимо учитывать нелинейные искажения, которые имеют переменные напряжение и ток. На практике, зачастую коэффициентом нелинейных искажений синусоиды пренебрегают, и значение косинуса фи принимают за приближенное значение коэффициента мощности.
Усредненные значения коэффициента мощности
Лампы накаливания и электрические нагревательные элементы, хотя и имеют в своих конструкциях спирали, намотанные с помощью специального провода, считаются чисто активной нагрузкой для сетей переменного тока. Так как индуктивность этих элементов настолько мала, что ею, как правило, просто пренебрегают. Для таких приборов cos ϕ (или коэффициент мощности) принимают равным 1.
Так как индуктивность этих элементов настолько мала, что ею, как правило, просто пренебрегают. Для таких приборов cos ϕ (или коэффициент мощности) принимают равным 1.
В разнообразных электрических ручных инструментах (дрелях, перфораторах, лобзиках и так далее) индуктивная составляющая мощности достаточно мала. Для них принято считать cos ϕ≈0,96÷0,97. Этот показатель достаточно близок к единице, поэтому его, практически, никогда не указывают в технических характеристиках.
Для мощных электродвигателей, люминесцентных ламп и сварочных трансформаторов cos ϕ≈0,5÷0,82. Этот коэффициент мощности необходимо учитывать, например, при выборе диаметра питающих проводов, чтобы они не нагрелись, и не сгорела их изоляция.
На что влияет низкий коэффициент мощности
К чему могут привести низкие показатели коэффициента мощности:
- При низком PF возрастает потребляемый нагрузкой ток. cos ϕ=P/S=P/(U•I), следовательно I=P/(U•cos ϕ). Допустим, для конкретной нагрузки необходима активная мощность P=10000 ВА при напряжении U=220 В.
 В идеальном варианте PF=cos ϕ=1. Тогда ток нагрузки: I=10000/(220•1)≈45 А. При PF=0,8 I=10000/(220•0,8)≈57 А. То есть при снижении PF с 1 до 0,8 ток возрастет приблизительно на 20%. Значит, это приведет к излишним затратам на электроэнергию.
В идеальном варианте PF=cos ϕ=1. Тогда ток нагрузки: I=10000/(220•1)≈45 А. При PF=0,8 I=10000/(220•0,8)≈57 А. То есть при снижении PF с 1 до 0,8 ток возрастет приблизительно на 20%. Значит, это приведет к излишним затратам на электроэнергию. - Снижение коэффициента мощности, и как следствие увеличение тока приводит к значительным энергетическим потерям в проводах, которые по закону Ома равны I•R², где R – активное сопротивление проводников. Для уменьшения этих потерь приходится увеличивать диаметр проводов, что опять же приводит к излишним экономическим затратам.
- Вышеуказанные потери расходуются на выделение тепла. В этом случае придется применять более термостойкие, а следовательно, и более дорогие изоляционные материалы).
В заключении
Смело можно утверждать, что чем ближе значение PF к единице, тем эффективнее используется электроэнергия. В некоторых мощных приборах производители устанавливают специальные приспособления, которые позволяют осуществлять коррекцию коэффициента мощности.
Косинус фи (cos φ) — Коэффициент мощности
На шильдиках двигателей и некоторых других устройств можно видеть непонятный параметр косинус фи (cos φ). Что этот параметр означает, в данной статье коротко объясняется, что это такое.
Косинус фи (cos φ) часто называют «Коэффициент мощности». Это почти одно и то же при правильной синусоидальной форме тока.
Иногда для обозначения коэффициента мощности используется λ, эту величину выражают в процентах, или PF.
Условные обозначения
P — активная мощность S — полная мощность Q — реактивная мощность, U — напряжение I — ток.
Что такое Косинус фи (cos φ) — «Коэффициент мощности»
Косинус фи (cos φ) это косинус угла между фазой напряжения и фазой тока.
При активной нагрузке фаза напряжения совпадает с фазой тока, φ (между фазами) равен 0 (нулю). А как мы знаем cos0=1. То есть при активной нагрузке коэффициент мощности равен 1 или 100%.
Активная нагрузка
При емкостной или индуктивной нагрузке фаза тока не совпадает с фазой напряжения. Получается «сдвиг фаз».
Получается «сдвиг фаз».
При индуктивной или активно-индуктивной нагрузке (с катушками: двигатели, дросселя, трансформаторы) фаза тока отстает от фазы напряжения.
При емкостной нагрузке (конденсатор) фаза тока опережает фазу напряжения
А почему тогда косинус фи (cos φ) это тоже самое что коэффициент мощности, да потому что S=U*I.
Посмотрите на графики ниже. Здесь φ равно 90 косинус фи (cosφ)=0(нулю).
Емкостная нагрузка
Индуктивная нагрузка
Попытаемся вычислить мощность для простоты возьмем максимальное значение напряжения равное 1(100%) в этот момент ток равен 0(нулю) соответственно их произведение, то есть мощность равны 0(нулю). И наоборот когда ток максимальный напряжение равно нулю.
Получается что полезная, активная мощность равна 0(нулю).
Коэффициент мощности это соотношение полезной активной мощности к полной мощности, то есть cosφ=P/S.
Треугольник мощностей
Посмотрите на треугольник мощностей. Вспомним тригонометрию (это что то из математики) вот здесь то она нам и пригодится.
Вспомним тригонометрию (это что то из математики) вот здесь то она нам и пригодится.
Q =U x I x sin φ
На практике. Если подключить асинхронный двигатель в сеть без нагрузки, в холостую. Напряжение вроде как есть, ток, если замерить тоже есть, при этом ни какой полезной работы не совершается. Соответственно активная мощность минимальна.
Если на двигателе увеличить нагрузку то сдвиг фаз начнет уменьшаться и соответственно косинус фи (cos φ) будет увеличиваться, а с ним и активная мощность.
К счастью счетчики активной мощности фиксируют соответственно только активную мощность. И нам не приходится переплачивать за полную мощность.
Однако у реактивной мощности есть большой минус она создает бесполезную нагрузку на электрическую сеть из-за этого образуются потери.
Что такое коэффициент мощности, косинус фи и тангенс фи
Одной из важнейших характеристик электрических устройств является мощность. Поэтому желательно знать, что такое коэффициент мощности и как он рассчитывается. Это поможет не только оценить эффективность использования электрической энергии, но и правильно организовать работу электроприбора.
Это поможет не только оценить эффективность использования электрической энергии, но и правильно организовать работу электроприбора.
Виды мощности
В цепи переменного электротока возникают три мощности: активная, реактивная и полная. Активную называют полезной или действующей мощностью. Это связано с тем, что она тратится на осуществление полезной работы. Обычно при этом электрическая энергия преобразуется в другие виды.
Реактивная мощность в процессе работы электроприбора не тратится, а лишь переходит из одной формы в другую. В данной мощности нуждаются устройства, принцип действия которых основывается на использовании электромагнитного поля.
Одним из примеров таких устройств может служить колебательный контур, включающий в себя индуктивность и ёмкость в предположении, что активное сопротивление деталей пренебрежимо мало. Ещё одним можно считать трансформатор. В нём ток и напряжение передаются по сердечнику с помощью колебаний электромагнитного поля.
Полную мощность можно получить векторным сложением активной и реактивной составляющих.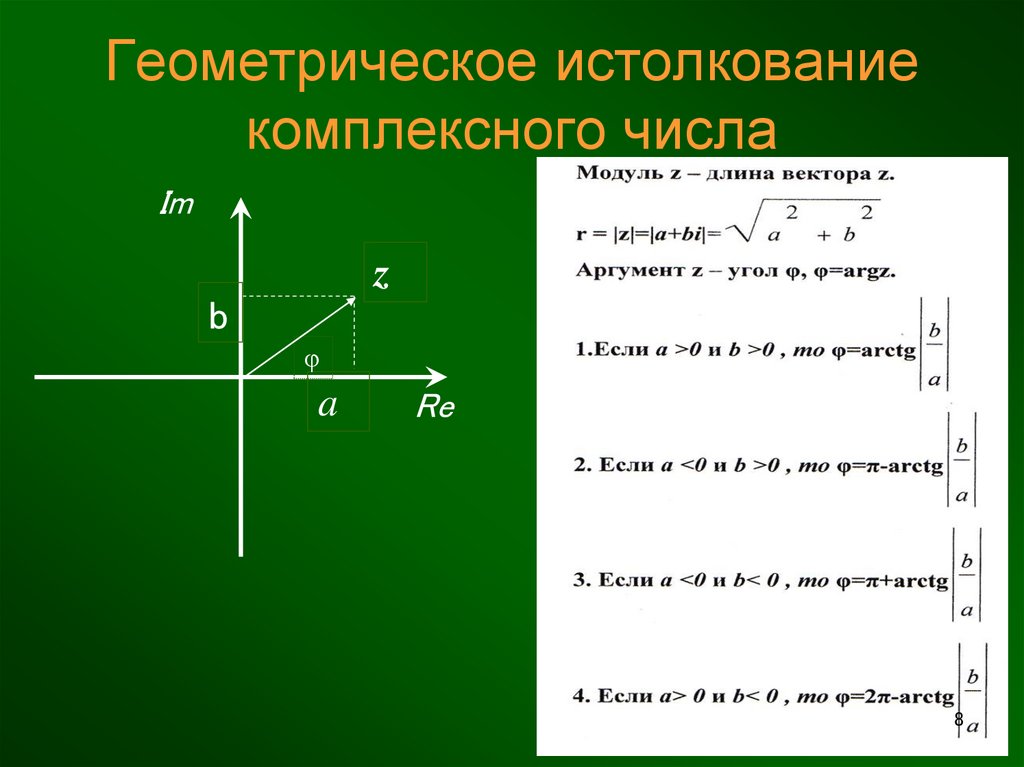
Что такое коэффициент мощности
Иногда бывает важно понять, какая часть мощности уходит на выполнение полезной работы. Для этого необходимо узнать активную и реактивную мощность рассматриваемого электрического прибора. Далее на их основе определяют полную.
В электротехнике для определения мощности в сети постоянного тока используется следующее соотношение:
В цепи переменного тока вычисление искомой величины производится более сложным образом. При этом следует учитывать, что изменения напряжения и тока по времени совпадать не будут. Электроток в ёмкостной нагрузке опережает напряжение, а в индуктивной, наоборот, отстает.
Поэтому при вычислении мощности принято использовать эффективные значения тока и напряжения. При этом рассматривается такая постоянная величина тока и напряжения, которая на активном сопротивлении выделит то же количество тепла, что и рассматриваемые переменные величины.
Конечно, в таких случаях можно также вычислить мгновенную мощность.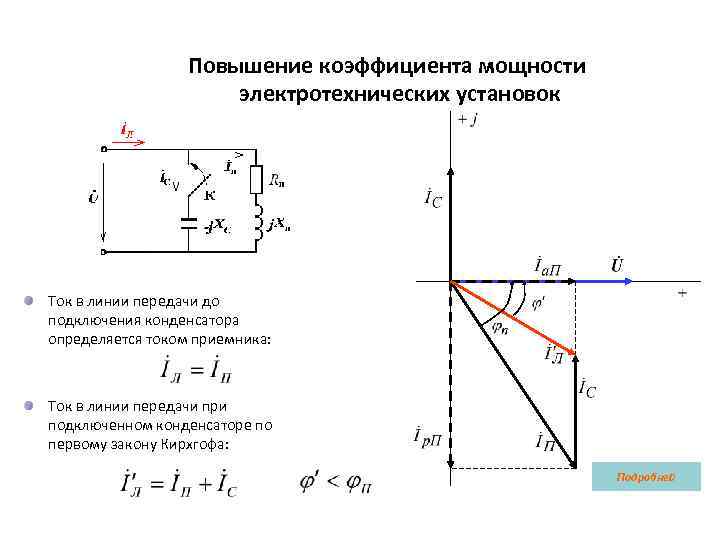 Для этого достаточно перемножить мгновенные значения тока и напряжения. Однако данная величина не учитывает сильную инерцию энергетических процессов, в связи с чем подобный расчет величин имеет ограниченное применение.
Для этого достаточно перемножить мгновенные значения тока и напряжения. Однако данная величина не учитывает сильную инерцию энергетических процессов, в связи с чем подобный расчет величин имеет ограниченное применение.
Чтобы определить коэффициент активной мощности нужно разделить активную мощность на полную. Данный коэффициент позволяет оценить эффективность использования рассматриваемого технического решения. Соотношение между реактивной и активной мощностью определяет тангенс «фи».
Полная мощность измеряется в вольт-амперах (ВА). Для активной используют ватты (Вт). Для реактивной применяется единица измерения вольт-ампер реактивный (ВАР).
Поскольку сложение мощностей происходит по векторным правилам, то нужно учитывать, что векторы активной и реактивной составляющих перпендикулярны друг к другу. Результат вычислений представляет собой гипотенузу прямоугольного треугольника с указанными катетами. Формула полной мощности выглядит следующим образом:
Это следует из теоремы Пифагора. Здесь применяется правило для нахождения гипотенузы прямоугольного треугольника. Если выразить катеты через гипотенузу и угол «фи», то можно получить формулу для определения активной мощности:
Здесь применяется правило для нахождения гипотенузы прямоугольного треугольника. Если выразить катеты через гипотенузу и угол «фи», то можно получить формулу для определения активной мощности:
Аналогичным образом выражается и реактивная:
Следовательно, из формулы для активной мощности можно найти cosφ:
Для трехфазного напряжения формула принимает следующий вид:
Поэтому следует понимать, что такое косинус «фи» в данной формуле. А это все тот же коэффициент мощности, который позволяет оценивать электроприемники при наличии реактивной составляющей в потребляемом токе.
Называется cosφ коэффициентом мощности в связи с тем, что при векторном сложении в прямоугольном треугольнике значение косинуса угла φ можно найти, разделив длину катета, соответствующего активной мощности, на длину гипотенузы, выражающей полную мощность. Следовательно, формула коэффициента мощности выглядит так:
Коэффициент активной мощности cosφ может иметь значение в диапазоне от 0 до 1. Иногда его выражают в процентах. В таком случае коэффициент обозначают греческой буквой «лямбда». Соотношение катетов в прямоугольном треугольнике определяет тангенс «фи».
Иногда его выражают в процентах. В таком случае коэффициент обозначают греческой буквой «лямбда». Соотношение катетов в прямоугольном треугольнике определяет тангенс «фи».
Коэффициент мощности является низким в тех случаях, когда активная составляющая мала по сравнению с полной мощностью. Это говорит о неэффективности применяемого оборудования.
Для тока и напряжения синусоидальной формы cosφ соответствует косинусу угла отставания по фазе для этих параметров.
Выгода электрооборудования с высоким коэффициентом мощности
Это связано с наличием следующих факторов:
- Поставщики электроэнергии в некоторых случаях контролируют коэффициент мощности оборудования, используемого потребителями. Они могут выставлять дополнительный счёт, если он будет ниже 0.95. В том случае, когда коэффициент меньше 0.85, поставка электроэнергии может быть ограничена.
- Низкий коэффициент приводит к тому, что при относительно небольшом объёме полезной работы происходят повышенные траты электроэнергии.
 Таким образом, за определённый объём полезной работы потребителю приходится переплачивать.
Таким образом, за определённый объём полезной работы потребителю приходится переплачивать. - В линиях электропередач наличие высоких показателей указывает на незначительные потери при передаче энергии.
- Низкий коэффициент в системе электроснабжения может приводить к уменьшению напряжения в сети. Это часто становится причиной перегрева используемых потребителем устройств.
При рассмотрении работы электрических устройств нужно учитывать, что часть из них генерирует реактивную мощность, а другие являются потребителями. Следовательно, применение первых приводит к возрастанию реактивной мощности, а использование вторых — к её уменьшению.
Реактивная мощность генерируется при работе асинхронного электродвигателя, трансформаторов, ветряных генераторов, систем освещения на разрядных лампах. Наличие реактивной нагрузки ухудшает эффективность работы оборудования. В качестве потребителей рассматриваются конденсаторы, синхронные двигатели и генераторы.
Для уменьшения реактивной мощности можно использовать следующие способы:
- В цепи устанавливаются конденсаторы.
 При их использовании совместно с индуктивностью они образуют колебательный контур. В нём мощность от индуктивности будет потребляться ёмкостью.
При их использовании совместно с индуктивностью они образуют колебательный контур. В нём мощность от индуктивности будет потребляться ёмкостью. - Следует избегать работы асинхронных двигателей вхолостую или с малой мощностью.
- Нужно исключить возможность работы оборудования при напряжении, которое превышает номинальное.
- Рекомендуется по мере замены двигателей переходить на те, которые имеют более высокий коэффициент полезного действия.
Оптимальной нагрузкой является номинальная. Если используется нагрузка, значение которой меньше или больше номинальной, то это существенно снижает эффективность работы оборудования.
Как узнать коэффициент мощности
Значение рассматриваемого коэффициента указывается в сопроводительной технической документации к приобретаемому промышленному оборудованию или бытовому прибору. Однако при этом речь идёт о номинальном значении.
Более точно коэффициент измеряется с помощью специализированного прибора, который называется фазометром.
Такие приборы могут быть электродинамическими или цифровыми. С помощью измерений можно достаточно просто и с большой точностью узнать чему равен cosφ и какова эффективность использования прибора.
Если фазометра нет в распоряжении, следует воспользоваться амперметром, вольтметром и ваттметром, с помощью которых измеряются такие физические величины, как сила тока, напряжение и мощность, а затем с помощью соответствующих формул вычислить коэффициент мощности.
Значения коэффициента для различных случаев
При измерении или вычислении коэффициента мощности необходимо знать характерные значения для различных видов оборудования:
- При использовании нагревательных устройств, несмотря на возможное присутствие индуктивных элементов, считается, что вся используемая мощность является активной. В таких случаях принимают косинус «фи» равный единице.
- Для перфораторов и ударных дрелей этот коэффициент составляет 0.95-0.97.
- Сварочные трансформаторы в значительной степени используют индуктивную нагрузку.
 Поэтому коэффициент мощности трансформатора обычно находится в диапазоне от 0.5 до 0.85.
Поэтому коэффициент мощности трансформатора обычно находится в диапазоне от 0.5 до 0.85.
Когда значения коэффициента являются широко известными, их могут не указывать в сопроводительной документации. Нужно помнить, что хотя в большинстве случаев напряжение меняется синусоидально, иногда оно может существенно отклоняться от этой формы. В такой ситуации говорят о присутствии высших гармоник в колебаниях.
Их появление ведёт к дополнительным затратам мощности, а также снижает компенсацию реактивной мощности, если она применялась. Подобное явление наблюдается при работе с дуговыми сталеплавильными печами, установками дуговой сварки, газоразрядными лампами.
Косинус фи — простое объяснение в 3-х словах. Таблицы коэффициента мощности для различных потребителей.
Многие из вас наверняка видели на электроинструментах, двигателях, а также люминесцентных лампах, лампах ДРЛ, ДНАТ и других, такие надписи как косинус фи — cos ϕ.
Однако люди далекие от электротехники и позабывшие школьные уроки физики, не совсем понимают, что же означает данный параметр и зачем он вообще нужен.
Давайте рассмотрим и объясним этот косинус, как можно более простыми словами, исключая всякие непонятные научные определения, типа электромагнитная индукция. В двух словах про него конечно не расскажешь, а вот в трех можно попробовать.
Когда ток отстает от напряжения
Предположим перед вами есть 2 проводника. Один из этих проводников имеет потенциал. Не суть важно какой именно — отрицательный (минус) или положительный (плюс).
У другого провода вообще нет никакого потенциала. Соответственно между этими двумя проводниками будет разность потенциалов, т.к. у одного он есть, а у другого его нет.
Эту разность потенциалов как раз таки и принято называть напряжением.
Если вы соедините кончики двух проводов не непосредственно между собой, а через лампочку накаливания, то через ее вольфрамовую нить начнет протекать ток. От одного провода к другому.
На первый взгляд может показаться, что лампочка загорается моментально. Однако это не так. Ток проходя через нить накала, будет нарастать от своего нулевого значения до номинального, какое-то определенное время.
Однако это не так. Ток проходя через нить накала, будет нарастать от своего нулевого значения до номинального, какое-то определенное время.
В какой-то момент он его достигает и держится на этом уровне постоянно. То же самое будет, если подключить не одну, а две, три лампочки и т.д.
А что случится, если вместе с лампой последовательно включить катушку, намотанную из множества витков проволоки?
Изменится ли как-то процесс нарастания тока? Конечно, да.
Данная катушка индуктивности, заметно затормозит время увеличения тока от нуля до максимума. Фактически получится, что максимальное напряжение (разность потенциалов) на лампе уже есть, а вот ток поспевать за ним не будет.
Его нарастание слишком медленное. Из-за чего это происходит и кто виноват? Виноваты витки катушки, которые оказывают влияние друг на друга и тормозят ток.
Если у вас напряжение постоянное, например как в аккумуляторах или в батарейках, ток относительно медленно, но все-таки успеет дорасти до своего номинального значения.
А далее, ток будет вместе с напряжением идти, что называется «нога в ногу».
А вот если взять напряжение из розетки, с переменной синусоидой, то здесь оно не постоянно и будет меняться. Сначала U какое-то время положительная величина, а потом — отрицательная, причем одинаковое по амплитуде. На рисунке это изображается в виде волны.
Эти постоянные колебания не дают нашему току, проходящему сквозь катушку, достигнуть своего установившегося значения и догнать таки напряжение. Только он будет подбираться к этой величине, а напряжение уже начинает падать.
Поэтому в этом случае и говорят, что ток отстает от напряжения.
Причем, чем больше в катушке намотано витков, тем большим будет это самое запаздывание.
Как же это все связано с косинусом фи — cos ϕ?
Что такое коэффициент мощности
А связано это таким образом, что данное отставание тока измеряется углом поворота. Полный цикл синусоиды или волны, который она проходит от нуля до нуля, вместив в себя максимальное и минимальное значение, измеряется в градусах. И один такой цикл равен 360 градусов.
И один такой цикл равен 360 градусов.
А вот угол отставания тока от напряжения, как раз таки и обозначается греческой буквой фи. Значение косинуса этого угла опаздывания и есть тот самый cos ϕ.
Таким образом, чем больше ток отстает от напряжения, тем большим будет этот угол. Соответственно косинус фи будет уменьшаться.
По научному, ток сдвинутый от напряжения называется фазовым сдвигом. При этом почему-то многие уверены, что синусоида всегда идеальна. Хотя это далеко не так.
В качестве примера можно взять импульсные блоки питания.
Не идеальность синусоиды выражается коэфф. нелинейных искажений — КНИ. Если сложить две эти величины — cos ϕ и КНИ, то вы получите коэффициент мощности.
Однако, чтобы все не усложнять, чаще всего под понятием коэфф. мощности имеют в виду только лишь один косинус фи.
На практике, данный коэффициент мощности рассчитывают не при помощи угла сдвига фаз, а отношением активной мощности к полной.
Активная и реактивная мощность
Существует такое понятие как треугольник мощностей. Сам косинус — это тригонометрическая функция, которая и появилась при изучении свойств прямоугольных треугольников.
Сам косинус — это тригонометрическая функция, которая и появилась при изучении свойств прямоугольных треугольников.
Она здорово помогает производить определенные вычисления с ними. Например, наглядно показывает отношение длин прилежащего катета (P-активная мощность) к гипотенузе (S-полная мощность).
То есть, зная угол сдвига, можно узнать, сколько активной мощности содержится в полной. Чем меньше этот угол, тем меньше реактивной составляющей находится в сети, и наоборот.
Только не путайте cos ϕ с КПД. Это разные понятия. Реактивная составляющая не расходуется, а «возвращается» на подстанцию в сеть, т.е. фактически потери ее нет. Только небольшая ее часть может тратиться на нагрев проводов.
В КПД все более четко — полезная мощность используется на нагрев — охлаждение — механическую работу, остальное уходит безвозвратно. Эта разница и показывается в КПД.
Более подробно, с графиками, рисунками и простыми словами, без особых научных формулировок обо всем этом говорится в ролике ниже.
Низкий коэффициент мощности и его последствия
Рассмотренное запаздывание тока относительно напряжения — это не хорошее явление. Как оно может сказаться на ваших лампочках или проводке?
- во-первых, это повышенное потребление электроэнергии
Часть энергии будет просто «болтаться» в катушке, при этом не принося никакой пользы. Правда не пугайтесь, ваш бытовой счетчик реактивную энергию не считает и платить вы за нее не будете.
Например, если вы включите в розетку инструмент или светильник с полной мощностью 100Ва, на блоке питания которого будет указано cos ϕ=0,5. То прибор учета накрутит вам только на половину от этой величины, то есть 50Вт.
Зато по проводам питания будет проходить вся нагрузка, разогревая их бесполезной работой.
- величина тока в проводке увеличится
Вот известное наглядное видео, демонстрирующее последствия этого для проводки.
- для эл.станций и трансформаторов оно вредно перегрузкой
Казалось бы, выбрось катушку и вся проблема исчезнет. Однако делать этого нельзя.
В большинстве светильников, лампы работают не отдельно, а в паре с источниками питания. И в этих самых источниках, как раз таки присутствуют разнообразные катушки.
Катушки просто необходимы как функциональная часть всей схемы и избавиться от них не получится. Например в тех же дроссельных лампах ДРЛ, ДНАТ, люминесцентных и т.п.
Поэтому характеристика коэфф. мощности, здесь больше относится к блоку питания, нежели к самой лампе. Данный cos ϕ может принимать значение от ноля до единицы.
мощности, здесь больше относится к блоку питания, нежели к самой лампе. Данный cos ϕ может принимать значение от ноля до единицы.
Ноль означает, что полезная работа не совершается. Единица — вся энергия идет на совершение полезной работы.
Чем выше коэффициент мощности, тем ниже потери электроэнергии. Вот таблица косинуса фи для различных потребителей:
Как измерить коэффициент мощности
Если вы не знаете точный коэфф. мощности своего прибора, или его нет на бирке, можно ли измерить косинус фи в домашних условиях, не прибегая к различным формулам и вычислениям? Конечно можно.
Для этого достаточно приобрести широко распространенный инструмент — цифровой ваттметр в розетку.
Подключая любое оборудование через него, можно легко без замеров и сложных вычислений, узнать фактический cos ϕ.
Зачастую, фактические данные могут быть даже точнее, чем написанные на шильдике, которые рассчитаны для идеальных условий.
Если он слишком низкий, что делать, чтобы привести его значение как можно ближе к единице? Можно это дело определенным образом компенсировать. Например, с помощью конденсаторов.
Например, с помощью конденсаторов.
Однако это тема совсем другой статьи.
Теорема косинусов и синусов треугольника. Формулы и примеры
Формулировка и доказательство теоремы косинусов
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Формула Теоремы Пифагора:
a2> + b2> = c2>, где a, b — катеты, с — гипотенуза.
Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними. Формула теоремы косинусов: a2 = b2 + c2 — 2bc cos α |
В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:
BC2 = (x2 — x1)2 + (y2 — y1)2
В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).
cos2α + sin
BC2 = a2 = (b cos α — c)2 + b2sin2α = b2cos2α + b2sin2α — 2bc cos α + c2 = b2(cos2α + sin2α) — 2bc cos α + c2
Что и требовалось доказать.
Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.
С помощью теоремы косинусов можно найти косинус угла треугольника:
- Когда b2 + c2 — a2 > 0, угол α будет острым.
- Когда b2 + c2 — a2 = 0, угол α будет прямым.
- Когда b2 + c2 — a2 < 0, угол α будет тупым.

Запоминаем
Когда угол α прямой, то теорема косинусов превращаеся в теорему Пифагора.
Сформулируем еще одно доказательство теоремы косинусов.
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:
- AD = b × cos α,
- DB = c – b × cos α.
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
- h2 = b2 — (b × cos α)2
- h2 = a2 — (c – b × cos α)2
Приравниваем правые части уравнений:
- b2 — (b × cos α)2 = a2 — (c — b × cos α)2
либо
- a2 = b2 + c2 — 2bc × cos α
Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.
Определим стороны b и c:
- b2
- c2 = a2 + b2 — 2ab × cos γ.

Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Формулировка теоремы для каждой из сторон треугольника
Теорема косинусов справедлива для всех сторон треугольника, то есть:
a2 = b2 + c2 — 2bc cos α
b2 = c2 + a2 — 2ca cos β
c2 = a2 + b2 — 2ab cos γ
Теорема косинусов может быть использована для любого вида треугольника.
Косинусы углов треугольника
Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:
Аналогично:
Учёба без слёз (бесплатный гайд для родителей)
Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.
Определение угла с помощью косинуса
А теперь обратим внимание на углы.
Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).
Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.
Рассмотрение пределов изменения cos α и sin α
Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.
Предел изменения косинуса: -1 < cos α < 1.
Предел изменения синуса: 0 < sin α ≤ 1.
- Если cos α > 0, то α ∈ (0°;90°)
- Если cos α < 0, то α ∈ (90°;180°)
- Если cos α = 0, то α = 90°
Примеры решения задач
При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.
Пример 1. Дан треугольник АВС. Найти длину СМ.
∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.
Как решаем:
- Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
Из треугольника АВС найдем cos B: - Из треугольника СМВ по теореме косинусов найдём СМ:
Ответ: СМ = .
Пример 2. Дан треугольник АВС, в котором a2 + b2 < c2. Доказать, что ∠C — тупой угол.
Как доказываем:
- Для доказательства нужно вспомнить теорему косинусов для угла ∠C:
- Так как a2 + b2 < c2, то cos C < 0, следовательно, ∠C — тупой.
Что и требовалось доказать.
Эта задача нам показала, что с помощью теоремы косинусов можно определить тупой угол или острый.
- Если c2 = a2 + b2, то ∠C = 90°.

- Если c2 < a2 + b2, то ∠C — острый.
Больше объяснений по этой и другим темам вы найдете в справочнике по математике — с формулами, чертежами и примерами решения задач.
| ГОСТы, СНиПы Карта сайта TehTab.ru Поиск по сайту TehTab.ru | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация/ / Физический справочник/ / Электрические и магнитные величины/ / Понятия и формулы для электричества и магнетизма. / / Коэффициент мощности (cos φ, косинус фи ), Полная (кажущаяся), активная и реактивная мощность электродвигателя=электромотора и не только его.
| |||||||
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу. | ||||||||
TehTab.ru Реклама, сотрудничество: [email protected] | Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями. | |||||||
Что такое косинус фи в электрике
Как найти электрическую мощность
Основная единица электрической мощности — Ватт. Электрическую мощность можно найти по следующей формуле:
Формула мощности
Давайте рассмотрим формулу, которую я привёл выше.
I (ток)- количество электричества, протекающее за определённый момент времени;
U(напряжение) — проделанная работа электрического поля по переносу заряду из точки А в точку В.
А теперь простыми словами: Два человека (это будет у нас ток) несут вместе один камень из точки А в точку В весом в 50 кг и тратят на это энергию (это напряжение), и один человек несёт камень массой 10 кг и тоже тратит энергию. Весовая категория у людей одинаковая. Если эти данные мы перенесём в нашу формулу, то выясним, что у двух людей мощность больше, чем у одного.
Приведу ещё формулы, по которым можно рассчитать электрическую мощность:
Формула мощности
Где: I-
ток, U- напряжение, R-
сопротивление
Как видите ничего сложного нет, потому что мы рассматриваем постоянный ток.
Косинус угла в электротехнике
Распределительная трансформаторная подстанция. рп в электрике что это. что такое рп в электрике
Итак, что такое косинус в электротехнике? Дело в том, что есть такое явление, как сдвиг фаз между током и напряжением
Он происходит по разным причинам, и иногда важно знать о его величине. Сдвиг фаз можно измерить в градусах, от 0 до 360
На практике степень реактивности (без указания индуктивного либо емкостного характера) выражают не в градусах, а в функции косинуса, и называют коэффициентом мощности:
cos fi
где:
- P – активная мощность, которая тратится на совершение полезной работы,
- S – полная мощность.
Полная мощность является геометрической суммой активной Р и реактивной Q мощностей, поэтому формулу коэффициента мощности можно записать в следующем виде:
Формула коэффициента мощности через активную и реактивную мощности
В иностранной литературе cos φ называют PF (Power Factor). Фактически, это коэффициент, который говорит о сдвиге сигнала тока по отношению к сигналу напряжения.
Фактически, это коэффициент, который говорит о сдвиге сигнала тока по отношению к сигналу напряжения.
Легендарный Алекс Жук очень толково рассказал, что такое реактивная мощность, и всё по этой теме:
В видео подробно и доступно изложена вся теория по теме.
«Звезда»
При соединении обмоток звездой к началам обмоток присоединяют питающие провода (на схемах обозначены цветами), а концы обмоток соединяют между собой в одну точку, при этом подключение нулевого проводника в точку соединения концов обмоток необязательно так как это симметричная нагрузка. В свою очередь, точка соединения концов обмоток также называется нейтралью.
Есть два варианта представления этого соединения на электрических схемах, как в наглядном виде, действительно напоминающем трёхлучевую звезду (А), так и в более классическом для схем представлении (Б). Вас не должно смущать это отличие, когда вы читаете схему.
Активная, реактивная и полная мощности
Что такое дин рейка в электрике
Мы знаем, что реактивные нагрузки (индуктивности и конденсаторы) не рассеивают мощность, но то, что на них падает напряжение и через них протекает ток, даёт обманчивое впечатление, что они всё-таки рассеивают мощность. Эта «фантомная мощность» называется реактивной мощностью, а её единицей измерения является вольт-ампер реактивный (вар), а не ватт.
Эта «фантомная мощность» называется реактивной мощностью, а её единицей измерения является вольт-ампер реактивный (вар), а не ватт.
Реактивная мощность в математических выражениях обозначается прописной буквой Q. Фактическое количество используемой или рассеиваемой в цепи мощности называется активной мощностью и измеряется в ваттах (обозначается, как обычно, прописной буквой P). Комбинация реактивной и активной мощностей называется полной мощностью и является произведением напряжения и тока цепи без учёта угла сдвига фаз. Полная мощность измеряется в вольт-амперах (ВА) и обозначается прописной буквой S.
Как правило, величина активной мощности определяется сопротивлением рассеивающих ее элементов цепи, обычно резисторов (R). Реактивная мощность определяется величиной реактивного сопротивления (X). Полная мощность определяется полным сопротивлением цепи (Z). Поскольку при определении мощности мы имеем дело со скалярными величинами, любые исходные комплексные величины (напряжение, ток и полное сопротивление) должны быть представлены в показательной форме, а не в виде действительных или мнимых составляющих. К примеру, при определении активной мощности по величинам тока и сопротивления необходимо использовать величину тока в полярной системе координат, а не действительную или мнимую часть. При определении полной мощности по напряжению и полному сопротивлению обе эти комплексные величины должны быть представлены в полярной системе координат для применения скалярной арифметики.
К примеру, при определении активной мощности по величинам тока и сопротивления необходимо использовать величину тока в полярной системе координат, а не действительную или мнимую часть. При определении полной мощности по напряжению и полному сопротивлению обе эти комплексные величины должны быть представлены в полярной системе координат для применения скалярной арифметики.
Имеется несколько выражений, связывающих три типа мощности со значениями активного, реактивного и полного сопротивления (во всех случаях используются скалярные величины).
P – активная мощность P = I2R P = E2/R Единицей измерения является ватт |
Q – реактивная мощность Q = I2X Q = E2/X Единицей измерения является вольт-ампер реактивный (вар) |
S – полная мощность S = I2Z S = E2/Z S = IE Единицей измерения является вольт-ампер (ВА) |
Обратите внимание, что для определения активной и реактивной мощности имеются два выражения. Для определения полной мощности есть три выражения, P = IE используется только для этой цели
Для определения полной мощности есть три выражения, P = IE используется только для этой цели
Изучите схемы, приведённые ниже, и посмотрите, как определяются эти три типа мощности при резистивной нагрузке, при реактивной нагрузке и при резистивно-реактивной нагрузке (см. рисунки ниже).
Как правильно рассчитать
Что такое коэффициент
Активная мощность, как сделать правильный расчет?
Мощность электрического тока влияет на то, как быстро прибор сможет выполнить работу. К примеру, дорогой обогреватель, имеющий в 2 раза большую мощность, обогреет помещение быстрее, чем два дешевых, с меньшей в 2 раза мощностью. Получается, что выгоднее купить агрегат, имеющий большую мощность, чтобы быстрее обогреть холодное помещение. Но, в то же время, такой агрегат будет тратить существенно больше энергии, чем его более дешевый аналог.
Потребляемая мощность всех приборов в доме учитывается и при подборе проводки для прокладки в доме. Если не учитывать этого и в последующем включить в сеть слишком много приборов, то это вызовет перегрузку сети. Проводка не сможет выдержать мощность электрического тока всех приборов, что приведет к плавлению изоляции, замыканию и самовоспламенению проводки. В результате может начаться пожар, который может привести к непоправимым последствиям.
Проводка не сможет выдержать мощность электрического тока всех приборов, что приведет к плавлению изоляции, замыканию и самовоспламенению проводки. В результате может начаться пожар, который может привести к непоправимым последствиям.
Однофазный синусоидальный ток в электрических цепях вычисляется по формуле Р = U x I x cos φ, где υ и Ι. Их обозначение шифруется следующим образом: среднеквадратичное значение напряжение и тока, а φ — фазный угол фаз между ними.
Для цепей несинусоидального тока электрическая ёмкость равна корню квадратному из суммы квадратов активной и реактивной производительности. Активная производительность характеризуется скоростью, которая имеет необратимый процесс преобразования электрической энергии в другие виды энергии. Данная ёмкость может вычисляться через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле P = I(2) x r = U(2) x g.
Реактивная мощность (Reactive Power)
Следует заметить, что:
- резистор потребляет активную мощность и отдаёт её в форме тепла и света.

- индуктивность потребляет реактивную мощность и отдаёт её в форме магнитного поля.
- конденсатор потребляет реактивную мощность и отдаёт её в форме электрического поля.
В любой электрической цепи как синусоидального, так и несинусоидального тока активная способность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая емкость определяется как сумма пропускной способности отдельных фаз. С полной производительностью S, активная связана соотношением P = S x cos φ.
В теории длинных линий (анализ электромагнитных процессов в линии передачи, длина которой сравнима с длиной электромагнитной волны) полным аналогом активной мощности является проходящая мощность, которая определяется как разность между падающей мощностью и отраженной производительностью.
Как найти реактивную полную мощность через активную? Данная производительность, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению среднеквадратичных значений напряжения U и тока I, умноженному на синус угла сдвига фаз φ между ними: Q = U x I x sin φ (если ток отстаёт от напряжения, сдвиг фаз считается положительным, если опережает — отрицательным).
Обозначение реактивной величины
Сдвиг фаз между напряжением и током
Фазовый сдвиг – показатель, описывающий разность исходных фаз двух параметров, имеющих свойство меняться во времени с одинаковыми скоростями и периодами. Именно сдвиг между силой и напряжением определяет, сколько будет значение угла фи.
В радиотехнической промышленности используются цепочки для получения асинхронного хода. Одна RC-цепь создает 60-градусный сдвиг, для получения 180-градусного для трехфазной структуры организуют последовательное соединение трех цепочек.
При трансформации электродвижущей силы во вторичных обмотках прибора для всех вариаций тока ее значение идентично по фазе таковому для первичной обмотки. Если обмотки трансформатора включить в противофазе, значение напряжения получает обратный знак. Если напряжение идет по синусоиде, происходит сдвиг на 180 градусов.
В простом случае (к примеру, включение электрического чайника) фазы двух показателей совпадают, и они в одно и то же время достигают пиковых значений. Тогда при расчете потребительской мощности применять угол фи не требуется. Когда к переменному току подключен электродвигатель с составной нагрузкой, содержащей активный и индуктивный компоненты (двигатель стиральной машинки и т.д.), напряжение сразу подается на обмотки, а ток отстает вследствие действия индуктивности. Таким образом, между ними возникает сдвиг. Если индуктивный компонент (обмотки) подменен использованием достижений химии в виде емкостного аккумулятора, отстающей величиной, напротив, оказывается напряжение.
Тогда при расчете потребительской мощности применять угол фи не требуется. Когда к переменному току подключен электродвигатель с составной нагрузкой, содержащей активный и индуктивный компоненты (двигатель стиральной машинки и т.д.), напряжение сразу подается на обмотки, а ток отстает вследствие действия индуктивности. Таким образом, между ними возникает сдвиг. Если индуктивный компонент (обмотки) подменен использованием достижений химии в виде емкостного аккумулятора, отстающей величиной, напротив, оказывается напряжение.
Косинус фи не следует путать с другим показателем, рассчитываемым для комплексных нагрузок, – коэффициентом демпфирования. Он широко используется в усилителях мощности и равен частному номинального сопротивлению прибора и выходному – усилка.
Угол фазового сдвига
Виды мощностей
Мощностью называется измеряемая физическая величина, которая равна скорости изменения с преобразованием, передачей или потреблением системной энергии. Согласно более узкому понятию, это показатель, который равен отношению затраченного времени на работы к самому периоду, который тратится на работу. Обозначается в механике символом N. В электротехнической науке используется буква P. Нередко можно увидеть также символ W, от слова ватт.
Обозначается в механике символом N. В электротехнической науке используется буква P. Нередко можно увидеть также символ W, от слова ватт.
Мощность переменного тока -это произведение силы тока с напряжением и косинусом сдвига фаз. При этом беспрепятственно можно посчитать только активную и реактивную разновидность. Узнать полное мощностное значение можно через векторную зависимость этих показателей и площади.
Основные мощностные разновидности
Активная мощность
Активной называется полезная сила, определяющая процесс прямого преобразования электроэнергии в необходимый вид силы. В каждом электроприборе преобразовывается она по-своему. К примеру, в лампочке получается свет с теплом, в утюге — тепло, а в электрическом двигателе — механическая энергия. Соответственно, показывает КПД устройства.
Активная разновидность
Реактивная мощность
Реактивной называется та, которая определяется при помощи электромагнитного поля. Образуется при работе электроприборов
Обратите внимание! Это вредная и паразитная мощностная характеристика, которая определяется тем, каков характер нагрузки. Для лампочки она равняется нулю, а для электродвигателя она может быть равна большим значением
Для лампочки она равняется нулю, а для электродвигателя она может быть равна большим значением
Разница между величинами в том, что активно действующая мощностная характеристика показывает КПД устройств, а реактивная является передачей этого КПД. Разница также наблюдается в определении, символе, формуле и значимости.
Обратите внимание! Что касается значения, то вторая нужна лишь для того, чтобы управлять создавшимся напряжением от первой величины и преодолевать мощностные колебания. Обе измеряются в ваттах и имеют большое значение в электромагнитном излучении, механической форме генератора или акустической волне
Активно применяются в промышленности.
Реактивная разновидность
Полная мощность
Полная — это сумма активной с реактивной мощностью. Равна сетевому мощностному показателю. Это произведение напряжения с током в момент игнорирования фазы угла между ними. Вся рассеиваемая с поглощаемой и возвращаемой энергией — это полная энергия.
Это произведение напряжения и тока, единица измерения которого это ватт, перемноженный на ампер. При активности цепи, полная равняется активной. Если речь идет об индуктивной или емкостной схеме, то полная больше, чем активная.
При активности цепи, полная равняется активной. Если речь идет об индуктивной или емкостной схеме, то полная больше, чем активная.
Полная разновидность
Комплексная мощность
Это сумма всех мощностных показателей фаз источника электроэнергии. Это комплексный показатель, модуль которого равняется полному мощностному показателю электроцепи. Аргументом является фазовый сдвиг между электротоком с сетевым напряжением. Может быть выражена уравнением, где суммарный мощностный показатель, который генерируют источники электроэнергии, равен суммарному мощностному показателю, который потребляется в электроцепи.
Обратите внимание! Вычисляется посредством использования соответствующей формулы. Так, необходимо комплексное напряжение перемножить на комплексны ток или же удвоенное значение комплексного тока перемножить на импеданс
Также можно удвоенное значение комплексного напряжения поделить на удвоенное значение импеданса.
Комплексная разновидность
Способы увеличения «косинуса фи»
Вышеперечисленные последствия низкого cos φ с достаточной убедительностью говорят о том, что необходимо вести борьбу за высокий cos φ. К мерам увеличения cos φ относятся:
К мерам увеличения cos φ относятся:
- Правильный выбор типа, мощности и скорости вновь устанавливаемых двигателей;
- Увеличение загрузки двигателей;
- Недопущение работы двигателей вхолостую продолжительное время;
- Правильный и высококачественный ремонт двигателей;
- Применение статических (то есть неподвижных, невращающихся) конденсаторов.
Малый вес конденсаторов, отсутствие вращающихся частей, незначительные потери энергии в них, легкость обслуживания, безопасность и надежность в работе дают возможность широкого применения статических конденсаторов для повышения cos φ двигателей.
Подбирая величину емкости при параллельном соединении и емкости, можно добиться уменьшения угла сдвига фаз между напряжением и общим током при неизменной активной и реактивной мощности, потребляемой ветвью с индуктивностью. Этот угол можно сделать равным нулю. Тогда ток, текущий на общем участке цепи, будет иметь наименьшую величину и совпадать по фазе с напряжением сети.
Это явление называется компенсацией сдвига фаз и широко используется на практике. По экономическим соображениям невыгодно доводить угол φ до нуля, практически целесообразно иметь cos φ = 0,9 – 0,95.
Рассмотрим расчет емкости конденсаторов, которые нужно включить параллельно индуктивной нагрузке, чтобы повысить cos φ до заданной величины.
На рисунке 1, а изображена схема включения индуктивной нагрузки в сеть переменного тока. Для увеличения коэффициента мощности параллельно потребителю включена батарея конденсаторов. Векторная диаграмма начинается с построения вектора напряжения U. Ток I1 вследствие индуктивного характера нагрузки отстает по фазе от напряжения сети на угол φ1. Необходимо уменьшить угол сдвига фаз между напряжением U и общим током до величины φ. Иначе говоря, увеличить коэффициент мощности от значения cos φ1 до значения cos φ.
Рисунок 1. Увеличение cos φ при помощи статических конденсаторов:а – схема включения; б – векторная диаграмма
Отрезок ос, представляющий активную слагающую тока I1, равен:
ос = I1 × cos φ1 = оа × cos φ1 .
Пользуясь выражением мощности переменного тока
P = U × I × cos φ ,
отрезок ос выразим так:
Ток на общем участке цепи I равен геометрической сумме тока нагрузки I1 и тока конденсатора IC.
Из треугольника оас и овс имеем:
ас = ос × tg φ1 ;bс = ос × tg φ .
Из диаграммы получаем:
ab = od – ac – bc = ос × tg φ1 – ос × tg φ = oc × (tg φ1 – tg φ) .
Так как
abIC
Вместе с этим, как было указано выше,
IC = U × ω × C .
Следовательно,
Пример 1. Электрические двигатели шахты потребляют мощность 2000 кВт при напряжении 6 кВ и cos φ1 = 0,6. Требуется найти емкость конденсаторов, которую нужно подключить на шины установки, чтобы увеличить cos φ до 0,9 при f = 50 Гц.
Решение.
cos φ1 = 0,6; φ1 = 53°10’; tg φ1 = 1,335;
cos φ = 0,9; φ = 25°50’; tg φ = 0,484;
Что такое полная мощность на примере простой R-L цепи
Графики изменения мгновенных значений u,i:
Графики изменения мгновенных значений u,i:
φ — фазовый сдвиг между током и напряжением
Уравнение для S примет следующий вид
Подставим вместо и заменим амплитудные значения на действующие:
Значение S рассматривается как сумма двух величин , где
и — мгновенные активные и реактивные мощности на участках R-L.
Графики p,q,s:
Как видим из графика, наличие индуктивной составляющей повлекло за собой появление отрицательной части в полной мощности (заштрихованная часть графика), что снижает ее среднее значение. Это происходит из-за фазового сдвига, в какой-то момент времени ток и напряжение находятся в противофазе, поэтому появляется отрицательное значение S.
Итоговые выражения для действующих значений:
Активная составляющая сети выражается в ваттах (Вт), а реактивная в вольт-амперах реактивных (вар).
Полная мощность сети S, обусловлена номинальными данными генератора. Для генератора она обусловлена выражением:
Для нормальной работы генератора ток в обмотках и напряжение на зажимах не должны превышать номинальные значения Iн, Uн. Для генератора значения P и S одинаковы, однако все-таки на практике условились S выражать в вольт-амперах (ВА).
Также энергию сети можно выразить через каждую составляющую отдельно:
Где S, P, Q – соответственно активное, реактивное и полное сопротивление сети. Они образуют треугольник мощностей:
Они образуют треугольник мощностей:
Треугольник мощностей с преобладающей индуктивной нагрузкой
Если вспомнить теорему Пифагора, то из прямоугольного треугольника можно получить такое выражение:
Реактивная составляющая в треугольнике является положительной (QL), когда ток отстает от напряжения, и отрицательной (QC), когда опережает:
Треугольник мощностей с преобладающей емкостной нагрузкой
Для реактивной составляющей сети справедливо алгебраическое выражение:
Из чего следует что индуктивная и емкостная энергия взаимозаменяемы. То есть если вы хотите уменьшить влияние индуктивной части цепи, вам необходимо добавить емкость, и наоборот. Ниже пример данной схемы :
Схема компенсации реактивной составляющей
Векторная диаграмма показывает влияние конденсатора на cosφ. Как видно, что при включении конденсатора cosφ2> cosφ1 иIл<I.
Векторная диаграмма
Связь между полной и реактивной энергии выражается:
Отсюда:
сosφ – это коэффициент мощности. он показывает какую долю от полной энергии составляет активная энергия. Чем ближе он к 1, тем больше полезной энергии потребляется из сети.
он показывает какую долю от полной энергии составляет активная энергия. Чем ближе он к 1, тем больше полезной энергии потребляется из сети.
Соединение в треугольник электроприемников и конденсаторных батарей.
Соединение в треугольник обмоток электродвигателей показано на рисунках 4, а – в. При этом на рисунке 4, а обмотки и соединены и расположены треугольником; на рисунке 4, б обмотки соединены треугольником, но расположены произвольно; на рисунке 4, в обмотки расположены звездой, но соединены в треугольник. На рисунке 4, г обмотки расположены треугольником, но соединены в звезду.
Рисунок 4. Соединение в треугольник электроприемников.
Все эти рисунки подчеркивают, что дело отнюдь не в том, как расположены изображения электроприемников на чертежах (хотя их часто удобно располагать в соответствии с видом соединения), а в том, что с чем соединено: концы (начала) всех обмоток между собой или конец одной обмотки с началом другой. В первом случае получается соединение в звезду, во втором – в треугольник.
Соединение в треугольник конденсаторных батарей показано на рисунке 4, д.
На рисунке 4, е показано соединение в треугольник ламп. Хотя лампы территориально разбросаны по разным квартирам, но они объединены сначала в группы в пределах каждой квартиры, затем в группы по стоякам 2 и, наконец, эти группы соединены в треугольник на вводном щите 1. Заметьте: до вводного щита нагрузка трехфазная, после вводного щита (в стояках и квартирах) однофазная, хотя она и включена между двумя фазами.
На каком основании нагрузка, питающаяся от двух фаз названа однофазной? На том основании, что изменения тока в обоих проводах, к которым присоединена нагрузка, происходят одинаково, то есть в каждый момент ток проходит через одни и те же фазы.
Видео 1. Соединение треугольником
1 Отсутствие тока в замкнутом контуре еще не означает, что в фазных обмотках нет тока. Токи в фазных обмотках соответствуют их нагрузкам.
Выводы обмоток
Для сетей переменного тока 50 Гц линейное напряжение выше фазного в квадратный корень из трёх раз то есть примерно в 1.
От того, выберем мы один или другой, будет зависеть в какую сторону начнет вращаться двигатель. Однако, по крайней мере, можно использовать 3-фазное подключение треугольником. Это позволяет использовать по полной КПД электродвигателя, согласно техпаспорта.
У каждого конца свое буквенное и числовое обозначение. На рисунке 4 приведена схема включения в трехфазную четырехпроводную сеть осветительной и силовой нагрузок.
К тому же агрегат сильно нагревается в процессе работы. Поэтому электродвигатели асинхронного типа со средней и большой мощностью чаще всего подключают по схеме звезда.
Концы всех трех обмоток соединяют в одну общую точку, так называемую нейтраль. При помощи тестера провода прозванивают, чтобы найти катушки. По полученным векторным уравнениям можно для равномерной нагрузки фаз построить векторную диаграмму рис.
Концы всех трех обмоток соединяют в одну общую точку, так называемую нейтраль. В таком случае этот двигатель можно будет использовать как в трёхфазной сети с линейным напряжением В подключение звезда , так и в однофазной сети В подключение треугольником через конденсатор. Форму треугольника предает эргономичное размещение соединения обмоток. При замыкании цепи поплавком будет замыкаться цепь катушки пускателя, и включаться электродвигатель, при размыкании — будет отключаться питание электродвигателя.
Форму треугольника предает эргономичное размещение соединения обмоток. При замыкании цепи поплавком будет замыкаться цепь катушки пускателя, и включаться электродвигатель, при размыкании — будет отключаться питание электродвигателя.
К тому же агрегат сильно нагревается в процессе работы. Фазные обмотки генератора образуют замкнутый контур с малым внутренним сопротивлением.
При большой мощности двигателя, в схему потребуется внесение пускового конденсатора. Каминский, г. Сдвиг на такой угол предназначен для создания вращения магнитного поля. Это может произойти из-за неисправного пускателя, или при перекосе фаз когда напряжение в одной из фаз сильно меньше, чем в двух других.
Подключение трехфазного двигателя по схеме звезды и треугольника
https://youtube.com/watch?v=PjZextDphQU
Оцените статью:
косинус фи для потребителей, единица измерения
§ 75. Коэффициент мощности («косинус фи»)
Коэффициентом мощности, или «косинусом фи» (cos φ), цепи называется отношение активной мощности к полной мощности.
| Коэффициент мощности = | активная мощность | |
| полная мощность |
или
cos φ = P/S = P/UI = P/√(P2 + Q2).
В общем случае активная мощность меньше полной мощности, т. е. у этой дроби числитель меньше знаменателя, и поэтому коэффициент мощности меньше единицы.
Только в случае чисто активной нагрузки, когда вся мощность является активной, числитель и знаменатель этой дроби равны между собой, и поэтому коэффициент мощности равен единице.
Чем большую часть полной мощности составляет активная мощность, тем меньше числитель отличается от знаменателя дроби и тем ближе коэффициент мощности к единице.
Величину cos φ можно косвенно определить по показаниям ваттметра, вольтметра и амперметра:
cos φ = P/UI.
Коэффициент мощности можно также измерить особым прибором — фазометром.
Пример 14. Амперметр показывает ток 10 а, вольтметр — 120 в, ваттметр — 1 квт. Определить cos φ потребителя:
Определить cos φ потребителя:
S = IU = 10 ⋅ 120 = 1200 ва,
cos φ = P/S = 1000/1200 = 0,83.
Пример 15. Определить активную мощность, отдаваемую генератором однофазного переменного тока в сеть, если вольтметр на щите генератора показывает 220 в, амперметр — 20 а и фазометр — 0,8:
Р = IU cos φ = 20 ⋅ 220 ⋅ 0,8 = 3520 вт = 3,52 квт.
Полная мощность
S = IU = 20 ⋅ 220 = 4400 ва = 4,4 ква.
Пример 16. Вольтметр, установленный на щитке электродвигателя, показывает 120 в, амперметр — 450 а, ваттметр — 50 квт. Определить z, r, xL, S, cos φ, Q:
z = U/I = 120/450 = 0,267 ом.
Так как Р = I2 ⋅ r, то
r = Р/I2 = 50000/4502 = 0/247 ом;
xL = √(z2 — r2) = √(0,2672 — 0,2472) = √0,01 = 0,1 ом;
S = IU = 450 ⋅ 120 = 54000 ва = 54 ква;
cos φ = Р/S = 50000/54000 = 0,927;
Q = √(S2 — Р2) = √(540002 — 500002) = √416000000 = 20396 вар = 20,396 квар.
Из построения треугольников сопротивлений, напряжений и мощностей для определенной цепи видно, что эти треугольники подобны один другому, так как их стороны пропорциональны. Из каждого треугольника можно найти «косинус фи» цепи, как показано на рис. 168. Этим можно воспользоваться для решения самых разнообразных задач.
Рис. 168. Определение коэффициента мощности из треугольников сопротивлений (а), напряжений (б) и мощностей (в)
Пример 17. Определить z, xL, U, Uа, UL, S, Р, Q, если I = 6 а, r = 3 ом, cos φ = 0,8 и ток отстает по фазе от напряжения.
Из треугольника сопротивлений известно, что
cos φ = r/z,
отсюда
z = r/cos φ = 3/0,8 = 3,75 ом;
U = I ⋅ z = 6 ⋅ 3,75 = 22,5 в;
xL = √(z2 — r2) = √(3,752 — 32) = √(14,06 — 9) = √5,06 = 2,24 ом;
Uа = Ir = 6 ⋅ 3 = 18 в;
UL = IxL = 6 ⋅ 2,24 = 13,45 в;
S = IU = 6 ⋅ 22,5 = 135 ва,
или
P = I2r = 36 ⋅ 3 = 108 вт;
Р = IU cos φ = 6 ⋅ 22,5 ⋅ 0,8 = 108 вт;
Q = IUL = 6 ⋅ 13,45 = 81 вар,
или
Q = √(S2 — P2) = √(1352 — 1082) = √6561 = 81 вар,
или
Q = I2xL = 62 ⋅ 2,24 = 81 вар.
Основными потребителями электрической энергии являются электрические двигатели, машины и электронагревательные устройства. Все они потребляют активную мощность, которую преобразуют в механическую работу и тепло. Электрические двигатели потребляют также реактивную мощность. Последняя, как известно, совершает колебательное движение от источника к двигателю и обратно.
У ламп и электрических печей сопротивления S = Р и cos φ = 1. У электрических двигателей S = √(P2 + Q2) и cos φ меньше 1.
При неизменной передаваемой активной мощности Р величина нагрузочного тока обратно пропорциональна значению cos φ:
I = P/U⋅cosφ
Это означает, что при тех же значениях активной мощности Р и напряжения U нагрузочный ток электрических двигателей больше, чем у электрических ламп. Если, например, коэффициент мощности электрического двигателя равен 0,5, то он потребляет в 2 раза больший ток, чем электрическая печь сопротивления той же мощности Р.
Потери мощности на нагрев проводов линии пропорциональны квадрату тока (ΔР = I2r).
Таким образом, при cos φ = 0,5 потери мощности в линии, по которой энергия передается потребителям, больше в 4 раза, чем при cos φ = 1. Кроме того, генераторы и трансформаторы будут загружены током в 2 раза больше и в этом случае требуется примерно в 2 раза большее сечение проводов для обмоток.
Отсюда видно, какое важное значение имеет величина cos φ в электроэнергетических установках. Для повышения коэффициента мощности промышленных установок, на которых преобладающая часть потребителей — электрические двигатели, параллельно им включают конденсаторы, т
е. добиваются резонанса токов, при котором cos φ близок к 1.
Сдвиг фаз между напряжением и током
Что такое электрическое сопротивление
Фазовый сдвиг – показатель, описывающий разность исходных фаз двух параметров, имеющих свойство меняться во времени с одинаковыми скоростями и периодами. Именно сдвиг между силой и напряжением определяет, сколько будет значение угла фи.
В радиотехнической промышленности используются цепочки для получения асинхронного хода. Одна RC-цепь создает 60-градусный сдвиг, для получения 180-градусного для трехфазной структуры организуют последовательное соединение трех цепочек.
Одна RC-цепь создает 60-градусный сдвиг, для получения 180-градусного для трехфазной структуры организуют последовательное соединение трех цепочек.
При трансформации электродвижущей силы во вторичных обмотках прибора для всех вариаций тока ее значение идентично по фазе таковому для первичной обмотки. Если обмотки трансформатора включить в противофазе, значение напряжения получает обратный знак. Если напряжение идет по синусоиде, происходит сдвиг на 180 градусов.
В простом случае (к примеру, включение электрического чайника) фазы двух показателей совпадают, и они в одно и то же время достигают пиковых значений. Тогда при расчете потребительской мощности применять угол фи не требуется. Когда к переменному току подключен электродвигатель с составной нагрузкой, содержащей активный и индуктивный компоненты (двигатель стиральной машинки и т.д.), напряжение сразу подается на обмотки, а ток отстает вследствие действия индуктивности. Таким образом, между ними возникает сдвиг. Если индуктивный компонент (обмотки) подменен использованием достижений химии в виде емкостного аккумулятора, отстающей величиной, напротив, оказывается напряжение.
Косинус фи не следует путать с другим показателем, рассчитываемым для комплексных нагрузок, – коэффициентом демпфирования. Он широко используется в усилителях мощности и равен частному номинального сопротивлению прибора и выходному – усилка.
Угол фазового сдвига
Косинус фи (cos φ) или Коэффициент мощности
На шильдиках двигателей и некоторых других устройств можно видеть непонятный параметр косинус фи (cos φ). Что этот параметр означает, в данной статье коротко объясняется, что это такое.Косинус фи (cos φ) часто называют «Коэффициент мощности». Это почти одно и то же при правильной синусоидальной форме тока.Иногда для обозначения коэффициента мощности используется λ, эту величину выражают в процентах, или PF.
Условные обозначения
P — активная мощность S — полная мощность Q — реактивная мощность, U — напряжение I — ток.
Что такое Косинус фи (cos φ) — «Коэффициент мощности»
Косинус фи (cos φ) это косинус угла между фазой напряжения и фазой тока. При активной нагрузке фаза напряжения совпадает с фазой тока, φ (между фазами) равен 0 (нулю). А как мы знаем cos0=1. То есть при активной нагрузке коэффициент мощности равен 1 или 100%.
При активной нагрузке фаза напряжения совпадает с фазой тока, φ (между фазами) равен 0 (нулю). А как мы знаем cos0=1. То есть при активной нагрузке коэффициент мощности равен 1 или 100%.
Активная нагрузка
При емкостной или индуктивной нагрузке фаза тока не совпадает с фазой напряжения. Получается «сдвиг фаз». При индуктивной или активно-индуктивной нагрузке (с катушками: двигатели, дросселя, трансформаторы) фаза тока отстает от фазы напряжения.При емкостной нагрузке (конденсатор) фаза тока опережает фазу напряженияА почему тогда косинус фи (cos φ) это тоже самое что коэффициент мощности, да потому что S=U*I.Посмотрите на графики ниже. Здесь φ равно 90 косинус фи (cosφ)=0(нулю).
Индуктивная нагрузка
Попытаемся вычислить мощность для простоты возьмем максимальное значение напряжения равное 1(100%) в этот момент ток равен 0(нулю) соответственно их произведение, то есть мощность равны 0(нулю). И наоборот когда ток максимальный напряжение равно нулю. Получается что полезная, активная мощность равна 0(нулю).
Получается что полезная, активная мощность равна 0(нулю).
Коэффициент мощности это соотношение полезной активной мощности к полной мощности, то есть cosφ=P/S.
Треугольник мощностей
Посмотрите на треугольник мощностей. Вспомним тригонометрию (это что то из математики) вот здесь то она нам и пригодится.
Q =U x I x sin φ
На практике. Если подключить асинхронный двигатель в сеть без нагрузки, в холостую. Напряжение вроде как есть, ток, если замерить тоже есть, при этом ни какой полезной работы не совершается. Соответственно активная мощность минимальна.Если на двигателе увеличить нагрузку то сдвиг фаз начнет уменьшаться и соответственно косинус фи (cos φ) будет увеличиваться, а с ним и активная мощность.
К счастью счетчики активной мощности фиксируют соответственно только активную мощность. И нам не приходится переплачивать за полную мощность.
Однако у реактивной мощности есть большой минус она создает бесполезную нагрузку на электрическую сеть из-за этого образуются потери.
Что вызывает низкий коэффициент мощности cos φ (cos фи) в электрической системе?
В разделе Техника на вопрос для чего нужен тангенс фи в электроэнергетики? При tgф<0 потребитель выдает реактивную мощность (емкостной характер) , при tgф>1 потребитель потребляет реактивную мощность (индуктивный характер).
Рассмотрев треугольник сопротивлений, можно понять смысл термина «тангенс фи». Это отношение между реактивной и активной составляющими нагрузки. Тангенс угла потерь также используется в электроэнергетике, но более привычным является показатель cos(φ).
Часть электрической мощности, пришедшая к потребителю, используется для совершения полезной работы и тепловое рассеяние на нагрузке у потребителя. Почему фазовый сдвиг приводит к потерям электроэнергии? Если активное сопротивление проводника просто рассеивает электроэнергию, переводя ее в тепловую, то фазовый сдвиг между током и напряжением приводит к повышенному расходу энергии на электростанции. Отношение активной мощности, потребляемой в нагрузке, и полной мощности, подаваемой на нагрузку по линии электропередач, численно равно cos(φ), где φ – угол фазового сдвига между током и напряжением. С другой стороны, 0% — крайне нежелательный вариант, когда φ=π/2, cos(φ)=0, при этом вся подаваемая мощность переменного тока отражается от реактивной нагрузки и рассеивается в подводящих проводах.
С другой стороны, 0% — крайне нежелательный вариант, когда φ=π/2, cos(φ)=0, при этом вся подаваемая мощность переменного тока отражается от реактивной нагрузки и рассеивается в подводящих проводах.
Р — мощность активная,Q — мощность реактивная. Главный инженер ЭнергосбытаА.
Мне тут в акте о разграничении балансовой ответственности МКС прописал Базовый коэффициент реактивной мощности тангенс Фи, который равен 0,2. Это как понимать?
Активный и реактивный токи, протекающие в проводе, складываются в один общий ток, который замеряется амперметром. Отношение активной мощности к полной называется коэффициентом мощности. Для удобства технических расчетов коэффициент мощности выражают через косинус условного угла «фи» (cosφ).
Коэффициент мощности (cos φ) это параметр, характеризующий искажения формы тока, потребляемого от электросети переменного тока. Важный показатель потребителя электроэнергии. Для оценки и расчетов цепей переменного тока используются действующие значения тока и напряжения. Вольтметры и амперметры переменного тока показывают именно действующие значения. Полная мощность в цепях переменного тока равна квадратному корню из суммы квадратов активной и реактивной мощностей. Фазового сдвига нет, cos φ = 1, вся энергия из сети переходит в активную мощность на нагрузке.
Вольтметры и амперметры переменного тока показывают именно действующие значения. Полная мощность в цепях переменного тока равна квадратному корню из суммы квадратов активной и реактивной мощностей. Фазового сдвига нет, cos φ = 1, вся энергия из сети переходит в активную мощность на нагрузке.
Косинус фи (cos φ) — это косинус угла между фазой напряжения и фазой тока. При активной нагрузке фаза напряжения совпадает с фазой тока, φ (между фазами) равен 0 (нулю). Попытаемся вычислить мощность для простоты возьмем максимальное значение напряжения равное 1(100%) в этот момент ток равен 0(нулю) соответственно их произведение, то есть мощность равны 0(нулю). И наоборот когда ток максимальный напряжение равно нулю. Получается что полезная, активная мощность равна 0(нулю). Счетчики активной мощности фиксируют соответственно только активную мощность.
Попробуем популярно объяснить причину такого уважения электриков к тригонометрической функции cos φ. «Косинус-фи» в электроэнергетике еще называют коэффициентом мощности. Численно коэффициент мощности равен косинусу этого фазового сдвига. Источниками реактивной мощности в сети переменного тока являются катушки индуктивности и конденсаторы. Большинство потребителей электрической энергии имеют обмотки на магнитопроводах, т.е. представляют собой индуктивность. Тогда в однофазной цепи cos φ = P / (U х I), где Р, U, I — показания ваттметра, вольтметра и амперметра, соответственно.
Численно коэффициент мощности равен косинусу этого фазового сдвига. Источниками реактивной мощности в сети переменного тока являются катушки индуктивности и конденсаторы. Большинство потребителей электрической энергии имеют обмотки на магнитопроводах, т.е. представляют собой индуктивность. Тогда в однофазной цепи cos φ = P / (U х I), где Р, U, I — показания ваттметра, вольтметра и амперметра, соответственно.
В тренде:
- Как Путин обошел Обаму в списке «Форбс»?Если это действительно так, то Путин с легкостью попадает в первую десятку богатейших людей мира по версии журнала Forbes. Этот журнал ежегодно проводит публикацию рейтинга самых богатых
- Когда можно съесть банан, а когда нельзяЛучше всего их кушать утром, когда ваш организм так жаден к питательным веществам. Возможно, банан – именно то, чего в этот момент так не хватает организму. Съеденный банан перед сном
- Типичные ошибки при приготовлении пломбираЕго разводят в молоке, а после заваривают до густоты.
 Если в пломбир добавляют ароматизаторы или ягоды и фрукты, то делать это нужно на заключительном этапе приготовления, уже пред тем как
Если в пломбир добавляют ароматизаторы или ягоды и фрукты, то делать это нужно на заключительном этапе приготовления, уже пред тем как
Способы улучшения коэффициента мощности
Повышение коэффициента мощности на предприятиях возможно двумя путями: естественным и искусственным.
Естественный путь повышения cos ф предусматривает: упорядочение технологических процессов таким образом, чтобы приводные двигатели были постоянно загружены и не работали продолжительное время на холостом ходу; замену незагруженных двигателей менее мощными; замену асинхронных двигателей с фазным ротором на асинхронные двигатели с короткозамкнутым ротором; замену тихоходных двигателей на быстроходные; применение синхронных двигателей вместо асинхронных.
Для осуществления вышеперечисленных мероприятий не требуются капитальные затраты, поэтому естественный путь улучшения коэффициента мощности является наиболее доступным и выгодным.
Для искусственного повышения коэффициента мощности применяют компенсирующие устройства на напряжение до 1000 В и выше.
На шахтах чаще всего применяются централизованная компенсация путем установки конденсаторов на шинах 6 кВ. При этом повышается общий коэффициент мощности, ио от передачи реактивной мощности разгружаютея только трансформаторы районных подстанций и линии, питающие ГПП.
Для разгрузки сетей участков от реактивной мощности необходимо конденсаторы устанавливать непосредственно на участках. В угольных шахтах такие установки конденсаторов не применяют из-за отсутствия их в нужном исполнении.
В связи с тем, что для установки конденсаторов необходимы определенные капитальные затраты, вопрос о применении искусственного способа повышения cos ф решается технико-экономичсскими расчетами при проектировании предприятия, а в период эксплуатации — технико-экономическими расчетами, которые производит электроснабжающая организация.
Средневзвешенный cos фср нельзя использовать для оценки состояния сети предприятия по реактивной мощности, особенно в часы максимальных нагрузок электроснабжающей системы. Зачастую при высоком средневзвешенном cos фср предприятие в часы максимума энергосистемы потребляет значительную часть реактивной мощности в системе.
Зачастую при высоком средневзвешенном cos фср предприятие в часы максимума энергосистемы потребляет значительную часть реактивной мощности в системе.
На основании технико-экономических расчетов предприятиям устанавливается экономически целесообразная величина реактивной мощности Q3l разрешенной к использованию с энергосистемы в часы максимальной нагрузки ее. Действительно потребляемую предприятием реактивную мощность QM определяют замерами в часы максимума нагрузок энергосистемы.
Сравнивая величину разрешенной к использованию реактивной мощности Q3 с величиной действительно потребляемой из сети реактивной мощности QM, можно определить эффективность мероприятий по компенсации реактивной мощности.
Коррекция коэффициента мощности
Коррекция коэффициента мощности при помощи конденсаторов
К ухудшению коэффициента мощности (непропорциональному потребляемому току относительно напряжения) приводят реактивная и нелинейная нагрузки. Реактивные нагрузки корректируется внешними реактивностями, именно для них определена величина cos φ.
Коррекция коэффициента мощности ((англ. power factor correction) PFC) — процесс приведения потребления конечного устройства, обладающего низким коэффициентом мощности при питании от силовой сети переменного тока, к состоянию, при котором коэффициент мощности соответствует принятым стандартам.
Технически реализуется в виде той или иной дополнительной схемы на входе устройства.
Данная процедура, необходимая для равномерного использования мощности фазы и исключения перегрузки нейтрального провода трёхфазной сети, обязательна для импульсных источников питания мощностью в 100 и более ватт[источник не указан 2743 дня]. Компенсация обеспечивает отсутствие всплесков тока потребления на вершине синусоиды питающего напряжения и равномерную нагрузку на силовую линию.
Разновидности коррекции коэффициента мощности
- Коррекция реактивной составляющей полной мощности потребления устройства. Выполняется путём включения в цепь реактивного элемента, производящего обратное действие.
 Например, для компенсации действия электродвигателя переменного тока, обладающего высокой индуктивной реактивной составляющей полной мощности, параллельно цепи питания включается конденсатор.
Например, для компенсации действия электродвигателя переменного тока, обладающего высокой индуктивной реактивной составляющей полной мощности, параллельно цепи питания включается конденсатор. - Коррекция нелинейности потребления тока в течение периода колебаний питающего напряжения. Если нагрузка потребляет ток непропорционально основной гармонике питающего напряжения, для повышения коэффициента мощности требуется схема пассивного (PPFC) или активного корректора коэффициента мощности (APFC). Простейшим пассивным корректором коэффициента мощности является дроссель с большой индуктивностью, включенный последовательно с питаемой нагрузкой. Дроссель выполняет сглаживание импульсного потребления нагрузки и выделение низшей, то есть основной, гармоники потребления тока, что и требуется.
Расчет электрического тока по мощности: формулы, онлайн расчет, выбор автомата
Проектируя электропроводку в помещении, начинать надо с расчета силы тока в цепях. Ошибка в этом расчете может потом дорого обойтись. Электрическая розетка может расплавиться под действием слишком сильного для нее тока. Если ток в кабеле больше расчетного для данного материала и сечения жилы, проводка будет перегреваться, что может привести к расплавлению провода, обрыва или короткого замыкания в сети с неприятными последствиями, среди которых необходимость полной замены электропроводки – еще не самое плохое.
Электрическая розетка может расплавиться под действием слишком сильного для нее тока. Если ток в кабеле больше расчетного для данного материала и сечения жилы, проводка будет перегреваться, что может привести к расплавлению провода, обрыва или короткого замыкания в сети с неприятными последствиями, среди которых необходимость полной замены электропроводки – еще не самое плохое.
Знать силу тока в цепи надо и для подбора автоматических выключателей, которые должны обеспечивать адекватную защиту от перегрузки сети. Если автомат стоит с большим запасом по номиналу, к моменту его срабатывания оборудование может уже выйти из строя. Но если номинальный ток автоматического выключателя меньше тока, возникающего в сети при пиковых нагрузках, автомат будет доводить до бешенства, постоянно обесточивая помещение при включении утюга или чайника.
Гармоники питающего напряжения
Кроме образования реактивной мощности, на промышленных предприятиях существует такой негативный фактор, как выработка гармоник напряжения питающей сети.
Гармоники – это та часть спектра питающего напряжения, которая отличается частоты промышленной сети 50 Гц. Как правило, гармоники образуются на частотах, кратных основной. Таким образом, 1-я (основная) гармоника имеет частоту 50 Гц, 2-я – 100, 3-я – 150, и так далее.
Для измерения гармоник напряжения существует формула:
Гармоники напряжения – формула расчета
где:
- Кu – коэффициент нелинейных искажений, или THD (Total Harmonic Distortion),
- U(1), U(2), и так далее – напряжение соответствующей гармоники, вплоть до 40-й.
Однако, эта формула не удобна на практике, поскольку не дает представления об уровне каждой гармонике в отдельности. Поэтому для практических целей используют формулу:
Коэффициент каждой гармоники напряжения
Где:
- Кu(n) – коэффициент n-й гармонической составляющей спектра напряжения,
- U(n) – напряжение n-й гармоники,
- U(1) – напряжение 1-й гармоники
Таким образом, при измерении мы получим детальное распределение гармоник в спектре питающего напряжения, что позволит провести детальный анализ полученной информации и сделать правильные выводы.
Есть ещё гармоники тока, но там всё гораздо хуже…
Самым мощным — отдельное питание
Отдельного внимания заслуживают электрическая плита, варочная поверхность и электрическая духовка, ведь это самые мощные «обитатели» на домашней кухне, если она не газифицирована. Для их подключения, в проекте электроснабжения дома, предусматривают отдельные линии, состоящие из медных проводников необходимого сечения (согласно нормативов — не менее 6 мм 2 для варочной поверхности, если ее мощность превышает 3,5 кВт) и обязательно защищенные индивидуальными автоматами.
Как правило, производитель не снабжает провода мощных устройств электрической вилкой для включения в розетку. В таком случае установка электрической розетки нецелесообразна, поскольку ее контакты будутсущественно нагреваться в моменты работы устройства на полной мощности. Разумней будет подключить электрический кабель из щитка напрямую, присоединив его ссразу к клеммам устройства или воспользовавшись гильзами для электрических соединений, то есть срастить два кабеля друг с другом. Так вы исключите ненужные дополнительные соединения и возникающие в них переходные сопротивления.
Так вы исключите ненужные дополнительные соединения и возникающие в них переходные сопротивления.
Коэффициент мощности
Коэффициент использования производственной мощности
Косинус фи является тем параметром, который характеризует деформацию синусоиды тока, используемого от электрической сети переменного тока, согласно картинке ниже. Он является основным критерием, определяющим потери в проводах и на внутреннем сопротивлении сети.
Искажение тока
Косинус фи, основываясь на таблице стандартов энергопотребления, имеет такие показатели:
- Отличный – при значениях от 0,95 до 1;
- Хороший – при значениях от 0,8 до 0,95;
- Удовлетворительный – при значениях от 0,65 до 0,8;
- Неудовлетворительный – при значениях ниже 0,65.

Коэффициент мощности асинхронного двигателя и генератора
Поскольку статор и ротор асинхронного двигателя выполнены путем намотки медного провода, то, помимо активной составляющей, имеется индуктивная и емкостная составляющая сопротивления. Соответственно, каждую половину периода колебания с частотой f в сеть возвращается некоторое количество электричества. Негативными последствиями такой операции, помимо паразитного нагрева проводов, является, по сути, вырабатывание генератором электроэнергии, часть которой расходуется впустую, путем циркулирования между генератором и двигателем. Для частных случаев величина реактивных токов является малой, однако если речь идет о больших предприятиях, то величина реактивной мощности может быть настолько велика, что может повлиять на энергосистему целого региона.
Наличие заниженного коэффициента мощности влечет за собой ряд неблагоприятных проявлений:
- Применение в линиях электропередач проводов большего сечения и использование электрических и трансформаторных станций большей мощности;
- Снижение коэффициента полезного действия генерирующих и трансформирующих элементов цепи;
- Снижение полезного напряжения и мощности в проводах.

Мероприятия по увеличению cosφ направлены на:
- Максимальное сокращение потерь электрической энергии;
- Применение оптимального количества цветных металлов в процессе формирования электропроводящей аппаратуры;
- Использование электрических двигателей, трансформаторов, генераторов и других устройств, работающих на переменном токе, с максимальной пользой и для увеличения их срока службы. Соответственно, улучшение коэффициента мощности неизбежно влечет за собой увеличение коэффициента полезного действия питающей сети.
К основным методам по увеличению коэффициента мощности относятся:
- Компенсация реактивного компонента путем включения в цепь элемента с обратным действием. Промышленные предприятия, имеющие в питающей сети большой индуктивный компонент, с целью его уменьшения применяют электротехнику, собранную на конденсаторах. В связи с этим циркуляция паразитных составляющих проходит между потребителями и установкой, не принося вред питающей сети;
- Осмысленный подход к технологическому процессу и разумное рассредоточение нагрузок с целью увеличения коэффициента мощности.

Для таких целей прибегают к таким мероприятиям:
- Использование оптимальной нагрузки на электрические двигатели в процессе эксплуатации;
- Исключить использование оборудования, потребляющего индуктивную мощность, без нагрузки или в режиме холостого хода;
- Использование электрических двигателей с другими характеристиками.
Разобравшись, что такое коэффициент мощности, и осознав техпроцессы, проходящие в питающей сети, при наличии паразитных мощностей можно обоснованно подходить к вопросу выбора оборудования, отвечающего характеристикам этой сети. Второстепенный, на первый взгляд, показатель косинус фи является важным критерием, как для поставщиков электрической энергии, так и для различных ее потребителей.
Активная и реактивная мощность
Существует такое понятие как треугольник мощностей. Сам косинус — это тригонометрическая функция, которая и появилась при изучении свойств прямоугольных треугольников.
Она здорово помогает производить определенные вычисления с ними. Например, наглядно показывает отношение длин прилежащего катета (P-активная мощность) к гипотенузе (S-полная мощность).
Например, наглядно показывает отношение длин прилежащего катета (P-активная мощность) к гипотенузе (S-полная мощность).
То есть, зная угол сдвига, можно узнать, сколько активной мощности содержится в полной. Чем меньше этот угол, тем меньше реактивной составляющей находится в сети, и наоборот.
В КПД все более четко — полезная мощность используется на нагрев — охлаждение — механическую работу, остальное уходит безвозвратно. Эта разница и показывается в КПД.
Более подробно, с графиками, рисунками и простыми словами, без особых научных формулировок обо всем этом говорится в ролике ниже.
Сферические координаты — Math Insight
Поначалу сферические координаты могут быть немного сложными для понимания. Сферические координаты определяют положение точки в трехмерном пространстве на основе расстояния $\rho$ от начала координат и двух углов $\theta$ и $\phi$. Если кто-то знаком с полярными координатами, то угол $\theta$ понять несложно, так как он практически такой же, как угол $\theta$ в полярных координатах. Но некоторым людям трудно понять, что
угол $\phi$ это все о.
Сферические координаты определяют положение точки в трехмерном пространстве на основе расстояния $\rho$ от начала координат и двух углов $\theta$ и $\phi$. Если кто-то знаком с полярными координатами, то угол $\theta$ понять несложно, так как он практически такой же, как угол $\theta$ в полярных координатах. Но некоторым людям трудно понять, что
угол $\phi$ это все о.
Следующая графика и интерактивные апплеты могут помочь вам понять сферические лучше координирует. На этой странице мы выводим взаимосвязь между сферическими и декартовыми координатами, показываем апплет, который позволяет исследовать влияние каждой сферической координаты, и иллюстрируем простые сферические координатные поверхности.
Связь между сферическими и декартовыми координатами
Сферические координаты определяются, как указано в следующий рисунок, который иллюстрирует сферические координаты точка $P$.
Координата $\rho$ — это расстояние от $P$ до начала координат. Если
точка $Q$ является проекцией $P$ на плоскость $xy$, тогда $\theta$
угол между положительной осью $x$ и отрезком от начала координат
до $Q$. Наконец, $\phi$ — это угол между положительной осью $z$ и
отрезок прямой от начала координат до $P$.
Наконец, $\phi$ — это угол между положительной осью $z$ и
отрезок прямой от начала координат до $P$.
Связь между декартовыми координатами $(x,y,z)$ точки $P$ и ее сферическими координатами $(\rho,\theta,\phi)$ можно вычислить с помощью тригонометрии. Розовый треугольник вверху — это прямоугольный треугольник, вершинами которого являются начало координат, точка $P$ и ее проекция на ось $z$. Поскольку длина гипотенузы равна $\rho$, а $\phi$ – это угол, который гипотенуза образует с катетом прямоугольного треугольника по оси $z$, координата $z$ точки $P$ (т. е. высота треугольника) равно $z=\rho\cos\phi$. Длина другого катета прямоугольного треугольника — это расстояние от $P$ до оси $z$, равное $r=\rho\sin\phi$. Столько же находится и расстояние точки $Q$ от начала координат.
Голубой треугольник, показанный как в исходной трехмерной системе координат слева, так и в плоскости $xy$ справа, представляет собой прямоугольный треугольник, вершинами которого являются начало координат, точка $Q$ и ее проекция на $x$-ось. На правом графике расстояние от $Q$ до начала координат, которое является длиной гипотенузы прямоугольного треугольника, обозначено как $r$. Поскольку $\theta$ — это угол, который эта гипотенуза образует с осью $x$, $x$- и $y$-компоненты точки $Q$ (которые совпадают с $x$- и $y$-компонентами точки $Q$ $-компоненты точки $P$) задаются выражениями $x=r\cos\theta$ и $y=r\sin\theta$. Поскольку $r=\rho\sin\phi$, эти компоненты можно переписать как $x=\rho\sin\phi\cos\theta$ и $y=\rho\sin\phi\sin\theta$. Таким образом, формулы для декартовых координат в терминах сферических координат:
\начать{выравнивать}
x &= \rho\sin\phi\cos\theta\notag\\
y &= \rho\sin\phi\sin\theta\label{spherical_cartesian}\tag{1}\\
z &= \rho\cos\phi\notag.
\end{выравнивание}
На правом графике расстояние от $Q$ до начала координат, которое является длиной гипотенузы прямоугольного треугольника, обозначено как $r$. Поскольку $\theta$ — это угол, который эта гипотенуза образует с осью $x$, $x$- и $y$-компоненты точки $Q$ (которые совпадают с $x$- и $y$-компонентами точки $Q$ $-компоненты точки $P$) задаются выражениями $x=r\cos\theta$ и $y=r\sin\theta$. Поскольку $r=\rho\sin\phi$, эти компоненты можно переписать как $x=\rho\sin\phi\cos\theta$ и $y=\rho\sin\phi\sin\theta$. Таким образом, формулы для декартовых координат в терминах сферических координат:
\начать{выравнивать}
x &= \rho\sin\phi\cos\theta\notag\\
y &= \rho\sin\phi\sin\theta\label{spherical_cartesian}\tag{1}\\
z &= \rho\cos\phi\notag.
\end{выравнивание}
Изучение влияния каждой сферической координаты
Приведенный ниже апплет позволяет увидеть, как положение точки изменяется при изменении
вы меняете $\rho$, $\theta$ и $\phi$. Точка $P$, соответствующая значению координат, показана большой фиолетовой точкой. Зеленая точка — это точка $Q$, т. е. проекция $P$ на $xy$-плоскость.
Зеленая точка — это точка $Q$, т. е. проекция $P$ на $xy$-плоскость.
Загрузка апплета
Сферические координаты. Учитывая значения сферических координат $\rho$, $\theta$ и $\phi$, которые можно изменить, перетаскивая точки на ползунках, большая красная точка показывает соответствующее положение в Декартовы координаты. Зеленая точка — это проекция точки на $xy$-плоскость. Вы можете визуализировать каждую из сферических координат с помощью геометрических структур, которые окрашены в соответствии с цветами ползунка. Длина отрезка красной линии от начала координат равна $\rho$. Угол зеленой части диска в плоскости $xy$ равен $\theta$. Угол синей части вертикального диска равен $\phi$. Вы также можете перемещать большую красную точку и зеленую проекцию этой точки непосредственно с помощью мыши.
Дополнительная информация об апплете.
Обратите внимание, как вы можете получить любую точку, даже если мы ограничиваем $\rho \ge 0$, $0 \le\тета
Эти ограничения устранили большую часть неуникальности сферических
координаты. Обратите внимание, что в точке $\rho =0$ все еще присутствует неединственность, в точке
$\phi = 0$ и при $\phi=\pi$. Когда любое из этих условий верно,
вы можете изменить значение одной или нескольких других координат
без перемещения точки.
Обратите внимание, что в точке $\rho =0$ все еще присутствует неединственность, в точке
$\phi = 0$ и при $\phi=\pi$. Когда любое из этих условий верно,
вы можете изменить значение одной или нескольких других координат
без перемещения точки.
К сожалению, соглашение об обозначении сферических координат не стандартизировано в разных дисциплинах. Например, в физике роли $\theta$ и $\phi$ обычно меняются местами. Чтобы правильно понять, как кто-то использует сферические координаты, вы должны сначала определить, какие обозначения используются при этом. Вы не можете предположить, что они следуют соглашению, используемому здесь.
Простые сферические координатные поверхности
Эти три следующих апплета могут помочь вам понять, что представляет собой каждый из трех значит сферические координаты. Они показывают, какие поверхности $\phi=$ константа, константа $\theta=$ и константа $\rho=$ выглядят так. значение константы определяется положением ползунков. Во всех случаях мы ограничиваем поверхности областью $\rho
Константа $\phi$
Что означает, что точка имеет сферическую координату $\phi=\pi/3$? Взгляните на поверхности, которые
определяется уравнением $\phi=$ постоянная.
Загрузка апплета
Поверхности постоянных $\phi$ в сферических координатах. Показана коническая поверхность константы $\phi=$, где значение $\phi$ определяется синей точкой на бегунке. Только часть поверхности где $\rho
Подробнее о апплете.
Поверхностная константа $\phi=$ представляет собой просто одиночный конус, направленный либо вверх или вниз. Если вы знаете, что $\phi=\pi/3$, то вы знаете точка находится где-то на (широком) единственном конусе, который открывается вверх, т. е. Уравнение $\phi=\pi/3$ задает поверхность, которая представляет собой одно конусное отверстие вверх. Уравнение $\phi=\pi/2$ соответствует плоскости $xy$. 92}$$ где $C=1/\tan \phi$, что действительно является уравнением для конуса.
Постоянная $\theta$
Поверхностная постоянная $\theta=$ представляет собой полуплоскость вне оси $z$. (Это отображается как полукруг только потому, что мы ограничиваем график $\ро
Загрузка апплета
Поверхности постоянных $\theta$ в сферических координатах. Показана полуплоская поверхность константы $\theta=$, где значение $\theta$ определяется синей точкой на бегунке. Только часть поверхности, где $\rho
Показана полуплоская поверхность константы $\theta=$, где значение $\theta$ определяется синей точкой на бегунке. Только часть поверхности, где $\rho
Дополнительная информация об апплете.
Если точка имеет $\theta=\pi/2$, то вы знаете, что точка находится на половина плоскости $yz$, где значения $y$ положительны. Уравнение $\theta=\pi/2$ — уравнение для этой полуплоскости.
Из соотношения \eqref{spherical_cartesian} отношение между $x$ и $y$ можно записать, например, как $y/x = \tan \theta$. Если $\theta$ поддерживается постоянным, то отношение между $x$ и $y$ остается постоянным. Таким образом, константа $\theta=$ дает прямую, проходящую через начало координат в плоскости $xy$. Так как $z$ не имеет ограничений, мы получаем вертикальную плоскость. Оглядываясь назад на отношение \eqref{spherical_cartesian}, мы видим, что это всего лишь полуплоскость, потому что $\rho\sin\phi$ не может быть отрицательным.
Константа $\rho$
У большинства людей нет проблем с пониманием того, что означает $\rho=3$. Это
сфера радиуса 3 с центром в начале координат. В общем, поверхность
Константа $\rho=$ — это сфера радиуса $\rho$ с центром в начале координат.
Это
сфера радиуса 3 с центром в начале координат. В общем, поверхность
Константа $\rho=$ — это сфера радиуса $\rho$ с центром в начале координат.
Загрузка апплета
Поверхности постоянных $\rho$ в сферических координатах. Показана сферическая поверхность постоянной $\rho=$, где значение $\rho$ определяется синей точкой на бегунке. 92 \конец{выравнивание*} проверяя, что константа $\rho=$ есть сфера радиуса $\rho$ с центром в начале координат.
Исчисление III — Сферические координаты
Онлайн-заметки Пола
Главная
/
Исчисление III
/
Трехмерное пространство
/ Сферические координаты
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 1-13: Сферические координаты
В этом разделе мы введем сферические координаты. К сферическим координатам нужно немного привыкнуть. Наверное, проще всего начать с наброска.
Сферические координаты состоят из следующих трех величин.
Сначала идет \(\rho \). Это расстояние от начала координат до точки, и нам потребуется \(\rho \ge 0\).
Далее идет \(\theta \). Это тот же самый угол, который мы видели в полярных/цилиндрических координатах. Это угол между положительной осью \(x\) и линией выше, обозначенной \(r\) (которая также является той же \(r\), что и в полярных/цилиндрических координатах). На \(\theta \) ограничений нет.
На \(\theta \) ограничений нет.
Наконец, есть \(\varphi \). Это угол между положительной осью \(z\) и линией от начала координат до точки. Нам потребуется \(0 \le \varphi \le \pi \).
Таким образом, \(\rho \) — это расстояние от начала координат до точки, \(\varphi \) — это угол, на который нам нужно повернуться вниз от положительной оси z-, чтобы добраться до точки и \(\theta\) — это то, сколько нам нужно повернуться вокруг оси \(z\), чтобы добраться до точки.
Сначала мы должны вывести некоторые формулы преобразования. Давайте сначала начнем с точки в сферических координатах и спросим, каковы цилиндрические координаты точки. Итак, мы знаем \(\left( {\rho,\theta,\varphi} \right)\) и хотим найти \(\left({r,\theta,z} \right)\). Конечно, нам действительно нужно найти только \(r\) и \(z\), так как \(\theta \) одно и то же в обеих системах координат.
Если мы посмотрим на рисунок выше прямо перед треугольником, мы получим следующий рисунок:
Мы знаем, что угол между осью \(z\) и \(\rho \) равен \(\varphi \) и с небольшим количеством геометрии мы также знаем, что угол между \(\rho \) и вертикальной стороной прямоугольного треугольника также равен \(\varphi \).
Затем с помощью небольшого треугольника мы получаем
\[\begin{align*}z & = \rho \cos \varphi \\ r & = \rho \sin \varphi \end{align*}\] 92}\]
Далее найдем декартовы координаты той же точки. Для этого мы начнем с цилиндрических формул преобразования из предыдущего раздела.
\[\begin{align*}x & = r\cos \theta \\ y & = r\sin \theta \\ z & = z\end{align*}\]
Теперь все, что нам нужно сделать, это использовать приведенные выше формулы для \(r\) и \(z\), чтобы получить
\[\begin{align*}x & = \rho \sin \varphi \cos \theta \\ y & = \rho \sin \varphi \sin \theta \\ z & = \rho \cos \varphi \end{ выровнять*}\] 92}\]
Преобразование точек из декартовых или цилиндрических координат в сферические координаты обычно выполняется с помощью тех же формул преобразования. Чтобы увидеть, как это делается, давайте рассмотрим пример каждого из них. 2}} = \sqrt {6 + 2} = \sqrt 8 = 2\sqrt 2 \]
9{ — 1}} \ влево ( {\ гидроразрыва {1} {2}} \ справа) = \ гидроразрыва {\ пи {3} \]
2}} = \sqrt {6 + 2} = \sqrt 8 = 2\sqrt 2 \]
9{ — 1}} \ влево ( {\ гидроразрыва {1} {2}} \ справа) = \ гидроразрыва {\ пи {3} \]
Обратите внимание, что существует много возможных значений \(\varphi \), которые дадут \(\cos \varphi = \frac{1}{2}\), однако мы ограничили \(\varphi \) до диапазон \(0 \le \varphi \le \pi \), так что это единственное возможное значение в этом диапазоне.
Таким образом, сферические координаты этой точки будут \(\left( {2\sqrt 2 ,\frac{\pi }{4}, \frac{\pi }{3}} \right)\).
b Преобразование точки \(\left( { — 1,1, — \sqrt 2 } \right)\) из декартовых координат в сферические. Показать решение 9{ — 1}}\left( {\ frac {{ — \ sqrt 2 }} {2}} \ right) = \ frac {{3 \ pi}} {4} \]
Как и в предыдущих частях, это будет единственная возможная \(\varphi \) в допустимом диапазоне.
Наконец, давайте найдем \(\theta \). Для этого мы можем использовать преобразование для \(x\) или \(y\). В этом случае мы будем использовать преобразование для \(y\).
В этом случае мы будем использовать преобразование для \(y\).
\[\ sin \ theta = \ frac {y} {{\ rho \ sin \ varphi}} = \ frac {1} {{2 \ left ( {\ frac {{\ sqrt 2}} {2}} \ right )}} = \ frac {1} {{\ sqrt 2 }} = \ frac {{\ sqrt 2}} {2} \ hspace {0,5 дюйма} \ Rightarrow \ hspace {0,25 дюйма} \ theta = \ frac {\ pi }{4}\,\,{\mbox{or}}\,\,\theta = \frac{{3\pi}}{4}\]
Теперь у нас на самом деле есть больше возможных вариантов для \(\theta \), но все они будут сведены к одному из двух углов, указанных выше, поскольку они будут просто одним из этих двух углов с одним или несколькими полными оборотами вокруг единицы. добавлен кружок.
Однако нам нужно решить, какой из углов является правильным, так как будет только один. Для этого заметим, что в двух измерениях точка с координатами \(x = — 1\) и \(y = 1\) лежит во втором квадранте. Это означает, что \(\theta \) должен быть углом, который поместит точку во второй квадрант. Следовательно, второй угол, \(\theta = \frac{{3\pi }}{4}\), должен быть правильным.
Следовательно, второй угол, \(\theta = \frac{{3\pi }}{4}\), должен быть правильным.
Тогда сферические координаты этой точки равны \(\left( {2,\frac{{3\pi }}{4},\frac{{3\pi }}{4}} \right)\).
Теперь давайте посмотрим на некоторые уравнения и определим поверхности, которые они представляют.
Пример 2 Определите поверхность для каждого из следующих уравнений.
- \(\ро = 5\)
- \(\displaystyle \varphi = \frac{\pi}{3}\)
- \(\displaystyle \theta = \frac{{2\pi}}{3}\)
- \(\ро \sin \varphi = 2\)
Показать все решения Скрыть все решения
a \(\rho = 5\) Показать решение
Есть несколько способов подумать об этом.
Сначала подумайте, что говорит это уравнение. Это уравнение говорит, что независимо от того, что такое \(\theta\) и \(\varphi\), расстояние от начала координат должно быть равно 5. Таким образом, мы можем вращать сколько угодно от \(z\) -оси и вокруг оси \(z\), но мы всегда должны оставаться на фиксированном расстоянии от начала координат. Это именно то, что представляет собой сфера. Итак, это сфера радиуса 5 с центром в начале координат. 92} & = 25\конец{выравнивание*}\]
Таким образом, мы можем вращать сколько угодно от \(z\) -оси и вокруг оси \(z\), но мы всегда должны оставаться на фиксированном расстоянии от начала координат. Это именно то, что представляет собой сфера. Итак, это сфера радиуса 5 с центром в начале координат. 92} & = 25\конец{выравнивание*}\]
Действительно, сфера радиуса 5 с центром в начале координат.
b \(\displaystyle \varphi = \frac{\pi }{3}\) Показать решение
В этом случае не существует простого способа преобразования в декартовы координаты, так что нам просто нужно немного подумать об этом. Это уравнение говорит о том, что независимо от того, насколько далеко мы отходим от начала координат и насколько сильно мы вращаемся вокруг оси \(z\), точка всегда должна находиться под углом \(\frac{\pi }{3 }\) от оси \(z\).
Именно это и происходит в конусе. Все точки конуса составляют фиксированный угол от оси \(z\). Итак, у нас есть конус, все точки которого расположены под углом \(\frac{\pi }{3}\) от оси \(z\).
c \(\displaystyle \theta = \frac{{2\pi }}{3}\) Показать решение
Как и в предыдущей части, здесь мы не сможем легко преобразовать в декартовы координаты. В этом случае независимо от того, как далеко мы отходим от начала координат или насколько мы поворачиваем вниз от положительной оси \(z\), точки всегда должны образовывать угол \(\frac{{2\pi }}{3} \) с осью \(x\).
Это сделают точки в вертикальной плоскости. Итак, у нас есть вертикальная плоскость, которая образует угол \(\frac{{2\pi }}{3}\) с положительной осью \(x\).
d \(\rho \sin \varphi = 2\) Показать решение
В этом случае мы можем преобразовать в декартовы координаты, так что давайте сделаем это. На самом деле есть два способа сделать это преобразование. Мы рассмотрим оба, так как оба будут использоваться время от времени.
Решение 1
В этом методе решения мы будем напрямую конвертировать в декартовы координаты. Для этого нам сначала нужно возвести в квадрат обе части уравнения. 92} & = 4\конец{выравнивание*}\]
Для этого нам сначала нужно возвести в квадрат обе части уравнения. 92} & = 4\конец{выравнивание*}\]
Итак, у нас есть цилиндр радиуса 2 с центром на оси \(z\).
Этот метод решения был не так уж и плох, но требовал некоторых не столь очевидных шагов.
Решение 2
Этот метод намного короче, но включает в себя то, что вы можете не увидеть в первый раз. В этом случае вместо того, чтобы сразу переходить к декартовым координатам, мы сначала преобразуем их в цилиндрические координаты.
Это не всегда будет работать, но в этом случае все, что нам нужно сделать, это признать, что \(r = \rho \sin \varphi \), и мы получим то, что сможем распознать. Используя это, мы получаем,
\[\begin{align*}\rho \sin \varphi & = 2\\ r & = 2\end{align*}\]
На данный момент мы знаем, что это цилиндр (помните, что мы находимся в трех измерениях, поэтому это не круг!). Однако давайте продолжим и завершим процесс преобразования. 92} & = 4\конец{выравнивание*}\]
Однако давайте продолжим и завершим процесс преобразования. 92} & = 4\конец{выравнивание*}\]
Итак, как мы видели в последней части предыдущего примера, иногда будет проще преобразовать уравнения в сферических координатах в цилиндрические координаты перед преобразованием в декартовы координаты. Это не всегда будет проще, но может сделать некоторые преобразования быстрее и проще.
Последнее, что мы хотим сделать в этом разделе, — это обобщить первые три части предыдущего примера.
\[\begin{align*}\rho & = a\hspace{0,5 дюйма}{\mbox{сфера радиуса}}a{\mbox{ с центром в начале координат}}\\ \varphi & = \alpha \hspace{ 0,5 дюйма {\ mbox {конус, образующий угол }} \ alpha {\ mbox { с положительным }} z — {\ mbox {ось}} \\ \ theta & = \ beta \ hspace {0,5 дюйма} { \mbox{вертикальная плоскость, образующая угол }}\beta {\mbox{ с положительным }}x — {\mbox{ось}}\end{align*}\]
14.
 1 — Тригонометрия 14.1 — Тригонометрия
1 — Тригонометрия 14.1 — Тригонометрия14.1 — Тригонометрия
Декартова плоскость
Декартова плоскость — это плоскость, на которой ось x нарисована горизонтально, а ось y нарисована вертикально. Любая точка на плоскости обозначается с помощью упорядоченных парных обозначений . как это: Это точка x = 1,5 и y = 2. Он указан на картинке справа. Этот метод использования значения x и значения y для определения точки называется прямоугольной системой координат (обратите внимание на пунктирный прямоугольник, показанный на рисунке).
Другая широко используемая система координат (особенно для
комплексные числа) полярная система координат .
Он использует расстояние от начала координат и направление к
найти точку.
Плоскость разделена на 4 квадранта . Квадрант 1 имеет положительные значения x и y . В другие квадранты можно попасть, двигаясь против часовой стрелки от первого.
Углы и их мера
- Угол в стандартном положении имеет вершину в начале координат и одна сторона вдоль 9Ось 0027 x .
- Угол образуется при повороте луча от начального к терминальное положение.
- Вращение против часовой стрелки считается положительным вращением.
- Вращение по часовой стрелке считается отрицательным вращением на .
Для измерения величины угла обычно используются две шкалы: шкала градусов и шкала радиан :
Градусы
В этой шкале угол выражается в единицах, называемых градусов , с вращением на один полный круг, составляющим 360 градусов (символ ° ).
Радиан
В этой шкале угол выражается в единицах, называемых радиан , с вращением на полный круг, равным 2π или примерно 6,28 радиан.Радианная шкала формально определяется следующим образом:
| Размер угла θ , выраженный в радианах равен с (длина дуги , стягиваемая углом) деленная на r (радиус окружности). |
Для одного полного круга с = C ( длины окружности ), а так как C = 2 π r мы получаем для угла в один полный круг.
Важным свойством радианов является то, что, поскольку s и r оба имеют размеры длины, радианы — единицы измерения без размеров.
Пример: Угол θ на рисунке справа равен 2 радианам. начиная с s = 6 и r = 3.
начиная с s = 6 и r = 3.
Перевод градусов в радианы
Для преобразования между градусами и радианами вы можете использовать тот факт, что π радианы = 180°. Это означает, что: Эти две фракции называются UFOO. (полезные формы одного). Умножение любого угла на один из них не меняет размер угла но меняет единицы измерения угла на .Пример: Преобразование 118° в радианы.
Решение:
Пример: Преобразование 0,438 радиана в градусы.
Решение:
Углы треугольника
Сумма углов любого треугольника равна 180° или π радианам.Теорема Пифагора и длины
Теорема Пифагора касается длин сторон прямоугольный треугольник. (Прямой угол — это угол 90° и прямоугольный треугольник — это треугольник, в котором угол равен 90°. )
Рассмотрим прямоугольный треугольник со сторонами длиной a , b и с показано справа. a называется высота , b это
называется основанием и c , самой длинной стороной, противоположной прямому углу,
называется гипотенузой .
Теорема Пифагора утверждает, что стороны связаны формулой:
)
Рассмотрим прямоугольный треугольник со сторонами длиной a , b и с показано справа. a называется высота , b это
называется основанием и c , самой длинной стороной, противоположной прямому углу,
называется гипотенузой .
Теорема Пифагора утверждает, что стороны связаны формулой:в 2 = а 2 + б 2Красивое анимированное геометрическое доказательство теоремы Пифагора приведено на википедия.
Пример: Найти длину прямой на декартовой плоскости простирающийся от точки ( x 1 , y 1 ) = (−1,5, 2) до точки ( x 2 , y 2 ) = (2, −1).
Решение: Растяните пунктирные линии по горизонтали и вертикали
для создания прямоугольного треугольника. Этот треугольник имеет основание b = 3,5 и высоту 9.0027 и = 3,
поэтому теорема Пифагора дает:
Этот треугольник имеет основание b = 3,5 и высоту 9.0027 и = 3,
поэтому теорема Пифагора дает:
с 2 = 3 2 + 3,5 2 = 21,25Извлечение квадратного корня из обеих сторон дает длину прямой как
Этот пример иллюстрирует следующее очень полезное применение Теорема Пифагора. Если ( x 1 , y 1 ) и ( x 2 , y 2 ) — любые две точки в декартовой плоскости, то расстояние c между ними можно получить по формуле:
Тригонометрические функции
Пока ограничимся прямоугольными треугольниками. Это означает, что угол θ должен иметь значение от 0° до 90°. Обратите внимание, что при увеличении размера треугольника стороны становятся длиннее, но отношение длин любых двух сторон не меняется.
Можно определить шесть различных коэффициентов. Пусть напротив и рядом с обозначают длины сторон, противоположных и смежный с углом θ и пусть гипотенуза обозначить длинную сторону. Шесть отношений называются синус, косинус, тангенс, котангенс, секанс и косеканс и определяются следующим образом:
Примечание:
- Названия шести соотношений сокращены как sin, cos, tan, кроватка, sec, csc.
- Шесть коэффициентов зависят (являются функциями) угла θ . Мы можем обозначить это, используя функциональную нотацию как это: sin( θ ), cos( θ ), tan( θ ) и т.д.
- Многие учебники по тригонометрии
опусти скобки и напиши sin θ вместо sin( θ ). Это нормально, но не пишите что-то вроде
грех х + у . Это двусмысленно, потому что не ясно, если вы
следует сначала добавить x и y и
затем возьмите синус или сначала возьмите синус x , а затем добавьте y .
 Также помните, что системы компьютерной алгебры, такие как Algebra Coach
нужны скобки.
Также помните, что системы компьютерной алгебры, такие как Algebra Coach
нужны скобки. - Три тригонометрические функции — синус, косинус и тангенс — встроены в ваш
калькулятор. Так как их значения зависят от угла θ ,
их можно найти, введя угол в свой калькулятор в
соответствующий режим (градусы или радианы), а затем нажатие соответствующей кнопки:
грех, кос или загар.
- Остальные три тригонометрические функции – косеканс, секанс и котангенс – не строятся в свой калькулятор. Чтобы найти их, вы должны сначала найти синус, косинус или тангенс на вашем калькуляторе, а затем принять обратное.
Примеры:
- sin(30°) = 0.500
- tan (57°) = 1.54
- cos(0.74 rads) = 0.738
- tan (1.1 rads) = 1.96
Example: Find y и r в треугольнике.

Решение:
- Чтобы найти y , используйте тот факт, что
.
Из калькулятора тангенс (35,8°) = 0,7212. Установка их равными друг другу дает которое можно решить, чтобы дать г = 8,94. - Чтобы найти r , используйте тот факт, что
.
Из калькулятора cos(35,8°) = 0,8111. Установка их равными друг другу дает которое можно решить, чтобы получить r = 15,3.
Обратные тригонометрические функции
Предположим, что мы хотим найти угол θ в показанном треугольнике. Одна вещь, которую мы знаем, это то, что .
В приведенных выше примерах мы подставили угол θ в калькулятора.
а затем нажал кнопку загара, чтобы получить значение из для касательной.
Здесь мы хотим сделать обратный процесс — мы хотим ввести значение тангенса в и получить угол. Для этого в вашем калькуляторе есть обратные тригонометрические функции sin −1 , cos −1 и коричневый −1 встроены. (Примечание: верхний индекс −1 не имеет ничего общего с показателями степени. просто ОБОЗНАЧЕНИЕ, означающее «обратная функция». Избегать из-за возможной путаницы эти функции часто называют арксинус, арккосинус и арктангенс; сокращенно arcsin, arccos и arctan.)
Для этого примера tan( θ ) = 0,7381, поэтому θ = тангенс -1 (0,7381). Калькулятор дает загар −1 (0,7381) = 36,4°, поэтому θ = 36,4°.
Обычно обратные тригонометрические функции определяются следующим образом:
- Если sin( θ ) = z , тогда θ = sin −1 ( z ) или θ = арксинус ( z ).

- Если cos( θ ) = z , тогда θ = cos −1 ( z ) или θ = arccos( z ).
- Если tan( θ ) = z , тогда θ = tan −1 ( z ) или θ = арктангенс ( z ).
Как решать прямоугольные треугольники
Решить треугольник означает найти все недостающие стороны и углы треугольника. Вот шаги, необходимые для решения прямоугольных треугольников.- Нарисуйте картинку (при необходимости со стандартным углом).
- Вам дадут как минимум (а) одну сторону и один угол или (б) две стороны (иначе треугольник не может быть решен).
- В случае (а) вы можете использовать sin, cos или tan по мере необходимости найти другую сторону.
- В случае (b) вы можете использовать sin −1 ,
cos -1 или тангенс -1 как уместно, чтобы найти угол.

- Используйте теорему Пифагора, чтобы найти окончательную сторону.
- Используйте тот факт, что сумма углов равна 180°, чтобы найти окончательный угол.
- Ответьте одним предложением.
Пример: Поезд движется по прямому участку пути. Пилот пролетел 4220 метров прямо над камбузом в задней части поезда. замечает, что угол наклона локомотива в передней части поезд составляет 68,2°. Найдите длину поезда.
Решение: Картинка слева описывает ситуацию. Обратите внимание, что угол подъема самолета от локомотива также 68,2°. Рисунки справа определяют термины «угол депрессии» и «угол возвышения», которые часто используются в маркшейдерских работах.
С помощью функции тангенса получаем:
Оценка функции тангенса дает 2,500, а определение длины поезда дает: Ответ на предложение состоит в том, что до 3 значащих цифр длина поезда 1690 м.
| Упражнения тренера по алгебре |
Тригонометрические функции любого угла
Когда мы впервые определили тригонометрические функции (нажмите здесь, чтобы просмотреть это) угол θ был между 0° и 90° и мы использовали термины рядом с , против и гипотенуза к относятся к сторонам треугольника. Но теперь мы хотим, чтобы угол θ имел значения вне этого диапазона.
Одна из причин заключается в том, чтобы уметь решать косые треугольники.
Эти треугольники могут иметь угол больше 90°.
Другая причина заключается в том, что мы хотим иметь возможность описать угол
вращающегося объекта, когда он совершает множество оборотов.
Примером может служить воздушный лыжник, который прыгает и делает 2 оборота в воздухе.
Они « делает 720 », что означает, что они вращаются
через 720°.
Чтобы учесть углы больше 90°, мы теперь представим стрелку (или вектор ) указывая из начала координат длиной r и ориентированной под углом θ , и со стрелкой, расположенной в ( x , y ).
Построим треугольник, проведя вертикальную линию от наконечника стрелки к х и еще одна линия горизонтально поперек оси и .
Теперь мы переопределим шесть тригонометрических функций следующим образом:
Если θ находится в диапазоне от 0° до 90°, тогда обе координаты x и y положительны и тригонометрические функции имеют те же значения, что и раньше. Но если θ равно вне , диапазон от 0° до 90° затем х или y или оба могут быть отрицательными. (Не забывайте, однако, что длина стрелки r равна определяется как положительный.) Это означает, что теперь тригонометрические функции могут быть отрицательными.
Пример: Вектор длиной r = 2,5 и углом θ = 127 ° имеет координаты x = -1,5 и y = 2,0. Таким образом:
Вот два способа запомнить квадранты, в которых находятся тригонометрические функции. положительный или отрицательный. Лучший способ, конечно, это просто изучить графики функций синуса, косинуса и тангенса. Нажмите здесь, чтобы увидеть их.
Многие студенты используют поговорку Все студенты сдают химию запомнить квадранты, в которых функции положительны.
Вычисление синуса, косинуса или тангенса теперь, когда угол может иметь
любое значение Это просто. Ваш калькулятор запрограммирован на нахождение синуса, косинуса, или тангенс любого угла (знак минус и все такое). Например, калькулятор дает cos(120°) = −0,5. Ответ, который дает калькулятор, уникален, но важно отметить, что
несколько углов имеют одинаковые синус, косинус или тангенс. Например, калькулятор дает sin(60°) = 0,866, а также sin(120°) = 0,866.
Например, калькулятор дает sin(60°) = 0,866, а также sin(120°) = 0,866.
Вычисление угла теперь, когда синус, косинус или тангенс могут иметь
любое значение Потому что у многих углов один и тот же синус (или косинус, или тангенс) и потому что калькулятор только находит один из них, это не так просто. Например, давайте перевернем последний пример: предположим, мы знаем, что синус некоторого неизвестного угла равен 0,866 и мы хотим найти угол. Мы используем кнопку sin −1 на калькуляторе, и она дает sin −1 (0,866) = 60°. Это не дает sin −1 (0,866) = 120°.Как найти все углов, синус которых равен 0,866? Одно решение состоит в том, чтобы используйте изображение, подобное одному из этих:
Пример: Найдите все значения θ между 0° и 360°, для которых sin( θ ) = +0,6293.
Решение: Так как ,
это означает, что .
Напомним, что r определяется положительно. Если мы позволим r = 1, например, тогда y = +0,6293. Это означает что углы должны находиться в квадрантах 1 и 2.
Калькулятор дает sin −1 (0,6293) = 39,0°. На рисунке видно, что это означает, что углы равны θ = 39,0° и θ = 180° − 39,0° = 141,0°
Пример: Найдите все значения θ между 0° и 360°, для которых тангенс ( θ ) = -1,24.
Решение: Так как , это означает, что .
На рисунке показано, что существует два способа получения этого соотношения.
Если мы допустим x = 1, то y = -1,24. Это означает этот угол находится в квадранте 4.
И если мы допустим x = -1, то y = + 1,24. Это означает, что другой угол находится в квадранте 2.
Калькулятор дает тангенс −1 (−1,24) = −51,1°.
На рисунке видно, что это означает, что углы равны θ = 128,9° и θ = 308,9°
(Эти значения получаются, если взять -51,1° и добавить 180° один раз и
еще раз. )
)
Пример: Найти все значения θ между 0° и 360° для которого sec( θ ) = −4,21
Решение: Так как , это то же самое, что сказать, что . Поскольку это означает, что .
Если мы допустим r = 1, то х = -0,2375. Это означает, что углы лежат в квадрантах 2 и 3.
Калькулятор дает cos −1 (−0,2375) = 103,7°
На рисунке видно, что это означает, что углы равны θ = 103,7° и θ = 360° — 103,7° = 256,3°.
Наклонные треугольники
Наклонный треугольник — это треугольник, не содержащий прямого угла.Соглашение об именах углов и сторон состоит в том, что угол и сторона напротив него имеет ту же букву, как показано на рисунке справа.
Закон синусов и закон косинуса (выведенный ниже) используются для решения косоугольных треугольников Обратите внимание на следующие моменты, касающиеся законов синусов и косинусов:
- Если С = 90°, то закон синусов уменьшает
к ,
а именно определение синуса, а закон косинуса сводит
к в 2 = а 2 + б 2 ,
а именно теорема Пифагора.

- В уголках A , B или C нет ничего особенного . С тем же успехом мы могли бы написать законы синусов и косинусов, и
Вывод закона синусов
Разбейте треугольник на 2 прямоугольных треугольников, отбрасывая перпендикуляр длиной h . Затем: а также Деление первого уравнения на второе дает что является другим способом записи закона синусов.Вывод закона косинусов
Снова разбейте треугольник на 2 прямоугольных треугольника. Применение теоремы Пифагора к двум прямоугольным треугольникам дает:Вычитание второго из первого дает:
Это закон косинусов: .Как использовать законы синусов и косинусов
Чтобы решить косой треугольник, комбинация не менее 3 углов и стороны должны быть указаны. Дела классифицированы САС, АСА, АСС и т.д.
Если даны сторона и противолежащий ей угол, то можно использовать закон синусов.
В противном случае вы должны использовать закон косинусов.
Дела классифицированы САС, АСА, АСС и т.д.
Если даны сторона и противолежащий ей угол, то можно использовать закон синусов.
В противном случае вы должны использовать закон косинусов.Если вы используете закон синусов, чтобы найти угол, который вам в конечном итоге понадобится для вычисления греха −1 . Если угол, который вы ищете острый, то калькулятор возвращает правильное значение. Но если угол тупой, то угол, указанный калькулятором не правильный. Вам нужен тот, что во втором квадранте (что можно получить, вычитая угол калькулятора из 180°.) (Напоминаем, что острый угол — это угол между 0° и 90°. Тупой угол — это угол между 90° и 180°.)
Пример: Решите косой треугольник.
Решение: Сумма углов равна 180°:
С = 180° — 32,5° — 49,7° = 97,8°Теперь используйте закон синусов, чтобы получить стороны b и c :
Решение для b дает
Решение для c дает
Неизвестные стороны и углы равны C = 97,8°, b = 321 и с = 417.

Пример. Неоднозначный случай: Решите косой треугольник с заданной информацией об угле и двух сторонах:
А = 25,3°, с = 152 и а = 95,0Решение: Обратите внимание, что данной информации недостаточно, чтобы решить, треугольник ABC или ABC’ показан здесь:
Это называется неоднозначностью ASS . Если мы используем закон синусов, чтобы получить угол C , мы получим:
Обратите внимание, что два значения sin −1 дают два значения C . в двух возможных треугольниках.- Первая возможность: C = 43,1° Тогда B = 180° — 25,3° — 43,1° = 111,6° и b получается из закона синусов:
- Второй вариант: C = 136,9° Тогда B = 180° — 25,3° — 136,9° = 17,8° и b получается из закона синусов:
или C = 136,9°, B = 17,8° и b = 68,1
Пример: Решите показанный косой треугольник.
Решение: Поскольку мы не знаем ни одной стороны — противоположной пару углов мы должны начать с закона косинуса:
Теперь найдем угол B используя закон синуса:
Из рисунка видно, что B острый и что единственная возможность состоит в том, что B = 30,2° Таким образом, A = 127,6°
Таким образом, c = 91,5, B = 30,2° и A = 127,6° Упражнения тренера по алгебре
Векторы
Определение: Вектор — это величина, имеющая направление а также звездной величины . Сравните это со скаляром , который является величиной, имеющей только величину. Примером вектора является сила. Чтобы ускорить объект в определенном направлении, вы необходимо приложить усилие в этом направлении. Примером скаляра является температура; температура не указывает ни в какую сторону.
Стрелка может использоваться для представления вектора. Длина стрелки представляет величину вектора а направление стрелки — это направление вектора.
Сложение векторов: Чтобы геометрически сложить два вектора A и B, положить хвост B в голову A или наоборот. Результирующий вектор A + B, показанный ниже красным, указывает от s (начало) до ф (финиш). Это называется параллелограммной конструкцией . Вектор A + B называется результатом сложения векторов A и B.
(Это добавление «хвост к голове» является продолжением того, как добавляются обычные числа. Нажмите здесь, чтобы увидеть числа 2 и 3 и их сумма 5.)
Определение вектора ничего не говорит о том, где находится вектор.
Векторы обычно рисуются хвостом в начале координат.
Это называется стандартной позицией .
Одним из преимуществ стандартного положения является то, что полная информация о векторе
задается координатами стрелки. Вот то же векторное сложение
сделано с векторами в стандартном положении.
Вот то же векторное сложение
сделано с векторами в стандартном положении.
Вычитание векторов: Вычитание векторов можно понимать двумя способами.
Во-первых, вычитание B − A эквивалентно сложению В + (-А). (Отрицательное значение вектора A, а именно −A, точки в направлении, противоположном направлению A.)
Второй способ состоит в том, чтобы думать о B − A как о разнице
между B и A. То есть разница между их наконечниками стрел.
Таким образом, это вектор, который указывает от наконечника стрелки A к наконечнику стрелки.
B, который показан серым цветом,
а затем перерисовывается в стандартное положение красным цветом.
Разложение вектора на его компоненты: Разложение вектора на его компоненты
Компоненты x и y выполняется путем проведения пунктирной линии от наконечника стрелки
параллельно оси y , пока не совпадет с осью x и другой пунктирной линией. линия, параллельная оси x , до пересечения с осью y ,
а затем рисование векторов по обеим осям до тех пор, пока они
прикоснуться к этим линиям.
линия, параллельная оси x , до пересечения с осью y ,
а затем рисование векторов по обеим осям до тех пор, пока они
прикоснуться к этим линиям.
Системы координат для векторов: Векторы могут быть выражены в
полярные координаты или прямоугольные координаты.
- В Полярные координаты величина вектора
и угол задаются напрямую.
Вектор V на картинке обозначается так:
В = 2,5 ∠ 53°
∠ называется символом угла. Число перед символом угла величина или длина вектора. Число после символа угла указывает направление вектор, выраженный как угол, измеренный против часовой стрелки от положительная часть действительной оси. - В Прямоугольные координаты координаты x и y координат
указана стрелка вектора.
Теперь вектор V на картинке обозначается так:
В = (1,5, 2)
 Например:
Например: Сложение двух векторов, выраженных в прямоугольных координатах, также просто. Вы добавляете два компонента x , чтобы получить результирующий компонент x . и добавьте два компонента y , чтобы получить результирующий компонент y . Например, если A = (2, 4) и B = (3, 1), то:
А + В = (2, 4) + (3, 1) = (5, 5)На рисунке показано, что это работает, потому что:
А + В = (2, 4) + (3, 1)
= (2, 0) + (0, 4) + (3, 0) + (0, 1)
= (2, 0) + (3, 0) + (0, 4) + (0, 1)
= (5, 0) + (0, 5)
= ( 5 , 5 )
Здесь мы описываем только двумерные векторы, но математики используют векторы в любом количестве измерений.
Преобразование полярных координат в прямоугольные
Часто необходимо преобразовать вектор, выраженный в полярных координатах в прямоугольные координаты или наоборот.
Ваш калькулятор может иметь полярную форму в прямоугольную. (обозначается P → R или → x y ) и прямоугольное преобразование в полярное (обозначается R → P или → r θ ) встроенный. См. руководство к калькулятору. Если нет, вы можете сделать следующее:
- Если задан вектор r ∠ θ в полярной, то в прямоугольной это ( x , y ), где:
x = r cos( θ ) и y = r sin( θ ).
- Если вам задан вектор ( x , y ) в прямоугольной форме, тогда в полярном это r ∠ θ где: Обратите внимание, что вам, возможно, придется добавить 180°, если θ находится не в первом квадранте.
Добавление полярных векторов
В общем, нет простого, прямого способа добавить два полярные векторы. Например получается, что (см. пример ниже):
Например получается, что (см. пример ниже):8 ∠ 30° + 10 ∠ −60° = 12,8 ∠ 21,3°
Единственным исключением является случай, когда два вектора лежат вдоль одной и той же линия. Например,
1 ∠ 50° + 2 ∠ 50° = 3 ∠ 50°
В общем, чтобы добавить два полярных вектора, вы должны:
- преобразовать оба в прямоугольные
- делать сложение в прямоугольной форме
- преобразовать полученный результат обратно в полярный
Пример: Сложите полярные векторы 8 ∠ 30° и 10 ∠ −60°.
Решение:
Применение векторов
Статика Если объект находится в статическом равновесии, то силы на нем должны в сумме равняться нулю. Другими словами, сумма силы справа равны сумме сил слева и силы вверх равны силам вниз.
Пример: Подвешен груз массой Вт = 510 Н
двумя веревками под указанными углами. (N обозначает ньютоны
которые являются единицами силы в метрической системе.)
(а) Каковы напряжения Т 1 T 2 в веревках?Решение: Силы Т 1 , Т 2 и W должны быть сбалансированы:(b) Если канаты имеют предел прочности на растяжение 1000 ньютонов, какой максимальный вес можно выдержать?
Замена 1.049 T 1 вместо T 2 во втором уравнении дает:
Таким образом, напряжения равны Тл 1 = 678 Н и T 2 = 711 Н.
Часть (b): Обратите внимание, что T 2 — это большее натяжение. Натяжения пропорциональны весу и когда Вт = 717 Н, тогда Т 2 = 1000 Н. Таким образом, максимальный вес
которую можно поддерживать, составляет 717 Н.
Натяжения пропорциональны весу и когда Вт = 717 Н, тогда Т 2 = 1000 Н. Таким образом, максимальный вес
которую можно поддерживать, составляет 717 Н.
Пример: Тележка весом Вт = 1250 ньютонов находится на плоскости, наклоненной под углом θ = 13°. Какая минимальная сила F должно быть применяется для предотвращения скатывания тележки под гору, если есть нет трения?
Решение: Вес W обусловлен гравитацией и поэтому действует вертикально вниз. Ключ состоит в том, чтобы разрешить W в компоненты параллельны и перпендикулярны наклонной плоскости. Компонент W , параллельный плоскости, равен W sin( θ ). F должен быть равен не менее столько, иначе тележка покатится под гору. Подставляем числа получаем:
F = Вт sin( θ ) = (1250 Н) sin(13°) = 281 НТаким образом, минимальная сила составляет 281 ньютон.

Применение радианного измерения
Выше мы видели, что углы могут быть измерены в 90 293 радианах 90 294 , при вращении на полный круг. составляет 2π или примерно 6,28 радиана.Размер угла θ в радианах равен с (длина дуги , стягиваемая углом) деленная на r (радиус окружности).
Для угла в один полный круг длина дуги с становится окружностью C . Поскольку C = 2 π r , мы получаем
для угла в один полный круг.Обратите внимание, что начиная с s и r оба имеют размеры длины радиан — это единица без размеров. Это важная особенность радианов.
Пример: Выразите угол θ на рисунке в радианах.
В равностороннем треугольнике три угла равны 60°.
 Изгиб одной стороны в дугу дает угол в 1 радиан.
Мы видим, что 1 радиан чуть меньше 60°.
Изгиб одной стороны в дугу дает угол в 1 радиан.
Мы видим, что 1 радиан чуть меньше 60°. Часто бывает полезно выразить угол в радианах
как кратное π. Для этого умножьте на символ π и
разделить на значение числа π, а именно на 3,14159.
Пример: Выразите 4,22 рад как кратное π.
Рисунок определяет сектор , хорду и сегмент .
площадь круга это:
А = π r 2Площадь сектора равна дроби s / C площади круга, где C — длина окружности. Таким образом:
Поскольку C = 2 π r площадь сектора составляет: Обратите внимание на сходство с формулой площади треугольника:
Пример: Каково расстояние между точкой на широте
43,6° северной широты и точка к югу от нее на экваторе?
(Используйте тот факт, что Земля имеет диаметр 7920 миль. )
)
Решение: Решение уравнения для длины дуги дает с = r θ . Эта формула требует радиус, , а угол θ выражено в радианах :
Таким образом, длина дуги равна:с = r θ = (3960 миль) (0,7610 рад) = 3010 миль,до 3 сиг фиг. Обратите внимание, что единицы измерения s такие же, как r (миль), поскольку единицы θ (радианы) фактически безразмерный.
Пример: На какое расстояние перемещается зубчатая рейка, если шестерня поворачивается на угол 300°?
Решение: Поскольку зубчатая рейка зацепляется, расстояние, на которое перемещается стойка, равно длине дуги s опирается на угол 300° на ведущей шестерне, что определяется как s = r θ . Радиус ведущей шестерни равен r = 11,25 мм, а угол θ , через которое поворачивается , выраженное в радианах , равно:
Таким образом:с = r θ = (11,25 мм) (5,236 рад) = 58,9 мм.Обратите внимание, что единицы измерения s такие же, как у r , а именно миллиметры.
Равномерное круговое движение
Предположим, что объект движется с постоянной скоростью v по окружности радиусом r и движется от A до B , преодолев расстояние с , по времени т . затем с скорость = пройденное расстояние / необходимое время .При этом угол θ увеличивается. Скорость, с которой θ увеличивается, равна угол заметания / необходимое время , а именно θ / t . Эта величина называется угловой скоростью ω (греческая буква омега). Таким образом:
Угловая скорость ω может иметь любые единицы измерения угла делится на время, но наиболее полезными единицами измерения являются радианы/сек.
Пример: Объект вращается с угловой скоростью ω = 48 π рад/сек. На какой угол он повернется за 0,25 с?
Решение: Решение для θ дает:
θ = ω t = (48 π рад/сек)(0,25 сек) = 12 π рад.(Обратите внимание, что 48 π рад/сек = 24 цикла/сек и что 12 π рад = 6 циклов)
Пример: Какова скорость в милях в час точки на экватора и точки Ванкувера из-за вращения Земли? Используйте тот факт, что радиус Земли составляет 3960 миль, что он вращается каждые 24 часа и что Ванкувер находится на широта 490,2° северной широты.
Решение: Первое изображение справа смотрит вниз на
Северный полюс и показывает, как далеко точка в Ванкувере и
точка на экваторе переместится за 1 час.
Оба имеют одинаковую угловую скорость ω , а именно:

Чтобы найти v , используйте уравнение v = r ω , где либо r = r E для экватора, либо r = r V для Ванкувера. Нам дали r E = 3960 миль. Чтобы найти r V , используйте изображение Земли сбоку. Направо. Тригонометрия дает:
Таким образом, скорости равны: Таким образом, скорость точки на экваторе равна 1037 миль в час, а скорость точка в Ванкувере составляет 677 миль в час из-за вращения Земли. (Эта дополнительная скорость является причиной того, что стартовые площадки для орбитальных ракет выбираются вблизи экватора.)Графики функций синуса, косинуса и тангенса
Напомним, что, а также ,где р это длина вектора, а x и y являются его x и Компоненты и .
 Пусть r = 1. Тогда
sin( θ ) = y и cos( θ ) = x .
Другими словами, sin( θ ) — это всего лишь компонент y .
а cos( θ ) представляет собой компонент вектора размером x длины 1.
Пусть r = 1. Тогда
sin( θ ) = y и cos( θ ) = x .
Другими словами, sin( θ ) — это всего лишь компонент y .
а cos( θ ) представляет собой компонент вектора размером x длины 1.- Функция синуса: Пусть угол θ изменяется от 0 до 2π радиан за 8
шаги. Вектор длины 1 поворачивается к позициям a через ч в кружке внизу (указано красными стрелками).
Вертикальные стрелки (синего цвета) обозначают и .
компоненты вектора в различных положениях.
График справа представляет собой график зависимости компонентов y от θ ,
следовательно, график sin( θ ) как функция θ .
Окружность, созданная вектором длины 1 при его вращении, называется единичной окружностью , и мы говорим, что функция синуса генерируется компонентом y этого вращающийся вектор.

- Функция косинуса: Снова пусть угол θ изменяется от 0 до 2π радиан за 8
шаги. Снова вектор длины 1 поворачивается в позиции и через ч в круге внизу (красные стрелки). горизонтальных стрелок (синие)
являются x компонентами вектора длины 1 в различных позициях.
График справа представляет собой график
Компонент x против θ , следовательно, график cos( θ )
как функция θ .
Мы говорим, что функция косинуса генерируется x компонент вращающийся вектор длины 1.
- Касательная функция: Этот график был построен путем вычисления отношения y / x для различных значений θ .
Обратите внимание, что тангенс(π/2) = ±∞ и tan(3π/2) = ±∞, поскольку x равно 0 (вызывая деление на 0) под этими углами.
- Ось θ для всех трех приведенных выше графиков может использовать градусы.
 Просто замените π радиан на 180° и т. д.
Просто замените π радиан на 180° и т. д. - sin( θ ), cos( θ ) и tan( θ )
являются периодическими функциями — это значит, что они повторяют свои
шаблоны для θ < 0 и θ > 2π радиан.
Функции sin( θ ) и cos( θ )
имеют период 2π радиан, так как они повторяются каждые 2π радиан.
Функция загар( θ ) имеет период π радиан, так как
повторяется каждые π радиан.
Синусоидальная функция
y = A sin ( ω t + φ ) Волны на воде, вибрации на струне, звук, свет, циклы популяции животных, хозяйственные циклы и переменный ток все они могут быть описаны синусоидальной функцией или синусоидальной формой волны :y = A sin ( ω t + φ )где y представляет процентную величину, а t представляет время.
 Поскольку y пропорционально
функция sin, она имеет характерную форму волны sin.
Изменяя на , ω и φ , мы можем изменить
высоту или ширину волны или сместить ее влево или вправо в соответствии с
заявление. Рассмотрим каждый из этих параметров, А , ω и φ , в свою очередь:
Поскольку y пропорционально
функция sin, она имеет характерную форму волны sin.
Изменяя на , ω и φ , мы можем изменить
высоту или ширину волны или сместить ее влево или вправо в соответствии с
заявление. Рассмотрим каждый из этих параметров, А , ω и φ , в свою очередь:
- В функции г = A sin ( ω t + φ ),
параметр A называется амплитудой волны.
Сама функция sin находится в диапазоне от
от −1 до +1 без единиц измерения. Умножение синусоидальной волны на A причины y растянуть по вертикали от − A до + A с агрегатами А .
- В функции г = A sin ( ω t + φ ),
параметр ω называется угловой скоростью волна.

(Примечание: это греческая буква «омега», а не латинская w.)
ω относится к скорости вращения вращающегося вектора, который генерирует волну. Он имеет единицы радианы/сек.
На рисунке сравниваются ω = 1, 2 и 3 рад/сек. Волна sin(3 t ) колеблется в 3 раза быстрее, чем волна sin( t ).
Алгебраический способ понять, почему ω = 3 сжимает волны по горизонтали в 3 раза, следует отметить, что в sin(3 t ), t должен быть только ⅓ настолько большой, насколько это необходимо в грехе ( т ) чтобы получить то же значение в скобках. Когда значение в скобках равно 2π радианам, функция sin завершает один цикл.
С угловой скоростью связаны частота f и период T .
- Частота число циклов волны,
происходят в секунду. Поскольку в 1 цикле 2π радиан,
угловая скорость и частота связаны формулой:
ω = 2 π f .
Единицы f — циклы/сек или Герц.
- Период — это время в секундах, необходимое для завершить один цикл. Это величина, обратная частоте: Единицы T — секунды. Потому что ω = 2 π f это также можно записать как:
- Частота число циклов волны,
происходят в секунду. Поскольку в 1 цикле 2π радиан,
угловая скорость и частота связаны формулой:
- В функции г = A sin ( ω t + φ ),
параметр φ называется фазовым сдвигом волны.
(Примечание: это греческая буква «фи», т. произносится как «фи» и рифмуется со словом «крик».)
Если φ положительно, то волна смещается влево. Если φ отрицательно, то волна смещается вправо. φ может быть указано в радианах или градусах.
- Чтобы понять насколько волна смещена, обратите внимание, что φ измеряет сдвиг фазы в ,
2π — сдвиг на целый цикл, π — сдвиг на половину цикла и т.
 д.
д.сдвиг во времени зависит от обоих ω и φ . Пример справа показывает, что начальная точка волны на t ось а не просто значение фазового угла φ , что многие начинающие студенты считают правдой.
Чтобы понять, как ω и φ действуют вместе, вызывая сдвиг во времени, думайте о sin() как о функциональной машине. В скобки ( ) входит угол, а на синусоиде точка выходит. Когда 0 идет в скобки начало цикла выходит и когда 2π радиан выходит в скобки конец выходит цикл.
Для красной кривой y = sin(4 t +1), цикл начинается когда в скобках стоит 0, а именно, когда t = −¼.
Для черной кривой y = sin(4 t ), цикл заканчивается когда в скобках 2π, а именно когда 4 t = 2π или (решение для t ), когда t = π/2.
Если представить, что синусоидальная кривая генерируется вращающимся вектором, то φ можно рассматривать как угол, под которым вращается точки вектора изначально, то есть в момент времени t = 0,
Вот некоторые специальные фазовые сдвиги:φ = 2π рад или 360°.
 Волна смещается влево на один полный цикл, поэтому волна выглядит неизменной.
Волна смещается влево на один полный цикл, поэтому волна выглядит неизменной.φ = π рад или 180°. Волна сдвинута влево на полпериода, поэтому волна кажется повернутой с ног на голову.
φ = π/2 рад или 90°. Волна смещается влево на четверть цикла, так что, например, волна синуса становится волной косинуса.
Синусоидальный сигнал плюс компонент постоянного тока
В некоторых приложениях синусоидальная функция, обсуждавшаяся в предыдущем разделе должен быть смещен вверх или вниз на некоторую величину. Для этого добавляем константу y DC в правую часть формулы, вот так:
y = A sin ( ω t + φ ) + у ДС
- График сдвинут вверх на величину y DC (или вниз, если y DC отрицательно).

- y DC среднее значение (средний рост), относительно которого и колеблется.
- В электричестве термин y DC называется DC (постоянный ток) составляющая y .
- Термин A sin ( ω t + φ ) называется составляющей переменного тока.
Нахождение уравнения синусоидальной кривой
Чтобы найти уравнение синусоидальной кривой, выполните следующие действия:- Начните с записи «шаблона» уравнения y = A sin( ω t + φ ) (при условии, что метка на вертикальной оси y и метка по горизонтальной оси t ). Затем используйте следующий три шага, чтобы получить A , ω и ф .
- Получите амплитуду A , считав пиковое значение кривой
от вертикальной оси.
 Получите единицы A с этикетки
на вертикальной оси.
Получите единицы A с этикетки
на вертикальной оси. - Читать t B и t E , значения времени t в начале и в конце цикл. Период T разница т Е − т Б . Затем вычислить угловую скорость ω из уравнения .
- Получите фазовый сдвиг φ , используя тот факт, что величина в скобках, ω t + φ , должно быть равно нулю когда t = t B , в начале цикла.
Пример: Найдите уравнение синусоидальной волны, приведенное к право. Это представляет собой переменное напряжение. в есть напряжение в вольтах и t время в секундах.
Решение:
Рисование графика синусоидальной функции
Чтобы нарисовать график синусоидальной функции, выполните следующие действия:- Начните с обозначения вертикальной оси « y » и
горизонтальная ось « t », предполагая, что уравнение y = A sin( ω t + φ ).

- Get t B , время начала цикла, воспользовавшись тем, что количество в скобках, ω t + φ , должно быть равно 0, когда т = т Б .
- Get t E , время окончания цикла, воспользовавшись тем, что количество в скобках, ω t + φ , должно быть равно 2π когда t = t E .
- Поместите ящик, простирающийся от t B до t E по горизонтальной оси и от −A до +A на вертикальной оси. Обозначьте края коробки.
- Нарисуйте один цикл кривой синусоиды, чтобы заполнить поле.
Пример: График функции , где v в вольтах и t в секундах.
Решение: Так как первый член в скобках, а именно
,
в радианах
мы должны изменить второй член, 60 °, на π / 3 радиана, чтобы единицы измерения согласовались. Таким образом, мы будем графически.
Таким образом, мы будем графически.
- Поместите коробку, растянувшуюся от −3 до +15 в горизонтальном направлении и от от −12 до +12 по вертикали. Обозначьте края коробки.
- Разбейте блок на четыре подблока и используйте их, чтобы очертить синусоидальную кривая (красные точки).
- Нарисуйте синусоиду, плавно соединив точки.
| Упражнения тренера по алгебре |
Если вы нашли эту страницу в веб-поиске, вы не увидите
Оглавление в рамке слева.
Щелкните здесь, чтобы отобразить его.
Суммарная мощность с использованием Калькулятора угла фи
✖Напряжение (общее) представляет собой величину общей разности потенциалов в сети. В этом случае это обычно разность напряжений на вольтметре. | 0003 | +10 % -10 % | |
✖Ток (общий) — это общий ток, протекающий через цепь с нагрузкой.ⓘ Ток (общий) [I] 9488 АбамперАмперАттоамперБиотСантиамперeCGS e.m.CGS e.s. Единица ДециамперДекаамперEMU токаESU токаExaampereФемтоамперГигаамперGilbertГектоамперKiloamperMegaampereMicroampereMilliampereNanoamperePetaamperePicoampereStatampereTeraampereYoctoampereYottaampereZeptoampereZettaampere | +10% -10% | ||
✖Angle is the angle of phase difference between different voltages.ⓘ Angle [ϕ] | CircleCycleDegreeGonGradianMilMilliradianMinuteMinutes of ArcPointQuadrantQuartercircleRadianRevolutionRight AngleSecondSemicircleSextantSignTurn | +10 % -10% |
✖Мощность — это общая мощность, потребляемая в n-фазной цепи. | Аттоджоуль в секундуАттоваттТормозная мощность (bhp)Btu (IT) в часBtu (IT) в минутуBtu (IT) в секундуBtu (th) в часBtu (th) в минутуBtu (th) в секундукалория (IT) в часкалория (IT) в минутукалория (IT) ) в секундуКалория (й) в часКалория (й) в минутуКалория (й) в секундуСантиджоуль в секундуСантиваттCHU в часДекаджоуль в секундуДекаваттДециджоуль в секундуДециваттЭрг в часЭрг в секундуЭксаджоуль в секундуЭксаджоуль в секундуФемтоджоуль в секундуФемтоваттФут-фунт-сила в часФут-фунт-сила в минутуФут-фунт-сила в секундуГигаджоуль-сила в секунду СекундаГигаваттГектоджоуль в секундуГектоваттЛошадиная силаЛошадиная сила (550 ft*lbf per s)Лошадиная сила (котла)Лошадиная сила (электрическая)Лошадиная сила (метрическая)Лошадиная сила (вода)Джоуль в часДжоуль в минутуДжоуль в секундуКилокалория (ИТ) в часКилокалория (ИТ) в минутуКилокалория (ИТ) в секундуКилокалория ( й) в часКилокалория (й) в минутуКилокалория (й) в секундуКилоджоуль в часКилоджоуль в минутуКилоджоуль в секундуКиловольт Ам pereKilowattMBHMBtu (IT) per hourMegajoule per SecondMegawattMicrojoule per SecondMicrowattMillijoule per SecondMilliwattMMBHMMBtu (IT) per hourNanojoule per SecondNanowattNewton Meter per SecondPetajoule per SecondPetawattPferdestarkePicojoule per SecondPicowattPlanck PowerPound-Foot per HourPound-Foot per MinutePound-Foot per SecondTerajoule per SecondTerawattTon (refrigeration)Volt AmpereVolt Ampere ReactiveWattYoctowattYottawattZeptowattZettawatt | ⎘ Копировать |
👎
Формула
Перезагрузить
👍
Полная мощность с использованием решения под углом фи
ШАГ 0: Сводка предварительного расчета
ШАГ 1: Преобразование входных данных в базовый блок
Напряжение (общее): 12 В —> 12 В Преобразование не требуется
Ток (всего): 9 Ампер —> 9 Ампер Преобразование не требуется
Угол: 10 радиан —> 10 радиан Преобразование не требуется
ШАГ 2: Вычисление формулы
ШАГ 3: Преобразование результата в единицу измерения выхода
-271,8520771 Ватт —> 920 Преобразование не требуется < 3 2 Калькуляторы метода ваттметра
Суммарная мощность по формуле угла фи
Мощность = 3*напряжение (всего)*ток (всего)*cos(угол)
P = 3*V*I*cos(ϕ)
Как рассчитать общую мощность?
Трехфазный ваттметр использует 2 установки ваттметра. Они могут быть как в конфигурации звезды, так и в конфигурации треугольника. Ее также называют трехпроводной системой. Общая потребляемая мощность представляет собой сумму мощности, потребляемой каждым ваттметром. При расчете мощности мы используем значение плеч токов и напряжений.
Они могут быть как в конфигурации звезды, так и в конфигурации треугольника. Ее также называют трехпроводной системой. Общая потребляемая мощность представляет собой сумму мощности, потребляемой каждым ваттметром. При расчете мощности мы используем значение плеч токов и напряжений.
Как рассчитать общую мощность, используя угол фи?
Калькулятор общей мощности с использованием угла фи использует Мощность = 3 * Напряжение (общее) * Ток (общий) * cos (угол) для расчета мощности. Общая мощность с использованием формулы угла фи используется для расчета полной мгновенной мощности, потребляемой в установка двухфазного ваттметра. Мощность обозначается символом P .
Как рассчитать общую мощность с использованием угла фи с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для полной мощности с использованием угла фи, введите напряжение (общее) (V) , Current (total) (I) & Angle (ϕ) и нажмите кнопку расчета. Вот как можно объяснить общую мощность с использованием расчета угла Фи с заданными входными значениями -> -271,859175 = 3*12*9*cos(10) .
Вот как можно объяснить общую мощность с использованием расчета угла Фи с заданными входными значениями -> -271,859175 = 3*12*9*cos(10) .
Часто задаваемые вопросы
Что такое общая мощность с использованием угла фи?
Общая мощность с использованием формулы угла фи используется для расчета полной мгновенной мощности, потребляемой в двухфазной установке ваттметра, и представлена как P = 3*V*I*cos(ϕ) или Мощность = 3*Напряжение (общее)*Ток (всего)*cos(Угол) . Напряжение (общее) — это величина общей разности потенциалов в сети. В этом случае обычно это разность напряжений на вольтметре, ток (общий) — это общая величина тока, протекающего через цепь с нагрузкой, а угол — это угол разности фаз между различными напряжениями.
Как рассчитать общую мощность с помощью угла фи?
Общая мощность с использованием формулы угла фи используется для расчета полной мгновенной мощности, потребляемой в двухфазной установке ваттметра, рассчитывается с использованием Мощность = 3*Напряжение (всего)*Ток (всего)*cos(Угол) . Чтобы рассчитать общую мощность с использованием угла фи, вам нужно напряжение (общее) (В) , ток (общий) (I) и угол (ϕ) . С помощью нашего инструмента вам нужно ввести соответствующее значение для напряжения (общего), тока (общего) и угла и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.
Чтобы рассчитать общую мощность с использованием угла фи, вам нужно напряжение (общее) (В) , ток (общий) (I) и угол (ϕ) . С помощью нашего инструмента вам нужно ввести соответствующее значение для напряжения (общего), тока (общего) и угла и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.
Доля
Скопировано!
Расчет фазового угла, частота задержки, вычисление фазового сдвига, сдвиг времени между разностью напряжений, время прихода ITD, осциллограф, измерение двух сигналов, формула, угол, ток, напряжение, phi, фазовый сдвиг, разность времени Осциллограф ITD измеряет формулу двух сигналов: угол, ток, напряжение, фазовый сдвиг, разность времени, phi — sengpielaudio Sengpiel Berlin
| Немецкая версия |
Phase in Acoustics
Calculation of phase angle − phase difference
phase shift from time delay , time of arrival difference и частота
Время задержки звука = Time Delay Δ t (разница во времени) осциллограф
— Запаздывание по фазе и сдвиг во времени
Связь между фазой, фазовым углом, частотой, временем прихода Δ t (задержка) и ITD
Угловая частота = частота среза = частота кроссовера
и ITD = интерауральная временная задержка
Используемый браузер не поддерживает JavaScript. Вы увидите программу, но функция не будет работать. |
| Вопрос: Какова формула для фазы синусоиды? Нет фазы синусоиды. Синусоида не имеет фазы. Фаза может развиваться только между двумя синусоидами. Две синусоидальные волны взаимно сдвинуты по фазе, если моменты времени его нулевых переходов не совпадают. |
| Слово фаза имеет четкое определение для двух чистых бегущих синусоидальных волн переменного тока, но не для музыкальных сигналов. Все эквалайзеры сдвигают фазу в зависимости от частоты. Без всяких неподвижной точки никакое «смещение» (перемещение) невозможно. Специальные приемы: 90° фильтр с двумя всепропускающими фильтрами. Фазы всегда равны разности фаз . Смена полярности (пол-оборот) никогда не бывает фазовым сдвигом на оси времени t .  Синусоидальные сигналы одной частоты могут иметь разность фаз. При наличии фазового сдвига (разности фаз) или фазовой задержки фазового угла φ (греческая буква фи) в градусах необходимо указать, между какими чистыми сигналами (синусоидами) это появляется. Так, например, фазовый сдвиг может быть между двумя стереофоническими сигналы канала слева и справа, между входным и выходным сигналом, между напряжением и ток, или между звуковым давлением p и скоростью частиц воздуха против . |
Что такое амплитуда?
| Один полный цикл волны связан с «угловым» смещением 2 π радиан. Фаза φ — угол участка сигнала, указывается в угловых градусах и обеспечивает ссылку на опорное значение всего сигнала.  Для периодических сигналов Для периодических сигналов полный фазовый угол 360 градусов и период, равный длительности периода. Типичный вопрос: какова частота и фазовый угол синусоидального сигнала? Может ли «один» сигнал действительно иметь фазу? Две «синфазные» волны имеют фазу (угол) φ = 0 градусов. Если частота = 0 Гц, то напряжения переменного тока нет — есть только постоянное. Тогда не будет Фазовый угол присутствует. |
Какое отношение временная задержка имеет к фазовому углу?
| Расчет между фазовым углом φ ° в градусах (град), временной задержкой Δ t и частота f равна: Фазовый угол (градусы) (Временной сдвиг) Разница во времени Частота λ = c / f = и м/с c c . Расчет между фазовым углом φ в радианах (rad), временным сдвигом или временной задержкой Δ t , |
Разность времени (длительность) звука на метр
Влияние температуры на разность времени Δ t
Зависимость только от температуры воздуха0003
| Температура воздуха в °C | Скорость звука c в м/с | Время на 1 м Δ t в мс/м |
| +40 | 354,9 | 2,818 |
| +35 | 352,0 | 2,840 |
| +30 | 349,1 | 2,864 |
| +25 | 346,2 | 2,888 |
| +20 | 343,2 | 2,912 |
| +15 | 340,3 | 2,937 |
| +10 | 337,3 | 2,963 |
| +5 | 334,3 | 2,990 |
| ±0 | 331,3 | 3,017 |
| −5 | 328,2 | 3,044 |
| −10 | 325,2 | 3,073 |
| −15 | 322,0 | 3. 103 103 |
| −20 | 318,8 | 3,134 |
| −25 | 315,7 | 3,165 |
| Звукорежиссеры обычно руководствуются эмпирическим правилом: На расстояние 90 294 90 293 90 027 r 90 028 90 294 90 293 = 1 м звуку требуется около 90 294 90 293 90 027 t 90 028 90 294 90 293 = 3 мс в воздухе. Δ t = r / c and r = Δ t × c Speed of sound c = 343 м/с при 20°С. |
следующий фазовый сдвиг φ ° (град) сигнала:
| Разность фаз φ ° (град) | Разность фаз φ Боген (рад) | Частота f | Длина волны λ = к/ф |
| 360° | 2 π = 6,283185307 | 2000 Гц | 0,171 м |
| 180° | π = 3,1415 | 1000 Гц | 0,343 м |
| 90° | π / 2 = 1,570796327 | 500 Гц | 0,686 м |
| 45° | π / 4 = 0,785398163 | 250 Гц | 1,372 м |
| 22,5° | π / 8 = 0,3 |
Преобразование: радианы в градусы и наоборот
Фазовый угол: φ ° = 360 × f × Δ t Для стереофонии на основе времени Δ t = a × sin α / c
Частота f = φ ° / 360 × 900
Фазовый угол (градусы) φ = временная задержка Δ t × Частота F × 360
, если вы принимаете разницу во времени δ T = Длина пути A / SPEED of Sound , затем GET , затем GET , затем GET , затем GET , затем GET , затем GET , затем GET , затем GET , затем GET , затем GET . Разность фаз φ ° = длина пути a × частота f × 360 / скорость звука c
Разность фаз φ ° = длина пути a × частота f × 360 / скорость звука c
Пожалуйста, введите два значения , третье значение будет рассчитано
Еще немного помощи: Время, частота, фаза и задержка
| Автор Лорд Рэлей (Джон Уильям Струтт, 3-й лорд Рэлей, 1907 г.) была показана дуплексная теория . Эта теория способствует пониманию процедуры «естественного слуха» у людей. Это очень простое понимание того, что интерауральное время прихода 90 091 различия ITD важны на частотах ниже 800 Гц, так как разности фаз с направление локализации как ушные сигналы , а на частотах выше 1600 Гц эффективны только межушные различия уровней ILD. Между ушами максимальная задержка составляет 0,63 мс. Разность фаз для отдельные частоты могут быть рассчитаны.  |
Схема фазовращателя для фазовых углов от φ = 0 до 180
Векторы напряжения фазовращателя
Для R = 0 Ом равно В OUT = В IN . Выход не должен быть нагружен низким импедансом.
Вы можете сдвигать отдельные чистые частоты (синусоиды),
но это невозможно с этой схемой для музыкальных программ.
Два синусоидальных напряжения — сдвинутые по фазе: φ = 45°
Условия для передачи без искажений
От Шопса — Йорга Вуттке: «Микрофонбух» — Глава 7
| Хотя потребность в постоянной частотной характеристике очевидна, для «линейной» фазы требуется скорее объяснение.  Есть инженеры, которые ожидают, что идеальная фаза будет такой же постоянной, как и амплитудная характеристика. Это неправда. Первоначально фаза начинается с 0°, потому что самая низкая частота заканчивается на 0 Гц, на . ОКРУГ КОЛУМБИЯ. (Фазовый угол между напряжениями постоянного тока отсутствует). В ходе на данной частоте фазовый угол не имеет значения, если фазовый угол равен только в два раза больше в случае двойной частоты и в три раза больше в случае тройной повторности и т. д. |
Предоставлено лабораториями Дэвида Моултона
(О гребенчатой фильтрации, фазовом сдвиге и изменении полярности)
| Электронный эквивалент потока сигнала и его задержанной итерации, объединенный в одиночный сигнал. В случае, который мы будем рассматривать, линия задержки имеет задержку в 1 миллисекунду, .  уровни как исходного, так и задержанного сигналов, поступающих в микшер, равны, и уровни как исходного, так и задержанного сигналов, поступающих в микшер, равны, и сигнал представляет собой синусоиду 1 кГц. |
| Синусоида 1500 Гц. частота (период T = 0,667 мс) и ее задержка итерация с задержкой 1 мс. Результирующий смешанный сигнал будет сигналом без . амплитуды или полное гашение сигнала. |
| |
| Фазовый сдвиг для любой частоты с задержкой в 1 миллисекунду. Диагональная линия представляет возрастающий фазовый сдвиг как функцию частоты. Обратите внимание, что мы можем думайте о 540 как о том же самом, что и 180. |
Время, Фаза, Частота, Задержка — Учебник по теории звуковых сигналов
Переполюсовка нет Фазовый сдвиг из 180 (временная задержка)
| (phi) = сдвиг фазы, сдвиг фазы, разность фаз, сдвиг фазы, отставание по фазе, угол фазы часто неправильно используются как: pol-rev = изменение полярности.  |
| «Это был соловей, а не жаворонок». Из: Ромео и Джульетта, Акт 3, Сцена 5, Уильям Шекспир. Это кнопка «POL-REV» (переключение полярности), а не кнопка «Phase (shift)». 1. Генерация отклика гребенчатого фильтра |
| Обратная полярность и фазовый сдвиг — разные термины (немецкий) Обратная полярность означает перестановку проводов a/b на b/a (немецкий) Фазовый сдвиг в отличие от обратной полярности (немецкий) Разница во времени Δ t и фазовый сдвиг Δ φ (немецкий) |
Полярность и фаза часто используются так, как будто они означают одно и то же. Они не.
«Кнопка реверса фазы» не меняет фазу. Он меняет полярность.
Переполюсовка без фазового сдвига. Переполюсовка (или Pol-Rev) — это термин, который часто путают с фазой Ø (phi) но не включает фазовый сдвиг или временную задержку. Смена полярности происходит всякий раз, когда мы «изменить знак» амплитудных значений сигнала. В аналоговом мире этот можно сделать с инвертирующим усилителем, трансформатором или в симметричной линии по просто переключая соединения между контактами 2 и 3 (разъем XLR) на одном конце кабель. В цифровом мире это делается простым изменением всех плюсов на 9.0091 минусы и наоборот в потоке данных аудиосигнала. |
Два пилообразных колебания
| вверху: исходный сигнал a/b (зуб пилы) в середине: 180 сдвинутый по фазе сигнал в виде сдвинутой во времени пилообразной формы T/2 внизу: b/a- сигнал обратной полярности (инвертированный) , зеркально отражено по оси времени |
Ясно видно, что обратная полярность не может быть такой же, как не в фазе. |
| Речь идет о широко обсуждаемой теме: «Фазовый сдвиг против инвертирования сигнала» и «фаза ». сдвиг по сравнению со сдвигом сигнала во времени». Термин фазовый сдвиг предположительно определен только для моночастотные синусоидальные сигналы и угол фазового сдвига явно определены только для синусоидальные величины. |
Стандартная кнопка Ø (фи) предназначена только для смены полярности
Абсолютно нет сдвига фаз
| Примечание. Время, частота и фаза тесно связаны друг с другом. Высота амплитуды не влияет на эти параметры. |
Угловая частота равна ω = 2 π × f
| Дано уравнение: y = 50 sin (5000 t) Определить частоту и амплитуду.  Answer: The amplitude is 50 and ω = 5000. So the frequency is f = 1/ T = ω / 2 π = 795.77 Hz. |
| Чтобы использовать калькулятор, просто введите значение. Калькулятор работает в обоих направлениях ↔ знак. |
| задняя часть | Поисковая система | дом |
Расстояние по большому кругу | Тригонометрия: составные углы
Как найти формулу расстояния по дуге большого круга?
В книге «Потерянный, но прекрасный: гаверсинус» мы исследовали расстояния по большому кругу на Земле и рассмотрели формулу гаверсинуса для их расчета: \[\mathop{\mathrm{haversin}} \left(\frac{d}{R}\ справа) = \mathop{\mathrm{haversin}} (\phi_2-\phi_1) + \cos{\phi_1}\cos{\phi_2} \mathop{\mathrm{haversin}} (\lambda_2-\lambda_1). \ ] 92{\left(\frac{\lambda_2-\lambda_1}{2}\right)}.\]
\ ] 92{\left(\frac{\lambda_2-\lambda_1}{2}\right)}.\]
В этой части мы исследуем, откуда взялась эта формула и почему мореплаватели могли использовать незнакомый гаверсинус, а не обычный синусов и косинусов в их расчетах.
Предварительные
При расчетах мы можем использовать любые единицы измерения расстояния: изменение единиц измерения не влияет на значение \(\frac{d}{R}\) (пока мы используем одни и те же единицы для обоих \(d \) и \(R\)). Удобнее всего выбрать единицы измерения так, чтобы радиус Земли был равен \(R=1\), а это означает, что мы работаем с 92 {\ влево (\ гидроразрыва {\ lambda_2-\ lambda_1} {2} \ вправо)}, \конец{уравнение}\]
выглядит немного проще. Мы будем работать с этими формами повсюду.
Расстояние по большому кругу, \(d\), представляет собой более короткую дугу, соединяющую две точки на большом круге. Мы также можем рассмотреть хорду (прямую), соединяющую две точки, и пусть ее длина равна \(C\).
Мы можем сразу заметить некоторые соотношения между \(d\), \(C\) и углом \(\сигма\) (измеряемым в радианах), который образует дуга большого круга с центром сферы: мы имеем \ (d=\sigma\) (поскольку радиус равен \(1\)), и рисуя равнобедренный треугольник \(POQ\), мы видим, что \(C=2\sin\bigr(\frac{\sigma} {2}\большой)\): 92 \ влево (\ гидроразрыва {d} {2} \ вправо) = 4 \ mathop {\ mathrm {haversin}} d. \конец{уравнение}\]
Теперь мы предлагаем четыре подхода к выводу формулы гаверсинуса. Первые два из них используют координаты, поэтому мы начнем с этого.
Координаты
Имея точку на единичной сфере с широтой \(\phi\) и долготой \(\lambda\), мы можем вычислить соответствующие декартовы координаты, как показано на следующей диаграмме.
Каковы декартовы координаты \(P\) (то есть его \((x,y,z)\) координаты)?
Зная декартовы координаты точек \(P\) и \(Q\) с широтами \(\phi_1\) и \(\phi_2\) и долготами \(\lambda_1\) и \(\lambda_2 \) соответственно, мы можем вычислить разность координат \(x\), \(y\) и \(z\) двух точек и использовать их для вычисления соответствующих расстояний или углов, чтобы найти \(d\ ).
Однако выражения станут довольно громоздкими с таким количеством переменных, поэтому мы ищем способ упростить ситуацию, прежде чем идти дальше.
Один трюк заключается в том, чтобы заметить, что расстояния и углы \(\сигма\) остаются неизменными, если мы вращаем сферу вокруг оси север-юг. Это изменяет только долготы точек, поэтому мы можем вращать его до тех пор, пока \(P\) не будет иметь долготу \(0\) и \(Q\) не будет иметь долготу \(\lambda_2-\lambda_1\), что мы назовем \ (\Delta\lambda\) (разница между \(\lambda\)s).
Тогда координаты \(P\) и \(Q\) становятся: \[\начать{выравнивать*} P &= (\cos\phi_1, 0, \sin\phi_1)\\ Q &= (\cos\phi_2\cos(\Delta\lambda), \cos\phi_2\sin(\Delta\lambda), \sin\phi_2). \конец{выравнивание*}\] 92\bigl(\frac{d}{2}\bigr)\)?
Затем мы можем продолжить точно так же, как в Подходе 1.
Подход 3: Сферическая тригонометрия
Точно так же, как существуют правила синусов и косинусов для треугольников на плоскости, существуют аналогичные правила для треугольников на сфере.
Вот рисунок сферического треугольника:
Углы \(A\), \(B\) и \(C\) — это углы при вершинах \(A\), \(B\) и \(C\) треугольника, а \(a\), \(b\) и \(c\) — длины сторон, как обычно. Но если мы возьмем сферу с радиусом \(1\), то их также можно рассматривать как углы: \(a\) — это угол \(\угол BOC\), например. Поэтому с этого момента мы предполагаем, что сфера имеет радиус \(1\).
Существует два правила сферических косинусов и одно правило сферических синусов, а именно:
правило сферических косинусов (1): \[\cos a=\cos b\cos c+\sin b\sin c\cos A\ ] (и аналогичные уравнения с переставленными \(a\), \(b\), \(c\) и \(A\), \(B\), \(C\))
сферическое правило косинусов (2): \[\cos A=-\cos B\cos C+\sin B\sin C\cos a\] (и аналогичные уравнения с \(a\), \(b\), \(c\) и \(A\), \(B\), \(C\) переставлены)
сферическое правило синусов: \[\dfrac{\sin A}{\sin a}=\dfrac{\sin B}{\sin b}=\dfrac{\sin C}{\sin c}\] 92=4\mathop{\mathrm{haversin}} d,\], где \(d\) — расстояние по большому кругу (или стягиваемый угол), а \(C\) — соответствующая длина хорды.

Требуется найти расстояние по окружности \(d\) между точками \(P\) и \(Q\) с широтами \(\phi_1\) и \(\phi_2\) и долготами \(\ лямбда_1\) и \(\лямбда_2\) соответственно.
Размышляя о симметрии, нам предлагается также рассмотреть точки \(R\) и \(S\) с широтами \(\phi_1\) и \(\phi_2\), но с переставленными долготами \(\lambda_2\ ) и \(\lambda_1\) соответственно. Это дает нам следующую конфигурацию:
На этой диаграмме все синие линии — это прямые хорды (хотя оптическая иллюзия заставляет их выглядеть иначе), а красная линия — это большой круг между \(P\) и \(Q\).
Можете ли вы использовать эту диаграмму, чтобы вывести формулу гаверсинуса?
Как сравнить эти четыре подхода?
Зачем использовать гаверсины?
Конечно, мы могли бы просто использовать \(\cos\bigl(\frac{d}{R}\bigr)=\cos\phi_1\cos\phi_2\cos(\Delta\lambda)+\sin\phi_1\sin\ phi_2\) для вычисления расстояний по большому кругу, как мы обнаружили в подходах 2 и 3? Зачем кому-то нужен гаверсин? (Мы повторно вставили радиус \(R\) здесь, так как в практических расчетах будут использоваться стандартные единицы измерения.


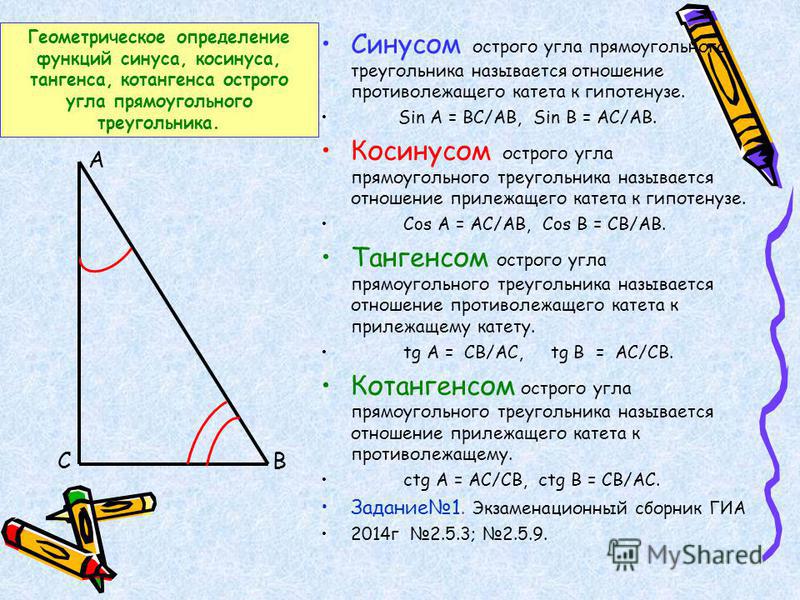 В идеальном варианте PF=cos ϕ=1. Тогда ток нагрузки: I=10000/(220•1)≈45 А. При PF=0,8 I=10000/(220•0,8)≈57 А. То есть при снижении PF с 1 до 0,8 ток возрастет приблизительно на 20%. Значит, это приведет к излишним затратам на электроэнергию.
В идеальном варианте PF=cos ϕ=1. Тогда ток нагрузки: I=10000/(220•1)≈45 А. При PF=0,8 I=10000/(220•0,8)≈57 А. То есть при снижении PF с 1 до 0,8 ток возрастет приблизительно на 20%. Значит, это приведет к излишним затратам на электроэнергию. Таким образом, за определённый объём полезной работы потребителю приходится переплачивать.
Таким образом, за определённый объём полезной работы потребителю приходится переплачивать. При их использовании совместно с индуктивностью они образуют колебательный контур. В нём мощность от индуктивности будет потребляться ёмкостью.
При их использовании совместно с индуктивностью они образуют колебательный контур. В нём мощность от индуктивности будет потребляться ёмкостью.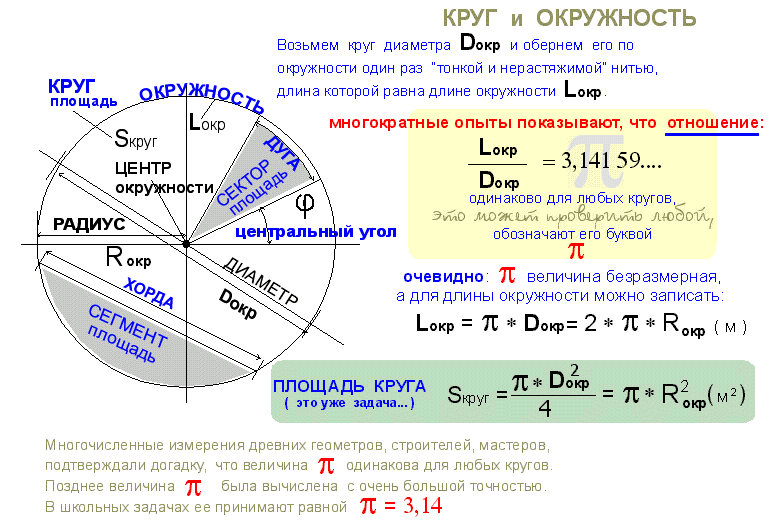 Поэтому коэффициент мощности трансформатора обычно находится в диапазоне от 0.5 до 0.85.
Поэтому коэффициент мощности трансформатора обычно находится в диапазоне от 0.5 до 0.85.
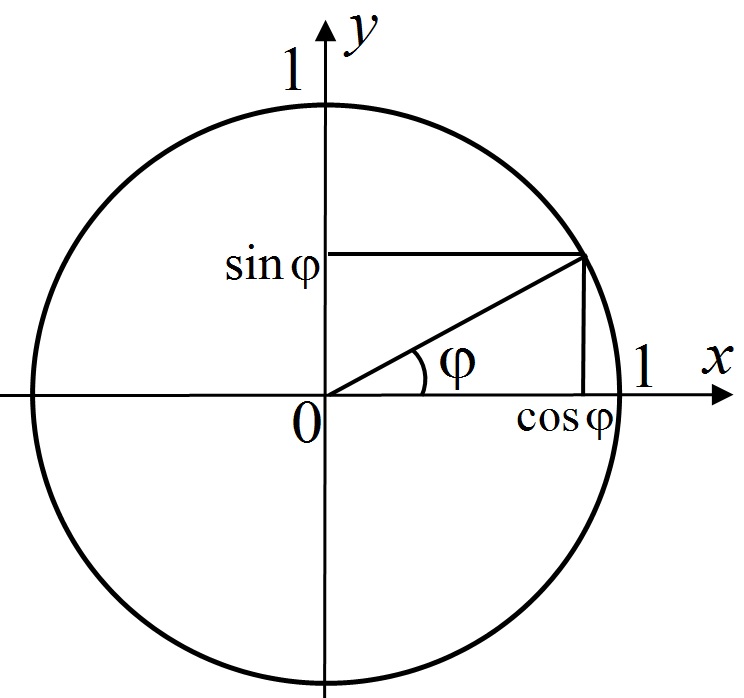

 Коэффициент мощности для трехфазного электродвигателя.
Коэффициент мощности для трехфазного электродвигателя.
 Для сетей переменного тока:
Для сетей переменного тока: