Действия с дробями, подробно с примерами
Действия с дробями. В этой статье разберём примеры, всё подробно с пояснениями. Рассматривать будем обыкновенные дроби. В дальнейшем разберём и десятичные. Рекомендую посмотреть весь список материалов и изучать последовательно.
1. Сумма дробей, разность дробей.
Правило: при сложении дробей с равными знаменателями, в результате получаем дробь – знаменатель которой остаётся тот же, а числитель её будет равен сумме числителей дробей.
Правило: при вычислении разности дробей с одинаковыми знаменателями получаем дробь – знаменатель остаётся тот же, а из числителя первой дроби вычитается числитель второй.
Формальная запись суммы и разности дробей с равными знаменателями:
Примеры (1):
Понятно, что когда даны обыкновенные дроби, то всё просто, а если смешанные? Ничего сложного…
Вариант 1 – можно перевести их в обыкновенные и далее вычислять.
Вариант 2 – можно отдельно «работать» с целой и дробной частью.
Примеры (2):
Ещё:
А если будет дана разность двух смешанных дробей и числитель первой дроби будет меньше числителя второй? Тоже можно действовать двумя способами.
Примеры (3):
*Перевели в обыкновенные дроби, вычислили разность, перевели полученную неправильную дробь в смешанную.
*Разбили на целые и дробные части, получили тройку, далее представили 3 как сумму 2 и 1, при чём единицу представили как 11/11, далее нашли разность 11/11 и 7/11 и вычислили результат. Смысл изложенных преобразований заключается в том, чтобы взять (выделить) единицу и представить её в виде дроби с нужным нам знаменателем, далее от этой дроби мы уже можем вычесть другую.
Ещё пример:
Вывод: имеется универсальный подход – для того, чтобы вычислить сумму (разность) смешанных дробей с равными знаменателями их всегда можно перевести в неправильные, далее выполнить необходимое действие.
После этого если в результате получаем неправильную дробь переводим её в смешанную.
Выше мы рассмотрели примеры с дробями, у которых равные знаменатели. А если знаменатели будут отличаться? В этом случае дроби приводятся к одному знаменателю и выполняется указанное действие. Для изменения (преобразования) дроби используется основное свойство дроби.
Рассмотрим простые примеры:
В данных примерах мы сразу видим каким образом можно преобразовать одну из дробей, чтобы получить равные знаменатели.
Если обозначить способы приведения дробей к одному знаменателю, то этот назовём СПОСОБ ПЕРВЫЙ.
То есть, сразу при «оценке» дроби нужно прикинуть сработает ли такой подход – проверяем делится ли больший знаменатель на меньший. И если делится, то выполняем преобразование — домножаем числитель и знаменатель так чтобы у обеих дробей знаменатели стали равными.
Теперь посмотрите на эти примеры:
К ним указанный подход не применим. Существуют ещё способы приведения дробей к общему знаменателю, рассмотрим их.
Существуют ещё способы приведения дробей к общему знаменателю, рассмотрим их.
Способ ВТОРОЙ.
Умножаем числитель и знаменатель первой дроби на знаменатель второй, а числитель и знаменатель второй дроби на знаменатель первой:
*Фактически мы приводим дроби к виду, когда знаменатели становятся равными. Далее используем правило сложения робей с равными знаменателями.
Пример:
*Данный способ можно назвать универсальным, и он работает всегда. Единственный минус в том, что после вычислений может получится дробь которую необходимо будет ещё сократить.
Рассмотрим пример:
Видно что числитель и знаменатель делится на 5:
Способ ТРЕТИЙ.
Необходимо найти наименьшее общее кратное (НОК) знаменателей. Это и будет общий знаменатель. Что это за число такое? Это наименьшее натуральное число, которое делится на каждое из чисел.
Посмотрите, вот два числа: 3 и 4, есть множество чисел, которые делятся на них – это 12, 24, 36, … Наименьшее из них 12. Или 6 и 15, на них делятся 30, 60, 90 …. Наименьшее 30. Вопрос – а как определить это самое наименьшее общее кратное?
Или 6 и 15, на них делятся 30, 60, 90 …. Наименьшее 30. Вопрос – а как определить это самое наименьшее общее кратное?
Имеется чёткий алгоритм, но часто это можно сделать и сразу без вычислений. Например, по указанным выше примерам (3 и 4, 6 и 15) никакого алгоритма не надо, мы взяли большие числа (4 и 15) увеличили их в два раза и увидели, что они делятся на второе число, но пары чисел могут быть и другими, например 51 и 119.
Алгоритм. Для того, чтобы определить наименьшее общее кратное нескольких чисел, необходимо:
— разложить каждое из чисел на ПРОСТЫЕ множители
— выписать разложение БОЛЬШЕГО из них
— умножить его на НЕДОСТАЮЩИЕ множители других чисел
Рассмотрим примеры:
50 и 60 => 50 = 2∙5∙5 60 = 2∙2∙3∙5
в разложении большего числа не хватает одной пятёрки
=> НОК(50,60) = 2∙2∙3∙5∙5 = 300
48 и 72 => 48 = 2∙2∙2∙2∙3 72 = 2∙2∙2∙3∙3
в разложении большего числа не хватает двойки и тройки
=> НОК(48,72) = 2∙2∙2∙2∙3∙3 = 144
* Наименьшее общее кратное двух простых чисел равно их произведению
Вопрос! А чем полезно нахождение наименьшего общего кратного, ведь можно пользоваться вторым способом и полученную дробь просто сократить? Да, можно, но это не всегда удобно. Посмотрите, какой получится знаменатель для чисел 48 и 72, если их просто перемножить 48∙72 = 3456. Согласитесь, что приятнее работать с меньшими числами.
Посмотрите, какой получится знаменатель для чисел 48 и 72, если их просто перемножить 48∙72 = 3456. Согласитесь, что приятнее работать с меньшими числами.
Рассмотрим примеры:
*51 = 3∙17 119 = 7∙17
в разложении большего числа не хватает тройки
=> НОК(51,119) = 3∙7∙17
А теперь применим первый способ:
*Посмотрите какая разница в вычислениях, в первом случае их минимум, а во втором нужно потрудиться отдельно на листочке, да ещё и дробь которую получили сократить необходимо. Нахождение НОК упрощает работу значительно.
Ещё примеры:
*Во втором примере и так видно, что наименьшее число, которое делится на 40 и 60 равно 120.
ИТОГ! ОБЩИЙ АЛГОРИТМ ВЫЧИСЛЕНИЙ!
— приводим дроби к обыкновенным, если есть целая часть.
— приводим дроби к общему знаменателю (сначала смотрим делится ли один знаменатель на другой, если делится то умножаем числитель и знаменатель этой другой дроби; если не делится действуем посредством других указанных выше способов).
— получив дроби с равными знаменателями, выполняем действия (сложение, вычитание).
— если необходимо, то результат сокращаем.
— если необходимо, то выделяем целую часть.
2. Произведение дробей.
Правило простое. При умножении дробей умножаются их числители и знаменатели:
Примеры:
Если есть возможность сократить дробь на стадии вычисления, то лучше это сделать:
Ещё правило относящееся к умножению!
Примеры, которые мы уже рассмотрели:
Определить, сколько составляет 3/7 от числа 63?
Задача. Весь путь составляет 180 километров. Турист в первый день прошёл 3/10 пути. Сколько километров турист прошёл в первый день?
Задача. На базу привезли 13 тонн овощей. Картофель составляет ¾ от всех завезённых овощей. Сколько килограмм картофеля завезли на базу?
С произведением закончим.
*Ранее обещал вам привести формальное объяснение основного свойства дроби через произведение, пожалуйста:
3. Деление дробей.
Деление дробей.
Деление дробей сводится к их умножению. Здесь важно запомнить, что дробь являющаяся делителем (та, на которую делят) переворачивается и действие меняется на умножение:
Данное действие может быть записано в виде так называемой четырёхэтажной дроби, ведь само деление «:» тоже можно записать как дробь:
Примеры:
На этом всё! Успеха вам!
С уважением, Александр Крутицких.
Делитесь информацией в социальных сетях.
ПРИМЕРЫ НА ВСЕ ДЕЙСТВИЯ С ОБЫКНОВЕННЫМИ ДРОБЯМИ.
ПРИМЕРЫ НА ВСЕ ДЕЙСТВИЯ С ОБЫКНОВЕННЫМИ ДРОБЯМИ.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Используются технологии uCoz
Действия с дробями
Дроби можно складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой. В принципе всё что можно делать с обычными числами, можно делать и с дробями.
Сложение дробей бывает двух видов:
- Сложение дробей с одинаковыми знаменателями;
- Сложение дробей с разными знаменателями.
Сначала изýчим сложение дробей с одинаковыми знаменателями. Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения.
Например, слóжим дроби и . Складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если к пиццы прибавить пиццы, то получится пиццы:
Пример 2. Сложить дроби и .
Опять же складываем числители, а знаменатель оставляем без изменения:
В ответе получилась неправильная дробь . Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два будет один:
В нашем случае целая часть выделяется легко — два разделить на два будет один:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к пиццы прибавить еще пиццы, то получится одна целая пицца:
Пример 3. Сложить дроби и .
Опять же складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если к пиццы прибавить ещё пиццы, то получится пиццы:
Пример 4. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить без изменения:
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы и ещё прибавить пиццы, то получится 1 целая и ещё пиццы.
Как видите в сложении дробей с одинаковыми знаменателями нет ничего сложного. Достаточно понимать следующие правила:
- Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.

Сложение дробей с разными знаменателями
Теперь научимся складывать дроби с разными знаменателями. Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, дроби и сложить можно, поскольку у них одинаковые знаменатели.
А вот дроби и сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Существует несколько способов приведения дробей к одинаковому знаменателю. Сегодня мы рассмотрим только один из них, поскольку остальные способы могут показаться сложными для начинающего.
Суть этого способа заключается в том, что сначала ищется наименьшее общее кратное (НОК) знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.
Затем числители и знаменатели дробей умножаются на свои дополнительные множители. В результате этих действий, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем.
Пример 1. Сложим дроби и
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
В первую очередь находим наименьшее общее кратное знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 2. Наименьшее общее кратное этих чисел равно 6
НОК (2 и 3) = 6
Теперь возвращаемся к дробям и . Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.
Полученное число 2 это первый дополнительный множитель. Записываем его к первой дроби. Для этого делаем небольшую косую линию над дробью и записываем над ней найденный дополнительный множитель:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3.
Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3.
Полученное число 3 это второй дополнительный множитель. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель:
Теперь у нас всё готово для сложения. Осталось умножить числители и знаменатели дробей на свои дополнительные множители:
Посмотрите внимательно к чему мы пришли. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Таким образом, пример завершается. К прибавить получается .
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы, то получится одна целая пицца и еще одна шестая пиццы:
Приведение дробей к одинаковому (общему) знаменателю также можно изобразить с помощью рисунка. Приведя дроби и к общему знаменателю, мы получили дроби и . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
Приведя дроби и к общему знаменателю, мы получили дроби и . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
Первый рисунок изображает дробь (четыре кусочка из шести), а второй рисунок изображает дробь (три кусочка из шести). Сложив эти кусочки мы получаем (семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили (одну целую пиццу и еще одну шестую пиццы).
Отметим, что мы с вами расписали данный пример слишком подробно. В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:
Но есть и обратная сторона медали. Если на первых этапах изучения математики не делать подробных записей, то начинают появляться вопросы рода «а откуда вон та цифра?», «почему дроби вдруг превращаются совсем в другие дроби?«.
Поэтому на первых этапах советуем записывать каждую мелочь. Хвастаться можно лишь в будущем, когда будут усвоены азы.
Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:
- Найти НОК знаменателей дробей;
- Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби;
- Умножить числители и знаменатели дробей на свои дополнительные множители;
- Сложить дроби, у которых одинаковые знаменатели;
- Если в ответе получилась неправильная дробь, то выделить её целую часть;
Пример 2. Найти значение выражения .
Воспользуемся инструкцией, которая приведена выше.
Шаг 1. Найти НОК знаменателей дробей
Находим НОК знаменателей обеих дробей. Знаменатели дробей это числа 2, 3 и 4
Шаг 2. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби
Делим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6. Записываем его над первой дробью:
НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6. Записываем его над первой дробью:
Теперь делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби это число 3. Делим 12 на 3, получаем 4. Получили второй дополнительный множитель 4. Записываем его над второй дробью:
Теперь делим НОК на знаменатель третьей дроби. НОК это число 12, а знаменатель третьей дроби это число 4. Делим 12 на 4, получаем 3. Получили третий дополнительный множитель 3. Записываем его над третьей дробью:
Шаг 3. Умножить числители и знаменатели дробей на свои дополнительные множители
Умножаем числители и знаменатели на свои дополнительные множители:
Шаг 4. Сложить дроби у которых одинаковые знаменатели
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби, у которых одинаковые (общие) знаменатели. Осталось сложить эти дроби. Складываем:
Осталось сложить эти дроби. Складываем:
Сложение не поместилось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке.
Шаг 5. Если в ответе получилась неправильная дробь, то выделить в ней целую часть
У нас в ответе получилась неправильная дробь. Мы должны выделить у неё целую часть. Выделяем:
Получили ответ
Вычитание дробей с одинаковыми знаменателями
Вычитание дробей бывает двух видов:
- Вычитание дробей с одинаковыми знаменателями
- Вычитание дробей с разными знаменателями
Сначала изучим вычитание дробей с одинаковыми знаменателями.
Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения.
Например, найдём значение выражения . Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения. Так и сделаем:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если от пиццы отрезать пиццы, то получится пиццы:
Пример 2. Найти значение выражения .
Опять же из числителя первой дроби вычитаем числитель второй дроби, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если от пиццы отрезать пиццы, то получится пиццы:
Пример 3. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Из числителя первой дроби нужно вычесть числители остальных дробей:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Выделим в ней целую часть:
Как видите в вычитании дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Вычитание дробей с разными знаменателями
Теперь научимся вычитать дроби у которых разные знаменатели. Когда вычитают дроби их знаменатели должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, от дроби можно вычесть дробь , поскольку у этих дробей одинаковые знаменатели. А вот от дроби нельзя вычесть дробь , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.
Пример 1. Найти значение выражения:
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
НОК (3 и 4) = 12
Теперь возвращаемся к дробям и
Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:
Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Получили ответ
Попробуем изобразить наше решение с помощью рисунка. Если от пиццы отрезать пиццы, то получится пиццы
Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:
Приведение дробей и к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Первый рисунок изображает дробь (восемь кусочков из двенадцати), а второй рисунок — дробь (три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков.
Пример 2. Найти значение выражения
У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.
Найдём НОК знаменателей этих дробей.
Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30
НОК (10, 3, 5) = 30
Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.
Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:
Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. Не забываем про знак равенства (=) на новой строке:
Не забываем про знак равенства (=) на новой строке:
В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще. А что можно сделать? Можно сократить эту дробь.
Чтобы сократить дробь , нужно разделить её числитель и знаменатель на наибольший общий делитель (НОД) чисел 20 и 30.
Итак, находим НОД чисел 20 и 30:
Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби на найденный НОД, то есть на 10
Получили ответ
Умножение дроби на число
Чтобы умножить дробь на число, нужно числитель данной дроби умножить на это число, а знаменатель оставить без изменений.
Пример 1. Умножить дробь на число 1.
Умножим числитель дроби на число 1
Запись можно понимать, как взять половину 1 раз. К примеру, если пиццы взять 1 раз, то получится пиццы
Из законов умножения мы знаем, что если множимое и множитель поменять местами, то произведение не изменится. Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Эту запись можно понимать, как взятие половины от единицы. К примеру, если имеется 1 целая пицца и мы возьмем от неё половину, то у нас окажется пиццы:
Пример 2. Найти значение выражения
Умножим числитель дроби на 4
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Выражение можно понимать, как взятие двух четвертей 4 раза. К примеру, если пиццы взять 4 раза, то получится две целые пиццы
А если поменять множимое и множитель местами, то получим выражение . Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:
Число, которое умножается на дробь, и знаменатель дроби разрешается сокращать, если они имеют общий делитель, бóльший единицы.
Например, выражение можно вычислить двумя способами.
Первый способ. Умножить число 4 на числитель дроби, а знаменатель дроби оставить без изменений:
Второй способ. Умножаемую четвёрку и четвёрку, находящуюся в знаменателе дроби , можно сократить. Сократить эти четвёрки можно на 4, поскольку наибольший общий делитель для двух четвёрок есть сама четвёрка:
Получился тот же результат 3. После сокращения четвёрок, на их месте образуются новые числа: две единицы. Но перемножение единицы с тройкой, и далее деление на единицу ничего не меняет. Поэтому решение можно записать покороче:
Сокращение может быть выполнено даже тогда, когда мы решили воспользоваться первым способом, но на этапе перемножения числа 4 и числителя 3 решили воспользоваться сокращением:
А вот к примеру выражение можно вычислить только первым способом — умножить число 7 на числитель дроби , а знаменатель оставить без изменений:
Связано это с тем, что число 7 и знаменатель дроби не имеют общего делителя, бóльшего единицы, и соответственно не сокращаются.
Некоторые ученики по ошибке сокращают умножаемое число и числитель дроби. Делать этого нельзя. Например, следующая запись не является правильной:
Сокращение дроби подразумевает, что и числитель и знаменатель будет разделён на одно и тоже число. В ситуации с выражением деление выполнено только в числителе, поскольку записать это всё равно, что записать . Видим, что деление выполнено только в числителе, а в знаменателе никакого деления не происходит.
Умножение дробей
Чтобы перемножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получится неправильная дробь, нужно выделить в ней целую часть.
Пример 1. Найти значение выражения .
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
Получили ответ . Желательно сократить данную дробь. Дробь можно сократить на 2. Тогда окончательное решение примет следующий вид:
Выражение можно понимать, как взятие пиццы от половины пиццы.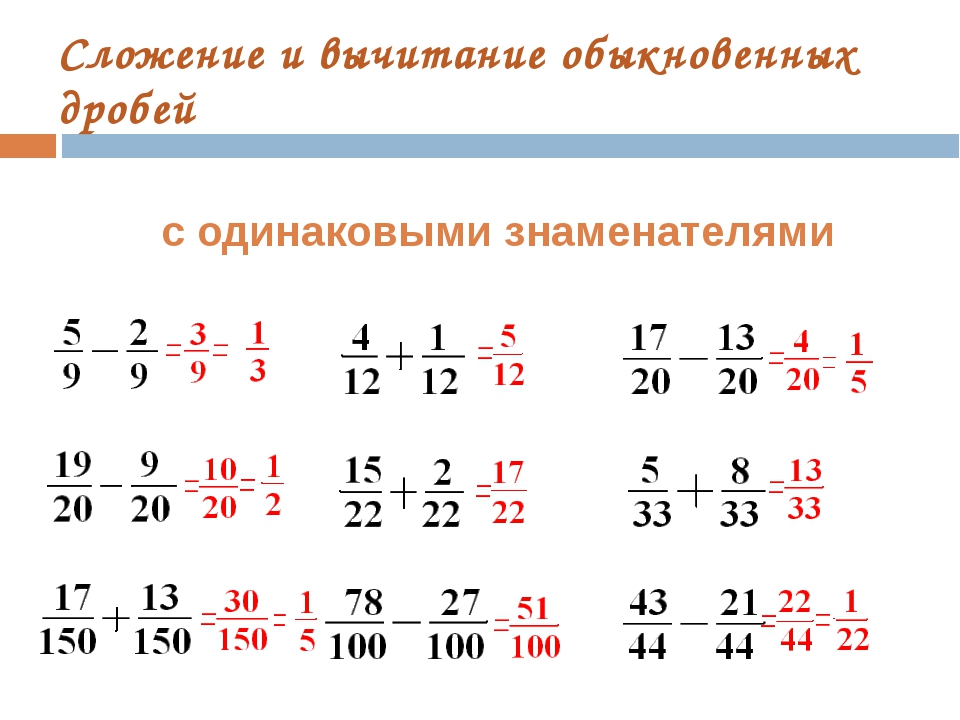 Допустим, у нас есть половина пиццы:
Допустим, у нас есть половина пиццы:
Как взять от этой половины две третьих? Сначала нужно поделить эту половину на три равные части:
И взять от этих трех кусочков два:
У нас получится пиццы. Вспомните, как выглядит пицца, разделенная на три части:
Один кусок от этой пиццы и взятые нами два кусочка будут иметь одинаковые размеры:
Другими словами, речь идет об одном и том же размере пиццы. Поэтому значение выражения равно
Пример 2. Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Пример 3. Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась правильная дробь, но будет хорошо, если её сократить. Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.
Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.
Итак, найдём НОД чисел 105 и 450:
Теперь делим числитель и знаменатель нашего ответа на НОД, который мы сейчас нашли, то есть на 15
Представление целого числа в виде дроби
Любое целое число можно представить в виде дроби. Например, число 5 можно представить как . От этого пятёрка своего значения не поменяет, поскольку выражение означает «число пять разделить на единицу», а это, как известно равно пятёрке:
Обратные числа
Сейчас мы познакомимся с очень интересной темой в математике. Она называется «обратные числа».
Определение. Обратным к числу a называется число, которое при умножении на a даёт единицу.
Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение:
Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу.
Можно ли найти такое число, которое при умножении на 5, даёт единицу? Оказывается можно. Представим пятёрку в виде дроби:
Затем умножить эту дробь на саму себя, только поменяем местами числитель и знаменатель. Другими словами, умножим дробь на саму себя, только перевёрнутую:
Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу:
Значит обратным к числу 5, является число , поскольку при умножении 5 на получается единица.
Обратное число можно найти также для любого другого целого числа.
Примеры:
- обратным числа 2 является дробь
- обратным числа 3 является дробь
- обратным числа 4 является дробь
Найти обратное число можно также для любой другой дроби. Для этого достаточно перевернуть её.
Примеры:
- для дроби обратной дробью является дробь
- для для дроби обратной дробью является дробь
- для дроби обратной дробью является дробь
Деление дроби на число
Допустим, у нас имеется половина пиццы:
Разделим её поровну на двоих. Сколько пиццы достанется каждому?
Сколько пиццы достанется каждому?
Видно, что после разделения половины пиццы получилось два равных кусочка, каждый из которых составляет пиццы. Значит каждому достанется по пиццы.
Деление дробей выполняется с помощью обратных чисел. Обратные числа позволяют заменить деление умножением.
Чтобы разделить дробь на число, нужно эту дробь умножить на число, обратное делителю.
Пользуясь этим правилом, запишем деление нашей половины пиццы на две части.
Итак, требуется разделить дробь на число 2. Здесь делимым является дробь , а делителем число 2.
Чтобы разделить дробь на число 2, нужно эту дробь умножить на число, обратное делителю 2. Обратное делителю 2 это дробь . Значит нужно умножить на
Получили ответ . Значит при делении половины на две части получается четверть.
Попробуем понять механизм этого правила. Для этого рассмотрим следующий простейший пример. Пусть у нас имеется одна целая пицца:
Умножим её на 2. То есть повторим её два раза (или возьмём два раза). В результате будем иметь две пиццы:
То есть повторим её два раза (или возьмём два раза). В результате будем иметь две пиццы:
Теперь угостим этими пиццами двоих друзей. То есть разделим две пиццы на 2. Тогда каждому достанется по одной пицце:
Разделить две пиццы на 2 это всё равно, что взять половину от этих пицц, то есть умножить число 2 на дробь
В обоих случаях получился один и тот же результат.
Тоже самое происходило, когда мы делили половину пиццы на две части. Чтобы разделить на 2, мы умножили эту дробь на число, обратное делителю 2. А обратное делителю 2 это дробь
Пример 2. Найти значение выражения
Умножим первую дробь на число, обратное делителю:
Допустим, имеется четверть пиццы и нужно разделить её на двоих:
Если разделить эту четверть на две части, то каждая получившаяся часть будет одной восьмой частью целой пиццы:
Заменять деление умножением можно не только при работе с дробями, но и с обычными числами. Например, все мы знаем, что 10 разделить на 2 будет 5
Например, все мы знаем, что 10 разделить на 2 будет 5
10 : 2 = 5
Заменим в этом примере деление умножением. Чтобы разделить число 10 на число 2, можно умножить число 10 на число, обратное числу 2. А обратное числу 2 это дробь
Как видно результат не изменился. Мы снова получили ответ 5.
Можно сделать вывод, что деление можно заменять умножением при условии, что вместо делителя будет подставлено обратное ему число.
Пример 3. Найти значение выражения
Умножим первую дробь на число, обратное делителю. Обратное делителю число это дробь
Допустим, имелось пиццы:
Как разделить такую пиццу на шестерых? Если каждый из трех кусков разделить пополам, то можно получить 6 равных кусков
Эти шесть кусков являются шестью кусками из двенадцати. А один из этих кусков составляет . Поэтому при делении на 6 получается
Деление числа на дробь
Правило деления числа на дробь такое же, как и правило деления дроби на число.
Чтобы разделить число на дробь, нужно умножить это число на дробь, обратную делителю.
Например, разделим число 1 на .
Чтобы разделить число 1 на , нужно это число 1 умножить на дробь, обратную дроби . А обратная дроби это дробь
Выражение можно понимать, как определение количества половин в одной целой пицце. Допустим, имеется одна целая пицца:
Если зададим вопрос «сколько раз половина содержится в этой пицце», то ответом будет 2. Действительно, половина содержится в одной целой пицце два раза
Пример 2. Найти значение выражения
Умножим число 2 на дробь, обратную делителю. А обратная делителю дробь это дробь
Допустим, у нас имеются две целые пиццы:
Если зададим вопрос «сколько раз половина содержится в двух пиццах», то ответом будет 4. Действительно, половина содержится в двух пиццах четыре раза:
Деление дробей
Чтобы разделить дробь на дробь, нужно первую дробь умножить на дробь, обратную второй.
Например, разделим на
Чтобы разделить на , нужно умножить на дробь, обратную дроби . А обратная дроби это дробь
Допустим, имеется половина пиццы:
Если зададим вопрос «сколько раз четверть пиццы содержится в этой половине», то ответом будет 2. Действительно, четверть пиццы содержится в половине пиццы два раза:
Пример 1. Найти значение выражения
Умножаем первую дробь на дробь, обратную второй. Грубо говоря, умножаем первую дробь на перевёрнутую вторую:
Пример 2. Найти значение выражения
Умножаем первую дробь на дробь обратную второй:
Здесь советуем остановиться и потренироваться. Решите несколько примеров, приведенных ниже. Можете использовать материалы сайта, как справочник. Это позволит вам научиться работать с литературой.
Каждая следующая тема будет более сложной, поэтому нужно тренироваться.
Задания для самостоятельного решения:
Задание 1. Найдите значение выражения:
Найдите значение выражения:
Решение:
Показать решение
Задание 2. Найдите значение выражения:
Решение:
Показать решение
Задание 3. Найдите значение выражения:
Решение:
Показать решение
Задание 4. Найдите значение выражения:
Решение:
Показать решение
Задание 5. Найдите значение выражения:
Решение:
Показать решение
Задание 6. Найдите значение выражения:
Решение:
Показать решение
Задание 7. Найдите значение выражения:
Решение:
Показать решение
Задание 8. Найдите значение выражения:
Решение:
Показать решение
Задание 9. Найдите значение выражения:
Решение:
Показать решение
Задание 10. Найдите значение выражения:
Решение:
Показать решение
Задание 11. Найдите значение выражения:
Решение:
Показать решение
Задание 12. Найдите значение выражения:
Решение:
Показать решение
Задание 13. Найдите значение выражения:
Решение:
Показать решение
Задание 14. Найдите значение выражения:
Найдите значение выражения:
Решение:
Показать решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Обыкновенные дроби — Определение, Примеры, Действия, Доли, Числитель и Знаменатель
Доля целого
Доля это каждая из равных частей, на которые поделено целое.
Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.
У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.
- Половина — одна вторая доля предмета или 1/2.
- Треть — одна третья доля предмета или 1/3.
- Четверть — одна четвертая доля предмета или 1/4.
Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Как устроена обыкновенная дробь
Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.
Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.
Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.
Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.
Знаменатель это делитель — то, на сколько делим.
Черта между числителем и знаменателем — символ деления.
Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.
Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.
Как устроена десятичная дробь
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
- 0,3
- 4,23
- 9,939
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Учёба без слёз (бесплатный гайд для родителей)
Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.
Свойства дробей
Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:
где a, b, k — натуральные числа.
Основные свойства
|
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
- Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.

- Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде, если в знаменателе обыкновенной дроби числа 10, 100, 1000 и т. д.
- Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби, если в знаменателе обыкновенной дроби числа 10, 100, 1000 и т. д. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
У нас есть отличные курсы по математике для учеников с 1 по 11 классы, записывайтесь! |
Действия с дробями
С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.
Сравнение дробей
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
Сравним 1/5 и 4/5. Как рассуждаем:
- В обеих дробях знаменатель равен 5.

- В первой дроби числитель равен 1, во второй дроби равен 4.
1 < 4
- Поэтому первая дробь 1/5 меньше второй 4/5.
Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.
Сравним 1/2 и 1/8. Как рассуждаем:
Представим, что у нас есть торт. Так как знаменатель первой дроби равен 2, то делим торт на две части и забираем себе одну, то есть половину торта.
Знаменатель второй дроби равен 8, делим торт на восемь частей и забираем крохотный кусочек. Половина торта больше больше маленького кусочка.
Таким образом 1/2 > 1/8.
Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.
Пример. Сравнить 2/7 и 1/14.
Как рассуждаем:
- Приведем дроби к общему знаменателю:
- Сравним дроби с одинаковыми знаменателями:
Ответ: 2/7 > 1/14.
Важно запомнить: любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.
Чтобы сравнить дроби с разными числителями и знаменателями, нужно:
- привести дроби к общему знаменателю;
- сравнить полученные дроби.
Чтобы привести дроби к общему знаменателю, нужно:
- Найти общее кратное знаменателей дробей, которое станет их общим знаменателем.
- Разделить общий знаменатель на знаменатель данных дробей, то есть найти для каждой дроби дополнительный множитель.
- Умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Сокращение дробей
Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81.
Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число.
В этом примере делим обе части дроби на двойку.
Можно никуда не спешить и сокращать дроби последовательно, в несколько действий.
Сложение и вычитание дробей
При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.
Не забудьте проверить, можно ли сократить дробь и выделить целую часть.
При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).
Вот, что делать:
- Найдем наименьшее общее кратное для определения единого делителя.
Для этого запишем в столбик числа, которые в сумме дают значения делителей.
 Далее перемножаем полученное и получаем НОК.
Далее перемножаем полученное и получаем НОК.НОК (15, 18) = 3 * 2 * 3 * 5 = 90
- Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:
90 : 15 = 6,
90 : 18 = 5.
Полученные числа запишем справа сверху над числителем.
- Воспользуемся одним из основных свойств дробей: перемножим числитель и знаменатель на дополнительный множитель. После умножения знаменатель должен быть равен наименьшему общему кратному, которое мы ранее высчитывали. Затем можно перейти к сложению.
- Проверим полученный результат:
- если числитель больше знаменателя, нужно преобразовать дробь в смешанное число;
- если есть что сократить, нужно выполнить сокращение.
Ход решения одной строкой:
Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:
- Сложить целые части.

- Сложить дробные части.
Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.
- Суммировать полученные результаты.
Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.
Умножение и деление дробей
Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:
Не забываем про сокращение. Это может облегчить вычисления.
Чтобы умножить два смешанных числа, надо:
- преобразовать смешанные дроби в неправильные;
- перемножить числители и знаменатели дробей;
- сократить полученную дробь;
- если получилась неправильная дробь, преобразовать в смешанную.
Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:
- числитель первой умножить на знаменатель второй, результат произведения записать в числитель новой дроби;
- знаменатель первой умножить на числитель второй, результат произведения записать в знаменатель новой дроби.

Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.
Числа, произведение которых равно 1, называют взаимно обратными.
Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше.
Для деления смешанных чисел необходимо:
- представить числа в виде неправильных дробей;
- разделить то, что получилось друг на друга.
Действия с дробями: правила, примеры, решения
Данная статья рассматривает действия над дробями. Будут сформированы и обоснованы правила сложения, вычитания, умножения, деления или возведения в степень дробей вида AB, где A и B могут быть числами, числовыми выражениями или выражениями с переменными. В заключении будут рассмотрены примеры решения с подробным описанием.
В заключении будут рассмотрены примеры решения с подробным описанием.
Правила выполнения действий с числовыми дробями общего вида
Числовые дроби общего вида имеют числитель и знаменатель, в которых имеются натуральные числа или числовые выражения. Если рассмотреть такие дроби, как 35, 2,84, 1+2·34·(5-2), 34+782,3-0,8, 12·2, π1-23+π, 20,5ln 3, то видно, что числитель и знаменатель может иметь не только числа, но и выражения различного плана.
Определение 1Существуют правила, по которым идет выполнение действий с обыкновенными дробями. Оно подходит и для дробей общего вида:
- При вычитании дробей с одинаковыми знаменателями складываются только числители, а знаменатель остается прежним, а именно: ad±cd=a±cd, значения a, c и d≠0 являются некоторыми числами или числовыми выражениями.
- При сложении или вычитании дроби при разных знаменателях, необходимо произвести приведение к общему, после чего произвести сложение или вычитание полученных дробей с одинаковыми показателями.
 Буквенно это выглядит таком образом ab±cd=a·p±c·rs, где значения a, b≠0, c, d≠0, p≠0, r≠0, s≠0 являются действительными числами, а b·p=d·r=s. Когда p=d и r=b, тогда ab±cd=a·d±c·db·d.
Буквенно это выглядит таком образом ab±cd=a·p±c·rs, где значения a, b≠0, c, d≠0, p≠0, r≠0, s≠0 являются действительными числами, а b·p=d·r=s. Когда p=d и r=b, тогда ab±cd=a·d±c·db·d. - При умножении дробей выполняется действие с числителями, после чего со знаменателями, тогда получим ab·cd=a·cb·d, где a, b≠0, c, d≠0 выступают в роли действительных чисел.
- При делении дроби на дробь первую умножаем на вторую обратную, то есть производим замену местами числителя и знаменателя: ab:cd=ab·dc.
Обоснование правил
Определение 2Существуют следующие математические моменты, на которые следует опираться при вычислении:
- дробная черта означает знак деления;
- деление на число рассматривается как умножение на его обратное значение;
- применение свойства действий с действительными числами;
- применение основного свойства дроби и числовых неравенств.
С их помощью можно производить преобразования вида:
ad±cd=a·d-1±c·d-1=a±c·d-1=a±cd;ab±cd=a·pb·p±c·rd·r=a·ps±c·es=a·p±c·rs;ab·cd=a·db·d·b·cb·d=a·d·a·d-1·b·c·b·d-1==a·d·b·c·b·d-1·b·d-1=a·d·b·cb·d·b·d-1==(a·c)·(b·d)-1=a·cb·d
Примеры
В предыдущем пункте было сказано про действия с дробями. Именно после этого дробь нуждается в упрощении. Подробно эта тема была рассмотрена в пункте о преобразовании дробей.
Именно после этого дробь нуждается в упрощении. Подробно эта тема была рассмотрена в пункте о преобразовании дробей.
Для начала рассмотрим пример сложения и вычитания дробей с одинаковым знаменателем.
Пример 1Даны дроби 82,7 и 12,7, то по правилу необходимо числитель сложить, а знаменатель переписать.
Решение
Тогда получаем дробь вида 8+12,7. После выполнения сложения получаем дробь вида 8+12,7=92,7=9027=313. Значит, 82,7+12,7=8+12,7=92,7=9027=313.
Ответ: 82,7+12,7=313
Имеется другой способ решения. Для начала производится переход к виду обыкновенной дроби, после чего выполняем упрощение. Это выглядит таким образом:
82,7+12,7=8027+1027=9027=313
Пример 2Произведем вычитание из 1-23·log23·log25+1 дроби вида 233·log23·log25+1.
Так как даны равные знаменатели, значит, что мы выполняем вычисление дроби при одинаковом знаменателе. Получим, что
1-23·log23·log25+1-233·log23·log25+1=1-2-233·log23·log25+1
Имеются примеры вычисления дробей с разными знаменателями. Важный пункт – это приведение к общему знаменателю. Без этого мы не сможем выполнять дальнейшие действия с дробями.
Важный пункт – это приведение к общему знаменателю. Без этого мы не сможем выполнять дальнейшие действия с дробями.
Процесс отдаленно напоминает приведение к общему знаменателю. То есть производится поиск наименьшего общего делителя в знаменателе, после чего добавляются недостающие множители к дробям.
Если складываемые дроби не имеют общих множителей, тогда им может стать их произведение.
Пример 3Рассмотрим на примере сложения дробей 235+1 и 12.
Решение
В данном случае общим знаменателем выступает произведение знаменателей. Тогда получаем, что 2·35+1. Тогда при выставлении дополнительных множителей имеем, что к первой дроби он равен 2, а ко второй 35+1. После перемножения дроби приводятся к виду 42·35+1. Общее приведение 12 будет иметь вид 35+12·35+1. Полученные дробные выражения складываем и получаем, что
235+1+12=2·22·35+1+1·35+12·35+1==42·35+1+35+12·35+1=4+35+12·35+1=5+352·35+1
Ответ: 235+1+12=5+352·35+1
Когда имеем дело с дробями общего вида, тогда о наименьшем общем знаменателе обычно дело не идет. В качестве знаменателя нерентабельно принимать произведение числителей. Для начала необходимо проверить, имеется ли число, которое меньше по значению, чем их произведение.
В качестве знаменателя нерентабельно принимать произведение числителей. Для начала необходимо проверить, имеется ли число, которое меньше по значению, чем их произведение.
Рассмотрим на примере 16·215 и 14·235, когда их произведение будет равно 6·215·4·235=24·245. Тогда в качестве общего знаменателя берем 12·235.
Рассмотрим примеры умножений дробей общего вида.
Пример 5Для этого необходимо произвести умножение 2+16 и 2·53·2+1.
Решение
Следую правилу, необходимо переписать и в виде знаменателя написать произведение числителей. Получаем, что 2+16·2·53·2+12+1·2·56·3·2+1. Когда дробь будет умножена, можно производить сокращения для ее упрощения. Тогда 5·332+1:1093=5·332+1·9310.
Используя правило перехода от деления к умножению на обратную дробь, получим дробь, обратную данной. Для этого числитель и знаменатель меняются местами. Рассмотрим на примере:
5·332+1:1093=5·332+1·9310
После чего должны выполнить умножение и упростить полученную дробь. Если необходимо, то избавиться от иррациональности в знаменателе. Получаем, что
Если необходимо, то избавиться от иррациональности в знаменателе. Получаем, что
5·332+1:1093=5·33·9310·2+1=5·210·2+1=32·2+1==3·2-12·2+1·2-1=3·2-12·22-12=3·2-12
Ответ: 5·332+1:1093=3·2-12
Данный пункт применим, когда число или числовое выражение может быть представлено в виде дроби, имеющую знаменатель, равный 1, тогда и действие с такой дробью рассматривается отдельным пунктом. Например, выражение 16·74-1·3 видно, что корень из 3 может быть заменен другим 31 выражением. Тогда эта запись будет выглядеть как умножение двух дробей вида 16·74-1·3=16·74-1·31.
Выполнение действие с дробями, содержащими переменные
Правила, рассмотренные в первой статье , применимы для действий с дробями, содержащими переменные. Рассмотрим правило вычитания, когда знаменатели одинаковые.
Необходимо доказать, что A, C и D (D не равное нулю) могут быть любыми выражениями, причем равенство AD±CD=A±CD равноценно с его областью допустимых значений.
Необходимо взять набор переменных ОДЗ. Тогда А, С, D должны принимать соответственные значения a0, c0 и d0. Подстановка вида AD±CD приводит разность вида a0d0±c0d0, где по правилу сложения получаем формулу вида a0±c0d0. Если подставить выражение A±CD, тогда получаем ту же дробь вида a0±c0d0. Отсюда делаем вывод, что выбранное значение, удовлетворяющее ОДЗ, A±CD и AD±CD считаются равными.
Тогда А, С, D должны принимать соответственные значения a0, c0 и d0. Подстановка вида AD±CD приводит разность вида a0d0±c0d0, где по правилу сложения получаем формулу вида a0±c0d0. Если подставить выражение A±CD, тогда получаем ту же дробь вида a0±c0d0. Отсюда делаем вывод, что выбранное значение, удовлетворяющее ОДЗ, A±CD и AD±CD считаются равными.
При любом значении переменных данные выражения будут равны, то есть их называют тождественно равными. Значит это выражение считается доказываемым равенством вида AD±CD=A±CD.
Примеры сложения и вычитания дробей с переменными
Когда имеются одинаковые знаменатели, необходимо только складывать или вычитать числители. Такая дробь может быть упрощена. Иногда приходится работать с дробями, которые являются тождественно равными, но при первом взгляде это незаметно, так как необходимо выполнять некоторые преобразования. Например, x23·x13+1 и x13+12 или 12·sin 2α и sin a·cos a. Чаще всего требуется упрощение исходного выражения для того, чтобы увидеть одинаковые знаменатели.
Вычислить:1) x2+1x+x-2-5-xx+x-2, 2)lg2x+4x·(lg x+2)+4·lg xx·(lg x+2), x-1x-1+xx+1.
Решение
- Чтобы произвести вычисление, необходимо вычесть дроби, которым имеют одинаковые знаменатели. Тогда получаем, что x2+1x+x-2-5-xx+x-2=x2+1-5-xx+x-2. После чего можно выполнять раскрытие скобок с приведением подобных слагаемых. Получаем, чтоx2+1-5-xx+x-2=x2+1-5+xx+x-2=x2+x-4x+x-2
- Так как знаменатели одинаковые, то остается только сложить числители, оставив знаменатель:lg2x+4x·(lg x+2)+4·lg xx·(lg x+2)=lg2x+4+4x·(lg x+2)
Сложение было выполнено. Видно, что можно произвести сокращение дроби. Ее числитель может быть свернут по формуле квадрата суммы, тогда получим (lg x+2)2из формул сокращенного умножения. Тогда получаем, что
lg2x+4+2·lg xx·(lg x+2)=(lg x+2)2x·(lg x+2)=lg x+2x - Заданные дроби вида x-1x-1+xx+1 с разными знаменателями. После преобразования можно перейти к сложению.
Рассмотрим двоякий способ решения.
Первый способ заключается в том, что знаменатель первой дроби подвергается разложению на множители при помощи квадратов, причем с ее последующим сокращением. Получим дробь вида
x-1x-1=x-1(x-1)·x+1=1x+1
Значит, x-1x-1+xx+1=1x+1+xx+1=1+xx+1.
В таком случае необходимо избавляться от иррациональности в знаменателе.
Получим:
1+xx+1=1+x·x-1x+1·x-1=x-1+x·x-xx-1
Второй способ заключается в умножении числителя и знаменателя второй дроби на выражение x-1. Таким образом, мы избавляемся от иррациональности и переходим к сложению дроби при наличии одинакового знаменателя. Тогда
x-1x-1+xx+1=x-1x-1+x·x-1x+1·x-1==x-1x-1+x·x-xx-1=x-1+x·x-xx-1
Ответ: 1) x2+1x+x-2-5-xx+x-2=x2+x-4x+x-2, 2)lg2x+4x·(lg x+2)+4·lg xx·(lg x+2)=lg x+2x, 3)x-1x-1+xx+1=x-1+x·x-xx-1.
В последнем примере получили, что приведение к общему знаменателю неизбежно. Для этого необходимо упрощать дроби. Для сложения или вычитая всегда необходимо искать общий знаменатель, который выглядит как произведение знаменателей с добавлением дополниетльных множителей к числителям.
Вычислить значения дробей: 1) x3+1×7+2·2, 2) x+1x·ln2(x+1)·(2x-4)-sin xx5·ln(x+1)·(2x-4), 3) 1cos2x-x+1cos2x+2·cos x·x+x
Решение
- Никаких сложных вычислений знаменатель не требует, поэтому нужно выбрать их произведение вида 3·x7+2·2, тогда к первой дроби x7+2·2 выбирают как дополнительный множитель, а 3 ко второй. При перемножении получаем дробь вида x3+1×7+2·2=x·x7+2·23·x7+2·2+3·13·x7+2·2==x·x7+2·2+33·x7+2·2=x·x7+2·2·x+33·x7+2·2
- Видно, что знаменатели представлены в виде произведения, что означает ненужность дополнительных преобразований. Общим знаменателем будет считаться произведение вида x5·ln2x+1·2x-4. Отсюда x4 является дополнительным множителем к первой дроби, а ln(x+1) ко второй. После чего производим вычитание и получаем, что:
x+1x·ln2(x+1)·2x-4-sin xx5·ln(x+1)·2x-4==x+1·x4x5·ln2(x+1)·2x-4-sin x·lnx+1×5·ln2(x+1)·(2x-4)==x+1·x4-sin x·ln(x+1)x5·ln2(x+1)·(2x-4)=x·x4+x4-sin x·ln(x+1)x5·ln2(x+1)·(2x-4) - Данный пример имеет смысл при работе со знаменателями дробями.
 Необходимо применить формулы разности квадратов и квадрат суммы, так как именно они дадут возможность перейти к выражению вида 1cos x-x·cos x+x+1(cos x+x)2. Видно, что дроби приводятся к общему знаменателю. Получаем, что cos x-x·cos x+x2.
Необходимо применить формулы разности квадратов и квадрат суммы, так как именно они дадут возможность перейти к выражению вида 1cos x-x·cos x+x+1(cos x+x)2. Видно, что дроби приводятся к общему знаменателю. Получаем, что cos x-x·cos x+x2.
После чего получаем, что
1cos2x-x+1cos2x+2·cos x·x+x==1cos x-x·cos x+x+1cos x+x2==cos x+xcos x-x·cos x+x2+cos x-xcos x-x·cos x+x2==cos x+x+cos x-xcos x-x·cos x+x2=2·cos xcos x-x·cos x+x2
Ответ:
1) x3+1×7+2·2=x·x7+2·2·x+33·x7+2·2, 2) x+1x·ln2(x+1)·2x-4-sin xx5·ln(x+1)·2x-4==x·x4+x4-sin x·ln(x+1)x5·ln2(x+1)·(2x-4), 3) 1cos2x-x+1cos2x+2·cos x·x+x=2·cos xcos x-x·cos x+x2.
Примеры умножения дробей с переменными
При умножении дробей числитель умножается на числитель, а знаменатель на знаменатель. Тогда можно применять свойство сокращения.
Пример 8Произвести умножение дробей x+2·xx2·ln x2·ln x+1 и 3·x213·x+1-2sin2·x-x.
Решение
Необходимо выполнить умножение. Получаем, что
Получаем, что
x+2·xx2·ln x2·ln x+1·3·x213·x+1-2sin(2·x-x)==x-2·x·3·x213·x+1-2×2·ln x2·ln x+1·sin (2·x-x)
Число 3 переносится на первое место для удобства подсчетов, причем можно произвести сокращение дроби на x2, тогда получим выражение вида
3·x-2·x·x13·x+1-2ln x2·ln x+1·sin (2·x-x)
Ответ: x+2·xx2·ln x2·ln x+1·3·x213·x+1-2sin(2·x-x)=3·x-2·x·x13·x+1-2ln x2·ln x+1·sin (2·x-x).
Деление
Деление у дробей аналогично умножению, так как первую дробь умножают на вторую обратную. Если взять к примеру дробь x+2·xx2·ln x2·ln x+1 и разделить на 3·x213·x+1-2sin2·x-x, тогда это можно записать таким образом, как
x+2·xx2·ln x2·ln x+1:3·x213·x+1-2sin(2·x-x), после чего заменить произведением вида x+2·xx2·ln x2·ln x+1·3·x213·x+1-2sin(2·x-x)
Возведение в степень
Перейдем к рассмотрению действия с дробями общего вида с возведением в степень. Если имеется степень с натуральным показателем, тогда действие рассматривают как умножение одинаковых дробей. Но рекомендовано использовать общий подход, базирующийся на свойствах степеней. Любые выражения А и С, где С тождественно не равняется нулю, а любое действительное r на ОДЗ для выражения вида ACr справедливо равенство ACr=ArCr. Результат – дробь, возведенная в степень. Для примера рассмотрим:
Но рекомендовано использовать общий подход, базирующийся на свойствах степеней. Любые выражения А и С, где С тождественно не равняется нулю, а любое действительное r на ОДЗ для выражения вида ACr справедливо равенство ACr=ArCr. Результат – дробь, возведенная в степень. Для примера рассмотрим:
x0,7-π·ln3x-2-5x+12,5==x0,7-π·ln3x-2-52,5x+12,5
Порядок выполнения действий с дробями
Действия над дробями выполняются по определенным правилам. На практике замечаем, что выражение может содержать несколько дробей или дробных выражений. Тогда необходимо все действия выполнять в строгом порядке: возводить в степень, умножать, делить, после чего складывать и вычитать. При наличии скобок первое действие выполняется именно в них.
Пример 9Вычислить 1-xcos x-1cos x·1+1x.
Решение
Так как имеем одинаковый знаменатель, то 1-xcos x и 1cos x, но производить вычитания по правилу нельзя, сначала выполняются действия в скобках, после чего умножение, а потом сложение. Тогда при вычислении получаем, что
Тогда при вычислении получаем, что
1+1x=11+1x=xx+1x=x+1x
При подстановке выражения в исходное получаем, что 1-xcos x-1cos x·x+1x. При умножении дробей имеем: 1cos x·x+1x=x+1cos x·x. Произведя все подстановки, получим 1-xcos x-x+1cos x·x. Теперь необходимо работать с дробями, которые имеют разные знаменатели. Получим:
x·1-xcos x·x-x+1cos x·x=x·1-x-1+xcos x·x==x-x-x-1cos x·x=-x+1cos x·x
Ответ: 1-xcos x-1cos x·1+1x=-x+1cos x·x.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р. Реферат
от 1 дня / от 700 р.
Реферат
от 1 дня / от 700 р.
Действия с дробями 7 класс, повторение, сравнение, сокращение, решение уравнений
В начале первой четверти семиклассники на уроках математики активно повторяют все действия, как с обыкновенными, так и с десятичными дробями. И делают они это не просто так.
В 7 классе по программе обучения начинается алгебра. Дроби будут состоять уже из алгебраических выражений, многочленов. Все действия с такими уже <<сложными>> дробями основываются на умении решать обыкновенные дроби в пятом шестом классе.
Содержание статьи
- Дроби повторение 7 класс
- Сравнение дробей 7 класс
- Правила дробей 7 класс
- Действия с дробями 7 класс
- Сложение и вычитание дробей 7 класс
- Деление и умножение дробей 7 класс
- Конечные десятичные дроби 7 класс
- Уравнения с дробями 7 класс на примерах с пояснением
- Сокращение дробей 7 класс
Дроби повторение 7 класс
Повторение начинается с самых простых примеров на все арифметические действия с обыкновенными дробями. Не забываем, что там где знаменатели разные следует найти общий, и только потом выполнять действия.
Сравнение дробей 7 класс
Для того, чтобы научиться сравнивать дроби, нужно узнать несколько способов по их сравнению, и выбрать для себя более понятный и удобный.
Основные правила сравнения дробей:
В первом правиле мы сравниваем только числители, так как знаменатели равны. Мы уже говорили, что знамен.-это общее количество долей, а числитель показывает сколько их взято из общего, следовательно, чем больше долей взято, тем и дробь соответственно больше.
При одинаковых числ-х сравнивают только знамен. Чем он меньше, тем больше дробь. Разберемся, почему так. К примеру разделите 10 на 5 и 10 на 2, очевидно, что второе частное больше первого. Поэтому, если сравнить 10/5 и 10/2, то 10/2 будет больше.
В десятичных дробях мы сравниваем их соответствующие целые части и дробные. Если первые равны, то мы сравниваем десятые, сотые и т.д. Поэтому для сравнения мы должны уравнивать количество дес.знаков.
Также можно сравнить две обыкн.дроби используя число, которое находится в ряду между ними. Какая из дробей окажется больше этого числа, та и будет большей в примере.
Вот несколько интересных способов, как можно сравнить дроби:
Если от вас требуется сравнить десятичную и обыкновенную дроби, можно перевести одну из них в более удобную для вас. И сравнивать вы уже будите либо обыкновенные, либо десятичные.
Еще один хороший способ, дополнить до единицы. Чем больше нужно добавить дроби, чтобы получить целое, тем она будет меньше.
Можно использовать и перекрестное правило, как в пропорции. Для этого умножаем смотрящие друг на друга числители и знаменатели.
Правила дробей 7 класс
Начиная изучать рациональные дроби в седьмом классе, стоит познакомиться с рядом правил, которым подчиняются действия с ними.
К рациональным дробям применяются те же правила, что и к обыкн-м.
Для выполнения всех арифметических действий, следует знать несколько формул сокращенного умножения:
Эти формулы понадобятся на уроках математики до 11 класса, поэтому их лучше выучить сразу в седьмом.
Действия с дробями 7 класс
Как в пятом и шестом, так же и в седьмом классе, дроби в основном складывают, вычитают, умножают и делят. Есть еще сокращение и сравнение. Рациональные дроби также называют алгебраическими.
Сложение и вычитание.
К примеру, b/3 + c/3. Это сумма рациональных или алгебраических дробей. Решением будет: b+c/3.
Еще пара примеров.
Умножение и деление.
Так же как и с обыкновенными дробями, умножать будем числитель на числитель, и знам. на знаменатель. Очень важно обратить внимание на то, что вы умножаете многочлены, поэтому каждый числитель и знаменатель лучше взять в скобки. Так вы сможете избежать ненужных ошибок.
И деление выполняется в точности также как и в обык.дробях. Первую дробь оставьте на месте без изменений, поменяйте частное на умножение, вторую дробь переверните.
Сложение и вычитание дробей 7 класс
Никогда не начинайте выполнять действия не упростив выражения. Выполните все возможные преобразования и пример решится намного легче и быстрее. Также числители второй и последующих дробей при сложении и вычитании стоит взять в скобки. Очень часто возникают ошибки только из-за одного неправильно поставленного знака. Будьте внимательны.
Если перед скобкой стоит <<+>>, раскрываем ее, не меняя знаки внутри. Если << — >>, то все меняем на противоположные.
Пример.
Знаменатели совершенно одинаковые, находим сумму числ. Приведите подобные, это с и 2с, d и -d, которые в свою очередь взаимно уничтожаются, так как имеют разные знаки. В итоге остается с+2с = 3с. Ответ: 3с/2а.
Все намного проще, если знам. одинаковые. С разными нужно немного подумать.
Пример.
В примере два знам. 15а и 3. Нам нужно найти общий. В этом случае проще домножить 3 так, чтобы получить 15а. Для этого 3 умножаем на 5а. Но чтобы действие было верным, применяем основное свойство дроби, и на 5а умножим еще и числитель. Далее складываем дроби с один.знам.
Деление и умножение дробей 7 класс
Разберем сразу примеры, так как правила уже обговорены выше.
В примере выше требуется разделить алгебраические дроби, содержащие выражения со степенью. Здесь важно вспомнить, что при сокращении степеней мы вычитаем из большей степени меньшую.
Первую дробь мы оставили без изменений, вторую перевернули, заменив действие на умножение. Теперь ищем, что можно сократить. Сначала смотри на числовые коэффициенты. Сокращаем 7 и 35, 9 и 18. Затем сокращаем буквенную часть.
Теперь ищем, что можно сократить. Сначала смотри на числовые коэффициенты. Сокращаем 7 и 35, 9 и 18. Затем сокращаем буквенную часть.
Для удобства возьмите каждый многочлен в скобки. Мы видим, что сразу можно сократить скобку (7-х). Многие допускают ошибку, считая что (a-b) и (a+b) сократимы, это большая ошибка. Ведь к примеру, 5-2 и 5+2 совершенно разные выражения.
Конечные десятичные дроби 7 класс
Десятичные дроби отличаются друг от друга по количеству знаков (цифр) после запятой. Соответственно своему названию, у конечной десятичной дроби после запятой, конечное число знаков: 5, 0235; 2,3654; 0,12 и т.д.
Любую такую дробь можно перевести обратно в обыкновенную. 2,36 = 2 целых 36/100. Но не каждую обыкновенную можно представить в виде конечной дес.дроби. В таком случае уже получается бесконечная дес.дробь.
Уравнения с дробями 7 класс на примерах с пояснением
Уравнения с дробями можно решить используя пропорцию, или светси решение к этому. Первое уравнение и ему подобные очень просто и быстро решается пропорцией. Используем умножение <<крест на крест>>.
Первое уравнение и ему подобные очень просто и быстро решается пропорцией. Используем умножение <<крест на крест>>.
Бывают и более сложные уравнения, которые нужно преобразовать.
Здесь уже нужно вспомнить правило умножения скобки на число или раскрытие скобок. На число перед скобкой умножаем каждое слагаемое в скобке. Значит 7 умножим и на 2, и на (-х). Далее решаем как обычное линейное уравнение.
В следующем уравнении разберем два способа решения.
Первый вариант решения основывается на избавлении от знаменателей, дабы превратить дробное уравнение в линейное. Для этого умножаем каждое слагаемое на общий для дробей знаменатель. В нашем случае 45.
Сокращаем и получаем линейное уравнение. Раскрываем в нем скобки, находим подобные слагаемые.
Вторым вариантом будет приведение к общему знаменателю в правой части, и сведению решения к пропорции.
Сокращение дробей 7 класс
При сокращении рациональных дробей используем правило сокращения обык. др. Числитель и знаменатель делим на один многочлен.
др. Числитель и знаменатель делим на один многочлен.
Запомните, что разные буквенные части мы не сокращаем, только одинаковые.
Дроби, в числ. и знамен. которых стоит выражение (многочлен) тоже сократимы. В таких дробях можно сокращать только одинаковые многочлены. Многочлены разделены между собой умножением.
Также можно использовать формулы сокращ. умножения.
Еще пара примеров:
Действия с дробями
Дроби можно складывать, вычитать, умножать и делить. Кроме того, дроби можно сравнивать друг с другом. По сути, все, что можно делать с обычными числами, можно делать и с дробями.
Сложение дробей с общим знаменателем
Сложение дробей:
- Сложение с общим знаменателем;
- Сложение с разными знаменателями.
Сначала научимся складывать дроби с общими знаменателями. Это просто.
Чтобы сложить дроби с одинаковыми знаменателями, сложите их числители и оставьте знаменатель без изменений.
Например, добавим дроби и . Сложите числители и оставьте знаменатель без изменений:
Этот пример легко понять, если представить себе пиццу, разделенную на четыре части. Если добавить к пицце пиццу, получится пицца:
Пример 2. Сложите дроби и .
Снова складываем числители и оставляем знаменатель без изменений:
Ответ — неправильная дробь.. Если наступает конец задачи, от неправильных дробей принято избавляться. Чтобы избавиться от неправильной дроби, нужно выделить ее целую часть. В нашем случае вся часть проста — два разделить на два равно одному:
Этот пример легко понять, если представить себе пиццу, разделенную на две части. Если к пицце добавить еще одну пиццу, то получится одна целая пицца:
Пример 3. Сложить дроби и .
Снова складываем числители и оставляем знаменатель без изменений:
Этот пример легко понять, если представить себе пиццу, разделенную на три части. Если к пицце добавить еще одну пиццу, то получится пицца:
Если к пицце добавить еще одну пиццу, то получится пицца:
Пример 4. Найдите значение выражения
Этот пример решается так же, как и предыдущие. Числители нужно сложить, а знаменатель оставить без изменений:
Попробуем изобразить наше решение на картинке. Если вы добавите пиццу к пицце и добавите еще одну пиццу, вы получите 1 целую пиццу и еще одну пиццу.
Как видите, ничего сложного в сложении дробей с общими знаменателями нет. Достаточно усвоить следующие правила:
- Чтобы сложить дроби с одинаковыми знаменателями, сложите их числители и оставьте знаменатель без изменений;
- Если ответом является неправильная дробь, нужно выделить всю ее часть.
Сложение дробей с разными знаменателями
Теперь научимся складывать дроби с разными знаменателями. При сложении дробей знаменатели этих дробей должны совпадать. Но они не всегда одинаковы.
Например, дроби и можно складывать вместе, потому что у них одинаковые знаменатели.
Но дроби и нельзя складывать сразу, потому что у этих дробей разные знаменатели. В таких случаях дроби необходимо привести к одному (общему) знаменателю.
Существует несколько способов приведения дробей к одному знаменателю. Сегодня мы рассмотрим только один из них, так как остальные могут показаться новичку сложными.
Суть этого метода в том, что сначала ищем наименьшее общее кратное (НОК) знаменателей обеих дробей. Затем LCM делится на знаменатель первой дроби и получается первый дополнительный множитель. Проделайте то же самое со второй дробью — LCM разделите на знаменатель второй дроби и получите второй дополнительный множитель.
Затем числители и знаменатели дробей умножаются на их дополнительные множители. В результате дроби с разными знаменателями преобразуются в дроби с одинаковыми знаменателями. И мы уже умеем складывать такие дроби.
Пример 1. Складываем дроби и
Эти дроби имеют разные знаменатели, поэтому нужно привести их к одному (общему) знаменателю.
Сначала найдите наименьшее общее кратное знаменателей обеих дробей. В знаменателе первой дроби число 3, а в знаменателе второй дроби число 2. Наименьшее общее кратное этих чисел равно 6
НОК (2 и 3) = 6
Теперь вернемся к дробям и . Сначала разделите НОК на знаменатель первой дроби и получите первый дополнительный множитель. НОК равен 6, а знаменатель первой дроби равен 3. Разделив 6 на 3, получим 2.
Полученное число 2 — это первый дополнительный множитель. Запишите это в первую дробь. Для этого над дробью проведите небольшую диагональную черту и над ней напишите найденный дополнительный множитель:
Проделайте то же самое со второй дробью. Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК равно 6, а знаменатель второй дроби равен 2. Разделив 6 на 2, получим 3.
Полученное число 3 является вторым дополнительным множителем. Запишите это во вторую дробь. Снова проведите маленькую диагональную линию над второй дробью и запишите над ней найденный дополнительный множитель:
Теперь все готово для сложения. Осталось умножить числители и знаменатели дробей на их дополнительные множители:
Осталось умножить числители и знаменатели дробей на их дополнительные множители:
Посмотрите внимательно, к чему мы пришли. Мы пришли к тому, что дроби с разными знаменателями превратились в дроби с одинаковыми знаменателями. И мы уже умеем складывать такие дроби. Решим этот пример до конца:
На этом пример закончен. Добавьте и получите.
Попробуем изобразить наше решение картинкой. Если добавить пиццу к пицце, получится одна целая пицца и одна шестая часть пиццы:
Также можно показать приведение дроби к одному (общему) знаменателю. Приведя дроби и к общему знаменателю, мы получили дроби и . Две фракции будут представлены одними и теми же кусочками пиццы. С той лишь разницей, что на этот раз они будут разделены на одинаковые дроби (приведены к одному знаменателю).
Первая картинка представляет дробь (четыре штуки по шесть), а вторая картинка представляет дробь (три штуки по шесть). Складывая эти кусочки, получаем (семь штук по шесть). Эта дробь неправильная, поэтому мы выделили всю ее часть. Получилось (одна целая пицца и еще шестая часть пиццы).
Эта дробь неправильная, поэтому мы выделили всю ее часть. Получилось (одна целая пицца и еще шестая часть пиццы).
Обратите внимание, что мы расписали этот пример слишком подробно. В школах не принято так подробно писать. Нужно уметь быстро находить НОК обоих знаменателей и дополнительных множителей к ним, а также быстро умножать найденные дополнительные множители на их числители и знаменатели. Если бы мы учились в школе, нам пришлось бы записать этот пример следующим образом:
Но есть и обратная сторона медали. Если вы не будете делать подробные заметки на первых этапах изучения математики, вы начнете получать вопросы вроде 9.0143 «откуда взялся этот номер?» , «почему дроби вдруг превращаются в совсем другие дроби?»
Поэтому на первых этапах желательно прописывать каждую мелочь. Похвастаться можно только в будущем, когда освоены азы.
Чтобы было проще складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:
- Найти НОК знаменателей дробей;
- Разделите НОК на знаменатель каждой дроби и получите дополнительный множитель для каждой дроби;
- Умножить числители и знаменатели дробей на их дополнительные множители;
- Сложите дроби с одинаковыми знаменателями;
- Если ответ представляет собой неправильную дробь, выберите всю ее часть;
Пример 2. Найдите значение выражения .
Найдите значение выражения .
Воспользуемся приведенными выше инструкциями.
Шаг 1. Найдите НОК знаменателей дробей
Найдите НОК знаменателей обеих дробей. Знаменатели дробей — числа 2, 3 и 4.
Шаг 2: Разделите НОК на знаменатель каждой дроби и получите дополнительный множитель для каждой дроби
Разделите НОК на знаменатель первой фракции. НОК равно 12, а знаменатель первой дроби равен 2. Разделим 12 на 2, получим 6. Получим первый дополнительный множитель 6. Запишем его над первой дробью:
Теперь разделите НОК на знаменатель второй дроби. НОК равно 12, а знаменатель второй дроби равен 3. Делим 12 на 3 и получаем 4. У нас есть второй дополнительный множитель 4. Запишем его над второй дробью:
Теперь разделим НОК на знаменатель третья дробь. НОК равно 12, а знаменатель третьей дроби равен 4. Делим 12 на 4 и получаем 3. У нас есть третий дополнительный множитель 3. Запишем его над третьей дробью:
Запишем его над третьей дробью:
Шаг 3: Умножьте числители и знаменатели фракций на их дополнительные множители
Умножьте числители и знаменатели на их дополнительные множители:
. установили, что дроби с разными знаменателями превращаются в дроби с одинаковыми (общими) знаменателями. Осталось сложить эти дроби. Складываем их:
Добавление не помещалось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это разрешено в математике. Когда выражение не помещается на одной строке, оно переносится на следующую строку, и вы должны поставить знак равенства (=) в конце первой строки и в начале новой строки. Знак равенства во второй строке указывает на то, что это продолжение выражения, которое было в первой строке.
Шаг 5. Если ответом является неправильная дробь, выберите всю ее часть
Наш ответ — неправильная дробь. Мы должны изолировать всю его часть. Делаем:
Делаем:
Получили ответ
Вычитание дробей с общим знаменателем
Вычитание дробей бывает двух видов:
- Вычитание дробей с общим знаменателем
- Вычитание дробей с разными знаменателями
Сначала мы научимся вычитать дроби с общими знаменателями.
Чтобы из одной дроби вычесть другую дробь, вычтите числитель первой дроби из числителя второй дроби и оставьте знаменатель без изменений.
Например, найдем значение выражения . Чтобы решить этот пример, вычтите числитель первой дроби из числителя второй дроби и оставьте знаменатель без изменений. Давайте сделаем так:
Этот пример легко понять, если представить себе пиццу, разделенную на четыре части. Если отрезать пиццу от пиццы, то получится пиццы:
Пример 2. Найдите значение выражения .
Снова вычитаем числитель второй дроби из числителя первой дроби и оставляем знаменатель без изменений:
Этот пример легко понять, если представить себе пиццу, разделенную на три части. Если отрезать пиццу от пиццы, то получится пицца:
Если отрезать пиццу от пиццы, то получится пицца:
Пример 3. Найдите значение выражения
Этот пример решается так же, как и предыдущие. Из числителя первой дроби вычесть числители остальных дробей:
Ответ — неправильная дробь. Выделим всю часть дроби:
Как видите, в вычитании дробей с равными знаменателями нет ничего сложного. Достаточно усвоить следующие правила:
- Чтобы из одной дроби вычесть другую дробь, вычтите числитель второй дроби из числителя первой дроби и оставьте знаменатель без изменений;
- Если ответом является неправильная дробь, нужно выделить всю ее часть.
Вычитание дробей с разными знаменателями
Теперь давайте научимся вычитать дроби с разными знаменателями. При вычитании дробей их знаменатели должны совпадать. Но они не всегда одинаковы.
Например, вы можете вычитать из дроби, потому что у этих дробей одинаковые знаменатели. Но вычитать из дроби нельзя, потому что у этих дробей разные знаменатели. В таких случаях дроби необходимо привести к одному (общему) знаменателю.
Но вычитать из дроби нельзя, потому что у этих дробей разные знаменатели. В таких случаях дроби необходимо привести к одному (общему) знаменателю.
Общий знаменатель находится по тому же принципу, который мы использовали при сложении дробей с разными знаменателями. Сначала находим НОК знаменателей обеих дробей. Затем делим НОК на знаменатель первой дроби и получаем первый дополнительный множитель, который записывается над первой дробью. Точно так же LCM делится на знаменатель второй дроби, чтобы получить второй дополнительный множитель, который записывается над второй дробью.
Затем дроби умножаются на их дополнительные множители. В результате этих операций дроби с разными знаменателями преобразуются в дроби с одинаковыми знаменателями. И мы уже умеем вычитать такие дроби.
Пример 1. Найдите значение выражения:
Эти дроби имеют разные знаменатели, поэтому нужно привести их к одному (общему) знаменателю.
Сначала найдите НОК знаменателей обеих дробей. В знаменателе первой дроби число 3, а в знаменателе второй дроби число 4. Наименьшее общее кратное этих чисел равно 12
В знаменателе первой дроби число 3, а в знаменателе второй дроби число 4. Наименьшее общее кратное этих чисел равно 12
НОК (3 и 4) = 12
Теперь вернемся к дробям и
Найдите дополнительный множитель для первой дроби. Для этого НОК разделите на знаменатель первой дроби. НОК равно 12, а знаменатель первой дроби равен 3. Делим 12 на 3 и получаем 4. Запишем четверку над первой дробью:
Проделываем то же самое со второй дробью. Разделите НОК на знаменатель второй дроби. НОК равно 12, а знаменатель второй дроби равен 4. Разделим 12 на 4, и получим 3. Запишем тройку над второй дробью:
Теперь мы готовы к вычитанию. Осталось умножить дроби на их дополнительные множители:
Мы обнаружили, что дроби с разными знаменателями превратились в дроби с одинаковыми знаменателями. И мы уже умеем вычитать такие дроби. Решим этот пример до конца:
Мы получили ответ.
Попробуем изобразить наше решение картинкой. Если отрезать пиццу от пиццы, получится пицца
Если отрезать пиццу от пиццы, получится пицца
Это подробная версия решения. Если бы мы учились в школе, нам пришлось бы решать этот пример в более короткой форме. Решение будет выглядеть так:
Приведение дробей и к общему знаменателю также можно представить с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут представлены одними и теми же кусками пиццы, но на этот раз они будут разделены на одинаковые дроби (приведенные к одному знаменателю):
На первом рисунке изображена дробь (восемь кусочков из двенадцати), а на втором рисунке дробь (три кусочка из двенадцати). Отрезав три ломтика от восьми ломтиков, мы получим пять ломтиков из двенадцати. Фракция и описывает эти пять частей.
Пример 2. Найдите значение выражения
Эти дроби имеют разные знаменатели, поэтому сначала нам нужно привести их к одному (общему) знаменателю.
Найдите НОК знаменателей этих дробей.
Знаменатели равны 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30
LCM (10, 3, 5) = 30
Теперь найдите дополнительные множители для каждой дроби. Для этого разделите НОК на знаменатель каждой дроби.
Найдите дополнительный множитель для первой дроби. НОК равно 30, а знаменатель первой дроби равен 10. Разделим 30 на 10, и получим первый дополнительный множитель 3. Запишем его над первой дробью:
Теперь найдите дополнительный множитель для второй дроби. Разделите НОК на знаменатель второй дроби. НОК равно 30, а знаменатель второй дроби равен 3. Разделив 30 на 3, получим второй дополнительный множитель 10. Запишите его над второй дробью:
Теперь найдите дополнительный множитель для третьей дроби. Разделите НОК на знаменатель третьей дроби. НОК равно 30, а знаменатель третьей дроби равен 5. Разделим 30 на 5, и получим третий дополнительный множитель 6. Запишем его над третьей дробью:
Теперь все готово для вычитания. Осталось умножить дроби на их дополнительные множители:
Осталось умножить дроби на их дополнительные множители:
Мы обнаружили, что дроби с разными знаменателями превратились в дроби с одинаковыми (общими) знаменателями. И мы уже умеем вычитать такие дроби. Закончим этот пример.
Продолжение примера не помещается на одной строке, поэтому переносим продолжение на следующую строку. Не забудьте знак равенства (=) в новой строке:
Ответ — правильная дробь, и нас вроде бы устраивает, но это слишком громоздко и некрасиво. Мы должны сделать это проще. Что мы можем сделать? Мы могли бы сократить дробь.
Чтобы сократить дробь , разделим ее числитель и знаменатель на наибольший общий делитель (НОД) 20 и 30.
Итак, находим НОД чисел 20 и 30:
Теперь вернемся к нашему пример и разделить числитель и знаменатель дроби на найденный НОД, то есть на 10
Мы получили ответ
Умножение дробей на целые числа
Чтобы умножить дробь на число, умножьте числитель дроби на это число и оставьте знаменатель без изменений.
Пример 1. Умножить дробь на число 1.
Умножить числитель дроби на число 1.
Запись можно понимать как занимающую половину 1 раза. Например, если вы возьмете пиццу один раз, вы получите 9 пицц.0003
Из законов умножения мы знаем, что если поменять местами множитель и множитель, произведение не изменится. Если написано как , то товар по-прежнему . Снова срабатывает правило умножения целого числа на дробь:
Эту запись можно понимать как получение половины от единицы. Например, если есть 1 целая пицца и мы берем половину, у нас есть пицца:
Пример 2. Найдите значение выражения
Умножьте числитель дроби на 4
Ответ — неправильная дробь. Выделим целую часть дроби:
Выражение можно понимать как взятие двух четвертей четыре раза. Например, если взять пиццу 4 раза, получится целых две пиццы
А если поменять местами множитель и множитель, то получится выражение . Оно также равно 2. Это выражение можно понимать как взятие двух пицц из четырех целых пицц:
Оно также равно 2. Это выражение можно понимать как взятие двух пицц из четырех целых пицц:
Число, которое умножается на дробь, и знаменатель дроби допускается сокращать, если они имеют общий делитель больше единицы.
Например, выражение можно вычислить двумя способами.
Первый метод . Умножьте 4 на числитель дроби и оставьте знаменатель без изменений:
Второй способ. Четверка, умноженная на четверку в знаменателе дроби, может быть сокращена. Эти четверки можно уменьшить на 4, потому что наибольшим общим делителем двух четверок является четверка:
Получаем тот же результат 3. После сокращения четверок на их месте образуются новые числа: две единицы. Но умножение одного на три и последующее деление на один ничего не меняет. Следовательно, решение можно записать в более короткой форме:
Сокращение может быть выполнено даже тогда, когда мы выбираем первый способ, но на этапе умножения числа 4 и числителя 3 мы выбираем использование сокращения:
А вот, например, выражение можно вычислить только первым способом — умножив число 7 на числитель дроби, а знаменатель оставить без изменений:
Это связано с тем, что число 7 и знаменатель дроби не имеют общего делителя больше единицы, а потому не сокращаются.
Некоторые учащиеся ошибочно сокращают умноженное число и числитель дроби. Этого делать не следует. Например, следующая запись неверна:
Сокращение дроби означает, что и числитель , и знаменатель будут делиться на одно и то же число. В случае делится только числитель, потому что писать то же самое, что писать . Мы видим, что деление производится только в числителе, а в знаменателе деления нет.
Умножение дробей
Чтобы умножить дроби, умножьте их числители и знаменатели. Если ответом является неправильная дробь, выберите целую часть дроби.
Пример 1. Найдите значение выражения .
Умножьте числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй дроби:
Ответ: . Желательно уменьшить эту фракцию. Дробь можно уменьшить на 2. Тогда окончательное решение будет выглядеть так:
Выражение можно понимать как взятие пиццы из половины пиццы. Предположим, у нас есть половина пиццы:
Предположим, у нас есть половина пиццы:
Как взять две трети этой половины? Сначала вы должны разделить эту половину на три равные части:
И взять из этих трех частей две:
У нас будет пицца. Вспомните, как выглядит пицца, разделенная на три части:
Один кусок этой пиццы и два взятых нами кусочка будут одинакового размера:
Другими словами, речь идет об одинаковом размере пиццы. Следовательно, значение выражения равно
Пример 2. Найдите значение выражения
Умножьте числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй дроби:
Ответ — неправильная дробь. Выделим целую часть дроби:
Пример 3. Найти значение выражения
Умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй дроби:
Ответ — правильная дробь, но было бы хорошо, если бы она была сокращена. Чтобы уменьшить эту дробь, разделите числитель и знаменатель дроби на наибольший общий делитель (НОД) чисел 105 и 450.
Чтобы уменьшить эту дробь, разделите числитель и знаменатель дроби на наибольший общий делитель (НОД) чисел 105 и 450.
Итак, найдем НОД 105 и 450:
Теперь разделим числитель и знаменатель нашего ответа на найденный НОД, то есть на 15
Представим целое в виде дробь
Любое целое можно представить в виде дроби. Например, число 5 можно представить как . Это не изменит значения числа пять, т.к. означает «число пять, деленное на один», а это, как мы знаем, равно пяти:
Обратные числа
Сейчас мы собираемся изучить очень интересную тему математики. Это называется «обратные числа».
Определение. Обратное к а — это число, которое при умножении на а дает единицу.
Давайте подставим число 5 вместо переменной a в этом определении и попробуем прочитать определение:
Число, обратное 5, — это число, которое при умножении на 5 дает единицу.
Можно ли найти число, которое при умножении на 5 дает единицу? Это возможно. Представим пять в виде дроби:
Представим пять в виде дроби:
Затем умножьте эту дробь саму на себя, но поменяйте местами числитель и знаменатель. Другими словами, умножьте дробь саму на себя, только перевернув:
Что получится в результате? Если мы продолжим решать этот пример, мы получим один:
Таким образом, число, обратное числу 5, является числом , потому что умножение 5 на дает один.
Обратное можно найти и для любого другого целого.
Примеры:
- число, обратное числу 2, равно дроби 9.0010
- обратная цифре 2 дробь
- обратная цифре 2 дробь
Также можно найти обратное число для любой другой дроби. Для этого все, что вам нужно сделать, это перевернуть его.
Примеры:
- Для дроби обратной дробью является дробь
- Для дроби обратной дробью является дробь
- Для дроби обратной дробью является дробь
Деление дроби на целое число
Допустим, у нас есть половина пиццы:
Разделите ее поровну между нами двумя. Сколько пиццы каждый из нас получит?
Сколько пиццы каждый из нас получит?
Вы можете видеть, что после разделения половины пиццы есть два равных куска, каждый из которых принадлежит пицце. Так что каждый человек получает по пицце.
Деление дробей производится обратными числами. Обратные числа позволяют заменить деление умножением.
Чтобы разделить дробь на число, умножьте дробь на число, обратное делителю.
Используя это правило, запишем деление половины нашей пиццы на две части.
Итак, вы хотите разделить дробь на число 2. Здесь делителем является дробь , а делителем является число 2.
Чтобы разделить дробь на 2, умножьте дробь на величину, обратную делителю 2. Обратное число делитель 2 равен . Так умножьте на .
Ответ . Итак, если вы разделите половину на два, вы получите четверть.
Попробуем разобраться в механизме этого правила. Для этого рассмотрим следующий простой пример. Допустим, у нас есть одна целая пицца:
Умножим на 2. То есть повторим дважды (или возьмем дважды). В итоге у нас будет две пиццы:
То есть повторим дважды (или возьмем дважды). В итоге у нас будет две пиццы:
Теперь давайте подадим эти пиццы двум друзьям. То есть разделить две пиццы на два. Затем каждый получает по одной пицце:
Разделить две пиццы на 2 — это все равно, что взять половину этих пицц, то есть умножить число 2 на дробь от
В обоих случаях результат был одинаковым.
То же самое произошло, когда мы разделили половину пиццы на две части. Чтобы разделить на 2, мы умножили эту дробь на число, обратное делителю 2. И обратное делителю 2 равно .
Пример 2. Найти значение выражения
Умножьте первую дробь на число, обратное делителю:
Допустим, у вас есть четверть пиццы и вам нужно разделить ее между двумя людьми:
Если вы разделите эту четвертинку на две части, каждая полученный кусок составляет одну восьмую часть целой пиццы:
Замена деления на умножение возможна не только при работе с дробями, но и с обычными числами. Например, все мы знаем, что 10 разделить на 2 равно 5.
Например, все мы знаем, что 10 разделить на 2 равно 5.
10 : 2 = 5
В этом примере вместо деления используется умножение. Чтобы разделить число 10 на число 2, вы можете умножить число 10 на число, обратное числу 2. И число, обратное 2, составляет дробь
Как видите, результат не изменился. Мы снова получили ответ 5.
Можно сделать вывод, что деление можно заменить умножением при условии, что вместо делителя подставлено обратное число.
Пример 3. Найдите значение выражения
Умножьте первую дробь на число, обратное делителю. Обратная делитель равна дроби
Допустим, пиццы было:
Как разделить такую пиццу между шестью людьми? Если вы разделите каждый из трех ломтиков пополам, вы получите шесть равных ломтиков
Эти шесть частей составляют шесть частей по двенадцать. И одна из этих частей. Поэтому при делении на 6 получается
Деление целого числа на дробь
Правило деления числа на дробь такое же, как правило деления дроби на число.
Чтобы разделить число на дробь, умножьте число на дробь, обратную делителю.
Например, разделите число 1 на .
Чтобы разделить число 1 на , нужно умножить число 1 на дробь, обратную дроби. И обратная дробь дробь .
Выражение можно понимать как определяющее количество половинок в одной целой пицце. Предположим, что есть одна целая пицца:
Если мы зададим вопрос «сколько раз половина содержится в этой пицце», ответ будет 2. Действительно, половина содержится в одной целой пицце дважды
Пример 2. Найдите значение выражения
Умножьте 2 на дробь, обратную делителю. А обратная делителю дробь
Допустим, у нас есть целых две пиццы:
Если мы зададим вопрос «сколько раз половина в двух пиццах», ответ будет 4. Действительно, половина содержится в двух пиццах четыре раза:
Деление дробей
Чтобы разделить дробь на дробь, умножьте первую дробь на дробь, обратную второй дроби.
Например, разделите на
Чтобы разделить на , вы должны умножить на дробь, обратную дроби . А обратная дробь это дробь
Допустим, есть половина пиццы:
Если мы зададим вопрос «сколько раз четверть пиццы содержится в этой половине», ответ будет 2. Действительно, четверть пиццы содержится в половине пиццы дважды:
Пример 1. Найдите значение выражения
Умножьте первую дробь на дробь, обратную второй дроби. Грубо говоря, умножаем первую дробь на перевернутую вторую дробь:
Пример 2. Найдите значение выражения
Умножьте первую дробь на обратную второй дроби:
Здесь вы должны остановиться и попрактиковаться. Решите несколько примеров ниже. Вы можете использовать материалы сайта в качестве справочной информации. Это позволит вам научиться работать с литературой.
Каждая следующая тема будет сложнее, поэтому нужно практиковаться.
Упражнения:
Задача 1. Найти значение выражения:
Решение:
Показать решение
Задача 2. Найти значение выражения:
Решение:
1 0 07 0 Показать решение3 9 0.0003 9 Найдите значение выражения:
Решение:
Показать решение
Задача 4. Найдите значение выражения:
Решение:
Показать решение
Задача 5. Найдите значение выражения :
Решение:
Показать решение
Задача 6. Найдите значение выражения:
Решение:
Показать решение
Задача 7. Найдите значение выражения:
Решение:
Показать решение
Задача 8. Найти значение выражения:
Решение:
Показать решение
Задача 9. Найти значение выражения:
Решение:
Показать решение
Задача 10. Найдите значение выражения:
Найдите значение выражения:
Решение:
Показать решение
Задача 11. Найдите значение выражения:
Решение:
Показать решение
Задача 12. Найти значение выражения:
Решение:
Показать решение
Задача 13. Найти значение выражения:
Решение:
Показать решение
Задача 14. Найдите значение выражения:
Решение:
Show Solution
Видео Урок
Реальные приложения фракций
Math & Beyond
Фракции. Beyond
Применение дробей в реальном мире
107,4 тыс. просмотров
Содержание
1. | Введение |
| 2. | Что такое дроби? |
| 3. | Дроби в математике |
| 4. | Дроби в реальном мире |
| 5. | Резюме |
| 6. | Часто задаваемые вопросы |
21 октября 2020 г.
Время считывания: 5 минут
ВведениеЗачем мне изучать дроби?
Существует несколько способов неосознанно использовать дроби в повседневной деятельности. Справедливо сказать, что мир не был бы без дробей, каким мы его видим сегодня. Этот блог прольет свет на дроби и то, как они применяются в различных разделах математики и как они влияют на нашу повседневную жизнь.
Читайте также:
- Как складывать дроби с разными комбинациями?
- Фракции: операции и свойства
Загружаемый PDF-файл
Для просмотра применения дробей и других вещей, связанных с дробями, загрузите приведенный ниже PDF-файл, нажав кнопку «Загрузить».
| 📥 | Применение дробей в реальном мире | Скачать |
Что такое дроби?
Дробь является частью целого. Другими словами, дробь — это число, представляющее целое число.
Например, торт разделен на 8 равных частей. Если съеден один кусочек, как мы можем представить оставшуюся часть торта?
Оставшаяся часть пирога может быть выражена численно как \(\frac{7}{8}\).
Здесь 7 — числитель , а 8 — знаменатель .
Дроби в математике
Дроби — это элементарная тема в математике, которая выступает в качестве строительного блока во многих других темах математики.
Вот некоторые способы использования дробей в математике:
- Мы можем определить часть любого числа , используя дроби.

Пример
\[\frac{3}{4}\; \text{часть }24 =\frac{3}{4} × 24 = 18\]
\[\text{Половина }90 = \frac{1}{2}× 90 = 45\]
- Дроби используются для определения десятичных и процентов чисел
Пример
\[\begin{align}\frac{3}{4}× 100 &= 75\% \\\frac{3}{4}&= 0,75\\[6pt]\frac{ 3}{8}&= 0,375 = 37,5\%\end{align}\]
- Дроби используются при расчете вероятности . Они используются для присвоения числового значения вероятности возникновения события.
Пример
Какова вероятность того, что число 3 выпадет при броске беспристрастной кости?
Вероятность того, что выпадет 3, равна \(\frac{1}{6} \)
- Мы также используем дроби в алгебре, когда решаем алгебраические уравнения.
- В соотношениях используются дроби.
- Эти понятия наряду с другими широко используются в математике и других науках для выполнения вычислений.

Дроби в реальном мире
Дроби окружают нашу повседневную деятельность. Вот несколько примеров использования дробей в реальной жизни:
Еда в ресторане: Вспомните случай, когда вы идете в ресторан с друзьями, и официантка приносит единственный счет. Чтобы разделить сумму между друзьями, вы используете дроби.
Покупки: Вспомните, как вы ходили по магазинам в поисках новой школьной сумки. Из-за распродажи на все была скидка в половину, поэтому вы рассчитываете новую цену, используя дроби.
По рецепту: Иногда в рецептах предлагается использовать \(\frac{1}{2}\) чайную ложку сахара, \(\frac{3}{4}\) столовую ложку соли. В некоторых рецептах также указано количество, рассчитанное на 2 человек. Если мы готовим одно и то же блюдо для 3 человек, для соответствующей корректировки ингредиентов используются дроби.
Спорт: Фракции часто используются для анализа производительности конкретного игрока или команды.

Фитнес: Мы используем дроби, чтобы понять наш индекс массы тела (ИМТ), чтобы определить, находимся ли мы в здоровом диапазоне массы тела или нет.
Напитки: Для приготовления напитков типа безалкогольных коктейлей различные фракции жидкостей смешиваются в нужном количестве для достижения наилучшего результата.
Пицца: Чтобы разделить кусочки пиццы поровну между всеми, нужны дроби.
Фото и видеосъемка: Выдержка камеры рассчитывается с использованием дробей.
Тесты и экзамены: Результаты тестов и экзаменов обычно выражаются дробями, например \(\frac{18}{20}\).
Медицинские рецепты: Когда кто-то болен, врач назначает разные дозы для людей разного телосложения. Взрослый человек может потреблять 500 мг, тогда как ребенок может потреблять половину этого количества.

Прогресс или спад: Можно измерить прогресс или спад любого проекта. Если продажи определенного продукта упали на 25 % или на \(\frac{1}{4}\)th.
Время: Полчаса — распространенный способ выражения 30 минут.
Резюме
Применение дробей в повседневной жизни безгранично; они имеют большое значение и глубоко влияют на все вокруг нас. В этом блоге рассказывается о некоторых вещах, связанных с дробями. Подумайте о других способах использования дробей в вашей жизни.
Часто задаваемые вопросыЧасто задаваемые вопросы (FAQ)
Что такое дробь?
Дробь является частью целого. Другими словами, дробь — это число, представляющее целое число.
Где дроби используются в математике?
Дроби используются в:
Определение части числа
Вычисление десятичных дробей и процентов
Соотношение и пропорция
Вероятность
Алгебраические уравнения
Какие есть примеры дробей в реальной жизни?
Вот некоторые применения дробей в реальной жизни:
Разделение счета во время еды в ресторане
Расчет цены со скидкой на объект при продаже.

По рецепту
Фракции часто используются для анализа производительности конкретного игрока и команды.
Мы используем дроби, чтобы понять наш индекс массы тела (ИМТ), чтобы определить, находимся ли мы в здоровом диапазоне массы тела или нет.
Различные фракции жидкостей смешиваются в нужных количествах для приготовления безалкогольных коктейлей.
Чтобы разделить куски пиццы поровну между всеми, нужны дроби.
Скорость затвора камеры рассчитывается с использованием дробей.
Результаты тестов и экзаменов обычно выражаются в виде дробей, например \(\frac{18}{20}\).
Врач прописывает разные дозировки для людей разного телосложения в зависимости от фракций.
Прогресс или спад любого проекта можно измерить. Если продажи определенного продукта упали на 25% или на \(\frac{1}{4}\) th.
Во времени, Half n часа является распространенным способом выражения 30 минут.

Как умножать дроби?
Чтобы умножить дроби, мы умножаем два числителя и два знаменателя друг на друга.
Пример
\[\frac{2}{3}\times\frac{4}{5}=\frac{2\times3}{4\times 5}=\frac{8}{15}\]
Статьи по теме
Математика и не только
Введение в общие базовые стандарты математики для 4 класса | Программа | Самые важные области
Чтобы удовлетворить потребность в целенаправленной и последовательной учебной программе по математике в США, Соединенные Штаты Common…
Введение в общие базовые стандарты математики для 3 класса | Программа | Наиболее важные области
Для удовлетворения потребности в целенаправленной и последовательной учебной программе по математике в США, Общем…
25 янв. павших: Как Математика спасла Мать-Землю?
Рони, Ниташа, я вижу последнюю треть куба. Давайте встретимся как можно скорее и покончим с этим. Читайте дальше…
2 апреля 21
Прочитать статью полностью
(3 минуты чтения)
Math & Beyond
Введение в общие базовые стандарты математики для 4 класса | Программа | Самые важные области
Чтобы удовлетворить потребность в целенаправленной и последовательной учебной программе по математике в США, Соединенные Штаты Common. ..
..
Введение в общие базовые стандарты математики для 3 класса | Программа | Наиболее важные области
Чтобы удовлетворить потребность в целенаправленной и последовательной учебной программе по математике в США, Общий…
25th Jan ’22
Прочитать статью полностью
(7 минут чтения)
Математика и не только
Восстание падших: как математика спасла Мать-Землю?
Рони, Ниташа, я вижу последнюю треть куба. Давайте встретимся как можно скорее и покончим с этим. Читайте дальше…
2 апреля 21
Прочитать статью полностью
(3 минуты чтения)
Дробные занятия Студенты любят — Учитель по соседству
Дроби могут быть трудными! Хотя учащимся требуется время и повторное знакомство с дробями, чтобы они действительно поняли их, есть много опыта и занятий, которые мы можем предоставить как учителя, чтобы продвинуть их понимание вперед!В этом посте я поделюсь с вами некоторыми из моих любимых занятий фракции!
1.
 Фракции, которые можно потрогать… и некоторые можно съесть!
Фракции, которые можно потрогать… и некоторые можно съесть!Первое, что мы хотим сделать, это предоставить много возможностей без давления, возможностей для игры с объектами, чтобы сделать концепцию дробей более ясной. Play-Doh — отличный способ сделать дроби!
Конечно, сначала вам нужно будет позволить детям играть с пластилином Play-Doh самостоятельно, но через несколько минут вы сможете вместе испечь дробное печенье или дробную пиццу, разрезанную на равные части, например половинки. , трети или четверти.
В зависимости от правил питания в вашей школе горсть (или небольшая упаковка) M&M’s или Skittles отлично подходят для сортировки по цветам и маркировки каждого цвета как дроби. Общее количество конфет будет знаменателем, а числитель будет конкретным цветом конфет в этой группе.
Цветной зефир или хлопья разных форм (например, Lucky Charms) также хорошо подходят. Я разрешаю ученикам есть их в конце урока после того, как я сам выборочно проверил их страницу дроби.
Пытаетесь держаться подальше от продуктов питания?
Есть множество мелких предметов, которые работают одинаково хорошо. Кнопки разных цветов, мини-ластики (отличный способ их использования), маленькие пластмассовые животные, деревянные формы танграма и т. д. — прекрасные примеры дробей!
2. Тексты наставников
Есть несколько действительно замечательных книжек с картинками, которые либо предназначены для обучения дробям, либо содержат некоторые темы в книгах, которые поддаются обсуждению дробей. Посмотрите на картинку выше, чтобы увидеть некоторые из моих любимых текстов наставников, если вы хотите добавить немного чтения к математике.
3. Дроби в стакане
Чтобы играть в эту игру, разделите учащихся на пары. Дайте каждой паре пластиковый стаканчик с двусторонними фишками (количество фишек на ваш выбор зависит от способностей ваших учеников). Учащиеся осторожно встряхивают чашку и осторожно выливают содержимое, чтобы осколки не разлетались повсюду. Затем учащиеся пишут две дроби, чтобы описать то, что они видят.
Затем учащиеся пишут две дроби, чтобы описать то, что они видят.
Например, если было всего семь жетонов и четыре приземлились на желтую сторону, эта дробь равна 4/7. Это будет означать, что также будет 3/7 красных жетонов, обращенных вверх, всего 7/7, то есть все жетоны.
Если вы хотите превратить это в игру, каждый ученик может выбрать один из цветов. После того, как учащиеся напишут свои дроби на доске, попросите одного из них бросить монету «Больше/Меньше», которая представляет собой просто пластиковую фишку с надписью «Больше» на одной стороне и «Меньше» на другой стороне либо на наклейке, либо с надписью маркером.
Ученик с наибольшей дробью выигрывает, если переворачивается Больше, а учащийся с меньшей дробью выигрывает, если показывается Меньше. Это поддерживает мотивацию учеников к игре, даже если у другого ученика дробь явно больше.
4. LEGOS или DUPLOS
Блоки LEGOS или DUPLOS являются прекрасными визуальными инструментами при обучении дробям. Хотя они могут быть дорогими, вы можете одолжить их или получить в дар от друзей, чьи дети уже выросли.
Хотя они могут быть дорогими, вы можете одолжить их или получить в дар от друзей, чьи дети уже выросли.
Если у вас есть небольшая сумма, они хорошо подойдут для математического занятия с гидом. Попросите детей показать вам определенные дроби (например, 1/3 или 2/5), и дети потренируются составлять дроби по мере их построения. Если у вас много LEGO, это можно сделать на уроке для всего класса.
Чтобы использовать LEGO или DUPLOS в качестве основной игры, вы можете объединить детей в группы по два человека. Каждый ребенок дважды бросает кубик, чтобы определить числа в дроби. Меньшее число, которое выпало, является числителем, а большее число — знаменателем.
Дети используют LEGOS, чтобы собрать эту фракцию, используя два разных цвета. Например, если ребенок выбросил 2 и 5, дробь будет 2/5, и можно построить башню из двух красных LEGO и трех синих LEGO, всего пять LEGO.
После того, как оба ученика построят башни своих фракций, используйте монету «Больше/Меньше», чтобы определить победителя, у которого останутся карты.
5. Игральные карты для сравнения дробей
Это игра для двух игроков. Сначала уберите все лицевые карты, но оставьте тузы, которые будут использоваться как единицы. Учащиеся перемешивают карточки и кладут их лицевой стороной вниз.
Каждый учащийся выбирает две карточки и кладет их так, чтобы меньшая карточка была в числителе, а большая – в знаменателе. Учащиеся сравнивают дроби, находя общий знаменатель.
После того, как будут определены большая и меньшая части, я предлагаю учащимся использовать описанную выше монету «Больше/Меньше», чтобы определить победителя. Победитель сохраняет карты, и тот, у кого больше карт в конце игры, побеждает.
6. Карточки с заданиями и игры с дробями
Один из моих любимых способов закрепить математические знания — использовать карточки с математическими заданиями и игры. Детям очень нравится играть в игровом формате, и я могу ориентироваться на конкретные типы концепций и стандартов, которые нам нужно практиковать. Если вы ищете готовые наборы карточек с заданиями для фракций, у меня есть несколько из них, которые могут вам понравиться.
Если вы ищете готовые наборы карточек с заданиями для фракций, у меня есть несколько из них, которые могут вам понравиться.
Щелкните здесь, чтобы получить набор фракций 3-го класса.
Вот набор фракций для 4-го класса.
Это набор фракций для 5-го класса.
7. Дроби О нас
Мне нравится начинать это задание с проведения урока для всего класса. Я задаю ученикам разные вопросы, и на основе ответов мы делаем дроби на доске.
Например, если есть 28 студентов, и я спрашиваю, сколько детей любят попкорн, мы можем получить дробь вроде 27/28 детей, которые любят попкорн.
Или я спрошу, у скольких детей есть братья, ходят ли они в школу, играют в баскетбол, любят брокколи и т. д. На каждого делаем дроби.
Затем, чтобы немного изменить ситуацию, я вытаскиваю группу из четырех детей вперед и задаю им только вопрос, который меняет знаменатель. Затем я прошу их сесть и вывести группу из шести детей вперед, чтобы они задали еще один вопрос. Опять же, подчеркивая, что общее число в группе является знаменателем.
Опять же, подчеркивая, что общее число в группе является знаменателем.
После того, как мы сделали это введение, я делю детей на группы примерно по пять человек и даю им большой лист цветной бумаги или лист бумаги с якорной диаграммой.
Сначала каждый ребенок пишет на плакате свое имя. Затем каждый ребенок по очереди задает вопрос и записывает ответы группы дробями. После того, как у каждого будет возможность один или два раза опросить свою группу, можно предложить детям совершить прогулку по галерее, чтобы увидеть плакаты всех остальных.
8. Игры в домино
A. Сравните дроби
В этой игре учащиеся кладут все кости домино лицевой стороной вниз. Каждый ребенок выбирает одну костяшку и переворачивает ее так, чтобы числитель был меньше знаменателя. С помощью общих знаменателей учащиеся определяют, какая дробь меньше, а какая больше. Монета «Больше/Меньше» используется для определения победителя, которому принадлежит домино.
B.
 Равные дроби
Равные дробиВсе кости домино кладутся лицевой стороной вниз. Каждый учащийся выбирает костяшку и на доске или на листе бумаги пытается написать эквивалентную дробь для этой костяшки. Например, 2/3 = 4/6, или 8/12, или 16/24. Чтобы превратить это в игру, каждый, кто напишет не менее трех одинаковых дробей, может оставить свое домино.
C. Неправильные дроби
Все кости домино кладутся лицевой стороной вниз. Каждый учащийся выбирает костяшку костяшки и ставит ее так, чтобы большее число было сверху в качестве числителя, а меньшее — в знаменателе. Получится неправильная дробь. Каждый учащийся заменяет неправильную дробь смешанным числом. После этого используйте монету «Больше/Меньше», чтобы определить, кто выиграет в этом раунде.
И, наконец, если вам нужен комплект карточек с математическими заданиями, содержащий 30 наборов карточек с заданиями, по одному для КАЖДОГО СТАНДАРТА, обратите внимание на эти:
3 -й класс по математике карты задач. Пакет
Пакет
4 -й класс по математическим картам
5 -й класс по математическим картам. Компания
Большое спасибо за остановку!
Математические игры с использованием игральных костей
На мой взгляд, игры являются важной частью занятий по математике. Дети могут не только практиковать навыки, которым мы уделяем особое внимание
Подробнее »
Математические игры с использованием домино
Математические игры всегда были частью нашей математики. Мне нравится тот факт, что каждый раз, когда я представляю математическую игру, я знаю, что
Подробнее »
Стратегии решения текстовых задач
Одно дело решить математическое уравнение, когда вам даны все числа, но со словами, когда вы начинаете складывать
Подробнее »
7 Вовлечение фракций Занятия для малых групп
Вы находите, что учить дроби только наполовину так весело, как вам хотелось бы? Считают ли две трети ваших учеников минуты до того, как они смогут уйти на обед, несмотря на то, что урок закончился только на четверть?
К сожалению, дроби — это одно из самых важных понятий, которое будут изучать ваши ученики. Это основополагающая концепция, которая будет использоваться даже в самых сложных математических концепциях. Кроме того, вы не сможете перейти к другим частям учебного плана, пока ваши ученики не получат базовое представление о том, как работают дроби.
Это основополагающая концепция, которая будет использоваться даже в самых сложных математических концепциях. Кроме того, вы не сможете перейти к другим частям учебного плана, пока ваши ученики не получат базовое представление о том, как работают дроби.
Пришло время пересмотреть планы уроков, чтобы сделать дроби более увлекательными. Вот как вы можете привлечь своих учеников, помогая им запоминать информацию в течение года.
1. Попросите учащихся решить вопросы о дробях
Это может быть разминка или способ применения концепции дробей для решения задач. Рейган Танстолл создал рабочий лист дробей, в котором учащиеся пишут свои имена, а затем составляют дроби на основе серии заданных вопросов. Например:
- Доля заглавных букв.
- Дробь для количества строчных букв Is.
- Доля количества высоких букв.
Ученица по имени Ники будет иметь 1/5 заглавных букв, 2/5 строчных букв Is и 2/5 высоких букв. Чтобы сделать это более продвинутым, попросите учащихся повторить это упражнение со своим отчеством и фамилией.
Чтобы сделать это более продвинутым, попросите учащихся повторить это упражнение со своим отчеством и фамилией.
2. Играйте в «Войну фракций»
Война — это базовая игра, в которую учащиеся играют с картами. Каждый ученик переворачивает карточку, и выигрывает тот, у кого выше. Цель состоит в том, чтобы собрать все карты, чтобы закончить игру. Та же концепция используется в войне фракций. Каждый учащийся переворачивает две карточки, чтобы составить дробь. Учащиеся определяют, какая дробь больше, и большая дробь берет все четыре карты.
Например:
- Один ученик переворачивает семерку в числителе и восьмерку в знаменателе.
- Другой ученик переворачивает тройку в числителе и четверку в знаменателе.
- 7/8 — более крупная дробь, чем 3/4 (которую также можно записать как 6/8), поэтому первый ученик выигрывает раздачу.
Вы даже можете провести турнир в своем классе, чтобы короновать короля или королеву войны фракций.
3. Предложите учащимся сыграть в лотерею Fraction Bingo
В то время как Fraction War — это игра, в которую учащиеся могут играть самостоятельно, Fraction Bingo предназначена для всего класса. Вы можете определить, насколько сложной является эта игра, в зависимости от уровня ваших учеников. На самом базовом уровне вы будете называть дробь, и учащиеся должны будут определить ее на своих досках (когда они услышат две трети, они должны понять, что это похоже на 2/3).
Тем не менее, вы можете сделать эту игру более сложной, поскольку ученики изучают разные понятия. Вы можете назвать наименьшую возможную дробь и попросить учеников найти соответствующую дробь на своих карточках (когда вы называете 1/2, один ученик может отметить 25/50, а другой — 33/66). Вы также можете вызывать задачи, в которых учащиеся добавляют и вычитают формулы, чтобы отметить свои карточки. Это игра, в которую вы можете играть несколько раз, пока ваши ученики изучают новые концепции фракций.
4.
 Формы бумажных тарелок с дробями
Формы бумажных тарелок с дробямиЭто занятие по изучению дробей требует от вас немного искусства и ремесла. Соберите несколько бумажных тарелок и раскрасьте их в разные цвета, затем разрежьте на разные фракции и подпишите. Например, вы можете разрезать бумажную тарелку на четыре части и пометить каждую часть как «одна четверть».
Отсюда раздайте ученикам разные кусочки бумажных тарелок и попросите их образовать полные круги (одно целое) из имеющихся у них тарелок. Учащиеся могут использовать половинную тарелку, четверть тарелки и две восьмерки, чтобы завершить полный круг. Вы можете смешивать кусочки в каждом раунде, поэтому учащиеся должны работать вместе в разных группах, чтобы сделать свои тарелки. Ничего страшного, если остались кусочки или некоторые группы не могут составить целые тарелки с данными дробями.
5. Добавьте еду в смесь
Ваши ученики оживятся, если вы принесете в класс угощения или другие вкусности. Это веселое занятие, если вы преподаете дроби в преддверии Хэллоуина, когда вы можете устроить вечеринку с пиццей или принести сладости своим ученикам. Подчеркните, как разные дроби означают, что учащиеся получают разное количество еды. Один ученик не может съесть целую пиццу, но трудно разделить одну пиццу на 30 учеников.
Подчеркните, как разные дроби означают, что учащиеся получают разное количество еды. Один ученик не может съесть целую пиццу, но трудно разделить одну пиццу на 30 учеников.
Вы также можете выполнить упражнение, в котором учащиеся «шутят или лечат» с дробями. Ученик случайным образом вытягивает из мешка дробь, которая соответствует количеству конфет, которые он получил. Если бы каждый учащийся потенциально мог получить 10 мармеладок, некоторые вытянули бы 8 мармеладок (4/5), а другие только одну (1/10). Вы можете дать своим ученикам, которые получили только несколько дополнительных конфет в конце урока, чтобы они не чувствовали себя обделенными.
6. Создайте «Дробь дня» Вопрос
Как только ваши учащиеся получат базовое представление о дробях, вы можете закрепить эту концепцию в течение года. Рассмотрите возможность создания вопроса «доля дня», когда учащиеся используют числа для ответа на вопрос. Каждый вопрос начинается с «какая дробь…», и вы можете либо потребовать от учащихся написать наименьший общий знаменатель, либо создать уникальную дробь из своих сверстников. Вот несколько примеров:
Вот несколько примеров:
- Какая часть учащихся носит шорты?
- … сегодня в красной рубашке?
- … у него голубые глаза?
- …есть младший брат?
Если у вас 25 учеников и у 15 из них есть младшие братья и сестры, то у 3/5 ваших учеников есть братья и сестры. Вы также можете сделать это более продвинутым по мере того, как ваши ученики учатся. Попросите свой класс найти долю учеников, которые носят брюки, за вычетом доли учеников, которые носят платья (или умножьте и разделите их).
7. Найдите своего партнера по фракции
Это может быть занятие, которое вы превратите в игру для обучения дробям, или это может быть еще один инструмент, который поможет вам закрепить концепцию у ваших учеников. Случайным образом раздайте ученикам карточки лицевой стороной вниз, а затем попросите их перевернуть их и найти своих партнеров по фракции. Вы можете попросить учащихся сформировать пары (учащиеся 2/4 и 1/2 могут объединиться) или небольшие группы, чтобы составить целое (1/3, 4/6 и 9/9).
В качестве отдельного занятия продолжайте собирать карточки и формировать или разбивать группы в течение урока. В качестве долгосрочного задания используйте этот метод для случайного распределения учащихся по парам и групповой работе.
Обучение дробям может быть забавным
Обучение дробям является неотъемлемой частью ваших уроков математики. В конечном итоге учащиеся будут складывать, вычитать, умножать и делить эти числа. Они будут использовать дроби в алгебре, геометрии и даже в исчислении. Эти занятия могут помочь вам впервые представить дроби своим ученикам или они могут ежедневно закреплять концепции, чтобы ваши ученики запоминали обсуждаемый материал и знали, как использовать его на своих уроках.
22 веселых и бесплатных дробных игр и занятий для детей
Изучение дробей может быть сложной задачей. Вот почему так важно иметь под рукой широкий спектр занятий, которые помогут детям усвоить эту сложную концепцию. Эти дробные игры — интересный способ попрактиковаться в классе или дома.
1. Рассортируйте стикеры
Разделите стикеры на секции, а затем попросите детей рассортировать их по якорным таблицам. Мы особенно любим использовать забавные формы, такие как сердца или звезды!
Подробнее: Smitten With First
2. Соединяйте дроби, чтобы учиться и выигрывать
Переделайте набор Connect Four, чтобы играть в дробные игры! Цель состоит в том, чтобы соответствовать не только вашим цветам, но и самим фракциям. Например, вам нужно четыре четверти подряд, но только три четверти, так что здесь тоже задействована стратегия.
Подробнее: Нет времени на карточки
3. Изучите дробь дня
Дроби — это одно из тех математических понятий, которые мы используем в повседневной жизни. Сделайте их частью повседневной практики, задавая новый вопрос «Часть дня» каждое утро.
Подробнее: Комната Рунде
4. Получите удовольствие от дробных ложек
Если вы уже играли в Spoons раньше, вы знаете, как это сделать. Сопоставьте четыре одинаковых карты (на этот раз с помощью бесплатных печатных карточек дробей, которые можно найти по ссылке ниже), и вы получите ложку — и все остальные тоже! Проигравший берет одну букву слова ЛОЖКА, и игра продолжается.
Сопоставьте четыре одинаковых карты (на этот раз с помощью бесплатных печатных карточек дробей, которые можно найти по ссылке ниже), и вы получите ложку — и все остальные тоже! Проигравший берет одну букву слова ЛОЖКА, и игра продолжается.
Подробнее: Игры 4 Выигрыши
5. Расположите их по порядку
Сравнение дробей, безусловно, непростая задача. Эта простая бесплатная игра для печати предлагает детям составить ряд из четырех дробей в порядке от наименьшего к наибольшему. Они могут участвовать в гонках, чтобы увидеть, кто финиширует первым, или просто бросить вызов самим себе, чтобы получить правильный ответ.
Узнайте больше: Приведи их в порядок/Math Geek Mama
6. Сразитесь в войне фракций
Вероятно, ваши дети уже знают, как играть в «Войну с картами». Эта версия просто добавляет фракционный аспект. Учащиеся раздают две карточки: числитель и знаменатель, а затем определяют, чья дробь наибольшая. Победитель сохраняет все четыре карты, и игра продолжается до тех пор, пока карты не закончатся. Вы также можете играть, используя эти бесплатные распечатанные карты фракций.
Вы также можете играть, используя эти бесплатные распечатанные карты фракций.
7. Лапша круглая с дробями
Эти математические манипуляции с лапшой для пула очень легко сделать, и вы сможете использовать их во всех играх с дробями. Узнайте, как их сделать, и почерпните идеи для их использования здесь.
8. Играйте в увлекательные игры с дробями LEGO
Визуализация того, что представляют собой дроби, проще (и намного веселее), если вы используете кубики LEGO! Выкладывайте их рядом или стройте башни. Независимо от того, как вы играете, это безошибочный хит.
Узнайте больше: Мама JDaniel4
9. Попробуйте составить дроби из бумажных тарелок
Такой веселый и красочный способ играть с дробями и эквивалентами! Получите полную инструкцию здесь.
10. Буги-вуги с газетными дробями
Включите музыку погромче! Начните с полной бумаги в качестве танцевальной площадки для каждого ученика, а затем сложите ее до половины. Продолжайте складывать бумагу, превращая ее в танцплощадку все меньше и меньше, и наблюдайте, как дети проявляют творческий подход, пытаясь удержаться на бумаге.
Продолжайте складывать бумагу, превращая ее в танцплощадку все меньше и меньше, и наблюдайте, как дети проявляют творческий подход, пытаясь удержаться на бумаге.
Подробнее: Музыкальный класс миссис Кинг
11. Двигайтесь по Fraction Avenue
Это такое веселое занятие! Возьмите бесплатную распечатанную уличную сцену по ссылке. Затем попросите детей следовать указаниям, чтобы добавить детали. Например, в 2/8 домов на улице есть собаки. Попросите детей уменьшить дробь, а затем нарисуйте правильное количество щенков.
Подробнее: Образовательное путешествие Эшли
12. Перейти в классики дроби
Это классики — с игрой дроби! Нарисуйте доску для игры в классики на игровой площадке (или обведите ее скотчем на полу в классе или коридоре). Обозначьте квадраты дробями, а не целыми числами. Дети бросают маркер и прыгают туда, куда он приземлился, а затем называют эквивалентные дроби для этого квадрата.
Узнайте больше: Захват идей в классе
13.
 Превратите свое имя в дроби
Превратите свое имя в дробиКто знал, что внутри вашего имени скрывается так много дробей? Задайте эти вопросы учащимся и попросите их также найти свои собственные дроби.
Узнайте больше: Tunstall’s Teaching Tidbits
14. Устройте небольшой пикник
Предоставьте различные изображения еды, вырезанные из журналов или распечатанные из Интернета. Студенты планируют пикник и выбирают еду, которую хотят взять с собой. С помощью линейки и ножниц вырежьте кусочки еды, которую они выбрали, и приклейте их на бумажную тарелку. Наконец, пометьте каждый элемент названием фракции. Приятного аппетита!
Подробнее: Fraction Picnic/E for Explore
15. Поиграйте с фракциями
Дети получают удовольствие от вращающихся вещей, поэтому им понравятся эти бесплатные распечатанные дроби. Поскольку спиннеры — это всего лишь карандаши и скрепки, каждый ребенок может иметь свой собственный, когда он отрабатывает свои навыки дроби. Получите весь бесплатный набор игр здесь.
Получите весь бесплатный набор игр здесь.
16. Раскрасьте свой путь к дробному бинго
Когда вы играете в дробное бинго, вам придется учиться и применять стратегию. Дети раскрашивают части кругов, чтобы получить пять в ряд, основываясь на дробях, которые называет учитель. Конечно, самое приятное — это кричать «БИНГО!»
Подробнее: School Time Snippets
17. Сокращайте дроби и бегите к финишу
Дети тянут карточку (карточки и доска для печати доступны по ссылке ниже) и уменьшают показанную дробь. Затем они перемещаются по доске к следующей совпадающей клетке. Побеждает первый до конца!
Подробнее: 123Homeschool4Me
18. Развивайте свои творческие способности с помощью дробей Pictionary
Можете ли вы нарисовать дробь, не используя цифры? Это задача этой игры фракций. Дети могут рисовать отдельные объекты, разделенные на части, или быть более творческими. Например, они могут нарисовать три яблока и два апельсина, чтобы представить три пятых.
Узнайте больше: Fraction Pictionary/E is for Explore
19. Попадите в фиаско дроби
Как только они усвоят правила, дети будут складывать дроби и проверять работу друг друга в этой бесплатной игре для печати. Все инструкции и игровое поле вы найдете по ссылке ниже.
Узнайте больше: Учитесь с математическими играми
20. Считайте с помощью дробей домино
Доминошки похожи на готовые дроби! Умножьте (или сложите, вычтите или разделите) их и уменьшите результаты. Превратите это в гонку, чтобы увидеть, кто сможет финишировать — правильно — первым.
Узнать больше: Неустанно весело, обманчиво познавательно
21. Играйте с кубиками узоров
Если у вас уже есть кубики узоров, используйте их в некоторых играх с дробями. В этом дети крутятся, чтобы узнать, сколько блоков они могут добавить на свою доску, чтобы первыми построить шесть полных фигур.
Узнайте больше: Pattern Block Fractions/Math Geek Mama
22.
 Встряхните его числовыми связями
Встряхните его числовыми связямиВсе, что вам нужно, это пластиковый стаканчик и двусторонние жетоны. Дети встряхивают чашку и высыпают фишки на стол, затем подсчитывают, сколько фишек каждого цвета выпало лицевой стороной вверх. Например, если выпало 13 жетонов, шесть красных и семь синих выпали лицом вверх. Шесть и семь являются частями тринадцатого (целого). Попросите учащихся написать числовое значение и дроби для каждого цвета.
Узнайте больше: Дроби с числовыми связями/E для Исследовать
Какие ваши любимые игры с дробями для детей? Приходите и поделитесь в нашей группе WeAreTeachers HELPLINE на Facebook.
Ищете другие математические игры? Попробуйте этот обзор математических онлайн-игр для каждого уровня.
Как умножать дроби с помощью простых шагов и 7 увлекательных заданий
Вы уже преуспели в обучении умножению, но теперь предстоит, казалось бы, сложная задача — научить их умножать дроби.
Глубокие вдохи.
Как учителя, так и ученики могут утверждать, что эта концепция более сложна, чем переход от вычитания и сложения к умножению.
К счастью, существуют стратегии, которые значительно облегчат понимание процесса умножения дробей, и мы собрали их для вас в четком руководстве.
Простой способ умножить фракции
Существует три простых шага, которые должны следовать вашим ученикам, когда мы должны следовать, как умножить фракции:
- Умножьте числители ( Верхние числа )
- Умножение денознаваторы () нижние номера )
- При необходимости упростите или уменьшите дробь
И прежде чем ваши увлеченные ученики спросят, ответ будет утвердительным — в отличие от сложения дробей, вы можете умножить две дроби с различными знаменателями.
Давайте рассмотрим пример вместе!
Пример умножения дробей
Понимание трех типов дробей и способов их умножения
Прежде чем мы углубимся в эту концепцию и объясним умножение дробей, мы подумали, что имеет смысл понять различные типа дроби.
Хорошо бы начать с простой терминологии, касающейся того, как состоит дробь:
- Числитель — верхнее число, которое указывает, сколько частей (целого) у вас есть.
- Знаменатель — нижнее число, которое относится к общему количеству частей, составляющих целое.
Авторы и права: Бретт Берри
Теперь мы рассмотрим три типа дробей и способы их умножения.
1. Умножение правильных дробей
У правильной дроби числитель на меньше знаменателя на . Это самое простое место для начала умножения дробей. Пример, который мы использовали выше, идеально подходит для умножения этого типа дроби.
Например: ½, ⅔, ¾, ⅘, ⅚
2. Умножение неправильных дробей
Неправильная дробь похожа по структуре, но имеет числитель больше знаменателя на .
Примечание : Когда числитель равен знаменателю, это считается «неправильным», потому что вы можете преобразовать его в целое число. То же правило применяется к неправильным дробям, таким как ²⁶⁄₁₃, которые при уменьшении становятся целыми (т. Е. Двойками).
То же правило применяется к неправильным дробям, таким как ²⁶⁄₁₃, которые при уменьшении становятся целыми (т. Е. Двойками).
Например: ³⁄₂, ⁵⁄₃, ⁷⁄₆, ¹¹⁄₁₀, ⁸⁄₈
Credit: Miranda Weenusk
Неправильные дроби умножаются точно так же. Однако иногда учащиеся могут столкнуться с неправильными дробями.
Возьмите эту проблему в качестве примера:
Решение : ⁵⁄₃ × ⁷⁄₆ Умноженные числиторы : 5 × 7 = 35 Умноженные знаменатели : 3 × 6 = 18 Новая фракция : ¼
: 3 × 6 = 18Если учащиеся знакомы со смешанными дробями, они могут заменить неправильную дробь на смешанную. В этом случае это смешанное число будет 1 ¹⁷⁄₁₈.
Но вы можете узнать больше о смешанных числах ниже!
3. Умножение смешанных дробей
Перед тем, как научить учащихся умножать дроби со смешанными числами, они должны знать три шага:
- Преобразование любых смешанных дробей в неправильные
- Умножение неправильных дробей
- Преобразование конечного произведения обратно в смешанное число
Чтобы выполнить первый шаг, научите своих учеников составлять смешанное число «БЕЗУМНО» .
Авторы и права: Fabulous Finch Facts
Помните: смешанное число состоит из целого числа и правильной дроби. Чтобы выполнить первый шаг и перевести смешанную дробь в неправильную, нужно:
- Найдите новый числитель — Умножьте целое число на знаменатель, затем добавьте к нему исходный числитель.
- Сохранить тот же знаменатель — Знаменатель не изменить.
Отсюда и полезная аббревиатура:
M умножить A dd D знаменатель
Шаг второй: умножьте неправильные дроби, как мы показали в этом разделе.
Шаг третий, превратите эту неправильную дробь обратно в смешанное число. Вот небольшой стишок, который поможет вашим ученикам запомнить, как это делать:
С неправильной дробью деление — это действие!
Предоставлено: Heather’s Show and Tell
Давайте используем пример, изображенный ранее: ¹⁶⁄₅.
Если деление — это действие, то нужно разделить числитель (16) на знаменатель (5) и посмотреть, есть ли остаток.
Пять входит в число 16 три раза равномерно , всего 15. Это означает, что целая часть смешанного числа будет три .
Но он не разделился идеально, что вы можете видеть по остатку один . Итак, дробная часть смешанного числа — это остаток от знаменателя исходной дроби (⅕).
В виде смешанной дроби это выглядит так: 3 ⅕ .
Чтобы получить более наглядное представление о том, как умножать смешанные числа, посмотрите этот четырехминутный видеоролик от Академии Хана:
И это то, что вам нужно знать при умножении дробей и смешанных чисел.
Как насчет умножения дробей на целые числа?
Кредит: Эрика Наджера
Умножение целых чисел и дробей может поставить ваших учеников в тупик. Почему? Потому что кажется, что дробь одна, а не две.
Но, изучая, как умножать дроби на целые числа, учащиеся могут переписать их как дроби. Вместо 4, например, превратите его в дробь ⁴⁄₁.
Вместо 4, например, превратите его в дробь ⁴⁄₁.
Теперь умножать стало проще и понятнее. Например, они могут переписать 2 × ⁵⁄₁₃:
Решение : 2 × ⁵⁄₁₃ Перепишите целое число в виде фракции : ²⁄₁ × ⁵– Умноженные числиторы : 2 × 5 = 10 Умноженные знаменатели : 1 × 13 Новая фракция. : ¹⁰⁄₁₃
Примечание : Если учащиеся затрудняются с целыми числами, объясните, что они могут думать о целом числе как о верхнем числе, а нижнее число всегда равно единице.
Модели площадей для умножения дробей
Идеально подходит для визуалов в вашем классе, модель площади эффективно иллюстрирует, как одна дробь умножается на другую.
Как видно из приведенного ниже рисунка, создать модель площади при умножении дробей очень просто:
- Нарисуйте умножаемые дроби в отдельных полях, используя для каждой из них свой цвет
- Объедините рисунки в одно поле, используя новый цвет для перекрывающихся частей
- Чтобы написать продукт, задайте себе два вопроса:
Сколько коробок имеют оба цвета? Это будет ваш числитель
Сколько всего коробок? Это будет ваш знаменатель
Кредит: миссис Коггинс
Броское напоминание
О! А если ваши ученики когда-нибудь забудут шаги, просто напомните им спеть эту песенку:
Умножение дробей? Это не большая проблема. Делайте верхние разы верхние над нижним временами нижние. И прежде чем попрощаться, не забудьте упростить!
Делайте верхние разы верхние над нижним временами нижние. И прежде чем попрощаться, не забудьте упростить!
2 Основные ошибки, которые учащиеся допускают при умножении дробей
Хотя некоторые ученики быстро усвоят ваши уроки по умножению дробей, другие могут испытывать трудности с этими новыми понятиями.
Чем раньше учителя обнаружат эти заблуждения, тем быстрее ученики смогут извлечь уроки из своих ошибок и исправить их.
В соответствии с практическим руководством Института педагогических наук What Works Clearinghouse «Разработка эффективных дробных инструкций для детского сада до 8-го класса», это одни из наиболее распространенных заблуждений в отношении обучения умножению дробей.
1. Верить, что целые числа имеют тот же знаменатель, что и дробь в задаче
Группа из восьми экспертов гида признала, что это заблуждение может привести к тому, что учащиеся берут задачу типа 4 – ⅜ и переписывают ее как ⁴⁄₈ – ⅜ для неправильного ответа ⅛.
При представлении смешанного числа учащиеся с таким неверным представлением могут добавить целое число к числителю, как в ³¹⁄₃ × ⁶⁄₇ = (³⁄₃ + ⅓) × ⁶⁄₇ = ⁴⁄₃ × ⁶ ⁄₇ = ²⁴⁄₂₁.
Помощь учащимся в понимании взаимосвязи между смешанными числами и неправильными дробями, а также в том, как перевести одно в другое, имеет решающее значение для работы с дробями.
Как помочь своим ученикам
Не поддавайтесь искушению взорвать фундаментальные уроки.
Потратьте время, необходимое вашим учащимся, чтобы помочь им понять взаимосвязь между неправильными дробями и смешанными числами, а также способы их преобразования из одних в другие.
Кредит: Once Upon a Creative Classroom
2. Оставить знаменатель без изменений
Учащиеся могут совершить ошибку, забыв умножить равные знаменатели. Вероятно, это связано с тем, что вам не нужно касаться равных знаменателей при сложении дробей.
Например, они могут увидеть ⅔ × ⅓ и неправильно ответить ⅔ вместо ²⁄₉.
Как помочь учащимся
В практическом руководстве эксперты-эксперты предлагают «объяснить концептуальную основу умножения дробей с помощью единичных дробей (например, ½ × ½ = половина половины = ¼)».
В частности, учителя могут показать, что задача ½ × ½ на самом деле спрашивает, какова ½ от ½, что подразумевает, что произведение должно быть меньше любой умножаемой дроби.
Вербализация этого заблуждения полезна, но визуализация особенно эффективна. Войдите в стену фракции !
Дробные стены — отличный способ помочь учащимся увидеть, как в данном случае выглядит абстрактная половина одной половины (т. е. одна четверть).
Теперь вы знаете о болевых точках многих студентов, изучающих умножение дробей, что дальше? Давайте рассмотрим, как закрепить уроки дробей и почему рабочие листы могут быть не лучшей стратегией.
Помогают ли рабочие листы умножать дроби?
Доктор Стивен Камарата, специалист по детскому развитию и порокам развития, считает, что природное любопытство детей рушится.
В эссе для Psychology Today он выразил недовольство предположением, что заполнение рабочих листов напрямую связано с улучшением обучения.
Но данные о баллах успеваемости в США по сравнению с остальным миром говорят об обратном. По иронии судьбы, по мере того, как все больше и больше рабочих листов выдвигают в более ранние классы и все больше механических и скучных домашних заданий навязывают развивающимся умам, успеваемость учащихся в США продолжает снижаться.
Источник: Источник: Исследователь данных NAEP, Национальный центр статистики образования
В отчете Центра исследований Пью отмечается снижение и без того удручающих показателей успеваемости в США. Д-р Камарата подчеркнул:
В 2011 году только 34% четвероклассников и 27% восьмиклассников были оценены как хорошо владеющие математикой, а в 2015 году этот показатель снизился до 33% среди четвероклассников и 25% среди восьмиклассников данные доступны). Невозможно оценить эти результаты положительно: в настоящее время 9 0017 более двух третей четвероклассников и трое из четырех восьмиклассников не владеют математикой
. Это 38-е место в мире.
Это 38-е место в мире.Означает ли это, что школы должны отказаться от рабочих листов? Не обязательно.
Корреляция не является причинно-следственной связью. На самом деле, многие учителя и ученики добились успеха с рабочими листами.
Тем не менее, преподаватели должны понимать, что образование быстро меняется, начиная с рабочих листов и заканчивая классными технологиями.
Итак, вот несколько творческих способов научить умножению дробей — без рабочих листов!
7 Увлекательные занятия для обучения учащихся умножению дробей
1. Prodigy
Prodigy — это математическая онлайн-игра, адаптированная к учебной программе, которая предлагает материалы по всем основным математическим темам с 1 по 8 класс.
Наряду со многими другими навыками и стандартами Prodigy может помочь учащимся научиться:
- Умножать две дроби
- Умножать дробь на целое число
- Умножать две дроби с помощью текстовых задач
- Умножение целого числа на недостающую дробь
И многое другое!
Играя в Prodigy, вы можете отправить своих учеников в увлекательное и познавательное путешествие, вдохновленное фэнтези. Кроме того, вы получите данные об их успехах, чтобы использовать их в своих повседневных стратегиях обучения.
Кроме того, вы получите данные об их успехах, чтобы использовать их в своих повседневных стратегиях обучения.
Готовы начать?
Зарегистрируйтесь прямо сейчас!2. Переверните дроби
Кредит: MathFileFolderGames
Для этого задания разделите учащихся на группы по четыре человека. Затем они делятся на команды по два человека, одна из которых является игроком А, а другая — игроком Б.
Дайте каждой группе по колоде перетасованных карт (тузы = 1, валеты = 10, дамы = 11 и короли = 12).
Как показано на рисунке выше, каждый учащийся вытягивает карту числителя (над карандашом) и карту знаменателя (под карандашом).
Оба игрока А перепишут и умножат дроби на бумаге, а затем, если возможно, упростят произведение. Как только они ответят, игрок Б сделает то же самое.
В зависимости от вашего расписания вы можете назначить всю колоду или дать учащимся таймер, чтобы заполнить столько, сколько они могут.
Предложите учащимся сдать листы для ответов после выполнения упражнения, чтобы вы могли их отметить, или вместе ответьте на 10+ вопросов всем классом.
Примечание : Вы также можете назвать эту игру «Slam-it дроби», заменив карты и карандаши домино.
3. Умножение дробей БИНГО
Кредит: jimmiehomeschoolmom
Каждый ученик получает карточку бинго с заполненными дробями вместе с небольшими листами бумаги (или «фишками бинго»), на которых находятся соответствующие задачи на умножение дробей.
Когда вы говорите «ВПЕРЕД», они могут начать решать каждую задачу одну за другой, кладя фишку поверх правильной дроби.
Вам решать, хотите ли вы, чтобы они завершили линию или всю карту бинго. Вы также можете выбрать, будут ли упрощены ответы на карты бинго.
Для простоты вы можете дать всем одну и ту же карточку бинго с одинаковыми вопросами. Таким образом, вы сможете потом пройтись по каждой проблеме и вместе решить, как их решить.
Примечание . Вы можете использовать этот и последующие примеры в качестве формативного оценивания для оценки знаний учащихся и выявления неправильных представлений на раннем этапе
4.
 Словесные задачи
Словесные задачиСловесные задачи — прекрасный способ сделать уроки математики актуальными для ваших учеников ‘ жизни.
Умение умножать дроби может показаться им чуждым, но простая история может полностью изменить их представление не только о дробях, но и о математике в целом.
Вот пример словесной задачи:
У вас есть ½ пакета чипсов в шкафу, но вы съели ½ после ужина. Сколько всего пакета ты съел? (Не сокращайте свой ответ до минимума.)
Конечно, это простой пример. Но секунду назад эта дробь была просто числом над и под короткой чертой. Однако теперь эта «повседневная» проблема со словами сделала умножение дробей применимым к реальной жизни.
5. Война фракций
Кредит: Шерри Фишер
Это занятие для двух человек взято из карточной игры «Война».
Примечание : Многие учителя отказываются от быстрого решения задач, потому что это не обязательно демонстрирует понимание учеником. У вас также могут быть дети в вашем классе, которые беспокоятся из-за необходимости быстро решать математику и поэтому не успевают. Поэтому лучше всего оценить свой класс, прежде чем играть в эту версию.
У вас также могут быть дети в вашем классе, которые беспокоятся из-за необходимости быстро решать математику и поэтому не успевают. Поэтому лучше всего оценить свой класс, прежде чем играть в эту версию.
У каждого ученика, сидящего рядом, будет половина колоды карт фракций (которую вы можете скачать здесь).
Положив стопку карт лицевой стороной вниз, каждый учащийся вытянет карту одновременно .
Первый учащийся, правильно умноживший две дроби, добавит эти карты в свою колоду.
Учащийся выигрывает, если у него в руке оказывается вся колода карт фракций или у него больше карт по истечении, например, 20 минут.
Более того, быстрое мышление на месте этого дробного задания может помочь улучшить навыки ментальной математики ваших учеников.
Кроме того, вы можете запустить версию этой игры, позволяющую всем играть против вас.
Кто не любит шанс перехитрить своего учителя!?
Разделите свой класс на пять групп.
Вы попадете в первую группу и ответите на один вопрос, прежде чем перейти во вторую группу и так далее. Помните: цель этой версии не в том, чтобы ответить перед вашими учениками, а в том, чтобы помочь улучшить их математические способности в уме.
Это позволяет учащимся отвечать коллективно, чтобы не выделять детей, у которых могут возникнуть проблемы с ментальной арифметикой.
6. Пищевые фракции
Дети любят поесть – это не секрет! Так почему бы не включить его в свой план урока?
Учитель в твиттере выше заставил своих детей попрактиковаться в умножении дробей путем преобразования рецептов вкусных блюд.
Каждый ученик может выбрать свою любимую еду и увеличить количество ингредиентов, чтобы накормить весь класс.
Поощрение тоже может помочь! Например, после того, как все переделают свою любимую еду, выберите безопасную закуску, которая понравится классу.
Откройте исходный рецепт. Теперь пусть ваши ученики поработают вместе, чтобы умножить ингредиенты, и, если они сделают это правильно, весь класс получит домашнюю (или купленную в магазине) выпечку!
7.
 Вымпел с умноженной дробью
Вымпел с умноженной дробьюКредит: Scaffolded Math
Вырежьте листы бумаги в форме ленты или треугольника для каждого учащегося. Вверху напишите «Я могу умножать…»
Ниже вы включите:
- Модель площади, иллюстрирующая дроби, которые они умножают
- Сама задача на умножение (с местом для демонстрации своей работы)
- Место внизу с надписью «Мой продукт сводится к…»
После того, как каждый учащийся заполнит и украсит свой вымпел на умножение дроби, клей или лента их в нитку!
Эта активная учебная деятельность не только поможет усвоить, как умножать дроби, но и придаст уверенности вашим ученикам. Это их работа на стене, проблема они разгадан, а каждый его видит.
Хотите научить своих учеников умножать дроби прямо сейчас?
Надеемся!
Умножение дробей может оказаться непростой задачей — выучить и научить.
Надеемся, что подробное описание различных типов дробей, способов их умножения и того, как сделать их изучение увлекательным, поможет вам и вашим ученикам обогатить опыт преподавания и обучения.

 После этого если в результате получаем неправильную дробь переводим её в смешанную.
После этого если в результате получаем неправильную дробь переводим её в смешанную.







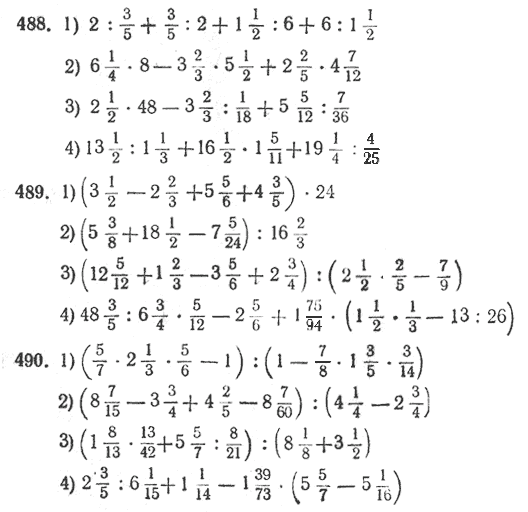
 Далее перемножаем полученное и получаем НОК.
Далее перемножаем полученное и получаем НОК.

 Буквенно это выглядит таком образом ab±cd=a·p±c·rs, где значения a, b≠0, c, d≠0, p≠0, r≠0, s≠0 являются действительными числами, а b·p=d·r=s. Когда p=d и r=b, тогда ab±cd=a·d±c·db·d.
Буквенно это выглядит таком образом ab±cd=a·p±c·rs, где значения a, b≠0, c, d≠0, p≠0, r≠0, s≠0 являются действительными числами, а b·p=d·r=s. Когда p=d и r=b, тогда ab±cd=a·d±c·db·d.