Как найти угол: Калькулятор расчета углов треугольника зная длину сторон

Как найти углы прямоугольного треугольника

1. Главная
2. /
3. Математика
4. /
5. Геометрия
6. /
7. Как найти углы прямоугольного треугольника

Чтобы найти углы прямоугольного треугольника воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Чтобы найти острые углы прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

• для угла α:
• угол β
• длины катетов a и b
• длину гипотенузы (с) и длину одного из катетов
• для угла β:
• угол α
• длины катетов a и b
• длину гипотенузы (с) и длину одного из катетов

Введите их в соответствующие поля и получите результат.

Найти угол α зная угол β и наоборот

Если ∠β = , то ∠α =

Если ∠α = , то ∠β =

Формула

α = 90° — β

β = 90° — α

Найти углы прямоугольного треугольника зная катеты

Катет a =
Катет b =

∠α =

∠β =

Чему равны острые углы (α и β) прямоугольного треугольника если известны оба катета (a и b)?

Формулы

tg(α) = ^a/_b

tg(β) = ^b/_a

или так:

α = arctg(^a/_b)

β = arctg(^b/_a)

Пример

Для примера определим чему равны углы α и β в градусах если катет a = 5 см, а катет b = 2 см:

∠α = arctg(5/2) = arctg(2. 5) ≈ 68.2°

∠β = arctg(2/5) = arctg(0.4) ≈ 21.8°

Найти углы прямоугольного треугольника по катету и гипотенузе

Гипотенуза c =
Катет ab =

∠α =

∠β =

Чему равны острые углы (α и β) прямоугольного треугольника если известны гипотенуза c и один из катетов (a или b)?

Формулы

sin(α) = ^a/_c

sin(β) = ^b/_c

cos(α) = ^b/_c

cos(β) = ^a/_c

или так:

α = arcsin(^a/_c) = arccos(^b/_c)

β = arcsin(^b/_c) = arccos(^a/_c)

Пример

Для примера определим чему равны углы α и β в градусах если гипотенуза c = 6 см, а катет b = 3 см:

∠α = arccos(3/6) = arccos(0.5) = 60°

∠β = arcsin(3/6) = arcsin(0.5) = 30°

См. также

Как найти стороны прямоугольного треугольника

Калькулятор площади прямоугольного треугольника

Калькулятор обратных тригонометрических функций (arcsin, arccos, arctg, arcctg)

Калькулятор тригонометрических функций (sin, cos, tg, ctg)

Углы в пространстве — Умскул Учебник

На этой странице вы узнаете

• Как мы сталкиваемся с двугранными углами, когда читаем книгу?
• Где в комнате можно найти перпендикулярные плоскости?
• Как с помощью линейки и листа воспроизвести в жизни теорему о трех перпендикулярах?

Стереометрия — это не просто раздел математики, который нужно долго и нудно учить. На самом деле стереометрия описывает всю нашу жизнь. Стало интересно? Давайте разбираться. 

Углы между плоскостями

Мы точно знаем, что угол между стеной и полом равен 90°. Также, как и угол между стеной и потолком, или полом и любым предметом мебели. 

Но чему равен угол между двумя открытыми страницами тетради? Или угол между стеной и полуоткрытой дверью? Угол между перилами и плоскостью пола? Все эти углы достаточно легко найти. И ответы на все эти вопросы нам дает именно стереометрия. 

Начнем разбирать в углах между плоскостями с того, что введем понятие двугранного угла. 

Двугранный угол — это часть пространства, заключенная между двумя полуплоскостями, имеющими общую границу. 

Если мы откроем книгу не полностью и посмотрим на пространство между двумя страницами, это пространство и будет двугранным углом.

На рисунке: 
АВ — общая прямая для плоскостей, ее называют ребром двугранного угла;
a, b  — плоскости, которые образуют двугранный угол, они называются гранями двугранного угла.   

Как мы сталкиваемся с двугранными углами, когда читаем книгу? Если раскрыть книгу не полностью, то ее страницы будут образовывать двугранный угол, то есть часть пространства, заключенную между двумя страницами.

Заметим, что при пересечении двух плоскостей обычно образуется четыре двугранных угла. Нас интересует меньший из них.

Настало время ввести понятие угла между двумя плоскостями. Но для этого нам нужно провести перпендикуляры к ребру двугранного угла в каждой плоскости. Важно, чтобы перпендикуляры пересекались в одной точке.

Проведенные перпендикуляры образовали четыре угла. Меньший из них и будет называться углом между плоскостями.

Угол между плоскостями — это угол между перпендикулярами, проведенными к линии пересечения плоскостей. Перпендикуляры должны лежать в данных плоскостях. 

Обозначим нужный нам угол на рисунке как угол COD. Он и будет являться углом между данными плоскостями. 

Угол COD также будет называться линейным углом двугранного угла. 

Линейный угол двугранного угла показывает градусную меру двугранного угла. Поскольку двугранный угол — это часть пространства, то в этом пространстве можно провести множество линейных углов, которые будут равны между собой. 

Как и обычные углы, углы между плоскостями бывают трех видов:

• Острые, то есть меньше 90⁰
• Прямые, равные 90⁰
• Тупые, которые больше 90и меньше 180⁰

Как уже было сказано выше, за угол между плоскостями всегда принимается острый угол, образованный этими плоскостями.

А что будет, если между плоскостями получится прямой угол?

Такие плоскости называются перпендикулярными. 

Где в комнате можно найти перпендикулярные плоскости? Достаточно посмотреть на стены и пол, или стены и потолок. А еще на углы потолка — в них будет три перпендикулярные плоскости.

У перпендикулярных плоскостей есть одна очень интересная особенность: все углы, образованные ими, равны между собой и равняются 90° градусам. 

Чтобы найти угол между плоскостями, необходимо следовать следующему алгоритму. 

Алгоритм нахождения угла между плоскостями 1 шаг. Найти линию пересечения плоскостей. 2 шаг. Достроить к этой линии перпендикуляр в каждой плоскости.  3 шаг. Найти острый угол между построенными перпендикулярами.

Углы между прямой и плоскостью

Если нарисовать две прямые на листе бумаги, мы с легкостью можем измерить угол между ними с помощью транспортира. А если провести прямую к плоскости, как точно измерить угол между ними?

И в этом вопросе к нам снова на помощь приходит стереометрия. Но для начала рассмотрим, что такое угол между прямой и плоскостью.

Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость. 

Что такое проекция? Предположим, мы проткнем лист бумаги (плоскость) очень длинной иглой. 

А теперь сделаем этот рисунок ближе к чертежу. Пусть плоскость а пересекает прямая а в точке О. 

Начнем строить проекцию. Прежде чем разобраться, что такое проекция прямой на плоскость, найдем проекцию точки на плоскость. 

Возьмем на нашей прямой а точку А и опустим из нее перпендикуляр к плоскости а. Точка, в которой перпендикуляр пересечет плоскость, будет называться проекцией точки на плоскость. На рисунке обозначим ее как А₁. 

Проекция точки на плоскость — это основание перпендикуляра, опущенного из этой точки на плоскость. 

Теперь, если мы будем брать каждую точку на прямой и проектировать ее на плоскость а, то получим проекцию этой прямой на плоскость. Но поскольку на прямой бесконечное множество точек, достаточно соединить точки А₁ и О, получаем, что А₁О — проекция прямой а на плоскость а. 

Заметим, что если мы проведем из любой точки прямой проекцию к плоскости, то попадем на прямую А₁О. 

Проекция прямой а на плоскость — это прямая а₁, образованная проекциями всех точек прямой а на плоскость. 

Таким образом можно построить проекции не только прямой, но и любой фигуры.

Мы построили угол из определения. Тогда углом между прямой а и плоскость а будет угол А₁ОА. 

В этом случае мы также берем острый угол, образованный прямой и плоскостью. 

Алгоритм нахождения угла между прямой и плоскостью Шаг 1. Построить проекцию прямой на плоскость. Шаг 2. Найти угол между прямой и построенной проекцией.

Если прямая параллельна плоскости угол будет равен 0. 

Проекция прямой на плоскость будет этой же прямой, просто лежащей в плоскости.  

Когда прямая перпендикулярна плоскости, проекцией прямой на плоскость будет точка пересечения прямой и плоскости. Угол между прямой и плоскостью будет равен 90°.

Чуть подробнее остановимся на случае, когда прямая перпендикулярна плоскости. 

Прямая, перпендикулярная плоскости — прямая, которая перпендикулярна к каждой прямой, лежащей в этой плоскости. 

А что делать, если прямая будет перпендикулярна только одной прямой из плоскости? По определению обязательно, чтобы она была перпендикулярна всем прямым из плоскости. Как тогда проверить перпендикулярность?

Для этого существует признак перпендикулярности прямой и плоскости:

• Если прямая перпендикулярна к двум пересекающимся прямым в этой плоскости, то она будет перпендикулярна этой плоскости.  

Следовательно, если необходимо в задаче доказать перпендикулярность прямой и плоскости, достаточно доказать, что прямая будет перпендикулярна всего двум пересекающимся прямым в этой плоскости, а не всему множеству прямых, лежащий в данной плоскости.

Рассмотрим несколько интересных свойств, связанных с прямой, перпендикулярной к плоскости. 

Свойство 1. Через любую точку пространства можно провести единственную прямую, перпендикулярную плоскости. 

Попробуйте подставить уголок к стене из любой точки. Получится ли у вас сделать так, что из одной и той же точки уголок встанет перпендикулярно стене несколько раз? Нет. 

Свойство 2. Если две прямые перпендикулярны одной и той же плоскости, то такие прямые параллельны. 

Здесь тоже просто все доказать. Достаточно построить в плоскости прямую, которая пересечет две данные прямые и посмотреть на рисунок “сбоку”. Заметим, что соответственные углы равны, а значит, прямые параллельны.  

Подробнее про соответственные углы и параллельные прямые можно прочитать в статье “Основы планиметрии”. 

Свойство 3. Если к одной прямой перпендикулярны две плоскости, то такие плоскости параллельны. 

Тут такие же рассуждения, как и в предыдущем свойстве: достаточно построить прямые, принадлежащие плоскостям, и посмотреть на них “сбоку”. 

Свойство 4. Если через перпендикулярную к плоскости прямую проходит плоскость, то данные плоскости будут перпендикулярны. 

Это легко проверить, если найти любой двугранный угол между построенными плоскостями. 

Теорема о трех перпендикулярах

Разберем еще одну очень интересную теорему, связанную с проекциями прямой на плоскость. А именно мы рассмотрим теорему о трех перпендикулярах. 

Для начала попробуем понять ее на реальных предметах. 

Как с помощью линейки и листа воспроизвести в жизни теорему о трех перпендикулярах?

Возьмем уголок и зафиксируем его строго вертикально на листе.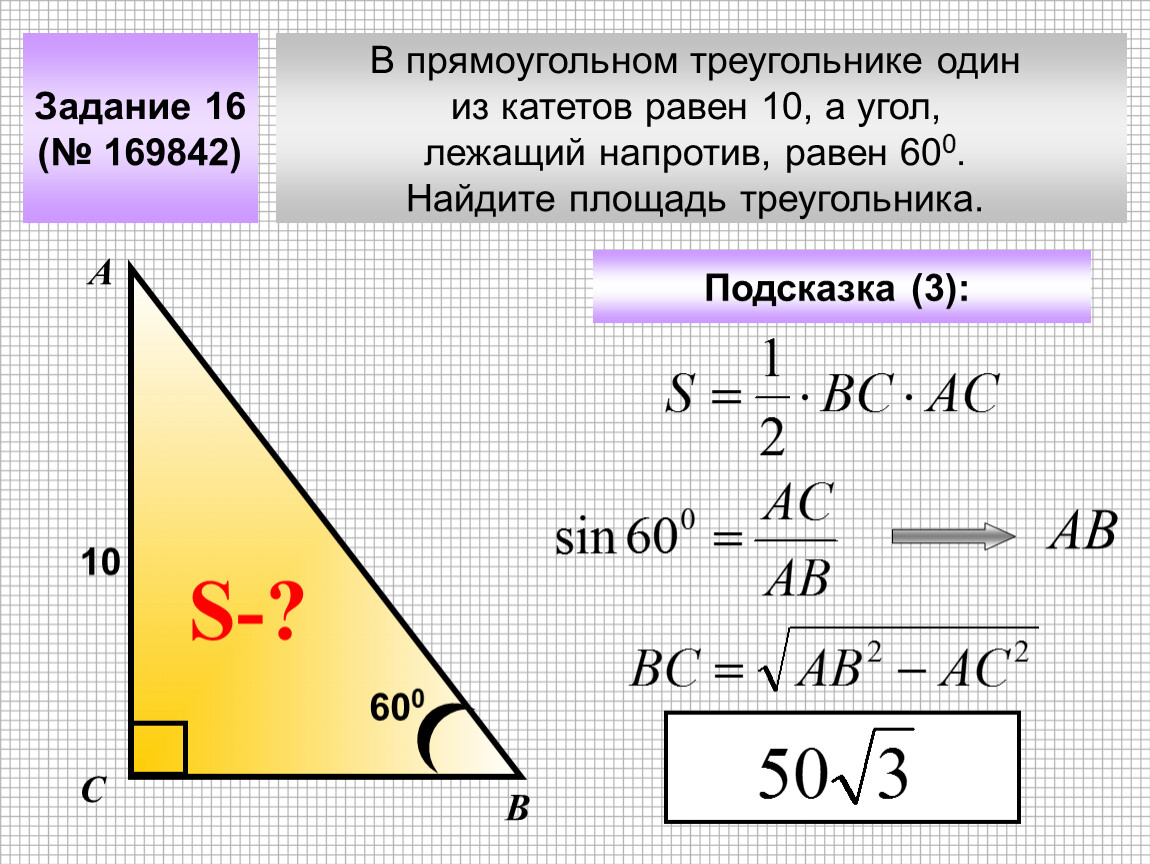 Для удобства назовем уголок АВС, где С — прямой угол. 

Сразу заметим, что прямая АС будет перпендикулярна плоскости листа (поскольку уголок стоит строго вертикально, а лист лежит строго горизонтально). 
Дальше заметим, что прямые АС и ВС также перпендикулярны, поскольку в уголке угол С равен 90°. 
Посмотрим чуть-чуть внимательнее и обратим внимание, что прямая ВС при этом будет проекцией на плоскость листа прямой АВ.

Немного достроим наш рисунок и через точку В проведем прямую, перпендикулярную ВС. Назовем эту прямую КМ. 
Сразу отмечаем, что прямая КМ перпендикулярна ВС по построению, а также перпендикулярна прямой АС (поскольку АС — перпендикуляр к плоскости листа).

Можем ли мы что-то еще сказать про нашу ситуацию? Оказывается, прямая АВ также будет перпендикулярна прямой КМ. 

Возникнет вопрос, почему? 

1. Вспомним признак перпендикулярности прямой и плоскости: если прямая перпендикулярна к двум пересекающимся прямым в этой плоскости, то она будет перпендикулярна этой плоскости.  

Теперь узнаем, как этот признак выполняется в данной ситуации. 

2. Посмотрим на ситуацию немного под другим углом и в этот раз возьмем за плоскость не лист, а нашу линейку. 

3. Тогда две пересекающиеся прямые в плоскости линейки будут перпендикулярны прямой КМ: BCKM по построению, а ACKM как прямая, перпендикулярная к плоскости листа, а значит, и перпендикулярная всем прямым в этой плоскости. 

4. Получается, что прямая КМ перпендикулярна плоскости АВС, следовательно, перпендикулярна и всем прямым в этой плоскости, в том числе прямой АВ. 

Таким образом, длинная сторона линейки будет наклонной прямой, основание — ее проекцией, а начерченная линия — перпендикуляром к проекции. 

Мы рассмотрели теорему о трех перпендикулярах. Осталось ее только сформулировать математическим языком. 

Теорема о трех перпендикулярах 
Если наклонная прямая АВ к плоскости а перпендикулярна прямой КМ в этой плоскости, то и проекция прямой АВ на плоскость а перпендикулярна к прямой КМ.  

Для построения чертежа заменим линейку на несколько отрезков. Тогда АВ — наклонная, ВС — проекция, КМ — прямая в плоскости. 

Как с помощью линейки и листа воспроизвести в жизни теорему о трех перпендикулярах? Для этого нужно взять лист бумаги и треугольную линейку. На листе бумаги построить произвольную прямую, а после поставить линейку строго вертикально так, чтобы основание линейки на листе было перпендикулярно начерченной прямой.  Таким образом, длинная сторона линейки будет наклонной прямой, основание — ее проекцией, а начерченная линия — перпендикуляром к проекции.

Вот и все, ничего сложного. А называется теорема так потому, что в построении действительно присутствуют три перпендикуляра, которые отлично видно на рисунке.

Теорему о трех перпендикулярах можно активно использовать для доказательства и решении задач. 

Фактчек

• Двугранный угол — это часть пространства, заключенная между двумя полуплоскостями, имеющими общую границу. Градусной мерой двугранного угла будет линейный угол двугранного угла или, другими словами, угол между плоскостями. 
• Угол между плоскостями — это угол между перпендикулярами, проведенными к линии пересечения плоскостей. Перпендикуляры должны лежать в данных плоскостях. За угол между плоскостями принимают острый угол, образованный этими плоскостями. Если угол между плоскостями равен 90°, то такие плоскости перпендикулярны. 
• Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость. Чтобы найти угол между прямой и плоскостью, необходимо построить проекцию прямой на плоскость и найти угол между прямой и ее проекцией. Если прямая параллельна плоскости, то угол между ними будет равен 0°. Если прямая перпендикулярна плоскости, то угол между ними будет равен 90°. 
• Прямая, перпендикулярная плоскости — прямая, которая перпендикулярна к каждой прямой, лежащей в этой плоскости. Чтобы доказать, что прямая перпендикулярна плоскости, достаточно доказать, что эта прямая перпендикулярна двум пересекающимся в плоскости прямым.  
• Теорема о трех перпендикулярах гласит, что если наклонная прямая а к плоскости а перпендикулярна прямой b в этой плоскости, то и проекция прямой а на плоскость а перпендикулярна к прямой b. 

Проверь себя

Задание 1. 
Выберите верное утверждение. 

1. Градусной мерой двугранного угла будет линейный угол двугранного угла. При этом все линейные углы двугранного угла равны между собой;
2. Градусной мерой двугранного угла будет линейный угол двугранного угла. При этом линейные углы двугранного угла не равны между собой;
3. Грань двугранного угла — это общая прямая плоскостей, которые его образуют;
4. Ребра двугранного угла — это плоскости, которые его образуют. 

Задание 2. 
Угол между плоскостями — это…

1. Тупой угол между перпендикулярами, проведенными к линии пересечения плоскостей;
2. Острый или прямой угол между перпендикулярами, проведенными к линии пересечения плоскостей;
3. Тупой угол между двумя произвольными линиями, проведенными к линии пересечения плоскостей;
4. Острый или прямой угол между двумя произвольными линиями, проведенными к линии пересечения плоскостей.

Задание 3. 
Что такое проекция прямой на плоскость?

1. Это любая прямая, проведенная из точки пересечения прямой и плоскости;
2. Это перпендикуляр, опущенный из любой точки на плоскость;
3. Это всегда точка пересечения прямой и плоскости;
4. Это прямая, образованная проекциями всех точек прямой на плоскость. 

Задание 4. 
Какой будет проекция прямой, перпендикулярной к плоскости, на эту плоскость?

1. Проекция будет равна этой прямой и параллельна ей;
2. Проекция будет меньше прямой и образовывать с ней угол;
3. Проекция будет точкой пересечения прямой и плоскости;
4. Проекция будет больше прямой и образовывать с ней угол.  

Задание 5. 
Как доказать, что прямая перпендикулярна плоскости?

1. Достаточно доказать, что прямая перпендикулярна одной любой прямой в плоскости;
2. Достаточно доказать, что прямая перпендикулярна двум параллельным прямым в плоскости;
3. Достаточно доказать, что угол между прямой и любой прямой в плоскости равен 90°;
4. Достаточно доказать, что прямая перпендикулярна к двум пересекающимся прямым в этой плоскости.

Ответы: 1. — 1 2. — 2 3. — 4 4. — 3 5. — 4

Как найти угол прямой

Все ресурсы по базовой геометрии

9 Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 4 5 6 Следующая →

Справка по базовой геометрии » Плоская геометрия » Линии » Как найти угол прямой

Рассмотрите схему. Какое из этих условий , а не доказывает это   ?

Возможные ответы:

Любое из этих утверждений может быть использовано для доказательства этого .

 и  

Правильный ответ:

Объяснение:

Если  и  , то , так как две прямые, параллельные одной и той же прямой, параллельны друг другу.

Если , то , так как два односторонних внутренних угла, образованных секущей, являются дополнительными.

Если , то , так как два альтернативных внутренних угла, образованных секущими, равны.

Однако, независимо от того, параллельны ли и ; это вертикальные углы, и по теореме о вертикальных углах они должны быть равны .

Сообщить об ошибке

Равнобедренный треугольник имеет внутренний угол, равный . Чему равны два его других угла?

Возможные ответы:

Этот треугольник не может существовать.

 

Правильный ответ:

 

Пояснение:

По теореме о равнобедренном треугольнике два внутренних угла должны быть равны. Однако, поскольку в треугольнике не может быть двух тупых внутренних углов, два недостающих угла должны быть равны. Поскольку общая мера угла треугольника  , каждый из отсутствующих углов измеряет .

Сообщить об ошибке

Как бы вы классифицировали следующий угол?

Возможные ответы:

Тупой

Прямой

Острый

Разносторонний

Правый

Правильный ответ:

Тупой

Объяснение:

Тупые углы больше .

Разнонаправленность — это обозначение треугольников, у которых один угол больше , но эта фигура не является треугольником.

Острые углы меньше , прямые углы равны , а прямые углы равны .

Следовательно, этот угол тупой.

Сообщить об ошибке

Что является мерой?

 

Возможные ответы:

Правильный ответ:

Объяснение:

Когда две параллельные прямые пересекаются третьей прямой (называемой секущей), угол измеряется по определенной схеме. Пары углов внутри двух прямых и по разные стороны называются альтернативными внутренними углами. Альтернативные внутренние углы, такие как и , имеют одинаковую градусную меру. Следовательно, мера .

Сообщить об ошибке

Марк тренируется для бега по пересеченной местности и натыкается на новый холм для бега. Пробежав несколько метров, Марк оказывается на метровой высоте. Каков угол падения холма, когда он находится на высоте  метров?

 

Возможные ответы:

То же, что и угол наклона

Невозможно определить

Правильный ответ:

Объяснение:

После прочтения вопроса у нас в голове остался этот пространственный образ Марка. После добавления данной информации изображение становится больше похоже на

Холм, по которому бежит Марк, можно увидеть в виде прямоугольного треугольника. Эта проблема быстро превращается в проблему, требующую загадочного угла, учитывая, что даны две стороны треугольника. Чтобы найти угол наклона, мы должны обратиться к принципам касательной функции. Tan, Sin или Cos обычно используются, когда имеется угол и цель состоит в том, чтобы вычислить одну из сторон треугольника. В этом случае обстоятельства обратные.

Вспомните «SOH CAH TOA». В этой задаче не дается никакой информации о гипотенузе, и мы не пытаемся вычислить гипотенузу. Поэтому у нас остается «ТОА». Если бы мы проверили, это сработало бы, потому что угол у ног Марка содержит информацию для противоположной стороны и соседней стороны.

Поскольку угол не задан, мы должны использовать принципы, лежащие в основе функции тангенса, при использовании дроби, состоящей из заданных сторон. Эта проблема будет решена с помощью arctan (иногда обозначается как ).

Сообщить об ошибке

Два угла являются дополнительными и имеют отношение 1:4. Какова величина меньшего угла?

Возможные ответы:

Правильный ответ:

Пояснение:

Поскольку углы смежные, их сумма равна 180 градусам. Поскольку они находятся в соотношении 1:4, можно записать следующее выражение:

Сообщить об ошибке

AB и CD — две параллельные линии, пересекаемые линией EF. Если угол 1 равен , то чему равен угол 2?

Возможные ответы:

Правильный ответ:

Пояснение:

Углы равны. При пересечении двух параллельных прямых секущей соответствующие углы имеют одинаковую величину.

Сообщить об ошибке

Линии A и B на диаграмме ниже параллельны. Треугольник в нижней части рисунка равнобедренный.

Что такое градусная мера угла?

Возможные ответы:

Правильный ответ:

Объяснение:

Поскольку A и B параллельны, а треугольник равнобедренный, мы можем использовать дополнительное правило для двух углов,  и  , которое в сумме даст . Составив для этого алгебраическое уравнение, получим . Решая для , получаем . При этом мы можем получить либо  (для меньшего угла), либо  (для большего угла — затем необходимо снова использовать дополнительное правило для внутреннего меньшего угла). В любом случае, мы находим, что внутренние углы при вершине равны 80 градусов каждый. Так как сумма углов внутри треугольника должна быть равна 180, мы можем составить уравнение как

 градуса.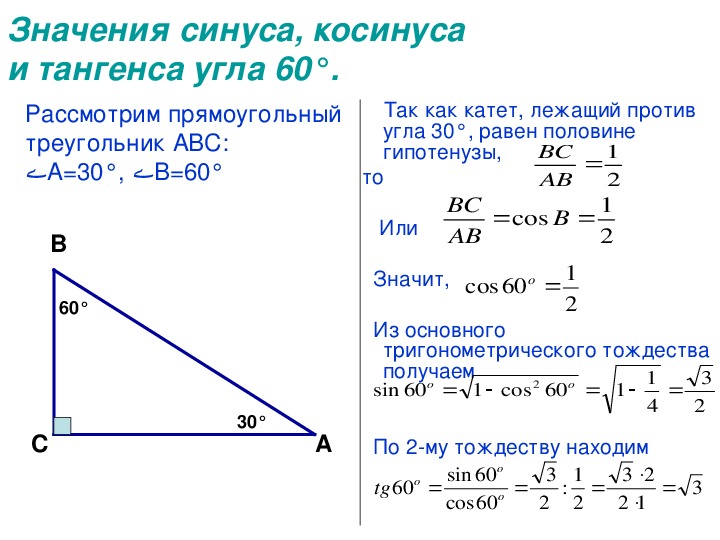

Сообщить об ошибке

Рисунок выполнен не в масштабе.

На рисунке выше APB образует прямую линию. Если мера угла APC на восемьдесят один градус больше, чем мера угла DPB, а меры углов CPD и DPB равны, то какова мера угла CPB в градусах?

Возможные ответы:

50

40

66

114

33

Правильный ответ:

66

Пояснение:

Пусть х равно мере угла DPB. Поскольку мера угла APC на восемьдесят один градус больше, чем мера DPB, мы можем представить меру этого угла как x + 81. Кроме того, поскольку мера угла CPD равна мере угла DPB, мы можем представить мера CPD как x.

Поскольку APB — прямая линия, сумма углов DPB, APC и CPD должна быть равна 180; поэтому мы можем написать следующее уравнение, чтобы найти x:

x + (x + 81) + x = 180

Упростите, собрав x членов.

3x + 81 = 180

Вычтите 81 с обеих сторон.

3x = 99

Разделить на 3.

x = 33.

Это означает, что углы DPB и CPD равны 33 градусам. Исходный вопрос требует от нас найти меру угла CPB, которая равна сумме мер углов DPB и CPD.

мера КПБ = 33 + 33 = 66.

Ответ: 66.

Сообщить об ошибке

Половина меры дополнительного угла ABC равна удвоенной мере угла ABC. Чему равен в градусах дополнительный угол ABC?

Верно ответ:

54

Пояснение:

Пусть x равно мере угла ABC, y равно мере дополнения угла ABC, а z равно мере дополнения угла ABC.

Так как x и y являются добавками, сумма их мер должна равняться 180. Другими словами, x + y = 180. 

Нам говорят, что половина меры добавки равна удвоенной мере меры азбука. Мы могли бы записать это уравнение следующим образом:

(1/2)y = 2x.

Поскольку x + y = 180, мы можем найти y через x, вычитая x из обеих частей. Другими словами, y = 180 – x. Затем мы можем подставить это значение в уравнение (1/2)y = 2x, а затем найти x.

(1/2)(180-х) = 2х.

Умножьте обе части на 2, чтобы избавиться от дроби.

(180 – х) = 4х.

Добавьте x с обеих сторон.

180 = 5х.

Разделите обе стороны на 5.

x = 36.

Угол ABC равен 36 градусам. Однако исходный вопрос требует от нас найти меру дополнения ABC, которую мы ранее обозначили как z. Поскольку сумма меры угла и меры его дополнения равна 90, мы можем написать следующее уравнение:

x + z = 90.

Теперь мы можем подставить 36 в качестве значения x и найти z.

36 + z = 90.

Вычесть 36 с обеих сторон.

z = 54.

Ответ: 54. 

Сообщить об ошибке

← Предыдущая 1 2 3 4 5 6 Следующая →

Уведомление об авторских правах

Все Ресурсы по базовой геометрии

9 Диагностические тесты 164 практических теста Вопрос дня Карточки Учитесь по концепции

Как найти недостающий угол треугольника (видео и примеры)

Автор:

Malcolm McKinsey

26 января 2023 г.

Проверено

Пол Маццола

Углы треугольника

Треугольник – это простейший из возможных многоугольников. Это двумерная (плоская) форма с тремя прямыми сторонами, образующими внутреннее замкнутое пространство. У него три внутренних угла . Одна из самых первых концепций, которую следует изучать в геометрии, заключается в том, что сумма внутренних углов треугольников равна 9.0405 180° . Но откуда ты знаешь? Как вы можете доказать, что это правда? Давай выясним!

Как найти угол треугольника

У вас может быть треугольник, в котором отмечены и измерены только два угла. Теперь, когда вы уверены, что все треугольники имеют внутренние углы в сумме с 180° , вы можете быстро вычислить недостающее измерение. Вы можете сделать это одним из двух способов:

1. Вычесть два известных угла из 180° .

2. Подставьте два угла в формулу и используйте алгебру: a+b+c=180°

Как найти недостающий угол треугольника

Два известных угла треугольника: 37°  и 24° . Каков недостающий угол?

Мы можем использовать два разных метода, чтобы найти наш недостающий угол:

Как найти угол треугольника

Вычесть два известных угла из  180° :

Подставьте два угла в формулу и используйте алгебру:  a + b + c = 180°

Формула угла треугольника

Нарисуем треугольник и обозначим его внутренние углы тремя буквами: a , b и c . Наш образец будет иметь сторону ac по горизонтали внизу и ∠b  наверху.

Теперь, когда мы обозначили углы, у нас есть формула, на которую мы можем ссылаться для углов. Это 90 405 a + b + c = 180 ° 90 406, что говорит нам о том, что если мы сложим все наши углы, они всегда будут равны 9.0405 180 .

Теперь давайте проведем линию, параллельную стороне ac , которая проходит через точку b (где вы также найдете ∠b ).

Теорема о чередующихся внутренних углах Чтобы найти недостающий угол в треугольнике

Эта новая параллельная прямая создала два новых угла по обе стороны от ∠b . Мы обозначим эти два угла ∠z и ∠w слева направо. Сторону ab нашего треугольника теперь можно рассматривать как поперечную, линию, пересекающую две параллельные линии.

Теорема о чередующихся внутренних углах

По теореме о альтернативных внутренних углах мы знаем, что ∠a сравнимо (равно) ∠z и ∠c 904 06 соответствует ∠w .

Мы потеряли тебя? Не отчаивайся! Теорема о чередующихся внутренних углах говорит нам, что поперечное сечение двух параллельных прямых создает конгруэнтные альтернативные внутренние углы. Чередующиеся внутренние углы лежат между параллельными прямыми по разные стороны от секущей. В нашем примере ∠a и ∠z являются альтернативными внутренними углами, как и ∠c  и ∠w .

Теперь у нас есть три угла нашего треугольника, тщательно перерисованные и имеющие общую точку Point b . У нас есть ∠z в качестве замены ∠a , затем ∠b и, наконец, ∠w  в качестве замены ∠c .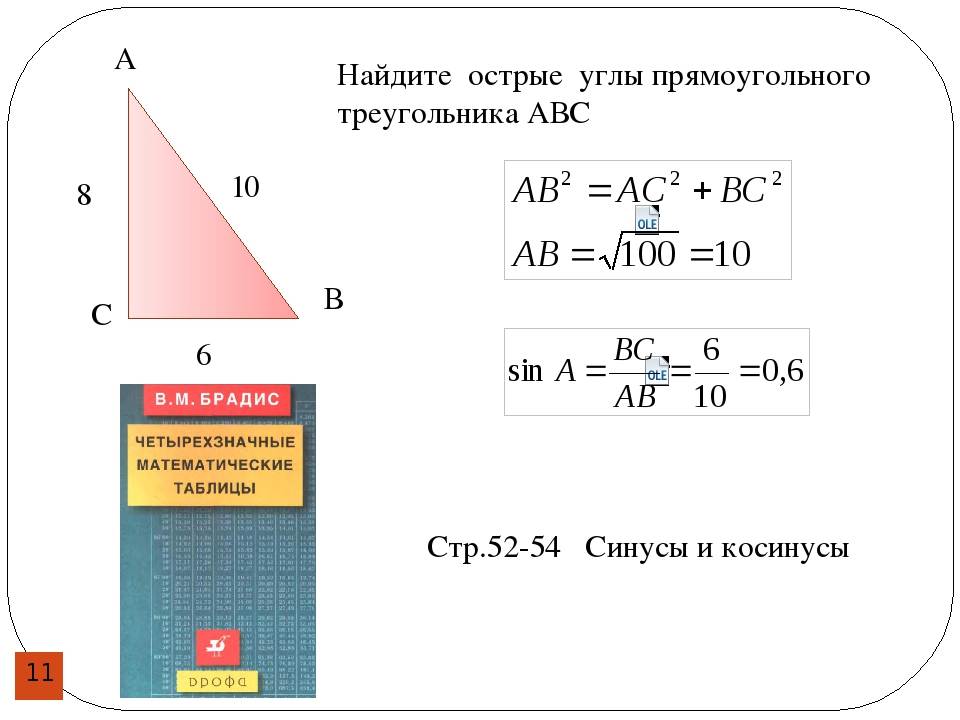 И посмотрите, они образуют прямую линию!

Прямая измеряет 180° . Это тот же тип доказательства, что и доказательство параллельных прямых. Три угла любого треугольника всегда дают в сумме 180° или прямая.

Теорема о сумме углов треугольника

Наша формула для этого: 90 406 – внутренние углы любого треугольника.

Сумма углов треугольника равна 180°.

Для выполнения этого удивительного математического трюка вам понадобятся четыре вещи. Вам понадобится линейка, ножницы, бумага и карандаш. На листе бумаги нарисуйте аккуратный большой треугольник. Любой треугольник — разносторонний, равнобедренный, равносторонний, остроугольный, тупоугольный — какой угодно.

Пометьте внутренние углы (вершины, образующие внутренние углы) тремя буквами, например  R-A-T . Вырежьте треугольник, оставив небольшую рамку вокруг него, чтобы вы могли видеть все три края.

Теперь оторвите три угла вашего треугольника. Не используйте ножницы, потому что вам нужны зубчатые края, которые помогут вам не перепутать их с прямыми сторонами, которые вы нарисовали. У вас будет три меньших треугольных фрезы, каждая с внутренним углом, обозначенным  R ,  A или T . Каждый маленький кусочек имеет две аккуратные стороны и шероховатый край.

У вас также будет грубый шестиугольник, который является оставшейся частью исходного большого треугольника.

Возьмите три маленьких отмеченных уголка и сложите их так, чтобы необработанные края были от вас. Единственный способ сделать это — заставить их выстроиться в прямую линию. Три внутренних угла RAT в сумме образуют прямой угол, также называемый прямой линией.

Есть; ты сделал это!

Итоги урока

Если вы внимательно изучили этот урок, то теперь вы можете определить и обозначить три внутренних угла любого треугольника, и вы можете вспомнить, что сумма внутренних углов всех треугольников составляет

Что вы узнали:

С помощью этого видео и урока вы научились:

• Определять и обозначать три внутренних угла любого треугольника

• Вспомнить, что сумма внутренних углов всех треугольников составляет 180°

• Продемонстрировать доказательство суммы внутренних углов треугольников

• Применить формулу суммы внутренних углов любого треугольника

• Вычислить недостающее измерение любого внутреннего угла любого треугольника

  904 22

Репетиторы

  180° .

No related posts.