СУНЦ УрФУ
Расписание
Электронный журнал
Поступающим
Олимпиады, турниры, конкурсы
Планы работы
Подготовительные курсы
Новости:
14.02.2023
«Науки юношей питают…» (М. Ломоносов)
В СУНЦ УрФУ в День российской науки состоялись тематические мероприятия.
12.02.2023
Lecture on the world economy Pupils 10Z and 11Z, или Приглашение на кейс-чемпионат
Математико-экономические классы СУНЦ встретились с представителями УрФУ.
10.02.2023
Урал… Уралу… Об Урале!
В общежитии состоялся поэтический вечер, посвященный Уралу.
09.02.2023
День Российской науки: астрономия с автором учебника
Лицеисты встретились с Владимиром Георгиевичем Сурдиным, автором учебника астрономии.
09.02.2023
Юрий Казарин о Тютчеве, интерфизике и «чуваках»
В СУНЦ прошла встреча с уральским поэтом, организованная кафедрой филологии.
06.02.2023
В СУНЦ УрФУ состоялся форум выпускников
Выпускники СУНЦ разных лет встретились с нынешними лицеистами.
Больше новостей
Видеогалерея:
Новогодние поздравления (декабрь 2022)
СУНЦ.АРТ (ноябрь 2022)
«Горнозаводской Урал» (октябрь 2022)
Больше видео
О нас:
Специализированный учебно-научный центр (СУНЦ) — структурное подразделение ФГАОУ ВО «УрФУ имени первого Президента России Б.Н. Ельцина», созданное в 1990 году как нетиповое структурное подразделение вуза, осуществляющее углубленное дифференцированное обучение по программам основного общего и среднего общего образования. Всего в России 10 СУНЦев. До мая 2011 года СУНЦ работал в составе Уральского государственного университета имени А. М. Горького (УрГУ).
В настоящее время СУНЦ имеет в своем составе 8 кафедр, укомплектованных профессорско-преподавательским составом УрФУ и учителями. Обучение производится по авторским программам, разработанным в соответствии с федеральными государственными образовательными стандартами; в составе СУНЦ — 8–11 классы различных профилей.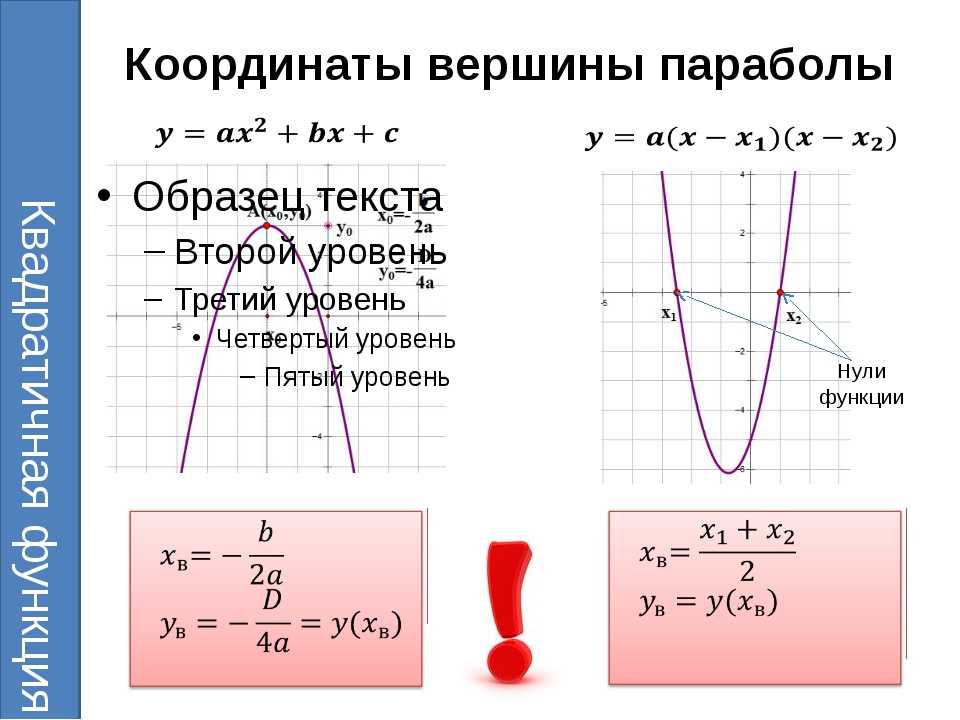
Иногородние обучающиеся проживают в уютном общежитии.
Прием производится в 8, 9, 10 и 11 классы. Работают подготовительные курсы.
Подробнее о правилах приема в СУНЦ можно узнать в отделе конкурсного отбора
по телефону +7 343 367-82-22 и в разделе нашего сайта «Поступающим».
Как нас найти:
Данилы Зверева ул., 30, Екатеринбург. N56°52´4˝ E60°39´16˝
Проезд:
- автобусами № 48, 52, 81 до остановки «Фирма Авангард»;
- автобусами № 28, 58 до остановки «Данилы Зверева», далее 7 минут пешком по улице Данилы Зверева;
- троллейбусом № 18 до остановки «Данилы Зверева», далее 14 минут пешком по улицам Сулимова, Данилы Зверева;
- троллейбусами № 4 до остановки «Сулимова», № 19, 32 до остановки «Боровая», далее 15 минут пешком по улицам Боровая, Вилонова, Данилы Зверева.
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
12.17Другие ответы
| ||||||||||||
12.17
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
В городе лжецов и рыцарей (рыцари всегда говорят правду, лжецы всегда лгут) 366 жителей, все родились в разные дни високосного года.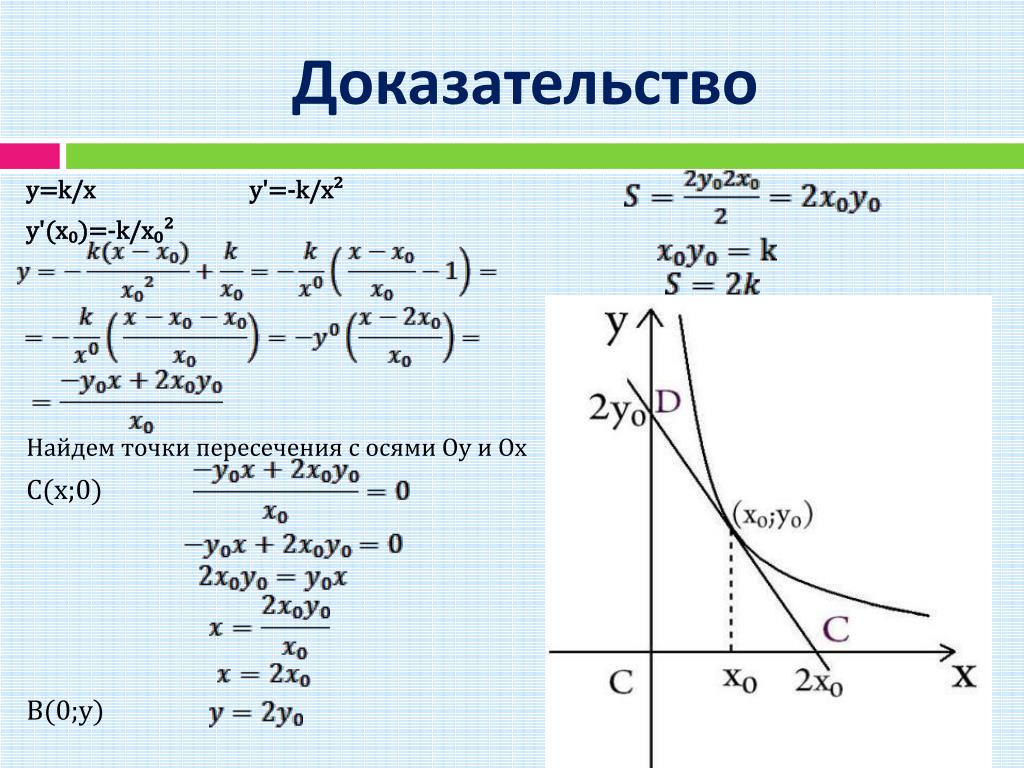
2. Найдите площадь полной поверхности цилиндра.
Имеется два сосуда, содержащие 30 кг и 20 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 81%
Луч AD – биссектриса угла А. На сторонах угла А отмечены точки В и С так, что АDВ = АDС . Докажите, что АВ = АС .
Полина старше Аллы на 9 лет. Вместе им 15 лет. Сколько лет будет Алле через 2 года
Пользуйтесь нашим приложением
элементарная теория чисел — Как найти решения линейного диофантова ax + by = c?
Диофантово уравнение $ax+by = c$ имеет решения тогда и только тогда, когда $\gcd(a,b)|c$. Если это так, то она имеет бесконечно много решений, и любое решение может быть использовано для генерации всех остальных.
Чтобы убедиться в этом, обратите внимание, что наибольший общий делитель $a$ и $b$ делит и $ax$, и $by$, а значит, делит $c$, если существует решение.
Это дает необходимость условия (которое у вас есть в обратном порядке). (исправлено в редактировании)
Обратное на самом деле является конструктивным доказательством , которое вы можете найти практически в каждом курсе или книге по элементарной теории чисел, и которое по существу совпадает с ответом Юнона выше (но без деления на первый ).
Используя расширенный алгоритм Евклида, для любых целых чисел $a$ и $b$ можно найти целые числа $s$ и $t$ такие, что $as+bt = \gcd(a,b)$; числа $s$ и $t$ не уникальны, но вам нужна только одна пара. Как только вы найдете $s$ и $t$, поскольку мы предполагаем, что $\gcd(a,b)$ делит $c$, существует целое число $k$ такое, что $\gcd(a,b)k = c $. Умножив $as+bt=\gcd(a,b)$ на $k$, вы получите $$a(sk) + b(tk) = \gcd(a,b)k = c.$$
Это дает одно решение с $x=sk$ и $y=tk$.
Теперь предположим, что $ax_1 + by_1 = c$ — это решение, а $ax+by=c$ — какое-то другое решение. Взяв разницу между ними, мы получим
$$a(x_1-x) + b(y_1-y) = 0.
$$
Следовательно, $a(x_1-x) = b(y-y_1)$. Это означает, что $a$ делит $b(y-y_1)$, а значит, $\frac{a}{\gcd(a,b)}$ делит $y-y_1$. Следовательно, $y = y_1 + r\frac{a}{\gcd(a,b)}$ для некоторого целого числа $r$. Подстановка в уравнение $a(x_1-x) = b(y-y_1)$ дает
$$a(x_1 — x) = rb\left(\frac{a}{\gcd(a,b)}\right)$$
который дает
$$\gcd(a,b)a(x_1-x) = rba$$
или $x = x_1 — r\frac{b}{\gcd(a,b)}$.
Таким образом, если $ax_1+by_1 = c$ — любое решение, то все решения имеют вид $$x = x_1 — r\frac{b}{\gcd(a,b)},\qquad y = y_1 + r\frac{a}{\gcd(a,b)}$$ точно так, как Юнон сказал.
Чтобы дать вам пример этого в действии, предположим, что мы хотим найти все целочисленные решения для $$258x + 147y = 369.$$
Сначала мы используем алгоритм Евклида, чтобы найти $\gcd(147,258)$; уравнение в скобках справа показывает, как мы будем использовать это равенство после завершения вычислений.
\начать{выравнивать*}
258 &= 147(1) + 111 &\quad&\mbox{(эквивалентно, $111=258 — 147$)}\\
147 &= 111(1) + 36&&\mbox{(эквивалентно $36 = 147 — 111$)}\\
111 &= 36(3) + 3&&\mbox{(эквивалентно $3 = 111-3(36)$)}\\
36 &= 3(12).
\конец{выравнивание*}
Итак, $\gcd(147 258)=3$. Начиная с $3|369$ уравнение имеет интегральные решения.
Затем мы находим способ записать $3$ как линейную комбинацию $147$ и $258$, используя алгоритм Евклида выше и равенство справа. У нас есть:
\начать{выравнивать*}
3 &= 111 — 3(36)\\
&= 111 — 3(147 — 111) = 4(111) — 3(147)\\
&= 4(258 — 147) — 3(147)\\
&= 4(258) -7(147).
\конец{выравнивание*}
Затем мы берем $258(4) + 147(-7)=3$ и умножаем на $123$; почему 123$? Потому что $3\times 123 = 369$. Мы получаем:
258 долларов США (492) + 147 (-861) = 369.$$
Таким образом, одно решение $x=492$ и $y=-861$. Все остальные решения будут иметь вид
\начать{выравнивать*}
х &= 492 — \frac{147r}{3} = 492 — 49r,\\
y &= -861 + \frac{258r}{3} =86r — 861, &\qquad&r\in\mathbb{Z}.
\конец{выравнивание*}
Вы можете уменьшить эти константы, сделав простую замену переменной. Например, если мы допустим $r=t+10$, то
\начать{выравнивать*}
х &= 492 — 49(t+10) = 2 — 49t,\\
y &= 86(t+10) — 861 = 86t — 1,&\qquad&t\in\mathbb{Z}.
\end{align*}
Калькулятор формул линейной аппроксимации | ААТ Биоквест
Линейная аппроксимация имеет решающее значение для многих хорошо известных численных методов, таких как метод Эйлера, методы Ранга Кутты и т. д., для аппроксимации решений обыкновенных дифференциальных уравнений. Расчет основан на близости касательной к графику функции вокруг точки.
Для данной точки x0, если x0 находится в области определения функции f(x), т. е. функция дифференцируема в этой точке, уравнение графика f(x) в точке (x0,y0), где y0 =f(x0) становится:
y-y0=f’(x0)(x-x0)
Для любого значения x1, достаточно близкого к x0, можно сказать, что x1=x0+Δx, где Δx — разница между x1 и x0.
Следовательно, значение y1 аппроксимируется f(x0+∆x) на касательной, определяемой как:
y1=y0+∆x*f'(x0)
функция f(x) в точке x0.
Для Δy=y1-y0 получаем Δy=Δx*f’(x0). В пределе, когда x приближается к x0, окончательное уравнение принимает вид:
L(x)≈f(x0)+f’(x)(x-x0)
где L(x) представляет собой линейную аппроксимацию функции f(x) в точке x0.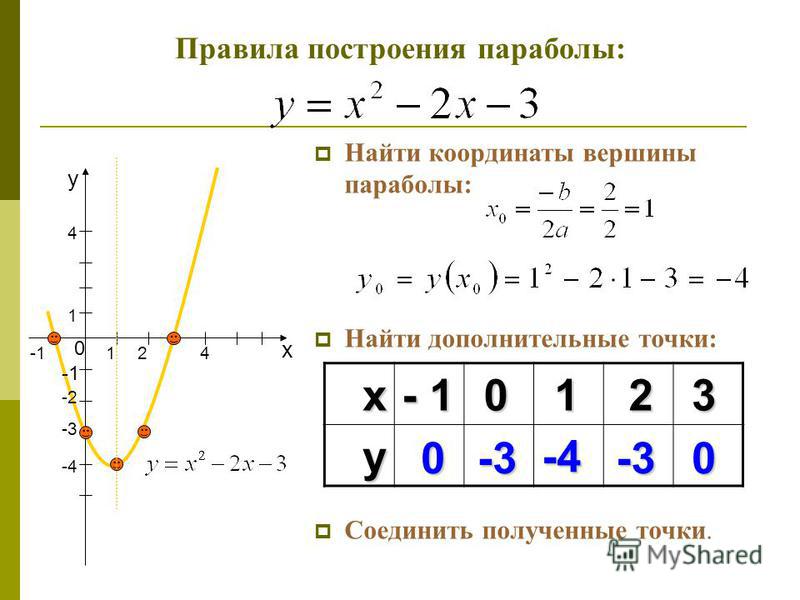
Калькулятор рассчитает линейную аппроксимацию явной кривой в любой заданной точке.
Как использовать этот инструмент
1. Введите функцию в поле справа с «x» в качестве независимой переменной. Круглые скобки должны быть заключены вокруг «x» в соответствии с типом и порядком операции. Например, в случае тригонометрических функций введите cos(x), а не cosx. Кроме того, оператор умножения должен быть явно определен с помощью «*», т.е. cos(2*x), а не cos(2x).
2. Введите числовое значение x0. Калькулятор не принимает «пи», поэтому при необходимости вводите значения в градусах, и калькулятор соответствующим образом преобразует их в радианы. Например, чтобы проверить линейную аппроксимацию в точке «pi/2», введите «90».
3. Убедитесь, что ваша функция и точка точны.
4. Нажмите кнопку «Вычислить линейное приближение», чтобы отобразить результаты.
Ввод данных
| Функция для аппроксимации | |
| x 0 (A) |
| Доступные экспрессии (Click To Add) | также известен как | |
x x| , также известный как | | |
x x x x x x x x x x x x| . |  к мощности N | |
| √x | квадратный корень, SQRT | |
| E x | Экспоненциальная функция | |
| LN (x) | LN (x) | 49.0067 |
| log 10 (x) | common log(arithm), log(arithmn) base 10 | |
| sin(x) | sine | |
| cos(x) | cosine | |
| tan(x) | tangent | |
| sinh(x) | hyperbolic sine | |
| cosh(x) | hyperbolic cosine | |
| tanh(x) | hyperbolic tangent | |
| asin(x ) | арксинус, арксинус, sin -1 | |
| ACOS (x) | Арккозин, обратный косинус, COS -1 | |
| ATAN (x) | Arctangent, Inverse Tangent, Tan -1 (x) | . |