Как обозначается середина отрезка: Координаты середины отрезка — как найти? Формулы и примеры

Координаты середины отрезка — как найти? Формулы и примеры

Поможем понять и полюбить математику

Начать учиться

Отрезок — понятие, которое знакомо даже первокласснику. С начальной школы мы учились рисовать их, находить длину, складывать и вычитать друг из друга. Сегодня же мы пойдем еще дальше и рассмотрим отрезки на плоскости и даже в пространстве! Звучит впечатляюще, правда? После этой статьи вы сможете с легкостью решать сложные геометрические задачи на нахождение середины отрезка, разберетесь в непростых формулировках и еще больше убедитесь в том, что геометрия прекрасна в своей простоте.

Что такое отрезок

Чтобы изучить эту тему досконально, давайте начнем с самого простого: с определения отрезка.

Отрезок — это прямая, у которой есть начало и конец, или же прямая, которая соединяет две произвольные точки, не совпадающие друг с другом.

Отрезок называют заглавными буквами латинского алфавита по названию конечных точек. Причем можно расставлять буквы в любом порядке: АВ и ВА — равноценные варианты. Рассмотрите иллюстрацию, посчитайте и назовите все отрезки.

Узнай, какие профессии будущего тебе подойдут

Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас

Что такое середина отрезка

Середина отрезка — это точка, которая находится на равном расстоянии от его концов. Иначе можно сказать так: это точка, которая делит отрезок пополам.

Так, на рисунке ниже D — середина отрезка СК, так как СD = DK. Обратите внимание, как на чертеже обозначаются равные по длине отрезки — мы ставим на них равное количество черточек.

Главный вопрос, который нас сегодня интересует, это координаты середины отрезка.

Координаты — это положение точки в пространстве.

Мы можем рассмотреть отрезок, который лежит на координатной прямой, тогда координата будет одна. В Декартовой системе координат оХУ будет две координаты, причем вначале записывают х, потом у. Например: С (5; 3): К (4; 8). Еще мы можем поместить отрезок в трехмерное пространство, тогда у каждой точки будет три координаты: х, у, z.

Кажется, что чем дальше, тем сложнее, но на самом деле это не совсем так. Хорошая новость: в каждом из случаев мы будем использовать один и тот же принцип, так что вы обязательно во всем разберетесь!

Как найти координаты середины отрезка на координатной прямой

Изобразим горизонтальную координатную прямую оХ и отметим на ней две точки: М и L. Координату точки М запишем как Хм, точки L — соответственно XL. Поставим лежащую на отрезке точку А — середину ML, MA = LA.

Определим координаты точек: Хм = {2}, XL = {8}. Чтобы найти середину отрезка, воспользуемся формулой X_A=(X_M+X_L)/2 и получим:

Х_А = (2 + 8)/2 = 5.

Проверим, верна ли формула. Для этого определим координаты середины отрезка графическим методом.Действительно: фактическая координата точки А совпадает со значением, которое мы получили.

Подумайте, взяли ли мы эту формулу случайно или же ее можно вывести. Да, конечно, второй вариант верный — в математике не используют ничего непроверенного. Давайте посмотрим, каким образом можно доказать истинность формулы, тем более, что мы возьмем ее за основу при решении более сложных задач.

1. Точка А — это середина отрезка, а значит, MA = LA.

2. Расстояние между точками можно рассчитать через разность модулей их координат: │Х_А – Х_М│=│Х_L – Х_А│.

3. Преобразуем правую часть, вынесем знак минуса: Х_А – Х_М= — (Х_А –Х_L).

4. Перенесем Х_А в левую часть, а все остальное — в правую: 2Х_А= Х_L+ Х_М.

5. Найдем Х_А: Х_А = (Х_L + Х_М)/2.

Вот мы и вывели формулу координат середины отрезков! Чтобы лучше закрепить материал, сделаем пару заданий.

Задача 1

Определите координаты середины отрезка АВ, если Х_А = –2, Х_B = 10.

Решение

Обозначим точку середины отрезка буквой Т. Тогда Хт = (Х_А + Х_B)/2 = (–2 + 10)/2 = 4.

Ответ: Хк = {4}.

Задача 2

Определите координаты начала отрезка КМ с серединой в точке Н, если Х_м = 5, Х_н = 10.

Решение

Вначале запишем формулу для середины отрезка: Х_н = (Х_к + Х_м)/2.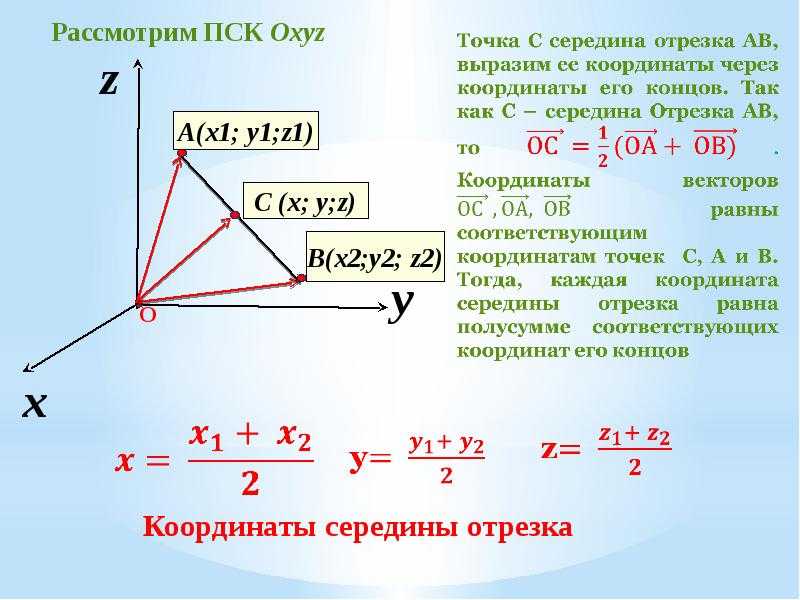

Выразим Х_к через нее:

Х_н = (Х_к + Х_м)/2,2Х_н = (Х_к + Х_м),2Х_н – Х_м = Х_к,Х_к = 2Х_н – Х_м = 2 * 5 – 10 = 0.

Ответ: Хк = {0}

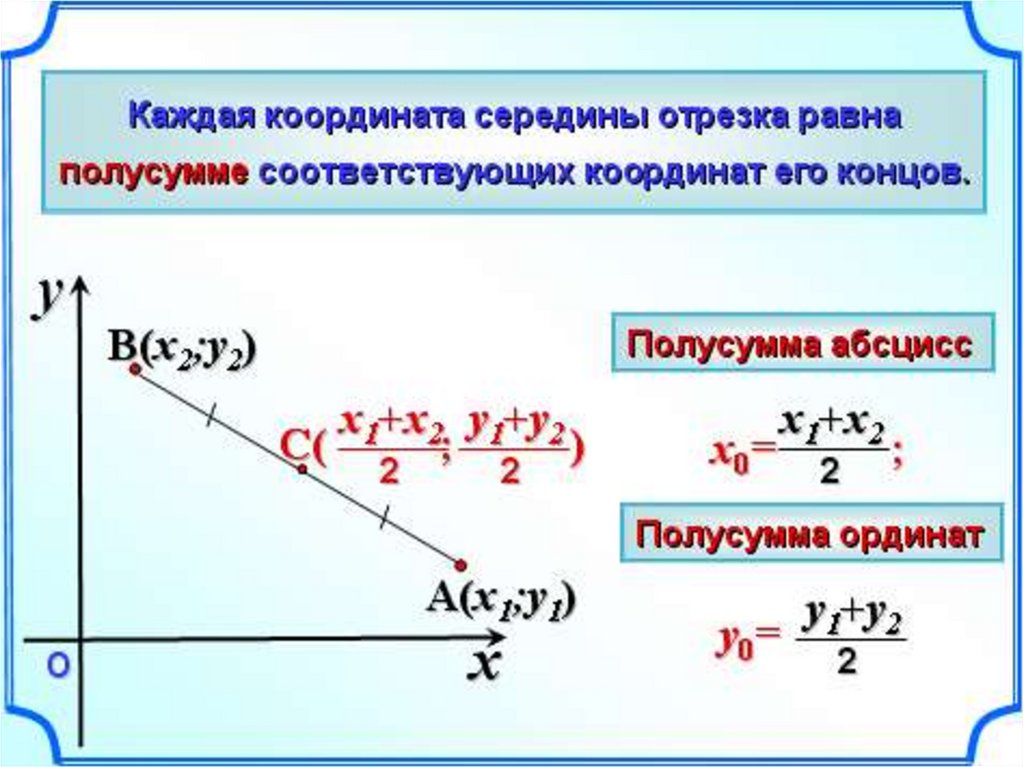
Как найти середину отрезка на плоскости

В Декартовой системе координат у каждой точки есть две координаты: по оси оХ и оУ. Изобразим отрезок АВ с координатами А (1; 3), В (3; 6) и точкой С — серединой отрезка.

Чтобы найти координаты точки С, мы воспользуемся уже известной нам формулой, но применим ее к каждой координате в отдельности. Вначале рассчитаем Х_с:

Х_с = (Х_А + Х_B)/2 = (1 + 3)/2 = 2.

Тогда У_C = (У_A + У_B)/2 = (3 + 6)/2 = 4,5.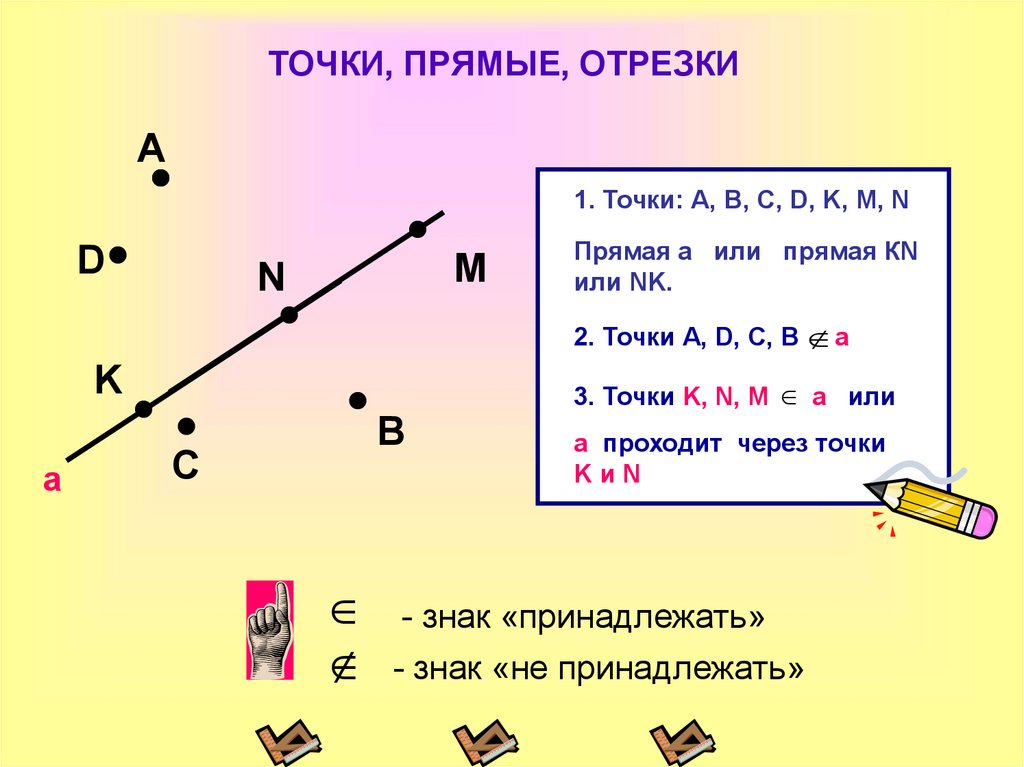 Значит С (2; 4,5).

Не пугайтесь, если отрезок на чертеже параллелен оси оХ или оУ: мы четко идем по нашему алгоритму и ничего не меняем.

Важно заметить: если отрезок параллелен оси оУ, координаты концов и середины отрезка по оХ будут совпадать, Х_А = Х_С = Х_В. Если же отрезок параллелен оси оХ, совпадут координаты по оУ: У_А = У_В = У_С.

И вновь пришло время задачек. Давайте разберем несколько примеров решения.

Задача 3

В системе координат находятся две точки: С (–6; 4) и К (2; 8). Определите координаты середины отрезка.

Решение

Обозначим середину отрезка точкой О. Тогда:

Х_О = (Х_С + Х_К)/2 = (–6 + 2)/2 = –2,У_О = (У_С + У_К)/2 = (4 + 8)/2 = 6.

Ответ: О (-2; 6).

Задача 4

Дан треугольник с вершинами АВС: А (-2; 4), В (4; 6), С (3; -5). Определите координаты точки М — медианы ВМ.

Решение

Медиана — отрезок, который проведен из вершины треугольника и делит противоположную сторону пополам. А значит, медиана ВМ делит на равные части сторону АС, АМ = МС. Тогда:

Х_М = (Х_А + Х_С)/2 = (–2 + 3)/2 = 0,5, У_М = (У_А + У_С)/2 = (4 – 5)/2 = –0,5.

Ответ: М (0,5; –0,5).

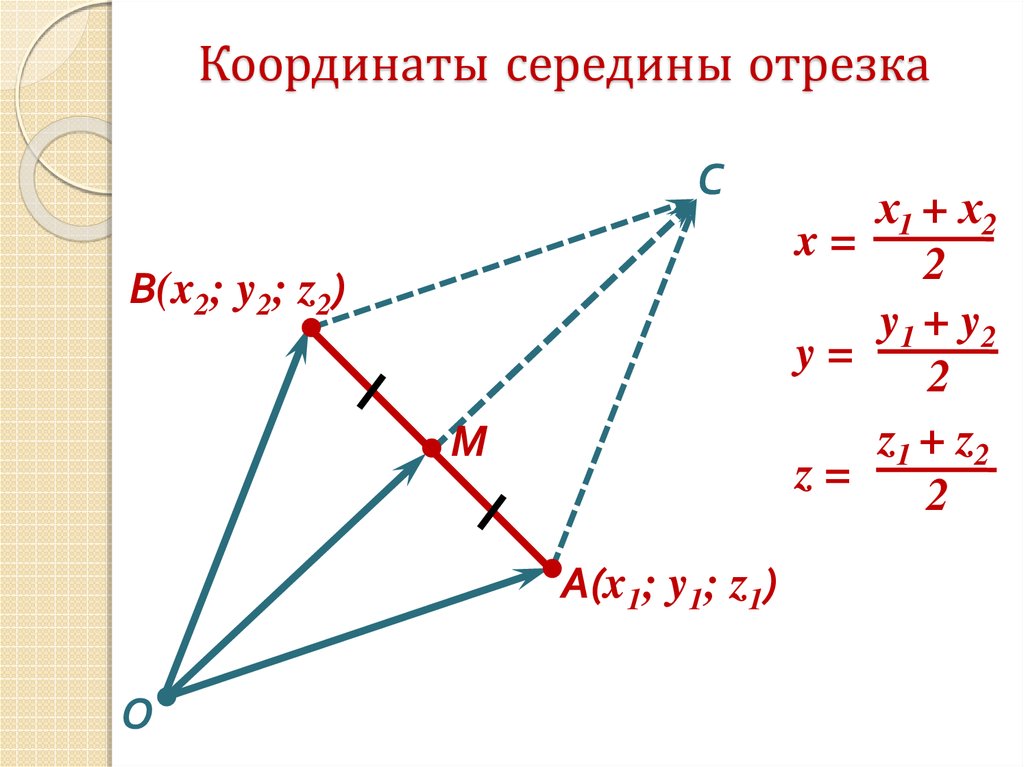
Координаты середины отрезка в пространстве

Вспомните, чем пространство отличается от плоскости. Правильно, третьим измерением! В том смысле, что добавляется еще одна координатная ось: оZ. Как это выглядит, можно посмотреть на рисунке ниже.

При этом формула нахождения середины отрезка остается неизменной. Если мы изобразим в трехмерном пространстве отрезок АВ с серединой в точке С, тогда:

Х_С = (Х_А + Х_В)/2,У_С = (У_А + У_В)/2,Z_С = (Z_А + Z_В)/2.

Координаты середины отрезка через радиус-векторы его концов

По сути, этот способ нельзя назвать каким-то новым и уникальным. Он лишь еще раз доказывает истинность формулы координат середины отрезков, только через алгебру. Чтобы разобраться в нем, давайте сначала вспомним определение вектора.

Вектор — это направленный отрезок прямой, то есть отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом.

Векторы — достаточно обширная тема. Чтобы разобраться в ней, не хватит и двух статей. Но сейчас мы с вами будем использовать всего несколько тезисов, которые помогут разобраться в теме.

1. Векторы можно изображать в системах координат оХУ и оХYZ, т. е. в двумерной и трехмерной.

2. Координаты начала и конца векторов записывают так же, как и для отрезков: (x; y) и (x; y; z).

3. Сумму векторов можно найти по методу треугольника или параллелограмма. Картинка ниже поможет вам вспомнить, как ими пользоваться.

Радиус-вектор — вектор, который задает положение точки в пространстве относительно некоторой заранее фиксированной точки — начала координат.

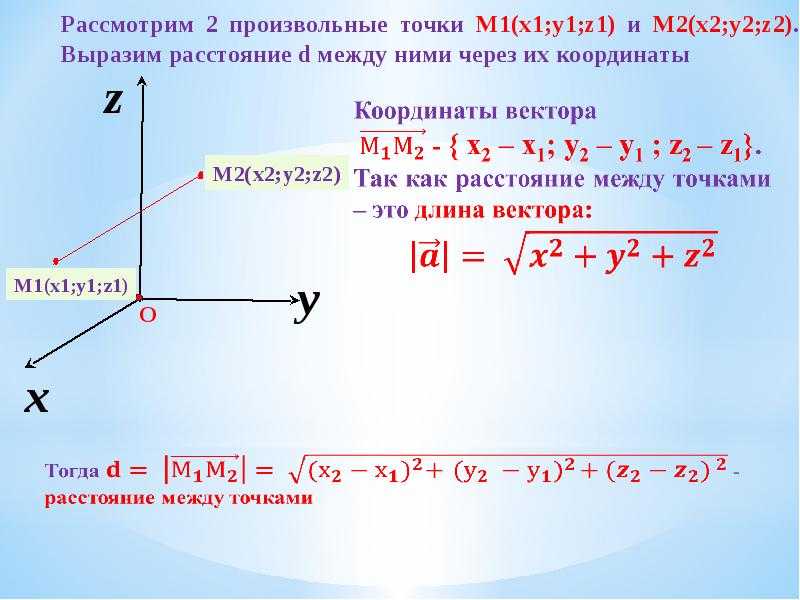
Давайте разберемся, как доказать формулу для нахождения координаты середины отрезка через радиус-векторы его концов. В Декартовой системе координат нарисуем вектор с серединой в точке К. Координаты точки А (Х_А; У_А; Z_А), К (Х_К; У_К; Z_К), С (Х_С; У_С; Z_С).Проведем радиус-векторы , , .

Согласно определению середины отрезка: ОК = ½(ОС + ОА). Координаты векторов ОА, ОК, ОС соответственно равны координатам точек А, К, С, так как координаты точки О (0; 0; 0).

ОА (Х_А – 0, У_А – 0, Z_А – 0) = (Х_А; У_А; Z_А),ОК (Х_К – 0, У_К – 0, Z_К – 0) = (Х_К; У_К; Z_К,),ОС (Х_С– 0, У_С – 0, Z_С – 0) = (Х_С; У_С; Z_С).

Тогда запишем равенство ОК = ½(ОС + ОА) через координаты:

Х_К = 1/2(Х_А + Х_О),У_К = 1/2(У_А + У_О),Z_К = 1/2(Z_А + Z_О).

Напоследок мы сделаем небольшой перерыв, забудем про формулы и числа. Давайте подумаем, как можно найти середину отрезка, если мы не знаем координат его концов.

Например, нарисуем отрезок на песчаном пляже во время каникул. Определить точные координаты в таком случае будет достаточно сложно, правда? Вряд ли вы взяли с собой в отпуск набор линеек, чтобы вычислить длину отрезка. С подобным заданием вы могли столкнуться и на уроках геометрии, где учитель раздавал вам чистые нелинованные листы бумаги и просил найти середину отрезка без использования линейки.

Сейчас мы обучим вас волшебному методу, приготовьтесь! Все что вам понадобится — это циркуль. Нарисуем на бумаге отрезок АВ любой длины. Поставим иголку циркуля в точку А и начертим окружность с радиусом, равным АВ. Далее повторим действие — прочертим такую же окружность с центром в точке В.

Мы видим, что окружности пересеклись дважды: снизу и сверху.

Если соединить эти две точки, эта прямая пересечет наш исходный отрезок ровно в его середине.

Скептики вспомнят наш пример с пляжем и скажут: «Линейку мы с собой в отпуск не берем, но и циркуль ведь тоже! Что вы скажете на это?» А ответим мы вот что: приходите на курсы по профильной математики в Skysmart! Там вы научитесь не только заменять настоящий циркуль на самодельный, но еще подготовитесь к экзаменам, разовьете логику и узнаете много всего интересного. Ждем вас на занятиях!

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Дарья Вишнякова

К предыдущей статье

Логарифмы

К следующей статье

Перпендикулярные прямые

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

формула, как по координатам его концов, блок схема

Содержание:

• Что такое середина отрезка
• Правила нахождения координат середины отрезка, формулы
  • Середина отрезка на координатной прямой
  • Середина отрезка на плоскости
  • Середина отрезка в пространстве
• Метод с использованием координат радиус-векторов концов отрезка
• Примеры решения задач

Содержание

• Что такое середина отрезка
• Правила нахождения координат середины отрезка, формулы
  • Середина отрезка на координатной прямой
  • Середина отрезка на плоскости
  • Середина отрезка в пространстве
• Метод с использованием координат радиус-векторов концов отрезка
• Примеры решения задач

Что такое середина отрезка

Отрезок — это геометрическая фигура, представляющая собой ограниченный с двух сторон участок прямой.  

Пусть точки A и B не совпадают. Если провести через них прямую, то образуется отрезок AB или BA, который ограничен точками A и B. Данные точки являются концами отрезка.

Длина отрезка — это расстояние между двумя точками, ограничивающими данный отрезок. Длина отрезка AB обозначается как модуль данной геометрической фигуры, то есть |AB|.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Серединой отрезка является такая точка C, принадлежащая отрезку AB, которая расположена в центре данного отрезка, то есть |AC|=|CB|.

Правила нахождения координат середины отрезка, формулы

Середина отрезка на координатной прямой

Предположим, что несовпадающие точки A и B лежат на координатной прямая Ох. Известно, что A и B соответствуют действительные числа x_A и x_B, а точка С делит AB пополам. Определите координату x_C, соответствующую С. 

Так как C — это середина AB, то справедливо следующее равенство:

\(\left|AC\right|=\left|CB\right|\)

Вычислим расстояние между A и C, а также между C и B. Для этого определим модуль разницы их координат. На математическом языке это будет иметь вид:

\(\left|AC\right|=\left|CB\right|\Leftrightarrow\left|x_C-x_A\right|=\left|x_B-x_C\right|\)

Опустим знак модуля и получим справедливость двух выражений:

\(x_C-x_A=x_B-x_C\)

\(x_C-x_A=-\left(x_B-x_C\right)\)

Исходя из первого равенства, получим формулу нахождения x_C, согласно которой координата точки С равна половине суммы координат A и B:

\(x_C=\frac{x_A+x_B}2\)

Следствием второго равенства будет следующее утверждение: 

\(x_A=x_B\)

Это противоречит заданным условиям, следовательно, формула определения координат середины отрезка выглядит так:

\(x_C=\frac{x_A+x_B}2\)

Середина отрезка на плоскости

В декартовой системе координат Oxy расположены две точки A(x_A,y_A) и B(x_B,y_B), которые не совпадают между собой. Точка C является центром AB. Необходимо произвести вычисление координат x_C и y_C, соответствующих С.

Пусть произвольные точки А и В лежат на одной координатной прямой, а также не принадлежат прямым, располагающимся перпендикулярно к оси абсцисс или ординат. Опустим от заданных точек A, B, C перпендикуляры на ось x на ось y. Полученные точки пересечения с осями координат A_x, A_y; B_x, B_y; C_x, C_y — это проекции исходных точек.

По построению прямые AA_x, BB_x, CC_x относительно друг друга находятся параллельно. Прямые AA_y, BB_y, CC_y не пересекаются, то есть являются параллельными. Согласно равенству AB=BC, далее применим теорему Фалеса и получим:

\(A_xC_x=C_xB_x\)

\(A_yC_y=C_yB_y\)

Это значит, что C_x и C_y являются серединами отрезков A_xB_x и A_yB_y соответственно. Теперь воспользуемся формулой определения координат середины отрезка на координатной прямой и получим:

\(x_C=\frac{x_A+x_B}2\)

\(y_C=\frac{y_A+y_B}2\)

Данные формулы подходят для вычисления координат середины отрезка в случае его расположения на осях абсцисс и ординат, а также при перпендикулярности одной из них. Следовательно, координаты центра отрезка AB, находящегося в плоскости и ограниченного точками A(x_A,y_A) и B(x_B,y_B), вычисляются следующим образом:

\(\left(\frac{x_A+x_B}2,\frac{y_A+y_B}2\right)\)

Середина отрезка в пространстве

Допустим, что в трехмерной системе координат Oxyz любые две точки с соответствующими им координатами A(x_A, y_A, z_A) и B(x_B, y_B, z_B). C(x_C, y_C, z_C) — это центр АВ. Задание заключается в том, чтобы определить x_C, y_C, z_C.

Проведем от исходных точек перпендикуляры к прямым Ox, Oy и Oz. Образовавшиеся точки пересечения с координатными осями — A_x, A_y, A_z; B_x, B_y, B_z; C_x, C_y, C_z — проекции точек A, B, C на них.

Воспользуемся теоремой Фалеса:

\(\left|A_xC_x\right|=\left|C_xB_x\right|\)

\(\left|A_yC_y\right|=\left|C_yB_y\right|\)

\(\left|A_zC_z\right|=\left|C_zB_z\right|\)

Исходя из полученных равенств следует, что C_x, C_y, C_z — делят A_xB_x, A_yB_y, A_zB_z пополам, то есть являются серединами перечисленных отрезков. Значит, для определения координат центра AB с концами A(x_A,y_A,z_A) и B(x_B,y_B,z_B) используем формулу:

\(\left(\frac{x_A+x_B}2,\frac{y_A+y_B}2,\;\frac{z_A+z_B}2\right)\)

Метод с использованием координат радиус-векторов концов отрезка

Трактовка векторов в алгебре позволяет составить формулу для расчета координат середины отрезка.

Дано: прямоугольная система координат Oxy, в которой лежат произвольные точки A(x_A,y_A) и B(x_B,y_B), а также C, делящая пополам отрезок, ограниченный A и B.

По определению действий над вектором в геометрии:

\((1)\;\overrightarrow{OC}=\frac12\times\left(\overrightarrow{OA}+\overrightarrow{OB}\right)\)

В рассматриваемой ситуации в точке C пересекаются диагонали параллелограмма с основаниями: \(\overrightarrow{OA},\;\overrightarrow{OB} \).

Это значит, что С — это центр диагоналей.

Поскольку координаты радиус вектора совпадают с координатами точки, имеем: \(\overrightarrow{OA}=\left(x_A,\;y_A\right),\;\overrightarrow{OB}=\left(x_B,\;y_B\right) \).

Произведем подстановку в формулу (1):

\(\overrightarrow{OC}=\frac12\times\left(\overrightarrow{OA}+\overrightarrow{OB}\right)=\left(\frac{x_A+x_B}2,\;\frac{y_A+y_B}2\right) \).

Получили формулу определения координат середины отрезка, находящегося в декартовой системе координат:

\(\left(\frac{x_A+x_B}2,\;\frac{y_A+y_B}2\right)\)

По аналогично схеме можно вывести формулу для расчета координат центра отрезка, лежащего в пространстве:

\(\left(\frac{x_A+x_B}2,\frac{y_A+y_B}2,\;\frac{z_A+z_B}2\right)\)

Примеры решения задач

Задача № 1

Дано: в декартовой системе координат имеются точки M(5,4) и N(1,−2). Найти координаты середины отрезка MN.

Решение:

Пусть точка O — центр MN. Тогда вычислим ее координаты, подставив в формулы:

\(x_O=\frac{x_A+x_B}2=\frac{5+1}2=\frac62=3\)

\(y_O=\frac{y_A+y_B}2=\frac{4+\left(-2\right)}2=\frac{4-2}2=\frac22=1\)

Точка O имеет координаты (3,1).

Ответ: (3,1).

Задача № 2

Дано: треугольник ABC лежит в прямоугольной системе координат. Известны координаты его вершин: A(7,3), B(−3,1), C(2,4). Вычислите длину медианы АМ.

Решение:

Поскольку АМ является медианой треугольника ABC, то точка М делит сторону ВС на два равных отрезка, то есть является серединой отрезка ВС. Отсюда можно вычислить координат точки М:

\(x_М=\frac{x_В+x_С}2=\frac{-3+2}2=\frac{-1}2=-0,5\)

\(y_М=\frac{y_В+y_С}2=\frac{1+4}2=\frac52=2,5\)

Теперь, зная координаты начала и конца отрезка АМ, применим формулу нахождения расстояния между точками:

\(AM=\sqrt{\left(x_M-x_A\right)^2+\left(y_M-y_A\right)^2}=\sqrt{\left(-0,5-7\right)^2+\left(-2,5-3\right)^2}=\sqrt{-7,5^2+\left(-5,5\right)^2}=\sqrt{56,25+30,25}=\sqrt{86,5} \).

Ответ: √86,5.

Насколько полезной была для вас статья?

У этой статьи пока нет оценок.

Как найти середину — математика GCSE

Введение

Как найти середину отрезка

Как найти рабочий лист средней точки

Поиск отсутствующей конечной точки

Распространенные заблуждения

Потренируйтесь находить середину вопросы

Как найти середину вопросов GCSE

Контрольный список обучения

Следующие уроки

Все еще застряли?

Индивидуальные занятия по математике, созданные для успеха KS4

Теперь доступны еженедельные онлайн-уроки повторения математики GCSE

Узнать больше

Введение

Как найти середину отрезка

Как найти рабочий лист средней точки

Поиск отсутствующей конечной точки

Распространенные заблуждения

Потренируйтесь находить середину вопросы

Как найти середину вопросов GCSE

Контрольный список обучения

Следующие уроки

Все еще застряли?

Здесь мы узнаем, как найти середину, в том числе найти середину отрезка с использованием декартовых координат и найти отсутствующую конечную точку, когда заданы середина и другая конечная точка.

Существуют также рабочие листы средней точки строки, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные указания о том, что делать дальше, если вы все еще застряли.

Что такое середина линии?

Середина отрезка линии — это точка, которая находится точно посередине между двумя точками. Это одинаковое расстояние от каждой конечной точки отрезка прямой.

Иногда это можно выяснить путем проверки — это проще сделать с положительными целыми числами.

Например, для двух точек (2,2) и (8,6) средняя точка находится ровно посередине между ними и лежит в (5, 4).

Мы видим, что 5 находится посередине между 2 и 8, а 4 — посередине между 2 и 6. В этом может помочь представление числового ряда.

Что такое середина линии?

Середина формулы линии

Если определить середину нелегко или координаты содержат дроби или отрицательные числа, мы можем использовать формулу средней точки.

Если точки \mathrm{A}\left(x_{1}, y_{1}\right) и \mathrm{B}\left(x_{2}, y_{2}\right) являются конечными точками отрезок, то середина отрезка, соединяющего точки A и B, равна \left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2} {2}\справа).

Это выглядит сложно, если записать алгебраически, но в основном мы вычисляем (среднее) среднее значение как значений x, так и значений y.

Мы суммируем две координаты x и делим на 2, чтобы найти координату x средней точки, и суммируем две координаты y и делим на 2, чтобы найти координату y средней точки.

Например, если даны две точки A \ (-1,2) и B \ (2,4), средняя точка (M) находится точно посередине между ними и лежит в (0,5, 3). 9{2}}=\sqrt{13} .

Пошаговое руководство: Теорема Пифагора

Если вы продолжите изучение координатной геометрии на уровне A, вы можете встретить общую формулу расстояния,

d=\sqrt{\left(x_{2}- x_{1}\right)+\left(y_{2}-y_{1}\right)}, где (x_{1},y_{1}) и (x_{2},y_{2}) – координаты двух точек, а d — расстояние между ними.

Как найти середину отрезка

Чтобы найти середину отрезка, соединяющего конечные точки A и B:

1. Найдите среднее значение \textbf{x} координат двух конечных точек.
2. Найдите среднее значение \textbf{y} координат двух конечных точек.
3. Запишите координаты точки.

Объясните, как найти середину отрезка

Рабочий лист с прямым графиком (включает в себя, как найти среднюю точку)

Получите бесплатный рабочий лист о том, как найти среднюю точку из более чем 20 вопросов и ответов по прямолинейному графику. Включает рассуждения и прикладные вопросы.

СКАЧАТЬ БЕСПЛАТНО

Икс

Рабочий лист с прямым графиком (включает в себя, как найти среднюю точку)

Получите бесплатный рабочий лист, как найти среднюю точку из 20+ вопросов и ответов по прямолинейному графику. Включает рассуждения и прикладные вопросы.

СКАЧАТЬ БЕСПЛАТНО

Как найти середину примеров

Пример 1: две положительные целые конечные точки

Найдите середину отрезка, соединяющего точки (0,6) и (4, 10).

1. Найдите среднее значение \textbf{x} координат двух конечных точек.

\frac{0+4}{2}=\frac{4}{2}=2

2 Найдите среднее значение \textbf{y} координат двух конечных точек.

\frac{6+10}{2}=\frac{16}{2}=8

3 Запишите координаты точки.

(2, \ 8)

В этом случае довольно легко увидеть среднюю точку путем осмотра, особенно при работе на графике.

Пример 2: две положительные целые конечные точки с дробным ответом

Найдите середину отрезка, соединяющего точки (1,5) и (6, 0).

Найдите среднее значение \textbf{x} координат двух конечных точек.

\frac{1+6}{2}=\frac{7}{2}=3,5

Найдите среднее значение \textbf{y} координат двух конечных точек.

\frac{5+0}{2}=\frac{5}{2}=2,5

Запишите координаты точки.

(3.5,\ 2.5)

Обычно допустимо задавать пары координат в виде коротких десятичных дробей в конце. Любые более длинные или повторяющиеся десятичные дроби следует по возможности указывать в виде дробей, не забывая об упрощении ответа.

Пример 3: пары координат, содержащие отрицательные числа

Найдите середину отрезка, соединяющего точки (-2,7) и (4, 10).

Найдите среднее значение \textbf{x} координат двух конечных точек.

\frac{-2+4}{2}=\frac{2}{2}=1

Найдите среднее значение \textbf{y} координат двух конечных точек.

\frac{7+10}{2}=\frac{17}{2}=8,5

Запишите координаты точки.

(1, \ 8,5)

Графически,

Пример 4: координаты, содержащие десятичные дроби

Найдите середину отрезка, соединяющего точки (0,5, 3) и (4, 2,5).

Найдите среднее значение \textbf{x} координат двух конечных точек.

\frac{0.5+4}{2}=\frac{4.5}{2}=2.25

Найдите среднее значение \textbf{y} координат двух конечных точек.

\frac{3+2.5}{2}=\frac{5.5}{2}=2.75

Запишите координаты точки.

(2,25, \ 2,75)

Графически,

Поиск отсутствующей конечной точки

Иногда вам может быть задана одна конечная точка и средняя точка, и вам придется работать с другой конечной точкой.

Чтобы добраться из первой конечной точки (1,3) в среднюю точку (3,7), мы перемещаем 2 в направлении x и 4 в направлении y. Поэтому мы просто повторяем это снова из средней точки, чтобы найти координату другой конечной точки, которая в данном случае будет (5,11).

Как найти отсутствующую конечную точку

Чтобы найти отсутствующую конечную точку при наличии одной конечной точки и средней точки:

1. Решите, как добраться от заданной конечной точки до средней точки.
2. Повторите это, чтобы перейти от средней точки к отсутствующей конечной точке.
3. Запишите координаты отсутствующей конечной точки.

Объясните, как найти отсутствующую конечную точку

Пример 5: поиск отсутствующей конечной точки при наличии одной конечной точки и средней точки

Отрезок соединяет точки A и B и имеет середину M.

A имеет координаты (4, 8), а M имеет координаты (6 , 9).

Найдите координаты точки B.

Решите, как добраться из заданной конечной точки в среднюю.

Чтобы добраться из A в M, мы добавляем 2 к координате x точки A и добавляем 1 к координате y точки A.

Повторите это, чтобы добраться от средней точки до недостающей конечной точки.

Чтобы добраться из M в B, мы добавляем 2 к координате x точки M и добавляем 1 к координате y точки M.

Запишите координату отсутствующей конечной точки.

Следовательно, координаты точки B равны (8,10).

Пример 6: поиск отсутствующей конечной точки с отрицательными координатами

Отрезок соединяет точки A и B и имеет середину M.

A имеет координаты (-9, 4), а M имеет координаты (-6, -1 ).

Найдите координаты точки B.

Решите, как добраться из заданной конечной точки в среднюю.

Чтобы перейти от A к M, мы добавляем 3 к координате x точки A и вычитаем 5 из координаты y точки A.

Повторите это, чтобы перейти от средней точки к отсутствующей конечной точке.

Чтобы добраться из M в B, мы добавляем 3 к координате x точки M и вычитаем 5 из координаты y точки M.

Запишите координату отсутствующей конечной точки.

Следовательно, координаты точки B равны (-3,-6).

Распространенные заблуждения

• Нахождение среднего значения каждой точки, а не среднего значения \textbf{x} координат и среднее значение \textbf{y} координат

Например, для точек (2, 3) и (5, 7) убедитесь, что вы не делаете \frac{2+3}{2} и \frac{5+7}{2}.

• Использование формулы средней точки при задании одной конечной точки и средней точки

Если одна конечная точка (3, 4), а средняя точка (6, 2), убедитесь, что вы определили, как добраться от конечной точки до средней точки, и повторите это, а не используйте формулу средней точки.

• Ошибки вычисления отрицательных чисел

Если вы не уверены в своем ответе, нарисуйте схему и посчитайте шаги.

Практика нахождения средней точки Вопросы

(5, \ 9)

(4, \ 10)

(7, \ 7)

(4, \ 9)

\frac{2+6}{2}=\frac{8}{2}=4, а среднее значение координат y равно \frac{8+12}{2}=\frac{20}{2}=10 .

(1, \ 3)

(6, \ 7.5)

(5.5, \ 7.5)

(6.5, \ 7.5)

Среднее значение координат x равно \frac{4+7}{2}=\frac{11}{ 2}=5,5, а среднее значение координаты Y равно \frac{10+5}{2}=\frac{15}{2}=7,5.

(2, \ 3)

(4, \ 5)

(4, \ 3)

(2, \ 5)

Среднее значение координат x равно \frac{-2+6}{ 2}=\frac{4}{2}=2, а среднее значение координат y равно \frac{8+(-2)}{2}=\frac{6}{2}=3.

(7, \ 7,5)

(7.5, \ 7.25)

(6, \ 8.5)

(7.25, \ 7.25)

Среднее значение координат x равно \frac{3.5+11}{2}=\frac{14. 5}{ 2}=7,25, а среднее значение координаты Y равно \frac{6+8,5}{2}=\frac{14,5}{2}=7,5.

(0, \ 7)

(14, \ 6)

(6.5, \ 3)

(5, \ 2)

Чтобы добраться из А в М, прибавьте 5 к координате x и прибавьте 2 к координате у. Повторите это, чтобы перейти от M к B, поэтому координата B равна (14, \ 6).

(1, \ 8.5)

(4, \ 3)

(-3, \ 13)

(-5, \ 13)

Чтобы получить из A в M, вычтите 4 из координаты x и добавьте 3 к координате y. Повторите это, чтобы перейти от M к B, поэтому координата B равна (-5, \ 13).

Как найти середину вопросов GCSE

1. Отрезок соединяет точки A и B и имеет середину M.

 

A имеет координаты (3, \ -12).

B имеет координаты (-5,\10).

 

Определите координаты точки M.

 

(2 балла)

Показать ответ

Исправьте координаты x или y или найдите среднюю точку с помощью \frac{3+(-5)}{ 2} или \frac{-12+10}{2} .

(1)

(-1, \-1)

(1)

2.

 

а) Запишите координаты точки А.

 

(c) На сетке отметьте крестиком точку (-2, \ 3). Обозначьте это C.

 

(3 балла)

Показать ответ

(a) (-2, \ 1)

(1)

  90

(1)

 

(c)

Точка отмечена в правильном положении.

(1)

3. Отрезок соединяет точки P и Q и имеет середину M.

P имеет координаты (9, \ 5), а M имеет координаты (15, \ 8).

Точка R расположена так, что треугольник PQR является прямоугольным.

Координата y R равна 5. Какова координата x R?

 

(3 балла)

Показать ответ

Метод определения координат конечной точки, например, +6 к координате x или +3 к координате y.

(1)

Q = (21, \ 11)

(1)

x координата R = 21 .

(1)

Учебный контрольный список

Теперь вы научились:

• Находить середину отрезка, соединяющего две точки
• Найти отсутствующую конечную точку по одной конечной точке и средней точке

Все еще зависает?

Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.

Узнайте больше о нашей программе повторения GCSE по математике.

Мы используем необходимые и необязательные файлы cookie для улучшения работы нашего веб-сайта. Пожалуйста, ознакомьтесь с нашей Политикой в ​​отношении файлов cookie, чтобы узнать, как мы используем файлы cookie и как управлять вашими настройками файлов cookie или изменять их. Примеры

Середина относится к точке, которая находится посередине линии, соединяющей две точки. Две опорные точки являются конечными точками линии, а средняя точка лежит между двумя точками. Середина делит линию, соединяющую эти две точки, на две равные половины. Кроме того, если провести линию, делящую пополам линию, соединяющую эти две точки, линия проходит через середину.

Формула средней точки используется для нахождения средней точки между двумя точками, координаты которых нам известны. Формула средней точки также используется для нахождения координат конечной точки, если известны координаты другой конечной точки и средней точки. В координатной плоскости, если провести линию, соединяющую две точки (4, 2) и (8, 6), то координаты середины линии, соединяющей эти две точки, равны ({4 + 8}/2, {2 + 6}/2) = (12/2, 8/2) = (6, 4). Давайте узнаем больше о формуле средней точки и различных методах нахождения середины линии.

1.	Что такое середина?
2.	Формула средней точки
3.	Как найти середину?
4.	Формулы, относящиеся к средней точке
5.	Часто задаваемые вопросы о Midpoint Formula

Что такое средняя точка?

Средняя точка — это точка, лежащая между двумя точками и находящаяся посередине линии, соединяющей эти две точки. Если провести линию, соединяющую две точки, то средней точкой будет точка в середине линии, равноудаленная от двух точек. Для любых двух точек, скажем A и C, середина — это точка B, расположенная посередине между точками A и C. Следовательно, чтобы вычислить середину, мы можем просто измерить длину отрезка и разделить ее на 2.

Обратите внимание, что точка B равноудалена от A и C. Середина существует только для отрезка прямой. Линия или луч не могут иметь середины, потому что линия неопределенна в обоих направлениях, а луч имеет только один конец и поэтому может быть продолжен.

Формула средней точки

Формула средней точки определяется для точек на осях координат. Пусть (x) ₁ , (y) ₁ и (x) ₂ , (y) ₂ — концы отрезка. Средняя точка равна половине суммы x-координат двух точек и половине суммы y-координат двух точек. Формула средней точки для вычисления середины отрезка, соединяющего эти точки, может быть представлена ​​​​как

Формула средней точки в математике

Даны две точки A (x) ₁ , (y) ₁ и B (x) ₂ , (y) ₂ , средняя точка между A и B определяется как ,

М(х) ₃ , (у) ₃ = [(х) ₁ + (х) ₂ ]/2, [(у) ₁ + (у) _{2 2 ]/2}

где M — середина между A и B, а (x) ₃ , (y) ₃ — ее координаты.

Давайте посмотрим на этот пример и найдем середину двух точек на одномерной оси. Предположим, у нас есть две точки, 5 и 9, на числовой прямой. Середина будет вычисляться как: (5 + 9)/2 = 14/2 = 7. Таким образом, 7 является серединой 5 и 9. , (х) ₁ , (у) ₁ и (х) ₂ , (у) ₂ . Для любого линейного отрезка средняя точка находится посередине между двумя его конечными точками. Выражение для координаты x средней точки равно [(x) ₁ + (x) ₂ ]/2, что является средним значением координат x. Точно так же выражение для координаты y имеет вид [(y) ₁ + (y) ₂ ]/2, что является средним значением координат y.

Таким образом, формула для средней точки имеет вид пример, чтобы увидеть применение формулы средней точки.

Пример: Используя формулу средней точки, найдите среднюю точку между точками X(5, 3) и Y(7, 8).

Решение: Пусть M будет серединой между X и Y.

M = ((5 + 7)/2, (3 + 8)/2) = (6, 11/2)

Следовательно, координаты середины между X и Y равны (6, 11/2).

Как найти середину?

Далее, на основе точек и значений их координат используются следующие два метода для нахождения середины линии, соединяющей две точки.

Метод 1: Если отрезок прямой вертикальный или горизонтальный, то, разделив длину на 2 и считая это значение от любой из конечных точек, мы получим середину отрезка прямой. Посмотрите на рисунок, показанный ниже. Координаты точек A и B равны (-3, 2) и (1, 2) соответственно. Длина горизонтальной линии \(\overline{AB}\) равна 4 единицам. Половина этой длины составляет 2 единицы. Перемещение на 2 единицы из точки (-3, 2) даст (-1, 2). Итак, (-1, 2) — это середина \(\overline{AB}\).

Метод 2: Другой способ найти среднюю точку — использовать формулу средней точки. Координаты точек A и B равны (-3, -3) и (1, 4) соответственно. Используя формулу средней точки, мы имеем: ({-3 + 1}/2, {-3 + 4}/2) = (-2/2, 1/2) = (-1,1/2).

Метод 3: Один из способов найти середину прямой, заданной на плоскости, — это построение. Мы можем использовать конструкцию циркуля и линейки, чтобы сначала построить линзу, используя дуги окружности одинакового (и достаточно большого) радиуса с центрами в двух конечных точках, а затем соединив вершины линзы (две точки, где дуги пересекаются). Точка пересечения линии, соединяющей бугры и отрезок, является серединой отрезка.

Вот пример поиска координат конечной точки по средней точке и координатам другой конечной точки.

Пример: Середина R между точками P и Q имеет координаты (4, 6). Если координаты Q равны (8, 10), то каковы координаты точки P? Решите его, используя формулу средней точки.

Решение:
Пусть координата x точки P равна m, а координата y точки P равна n.

Р = (м, н)
Q = (8, 10)
R = (4, 6)
Используя формулу средней точки,

R = ((m + 8)/2, (n + 10)/2) = (4, 6)
Решение для m,
(м + 8)/2 = 4
м + 8 = 8
m = 0

Решение для n,
(n + 10)/2 = 6
п + 10 = 12
n = 2

Следовательно, координаты P равны (0, 2).

Важные примечания относительно средней точки:

Следующие точки являются важными свойствами средних точек.

• Середина делит отрезок в равном соотношении, то есть 1:1.
• Середина делит отрезок на две равные части.
• Биссектриса отрезка пересекает его середину.

Формула средней точки включает вычисления отдельно для x-координаты точек и y-координаты точек. Кроме того, вычисления точек между двумя заданными точками также включают в себя аналогичные вычисления координаты x и координаты y заданных точек. Следующие две формулы тесно связаны с формулой средней точки.

• Центроид формулы треугольника
• Формула сечения

Центроид треугольника Формула

Точка пересечения медиан треугольника называется центром треугольника. Медиана — это линия, соединяющая вершину с серединой противоположной стороны треугольника. Центроид делит медиану треугольника в отношении 2:1. Для треугольника с вершинами (x) ₁ , (y) ₁ , (x) ₂ , (y) ₂ , (x) ₃ , (y) ₃ формула для нахождения координат центра тяжести треугольника выглядит следующим образом.

Формула сечения

Формула сечения помогает найти координаты любой точки, которая находится на линии, соединяющей две точки. Далее, отношение, в котором точка разделила линию, соединяющую две заданные точки, необходимо, чтобы узнать координаты точки. Точка может располагаться между точками или в любом месте за точками, но на одной линии. Формула сечения для нахождения координат точки, которая делит линию, соединяющую точки (x) ₁ , (у) ₁ и (х) ₂ , (у) ₂ в соотношении m:n выглядит следующим образом. Знак плюс используется в формуле для нахождения координат точки, которая делит точки внутри, а знак минус используется, если точка делится снаружи.

☛ Связанные темы:

Ознакомьтесь с еще несколькими интересными статьями, которые содержат дополнительные концептуальные идеи, вращающиеся вокруг формулы средней точки.

• Медиана треугольника
• Геометрия
• Равноудаленный
• Калькулятор средней точки
• Центроид Формула

Часто задаваемые вопросы о Midpoint Formula

Что такое формула средней точки в координатной геометрии?

Формула средней точки в координатной геометрии определяется как формула для нахождения центральной точки прямой с использованием координат ее концов. Формула средней точки используется для нахождения половины пути, то есть точки, которая делит прямую на две равные части.

Что означает середина?

Средняя точка определяется как точка, которая находится в середине линии, соединяющей две точки. Это точка, которая равноудалена от обеих конечных точек и, таким образом, делит отрезок пополам.

Как использовать формулу средней точки?

Формула средней точки очень проста, когда дело доходит до ее применения.

• Шаг 1: Определите сегмент линии или две конечные точки.
• Шаг 2: Найдите их координаты.
• Шаг 3: Сложите координаты x обеих конечных точек и разделите на 2.
• Шаг 4: Сложите координаты Y обеих конечных точек и разделите на 2.
• Шаг 5: Запишите значения, полученные на шагах 3 и 4, при упоминании координат любой точки.

☛ Также проверьте: Вы можете попробовать этот калькулятор средней точки, чтобы проверить результат, полученный для средней точки отрезка линии — Калькулятор средней точки

Что такое формула средней точки в Word?

Для середины линии, соединяющей две точки, координаты которых заданы, формула середины точки словесно может быть описана как половина суммы x-координат двух точек и половина суммы y-координат две точки.

Почему важна формула средней точки?

Формула средней точки имеет различные применения в реальной жизни, например, для целей строительства и т. д. Она имеет важное значение в геометрии, например,

• Нахождение координат центра тяжести треугольника.
• Нахождение медианы треугольника.
• Нахождение середины отрезка.

Может ли середина быть дробью?

Да, среднее значение также может быть дробным. Это в основном зависит от числового значения двух точек. Средняя точка представляет собой сумму числового значения двух точек, деленную на 2. Для таких точек, как -4 и 5 на числовой прямой, средняя точка равна +1/2.

Как рассчитать среднюю точку?

Середину можно найти по формуле [(x) ₁ + (x) ₂ ]/2, [(y) ₁ + (y) ₂ ]/2. Здесь (x) ₁ , (y) ₁ и (x) ₂ , (y) ₂ — координаты двух точек, а середина — точка, лежащая на равном расстоянии между этими двумя точками.

Может ли середина быть нулем?

Средняя точка может быть нулевой. Это зависит от значения двух точек. Для двух точек на числовой прямой в точках со значениями -4 и 4 середина равна 0. А для двух точек, таких как (-2, 5) и (2, -5), середина равна (0 , 0).

Что такое середина линии?

Середина линии — это точка, равноудаленная от концов линии и в середине линии. Если конечные точки линии (x) ₁ , (y) ₁ и (x) ₂ , (y) ₂ , то формула для середины линии {[(x ) ₁ + (x) ₂ ]/2, [(y) ₁ + (y) ₂ ]/2}

Что такое середина кривой?

Середина кривой — это середина наибольшей хорды, которую можно провести для кривой. Середина окружности — это середина ее наибольшей хорды, которая является диаметром окружности.

Что такое середина треугольника?

Середина треугольника является центром тяжести треугольника. Центроид – это точка пересечения медиан треугольника.