Как обозначать периметр и площадь: Какой буквой обозначается площадь? — ответ на Uchi.ru

Содержание

Тест для учащихся 8 класса «Периметр. Площадь и единицы площади»

Тест для учащихся 8 класса

по теме «Периметр. Площадь и единицы площади»

по учебнику В.В.Эк

(по программе для умственно отсталых детей)

1. Выбери правильное утверждение и подчеркни его

а) Периметр – это внутренняя часть геометрической фигуры.

Периметр – это все отрезки, из которых состоит фигура.

Периметр – это сумма длин всех сторон геометрической фигуры.

Б) Площадь – это внутренняя часть геометрической фигуры.

Площадь – это сумма длин всех сторон геометрической фигуры.

Площадь — это сумма длин всех сторон геометрической фигуры.

2. Обведи кружочком букву, которой принято обозначать:

N L S F P Q

3.Среди условных обозначений выбери и подпиши те, которые обозначают единицы измерения площади:

мм, ч, кг, кв. см, т, с, см, км, сут., м ², см ², м, л, г, мин, дм ² .

4.Заштрихуй площадь треугольника. Что больше: площадь треугольника или круга? (Подчеркни правильный ответ)

а) площадь круга больше

б) площадь треугольника больше

5. Заполни пропуски.

1 м ² = дм ² 1 м ² = см ² 1 дм ²= см ²

5 м ² = см ² 600 см ² = дм ² 7 дм ²= см ²

6. Сравни.

2 см ²….. 2 дм ² 300 см ²….. 3 м ²

4 см ²….. 40 см ² 1000 дм ² ….. 1 м ²

18 м ²….. 1800 дм ² 5300 м

² …… 530 000 см ²

7. Найди правильные утверждения и обведи кружочком букву.

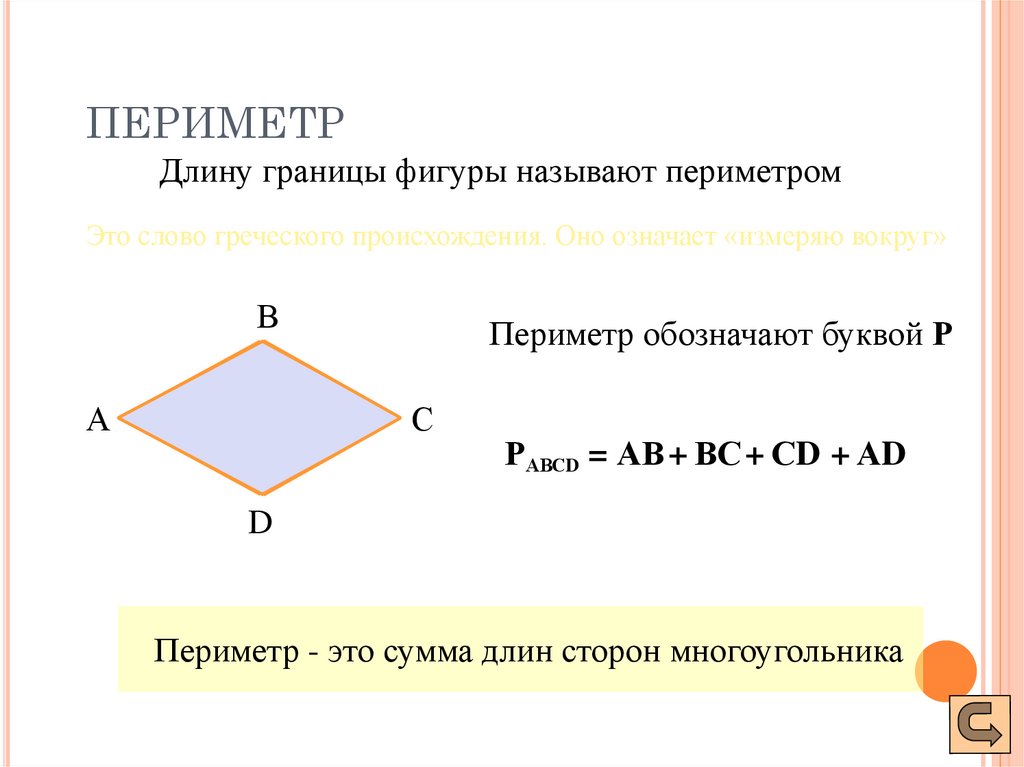
А) Чтобы вычислить площадь прямоугольника, надо узнать его длину и ширину (в одинаковых единицах) и найти произведение полученных чисел.

Б) Чтобы найти площадь квадрата, надо сложить его стороны и полученную сумму умножить на 4.

В) S прямоуг. = а x b

Г) S кв. = а x 4

Д) Чтобы найти площадь квадрата, надо умножить длину стороны на саму себя.

Е) Чтобы найти площадь прямоугольника, надо сложить его длину и ширину и полученную сумму умножить на 2.

8. Прочитай задачу и рассмотри несколько её решений. Обведи кружочком номер правильного решения этой задачи.

Площадь прямоугольника равна 45 м ² . Его длина равна 15 м. Чему равна ширина прямоугольника?

1) (45-15) : 2 = 15 м

2) 45-15 = 30 м

3) 45 : 15 = 3 м

9. Заполни таблицу.

Длина (м)	Ширина (м)	Площадь (м ²)
2	3
	6	54
12		48
14	7
13		91

10. Найди верные утверждения и обведи кружочком правильную букву.

А) Чтобы найти периметр прямоугольника, надо сложить длины всех его сторон и умножить на 2.

Б) Чтобы найти периметр квадрата, надо длину его стороны умножить на 4.

В) Чтобы найти периметр прямоугольника, надо сложить значения его длины и ширины и полученную сумму увеличить в 2 раза.

Г) Чтобы найти сторону квадрата, надо его периметр разделить на 4.

Д) P прямоуг. = (а + b ) x 2

11. Реши задачу.

Сумма длин сторон квадрата равна 20 дм. Чему равна площадь этого квадрата?

Опубликовано

02.12.17 в 19:58 в группе «УРОК.РФ: группа для участников конкурсов»

как найти периметр. Что мы узнали

, ломаная и т. д.:

Если внимательно посмотреть на все эти фигуры, то можно выделить две из них, которые образованы замкнутыми линиями (окружность и треугольник). Эти фигуры имеют своего рода границу, отделяющую то что находится внутри, от того что находится снаружи. То есть граница делит плоскость на две части: внутреннюю и внешнюю область относительно фигуры, к которой она относится:

Периметр

Периметр — это замкнутая граница плоской геометрической фигуры, отделяющая её внутреннюю область от внешней.

Периметр есть у любой замкнутой геометрической фигуры:

На рисунке периметры выделены красной линией. Обратите внимание, что периметр окружности часто называют длиной.

Периметр измеряется в единицах измерения длины: мм, см, дм, м, км.

У всех многоугольников нахождение периметра сводится к сложению длин всех сторон, то есть периметр многоугольника всегда равен сумме длин его сторон. При вычислении периметр часто обозначают большой латинской буквой P:

Площадь

Площадь — это часть плоскости, занимаемая замкнутой плоской геометрической фигурой.

Любая плоская замкнутая геометрическая фигура имеет определённую площадь.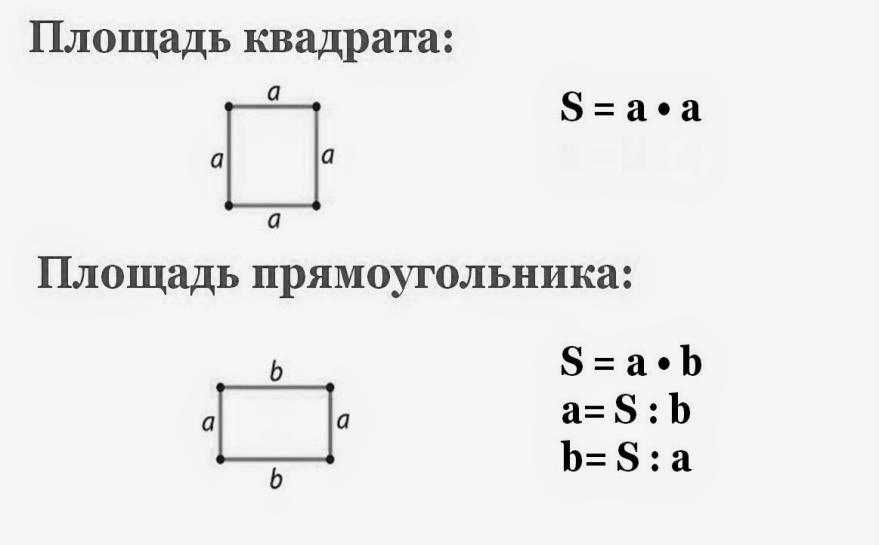 На чертежах площадью геометрических фигур является внутренняя область, то есть та часть плоскости, которая находится внутри периметра.

Измерить площадь фигуры — значит найти, сколько раз в данной фигуре помещается другая фигура, принятая за единицу измерения. Обычно за единицу измерения площади принимается квадрат, у которого сторона равна единице измерения длины: миллиметру, сантиметру, метру и т. д.

На рисунке изображён квадратный сантиметр. — квадрат, у которого каждая сторона имеет длину 1 см:

Площадь измеряется в квадратных единицах измерения длины. К единицам измерения площади относятся: мм 2 , см 2 , м 2 , км 2 и т. д.

Таблица перевода квадратных единиц

	мм 2	см 2	дм 2	м 2	ар (сотка)	гектар (га)	км 2
мм 2	1 мм 2	0,01 см 2	10 -4 дм 2	10 -6 м 2	10 -8 ар	10 -10 га	10 -12 км 2
см 2	100 мм 2	1 см 2	0,01 дм 2	10 -4 м 2	10 -6 ар	10 -8 га	10 -10 км 2
дм 2	10 4 мм 2	100 см 2	1 дм 2	0,01 м 2	10 -4 ар	10 -6 га	10 -8 км 2
м 2	10 6 мм 2	10 4 см 2	100 дм 2	1 м 2	0,01 ар	10 -4 га	10 -6 км 2
ар	10 8 мм 2	10 6 см 2	10 4 дм 2	100 м 2	1 ар	0,01 га	10 -4 км 2
га	10 10 мм 2	10 8 см 2	10 6 дм 2	10 4 м 2	100 ар	1 га	0,01 км 2
км 2	10 12 мм 2	10 10 см 2	10 8 дм 2	10 6 м 2	10 4 ар	100 га	1 км 2

10 4 = 10 000	10 -4 = 0,000 1
10 6 = 1 000 000	10 -6 = 0,000 001
10 8 = 100 000 000	10 -8 = 0,000 000 01
10 10 = 10 000 000 000	10 -10 = 0,000 000 000 1
10 12 = 1 000 000 000 000	10 -12 = 0,000 000 000 001

Знания о том, как найти периметр, учащиеся получают еще в начальной школе. Потом эта информация постоянно используется на протяжении всего курса математики и геометрии.

Общая для всех фигур теория

Стороны принято обозначать латинскими буквами. Причем их можно обозначать как отрезки. Тогда букв потребуется по две для каждой стороны и записанные большими. Или ввести обозначение одной буквой, которая обязательно будет маленькой.
Буквы всегда выбирают по алфавиту. Для треугольника они будут первыми тремя. У шестиугольника их будет 6 — от а до f. Это удобно для введения формул.

Теперь о том, как найти периметр. Он является суммой длин всех сторон фигуры. Количество слагаемых зависит от ее вида. Обозначается периметр латинской буквой Р. Единицы измерения совпадают с теми, которые даны для сторон.

Формулы периметров разных фигур

Для треугольника: Р=а+в+с. Если он равнобедренный, то формула преобразуется: Р=2а+в. Как найти периметр треугольника, если он равносторонний? Поможет такая: Р=3а.

Для произвольного четырехугольника: Р=а+в+с+d. Его частным случаем является квадрат, формула периметра: Р=4а. Есть еще прямоугольник, тогда требуется такое равенство: Р=2(а+в).

Как быть, если неизвестна длина одной или нескольких сторон треугольника?

Воспользоваться теоремой косинусов, если среди данных есть две стороны и угол между ними, который обозначается буквой А. Тогда до того, как найти периметр, придется посчитать третью сторону. Для этого пригодится такая формула: с² = а² + в² — 2 ав cos(А).

Частным случаем указанной теоремы является сформулированная Пифагором для прямоугольного треугольника. В ней значение косинуса прямого угла становится равным нулю, а значит, последнее слагаемое просто исчезает.

Бывают ситуации, когда узнать, как найти периметр треугольника, можно по одной стороне. Но при этом известны еще и углы фигуры. Здесь на помощь приходит теорема синусов, когда отношения длин сторон к синусам соответствующих противолежащих углов равны.

В ситуации, когда периметр фигуры нужно узнать по площади, пригодятся другие формулы.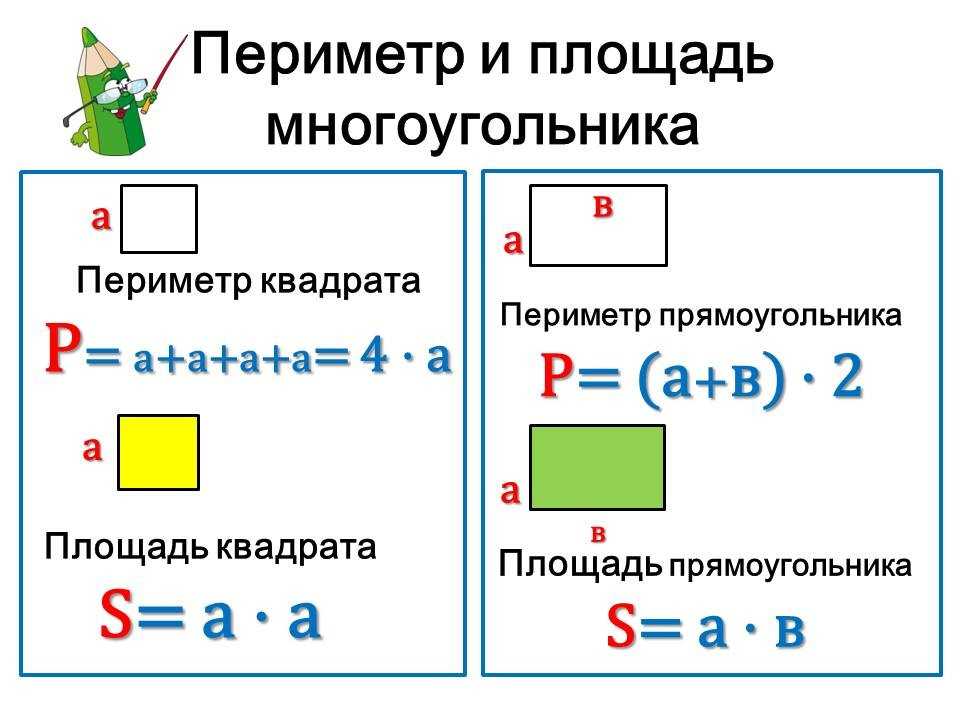 Например, если известен радиус вписанной окружности, то в вопросе о том, как находить периметр треугольника, пригодится следующая формула: S=р*r, здесь р — полупериметр. Его нужно вывести из данной формулы и умножить на два.

Примеры задач

Условие первой. Узнать периметр треугольника, стороны у которого 3, 4 и 5 см.
Решение. Нужно воспользоваться равенством, которое указано выше, и просто подставить в него данные в задаче значения. Расчеты легки, они приводят к числу 12 см.
Ответ. Периметр треугольника равен 12 см.

Условие второй. Одна сторона треугольника равна 10 см. Известно, что вторая на 2 см больше первой, а третья в 1,5 раза больше первой. Требуется вычислить его периметр.
Решение . Для того чтобы его узнать, потребуется сосчитать две стороны. Вторая определится как сумма 10 и 2, третья равна произведению 10 и 1,5. Потом останется только сосчитать сумму трех значений: 10, 12 и 15. Результатом будет 37 см.
Ответ.

Периметр равняется 37 см.

Условие третьей. Имеются прямоугольник и квадрат. Одна сторона прямоугольника равна 4 см, а другая на 3 см больше. Нужно вычислить значение стороны квадрата, если его периметр меньше на 6 см, чем у прямоугольника.
Решение. Вторая сторона прямоугольника равна 7. Зная это, легко вычислить его периметр. Расчет дает 22 см.
Чтобы узнать сторону квадрата, нужно сначала вычесть 6 из периметра прямоугольника, а потом разделить полученное число на 4. В результате имеем число 4.
Ответ. Сторона квадрата 4 см.

Наверняка каждый из нас учил в школе такую важную составляющую геометрии, как периметр. Нахождение периметра просто необходимо для решения множества задач. О том, как найти периметр, расскажет наша статья.

Стоит помнить, что периметр любой фигуры это почти всегда сумма ее сторон. Давайте рассмотрим несколько разных геометрических фигур.

Прямоугольник — это такой четырехугольник, у которого параллельные стороны равны попарно между собой.
Если одна сторона X, а другая Y, то мы получим такую формулу для нахождения периметра этой фигуры:
P = 2(X+Y) = X+Y+X+Y = 2X+2Y.
Пример решения задачи:
Допустим, что сторона X = 5 см, сторона Y = 10 см. Значит, подставив эти значения в нашу формулу, мы получим — P = 2*5 см + 2* 10см = 30 см.
Трапеция — это четырехугольник, у которого две противоположные стороны параллельны, но не равны между собой. Периметр трапеции — это сумма всех четырех её сторон:
P = X+Y+Z+W, где X, Y, Z, W — стороны фигуры.
Пример решения задачи:
Допустим, что сторона X = 5 см, сторона Y = 10 см, сторона Z = 8 см, сторона W = 20 см. Значит, подставив эти значения в нашу формулу, мы получим — P = 5 см + 10 см + 8 см + 20 см = 43 см.
Периметр круга (длину окружности) можно вычислить по формуле:
P = 2rπ = dπ, где r — это радиус круга, d — диаметр круга.
Пример решения задачи:
Допустим, что радиус r нашего круга равен 5 см, тогда диаметр d будет равен 2*5 см = 10 см. Известно, что π = 3,14. Значит, подставив эти значения в нашу формулу, мы получим — P = 2*5 см*3,14 = 31,4 см.
Если Вам необходимо найти периметр треугольника, то Вы можете столкнуться с рядом проблем при этом, поскольку треугольники могут иметь очень разные формы. Например, есть острый, тупой, равнобедренный, прямоугольный или равносторонний треугольники. Хотя формула для всех видов треугольников такая:
P = X+Y+Z, где X, Y, Z — стороны фигуры.
Проблема в том, что при решении многих задач на нахождение периметра этой фигуры Вам не всегда будут известны длины всех сторон. Например, вместо информации о длине одной из сторон Вы можете иметь градус угла или длину высоты конкретного треугольника. Это существенно осложнит задачу, но не сделает ее решение нереальным. О том, как найти периметр треугольника, какой формы бы он не был можно прочитать » «.
Периметр такой фигуры, как ромб находят также как и периметр квадрата, ведь ромб — это параллелограмм, который имеет равные стороны. Узнать, как найти периметр квадрата можно прочитав статью на нашем сайте » «.
Теперь Вы знаете, как найти сторону периметра той геометрической фигуры, какой Вам нужно!

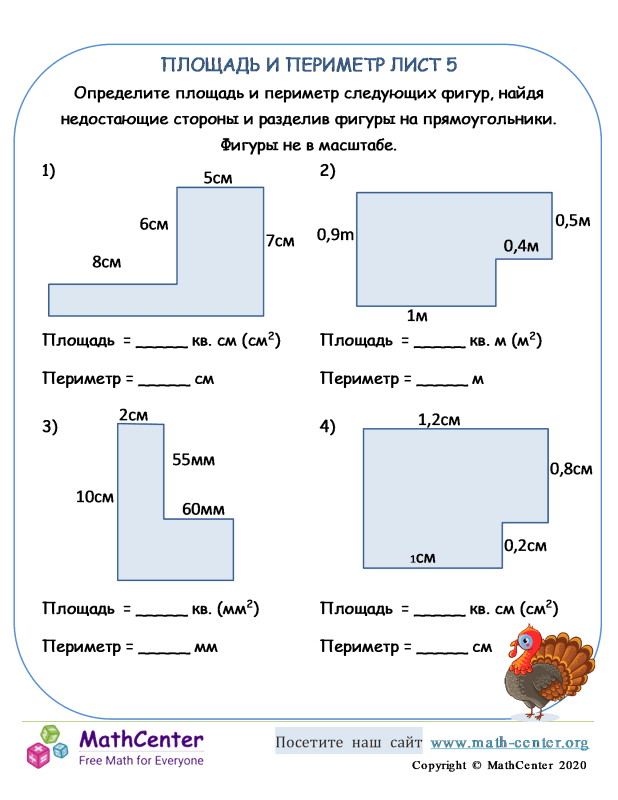
В следующих тестовых заданиях требуется найти периметр фигуры, изображенной на рисунке.

Найти периметр фигуры можно разными способами. Можно преобразовать исходную фигуру таким образом, чтобы периметр новой фигуры можно было бы легко вычислить (например, перейти к прямоугольнику).

Другой вариант решения — искать периметр фигуры непосредственно (как сумму длин всех её сторон). Но в этом случае нельзя полагаться только на рисунок, а находить длины отрезков, исходя из данных задачи.

Хочу предупредить: в одном из заданий среди предложенных вариантов ответов я не нашла того, который получился у меня.

C) .

Перенесем стороны маленьких прямоугольников с внутренней области во внешнюю. В результате большой прямоугольник замкнулся. Формула для нахождения периметра прямоугольника

В данном случае, a=9a, b=3a+a=4a.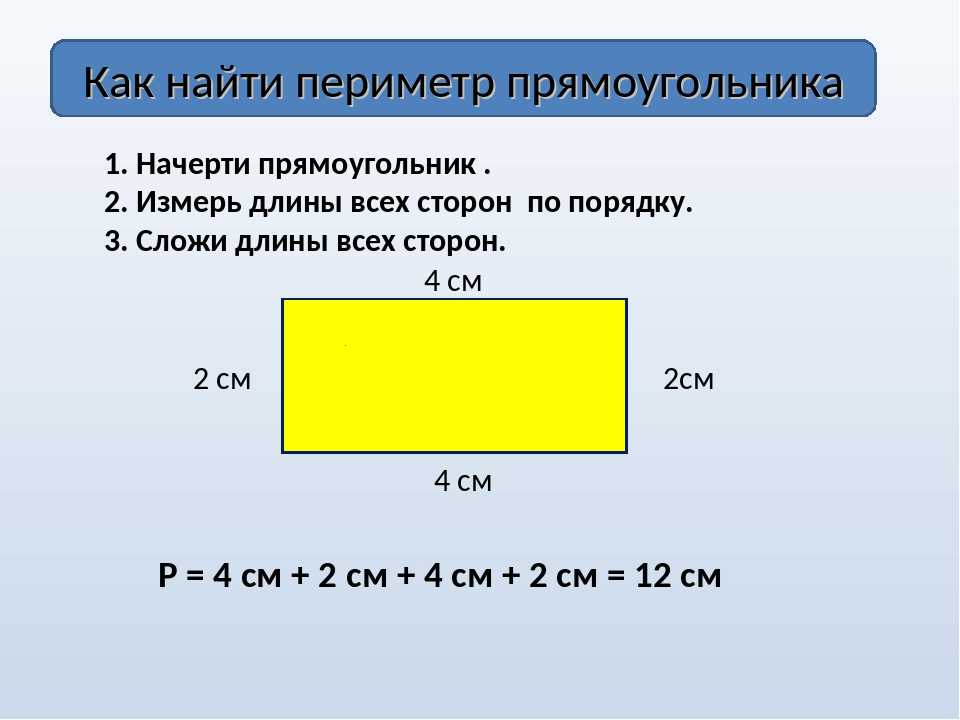 Таким образом, P=2(9a+4a)=26a. К периметру большого прямоугольника прибавляем сумму длин четырех отрезков, каждый из которых равен 3a. В итоге, P=26a+4∙3a=38a .

C) .

После переноса внутренних сторон маленьких прямоугольников во внешнюю область, получаем большой прямоугольник, периметр которого равен P=2(10x+6x)=32x, и четыре отрезка, два — диной по x, два — по 2x.

Итого, P=32x+2∙2x+2∙x=38x .

?) .

Перенесем 6 горизонтальных «ступенек» из внутренней части во внешнюю. Периметр полученного большого прямоугольника равен P=2(6y+8y)=28y. Осталось найти сумму длин отрезков внутри прямоугольника 4y+6∙y=10y. Таким образом, периметр фигуры равен P=28y+10y=38y .

D) .

Перенесем вертикальные отрезки из внутренней области фигуры влево, во внешнюю область. Чтобы получить большой прямоугольник, перенесём одни из отрезков длиной 4x в нижний левый угол.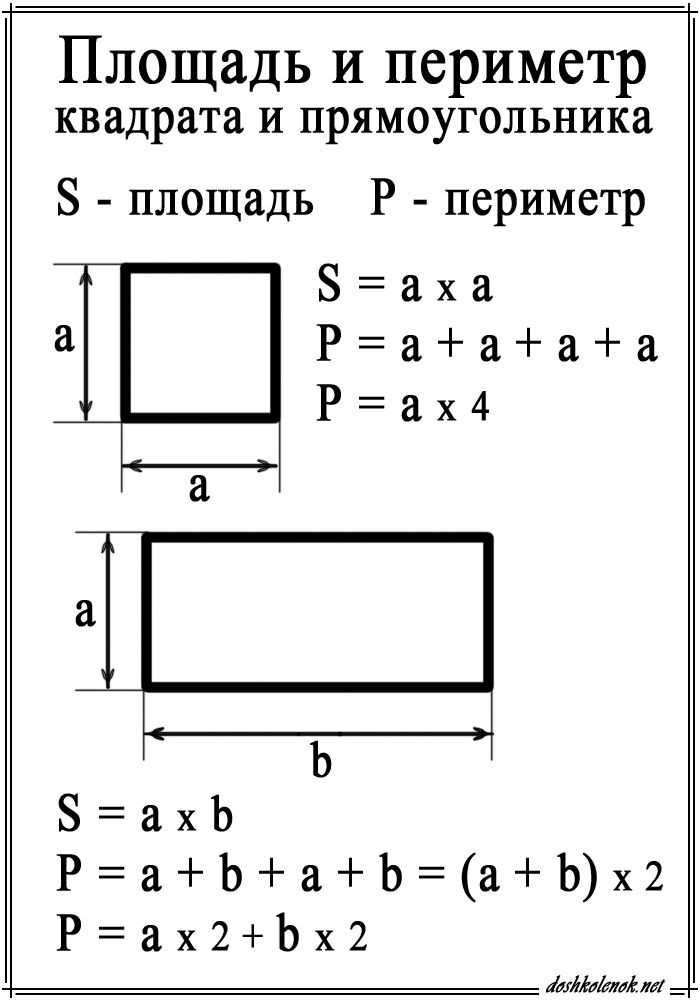

Периметр исходной фигуры найдём как сумму периметра этого большого прямоугольника и длин оставшихся внутри трёх отрезков P=2(10x+8x)+6x+4x+2x=48x .

E) .

Перенеся внутренние стороны маленьких прямоугольников во внешнюю область, получим большой квадрат. Его периметр равен P=4∙10x=40x. Чтобы получить периметр исходной фигуры, нужно у периметру квадрата прибавить сумму длин восьми отрезков, каждый длиной 3x. Итого, P=40x+8∙3x=64x .

B) .

Перенесём все горизонтальные «ступеньки» и вертикальные верхние отрезки во внешнюю область. Периметр полученного прямоугольника равен P=2(7y+4y)=22y. Чтобы найти периметр исходной фигуры, нужно к периметру прямоугольника прибавить сумму длин четырех отрезков, каждый длиной y: P=22y+4∙y=26y .

D) .

Перенесем из внутренней области во внешнюю все горизонтальные линии и передвинем две вертикальные внешние линии в левом и правом углах, соответственно, на z левее и правее.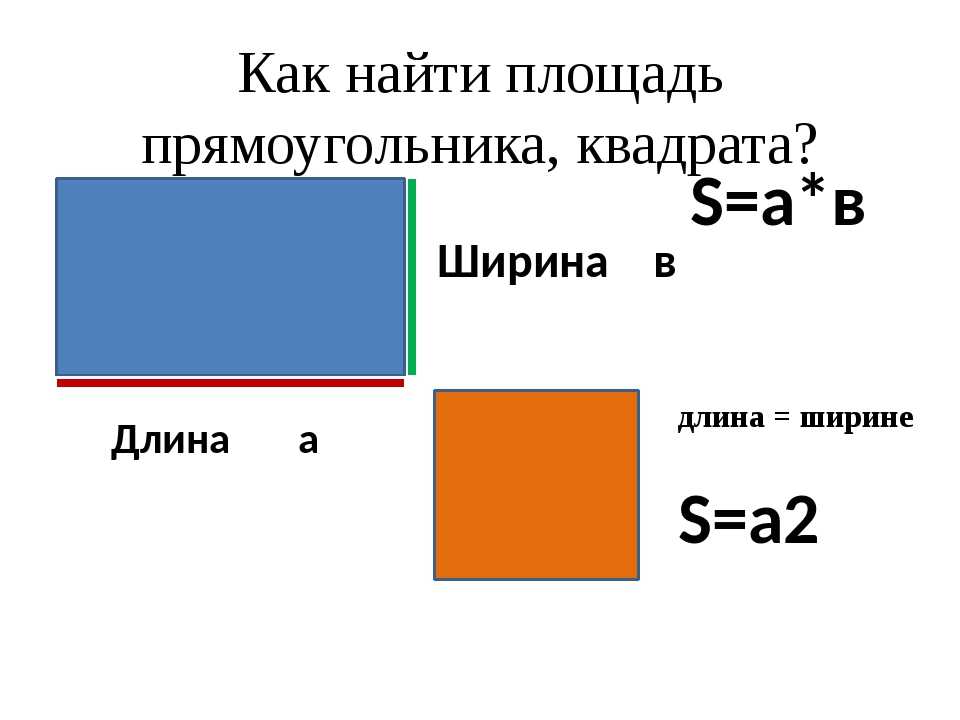 В результате получим большой прямоугольник, периметр которого равен P=2(11z+3z)=28z.

Периметр исходной фигуры равен сумме периметра большого прямоугольника и длин шести отрезков по z: P=28z+6∙z=34z .

B) .

Решение полностью аналогично решению предыдущего примера. После преобразования фигуры находим периметр большого прямоугольника:

P=2(5z+3z)=16z. К периметру прямоугольника прибавляем сумму длин оставшихся шести отрезков, каждый из которых равен z: P=16z+6∙z=22z .

Геометрия, если не ошибаюсь, в мое время изучалась с пятого класса и периметр был и есть одним из ключевых понятий. Итак, периметр — это сумма длин всех сторон (обозначается латинской литерой P) . Вообще, трактуют данный термин по разному, например,

общая длина границы фигуры,
длина всех ее сторон,
сумма длин ее граней,
длина ограничивающей фигуру линии,
сумма всех длин сторон многоугольника

Для различных фигур существуют свои формулы определения периметра.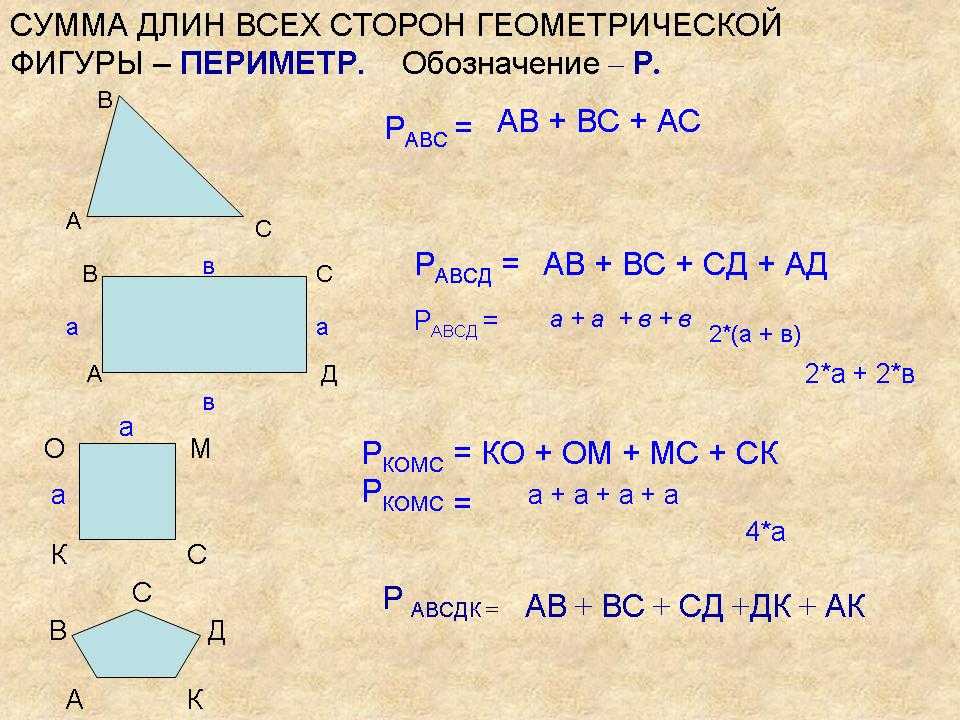 Чтобы понять сам смысл, предлагаю самостоятельно вывести несколько несложных формул:

для квадрата,
для прямоугольника,
для параллелограмма,
для куба,
для параллелепипеда

Периметр квадрата

Для примера возьмем самое простое — периметр квадрата.

Все стороны квадрата равны. Пусть одна сторона носит название «a» (также, как и остальные три), тогда

P = a + a + a + a

или более компактная запись

Периметр прямоугольника

Усложним задачу и возьмем прямоугольник. В данном случае уже нельзя сказать, что все стороны равны, поэтому пусть длины сторон прямоугольника будут равны a и b.

Тогда формула будет иметь следующий вид:

P = a + b + a + b

Периметр параллелограмма

Аналогичная ситуация будет и с параллелограммом (см. периметр прямоугольника)

Периметр куба

Что же делать, если мы имеем дело с объемной фигурой? Например, возьмем куб. Куб имеет 12 сторон и все они равны. Соответственно, периметр куба можно вычислить следующим образом:

Периметр параллелепипеда

Ну, и для закрепления материала вычислим периметр параллелепипеда. Тут необходимо немного поразмышлять. Давайте делать это вместе. Как мы знаем, прямоугольный параллелепипед представляет собой фигуру, сторонами которой являются прямоугольники. У каждого параллелепипеда есть два основания. Возьмем одно из оснований и посмотрим на его стороны — они имеют длину a и b. Соответственно, периметр основания есть P = 2a + 2b. Тогда периметр двух оснований есть

(2a + 2b) * 2 = 4a + 4b

Но ведь у нас есть еще и сторона «c». Значит формула для вычисления периметра параллелепипеда будет иметь следующий вид:

P = 4a + 4b + 4c

Как видно из примеров выше, всё, что необходимо сделать для определения периметра фигуры — найти длину каждой из сторон, а затем их сложить.

В заключение хочется отметить, что не всякая фигура имеет периметр. К примеру, у шара периметра нет.

Периметр и площадь: определение, формула, примеры решения

Автор Гурудат
Последнее изменение 25-10-2022

Площадь и периметр — две важные характеристики двумерных фигур в математике. Дети младших классов часто путают Периметр и Зону . Площадь определяется как количество пространства, занимаемого любой формой в двух измерениях. С другой стороны, периметр — это граница или контур плоской формы. Это определение применимо к любой двумерной форме любого размера, независимо от того, является ли она правильной или неправильной. Каждая фигура имеет свою уникальную формулу площади и периметра. В этой статье мы обсудим различия между этими двумя терминами, формулами площади и периметра для различных форм, таких как треугольник, квадрат, прямоугольник, круг, сфера и т. д. Читайте дальше, чтобы узнать больше.

Периметр: Периметр — это расстояние, пройденное вдоль границы замкнутой фигуры, когда вы обойдете фигуру один раз. Периметр фигуры определяется как общее расстояние вокруг фигуры. Это длина любой фигуры, которую можно разложить в линейную форму. Периметры разных фигур могут быть одинаковыми в зависимости от измерений. Например, представьте себе прямоугольник, сделанный из проволоки длиной \(L,\), из той же проволоки можно сделать квадрат, учитывая, что все стороны равны по длине.

На рисунке ниже, если мы начнем с точки \(P\) и будем двигаться вдоль отрезка, мы снова достигнем точки \(P.\) Мы сделали полный круг фигуры.

Пройденное расстояние равно длине проволоки, используемой для рисования фигуры. Таким образом, расстояние известно как периметр замкнутой фигуры.

Проверить Важные формулы измерения

Площадь : Площадь поверхности замкнутой фигуры называется ее площадью. Площадь фигуры обычно определяют с помощью ее длины и ширины. Площадь фигуры есть двумерная величина. Следовательно, он рассчитывается в квадратных единицах, таких как квадратные дюймы или квадратные футы, квадратные ярды и т.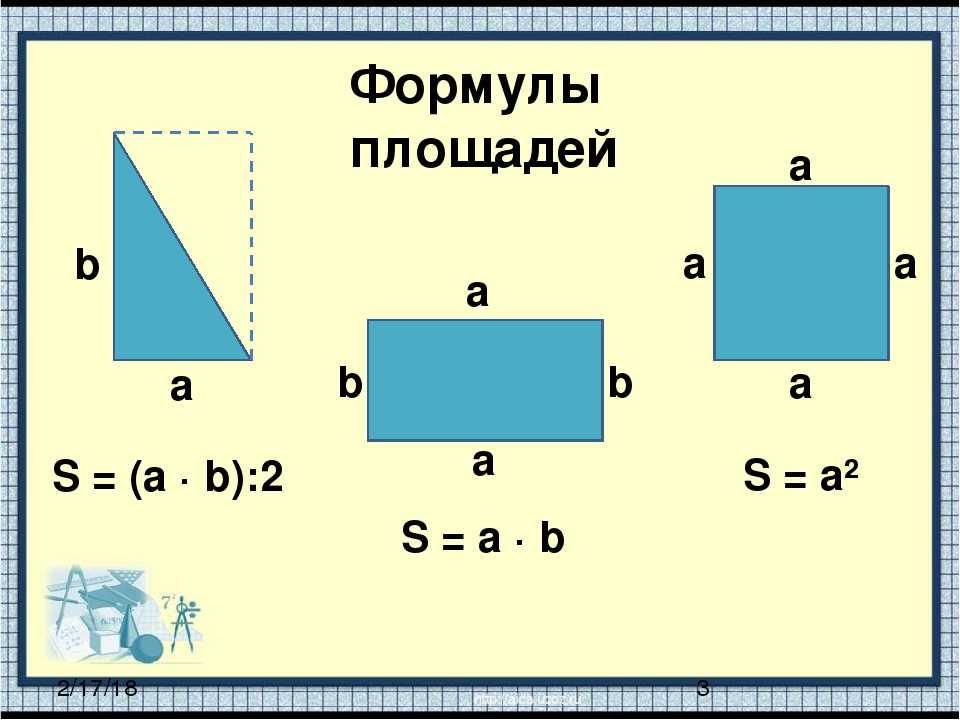 д.

У большинства фигур есть края и углы. Длина и ширина этих краев берутся при расчете площади определенной формы.

Преобразование единиц

Единица может быть преобразована в другую с помощью следующих преобразований:

(i) \(1~{\text{километр}}\left({{\text{км}}} \ справа) = 1000~\,{\text{метр}}\влево({\text{м}} \справа)\)
(ii) \(1\,{\text{метр}}\влево({\ text{m}} \right) = 100\,{\text{сантиметров}}\left( {{\text{см}}} \right)\)
(iii) \(1\,{\text{дециметр}}\влево({{\text{дм}}} \вправо) = 10\,{\text{сантиметров}}\влево({{\text{ см}}} \right)\)
(iv) \(1\,{\text{сантиметры}}\left({{\text{см}}} \right) = 10\,{\text{миллиметры} }\left( {{\text{мм}}} \right)\)
(v) \(1{\mkern 1mu} {\rm{foot}}\,{\rm{=}}\,{\ rm {12}} {\ mkern 1mu} {\ rm {дюймы}} \)
(vi) \ (1 {\ mkern 1mu} {\ rm {ярд}} \, {\ rm { = }} \, { \rm{3}}{\mkern 1mu} {\rm{футы}}\)
(vii) \(22{\mkern 1mu} {\rm{ярд}}\,{\rm{=}}\, {\ rm {1}} {\ mkern 1mu} {\ rm {цепь}} \)

Изучение концепций экзамена на Embibe

Формула периметра плоских фигур

Периметр квадрата: Квадрат — это плоская фигура с четырьмя равными прямыми сторонами и четырьмя прямыми углами.

Таким образом, периметр квадрата с длиной каждой стороны \(a\) единиц равен \(4a\,{\text{единиц}}.\)

Периметр прямоугольника : Плоскость Фигура с параллельными сторонами, равными между собой, и четырьмя прямыми углами называется прямоугольником.

Итак, периметр прямоугольника с длиной \(l\,{\text{единицы}}\) и шириной \(b\,{\text{единицы}}\) единиц равен \(2\left ( {l + b} \right)\,{\text{единицы}}\)

Периметр параллелограмма : Параллелограмм — это четырехугольник, каждая пара противоположных сторон которого параллельна.

Итак, периметр параллелограмма с длиной \(a\,{\text{единицы}}\) и шириной \(b\,{\text{единицы}}\) равен \(2\left( {a + b} \right)\,{\text{единицы}}{\text{.}}\)

Периметр ромба: Частным случаем параллелограмма, у которого четыре равные стороны и противоположные стороны, параллельные с противоположными углами, равны, является ромб.

Итак, периметр ромба со стороной \(a\,{\text{единицы}}\) равен \(4 a\,{\text{единицы}}{\text{. }}\)

Периметр круга : Замкнутая двумерная фигура, в которой множество всех точек на плоскости равноудалены от центра, называется окружностью.

Итак, периметр круга — это не что иное, как его окружность. Итак, периметр круга с радиусом \(r\) равен \(2\pi r\,{\text{единицы}}{\text{.}}\) 9\circ }.\)

Таким образом, периметр треугольника с длинами сторон \(a,b\) и \(c\,{\text{единицы}}\) равен \(P = a + b + c\,{\text{единицы}}{\text{.}}\)

Периметр равностороннего треугольника : Равносторонний треугольник – это треугольник, все три стороны которого имеют одинаковую длину и равные угол.

Итак, периметр равностороннего треугольника с длиной сторон \(a\) единиц определяется выражением \(P = 3a\,{\text{единицы}}.\)

Формула площади плоских фигур 92}\,{\text{sq}}{\text{.units}}{\text{.}}\)

(ii) Площадь прямоугольника : Площадь прямоугольника с длиной \(l\ ) и ширина \(b\) определяется выражением \(l \times b\,{\text{sq}}{\text{. units}}\)

(iii) Площадь параллелограмма : Площадь параллелограмма с основанием \(b\) и высотой \(h\) определяется выражением \(b \times h\,{\text{sq}}{\text{.units}}\)

(iv )Площадь ромба : Площадь ромба \( = \frac{1}{2} \times \left( {\rm{product}}\,{\rm{of}}\,{\rm{length }}\,{\rm{из}}\,{\rm{диагоналей}}} \right)\,{\rm{sq}}{\rm{.}}\,{\rm{единиц}}\ ) 92}\) \(2\pi b\)

Решаемые примеры – периметр и площадь

Q.1. Спортсмен совершает 10 раундов по прямоугольному парку, \(50\,{\text{м}}\) в длину и \(25\,{\text{м}}\) в ширину. Найдите полный путь, пройденный им.

Ответ: Дано: Длина прямоугольного парка \( = 50\,{\text{м}}\)
Ширина прямоугольного парка \( = 25\,{\text{м} }\)
Общее расстояние, пройденное спортсменом за один раунд, будет периметром парка.
Теперь периметр прямоугольного парка \( = 2\left({l + b} \right)\)
\( = 2\left({50 + 25} \right){\text{m}}\)
\( = 2\left({75} \right){\text{m}} = 150\,{\text{m}}\)
Значит, расстояние, пройденное спортсменом за один раунд, равно \(150 \,{\text{м}}. \)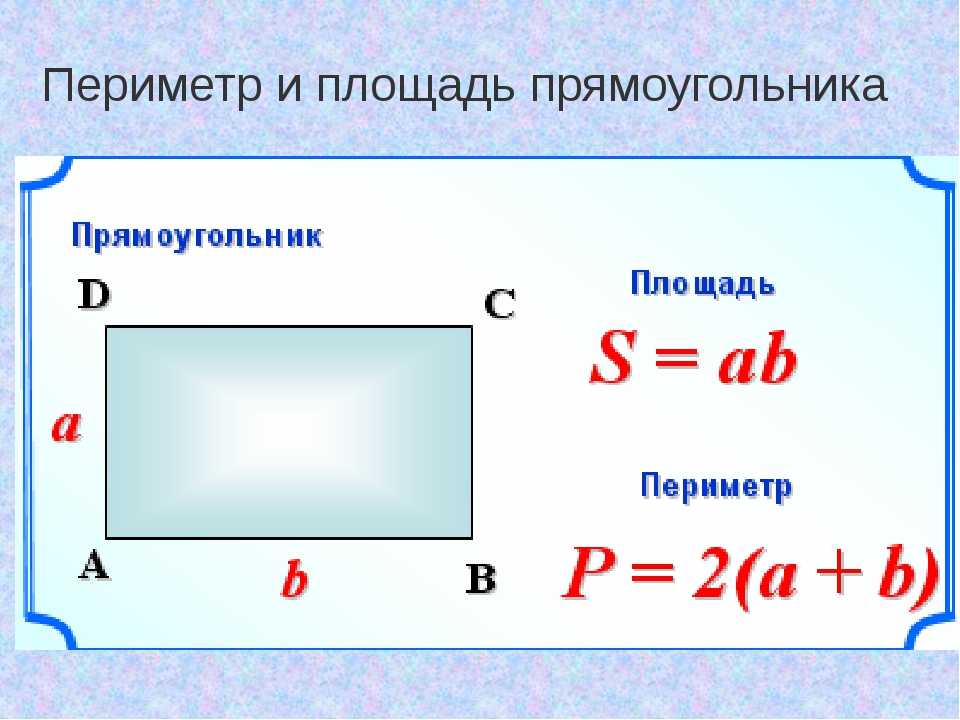
Следовательно, расстояние, пройденное спортсменом за \(10\) раундов \(10\, \times 150{\text{м=1500}}\,{\text{ м}}\)
Следовательно, общее расстояние, пройденное спортсменом, равно \({\text{1500}}\,{\text{м}}{\text{.}}\)

Q.2. Найти стоимость ограждения прямоугольного парка длиной \( 250\,{\text{м}}\) и шириной \( 175\,{\text{м}}\) из расчета \(₹12\, {\rm{per}}\,{\rm{метр}}.\)

Ответ: Длина прямоугольного парка \(=250\,{\rm{м}}\)
Ширина прямоугольного парка \( = 175\,{\rm{м}}\)
Для расчета стоимости ограждения нам потребуется периметр.
Мы знаем, что периметр прямоугольника \( = 2\left({l + b} \right)\)
Итак, площадь прямоугольного парка \( = 2\left({250 + 175} \right){\text {m}} = 2\left({425} \right){\text{m}} = 850\,{\text{m}}\) 92,}\) высота \(h = 3\,{\text{см}}{\text{.}}\)
Мы знаем, что площадь треугольника \( = \frac{1}{2} \ раз b \times h\)
\( \Rightarrow 36 = \frac{1}{2} \times b \times 3\)
\( \Rightarrow b = \frac{{72}}{3}\,{ \text{см}}\)
\( \Rightarrow b = 24\,{\text{см}}\) Следовательно, основание треугольника равно \(24\,{\text{см}}{\text {. }}\)

Q.5. Периметр правильного шестиугольника равен \(18\,{\text{см}}{\text{.}}\). Какова длина его стороны?

Ответ: Периметр правильного шестиугольника \( = 18\,{\text{см}}{\text{.}}\)
Правильный шестиугольник имеет \(6\) сторон, поэтому мы можем разделить периметр на \(6\), чтобы получить длину одной стороны.
Одна сторона шестиугольника \( = 18\,{\text{см}} \div 6 = 3\,{\text{см}}.\)
Следовательно, длина каждой стороны правильного шестиугольника равна \( 3\,{\text{см}}.\)

Резюме

В этой статье мы узнали об определении площади и периметра. Кроме того, мы изучили различные формулы для нахождения площади и периметра различных фигур и решили некоторые практические задачи.

Попытка пробных тестов

Часто задаваемые вопросы (FAQ) — периметр и площадь

Ответы на некоторые часто задаваемые вопросы о периметре и площади приведены здесь:

Q. 1. Как найти периметр и площадь?
Ответ: У нас есть разные формулы для разных фигур, чтобы найти периметр и площадь.
Пример: Периметр квадрата с длиной стороны a=4 кв.ед.
Площадь квадрата с длиной стороны a=a2кв.единиц

Q.2. Какая формула площади и периметра круга?
Ответ: Площадь круга с радиусом runits равна πr2, а периметр круга равен 2πr.

Q.3. Какой пример для периметра?
Ответ: Представление о периметре широко используется в нашей повседневной жизни.

Фермер, который хочет оградить свое поле.
Лицо, готовящее трассу для занятий спортом.
Во всех приведенных выше примерах используется идея периметра.

Q.4. Какая формула площади и периметра треугольника?
Ответ: Площадь треугольника =12×b×h, где b=основание и h=высота
Периметр треугольника с длинами сторон a,b и c в единицах равен p=a+b+cunits.

Q.5. Какова формула периметра?
Ответ: Периметр — это расстояние, пройденное вдоль границы, образующей замкнутую фигуру, когда вы обойдете фигуру один раз. Периметр фигуры определяется как общее расстояние вокруг фигуры. Таким образом, это длина любой фигуры, которую можно разложить в линейную форму.

Итак, формула периметра зависит от формы и измерения данной формы или предмета.
Пример: Периметр квадрата с длиной каждой стороны равен 4 единицам.
Периметр прямоугольника с единицами длины и ширины равен 2(l+b)единицам.
Периметр параллелограмма с единицами длины и ширины равен 2(a+b)единицам.

Некоторые другие полезные статьи Embibe приведены ниже:

Решения NCERT для периметра и площади Глава

Мы надеемся, что эта статья о периметре и площади принесла значительную пользу вашим знаниям. Если у вас есть какие-либо вопросы или предложения, не стесняйтесь записывать их в разделе комментариев ниже. Мы будем рады услышать от вас. Embibe желает вам удачи!

Изучение света и соли. Площадь и периметр по определению

Когда дело доходит до двумерных фигур, вам нужно очень хорошо понимать две концепции: площадь и периметр.

Помогите мне держать все мои ресурсы открытыми и бесплатными

Стать покровителем

УЗНАТЬ ЭТО

Представьте двумерную фигуру, такую как прямоугольник, треугольник или трапецию; есть два способа думать об их «измерении». Вы можете измерить длину линии вокруг внешней стороны фигуры, это периметр, или вы можете измерить пространство, чтобы покрыть фигуру, это площадь. Когда двумерная фигура, на которую вы смотрите, представляет собой прямоугольник, оба измерения довольно просты. Чтобы найти периметр, сложите все стороны. Чтобы найти площадь, умножьте два измерения прямоугольника, длину и ширину.

Посмотрите видео класса Virtual GED ниже, чтобы получить полное объяснение и множество примеров задач.