1. Действительные числа
Понятие действительного числа является одним из основных математических понятий. Свойства действительных чисел служат тем фундаментом, на котором строится теория пределов, а вместе с ней и весь современный математический анализ. Существуют различные подходы к определению действительного числа (теории Дедекинда, Кантора и другие). Однако наиболее логичным и простым является аксиоматический метод введения действительного числа.
Определение 1.1.СовокупностьRиз более чем одного элемента называетсямножеством действительных чисел, если:
а) в множестве Rопределена операция сложения элементов, сопоставляющая каждой паре элементовx, y є Rнекоторый элемент изR, называемый их суммой и обозначаемыйх+у, такой, что выполняются следующие условия (аксиомы):
1а) х+у=у+хдля любыхх, у є R;
2а) х+(у+z)=(х+у)+zдля любыхх,у,z є R;
3a) вRсуществует такой элемент, называемыйнулем и обозначаемый 0, чтох+0=хдля всехх є R;
4a) для любогох є Rсуществует элемент изR, называемыйпротивоположным хи обозначаемый —х, для которогох+(-х)=0;
б) в множестве Rопределена операция умножения элементов, сопоставляющая каждой паре элементовх, у є Rнекоторый элемент изR, называемый их произведением и обозначаемыйху, такой, что выполняются следующие условия (аксиомы):
1б) ху=ухдля любыхх, у є R;
2б) х (уz)=(ху) zдля любыхх, у, z є R;
3б) в Rсуществует такой элемент, называемый единицей и обозначаемый1, чтох·1=х, для всехх є R;
4б) для любого Rэлементах≠0существует элемент изR,
называемый обратным к х и обозначаемый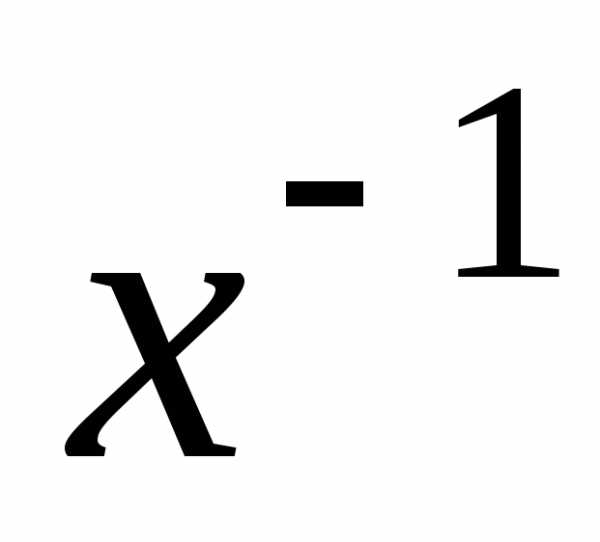 или
или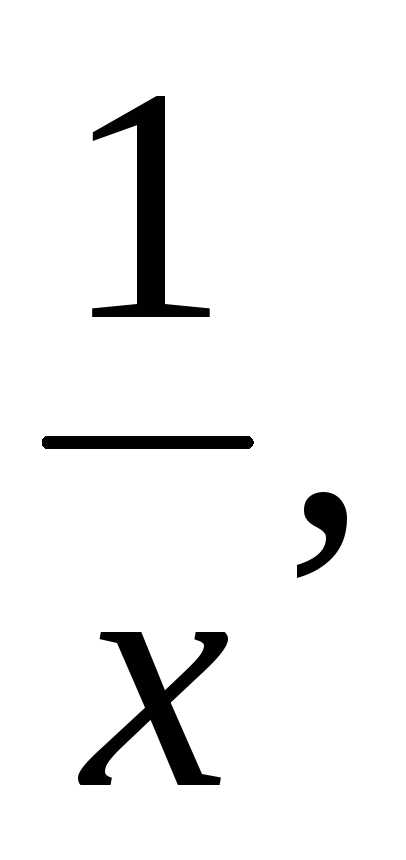 для
которого
для
которого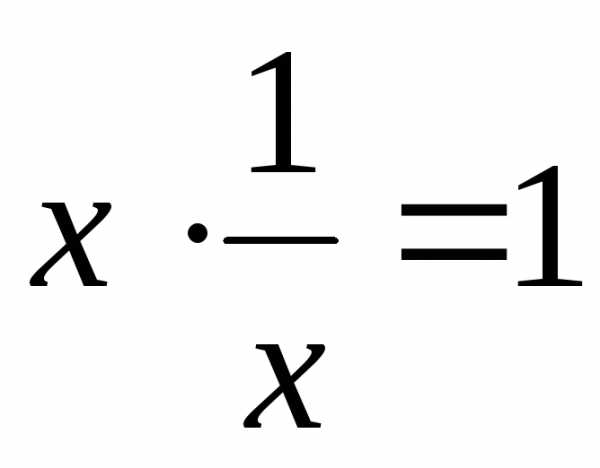 ;
;
в) операции сложения и умножения удовлетворяют условию (аксиоме):
1 в) (х+у)z=хz+уzдля всехх, у, z є R;
г) в множестве R определено отношение порядка<, определяемое следующим образом: любые два различныч элементах, у, є Rсвязаны либо отношениемх < у
1 г) если х<yиy<z, тох<z;
2 г) если х<y, то
для любого  имеет местоx+z<y+z;
имеет местоx+z<y+z;
3 г) если х<yиz>0, тоxz<yz;
д) для любых непустых множеств Х, У  Rтаких, что для
каждой пары элементовх є Хиу є
Увыполняется условиех ≤ у(либох < у, либох=у), вRсуществует элементz,
удовлетворяющий условию
Rтаких, что для
каждой пары элементовх є Хиу є
Увыполняется условиех ≤ у(либох < у, либох=у), вRсуществует элементz,
удовлетворяющий условию
Элементы множества R называютсядействительными или вещественными числами. Аксиомы групп а), б), в) есть аксиомы сложения и умножения действительных чисел, аксиомы группы г) – аксиомы сравнения действительных чисел, а аксиома группы д) – аксиома непрерывности.
Теорема 1.1.Числа0,-х,1и единственны.
единственны.
Докажем, например, единственность нуля (остальные утверждения проверяются аналогично). Допустим, что существуют два нуля 0и0/. Тогда, согласно аксиоме 3(а),0+0/=0и0/+0=0/.В силу аксиомы (а) левые части этих равенств одинаковы, следовательно, одинаковы и правые, т.е.0=0/
Число х+(-у)называетсяразностьючиселх иуобозначаетсях-у.
Число
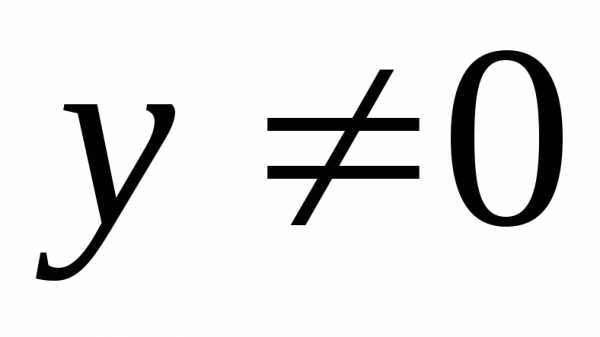 ,
называютсячастным от деленияхиуи обозначается
,
называютсячастным от деленияхиуи обозначается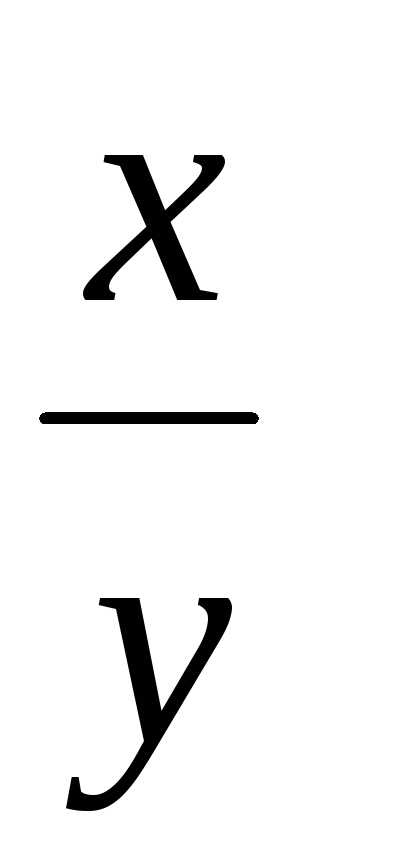 или
или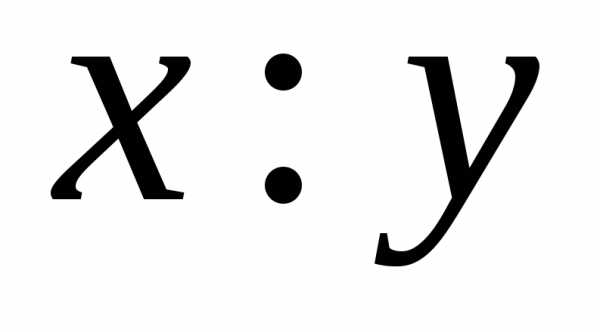 .
Соотношенияназывается неравенствами. Числох,
удовлетворяющее неравенствух>0,
называют положительным, а числох,
удовлетворяющее неравенствух<0,
называют отрицательным.
.
Соотношенияназывается неравенствами. Числох,
удовлетворяющее неравенствух>0,
называют положительным, а числох,
удовлетворяющее неравенствух<0,
называют отрицательным. Числа 1,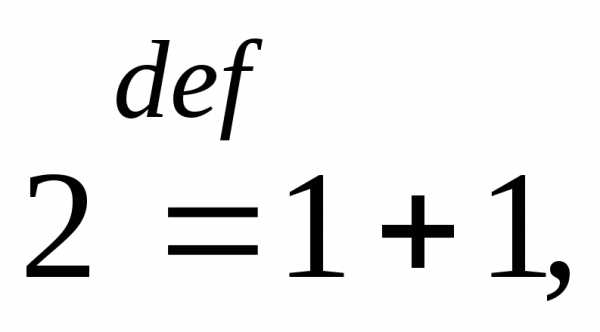
 и т.д. называются натуральными числами,
а их множество обозначаетсяN.
Числаназываются целыми числами, их множество
обозначаютZ. Числа
вида
и т.д. называются натуральными числами,
а их множество обозначаетсяN.
Числаназываются целыми числами, их множество
обозначаютZ. Числа
вида
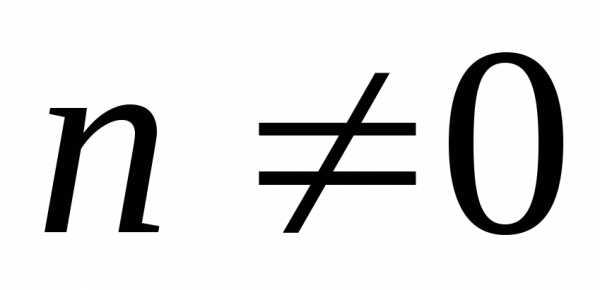 ,
называются рациональными числами, их
множество обозначаетсяQ.
Действительные числа, не являющиеся
рациональными, называют иррациональными,
а их множествообозначаютI.
,
называются рациональными числами, их
множество обозначаетсяQ.
Действительные числа, не являющиеся
рациональными, называют иррациональными,
а их множествообозначаютI.Теорема 1.2.(Плотность действительных чисел). Для любых двух различных действительных чиселхиу, существует такое числоz, что.
Доказательство.Пусть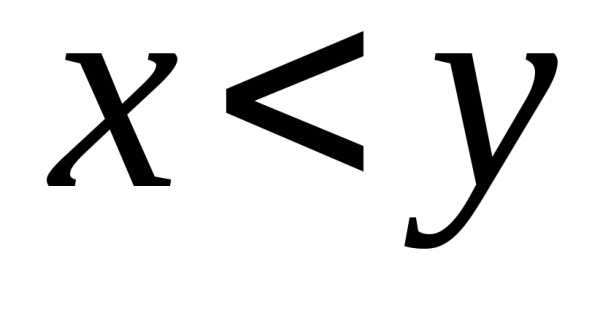 .
Отсюда по аксиоме 2(г)или в силу аксиом 1(а) и 3(б)или согласно 1(в)или на основании 1(б) и 1(г)
или, наконец, по аксиоме 3(г)
.
Отсюда по аксиоме 2(г)или в силу аксиом 1(а) и 3(б)или согласно 1(в)или на основании 1(б) и 1(г)
или, наконец, по аксиоме 3(г)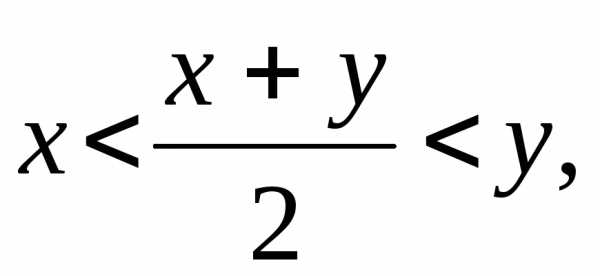 т.е. в качестве числаzможно взять
т.е. в качестве числаzможно взять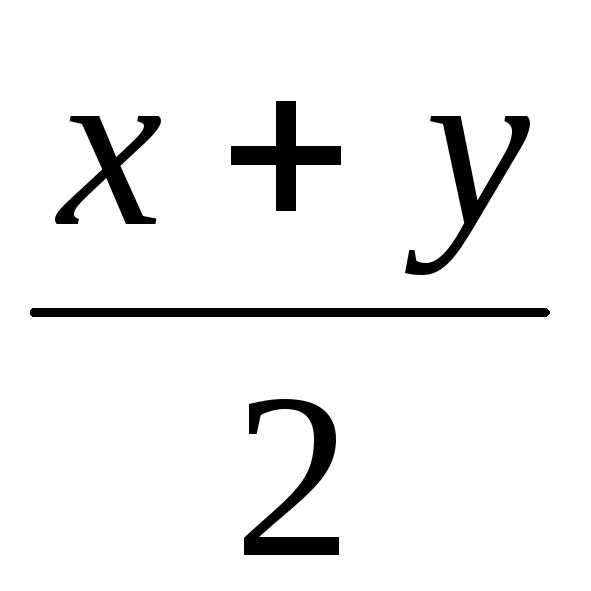 .
.
Доказывается, что любое действительное
число можно представить в виде бесконечной
десятичной дроби
Геометрически множество действительных
чисел изображается числовой осью, т.е.
прямой, не которой заданы начало отсчета,
единица масштаба и положительное
направление, а отдельные числа – точками
этой оси. Поэтому совокупность
действительных чисел часто называют
числовой осью, а отдельные числа – ее
точками. Введем на числовой оси декартову
систему координат, взяв в качестве
начала координат начало отсчета, а в
качестве единичного вектора 
Определение 1.2.Абсолютной величиной
или модулем действительного числа х называется неотрицательное число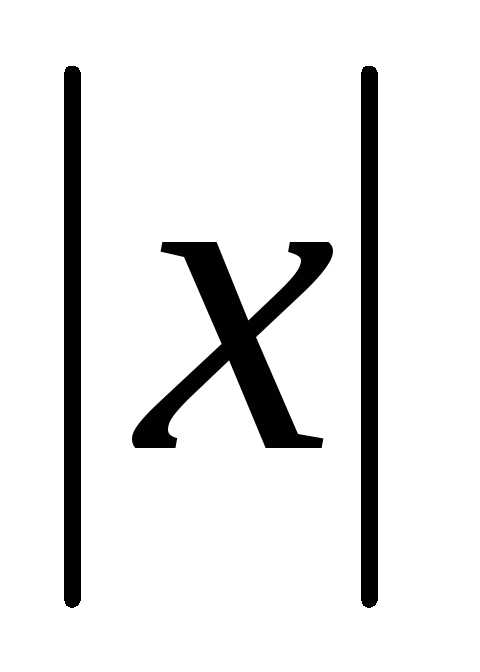 ,
определенное формулой
,
определенное формулой
.
Отметим ряд свойств модуля.
В самом деле, по определению модуля и свойству неравенств
при 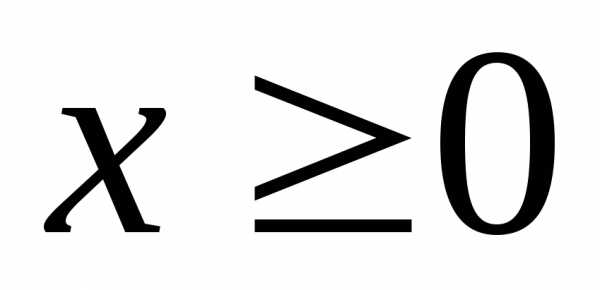 мы имеем:
мы имеем:
а при 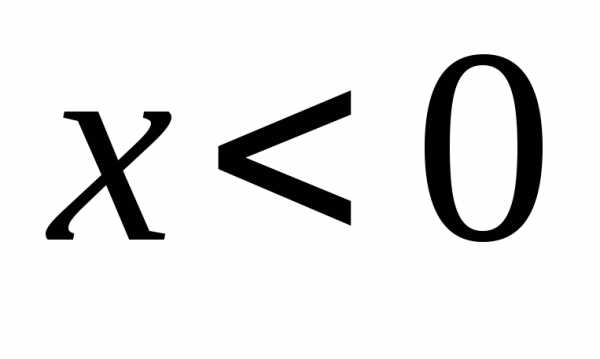 :.
:.
.
Для доказательства воспользуемся очевидными неравенствами:
.
Почленное сложение этих неравенств дает
.
По свойству 1) полученное двойное неравенство равносильно неравенству
.
.
В самом деле, для любых чисел хиуимеем:
Отсюда по свойству 2) или.
,
 .
.
Эти равенства легко проверяются путем рассмотрения различных комбинаций знаков чисел хиу.
Пополним множество действительных
чисел тремя элементами -∞,+∞,∞, определив их соответственно
условиями:,.
Бесконечностиназываются также бесконечно удаленными
точками в отличие от остальных точек,
которые называются конечными точками
числовой оси. Множество действительных
чисел R, дополненное
элементами и
и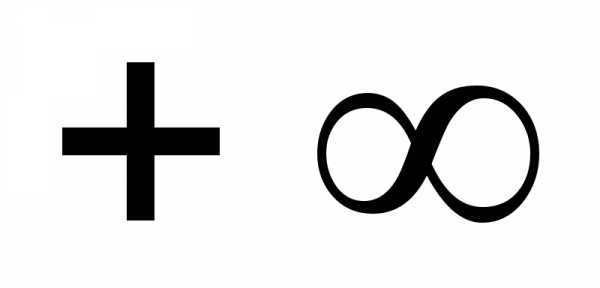 будем называтьрасширенным множеством
действительных чисели обозначать
будем называтьрасширенным множеством
действительных чисели обозначать
Рассмотрим некоторые важные типы
подмножеств расширенного множества
действительных чисел  .
Пусть.
Множество
.
Пусть.
Множество называетсяотрезкомилисегментом,
множество-
интервалом, множества-
полуинтервалами.
называетсяотрезкомилисегментом,
множество-
интервалом, множества-
полуинтервалами.
studfiles.net
§ 2. Действительные числа п.1. Действительные числа и координатная прямая
N – множество натуральных чисел,
Z– множество целых чисел,
Z0– множество целых неотрицательных чисел,
Q– множество рациональных чисел,
I– множество иррациональных чисел,
R – множество действительных чисел.
В курсе СШ под действительным числомпонимают бесконечную десятичную дробь без 9 в периоде. Если бесконечная десятичная дробь – периодическая, то эторациональноечисло, а если бесконечная десятичная дробь – непериодическая, то этоиррациональноечисло.
Из курса математики СШ известно, что множество, состоящее и рациональных и иррациональных чисел, называется множеством действительных чисел(R). На множестве Rвводятся операции «сложения», «умножения», отношение порядка (сравнение). Формулируются 3 группы аксиом:
I. Аксиомы сложения и умножения
1.a+b=b+a
2. a+ (b + c )= (a + b) + c
3. a ∙ b = b ∙ a
4. a ∙ (b ∙ c )= (a ∙ b) ∙ c
5.(a + b) ∙ c= a∙ c +b∙ c
6.Существует число 0 такое, чтоа+ 0 =адля любого действительного числаа
7.Для любого действительного числаа существует число –атакое, чтоа+ (–а) = 0
8.Существует число 1≠0 такое, чтоа∙1 =адля любого действительного числаа
9.Для любого действительного числаа≠0 существует числоа–1 такое, чтоа∙ а–1 = 1
II. Аксиомы порядка
Для любых
1.Для любых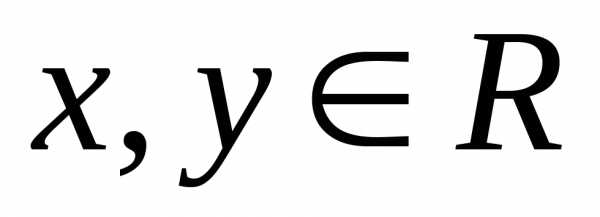 либо
либо 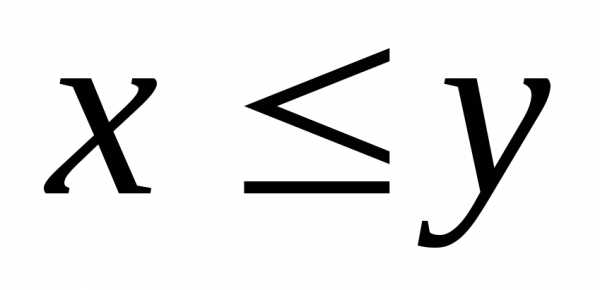 ,
либо
,
либо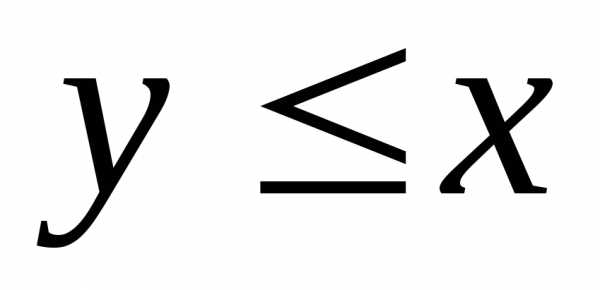 .
.
2.Если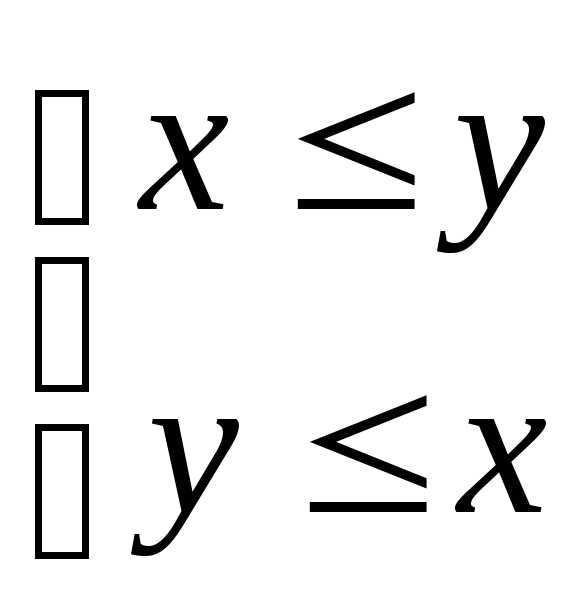 ,
тоx=y.
,
тоx=y.
3.Если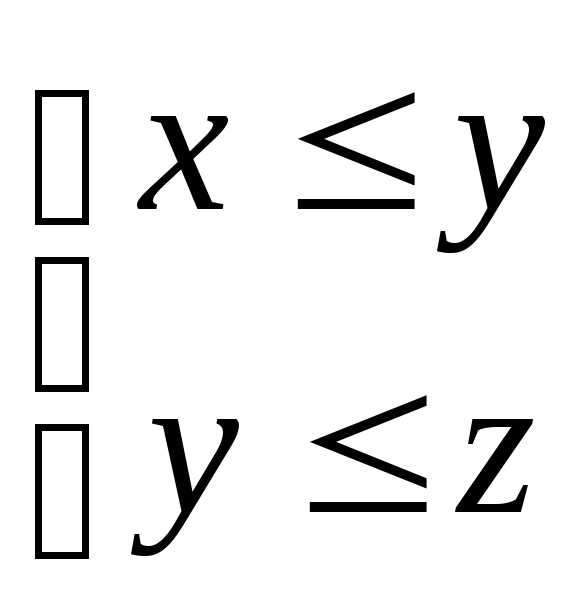 ,
то
,
то 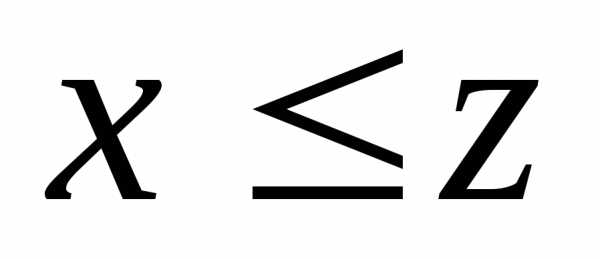 .
.
4. Еслих≤у, то для любогоzвыполняетсях+z≤у+ z
5. Еслих≤у, то для любогоz> 0 выполняетсях∙z≤у∙ z,
а для любого z< 0 выполняетсях∙z≥ у∙ z.
III. Аксиома
непрерывности. Пусть X и Y два непустых
множества действительных чисел. Если выполняется
неравенство ,
то
,
то ,
такое, что .
,
такое, что .
Все остальные свойства можно получить из этих аксиом.
Такой подход к определению множества действительных чисел называется аксиоматическим, действительные числа – это множество, элементы которого удовлетворяют аксиомам группI–III.
Между множеством действительных чисел и точками любой прямой можно установить взаимно однозначное соответствие.
Рассмотрим любую прямую и отметим на ней произвольно точку 0 – начало отсчёта. Точка 0 разбивает данную прямую на два луча. Один из них назовём положительным и обозначим стрелкой, а другой отрицательным. От точки 0 отложим на положительном луче произвольный отрезок и назовём его единичным (его длину примем за единицу измерения длин). Из СШ известно, что прямая, с выбранным на ней началом отсчёта 0, положительным направлением и единичным отрезком, называется координатной прямой.
Возьмем произвольное действительное число х. Возможны случаи:
1) x>0. Отложим на положительном луче координатной прямой от точки 0 отрезок длиныx. Правый конец полученного отрезка – соответствующаяx точка.
2) x<0. Отложим на отрицательном луче координатной прямой от точки 0 отрезок длины (–x). Левый конец полученного отрезка – соответствующаяx точка.
3) x=0, соответствующая ему точка – точка 0.
Возьмем произвольную точку хна координатной прямой. Возможны случаи:
1) точка xпопала на положительный луч координатной прямой. Тогда ей соответствует числоx>0, равное расстоянию от точки 0 до точкиx.
2) точка xпопала на отрицательный луч координатной прямой. Тогда ей соответствует числоx<0, равное расстоянию от точки 0 до точкиx,взятому со знаком минус
3) точка xпопала в начало атсчета координатной прямой. Тогда ей соответствует числоx=0.
Таким образом, установили взаимно однозначное соответствие между множеством действительных чисел и точками координатной прямой. Поэтому в математике принято множество R (действительных чисел) называть числовой прямой, а его элементы, т.е. действительные числа, точками числовой прямой. Часто для наглядности вместо действительного числахрассматривают ту точку на координатной прямой, которая соответствует этому действительному числу. Эту точку называютгеометрическим изображением числахи обозначают так же черезх.
studfiles.net
Действительные числа
Действительные числа
Все рациональные и иррациональные числа образуют множество действительных (вещественных) чисел. Множество всех действительных чисел обозначают буквой R. Очевидно, что R Q Z N .
Основные свойства действительных чисел:
1.множество действительных чисел упорядоченное, то есть для каждых двух различных действительных чисел a и b можно указать, какое из них меньшее;
2.множество действительных чисел всюду плотное, то есть между каждыми двумя
действительными | числами | a и | b | a b существует | еще | по крайней | мере одно |
действительное | число c | a c b , | а следовательно, | и | бесконечное | множество | |
действительных чисел;
3.множество действительных чисел непрерывно, то есть в множестве действительных чисел нет ни скачков, ни пробелов, а геометрически это означает, что каждому действительному числу a на числовой прямой соответствует точка, имеющая координату a , и, обратно, каждая точка числовой прямой имеет действительную координату;
4.арифметические действия над действительными числами всегда возможны (кроме деления на нуль) и в результате дают действительное число.
| Множество действительных чисел |
| R дополняют двумя элементами, обозначаемыми | |||||||||
| и | (плюс | и | минус |
| бесконечность). При | этом полагают, что | |||||
; ; ; |
| |||||||||||
|
| ; . | ||||||||||
| Но операции | , |
|
| , |
| , |
| не определены. Кроме того, для любого числа | |||
|
|
|
|
| ||||||||
|
|
|
|
|
|
|
|
| ||||
a R полагают, что справедливо неравенство a |
| |||||||||||
| и справедливы операции a a ; a a ; | |||||||||||
| для a 0 | a a ; | a a ; |
| ||||||||
| для a 0 | a a ; | a a . |
| ||||||||
| Операции 0 и | 0 не определены. Бесконечности | и называют иногда | |||||||||
«бесконечными числами» в отличие от действительных чисел, которые называют «конечными числами». В дальнейшем под числом будем понимать конечное число.
Определение 1. Абсолютной величиной, или модулем, действительного числа a
называют неотрицательное число обозначаемое | a | и определяемое следующим образом: | ||||
| a |
| a, | если | a 0; | |
|
| |||||
| a |
| a, | если | a 0. | |
|
| |||||
|
|
|
|
|
|
|
1
Ясно, | что |
| a |
| 0, |
| a |
|
|
|
|
| a |
| , |
|
| a |
| 2 | a2 , |
|
|
|
|
|
| a2 |
|
|
|
|
| a |
| . | Если |
| a |
| 0, то это эквивалентно | ||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
тому, что | a 0 . |
| Для |
| любых | действительных | чисел |
| a и |
| b |
| справедливы | следующие | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
соотношения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
| a b |
|
|
|
|
| a |
|
|
|
| b |
| ; |
|
|
| a |
|
|
|
|
| a |
|
|
| , если b 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| b |
|
| b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
|
|
|
|
|
| a |
|
|
| b |
|
|
| a b |
|
|
| a |
|
|
| b |
| ; |
|
| a |
|
|
| b |
|
|
| a b |
|
|
| a |
|
|
| b |
|
|
| |||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Определение 2. Подмножество X множества всех действительных чисел R | называется | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ограниченным снизу, если существует действительное число |
| a |
| a R такое, | что оно не | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
больше каждого числа x |
| из X, то есть для любого x |
|
| x X выполняется неравенство a x . | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Число a называют числом, ограничивающим множество X снизу.
Множество, не являющиеся множеством ограниченным снизу, называют множеством неограниченным снизу. Термин «множество неограниченное снизу» означает, что каково бы ни
было отрицательное, сколь угодно большое по абсолютной величине | число a , в данном |
множестве обязательно найдется еще меньшее число x x a . |
|
Если множество X ограничено снизу числом m , и число m принадлежит множеству X | |
m X , то число m называют наименьшим или минимальным | числом множества |
X : m min X . Если в множестве есть наименьшее число, то оно единственно.
Пример. а) множество чисел X 1; 3; 8; 17 ограничено снизу числом 1, причем это число 1 является наименьшим;
б) множество X – множество всех неотрицательных чисел x (т.е. чисел, удовлетворяющих неравенству x 0 ) тоже является ограниченным снизу и его наименьшим значением является число 0 ;
в) множество Y – множество всех положительных чисел y (т.е. чисел, удовлетворяющих неравенству y 0 ) тоже является ограниченным снизу числом 0 , но множество Y не имеет наименьшего, так как число 0 не принадлежит Y. При этом число 0 является наибольшим из всех чисел, ограничивающих множество Y снизу, а элементы y множества Y в силу свойств плотности и непрерывности действительных чисел могут быть сколь угодно близки к числу 0 , оставаясь больше его;
г) множество D – множество всех отрицательных чисел неограниченно снизу, так как какое бы отрицательное число ни взять, найдется еще меньше число.
Определение 3. Подмножество X множества всех действительных чисел R называется ограниченным сверху, если существует такое число b b R , что оно не меньше каждого
числа x x X , то есть для любого | x X , выполняется неравенство | x b. Число b |
называют числом ограничивающим множество X сверху. |
| |
Множество, не являющееся множеством ограниченным сверху, называют множеством неограниченным сверху. Термин «множество неограниченное сверху» означает, что каково бы ни было сколь угодно большое положительное число b , в данном множестве обязательно найдется еще большее число.
2
Если множество | X ограничено сверху числом | M и M X , то число M называют | |||
наибольшим или максимальным числом множества | X : M max X . Если есть в множестве | ||||
наибольшее число, то оно единственное. |
|
|
| ||
Определение 4. Множество, ограниченное и снизу и сверху, называется ограниченным | |||||
множеством. |
|
|
|
|
|
Другими словами, | множество X R | ограничено, если существуют числа | |||
a , b a R , b R такие, что для каждого x X | справедливо неравенство: a x b. | ||||
Множество, не являющееся ограниченным, | называют неограниченным. | ||||
Пример. а) множество | X 1; 3; 8; 17 ограничено, т.к. для всякого | x X справедливо | |||
1 x 17 , причем оно имеет и наименьшее значение m 1 и наибольшее | M 17 ; | ||||
б) множество Y — множество положительных чисел, являясь ограниченным снизу, | |||||
неограниченно сверху, | 0 y ; |
|
|
| |
в) множество Z — | множество всех целых чисел неограниченно как снизу, так и сверху | ||||
z .
Ясно, что чисел ограничивающих множество снизу (сверху) может быть много.
Определение 5. Наибольшее число среди всех чисел, ограничивающих снизу множество X R , называется нижней гранью (или инфимумом) множества X и обозначается через inf X (инфимум — от латинского слова infimum – наименьший).
Например, для множества Y — множества всех положительных чисел нижней гранью является число 0, а для множества всех натуральных чисел N нижней гранью является число 1, оно является и наименьшим.
Определение 6. Наименьшее среди всех чисел, ограничивающих сверху множествоX R , называется верхней гранью (или супремумом) множества X и обозначается через sup X (супремум – от латинского слова supremum – наибольший).
Например, для множества всех отрицательных чисел число 0 является верхней гранью.
Если в множестве существует наименьшее (наибольшее) число, то оно является нижней (верхней) гранью этого множества. Всякое ограниченное сверху непустое множество имеет верхнюю грань, а всякое ограниченное снизу непустое множество имеет нижнюю грань.
Множество | всех | действительных | чисел | x , удовлетворяющих двойному неравенству | ||||
a x b , называют открытым промежутком или интервалом и обозначают a ; b . | ||||||||
Множество | всех | действительных | чисел | x , удовлетворяющих двойному неравенству | ||||
a x b , называют закрытым промежутком или отрезком и обозначают a ; b . | ||||||||
Пример 5. Примеры числовых множеств: |
|
|
| |||||
1. | [a ; b) , если a x b; | 2. | (a ; b], | если a x b; | ||||
3. | [a ; ) , | если | a x ; |
| 4. | a; , | если | a x ; |
5. | ( ; b], | если | x b; |
| 6. | ; b , | если | x b; |
|
|
|
|
|
| 3 |
|
|
7. | ; , если x ; | 8. a; a , если a x a | a 0 ; |
|
9. | a; a , если a x a a 0 ; | 10. a ; a , если a | x a | 0 . |
Множества, приведенные под номерами 1 и 2, называют полуоткрытыми промежутками, множества под номерами 3, 4, 5, 6, 7 называют неограниченными промежутками, причем множество под номером 7 есть множество всех действительных чисел R.
Определение 7. Множество всех действительных чисел x , удовлетворяющих двойному неравенству a x a , где 0 , называют — окрестностью точки a.
Этот факт можно записать следующим образом x a . Для любых двух неравных действительных чисел a и b существуют непересекающиеся — окрестности.
Числовое множество X называют симметричным относительно начала координат, если этому множеству вместе с числом x принадлежит и ему противоположное число x , то есть, если x X , то и x X .
Примерами таких множеств являются множества под номерами 7, 8, 9, а так же множество всех рациональных чисел Q и множество [ 5; 1) (1; 5] и т.д.
Вопросы и задания
1.Записать определения ограниченного снизу, ограниченного сверху, ограниченного множества. Привести примеры таких множеств. Что такое наименьшее (наибольшее) число множества?
2.Дать опеределение нижней грани (инфимума), верхней грани (супремума).
3.Что такое — окрестность точки a? Изобразить на числовой прямой Ox — окрестность точек A(2), В(3) так, чтобы они: а) не пересекались; б) пересекались. Указать возможные значения для каждого из случаев.
4. | Перечислить операции с | и |
| , которые не определены. | ||||||||||||||||||||||||
5. | Даны множества | A 0; 4 , | B 3; 2 . |
|
| Указать наименьшее и наибольшее числа | ||||||||||||||||||||||
каждого из множеств: а) A; б) B ; в) A B; г) A B. |
|
|
| |||||||||||||||||||||||||
6. | Даны множества | A 0; 4 , | B 3; 2 . Указать точные нижние грани (инфимумы) и | |||||||||||||||||||||||||
точные верхние грани (супремумы) множеств: а) | A; б) B ; в) | A B; г) A B. Имеют ли эти | ||||||||||||||||||||||||||
множества наименьшее и наибольшее числа? |
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||
7. | Даны множества | A ; 3 , B 1; . Имеют ли эти множества точные нижние и | ||||||||||||||||||||||||||
верхние грани, наименьшее и наибольшее числа? Если имеют, то указать их. | ||||||||||||||||||||||||||||
8. | Изобразить на числовой прямой Ox | множества, точки которых удовлетворяют | ||||||||||||||||||||||||||
следующим соотношениям: а) |
|
|
| x |
| 5; б) |
| x |
| 1; в)1 |
| x |
| 5. |
|
|
| |||||||||||
|
|
|
|
|
|
|
|
| ||||||||||||||||||||
9. | Изобразить на числовой прямой Ox | множества, | точки которых удовлетворяют | |||||||||||||||||||||||||
следующим соотношениям: а) |
| x 3 |
| 2; б) |
| x 3 |
|
| 2; в) 1 |
|
| x 3 |
| 2. | ||||||||||||||
|
|
|
|
|
| |||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
| 4 |
|
|
|
|
|
|
|
|
| ||||||||
studfiles.net
Действительное число — это… Что такое Действительное число?
Веще́ственные, или действи́тельные[1]числа — математическая абстракция, служащая, в частности, для представления и сравнения значений физических величин. Такое число может быть интуитивно представлено как описывающее положение точки на прямой.
Множество вещественных чисел обозначается (Unicode: ℝ) и часто называется вещественной прямой.
Относительно операций сложения и умножения вещественные числа образуют поле. Поле вещественных чисел является важнейшим объектом математического анализа.
Примеры
Определения
Существует несколько стандартных путей определения вещественных чисел:
Аксиоматическое определение
См. основную статью Аксиоматика вещественных чисел.
Множество вещественных чисел можно определить как топологически полное, упорядоченное поле, то есть поле с отношением , которое удовлетворяет следующим аксиомам:
- Отношение является отношением линейного порядка:
- Порядок согласован со структурой поля:
- Порядок на удовлетворяет условию полноты:
Примечания
Из свойства 3 следует, что у любого непустого ограниченного сверху множества (то есть такого, что для всех x из A все для некоторого ) существует точная верхняя грань (минимальная из всех), то есть число такое, что
- Для всех x из A все
- Если свойству (1) удовлетворяет также число , то .
Наличие точных верхних граней у ограниченных сверху множеств эквивалентно аксиоме полноты и часто заменяет её в аксиоматике поля .
Любые два поля с отношением порядка, удовлетворяющим этим аксиомам, изоморфны, поэтому можно говорить, что существует единственное такое поле. (На самом деле, правильней говорить, что единственна структура полного упорядоченного поля, каждое поле, которое её имеет, служит моделью множества вещественных чисел, так как любые две модели изоморфны.)
Пополнение рациональных чисел
Вещественные числа могут быть построены как пополнение множества рациональных чисел по отношению к обычной метрике .
Более точно, рассмотрим все фундаментальные последовательности рациональных чисел {ri}. На таких последовательностях можно естественным образом ввести арифметические операции: {ri} + {qi} = {ri + qi} и .
Две такие последовательности и считаются эквивалентными , если при .
Множество вещественных чисел можно определить как классы эквивалентности этих последовательностей.
Дедекиндовы сечения
См. основную статью Дедекиндово сечение.
Дедекиндово сечение — это разбиение множества рациональных чисел на два подмножества A и B такие, что:
- для любых и ;
- B не имеет минимального элемента.
Множество вещественных чисел определяется как множество дедекиндовых сечений. На них возможно продолжить операции сложения и умножения.
Например, вещественному числу соответствует дедекиндово сечение, определяемое или и и x2 > 2}. Интуитивно, можно представить себе, что для того чтобы определить мы рассекли множество на две части: все числа, что левее и все числа, что правее ; соотвеетственно, равно точной нижней грани множества B.
Бесконечные десятичные дроби
Такое задание, как правило, практикуется в школьной программе и во многом похоже на пополнение рациональных чисел.
Бесконечной десятичной дробью (со знаком) называется последовательность вида , где di являются десятичными цифрами, то есть .
Две последовательности называются эквивалентными, если они либо совпадают, либо их различающиеся «хвосты» имеют вид и , где , либо если это «нулевые» последовательности (все di равны 0), отличающиеся только знаком.
Вещественные числа определяются как классы эквивалентности десятичных дробей. Операции на десятичных дробях определяются позиционно подобно операциям над целыми числами в позиционных системах счисления.
Значение десятичной дроби формально задаётся суммой ряда .
Счетность множества
TODO:
Примечания
- ↑ Традиционно в Петербурге (СПбГУ) принято название вещественные, а в Москве (МГУ) — действительные.
Ссылки
- Кириллов, А. А. Что такое число? // Выпуск 4-й серии «Современная математика для студентов». — М.: Физматлит, 1993.
- Понтрягин, Л. С. Обобщения чисел // Серия «Математическая библиотечка». — М.: Наука, 1965.
См. также
Wikimedia Foundation. 2010.
dic.academic.ru
Действительные числа. Расширенная числовая прямая. Модуль вещественного числа
Из элементарной математики известно, что действительные числа можно складывать, вычитать, умножать, делить и сравнивать по величине. Перечислим основные свойства, которыми обладают эти операции. Множество всех действительных чисел будем обозначать через R, а его подмножества называть числовыми множествами.
I. Операция сложения. Для любой пары действительных чисел а и b определено единственное число, называемое их суммой и обозначаемое а + b, так, что при этом выполняются следующие условия:
I.1. a + b = b + a, a,b R.
I.2. a + (b + с) = (a + b) + с, a,b,c R.
I.3. Существует такое число, называемое нулем и обозначаемое О,
что для любого a R выполняется условие а + 0 = а.
I.4. Для любого числа a Rсуществует число, называемое ему
противоположным и обозначаемое -а, для которого а + (-а) = 0.
Число а + (—b), а, b R, называется разностью чисел а и b и обозначается а — b.
П. Операция умножения. Для любой пары действительных чисел а и b определено единственное число, называемое их произведением и обозначаемое ab (a • b), такое, что выполняются следующие условия:
II.1. ab = ba, a, b R.
II.2. а(bс) = (ab)c, a,b, R
II.3. Существует такое число, называемое единицей и обозначаемое 1, что для любого а е R выполняется условие а • 1 = а.
II.4. Для любого числа существует число, называемое ему обратным и обозначаемое a-1 или , для которого = 1.
Число а , называется частным от деления а на b и обозначается а : b или или а/b.
III. Связь операций сложения и умножения:
для любых a,b,c R выполняется условие (а + b)с = ac+bc
IV. Упорядоченность. Для действительных чисел определено отношение порядка. Оно состоит в следующем. Для любых двух различных чисел а и b имеет место одно из двух
соотношений: либо а < b (читается «а меньше b»), или, что то же самое, b > а (читается «b больше а»), либо а > b, или, что то же самое, b < а. При этом предполагается, что выполняются следующие условия:
IV1. Транзитивность. Если а<b и b < с, то а < с.
IV2— Если а < b, то для любого числа с имеет место а + с < b + с.
IV3. Если а > b и с > 0, то ас> bc.
Соотношения порядка называют также сравнением действительных чисел по величине или неравенствами. Запись а ≤ b, равносильная записи b ≥ а, означает, что либо а < b, либо а = b.
Из выполнения условий IV2 и IV3 вытекает одно важное свойство, называемое плотностью действительных чисел: для любых двух различных действительных чисел а и b, например, таких, что а < b, существует такое число с, что а < с < b. В самом деле, сложив каждое из равенств a = a, b = b c неравенством а < b, получим 2a<a + b<2b,
откуда а < < b, т. е. в качестве числа с можно взять .
Множество действительных чисел обладает еще свойством непрерывности.
V. Непрерывность. Для любых непустых числовых множеств X и Y таких, что для каждой пары чисел х X и у Y выполняется неравенство x≤y, существует число а, удовлетворяющее условию x≤a≤y, х X и у Y (см рис.7.1.)
Рис. 7.1.
Перечисленные свойства полностью определяют множество действительных чисел в том смысле, что из этих свойств следуют и все остальные его свойства. Поэтому можно дать аксиоматическое определение множества действительных чисел следующим образом.
Определение 7.1.
Множество элементов, обладающих свойствами I-V, содержащее более одного элемента, называется множеством действительных чисел, а каждый его элемент — действительным числом.
Это определение однозначно задает множество действительных чисел с точностью до конкретной природы его элементов. Оговорка о том, что в множестве содержится более одного элемента, необходима потому, что множество, состоящее из одного только нуля, очевидным образом удовлетворяет условиям I-V.
Геометрически множество действительных чисел изображается направленной (ориентированной) прямой, а отдельные числа — точками этой прямой (см.рис. 7.1.(2))
Рис. 7.1. (2)
Поэтому совокупность действительных чисел часто называют числовой прямой или числовой осью, а отдельные числа — ее точками. В связи с этим иногда вместо а < b (соответственно вместо b > а) говорят, что точка а лежит левее точки b (точка b лежит правее точки а).
Часто бывает удобно дополнить множество действительных чисел элементами, обозначаемыми через +∞ и — ∞ и называемыми соответственно плюс бесконечностью и минус бесконечностью, считая при этом по определению, что для любого числа х R. выполняется неравенство -∞< х < +∞.
Множество действительных чисел R, дополненное элементами +∞ и —∞, называется расширенным множеством действительных чисел (расширенной числовой прямой) и обозначается
Иногда бывает удобно дополнить множество действительных чисел R одним элементом ∞ (бесконечностью без знака), в этом случае бесконечность ∞ уже не связана соотношением порядка с действительными числами. Бесконечности +∞, ∞и ∞ называются также бесконечно удаленными точками числовой прямой, в отличие от ее остальных точек, которые называются конечными точками числовой прямой.
Сформулируем определения некоторых важных типов подмножеств расширенной числовой прямой R. Пусть a , b , а ≤b. Множество
[а, b] = {х: х , а ≤x≤b}
называется отрезком, множество
(a,b) = {х: х , а < х < b}
— интервалом, множества
[а, b) = {х: х , а ≤ х < b},
(а,b] = {х: х , а < х ≤b}
— полуинтервалами, а все они — промежутками расширенной числовой оси. Точки а и b называются концами этих промежутков, а точки х такие, что а < х < b, — их внутренними точками. Если а и b — числа, а ≤b, то число b — а называется длиной соответствующего промежутка, а сам промежуток называется конечным.
Определение 7.1(2).
U(a, ε) = (a — ε, a + ε ) (см рис.7.1(3)
Рис. 7.1(3).
Модуль вещественного числа
Определение 7.2.
Модулем действительного числа х называется такое неотрицательное число, обозначающееся |x|, такое, что:
Например, |6|=6, 6≥0, |-7| = -(-7)=+7, -7<0
Если расположить действительные числа на числовой оси, то модуль |x| любого числа х представляет собой расстояние от начала отсчета 0 до соответствующей точки А с абсциссой х: |x|=OA (см.рис. 4.2(1))
Рис.7.2(1).
Наконец, модуль вещественного числа х можно определить следующим образом:
|x| = max {x, -x}.
где max{a,b} – наибольшее из чисел a и b
Например, |2| = max {2, -2}=2,
|-9| = max {-9, -(-9))} = max{-9, 9} = 9.
Если модуль числа х удовлетворяет неравенству
(см. рис.7.2(2))
Рис.4.2.(2)
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
zdamsam.ru
| ЛЕКЦИЯ 1 Понятие величины – основное понятие, с которым встречаются в естественнонаучной и технической областях. Под величиной понимают всё то, что может быть измерено и выражено числом. Среди величин различают постоянные и переменные. Действительные числа, числовая ось. Целые положительные числа 1,2,3… называются натуральными. Множество натуральных чисел обозначают N. Рациональные числа – все целые, нуль и дробные числа. Каждое рациональное число можно представить в виде , где p – целое число, q – натуральное число. Рациональное число можно представить также в виде периодической десятичной дроби. Иррациональные числа – бесконечная непериодическая дробь. Все рациональные и иррациональные числа образуют множество действительных чисел, которое обозначают R. Каждое действительное число изображается точкой числовой оси и, обратно, каждой точке числовой оси соответствует единственное действительное число.
(— ∞, a]. Абсолютная величина (модуль) действительного числа. Определение. Абсолютной величиной (или модулем) действительного числа а называется неотрицательное действительное число, удовлетворяющее условиям:
Свойства абсолютных величин.
.
.
.
.
Определение: Переменная у называется функцией переменной х, если: 1) задано множество D значений х; 2) задан закон, по которому любому значению хD соответствует одно или несколько значений у, где х – независимая переменная (аргумент), у – зависимая переменная (функция). Множество всех значений, которые может принимать х, называется областью определения этой функции.
Частное значение функции – это значение при конкретном значении аргумента, пусть у=f(x), при х = х0 получаем частное значение у0 = f(x0). Определение 1. Значение переменной х, при котором функция обращается в нуль, то есть f(x) = 0 называется нулём (или корнем) функции. Определение 2. Функция у=f(x) называется чётной, если при изменении знака у аргумента значение функции не меняется: f(-x)=f(x). График чётной функции симметричен относительно оси ОY. Определение 3. Функция у=f(x) называется нечётной, если при изменении знака у аргумента изменяется только знак значения функции: f(-x) = — f(x). График нечётной функции симметричен относительно начала координат. Определение 4. Функция у=f(x) называется периодической, если существует такое постоянное число Т ≠ 0, что f(x+Т) = f(x). Наименьшее положительное число Т называют периодом. Определение 5. Элементарной функцией называется функция, которую можно задать одной формулой, составленной из простейших функций и постоянных с помощью конечного числа арифметических действий и конечного числа операций взятия функции от функции. Функции, заданные различными аналитическими выражениями, называются неэлементарными. Определение 6. Графиком функции у=f(x) называется геометрическое место точек плоскости ОХY, для каждой из которых аргумент х является абсциссой, а соответствующее значение функции у – ординатой.
Пусть известен график функции у=f(x). Зная правила преобразования графиков, можно построить графики функции у=f(x-a), y=f(x)+b, y=f(Ax), y=Bf(x), y=-f(x), y=f(-x).
Сжатие вдоль оси ОХ – это уменьшение абсцисс точек исходного графика без изменения ординат. Растяжение вдоль оси ОХ – это увеличение абсцисс точек исходного графика без изменения ординат.
Сжатие вдоль оси ОY – это уменьшение ординат точек исходного графика без изменения абсцисс. Растяжение вдоль оси ОY– это увеличение ординат точек исходного графика без изменения абсцисс.
ЛЕКЦИЯ 2
Рассмотрим свойства и графики основных простейших функций. 1. Линейная функция. Линейной функцией называется такая функция, которая задаётся формулой , где k и b– действительные числа. Если, в частности, k=0, то получаем постоянную функцию ; если b=0, то получаем прямую пропорциональность . Свойства линейной функции при k≠0, b≠0:
Теорема. Графиком линейной функции является прямая. Рис. 1. Число k называется угловым коэффициентом прямой, оно равно тангенсу угла между прямой и положительным лучом оси х, то есть . 2. Обратная пропорциональность. Обратной пропорциональностью называют функцию, заданную формулой , где k≠0. Число k называют коэффициентом обратной пропорциональности.
Рис. 2. График обратной пропорциональности называют гиперболой. 3. Функция .
Графиком функции является парабола. Этот график изображен на рисунке 3. Рис. 3. 4. Функция .
График функции изображен на рисунке 4. Он называется кубической параболой. Рис. 4. 5. Функция .
График функции изображен на рисунке 5. Рис. 5. 6. Функция — целая часть числа. Если 1, то ; если 2, то ; если 0, то и т.д. График функции изображен на рисунке 6. Рис. 6. 7. Функция — дробная часть числа. Построим график функции . Заметим, что , поэтому достаточно сначала построить ветвь графика на любом промежутке длиной 1, например на . Если 1, то , а потому. На рисунке 7 изображен график функции на промежутке , а на рисунке 8 изображен график функции на всей числовой оси. Рис. 7. Рис. 8. 8. Показательная функция. Показательная функция задается формулой , где 0 и .
График показательной функции изображен на рисунке 9. Рис. 9. 9. Логарифмическая функция. Логарифмическая функция является обратной к показательной функции и обладает следующими свойствами:
График функции изображен на рисунке 10. Рис. 10. 10. Функция .
Функция возрастает на промежутках и убывает на промежутках , . График функции изображен на рисунке 11. Рис. 11. 11. Функция .
График функции изображен на рисунке 12. Рис. 12. 12. Функция .
График функции изображен на рисунке 13. Рис. 13. 13. Функция .
График функции изображен на рисунке 14. Рис. 14. 14. Функция является обратной к функции .
Из сказанного выше следует, что записи и , , эквивалентны. Подставив в равенство вместо его выражение, то есть , получим . Следовательно, для любого из имеем: , . Последние два соотношения позволяют истолковать, где , так: — это число, взятое в пределах от до и такое, что его синус равен . График функции изображен на рисунке 15. Рис. 15. 15. Функция является обратной к функции .
Из сказанного выше следует, что записи и , , эквивалентны. Подставив в равенство вместо выражение , получим . Следовательно, для любого из имеем: , . Последние два соотношения позволяют истолковать , где , так: — это число, взятое в пределах от до и такое, что его косинус равен . Отметим, что имеет место следующее тождество: . В его справедливости можно убедиться с помощью графика функции , изображенного на рисунке 16. Рис. 16. 16. Функция является обратной к функции .
Из сказанного выше следует, что записи и , , эквивалентны. Для любого имеем: , . Последние соотношения позволяют истолковать так: — это число, взятое в пределах от до (исключая сами значения и ) и такое, что его тангенс равен . График функции изображен на рисунке 17. Рис. 17. 17. Функция является обратной к функции .
Из сказанного выше следует, что записи и , , эквивалентны. Для любого имеем: , . Последние соотношения позволяют истолковать так: — это число, взятое в пределах от до (исключая сами значения и) и такое, что его котангенс равен . Имеет место тождество . График функции изображен на рисунке 18. Рис. 18.
Определение: Дробно-линейной функцией называется функция вида: , где a, b, c, d – const, c ≠ 0. Эта функция определена всюду, кроме . Выясним, как выглядит график этой функции. Приведем функцию к виду: . Обозначим . Тогда получим (1) Согласно правилам преобразования графиков, график функции (1) может быть построен с помощью следующих действий:
Таким образом, графиком дробно-линейной функции является гипербола, центр которой находится в точке О1 (а1, b1). ЛЕКЦИЯ 3 |
uz.denemetr.com

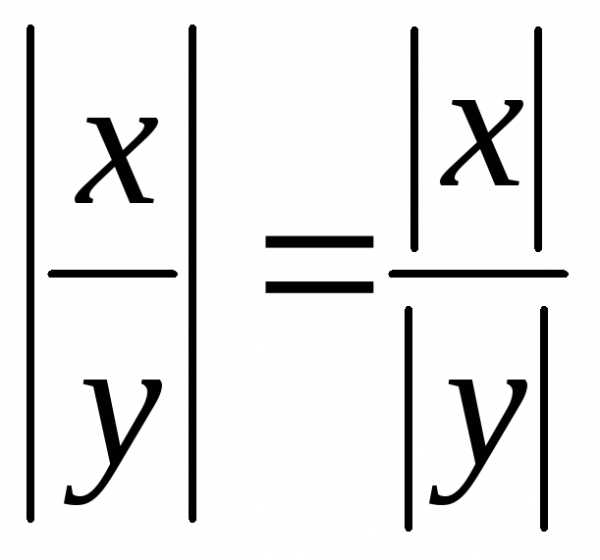 .
.