Как определить чётную функцию. Основные свойства функции: четность, нечетность, периодичность, ограниченность
Графики четной и нечетной функции обладают следующими особенностями:
Если функция является четной, то ее график симметричен относительно оси ординат. Если функция является нечетной, то ее график симметричен относительно начала координат.
Пример. Построить график функции \(y=\left|x \right|\).
Решение. Рассмотрим функцию: \(f\left(x \right)=\left|x \right|\) и подставим вместо \(x \) противоположное \(-x \). В результате не сложных преобразований получим: $$f\left(-x \right)=\left|-x \right|=\left|x \right|=f\left(x \right)$$ Другими словами, если аргумент заменить на противоположный по знаку, функция не изменится.
Значит эта функция — четная, а ее график будет симметричен относительно оси ординат (вертикальной оси). График этой функции приведен на рисунке слева. Это означает что при построении графика, можно строить только половину, а вторую часть (левее вертикальной оси рисовать уже симметрично правой части).
Пример. Построить график функции \(y=x\left|x \right|\).
Решение. Выполним проверку так же как в предыдущем примере: $$f\left(-x \right)=x\left|-x \right|=-x\left|x \right|=-f\left(x \right)$$ Это означает, что исходная функция является нечетной (знак функции поменялся на противоположный).
Вывод: функция симметрична относительно начала координат. Можно строить только одн половину, а вторую рисовать симметрично.
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −4 | −3 | −2 | −1 | 0 | 1 |
Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3 ; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.
Еще функции возможно задать, используя графики. С помощью графика устанавливается какое значение функции соотносится с определенным значением x . Наиболее часто, это будет приближенное значение функции.
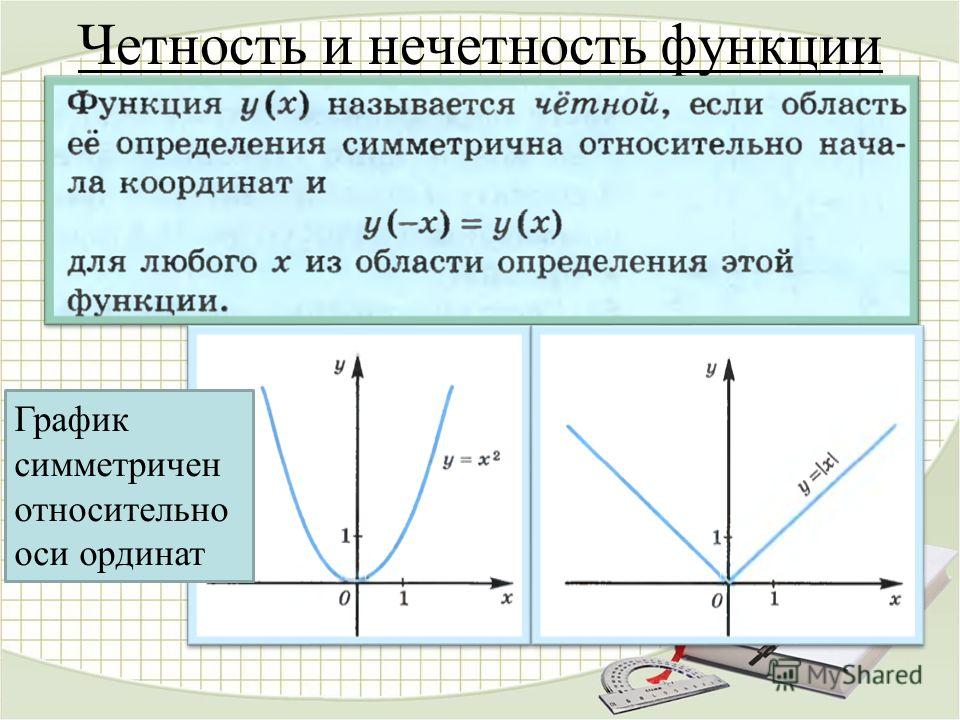
Четная и нечетная функция
Функция является четной функцией , когда f(-x)=f(x)
для любого x
из области определения. Такая функция будет симметрична относительно оси Oy
. {2}} \neq 1
для любого x \in [-1;1]
.
{2}} \neq 1
для любого x \in [-1;1]
.
Ограниченной принято называть функцию y=f(x), x \in X тогда, когда существует такое число K > 0 , для которого выполняется неравенство \left | f(x) \right | \neq K для любого x \in X .
Пример ограниченной функции: y=\sin x ограничена на всей числовой оси, так как \left | \sin x \right | \neq 1 .
Возрастающая и убывающая функция
О функции, что возрастает на рассматриваемом промежутке принято говорить как о возрастающей функции тогда, когда большему значению x будет соответствовать большее значение функции y=f(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значения аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1}) > y(x_{2}) .
Функция, что убывает на рассматриваемом промежутке, называется убывающей функцией тогда, когда большему значению x будет соответствовать меньшее значение функции y(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значений аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1})
Корнями функции принято называть точки, в которых функция F=y(x)
пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0
).
а) Если при x > 0 четная функция возрастает, то убывает она при x
б) Когда при x > 0 четная функция убывает, то возрастает она при x
в) Когда при x > 0 нечетная функция возрастает, то возрастает она и при x
г) Когда нечетная функция будет убывать при x > 0 , то она будет убывать и при x
Экстремумы функции
Точкой минимума функции
Точкой максимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняется неравенство f(x)
Необходимое условие
Согласно теореме Ферма: f»(x)=0
тогда, когда у функции f(x)
, что дифференцируема в точке x_{0}
, появится экстремум в этой точке.
Достаточное условие
- Когда у производной знак меняется с плюса на минус, то x_{0} будет точкой минимума;
- x_{0} — будет точкой максимума только тогда, когда у производной меняется знак с минуса на плюс при переходе через стационарную точку x_{0} .
Наибольшее и наименьшее значение функции на промежутке
Шаги вычислений:
- Ищется производная f»(x) ;
- Находятся стационарные и критические точки функции и выбирают принадлежащие отрезку ;
- Находятся значения функции f(x) в стационарных и критических точках и концах отрезка. Меньшее из полученных результатов будет являться наименьшим значением функции , а большее — наибольшим .
Четность и нечетность функции являются одним из основных ее свойств, и на четность занимает внушительную часть школьного курса по математике. Она во много определяет характер поведения функции и значительно облегчает построение соответствующего графика.
Определим четность функции. Вообще говоря, исследуемую функцию считают четной, если для противоположных значений независимой переменной (x), находящихся в ее области определения, соответствующие значения y (функции) окажутся равными.
Вообще говоря, исследуемую функцию считают четной, если для противоположных значений независимой переменной (x), находящихся в ее области определения, соответствующие значения y (функции) окажутся равными.
Дадим более строгое определение. Рассмотрим некоторую функцию f (x), которая задана в области D. Она будет четной, если для любой точки x, находящейся в области определения:
- -x (противоположная точка) также лежит в данной области определения,
- f (-x) = f (x).
Из приведенного определения следует условие, необходимое для области определения подобной функции, а именно, симметричность относительно точки О, являющейся началом координат, поскольку если некоторая точка b содержится в области определения четной функции, то соответствующая точка — b тоже лежит в этой области. Из вышесказанного, таким образом, вытекает вывод: четная функция имеет симметричный по отношению к оси ординат (Oy) вид.
Как на практике определить четность функции?
Пусть задается с помощью формулы h(x)=11^x+11^(-x).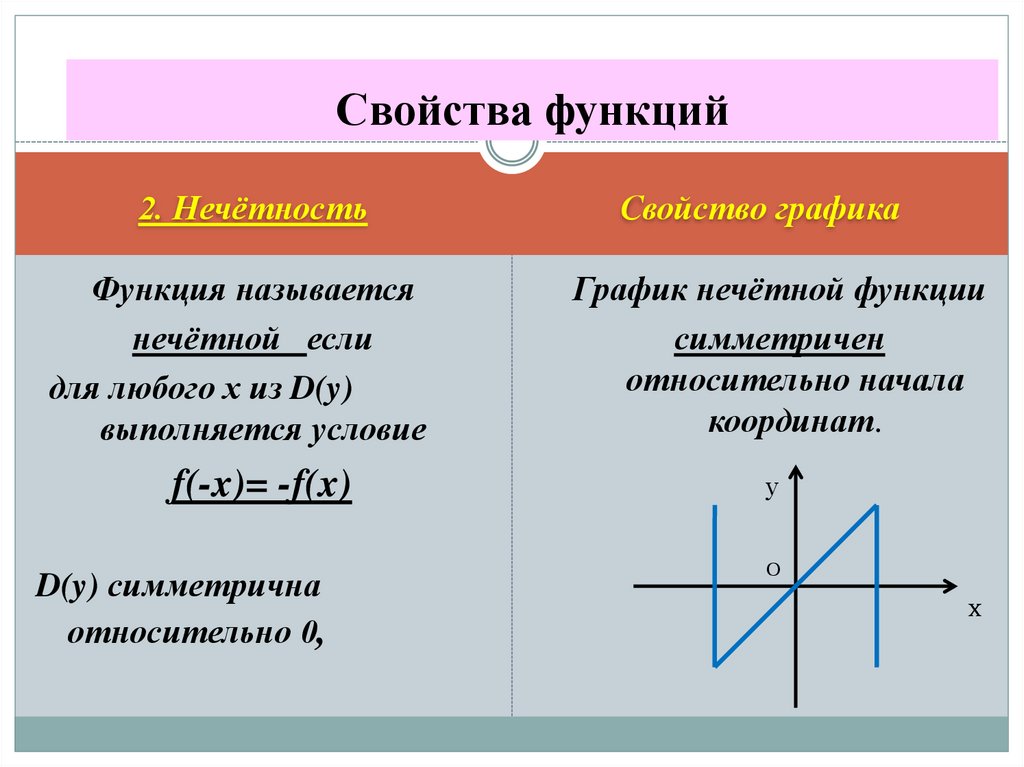 (-x))=- h(x). Следовательно, h(x) — нечетная.
(-x))=- h(x). Следовательно, h(x) — нечетная.
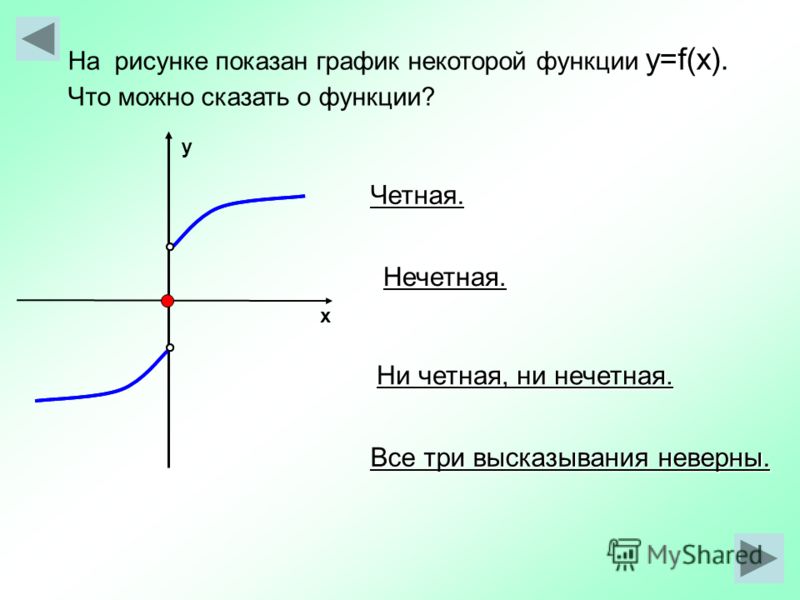
Кстати, следует напомнить, что есть функции, которые невозможно классифицировать по этим признакам, их называют ни четными, ни нечетными.
Четные функции обладают рядом интересных свойств:
- в результате сложения подобных функций получают четную;
- в результате вычитания таких функций получают четную;
- четной, также четная;
- в результате умножения двух таких функций получают четную;
- в результате умножения нечетной и четной функций получают нечетную;
- в результате деления нечетной и четной функций получают нечетную;
- производная такой функции — нечетная;
- если возвести нечетную функцию в квадрат, получим четную.
Четность функции можно использовать при решении уравнений.
Чтобы решить уравнение типа g(x) = 0, где левая часть уравнения представляет из себя четную функцию, будет вполне достаточно найти ее решения для неотрицательных значений переменной. Полученные корни уравнения необходимо объединить с противоположными числами.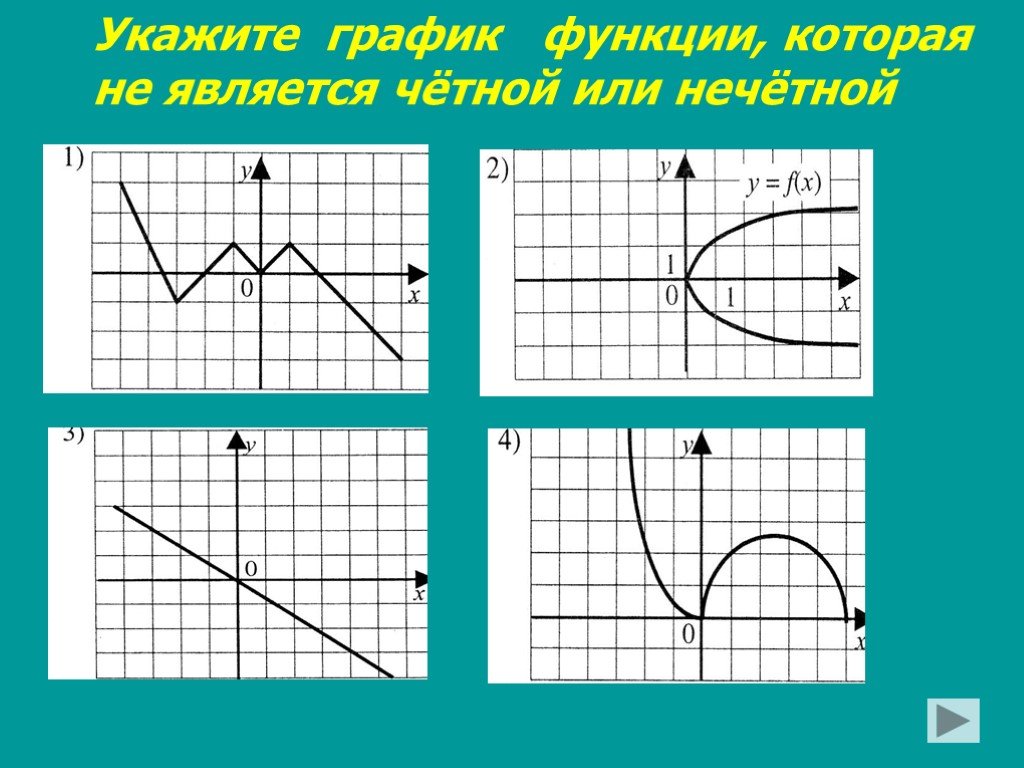 2+2 может быть нечетным, причем для любого значения параметра. Действительно, легко проверить, что множество корней данного уравнения содержит решения «парами». Проверим, является ли 0 корнем. При подстановке его в уравнение, получаем 2=2 . Таким образом, кроме «парных» 0 также является корнем, что и доказывает их нечетное количество.
2+2 может быть нечетным, причем для любого значения параметра. Действительно, легко проверить, что множество корней данного уравнения содержит решения «парами». Проверим, является ли 0 корнем. При подстановке его в уравнение, получаем 2=2 . Таким образом, кроме «парных» 0 также является корнем, что и доказывает их нечетное количество.
Функция
называется четной (нечетной), если для
любогои выполняется равенство
.
График четной
функции симметричен относительно оси
.
График нечетной функции симметричен относительно начала координат.
Пример 6.2. Исследовать на четность или нечетность функции
1)
;
2)
;
3)
.
Решение .
1) Функция определена
при
.
Найдем
.
Т.е.
.
Значит, данная функция является четной.
2) Функция определена
при
Т.е.
.
Таким образом, данная функция нечетная.
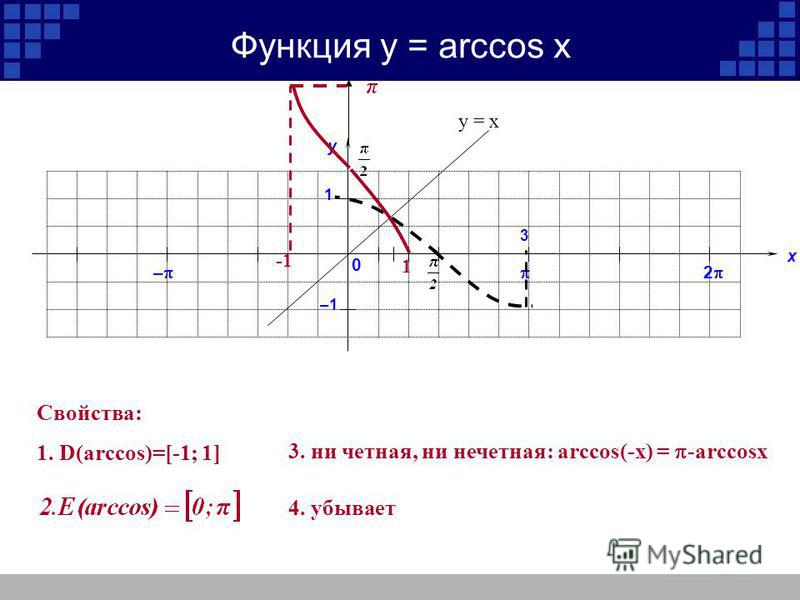
3) функция определена для , т.е. для
,
.
Поэтому функция не является ни четной,
ни нечетной.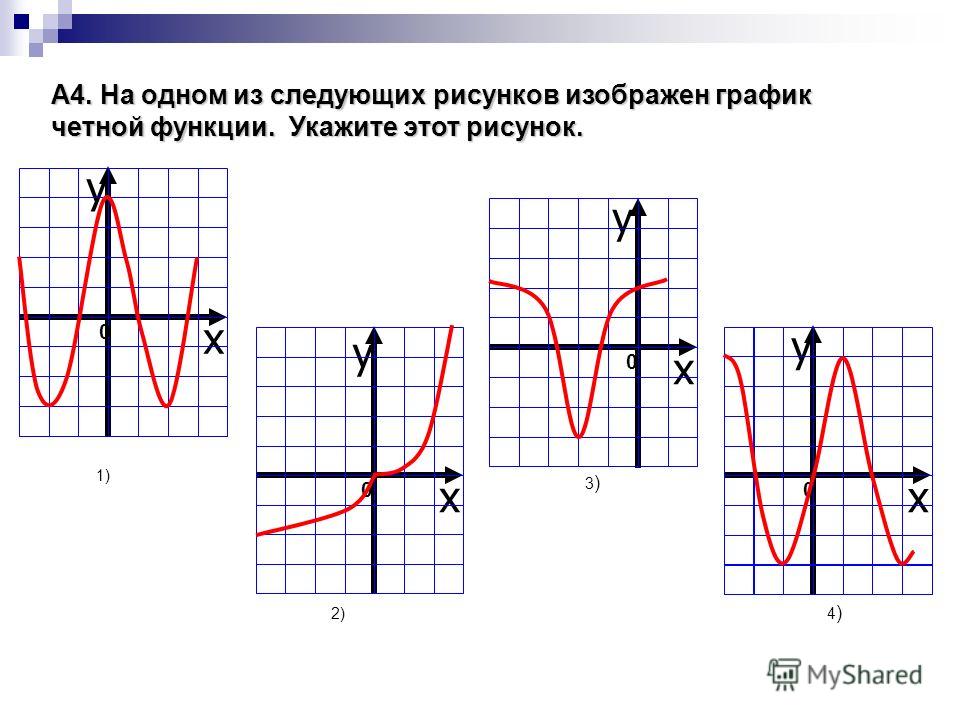 Назовем ее функцией общего
вида.
Назовем ее функцией общего
вида.
3. Исследование функции на монотонность.
Функция
называется возрастающей (убывающей) на
некотором интервале, если в этом интервале
каждому большему значению аргумента
соответствует большее (меньшее) значение
функции.
Функции возрастающие (убывающие) на некотором интервале называются монотонными.
Если функция
дифференцируема на интервале
и имеет положительную (отрицательную)
производную
,
то функция
возрастает (убывает) на этом интервале.
Пример 6.3 . Найти интервалы монотонности функций
1)
;
3)
.
Решение .
1) Данная функция определена на всей числовой оси. Найдем производную .
Производная равна
нулю, если
и
.
Область определения – числовая ось,
разбивается точками
,
на интервалы. Определим знак производной
в каждом интервале.
В интервале
производная отрицательна, функция на
этом интервале убывает.
В интервале
производная положительна, следовательно,
функция на этом интервале возрастает.
2) Данная функция
определена, если
или
.
Определяем знак квадратного трехчлена в каждом интервале.
Таким образом, область определения функции
Найдем производную
,
,
если
,
т.е.
,
но
.
Определим знак производной в интервалах
.
В интервале
производная отрицательна, следовательно,
функция убывает на интервале
.
В интервале
производная положительна, функция
возрастает на интервале
.
4. Исследование функции на экстремум.
Точка
называется точкой максимума (минимума)
функции
,
если существует такая окрестность точки,
что для всех
из этой окрестности выполняется
неравенство
.
Точки максимума и минимума функции называются точками экстремума.
Если функция
в точкеимеет экстремум, то производная функции
в этой точке равна нулю или не существует
(необходимое условие существования
экстремума).
Точки, в которых
производная равна нулю или не существует
называются критическими.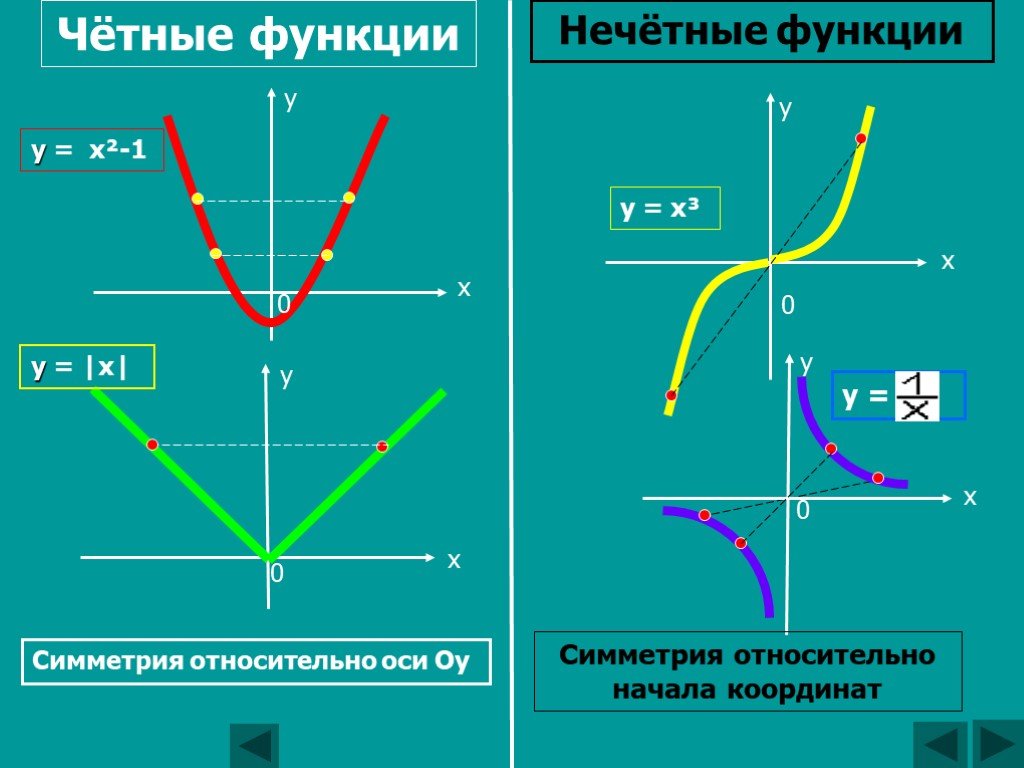
5. Достаточные условия существования экстремума.
Правило 1 .
Если при переходе (слева направо) через
критическую точку
производная
меняет знак с «+» на «–», то в точкефункция
имеет максимум; если с «–» на «+», то
минимум; если
не меняет знак, то экстремума нет.
Правило 2 .
Пусть в точке
первая производная функции
равна нулю
,
а вторая производная существует и
отлична от нуля. Если
,
то– точка максимума, если
,
то– точка минимума функции.
Пример 6.4 . Исследовать на максимум и минимум функции:
1)
;
2)
;
3)
;
4)
.
Решение.
1) Функция определена
и непрерывна на интервале
.
Найдем производную
и решим уравнение
,
т.е.
.Отсюда
– критические точки.
Определим знак
производной в интервалах
,
.
При переходе через
точки
и
производная меняет знак с «–» на «+»,
поэтому по правилу 1
– точки минимума.
При переходе через
точку
производная меняет знак с «+» на «–»,
поэтому
– точка максимума.
,
.
2) Функция определена
и непрерывна в интервале
.
Найдем производную
.
Решив уравнение
,
найдем
и
– критические точки. Если знаменатель
,
т.е.
,
то производная не существует. Итак,
– третья критическая точка. Определим
знак производной в интервалах.
Следовательно,
функция имеет минимум в точке
,
максимум в точках
и
.
3) Функция определена
и непрерывна, если
,
т.е. при
.
Найдем производную
.
Найдем критические
точки:
Окрестности точек
не принадлежат области определения,
поэтому они не являются т. экстремума.
Итак, исследуем критические точки
и
.
4) Функция определена
и непрерывна на интервале
.
Используем правило 2. Найдем производную
.
Найдем критические точки:
Найдем вторую
производную
и определим ее знак в точках
В точках
функция имеет минимум.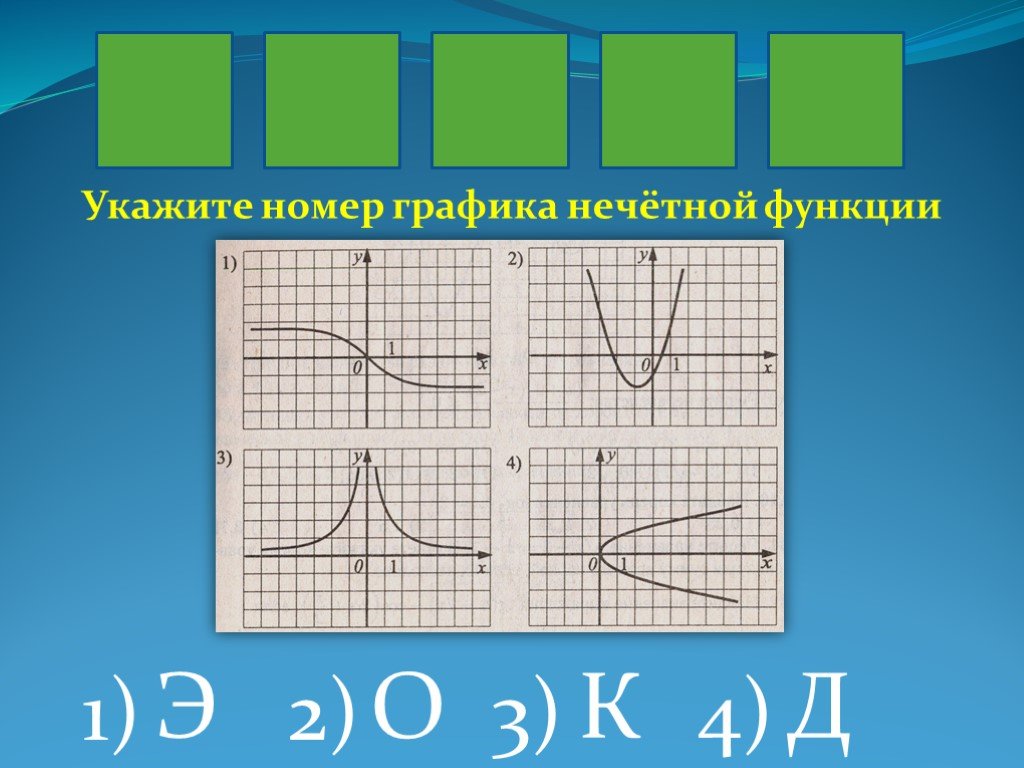
В точках
функция имеет максимум.
Четные и нечетные функции — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
2. Цели урока
• сформировать понятие чётности инечётности функции, учить умению
определять и использовать эти свойства
при исследовании функций, построении
графиков;
• развивать творческую активность
учащихся, логическое мышление, умение
сравнивать, обобщать;
• воспитывать трудолюбие,
математическую культуру; развивать
коммуникативные качества.
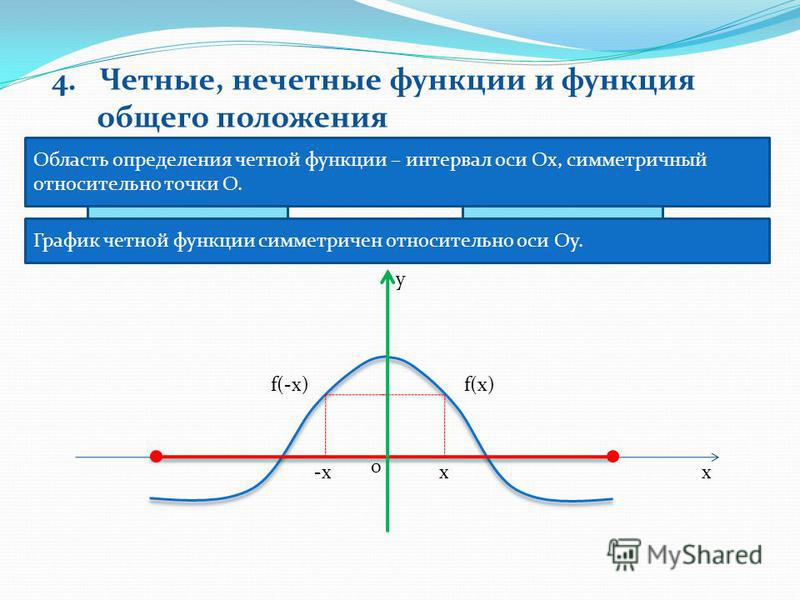
3. Чётные функции
Функция f(х) называется четной, если область её определениясимметрична относительно начала координат и f(-x) = f(x) для
любого х из области определения функции.
Графики чётных функций симметричны относительно оси
ординат.
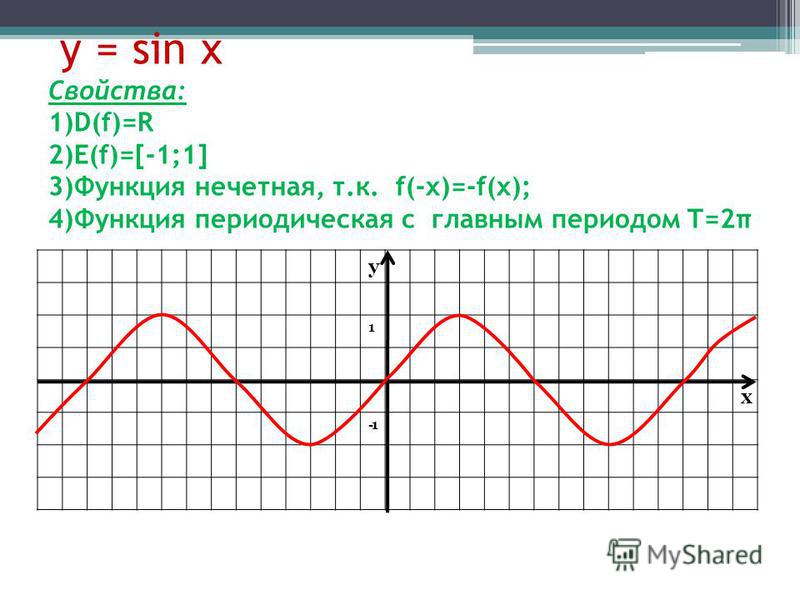
4. Нечётные функции
Функция f(х) называется нечетной, если область еёопределения симметрична относительно начала координат и
f(-x) = -f(x) для любого х из области определения функции.
Графики нечётных функций симметричны относительно
начала координат.
5. Алгоритм исследования функции на чётность.
1. Установить, симметрична ли областьопределения функции. Если нет, то функция
не является ни чётной, ни нечётной. Если да,
то перейти к шагу 2 алгоритма.
2. Составить выражение для f(-х).
3. Сравнить f(-х) и f(х):
– если f(-х) = f(х), то функция чётная;
– если f(-х) = — f(х), то функция нечётная;
– если f(-х) ≠ f(х) и f(-х) ≠ — f(х), то функция не
является ни чётной, ни нечётной.
6. Определите, являются ли заданные множества симетричными?
А) (-2;2)
Б) (-2;2]
В)
Г)
Д) [0; ∞)
Е)
Исследуйте функцию на четность.
f(x)= 4х6 -х2.
Решение:
D(f)=R
f(-x)= 4·(-х)6 -(-х)2 =4х6 – х2
f(-x)=f(x).Функция четная
Исследуйте функцию на четность.
f(x)= 7х5 -х3.
Решение:
D(f)=R
f(-x)= 7·(-х)5 -(-х)3 =-7х5 + х3
=-(7×5-x3)=-f(x)
f(-x)=-f(x). Функция нечетная
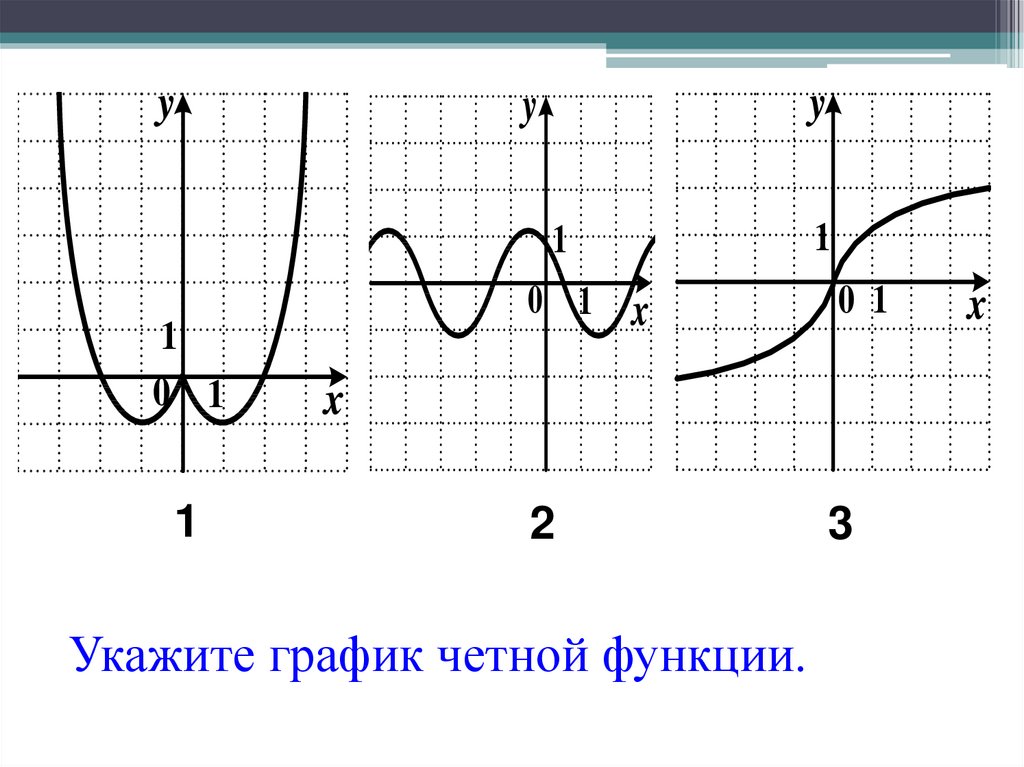
12. Укажите график четной функции.
yy
y
1
1
1
0 1
1
x
0 1
2
x
0 1
3
x
13. Укажите график четной функции.
yy
y
1
1
0 1
1
1
0 1 x
0 1
2
3
x
x
16. Укажите график нечетной функции.
yy
1
0 1
y
1
x
0 1
1
0 1
x
1
3
2
x
17. Укажите график нечетной функции
yy
y
1
0 1
1
0 1
x
1
0 1
1
x
3
2
x
18.
 Укажите график нечетной функции.y
Укажите график нечетной функции.yy
y
1
0 1
1
x
0 1
1
0 1
1
x
3
2
x
19. Подведение итогов урока
20. Рефлексия
Разобрался полностьюПонял, но есть некоторые
затруднения
Не понял
Отлично
Хорошо
Плохо
Определение четной и не
четной функции
Алгоритм исследования
функций на четность
Графическое изображение
четных и не четных
функций
Настроение на уроке
21. Домашнее задание
Выучить определения из презентации, алгоритм определения четной
функции.
Изучить материал по интернет-ресурсам
http://school-collection.edu.ru — Электронный учебник «Математика в
школе, XXI век».
http://fcior.edu.ru — информационные, тренировочные и контрольные
материалы.
www.school-collection.edu.ru — Единая коллекция цифровых
образовательных ресурсов
Выучить материал по учебнику: Колмогоров А.Н. Алгебра 10-11. Параграф
2, пункт 4, подпункт 1 (страницы 30-32).

Выполнить письменно по указанному учебнику №57 (а,б) и №59 (а,б).
Выполнить проверочный тест (смотри последний слайд №22
презентации), если Ваш № по журналу нечетный- вариант 1, четныйвариант 2.
Фото записанного материала презентации, выполненных номеров и
теста прислать учителю в личном сообщении.
English Русский Правила
{3}\text{}[/latex]или[latex]\text{}f\left(x\right)=\frac{1}{x}\text{}[/latex] были отражены по и по осей, результатом будет исходный график, как показано на рисунке 3-11. Рисунок 3-11: (a) Кубическая функция набора инструментов (b) Горизонтальное отражение кубической функции набора инструментов (c) Горизонтальные и вертикальные отражения воспроизводят исходную кубическую функцию. Мы говорим, что эти графы симметричны относительно начала координат. Функция с графиком, симметричным относительно начала координат, называется 9{x}\text{}[/latex] не является ни четным, ни нечетным. Кроме того, единственная функция, которая одновременно является четной и нечетной, — это константная функция [латекс]\текст{}f\left(x\right)=0[/latex].
Функция называется четной функцией , если для каждого ввода [латекс]\текст{}х[/латекс]
[латекс]f\left(x\right)=f\left(-x\right)[ /latex]
График четной функции симметричен относительно оси [latex]y\text{-}[/latex].
Функция называется нечетной функцией , если для каждого ввода [latex]\text{}x[/latex]
[латекс]f\влево(х\вправо)=-f\влево(-х\вправо)[/латекс]
График нечетной функции симметричен относительно начала координат.
Зная формулу функции, определите, является ли функция четной, нечетной или ни одной из них.
- Определите, удовлетворяет ли функция [латекс]\текст{}f\left(x\right)=f\left(-x\right)\text{}[/latex]. Если да, то даже.
- Определите, удовлетворяет ли функция [латекс]\текст{}f\left(x\right)=-f\left(-x\right)\text{}[/latex]. Если это так, то это странно. 9{3}+2x\text{}[/latex] четное, нечетное или ни то, ни другое? Анализ
Рассмотрим график [latex]\text{}f\text{}[/latex] на рис.
 3-12. Обратите внимание, что график симметричен относительно начала координат. Каждой точке [латекс]\текст{}\левый(х,у\правый)\текст{}[/латекс] на графике соответствует точка [латекс]\текст{}\левый(-х,-у\ справа)\text{}[/latex] также находится на графике. Например, (1, 3) находится на графике [латекс]\текст{}f\текст{}[/латекс], а соответствующая точка [латекс]\влево(-1,-3\вправо)[/ латекс] также находится на графике. 9{2}+7\text{}[/latex] четное, нечетное или ни то, ни другое?
3-12. Обратите внимание, что график симметричен относительно начала координат. Каждой точке [латекс]\текст{}\левый(х,у\правый)\текст{}[/латекс] на графике соответствует точка [латекс]\текст{}\левый(-х,-у\ справа)\text{}[/latex] также находится на графике. Например, (1, 3) находится на графике [латекс]\текст{}f\текст{}[/латекс], а соответствующая точка [латекс]\влево(-1,-3\вправо)[/ латекс] также находится на графике. 9{2}+7\text{}[/latex] четное, нечетное или ни то, ни другое?Раствор
Бесплатный доступ на https://openstax.org/books/precalculus/pages/1-introduction-to-functions
Как определить, является ли функция четной, нечетной или ни одной — Криста Кинг Математика
Что такое четные и нечетные функции?
Когда мы говорим «четное, нечетное или ни то, ни другое», мы говорим о симметрии функции. Легче всего визуально увидеть четное, нечетное или ни то, ни другое, глядя на график.
 Иногда сложно или невозможно построить график функции, поэтому есть и алгебраический способ проверки.
Иногда сложно или невозможно построить график функции, поэтому есть и алгебраический способ проверки.Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Четные функции
Симметрично относительно оси ???y???
При подключении ???-x??? в функцию, она упростится, чтобы быть такой же, как исходная функция. Это означает, что не имеет значения, подключаете ли вы ???x??? или ???-x???, ваш вывод будет таким же. Итак,
???f(-x)=f(x)???
Ниже приведены четные и симметричные относительно оси ???y??? графики.
Нечетные функции
Симметрично относительно происхождения
При подключении ???-x??? в функцию, это упростит получение отрицательной исходной функции или исходной функции, умноженной на ???-1???. Это означает, что при подключении ???-x??? в функцию, вы получите тот же вывод, что и при подключении ???x???, за исключением того, что он будет отрицательным (или будет иметь противоположный знак, чем исходный вывод).
 Так
Так???f(-x)=-f(x)???
Ниже приведены нечетные и симметричные относительно начала координат графики. Обязательно визуально сравните квадранты, расположенные по диагонали друг от друга (квадранты 1 и 3 и квадранты 2 и 4).
Ни четная, ни нечетная
Несимметричная относительно оси ???y??? и несимметричная относительно начала координат
Функция не имеет симметрии. Вполне возможно, что график может быть симметричен относительно оси ???x???, но тогда он не пройдет тест вертикальной линии и, следовательно, не будет функцией.
Как определить, является ли функция четной, нечетной или ни одной из них
Пройти курс
Хотите узнать больше об Алгебре 1? У меня есть пошаговый курс для этого.


 3-12. Обратите внимание, что график симметричен относительно начала координат. Каждой точке [латекс]\текст{}\левый(х,у\правый)\текст{}[/латекс] на графике соответствует точка [латекс]\текст{}\левый(-х,-у\ справа)\text{}[/latex] также находится на графике. Например, (1, 3) находится на графике [латекс]\текст{}f\текст{}[/латекс], а соответствующая точка [латекс]\влево(-1,-3\вправо)[/ латекс] также находится на графике. 9{2}+7\text{}[/latex] четное, нечетное или ни то, ни другое?
3-12. Обратите внимание, что график симметричен относительно начала координат. Каждой точке [латекс]\текст{}\левый(х,у\правый)\текст{}[/латекс] на графике соответствует точка [латекс]\текст{}\левый(-х,-у\ справа)\text{}[/latex] также находится на графике. Например, (1, 3) находится на графике [латекс]\текст{}f\текст{}[/латекс], а соответствующая точка [латекс]\влево(-1,-3\вправо)[/ латекс] также находится на графике. 9{2}+7\text{}[/latex] четное, нечетное или ни то, ни другое? Иногда сложно или невозможно построить график функции, поэтому есть и алгебраический способ проверки.
Иногда сложно или невозможно построить график функции, поэтому есть и алгебраический способ проверки.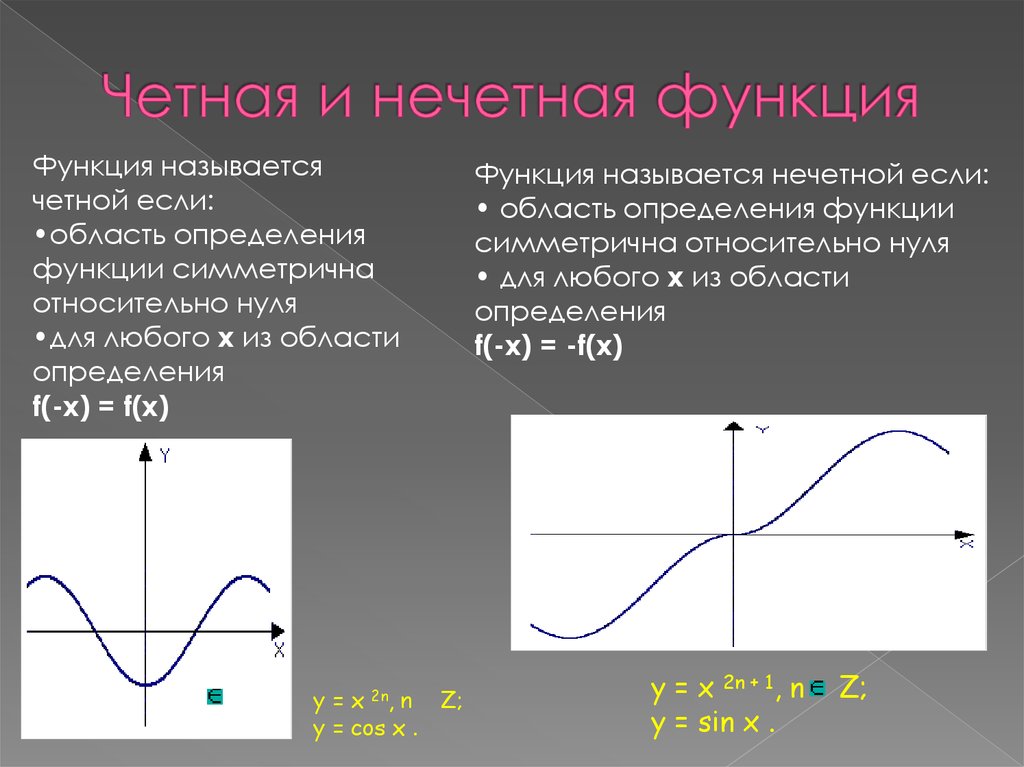 Так
Так