Как определить область значения функции по формуле: виды, свойства, примеры решения задач

Функции — что это, определение и ответ

Функция – это соответствие между двумя множествами, при котором каждому элементу одного множества соответствует единственный элемент второго множества.

СУТЬ ФУНКЦИИ:

Чтобы понять суть функции, можно рассмотреть формулу периметра квадрата. Мы знаем, что периметр квадрата находится так: \(P = 4a\), где a – это сторона квадрата.

Мы можем сами подставить любую длину стороны квадрата, чтобы получить соответствующий ей периметр. Если между двумя какими-либо величинами есть такое соответствие, то между ними существует функция.

Рассмотрим это соответствие на примере квадрата:

Если \(а = 1\), то \(Р = 1 \bullet 4 = 4\)

Если а\(= 2\), то \(Р = 2 \bullet 4 = 8\)

Если \(а = 3\), то \(Р = 3 \bullet 4 = 12\)

и так далее.

Мы говорим, что чтобы получить периметр квадрата, нужно его сторону умножить на 4. Это будет верно для любой стороны квадрата, которую мы сами зададим.

ОПРЕДЕЛЕНИЯ, СВЯЗАННЫЕ С ФУНКЦИЕЙ:

Величина, которую мы подставляем в формулу, называется переменной величиной или аргументом.

Та величина, которая получается в итоге преобразования переменной, называется зависимой величиной или значением функции.

Закон (или принцип) по которому меняется переменная, превращаясь в зависимую, называется функцией.

В нашем примере a – это переменная, P – это зависимая, а действие ( \(\bullet 4\)) – функция.

В общем виде переменную, зависимую и функцию записывают следующим образом:

\(y = f(x)\)

Она означает, что чтобы получить y, нужно преобразовать x по функции f. Такую запись можно читать как «\(y\ \)равен \(f\) от\(\ x\)».

При этом не только сама закономерность, по которой меняется \(x\), называется функцией. Для краткости функцией называют всё выражение, в котором есть зависимость. То есть мы можем сказать, что \(Р = 4a\) – это функция, хотя формально это выражение, содержащее аргумент, зависимую и функцию.

Далее, когда мы будем говорить о функции, мы будем иметь в виду целое выражение, подобно формуле площади квадрата, а не только действие преобразования аргумента.

Также каждая функция имеет свою область значений и область определения.

Область определения – это множество чисел, которые могут являться аргументами данной функции.

Область значений – это множество чисел, которые могут являться значением функции.

Например, в случае с периметром квадрата мы можем точно сказать, что сторона квадрата должна быть положительным числом. Потому что длина не может иметь отрицательное значение и не может быть равна 0, ведь в таком случае, квадрата не получится.

А если аргумент функции должен быть положительным, то при умножении положительного числа на 4 получится тоже только положительное число.

Таким образом область значений и областью определений в данном примере являются множества положительных чисел.

СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ:

Описать суть функции можно по-разному. Также можно по-разному описать зависимость, чтобы какую-либо функцию задать.

Рассмотрим различные способы задания одной и той же функции.

1. Словесный способ задания функции.

«У Даши есть яблоки. При этом у её старшего брата Вани всегда на два яблока больше.»

Чтобы словесно задать функцию, нужно описать, как изменяется аргумент. В данном случае в описании ситуации уже словесно задана функция словами «у Вани всегда на два яблока больше, чем у Даши». Эти слова определяют конкретную зависимость количества яблок у Вани от количества яблок у Даши.

2. Табличный способ задания функции.

Посмотрим на таблицу аргументов и зависимых от них величин.

Можем заметить, что каждый y больше своего x на 2. Эта зависимость есть у каждой из пар «аргумент – значение функции».

3. Способ задания функции формулой.

Этот способ мы рассматривали ранее через формулу периметра квадрата. Рассмотрим более общий вид функции, заданной формулой – через \(x\ \)и \(y\):

\(y = x + 2\)

По формуле мы видим, что каждый y на 2 больше, чем соответствующий ему x.

Пример №1

Найдите значение функции:

\(y = \frac{x\ –\ 2}{5}\) при \(x = 2;\ x = 27\).

1. Чем являются значение и аргумент функции мы знаем, это y и x. А вот именно функцией является более сложное действие – «вычесть 2, разделить на 5». Найдем значение этой функции при \(x = 2\):

\(y = f(x) = \frac{x\ –\ 2}{5}\)

\(f(2) = \frac{2\ –\ 2}{5} = \frac{0}{5} = 0\)

Таким образом мы узнали, что аргументу 2 соответствует значение функции 0.

2. Аналогично найдем значение функции при \(x = 27\):

\(f(27) = \frac{27\ –\ 2}{5} = \frac{25}{5} = 5\)

Значит аргументу 27 соответствует значение функции 5.

Ответ: 0; 5.

ГРАФИК ФУНКЦИИ:

Любую функцию можно изобразить на координатной плоскости. Если координатная плоскость состоит из точек, каждая из которой имеет две координаты, то одна координата будет равна аргументу, а вторая координата значению функция, который ей соответствует.

Из этого следует, что точка принадлежит графику некоторой функции, если её координаты равны аргументу и соответствующему ей значению функции.

Пример №2:

Постройте график функции \(y = x + 2.\)

1. Для построения графиков удобнее всего задавать функцию таблицей. Выберем несколько любых аргументов и найдем для них значения функции:

2. У нас есть координаты для четырех точек – А\((–2;\ 0)\), В(\(0;\ 2),\) С\((3;\ 5)\), D\((6;\ 8).\) Построим их на координатной плоскости и соединим. Полученный рисунок будет являться графиком функции \(y = x + 2:\)

График функции не обязательно должен быть прямой линией. {2}–\ 4.\)

1. Выберем любые аргументы и найдем им соответствующие значения функции. Запишем их в таблице:

2. Построим и соединим на координатной плоскости получившиеся точки:

На данном графике мы видим что одно значение функции может быть у двух аргументов, например точки В\((–2;\ 0)\) и F(\(2;\ 0)\) или С\((–1;\ –3)\) и Е(\(1;\ –3)\) имеют разные аргументы, но одинаковые значения функции. Это не противоречит определению функции.

Для разных аргументов могут совпадать значения функции

Но при этом, НЕ может быть такой ситуации, когда одному аргументу соответствуют несколько значений функций. Так нарушается принцип соответствия и рисунок на координатной плоскости перестает быть графиком функций по определению

Для одного аргумента НЕ может существовать несколько значений функции

Например, вот такой график нельзя назвать графиком функций, потому что одному аргументу соответствует несколько значений:

Пример №4:

Определите без построения графика, принадлежат ли точки А\((2;\ 10)\) и В(\(–3;\ 6)\) графику функций \(y\ = \ 8\ + \ x\)?

1. Точка принадлежит графику функций, если её координате x соответствует координата соответствует координата y именно как \(y\ = \ 8\ + \ x.\)

2. Определим принадлежность точки А к графику данной функции. Для этого подставим координату её абсциссы в функцию и найдем соответствующее ей значение:

\({y = 8 + x }{y\left( 2 \right) = 8 + 2 = 10}\)

Мы получили некую точку графика с координатами \((2;\ 10)\). Такие же координаты и у точки А Получается, что точка А\((2;\ 10)\) – это точка графика функции. Значит А принадлежит графику.

3. Аналогично определим принадлежность точки В к графику функции.

\({y = 8 + x }{y(–3) = 8\ –\ 3 = 5}\)

Мы получили точку графика \((–3;\ 5),\) а у точки В координаты \((–3;\ 6)\), значит тока В НЕ принадлежит графику.

Ответ: да; нет.

Как находится область определения функции заданной формулой

Статьи › Находится

Как найти область определения функции по формуле? Если a — положительное целое число, то область определения функции есть множество действительных чисел: (−∞, +∞). Для нецелых действительных положительных показателей степени: D(f) = [0, +∞). Если a — отрицательное целое число, то область определения функции представляет собой множество (−∞, 0) ∪ (0, +∞).

1. Как обозначается область определения функции f
2. Как найти область определения функции y 4x 8
3. Что считают областью определения функции Если она задана формулой
4. Как найти область определения функции y sin2x
5. Как найти область определения функции sin
6. Как найти область определения и значения функции
7. Что такое область определения функции
8. Что такое F В функции
9. Что такое область определения функции 9 класс
10. Как найти область определения функции y 3x 7
11. Как найти область определения функции с двумя переменными
12. Какое число не входит в область определения функции заданной формулой
13. Что понимают под областью определения функции заданной аналитически
14. Как найти значение функции
15. Как найти область определения квадратичной функции
16. Что такое область определения уравнения
17. Что такое функция в графике
18. Что такое область определения функции своими словами
19. Как найти область определения функции гиперболы

Как обозначается область определения функции f

Множество всех значений, которые принимает аргумент функции, называется областью определения функции: D(f) т.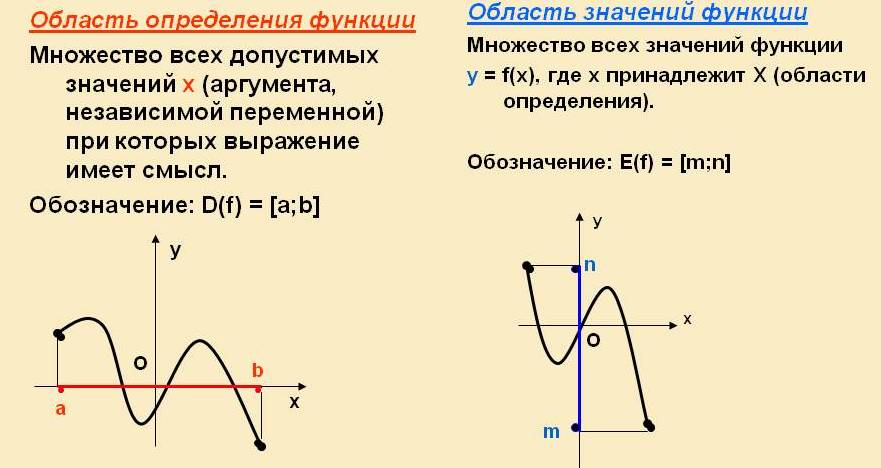

Как найти область определения функции y 4x 8

Так как в формуле функции y = 4x — 8 нет ни деления, ни корня, значит допустимы любые значения переменной х. Ответ: D(f) = (-∞; +∞).

Что считают областью определения функции Если она задана формулой

Если функция задана формулой, то считают, что область определения состоит из всех значений переменной, при которых эта формула имеет смысл. Графиком функции называется множество всех точек на координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.

Как найти область определения функции y sin2x

Y = sin 2x. Синус — тригонометрическая функция, непрерывная, значит, область определения функции — любое число. Функция независимо от своего аргумента принимает значения, находящиеся в промежутке от -1 до 1.

Как найти область определения функции sin

Итак, Областью определения функций y = sin x и y = cos x является множество R всех действительных чисел.

Как найти область определения и значения функции

Областью определения функции являются все значения Х, на которых существует функция. Иными словами, те Х, которые можно подставить в уравнение функции и получить в результате Y. Область значения функции определяется значениями, которое принимает Y на всей своей области определения.

Что такое область определения функции

Область определения — множество, на котором задаётся функция. В каждой точке этого множества значение функции должно быть определено.

Что такое F В функции

Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой. Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.

Что такое область определения функции 9 класс

Область определения —- множество всех значений аргумента (переменной x). Область значений —- множество всех значений функции (переменной y).

Как найти область определения функции y 3x 7

Функции y=3x-7 — является линейной функцией. Областью определения функции y=3x-7 является множество всех действительных чисел, то есть при любом значении х — функция будет существовать. Ответ: область определения функции y=3x-7 — множество всех действительных чисел.

Как найти область определения функции с двумя переменными

Областью определения функции двух переменных называется множество всех пар, для которых существует значение. Графически область определения представляет собой всю плоскость либо её часть. Так, областью определения функции является вся координатная плоскость — по той причине, что для любой точки существует значение.

Какое число не входит в область определения функции заданной формулой

Ответы1. Областью определения функции называют все допустимые значения аргумента (то есть х). Недопустимыми считаются такие значения х, при подстановке которых в формулу функции получается деление на ноль или извлечение корня из отрицательного числа.

Что понимают под областью определения функции заданной аналитически

При аналитическом способе задания функции, т. е. с помощью некоторого аналитического выражения, под областью определения функции понимают множество всех значений независимых переменных, при которых это выражение имеет смысл.

Как найти значение функции

Чтобы найти значение функции при заданном значении аргумента, надо значение аргумента подставить в уравнение функции вместо x и вычислить ее значение.

Как найти область определения квадратичной функции

Графиком квадратичной функции является парабола, вершина которой находится в точке (− b 2 a; − b 2 − 4 a c 4 a). Область определения функции — вся числовая прямая: D (f) = R = (− ∞; ∞). Область значений функции зависит от знака коэффициента.

Что такое область определения уравнения

Областью определения уравнения f (x) = g (x) называют множество всех тех значений переменной x, при которых и выражение f (x), и выражение g (x) имеют смысл. Область определения уравнения иногда называют областью допустимых значений переменной (аргумента).

Что такое функция в графике

Понятие графика функции

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу. Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.

Что такое область определения функции своими словами

Область определения — множество, на котором задаётся функция. В каждой точке этого множества значение функции должно быть определено.

Как найти область определения функции гиперболы

Область определения — любое число, кроме нуля. Область значения — любое число, кроме нуля. Функция не имеет наибольших или наименьших значений.

• Как найти значение функции
• Как найти область определения функции y sin2x
• Как найти область определения функции гиперболы

pine script — Функция должна вызываться при каждом расчете для согласованности, вывод консоли?

спросил 2 года, 7 месяцев назад

Изменено 6 месяцев назад

Просмотрено 11 тысяч раз

Недавно мой скрипт начал показывать эти строки в консоли, когда я добавляю на график или сохраняю.

 "Функция 'anonym_function_10' должна вызываться при каждом вычислении для согласованности. Рекомендуется извлекать вызов из тернарного оператора или из области видимости."
«Функция« anonym_function_11 »должна вызываться при каждом расчете для согласованности. Рекомендуется извлекать вызов из тернарного оператора или из области».
 

Нужна помощь, чтобы понять это, скомпрометирована ли точность кода, или это может стать возможной проблемой в будущем? Каким было бы решение, чтобы исправить это?

 // @версия=4
f_top_fractal(src) => src[4] < src[2] и src[3] < src[2] и src[2] > src[1] и src[2] > src[0]
f_bot_fractal(src) => src[4] > src[2] и src[3] > src[2] и src[2] < src[1] и src[2] < src[0]
f_fractalize(src) => f_top_fractal(src) ? 1: f_bot_fractal(источник)? -1 : 0
 

Последняя строка вызывает вопросы…

• pine-script
• trade

Если ваш код похож на этот, вы, вероятно, получите эту ошибку.

 мав = na(xem[1]) ? sma(src, длина): (xem[1] / длина)`
 

попробуй так. ..

 _sma= sma(src, len)
mav = na(xem[1]) ? _sma : (xem[1] / длина)
 

3

Функции, использующие переменные серии, должны выполняться на каждом баре, чтобы у функции была полная история серии; иначе индексы серий внутри функции будут неверными. Поэтому Pine выдает предупреждение для таких функций, когда они встроены в условное выражение, что может привести к тому, что они не будут выполняться на каждом такте.

Чтобы решить эту проблему, либо выполните функцию в глобальном масштабе, вне любых условных выражений, либо переопределите функцию, чтобы она принимала значения отдельных рядов в качестве аргументов функции.

Последнее решение будет работать в случае OP.

См. объяснение в разделе «Выполнение функций Pine и исторический контекст внутри функциональных блоков» по ​​адресу https://www.tradingview.com/pine-script-docs/en/v4/language/Functions_and_annotations.html

 f_fractalize(_src) => f_top_fractal(_src) ? 1: f_bot_fractal(_src)? -1 : 0
Ниже альтернатива
f_fractalize(_src)=>
    bool rhign = f_top_fractal(_src)
    логический rlow = f_bot_fractal(_src)
    если прав
        1
    иначе, если rlow
        -1
    еще
        0
 

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания и подтверждаете, что прочитали и поняли нашу политику конфиденциальности и кодекс поведения.

R функция add1, аргумент области для ссылки на все переменные

Задавать вопрос

спросил 9 лет, 6 месяцев назад

Изменено 9 лет, 6 месяцев назад

Просмотрено 2к раз

Часть R Language Collective

При использовании функции add1 для учета новых переменных я хотел бы сослаться на все переменные (либо в каком-то фрейме данных, либо в глобальной среде), но я не могу понять, как использовать для этого аргумент области видимости.

Я знаю, что могу использовать это так

 X = data.frame(replicate(4,rnorm(20))) ; у = rn(20)
lm1 = lm(y ~ 1)
out = add1(lm1, область видимости= ~X$X1 + X$X2 + X$X3)
 

, но я не хочу вручную записывать каждую переменную.

Как я уже видел в других вопросах, я знаю . символ не будет работать, но я не уверен, почему. Это означает то, что уже есть, поэтому, если я сделаю

 x1 = rnorm(20) ; x2 = rnorm(20) ; x3 = rnorm(20) ; x4 = rnorm(20) ; у = rn(20)
out = add1(lm1, область видимости= ~ . )
 

не использует то, что уже есть в глобальной среде.

Я знаю, что в документации говорится, что объем должен быть «формулой, дающей условия для рассмотрения», но обычно это происходит там, где . может использоваться для ссылки на все переменные.

Заранее спасибо.

Также обратите внимание, что я прочитал главу 7 MASS, и эти связанные темы

область действия команды add1() в R

http://tolstoy.newcastle.edu.au/R/help/02b/3588.html

2

Это еще более простой ответ, который я нашел после просмотра этого вопроса.

http://r.789695.n4.nabble.com/glm-formula-vs-character-td2543061.html ) х2 = рнорм(100) х3 = рнорм(100) у = рнорма(100) BaseReg = lm(y ~ 1) newdf = data. frame(x1,x2,x3) out = add1 (BaseReg, имена (newdf))

Озадачивает, что такой простой способ получить это не был указан в документации для add1.

Как сказано на странице справки для add1, формула ~. означает «то, что уже есть». Не проще использовать как формулу для небольшого количества имен, но этот подход можно использовать в функции или скрипте. (Как правило, можно было бы ожидать, что X и Y помещаются в один и тот же фрейм данных.)

 as.formula(paste("~", paste(names(YX)[-c(1,5)],collapse="+" )))
#~Х1 + Х2 + Х3
YX <- cbind(y,X)
form <- as.formula(paste("~", paste(names(YX)[-c(1,5)],collapse="+")))
add1(lm1, форма)
 

Кажется, вы наткнулись на более эффективную стратегию. При использовании объекта данных с именами столбцов: "y" "X1" "X2" "X3"

 "X4:
> формула (YX)
у ~ Х1 + Х2 + Х3 + Х4
> формула(YX)[-2]
~Х1 + Х2 + Х3 + Х4
> as.list(формула(YX))
[[1]]
`~`
[[2]]
у
[[3]]
Х1 + Х2 + Х3 + Х4
> имена (YX)
[1] «у» «Х1» «Х2» «Х3» «Х4»
 

Вы можете видеть, что объект-формула имеет в качестве первого элемента определяющую формулу тильду, которая на самом деле является функцией R.