X 2y 3x y: Mathway | Popular Problems

36Risolvere per ?cos(x)=1/27Risolvere per xsin(x)=-1/28Преобразовать из градусов в радианы2259Risolvere per ?cos(x)=( квадратный корень из 2)/210Risolvere per xcos(x)=( квадратный корень из 3)/211Risolvere per xsin(x)=( квадратный корень из 3)/212Графикg(x)=3/4* корень пятой степени из x 13Найти центр и радиусx^2+y^2=914Преобразовать из градусов в радианы120 град. 2+n-72)=1/(n+9)

Задачи с системами уравнений

Задача 1 Две следующие системы уравнений имеет решение (1, 3). Найдите их, выполняя проверку.
a)
|x + y = 5
|2x — y = 7;
b)
|2x + y = 5
|x — y = 2
c)
|3x + y = 6
|4x — 3y = -5
d)
|1/(x — 1) = y — 3
|x — y = -2
e)
|(9x + 4y)/3 — (5x — 11)/2 = 13 — y
|13x — 7y = -8
Ответ:c) и e).

Задача 2 Равны ли системы уравнений?
|4x + 5y = 11
|x — y = 5
and
|4x — 5y = 11
|2x + y = 9 ?
Ответ: Нет.

(3-32) Решите систему уравнений:

Задача 3
|2y — x = -5
|y = 1 — 3x
Ответ:(1; -2).

Задача 4
|3x — y = 13
|3y — 2x = -4
Ответ:(5; 2).

Задача 5
|6x — y = 11
|12x — 2y — 22 = 0
Ответ: Решением является каждая пара чисел, которая есть решениея уравнения 6x — y = 11.

Задача 6
|5u — 6v = -2
|7u + 18v = 2
Ответ:(-1; 1/2).

Задача 7
|8x — 5y + 16 = 0
|1x + 3y — 17 = 0
Ответ:(1/2; 4).

Задача 8
|4(x + 2) — 7(x — y) = 7
|7(x + y) + 10(x — 2) = 79
Ответ:(5; 2).

Задача 9
|3x + 4(x — 3) = 3(2y — 3) — 3y
|3y + 2(x — 4) = 5(y + 2) — 28
Ответ:(-4; 1).

Задача 10
|(x + 3)(x — 1) = 4y + x² + 5
|(x — 3)(3x + 2) = 3x² — 14y + 15
Ответ: Нет решения.

Задача 11
|(x — 1)(y + 2) — (x — 2)(y + 5) = 0
|(x + 4)(y — 3) — (x + 7)(y — 4) = 0
Ответ:(5; 7)

Задача 12
|(x + 2)² — (x + 3)(x — 3) — 3(y + 5) = 0

|(2y — 3)² — y(4y — 3) + 12x — 15 = 0
Ответ: Решением является каждая пара чисел, которая есть решением уравнения 4x — 3y — 2 = 0.

Задача 13
|(y + 2)/6 — (y — 4)/2 = x/3
|(4/3)(y — 1) — 2x = -2
Ответ:(3; 4)

Задача 14
|0,25x — 0,04y = 1
|0,4x + 1,5y = 40,7
Ответ:(8; 25)

Задача 15
|(5x — 3y)/4 = (x — 5y)/3
|7x + y = 12
Ответ:(2; -2)

Задача 16
|(3x + 1)/5 + 2y -3 = 0
|(4y — 5)/6 + 3y — 9 = -1/2
Ответ:(-42/11; 28/11)

Задача 17
|(3x — 1)/5 + 3y — 4 = 15
|(3y — 5)/6 + 2x — 8 = 23/3
Ответ:(7; 5)

Задача 18
|(2x — z)/6 + (2x — z)/9 = 3
|(x + z)/3 — (x — z)/4 = 4
Ответ:(6; 6)

Задача 19
|(x — 1)/3 + (5y + 1)/2 = (x + 10y — 8)/6
|(x + 2)(5y — 2)/2 = 5 + 5xy/2 — 2(x + 1)
Ответ: Нет решения.

Задача 20
|(5x — 1)/6 + (3y — 1)/10 = 3
|(11 — x)/6 + (11 + y)/4 = 3
Ответ:(5; -3).

Задача 21
|y — 0,2(x — 2) = 1,4
|5/2 — (2y — 3)/4 = (4x — y)/8
Ответ:(5; 2).

Задача 22
|x/5 + 0,03(10y — 20) = 0,8
|(2x + 4,5)/20 — 0,75 = (y — 3)/8
Ответ:(4; 2).

Задача 23
|y — x — (5x — 4)/2 = 3 — (11y + 17)/4
|x + (9y + 11)/4 — (3y + 4)/7 = 6
Ответ:(2; 1).

Задача 24
|(5x — 3y)/3 — (2y — 3x)/5 = x + 1
|(2x — 3y)/3 — (3y — 4x)/2 = y + 1
Ответ:(3; 2).

Задача 25
|(x — 1)/4 (1 + y)/2 = 1/6 — (x + 2y)/6
|(x — 2)/3 + x/15 = (y + 4)/5 — (4x — y)/15
Ответ: Решением является каждая пара чисел, которая есть решением уравнения 5x — 2y = 11.

Задача 26
|(x + 2y)/4 — (x — 2y)/2 = 1 — [x — (7 — 2y)/3]
|3x — 2y = 8
Ответ:(3; 1/2).

Задача 27
|(7 + x)/5 — (2x — y)/4 — 3y = -5

|(5y — 7)/2 + (4x — 3)/6 — 18 = -5x
Ответ:(3; 2).

Задача 28
|11y/20 — 0,8(x/4 + 2,5) = 5/2
|(6x — 0,3y)/2 — 3/2 = 2(1 + x)
Ответ:(5; 10).

Задача 29
|0,5x — (y — 4)/5 = 0,3x — (y — 4)/2
|0,5y — (x — 4)/6 = 7y/12 — (x — 3)/3
Ответ:(3; 2).

Задача 30
|2(x — y)/3 + 1,6 = 8x/15 — (3y — 10)/5
|(3x + 4)/4 + y/8 = 5x/6 — (y — 17)/12
Ответ:(5; 4).

Задача 31
|(2 + x)(5y — 2)/2 = 5 + 5xy/2 — 2(1 + x)
|(x — 1)² + (2y + 1)² = 2(1 + 2y)(x — 1)
Ответ: Решением является каждая пара чисел, которая есть решением уравнения x + 5y = 5

3 6 Решить для ? cos(x)=1/2 7 Найти x sin(x)=-1/2 8 Преобразование градусов в радианы 225 9 Решить для ? cos(x)=(квадратный корень из 2)/2 10 Найти x cos(x)=(квадратный корень из 3)/2 11 Найти x sin(x)=(квадратный корень из 3)/2 92=9 14 Преобразование градусов в радианы 120 градусов 15 Преобразование градусов в радианы 180 16 Найти точное значение желтовато-коричневый(195) 92-4 38 Найти точное значение грех(255) 39 Оценить лог база 27 из 36 40 Преобразовать из радианов в градусы 2 шт. 92-3sin(x)+1=0 43 Найти x tan(x)+ квадратный корень из 3=0 44 Найти x sin(2x)+cos(x)=0 45 Упростить (1-cos(x))(1+cos(x)) 92=25 59 График f(x)=- натуральный логарифм x-1+3 60 Найдите значение с помощью единичного круга угловой синус(-1/2) 61 Найти домен квадратный корень из 36-4x^2 92=0 66 Найти x cos(2x)=(квадратный корень из 2)/2 67 График у=3 68 График f(x)=- логарифмическая база 3 x-1+3 92 71 Найти x квадратный корень из x+4+ квадратный корень из x-1=5 72 Решить для ? cos(2x)=-1/2 73 Найти x логарифмическая база x из 16=4 9х 75 Упростить (cos(x))/(1-sin(x))+(1-sin(x))/(cos(x)) 76 Упростить сек(х)sin(х) 77 Упростить кубический корень из 24 кубический корень из 18 92=0 96 Найти x 3x+2=(5x-11)/(8г) 97 Решить для ? sin(2x)=-1/2 98 Найти x (2x-1)/(x+2)=4/5 92+n-72)=1/(n+9)

Решите следующее алгебраическое выражение: [5z-(x+2y)]-[3x-(y-2z)]

Выберите область веб-сайта для поиска

MathAllУчебные пособияПомощь по выполнению домашних заданийПланы уроков

Искать на этом сайте

Цитата страницы Начать эссе значок-вопрос Задайте вопрос Начать бесплатную пробную версию

Скачать PDF PDF Цитата страницы Цитировать Поделиться ссылкой Делиться

Ссылайтесь на эту страницу следующим образом:

«Решите следующее алгебраическое выражение: [5z-(x+2y)]-[3x-(y-2z)]» eNotes Editorial , 21 декабря 2009 г. , https://www.enotes.com/homework-help /алгебраическое-выражение-124719. По состоянию на 21 мая 2023 г.

Ответы экспертов

Привет. Это алгебраическое выражение (кстати, в чем разница между выражением и уравнением? Ответ следует далее) требует, чтобы вы увидели, что отрицательный знак можно интерпретировать как (-1) и распределять с помощью распределительного свойства умножения.

Используя стратегию решения проблем «Упрости и реши», мы сначала пытаемся определить, можем ли мы комбинировать похожие термины. Еще нет. Итак, давайте обратимся к этим неприятным (-) знакам минус. Чтобы устранить путаницу, которую они создают, изменим ли мы все знаки операций на (+) знаки сложения? Сделаем так:

[5z + -1(x + 2y)] + -1[3x + -1(y + -2z)]

= 5z + -1x + -2y + -1[3x + -1y + 2z]

= 5z + -1x + -2y + -3x + 1y + -2z Теперь объединим похожие термины

= -4x + -y + 3z

(О да! В выражении нет знака равенства, но в уравнении он есть).

Утверждено редакцией eNotes

Примечание:

Многие учебники по алгебре предлагают записывать переменные в алфавитном порядке с убывающими показателями степени, а вторичные переменные имеют возрастающие степени.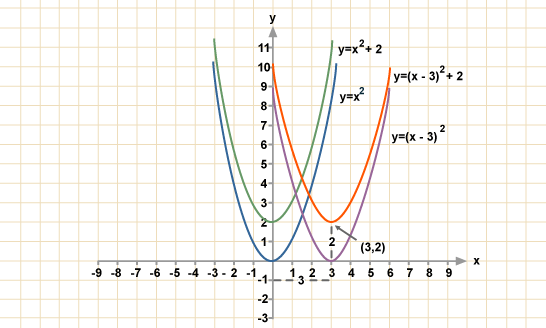 Например, 92 +2xy – нет.

Для исходной задачи, описанной выше, лучшим ответом будет

— 4x — y + 3z

вместо того, чтобы требовать, чтобы первый член всегда был положительным.

Утверждено редакцией eNotes

Эта проблема заключается в перемещении знака минус внутри скобки, чтобы сохранить порядок операций.

[5z-(x+2y)]-[3x-(y-2z)]

5z — x — 2y — (3x — y + 2z)

5z — x — 2y — 3x + y — 2z

3z — 4x — y

См. eNotes без рекламы

Начните 48-часовую бесплатную пробную версию , чтобы получить доступ к более чем 30 000 дополнительных руководств и более чем 350 000 вопросов помощи при выполнении домашних заданий, на которые ответили наши эксперты.

Получите 48 часов бесплатного доступа

Уже зарегистрированы? Войдите здесь.

Утверждено редакцией eNotes

Задайте вопрос

Похожие вопросы

Просмотреть все

Математика

Последний ответ опубликован 07 сентября 2010 г. в 12:47:25.

Что означают буквы R, Q, N и Z в математике?

14 Ответы педагога

Математика

Последний ответ опубликован 07 октября 2013 г. в 20:13:27.

Как определить, является ли это уравнение линейной или нелинейной функцией?

84 Ответы педагога

Математика

Последний ответ опубликован 25 февраля 2016 г. в 18:48:45.

Сколько времени (в часах) займет ваше путешествие, если вы проедете 350 км со средней скоростью 80 км/ч? Какова формула с данными: время, расстояние, скорость или скорость?

1 Ответ воспитателя

Математика

Последний ответ опубликован 02 сентября 2012 г. в 3:00:53.

Как ограничения (пределы исчисления) используются или применяются в повседневной жизни? Или применительно к проблемам реального мира? Мне нужно пару примеров! Спасибо!

1 Ответ учителя

Математика

Последний ответ опубликован 09 октября 2017 г.