Определение синуса, косинуса и тангенса угла. Знаки синуса, косинуса и тангенса. Синус, косинус и тангенс углов α и –α
Определение синуса, косинуса, тангенса и котангенса угла
План урока
- Введение понятий синуса, косинуса угла
- Частные случаи тригонометрических уравнений.
- Введение понятий тангенса, котангенса угла
- Таблица некоторых значений синуса, косинуса, тангенса, котангенса угла
- Решение задач на нахождение синуса, косинуса, тангенса угла, вычисление значений тригонометрических выражений, решение тригонометрических уравнений
Цели урока
- Знать определения синуса, косинуса, тангенса и котангенса угла, их некоторые табличные значения, решения частных случаев тригонометрических уравнений
- Уметь вычислять значения выражений, содержащих синус, косинус, тангенс или котангенс угла, решать тригонометрические уравнения типа sinx=0, sinx=±1, cosx=0, cosx=±1
Разминка
1.
Найдите координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол: π2, 5π, -2700, 5400, -π2+2πk, k∈Z.
2. Определите четверть, в которой расположена точка, полученная путем поворота точки (1; 0) на угол: 2π3, -4π3,-6270.
Что такое синус, косинус и тангенс угла вы уже знаете из курса геометрии, углы рассматривались от 00 до 1800. Введем определение синуса и косинуса для произвольного угла.
Рис. 1
Синусом угла α называется ордината точки, полученной поворотом точки (1; 0) вокруг начала координат на угол α (Рис. 1). Обозначается sinα.
Косинусом угла α называется абсцисса точки, полученной поворотом точки (1; 0) вокруг начала координат на угол α (Рис. 1). Обозначается cosα.
Например, при повороте точки (1; 0) на угол π получается точка (–1; 0). Так как синус это ордината, а косинус — абсцисса, то sinπ=0, cosπ=-1.
Пример 1
Найти sin-π2 и cos-π2.
Решение
Так как при повороте на угол -π2 точка (1; 0) попадает в точку (0; –1), то sin-π2=-1, cos-π2=0.
Ответ: sin-π2=-1, cos-π2=0.
Радианную меру угла α можно рассматривать как действительное число, значит sinα и cosα являются числовыми выражениями. В уравнении sinx=a, где a∈R, x считается неизвестным.
Рис. 2
Решим уравнение cosx=0. Найдем все углы, косинус которых 0. У двух точек единичной окружности (0; 1)и (0; –1) абсциссы равны нулю (Рис. 2). Они получаются из точки (1; 0) путем поворота вокруг начала координат на углы π2,3π2,5π2,7π2и т. д., и на углы -π2,-3π2,-5π2,-7π2 и т. д.
Тогда cosx=0 при x=π2+πk, k∈Z. (1)
Аналогично, при помощи единичной окружности можно решить уравнения sinx=0, sinx=±1, cosx=±1.
Их называют частными случаями тригонометрических уравнений .
Приведем их решения.
sinx=0, x=πk, k∈Z.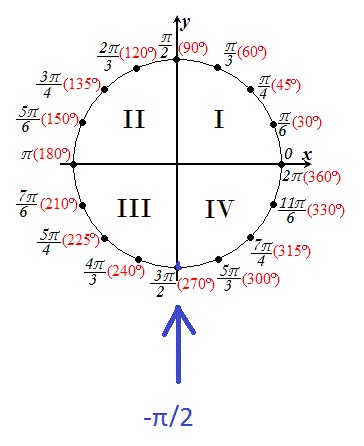
(2)
sinx=1, x=π2+2πk, k∈Z. (3)
sinx=-1, x=-π2+2πk, k∈Z. (4)
cosx=1, x=2πk, k∈Z. (5)
cosx=-1, x=π+2πk, k∈Z. (6)
sinα и cosα определены для любого угла, а их значения находятся в промежутке [–1; 1].
Тангенсом угла α называется отношение синуса угла α к его косинусу. Обозначается tg α.
tg α=sinαcosα.
Котангенсом угла α называется отношение косинуса угла α к его синусу. Обозначается ctg α.
ctg α=cosαsinα.
Тангенс угла определен тогда, когда cosα≠0, т. е. α≠π2+πk, k∈Z. Котангенс угла определен когда sinα≠0, α≠πk, k∈Z.
Таблица некоторых значений синуса, косинуса, тангенса и котангенса
Пример 2
Найти все углы из промежутка [-2π; 2π], на которые нужно повернуть точку
А(1; 0), чтобы получить точку Aα, если:
а)sinα=32; б)cosα=-12.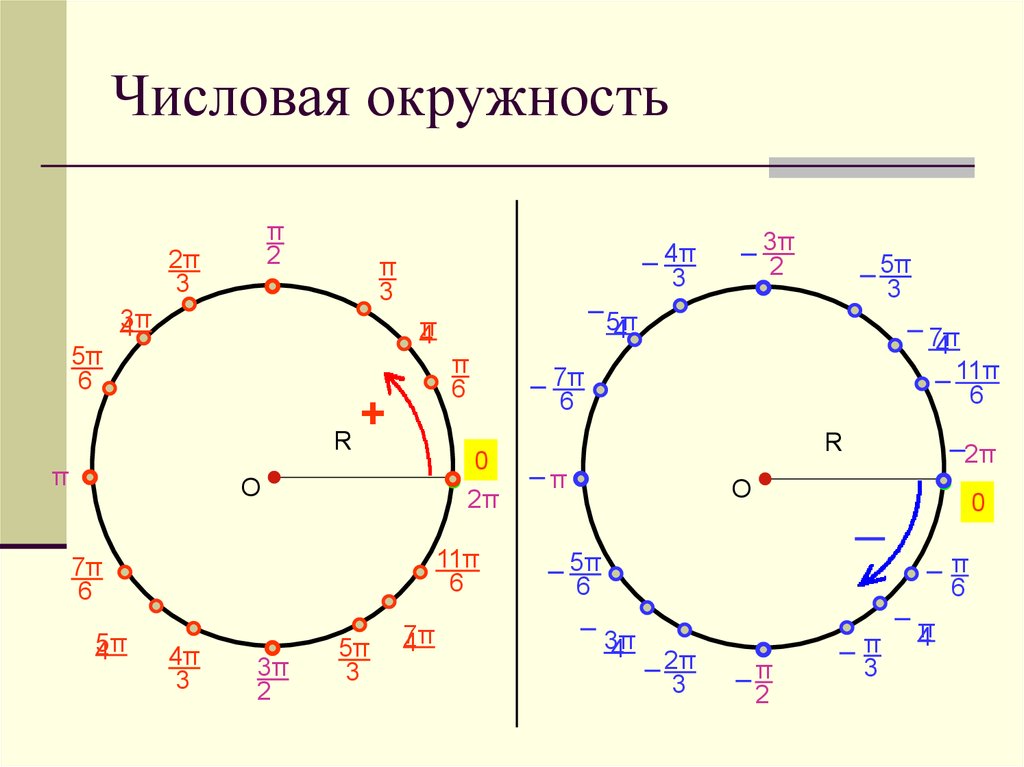
Решение
а) По определению синус угла это ордината точки. Ординату, равную 32, имеют две точки единичной окружности – В и С (Рис. 3). Точка С получена путем поворота точки А на угол α1=π3 или на угол α2=-2π+π3=-5π3. Точка В получена из А поворотом на α3=π-π3=2π3 или на угол α4=-π-π3=-4π3.
Рис. 3
б) Абсциссу, равную -12, имеют точки В и Е единичной окружности. С углами поворота точки А для получения точки В
Ответ: а) π3,-5π3, 2π3,-4π3;
б) 2π3,-4π3, 4π3,-2π3.
Пример 3
Найти sinα, cosα, tgα, если:
а) α=-7π; б) α=5π2; в) α=19800.
Решение
а) Представим α в виде α=2πκ+β, k∈Z, β<2π, или, другими словами, выделим в α полные обороты окружности: α=-6π-π.
Значит, точка, полученная из точки A(1; 0) поворотом на угол -7π совпадает с точкой, полученной поворотом на -π, координаты которой (–1; 0). Тогда sinα=0, cosα=-1, tgα=sinαcosα=0.
б) α=5π2=2π+π2. Точка, полученная из начальной точки поворотом на 5π2 совпадает с точкой, полученной поворотом на π2. Она имеет координаты (0; 1). Значит, sinα=1, cosα=0, tgα не существует.
в) α=19800=5×3600+1800. Тогда sinα=0, cosα=-1, tgα=0.
Ответ:
а) sinα=0, cosα=-1, tgα=0;
б) sinα=1, cosα=0, tgα не существуют;
в) sinα=0, cosα=-1, tgα=0.
Пример 4
Вычислить:
а) sinπ3+cos-3π2;
б) cos-π+tgπ4.
Решение
а) Воспользуемся таблицей некоторых значений синуса, косинуса, тангенса и котангенса.
sinπ3+cos-3π2=32+0=32.
б) cos-π+tgπ4=-1+1=0.
Ответ: а) 32;
б) 0.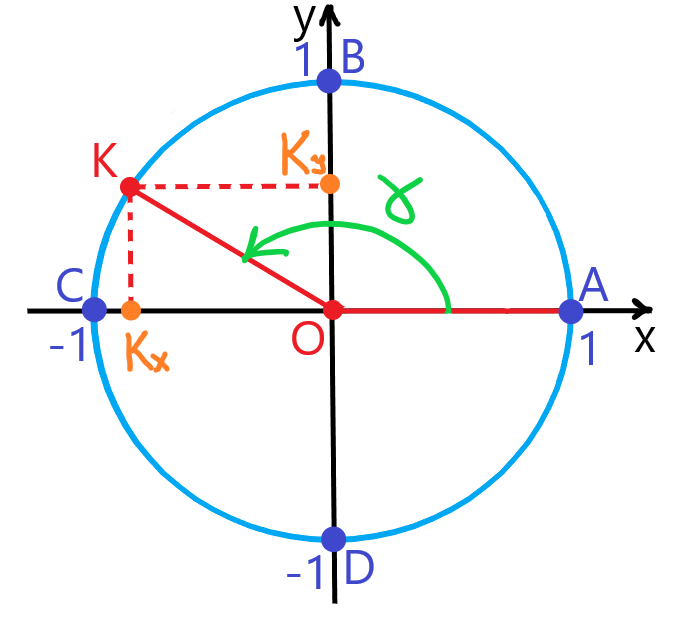
Пример 5
Решить уравнение:
а) 4cosx=-4;
б) sin3x=1;
в) cos2x+π3=1.
Решение
а) 4cosx=-4. Разделим обе части уравнения на 4: cosx=-1. Согласно уравнению (6) x=π+2πk, k∈Z.
б) sin3x=1. Воспользуемся уравнением (3): 3x=π2+2πk, k∈Z.
Выразим x из этого уравнения:
x=π6+2πk3, k∈Z.
в) cos2x+π3=1. По уравнению (5) имеем:
2x+π3=2πk, κ∈Z, 2x=-π3+2πk, k∈Z, x=-π6+πk, k∈Z.
Ответ: а) π+2πk, k∈Z;
б) π6+2πk3, k∈Z;
в) -π6+πk, k∈Z.
Упражнение 1
Найти все углы из промежутка [-2π; 2π], на которые нужно повернуть точку
А(1; 0), чтобы получить точку Аа, если:
а)sinα=-22; б)cosα=32.
Упражнение 2
Найти sinα, cosα, tgα, если:
а) α=5π; б) α=9π2; в) α=-12600.
Упражнение 3
Вычислить:
а)cosπ6-sin-π2;
б)sin-2π+cosπ4.
Упражнение 4
Решить уравнение:
а) 5sinx-5=0;
б) cos4x=1;
в) cos5x+π6=0.
Контрольные вопросы
1. Какая область допустимых значений переменной в выражении tg x?
2. Какая область допустимых значений переменной в выражении ctg x?
3. Как можно найти котангенс угла, если известен тангенс этого угла?
Ответы
Упражнение 1
а) -π4;-3π4;5π4;7π4; б)π6;-π6;11π6;-11π6.
Упражнение 2
а)sinα=0, cosα=-1, tg α=0;
б)sinα=1, cosα=0, tg α не существует;
в)sinα=0, cosα=-1, tg α=0.
Упражнение 3
а)32+1; б)22.
Упражнение 4
а)π2+2πk, k∈Z; б)πk2, k∈Z; в)π15+πk5, k∈Z.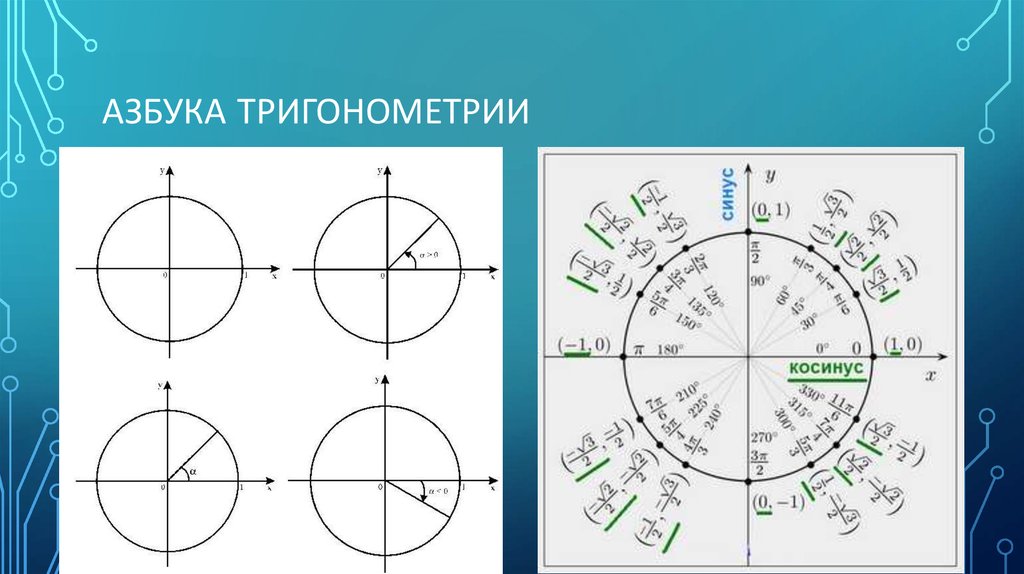
Знаки синуса, косинуса и тангенса угла
Вспомним, что синусом угла называется ордината точки , полученной поворотом точки вокруг начала координат на угол .
Косинусом угла называется абсцисса точки , полученной поворотом точки вокруг начала координат на угол .
Тангенсом угла называется отношение синуса угла к его косинусу.
Котангенсом угла называется отношение косинуса угла к его синусу.
Также напомним, что оси координат делят плоскость на четыре четверти.
А сейчас давайте выясним, какие знаки имеют синус и косинус в зависимости от того, в какой четверти единичной окружности располагается точка.
Пусть на координатной плоскости изображена единичная окружность с
центром в начале координат. Точка совершает поворот против часовой стрелки на угол и оказывается в точке , которая расположена в первой четверти. Для точек, расположенных
в первой четверти, абсцисса и ордината положительны, а значит, и будут иметь положительные значения.
Пусть точка совершает поворот против часовой стрелки и оказывается в точке , которая расположена во второй четверти. Для точек, которые расположены во второй четверти, абсциссы отрицательны, а ординаты положительны, а значит, будет принимать отрицательные значения, а – положительные значения. То есть и при .
Теперь пусть точка совершает поворот против часовой стрелки и оказывается в точке , которая расположена в третьей четверти. Для точек, которые расположены в третьей четверти, абсциссы и ординаты отрицательны, а значит, и будут принимать отрицательные значения. То есть и , если .
И пусть точка совершает поворот против часовой стрелки и оказывается в точке , которая расположена в четвёртой четверти. У точек, которые
расположены в четвёртой четверти, абсциссы положительны, а ординаты
отрицательны, а значит, будет принимать положительные значения, а – отрицательные значения. То есть и при .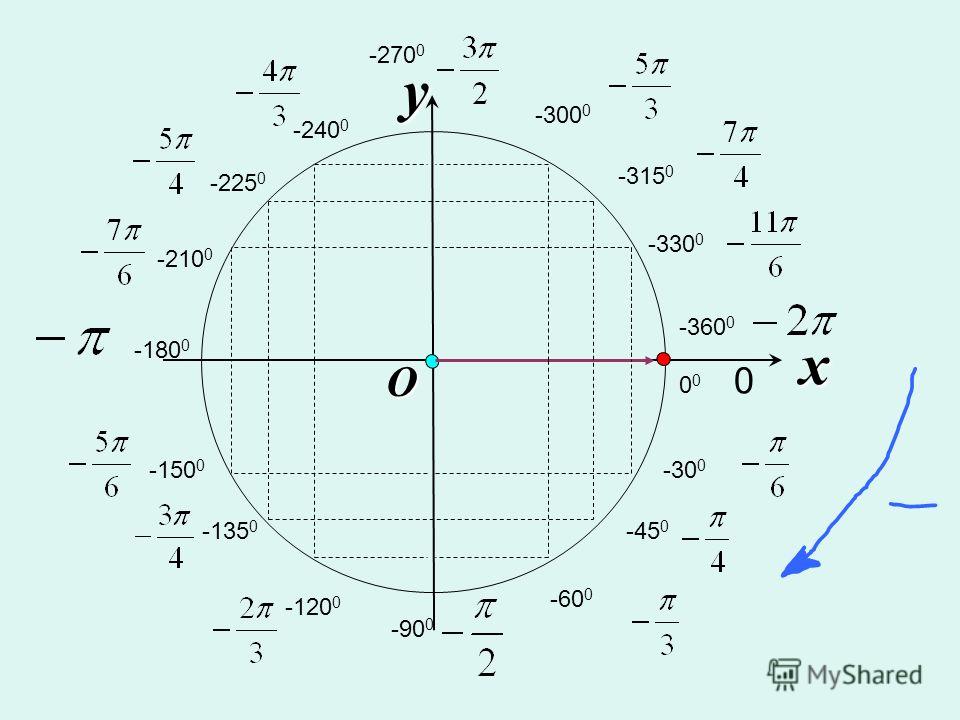
При этом важно помнить, что при повороте точки против часовой стрелки на угол, больший , а также при повороте точки по часовой стрелке на любой угол, знаки синуса и косинуса определяются тем, в какой четверти окажется точка.
Давайте определим знаки синуса и косинуса углов: , , , .
Итак, . Тогда углу соответствует точка единичной окружности, расположенная в третьей четверти. Мы с вами выяснили, что в третьей четверти синус и косинус принимают отрицательные значения. Поэтому и .
. А значит, углу в соответствует точка единичной окружности, расположенная во второй четверти. Мы выяснили, что во второй четверти синус принимает положительные значения, а косинус – отрицательные. Следовательно, , а .
Углу соответствует точка единичной окружности, расположенная в четвёртой четверти. В четвёртой четверти синус принимает отрицательные значения, а косинус – положительные. Следовательно, , .
И последний угол – угол .
Запишем , . Тогда можем сказать, что повороту точки с координатами на угол д соответствует точка, расположенная в первой четверти. Поэтому и .
Давайте выясним, какие знаки имеет тангенс. Мы знаем, что .
Если и имеют одинаковые знаки, то . Если же и имеют разные знаки, то .
Итак, в первой четверти синус и косинус принимают положительные значения, то есть имеют одинаковые знаки, а значит, тангенс в первой четверти также принимает положительные значения.
Во второй четверти синус принимает положительные значения, а косинус – отрицательные, то есть они имеют разные знаки, а значит, тангенс принимает отрицательные значения во второй четверти.
В третьей четверти синус и косинус принимают отрицательные значения, то есть имеют одинаковые знаки. Следовательно, тангенс в третьей четверти принимает положительные значения.
В четвёртой четверти синус принимает отрицательные значения, а
косинус – положительные, они имеют разные знаки.
Следовательно, в четвёртой
четверти тангенс принимает отрицательные значения.
А какие знаки имеет котангенс? . А значит, если и имеют одинаковые знаки, то . Если и имеют разные знаки, то . Следовательно, значения котангенса имеют те же знаки, что и значения тангенса.
Давайте определим знаки тангенса и котангенса углов: и .
. Тогда углу соответствует точка единичной окружности, расположенная во второй четверти. Мы с вами выяснили, что во второй четверти тангенс и котангенс принимают отрицательные значения. Поэтому и .
. А значит, углу, равному единице, соответствует точка единичной окружности, расположенная в первой четверти. В первой четверти тангенс и котангенс принимают положительные значения. Следовательно, и .
А сейчас давайте выполним несколько заданий.
Задание первое. Определите знак числа , если равняется: , .
Решение.
Второе задание. Определите
знак числа , если равняется: , .
Решение.
И ещё одно задание. Определите знак числа , если равняется: , .
Решение.
Синус, косинус и тангенс в четырех квадрантах
Синус, косинус и тангенс
Три основные функции в тригонометрии — это синус, косинус и тангенс.
Их легко вычислить:
Разделить длину одной стороны прямоугольного треугольника
на другую сторону
… но надо знать с каких сторон!
Для угла θ функции вычисляются следующим образом:
Синусоидальная функция: | sin( θ ) = Противоположность / Гипотенуза |
Функция косинуса: | cos( θ ) = Смежный / Гипотенуза |
Функция касания: | tan( θ ) = Противоположный / Смежный |
Пример: чему равен синус 35°?
Используя этот треугольник (длина только до одного десятичного знака): sin(35°) = противоположность / гипотенуза = 2,8/4,9 = 0,57. |
.. Декартовы координаты
Используя декартовы координаты, мы отмечаем точку на графике , как далеко вдоль и , как далеко вверх по :
Точка (12,5) находится на 12 ед. вдоль и на 5 ед. вверх.
Четыре квадранта
Когда мы включаем отрицательных значений , оси x и y делят пространство на 4 части:
Квадранты I, II, III и IV
(Нумерация против часовой стрелки)
- В квадранте I и x, и y положительны,
- в квадранте II x отрицательное (y все еще положительное),
- в квадранте III и x, и y отрицательны, а
- в квадранте IV x снова положительный, а y отрицательный.
Вот так:
| Квадрант | X (по горизонтали) | Y (вертикальный) | Пример |
|---|---|---|---|
| я | Положительный | Положительный | (3,2) |
| II | Отрицательный | Положительный | (−5,4) |
| III | Отрицательный | Отрицательный | (-2,-1) |
| IV | Положительный | Отрицательный | (4,−3) |
Пример: Точка «C» (−2,−1) находится на 2 единицы вперед в отрицательном направлении и на 1 единицу вниз (т.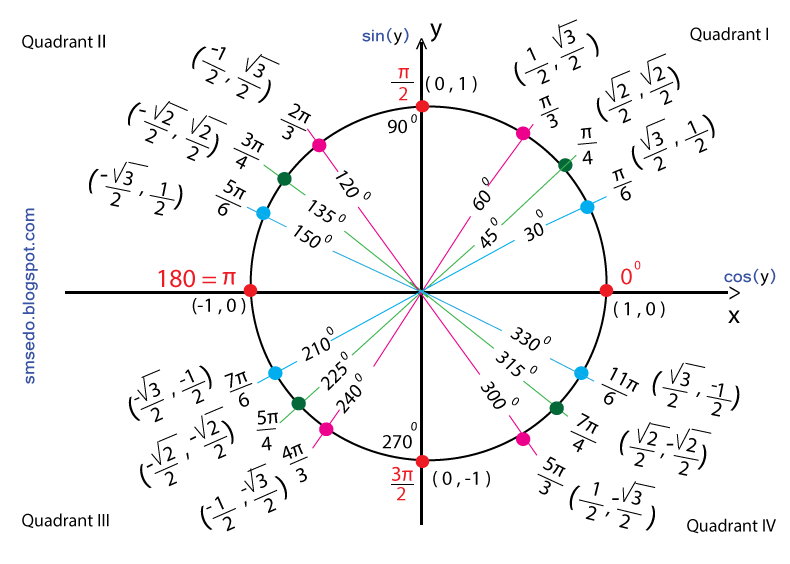
е. в отрицательном направлении).
И x, и y отрицательны, поэтому эта точка находится в «Квадранте III»
Контрольный угол
Углы могут быть больше 90º
Но мы можем вернуть их ниже 90º, используя ось X в качестве точки отсчета.
Думайте, что «ссылка» означает «ссылка x»
Самый простой способ — сделать набросок!
Пример: 160º
Начните с положительной оси x и поверните на 160º
Затем найдите угол к ближайшей части оси x,
в данном случае 20º
Исходный угол для 160º равен 20º
Здесь мы видим четыре примера с опорным углом 30º:
Вместо эскиза можно использовать следующие правила:
| Квадрант | Контрольный угол |
| я | θ |
| II | 180º − θ |
| III | θ − 180º |
| IV | 360º − θ |
Синус, косинус и тангенс в Четыре квадранта
Теперь давайте посмотрим на детали прямоугольного треугольника с углом 30° в каждом из 4 квадрантов.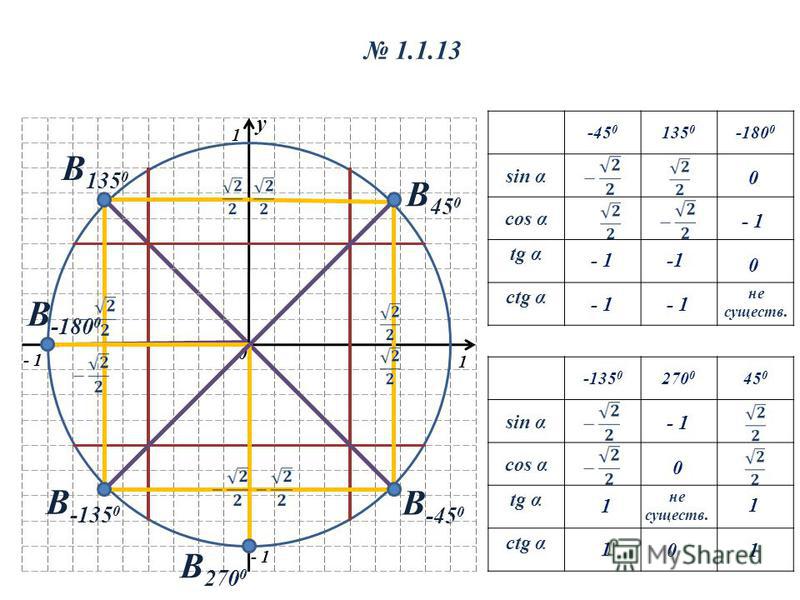
В квадранте I все в норме, а синус, косинус и тангенс положительны:
Пример: синус, косинус и тангенс угла 30°
Синус | sin(30°) = 1/2 = 0,5· |
Косинус | cos(30°) = 1,732 / 2 = 0,866 |
Касательная | тангенс (30°) = 1 / 1,732 = 0,577 |
Но в квадранте II направление x отрицательно , а косинус и тангенс становятся отрицательными:
Пример: синус, косинус и тангенс 150°
Синус | sin(150°) = 1/2 = 0,5 |
Косинус | cos(150°) = −1,732 / 2 = −0,866 |
Касательная | тангенс (150°) = 1 / −1,732 = −0,577 |
В квадранте III синус и косинус отрицательны:
Пример: синус, косинус и тангенс 210°
Синус | sin(210°) = −1 / 2 = −0,5 |
Косинус | cos(210°) = −1,732 / 2 = −0,866 |
Касательная | тангенс (210°) = −1 / −1,732 = 0,577 |
Примечание.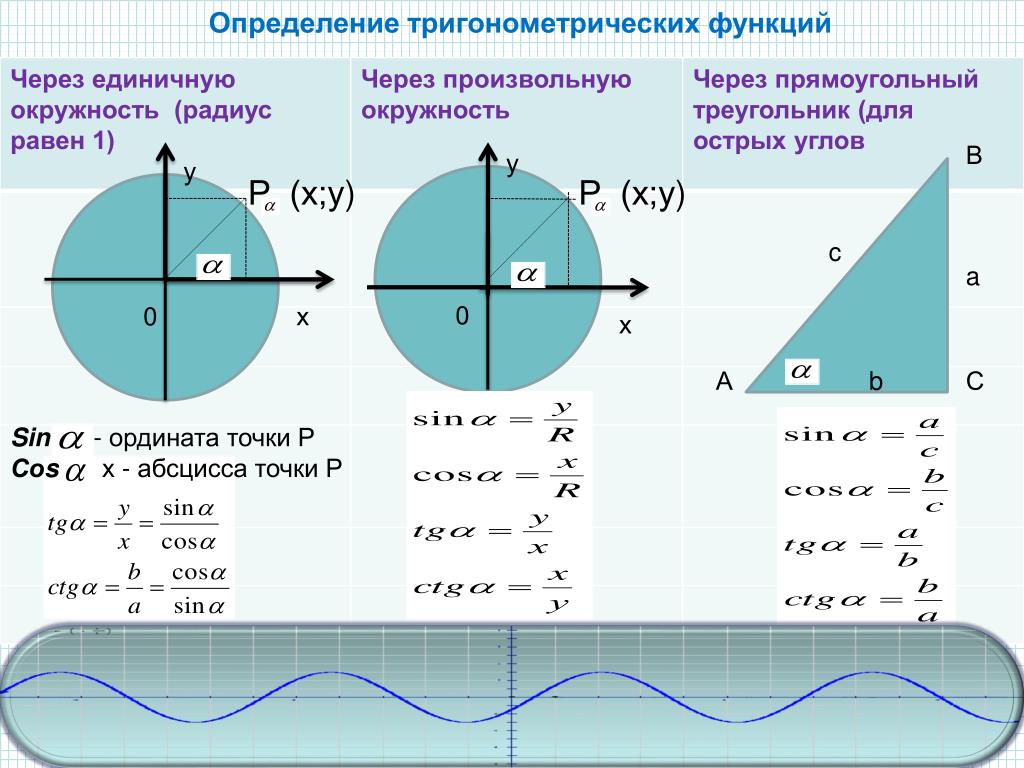
Тангенс равен положительному числу , потому что деление отрицательного числа на отрицательное дает положительное значение.
В квадранте IV синус и тангенс отрицательны:
Пример: синус, косинус и тангенс 330°
Синус | sin(330°) = −1 / 2 = −0,5 |
Косинус | cos(330°) = 1,732 / 2 = 0,866 |
Касательная | тангенс (330°) = −1 / 1,732 = −0,577 |
Выкройка есть! Посмотрите, когда синус, косинус и тангенс положительны …
- Все три из них положительные в квадранте I
- Синус положительный только в Квадранте II
- Только тангенс положителен в квадранте III
- Косинус положителен только в Квадранте IV
Это можно показать еще проще:
На этом графике также отображается «ASTC».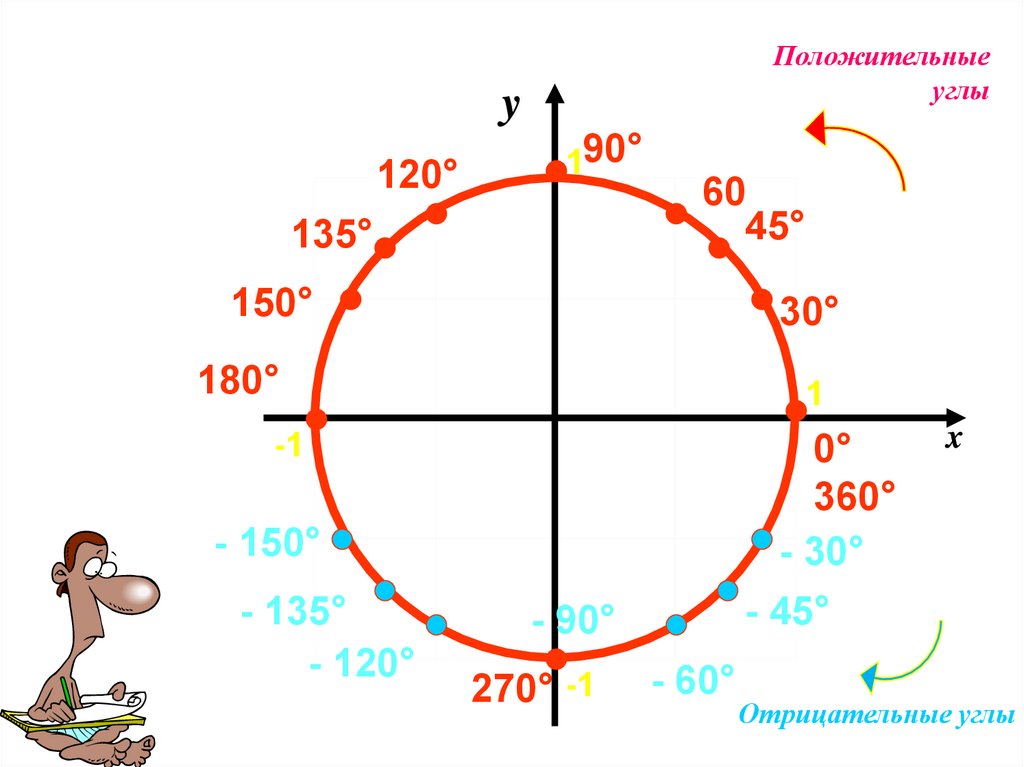
Некоторым людям нравится запоминать четыре буквы ASTC по одной из следующих:
- Все учащиеся сдают химию
- Все учащиеся сдают математический анализ
- Все глупые коты Том
- Все станции к центральному
- A dd S сахар T o C офис
Может быть, вы могли бы придумать свой собственный. Или просто помните ASTC.
Инверсия Sin, Cos и Tan
Что такое арксинус 0,5?
sin -1 (0,5) = ?
Другими словами, когда на графике ниже у равно 0,5, чему равен угол?
Существует много углов где y=0,5
Проблема в следующем: калькулятор выдаст вам только одно из этих значений …
… но всегда есть два значения между 0º и 360º
(и бесконечно много дальше):
| | Первое значение | Второе значение |
| Синус | θ | 180º − θ |
| Косинус | θ | 360º − θ |
| Касательная | θ | θ + 180º |
Теперь мы можем решить уравнения для под любым углом!
Пример: Решаем sin θ = 0,5
Получаем первое решение из калькулятора = sin -1 (0,5) = 30º (это в квадранте I)
Следующее решение 180° − 30° = 150° (квадрант II)
Пример: вычислить cos θ = −0,85
Получаем первое решение из калькулятора = cos -1 (−0,85) = 148,2º (квадрант II)
Другое решение: 360º − 148,2º = 211,8º (квадрант III)
Возможно, нам потребуется изменить угол между 0º и 360º, прибавив или вычитая 360º
Пример.
Решите тангенс θ
= −1,3Получаем первое решение из калькулятора = tan -1 (−1,3) = −52,4º
Это меньше 0º, поэтому мы прибавляем 360º: −52,4º + 360º = 307,6º (квадрант IV)
Другое решение: −52,4º + 180º = 127,6º (квадрант II)
3914, 3915, 3916, 3917, 3918, 3919, 3920, 3921, 3922, 3923
Упражнение: Прогулка по пустыне 2
Видео-урок: Тригонометрические отношения на единичной окружности
Стенограмма видео
В этом видео мы научимся использовать тот факт, что квадрант, в котором лежит угол, определяет знак его тригонометрические функции синуса, косинуса и тангенса для решения уравнений. Начнем с размышлений о том, что мы знаем об углах на координатной плоскости.
На координатной плоскости центр
является источником. Для стандартных углов, измеренных в
координатная плоскость, положительная ось 𝑥 будет начальной стороной, начальной точкой
нашего измерения.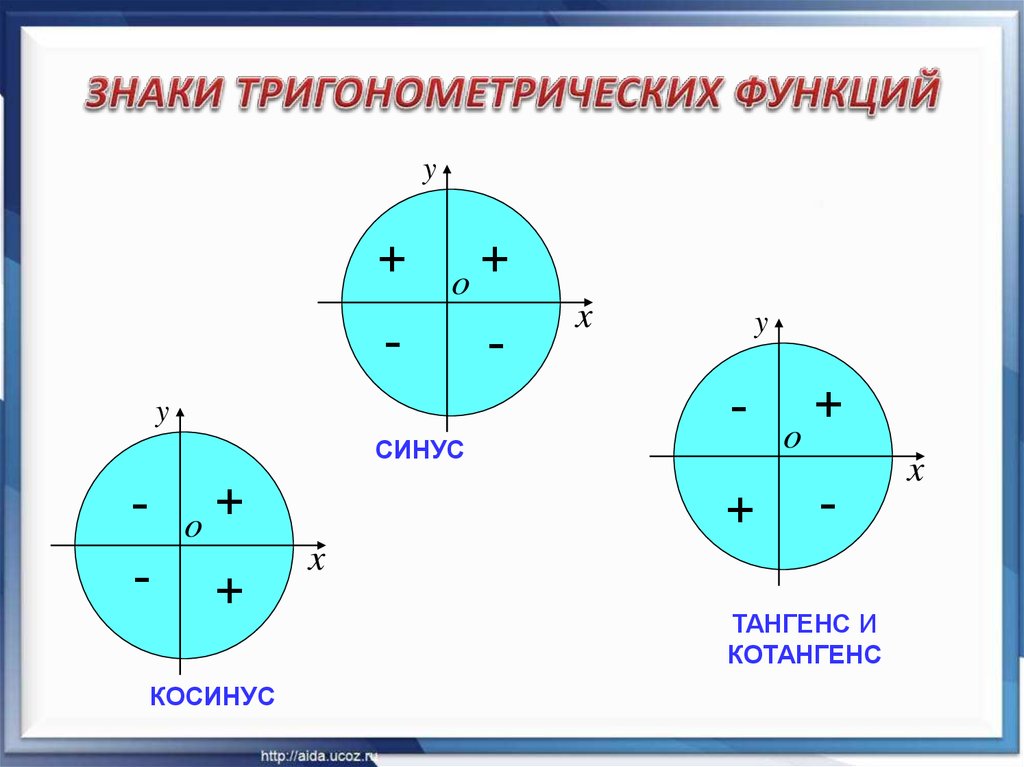
Эта положительная 𝑥-ось и
начало представляет ноль градусов. К тому времени, когда мы доберемся до положительного
𝑦-ось, мы пошли на 90 градусов. Отрицательная ось 𝑥 будет равна 180
градусов. Отрицательная 𝑦-ось будет 270
градусов. И весь обратный путь для
полный оборот 360 градусов. В радианах это будет ноль, 𝜋
больше двух, 𝜋, три 𝜋 больше двух, а затем два 𝜋.
Луч, обозначающий, где мы
остановка измерения нашего угла называется конечной стороной. И угол и стандартное положение
будет располагаться между начальной и конечной сторонами. Но мы хотим специально
рассмотрим углы, лежащие на единичной окружности. Единичный круг имеет центр в
начало координат и имеет радиус в одну единицу. Для некоторой координаты 𝑥, 𝑦 в
первом квадранте длины 𝑥 и 𝑦 становятся катетами прямоугольного треугольника. А поскольку мы знаем, что радиус
этого круга один, гипотенуза этого прямоугольного треугольника будет один.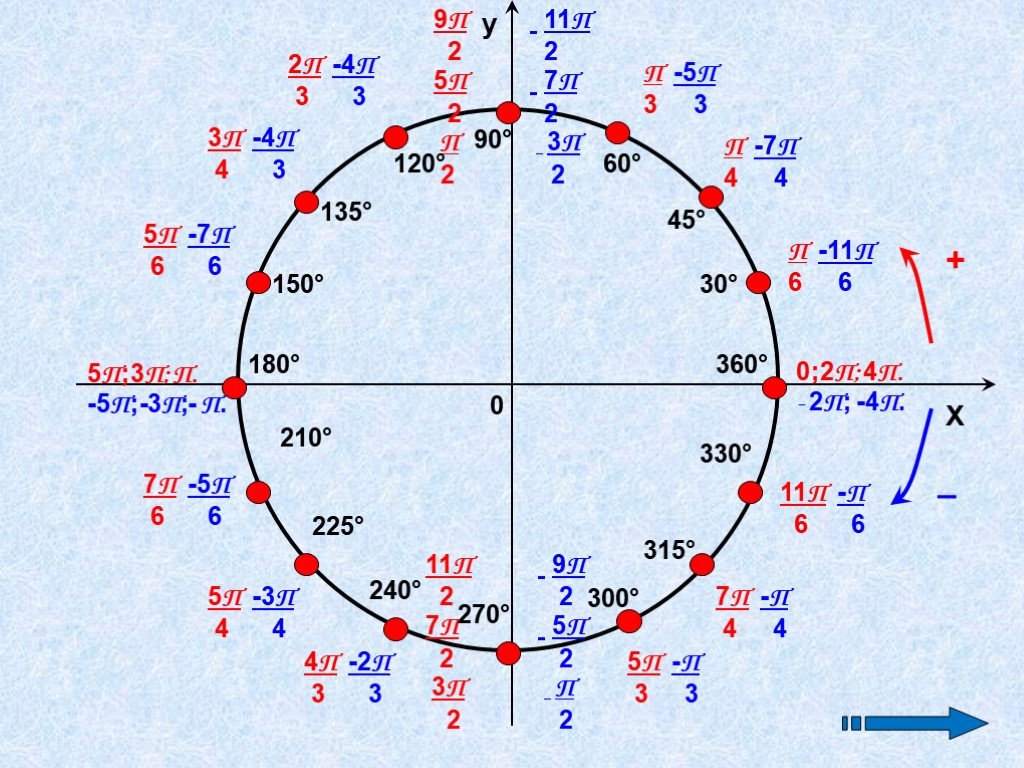
Если мы обозначим здесь длины сторон 𝑥 и 𝑦, мы можем взять теорему Пифагора, которая говорит нам 𝑎 в квадрате плюс 𝑏 в квадрате равно 𝑐 в квадрате, в единичном круге 𝑥 в квадрате плюс 𝑦 в квадрате равно один. Можно также сказать, что уравнение единичного круга должно быть 𝑥 в квадрате плюс 𝑦 в квадрате равно единице. Но то, что мы хотим сделать сейчас, это рассмотрим немного тригонометрии в отношении синуса единичной окружности, косинуса и касательная. Мы знаем синус угла представляет длину противоположной стороны по гипотенузе, косинус угла 𝜃 представляет длину прилегающей стороны по гипотенузе, а касательная Отношение угла — это отношение длины противоположной стороны к прилежащей стороне длина.
Для нашего угла 𝜃 внутри блока
круг, длина противоположной стороны всегда будет 𝑦-значением, это вертикаль
нога.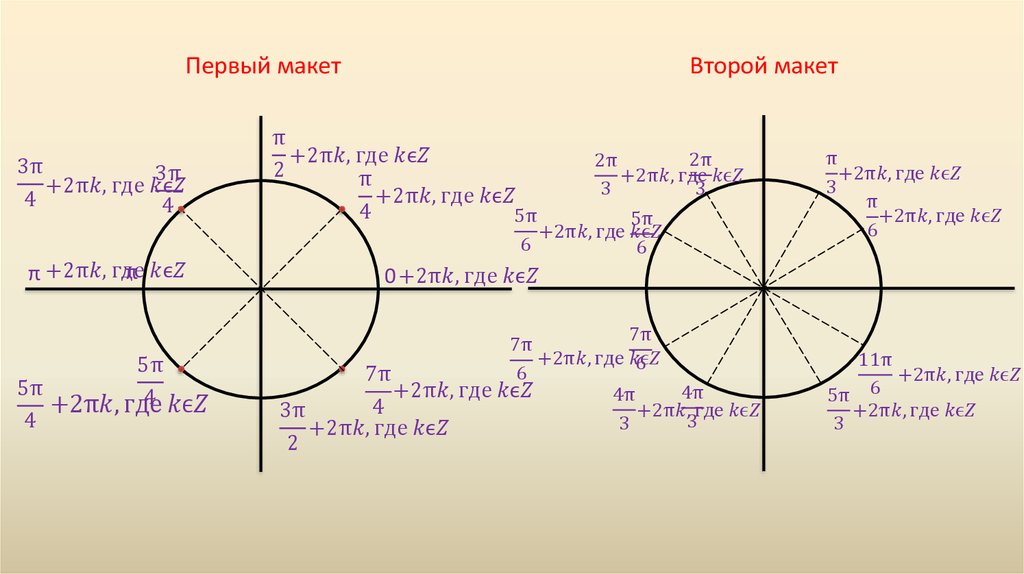
Грех 𝜃 тогда 𝑦 над одним
так как в единичной окружности гипотенуза всегда равна единице. грех 𝜃, следовательно, равен
𝑦 в единичном круге. Аналогично, соседняя сторона будет
быть горизонтальной ногой, 𝑥-значением. А значит в единичном круге,
cos 𝜃 будет равен 𝑥. А это значит, что загар
угол 𝜃 будет равен 𝑦 над 𝑥.
Прежде чем мы рассмотрим несколько примеров,
есть еще одна вещь, которую нам нужно рассмотреть. А это синус углов
квадранты. Если мы сохраним наш единичный круг, и мы
посмотрите на наши 𝑥, 𝑦 в первом квадранте, в первом квадранте все 𝑥-значения
положительный и все 𝑦-значения положительны. Это означает, что грех 𝜃 будет
положительна, так как 𝑦 положительна, то cos 𝜃 будет положительным, так как 𝑥
положительный, а поскольку 𝑥 и 𝑦 оба положительны, тангенс 𝜃 также будет
положительный.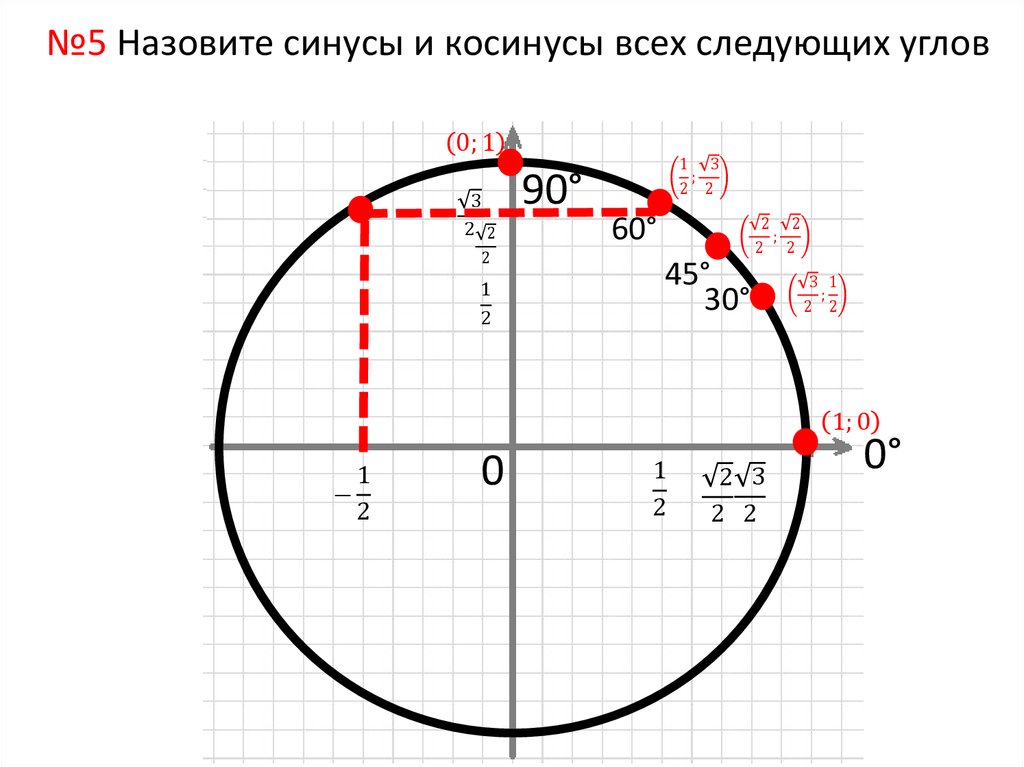
Это означает, что в первом квадранте
все триггерные отношения положительны.
Но когда мы движемся ко второму квадранту и создадим прямой угол из точки отрицательный 𝑥, 𝑦, мы имеем дело с отрицательным 𝑥-значения и положительные 𝑦-значения. 𝑦-значение положительно в второй квадрант, делая значение синуса положительным. Но 𝑥-значение отрицательное. А это означает, что во втором квадранте косинус будет отрицательным. С положительным значением и отрицательное значение, тогда тангенс становится отрицательным. Итак, мы можем обобщить и сказать в во втором квадранте синус положительный, а косинус и тангенс отрицательные.
Переход к третьему квадранту, в
третий квадрант, значение 𝑥 и значение 𝑦 будут отрицательными. Это означает, что синус будет
отрицательный, косинус будет отрицательным. Однако с касательной отрицательное 𝑦
над отрицательным 𝑥 будет положительным.
Итак, в третьем квадранте синус и
косинус отрицательный, а тангенс положительный. И, наконец, в четвертом квадранте
𝑥-значения будут положительными, а 𝑦-значения будут отрицательными. Это дает нам отрицательный синус
значение, положительное значение косинуса и отрицательное значение тангенса.
Один из способов запомнить эти синусоидальных значений с помощью диаграммы CAST, которая выглядит следующим образом. Диаграмма CAST показывает, какие значение триггера будет положительным в каком квадранте. В первом квадранте все положительный. Во втором квадранте синус равен положительный. В третьем квадранте тангенс равен положительный. А в четвертом квадранте косинус равен положительный. Теперь мы готовы рассмотреть некоторые Примеры.
Найти грех 𝜃, если 𝜃 находится в
стандартное положение и его крайняя сторона проходит через точку три пятых,
отрицательные четыре пятых.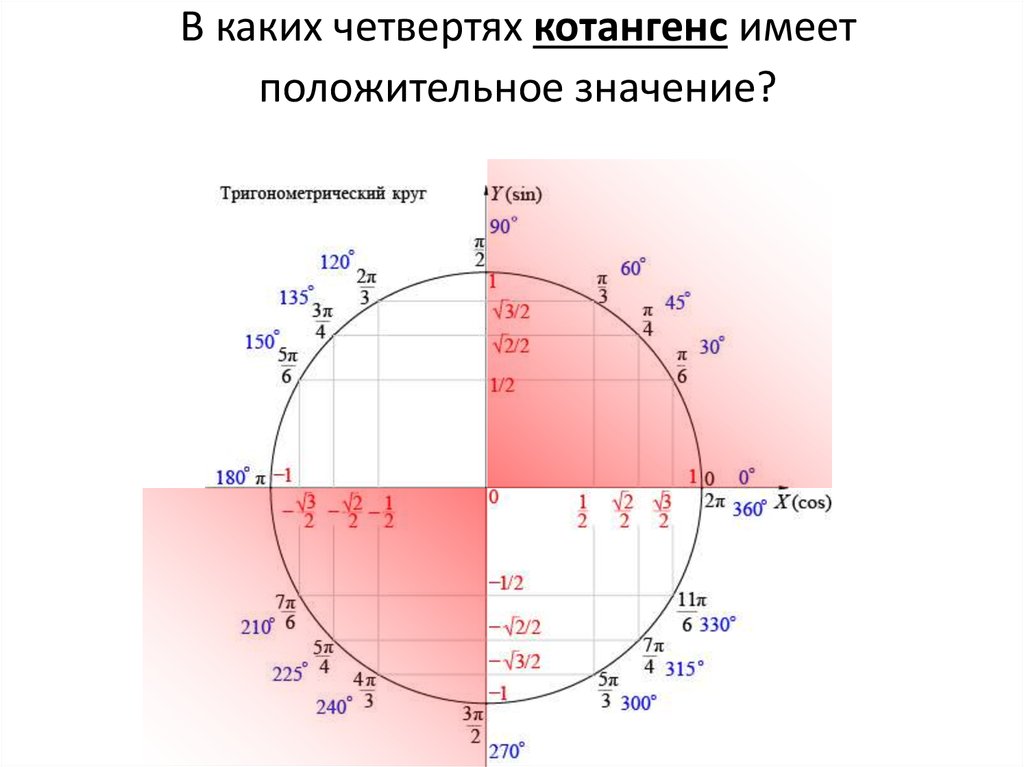
Возможно, здесь будет полезно нарисовать координатную плоскость. На этой координатной плоскости мы хотите построить точку три пятых, минус четыре пятых, которая здесь. Если мы знаем, что терминал сторона нашего угла проходит через эту точку и что наш угол находится в стандарте положение, то начальной стороной будет луч, который начинается в начале координат и проходит через положительную 𝑥-ось. Это означает, что мы интересует пространство от начальной стороны до конечной стороны. Однако для расчета этого мы образуем прямой угол с осью 𝑥.
Когда мы это делаем, мы получаем
прямоугольный треугольник. И мы будем использовать созданный угол
с осью 𝑥 для решения. Мы можем решить это, используя
тригонометрия прямоугольного треугольника, где у нас есть прямоугольный треугольник с длинами сторон
три пятых и четыре пятых.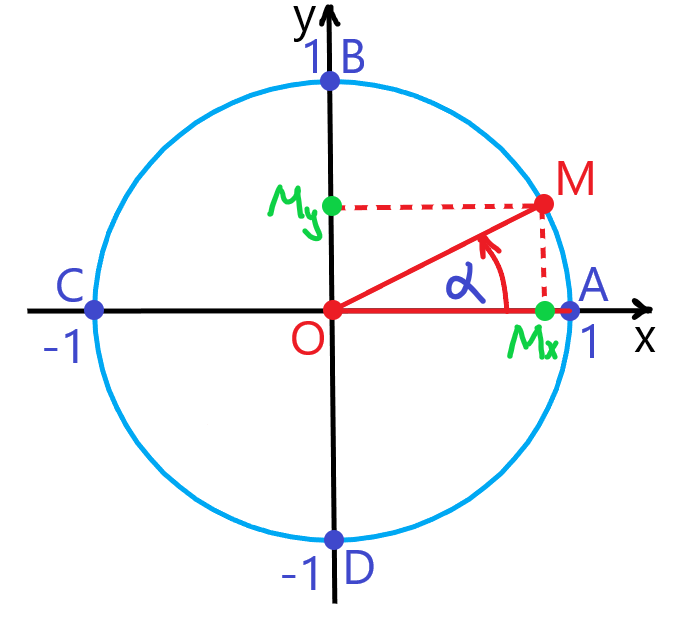
Мы помним, что грех 𝜃 будет
быть противоположным относительно гипотенузы. Однако в настоящее время мы не
знать гипотенузу. Мы не знаем расстояния от
начало координат до точки три пятых, минус четыре пятых. Мы можем использовать пифагорейскую
теорема, чтобы найти то, что означает три пятых в квадрате плюс четыре пятых в квадрате
равно 𝑐 в квадрате. Девять двадцать пятых плюс шестнадцать
двадцать пятых равно 𝑐 в квадрате. 25 больше 25 равно единице. И если 𝑐 в квадрате равно единице,
тогда 𝑐 должно быть равно единице.
Теперь, когда мы знаем гипотенузу
равен единице, мы можем сказать кое-что еще об этом угле в нашей координате
самолет. И в этом наша точка
падает на единичную окружность. Единичный круг имеет свой центр
в начале координат и имеет радиус, равный единице.
Мы ищем грех
𝜃. Это равносильно обратному
гипотенуза. Также в единичном круге грех
𝜃 равна его 𝑦-координате. 𝑦-координата для этого
точка минус четыре пятых. Итак, мы говорим, что грех
𝜃 равно отрицательным четырем пятым. И если бы мы хотели это проверить,
мы могли вспомнить, основываясь на нашей диаграмме CAST, что для углов, падающих в
в четвертом квадранте косинус положителен, но синус и тангенс будут
отрицательное, что подтверждает, что грех нашего угла 𝜃 равен отрицательному
четыре пятых.
Рассмотрим другой пример.
Предположим, 𝑃 — точка на
единичный круг, соответствующий углу четыре 𝜋 больше трех. Есть ли еще один момент на
единичный круг, представляющий угол в интервале от нуля до двух 𝜋, который имеет
одинаковое значение тангенса? Если да, укажите угол.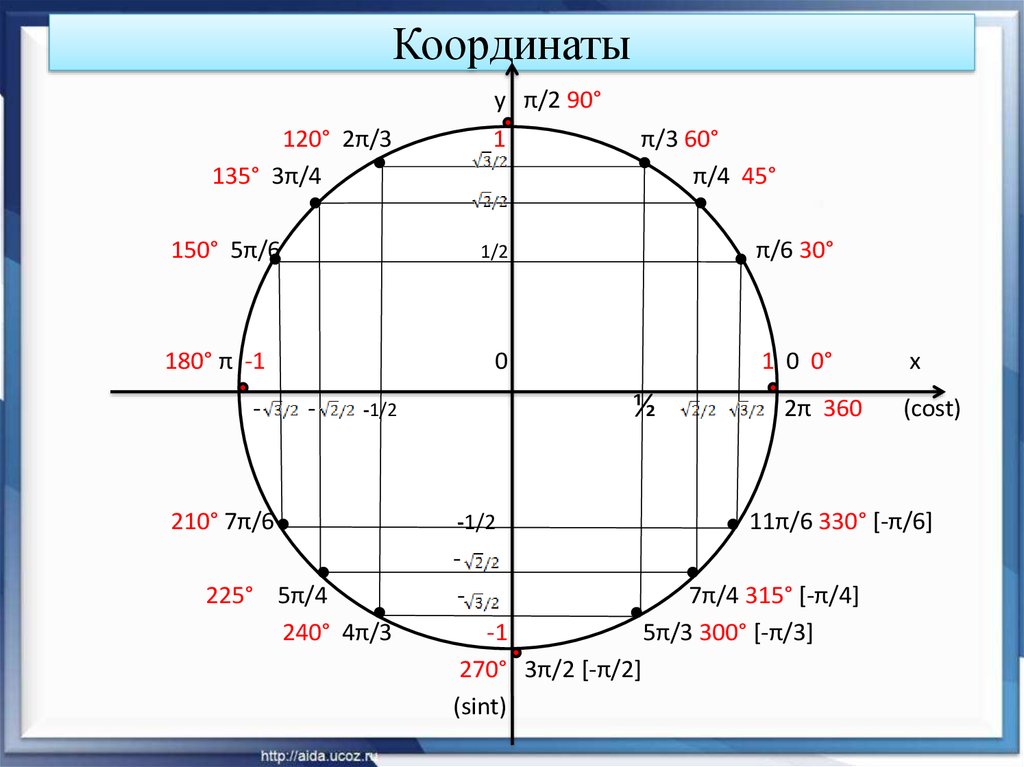
Во-первых, мы могли бы сделать набросок координатной плоскости, а затем добавьте единичный круг, который представляет собой круг с центром в начале координат и радиусом единицы. Оттуда мы также можем захотеть чтобы пометить нашу координатную плоскость радианами, начинающимися с нуля, 𝜋 более двух, 𝜋, три 𝜋 больше двух и два 𝜋. Потому что у нас есть интервал от нуля до двух 𝜋, мы знаем, что нас интересует только один полный оборот. Наша точка 𝑃 находится на единице окружности и соответствует углу четыре 𝜋 над тремя. Это означает, что наша первая задача состоит в том, чтобы узнайте, где приземлится угол четыре 𝜋 больше трех.
Я знаю, что 𝜋 больше трех
больше, чем 𝜋, но, вероятно, стоит сравнить, чтобы узнать, если четыре 𝜋 больше
три больше или меньше трех 𝜋 больше двух. Если дать этим дробям
общие знаменатели, четыре 𝜋 больше двух становится восемью 𝜋 больше шести и трех 𝜋
больше двух становится девятью 𝜋 больше шести.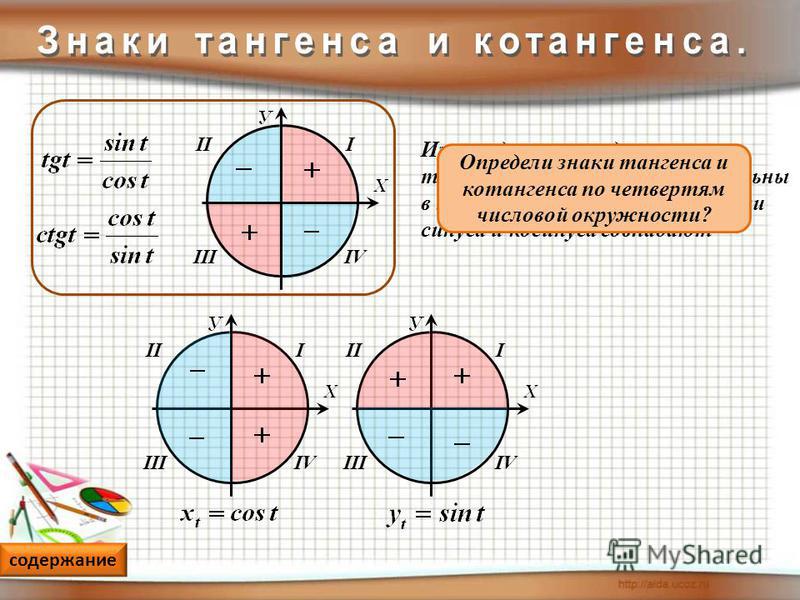
Так как восемь 𝜋 больше шести меньше
чем девять 𝜋 больше шести, мы можем сказать, что четыре 𝜋 больше трех меньше трех 𝜋
больше двух. А это значит, что точка 𝑃
мы попадем в наш третий квадрант, и четыре 𝜋 больше трех будут такими
угол.
Так как мы знаем, что наш угол попадает в третий квадрант, мы можем использовать диаграмму CAST, которая покажет нам что тангенс угла в третьей четверти будет положительным. Чтобы мы нашли другого точка внутри единичного круга, имеющая такое же значение касательной, мы будем искать для другого места, где значение тангенса может быть положительным. И это будет в первую квадрант. В первом квадранте все триггеры значения будут положительными.
Но для того, чтобы мы нашли
какое значение этого угла будет в первом квадранте, нам нужно разбить
наш угол четыре 𝜋 над тремя на более мелкие части.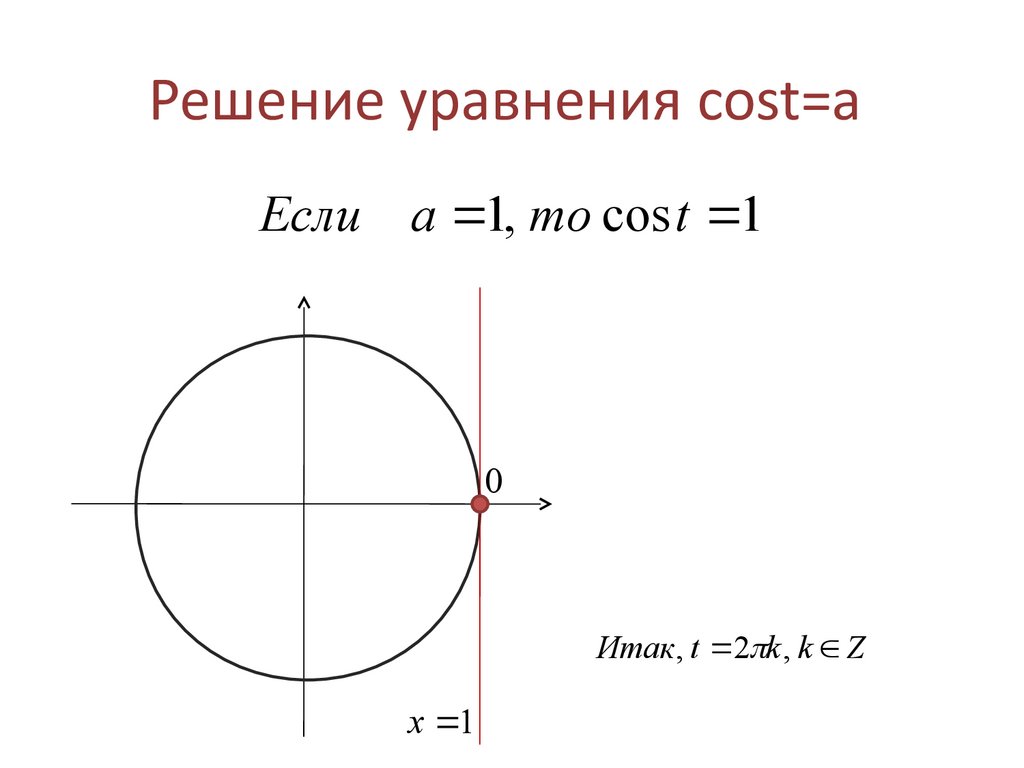
Можно сказать, что четыре 𝜋 более
три равно 𝜋 плюс 𝜋 на три, расстояние от нуля до 𝜋, а затем
дополнительный 𝜋 сверх трех. Создан прямоугольный треугольник
внутри единичного круга четыре 𝜋 больше трех в третьем квадранте будет выглядеть так
этот.
И в первом квадранте,
была бы некоторая точка, в которой мы имели бы дело с углом 𝜋
более трех. В первом квадранте это
будет иметь 𝑥, 𝑦 координаты. А в третьем квадранте это
будет иметь отрицательные 𝑥, отрицательные 𝑦 координаты. И мы знаем, что в единице
круг, тангенс 𝜃 будет равен 𝑦 над 𝑥. И мы бы сказали, что загар
из четырех третей 𝜋 равно отрицательному 𝑦 над отрицательным 𝑥 и тангенсом 𝜋
больше трех равно 𝑦 больше 𝑥. Но мы упрощаем отрицательное 𝑦
над отрицательным 𝑥 просто 𝑦 𝑥. Итак, мы показали, что да,
в этом интервале есть другой угол с таким же значением тангенса.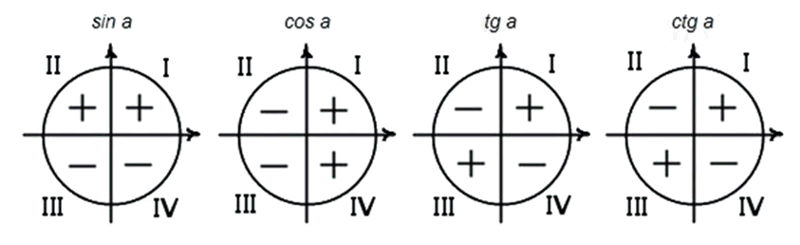
И это угол 𝜋 закончился
три.
В нашем следующем примере мы рассмотрим применение единичного круга.
Рассмотрим ветряную мельницу с лезвия длиной один метр. Положение вершины 𝑃 данная лопасть задается координатами 𝑎, 𝑏, которые зависят от угла 𝜃 как показано. Выразите 𝑎 и 𝑏 как функции меры угла 𝜃 в радианах. Если угол 𝜃 в определенный момент времени составляет пять третей 𝜋, какой она будет после того, как лезвие пройдет половину вращение?
Поскольку длина
лезвия составляют один метр, и на нашей диаграмме это представляет собой радиус
ветряная мельница, мы можем использовать наши знания об единичном круге, чтобы решить эту задачу.
проблема. Расстояние от центра г.
ветряная мельница в точку 𝑃 будет одной. И нам говорят, что суть
𝑃 находится по адресу 𝑎, 𝑏.
Итак, мы можем создать право
треугольник с осью 𝑥 и говорят, что длины его сторон равны 𝑎 и 𝑏,
соответственно. Мы используем расстояние от
конечной стороной к оси 𝑥, чтобы вычислить угол 𝜃. Мы знаем, что в блоке
окружности, мы можем представить угол как отношение синуса и косинуса. Для нашего угла 𝜃 наоборот
длина стороны будет 𝑏, а ее гипотенуза равна одному метру, поэтому у нас есть грех 𝜃
равно 𝑏 больше единицы. И мы можем представить 𝑏 как грех
из 𝜃.
Точно так же, если мы посмотрим на
косинус, мы получаем длину стороны 𝑎 больше единицы, что означает, что мы можем сказать, что
расстояние 𝑎 должно быть равно cos угла 𝜃. И без дополнительной информации,
это все, что мы можем сделать с этими двумя функциями. Мы можем сказать, что 𝑏 равно греху
𝜃 и 𝑎 равно потому что 𝜃.
Во второй части наших вопросов говорится если угол 𝜃 в определенный момент времени пять 𝜋 больше трех, то каким он будет после того, как лезвие совершило пол-оборота? Во-первых, мы уже нам сказали, что мы работаем в радианах, поэтому может быть полезно обозначить наша координатная плоскость. Начиная с оси 𝑥, ноль радиан, затем 𝜋 более двух радиан, 𝜋 радиан, три 𝜋 более двух радиан и полный оборот, что составляет два 𝜋 радиана. В такой системе полный очередь — два 𝜋. И, следовательно, пол-оборота будет равно 𝜋 радианам.
Если мы начнем с угла 𝜃
пять 𝜋 на три радиана, и мы добавляем половину оборота, мы добавляем 𝜋 к этому
угол. И так же, как добавление любого
дроби, нам нужен общий знаменатель. Мы можем написать 𝜋 как три 𝜋
более трех.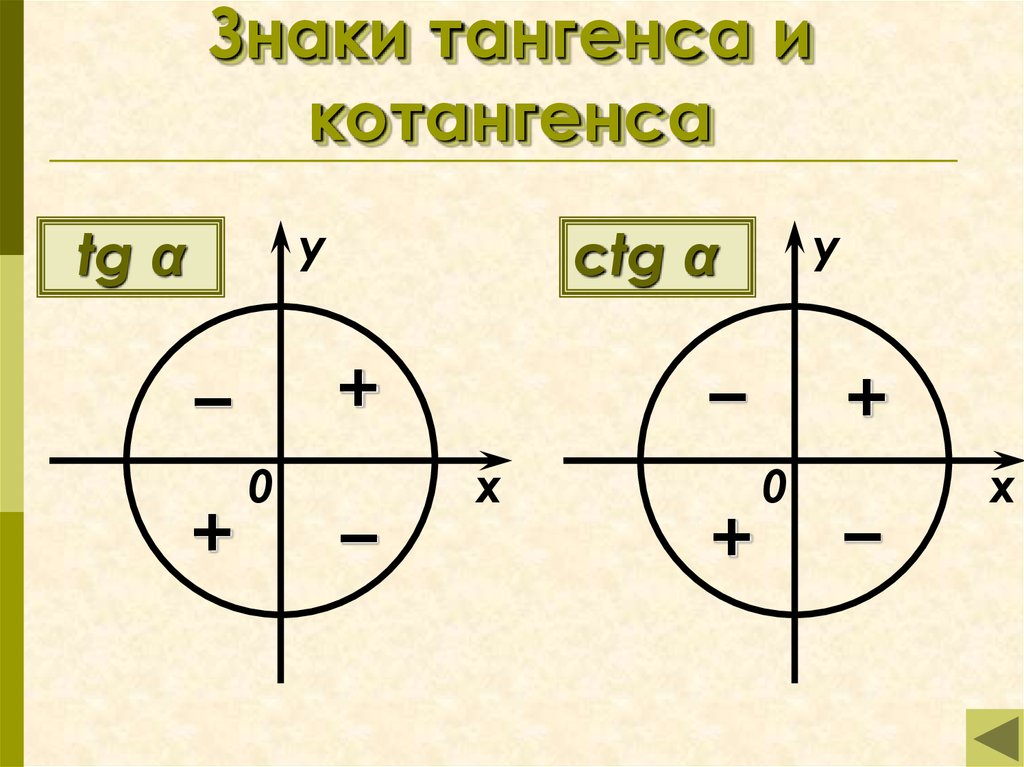