Полная вероятность формула: Полная вероятность и формула Байеса, формула полной вероятности, примеры

01Математика — Теория вероятностей — Формула полной вероятности и рекурсия

Пусть событие \(\displaystyle A\) – сумма выпавших очков  превысила число \(\displaystyle 3\) ровно за два броска.

Начнём строить граф возможных исходов, учитывая результаты первого броска кости.

Обозначим зелёным цветом исходы, для которых наступление события \(\displaystyle A\) возможно, красным – невозможно.

Получаем:

Введем события:

• \(\displaystyle B_{1}\) – при первом броске выпало \(\displaystyle 1{\small , }\)
• \(\displaystyle B_{2}\) – при первом броске выпало \(\displaystyle 2{\small , }\)
• \(\displaystyle B_{3}\) – при первом броске выпало \(\displaystyle 3\) очка.

Тогда вероятность наступления каждого из событий \(\displaystyle B_{1}{ \small ,}\,B_2\) и \(\displaystyle B_{3}\) равна

\(\displaystyle P(B_{1})=P(B_{2})=P(B_{3})=\frac{1}{6}{\small . }\)

Обозначим на рисунке эти вероятности:


Продолжим строить граф возможных исходов.

Будем его достраивать по результатам второго броска кости.  

Опять обозначим зелёным цветом исходы, для которых событие \(\displaystyle A\) наступает, красным – не наступает.

Получаем:

Найдем условную вероятность \(\displaystyle P_{B_{1}}(A)\) – вероятность наступления события \(\displaystyle A\) при условии, что событие \(\displaystyle B_{1}\)  произошло.

\(\displaystyle B_{1}\) – это выпадение в первом броске \(\displaystyle 1\) очка. Значит, для наступления \(\displaystyle A\) во втором броске должно выпасть \(\displaystyle 3\),  \(\displaystyle 4\),  \(\displaystyle 5\) или \(\displaystyle 6{\small . }\)

Тогда

\(\displaystyle P_{B_{1}}(A)=\frac{4}{6}{\small . }\)

Аналогично,

\(\displaystyle P_{B_{2}}(A)=\frac{5}{6}\) и \(\displaystyle P_{B_{3}}(A)=\frac{6}{6}{\small . }\)


Подсчитаем вероятность одновременного наступления событий \(\displaystyle A\) и \(\displaystyle B_1{\small . }\)

На рисунке это выглядит как подсчет вероятности для первой ветки графа:

Тогда

\(\displaystyle P(\)в первом броске выпало \(\displaystyle 1\) очко и сумма больше \(\displaystyle 3)=P(B_{1}) \cdot P_{B_{1}}(A)=\frac{1}{6}\cdot\frac{4}{6}=\frac{4}{36}{\small . }\)

Аналогично получаем:

\(\displaystyle P(\)в первом броске выпало \(\displaystyle 2\) очка и сумма больше \(\displaystyle 3)=P(B_{2}) \cdot P_{B_{2}}(A)=\frac{1}{6}\cdot\frac{5}{6}=\frac{5}{36}{\small . }\)

\(\displaystyle P(\)в первом броске выпало \(\displaystyle 3\) очка и сумма больше \(\displaystyle 3)=P(B_{3}) \cdot P_{B_{3}}(A)=\frac{1}{6}\cdot\frac{6}{6}=\frac{6}{36}{\small . }\)


Осталось найти полную вероятность наступления события \(\displaystyle А{\small . }\)

Для этого необходимо просуммировать вероятности, полученные для каждой ветки нашего графа.

Тогда 

\(\displaystyle P(A)=\frac{4}{36}+\frac{5}{36}+\frac{6}{36}=\frac{15}{36}\approx0{,}42{\small . }\)

 

Ответ: \(\displaystyle 0{,}42{\small .}\)

Формула полной вероятности. Формула Байеса. Примеры решения задач



Образовательные онлайн сервисы: теория и практика

• Главная
• Примеры
  • Математический анализ
  • Векторная алгебра и аналитическая геометрия
  • Линейная алгебра
  • Теория вероятностей и математическая статистика
  • Математическое программирование
    Методы оптимизации
  • Математика в экономике
    Экономическая статистика
• Видео-уроки
  • Математический анализ
  • Векторная алгебра и Аналитическая геометрия
  • Линейная алгебра
  • Теория вероятностей и математическая статистика
  • Математическое программирование. Методы оптимизации
• Готовые работы
  • Математический анализ
  • Векторная алгебра и аналитическая геометрия
  • Линейная алгебра
  • Теория вероятностей и математическая статистика
  • Математическое программирование
    Методы оптимизации
  • Математика в экономике
    Экономическая статистика
  • Другое
• Контакты


Полезные материалы:

• Учебники
• Справочники
• Онлайн калькуляторы
• Помощь в решении
• Онлайн занятия в Zoom

Формула полной вероятности. Формула Байеса.

Формула полной вероятности
,
где B1, B2 ,…, Bn  — полная группа попарно несовместных событий.
Формула Байеса
,
где B1, B2, …, Bn — полная группа событий.

Задача 1.


Фирма имеет три источника поставки комплектующих – фирмы А,В,С. На долю фирмы А приходится 50 % общего объема поставок, В – 30% и С – 20%. Из практики известно, что 10% поставляемых фирмой А деталей – бракованные, фирмой В – 5% и С – 6%.
Найти вероятность того, что наудачу выбранная деталь будет бракованной.

Решение. Производится испытание – извлекается одна деталь.
Событие А – появилась бракованная деталь.
Гипотеза Н1 – деталь фирмы А.
Гипотеза Н2 – деталь фирмы В.
Гипотеза Н3 – деталь фирмы С.
Тогда, согласно формуле полной вероятности, искомая вероятность равна:


Задача 2.
В центральную бухгалтерию корпорации поступили пачки накладных для проверки и обработки. 90 % пачек были признаны удовлетворительными: они содержали только 1 % неправильно заполненных накладных.

Остальные 10 % пачек были признаны неудовлетворительными, так как содержали 5 % неверно оформленных накладных. Взятая наугад из пачки накладная оказалась оформленной неверно. Учитывая это, какова вероятность того, что вся пачка накладных будет признана несоответствующей стандарту?

Решение. Испытание – проверяется пачка накладных.
Событие А – взятая наугад накладная оказалась неверной. 
Гипотеза Н1 – пачка не соответствует стандарту.
Гипотеза Н2 – пачка соответствует стандарту.
Необходимо узнать вероятность гипотезы Н1 при условии, что событие А произошло. Согласно формуле Бейеса имеем:


Задача 3.
Имеется три урны с различным составом шаров в каждой. В первой - 5 белых и 5 черных, во второй - 3 белых и 3 черных, в третьей - 2 белых и 4 черных. Из случайно выбранной урны извлекается шар. Он оказался белым. Определить вероятность того, что он был вынут из третьей урны.

Решение: Введем обозначения для рассматриваемых событий.
Пусть А — извлечен белый шар. — выбрана первая урна.
— выбрана вторая урна. — выбрана третья урна.
— вероятность извлечения белого шара из первой урны.
— вероятность извлечения белого шара из второй урны.
— вероятность извлечения белого шара из третьей урны.
Определим вероятности, соответствующие этим событиям . Так как все урны одинаковы, то
.
,   ,   .
Тогда, используя формулу полной вероятности, получим:
.
Пересчитаем вероятность третьей гипотезы с условием, что произошло рассматриваемое событие, используя формулу Байеса.







Задать вопрос
Заказать помощь

Отзывы

+7-911-7987704

vk.com/id286009794

Написать в Whatsapp

Написать в Viber

@matem96

Skype: matem96.ru



Теорема о полной вероятности

Вероятность — это понятие, используемое в математике, особенно в статистике, для предсказания вероятности возникновения события. Вероятность дает представление о том, произойдет событие или нет, и если прогнозируется, что событие произойдет, насколько мы можем полагаться на его возникновение. Вероятность события — безразмерная величина. Это может быть любое числовое значение в диапазоне от нуля до единицы. Если вероятность события равна 1, то событие обязательно произойдет и, следовательно, называется достоверным событием или определенным событием. Если вероятность события равна «0», событие вообще не произойдет и, следовательно, называется невозможным событием. Теорема о полной вероятности — это теорема, которая связывает условную вероятность с предельной вероятностью.

Теорема об общей вероятности:

Рассмотрим два события A и B, как показано на диаграмме Венна, показанной на рисунке 1. Предположим, что эти два события связаны с одним и тем же пространством выборки, представленным как «S». Все пространство выборки можно разделить на следующие части, обозначающие подмножества пространства выборки «S»: (A ⋂ B’), (A’ ⋂ B’), (A ⋂ B) и (A’ ⋂ B). Эти подмножества являются взаимно непересекающимися множествами, потому что они не пересекаются попарно. Для любых парных комбинаций четырех наборов они остаются непересекающимися. Однако вероятность возникновения любого из этих событий зависит от возникновения других событий в пространстве выборки. В тех случаях, когда вероятность события зависит от вероятности других событий в том же пространстве выборки, для определения вероятности события используется теорема о полной вероятности. 9{n}\] P(Ai).P(E | Ai)

Доказательство теоремы о полной вероятности:

(Изображение будет загружено в ближайшее время)

Рассмотрим примерное пространство, показанное на рисунке выше, такое, что C1, C2, C3 ………… Cn — это разбиения выборочного пространства ‘S’ такие, что Cp ⋂ Cq = ∅ (нулевое множество). т. е. разбиения не пересекаются, когда p ≠ q, где p и q = 1, 2, 3, 4…. н. Также верно, что P (Cm) ≠ 0, т. е. ни одно событие в пространстве выборки не имеет ненулевой вероятности.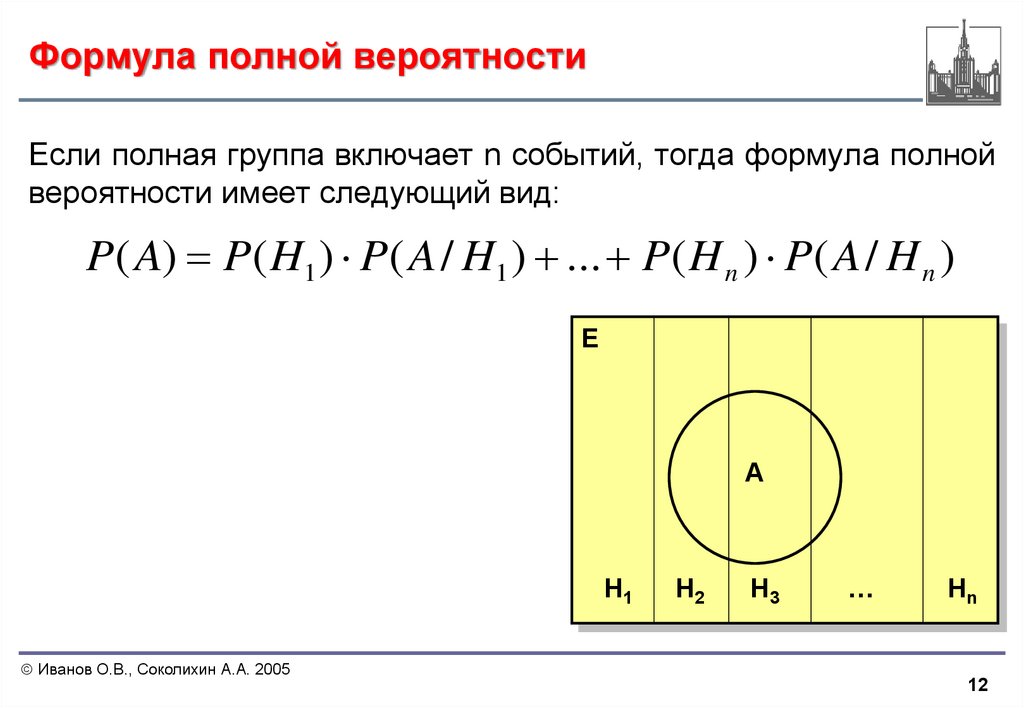 Пространство выборки можно представить в виде:

S = C1 U C2 U C3 U ………… U Cn → (1)

Для любого события «A» в выборочном пространстве S событие «A» может быть обозначено как:

A = A ⋂ S

Подставляя (1) в приведенное выше уравнение, оно дает

A = A ⋂ (C1 U C2 U C3 U ………… U Cn)

A = (A ⋂ C1) U (A ⋂ C2) U (A ⋂ C3) U ……… U (A ⋂ Cn)

It ясно, что A ⋂ Cp и A ⋂ Cq являются подмножествами Cp и Cq соответственно. Следовательно, верно, что

A ⋂ Cp и A ⋂ Cq также не пересекаются при p ≠ q. Итак, вероятность события «А» можно рассчитать как:

P(A) = P [(A ⋂ C1) U (A ⋂ C2) U (A ⋂ C3) U ……… U (A ⋂ Cn)]

P(A) = P (A ⋂ C1) + P (A ⋂ C2) + P (A ⋂ C3) + ……… + P (A ⋂ Cn) → (3)

Однако правило умножения вероятности утверждает, что

P (A ⋂ Cp) = Р (Ср). P (A | Cp)  → (4) 

Подставляя (3) в (4), получаем

P (A) =  P (C1) . Р (А | С1) + Р (С2) . Р (А | С2) + Р (С3) . Р(А|С3)+…. + P (Cn) . P (A | Cn)

Приведенное выше уравнение может быть кратко записано как: 9{n}\] P(Ci).P(A | Ci)

Теорема полной вероятности Примеры: 

1. У Шэрон есть три мешка по 100 шариков в каждом. В первом мешке 25 синих и 75 красных шариков, во втором мешке 40 синих и 60 красных шариков, а в третьем мешке 55 синих и 45 красных шариков. Из одного из мешков случайным образом выбирается шарик. Какова вероятность того, что это красный шарик? (Подсказка: рассмотрите это как пример теоремы о полной вероятности)

Решение:

Пусть «A» представляет событие выбора красного шарика, а Ci представляет событие выбора мешка. Из приведенных данных мы можем сделать следующий вывод.

Вероятность выбора красного шарика из мешка 1 равна

P (A | C1) = 75 / 100 = 0,75

Вероятность выбора красного шарика из мешка 2 равна

P (A | C2) = 60 / 100 = 0,6

Вероятность выбора красного шарика из мешка 3 равна

P (A | C3) = 45 / 100 = 0,45

Вероятность выбора одного из трех мешков остается прежней.

P (Ci) = ⅓ 

Формула, представляющая доказательство теоремы о полной вероятности  9{3}\] P(Ci).P(A | Ci)

P(A) = P(C1).P(A | C1) + P(C2).P(A | C2) + P(C3 ).P(A | C3)

P(A) = ⅓(0,75) + ⅓(0,6) + ⅓(0,45) = 0,25 + 0,2 + 0,15 = 0,6

Следовательно, вероятность выбора красного шара на случайное из одного из трех мешков равно 0,6

Забавные факты об общей вероятности Доказательство теоремы:

В теории вероятностей условная вероятность рассчитывается, когда наступление одного события возможно только тогда, когда другое событие уже произошло.

Предельная вероятность рассчитывается, когда события в выборочном пространстве независимы друг от друга. События не зависят друг от друга в случае предельной вероятности.

Доказательство теоремы о полной вероятности устанавливает связь между условной вероятностью и предельной вероятностью и определяет вероятность события как сумму вероятностей других событий в пространстве выборки.

Дерево решений — это простой и легкий способ взглянуть на проблемы с помощью полной стратегии закона вероятности. Дерево решений последовательно показывает все возможные события. С помощью дерева решений можно быстро определить отношения между событиями и рассчитать условные вероятности.

Чтобы понять, как можно использовать дерево решений для расчета полного потенциала, рассмотрим следующий пример:

• Рассматриваемый человек — фондовый аналитик из ABC Corp. Он обнаружил, что компания планировала запустить новый проект, который может повлиять на цену акций компании. Определите следующие вероятности:

• Вероятность начала нового проекта составляет 60%.

• Когда компания запускает проект, вероятность того, что ее акции вырастут, составляет 75%.

• Если компания не начинает проект, то вероятность того, что ее акции вырастут, составляет 30%.

Тогда шансы на то, что вторая карта станет королем или нет, будут представлены законом полных вероятностей, например:

P (E) = P (A) P (E | A) + P (B) P (E | B)

Там,

• P (E) вероятность того, что вторая карта будет королем,

• P (A) вероятность того, что первая карта будет королем,

• P (E | A) — вероятность того, что вторая карта — король, при условии, что первая карта — король,

• P (B) — вероятность того, что первая карта не король, | B) вероятность того, что вторая карта будет королем, а первая выпущенная карта не будет королем.

Объяснение теоремы полной вероятности на следующих примерах:

• Врач обращается к пациенту за лечением, пользуется разными видами транспорта, и его шансы прибыть вовремя равны уменьшению его или ее шансы прибыть вовремя из разных видов транспорта.

• Учащийся должен представлять школу на внешнем конкурсе. Шансы выбрать ученика на конкурсе такие же, как и сократить шансы выбрать этого ученика в разных классах школы.

• Шансы найти некачественный манго уменьшаются.

Основой теоремы Байеса является теорема о полной вероятности, которая помогает учащимся вывести обратную вероятность того, что событие происходит из частей выборки S. Расчет наступления события из-за разделение определенного пространства выполняется с помощью теоремы о полной вероятности , а обратная вероятность от конкретного раздела выборочного пространства S из-за данной вероятности события может быть установлена ​​с помощью Теорема Байеса. Следовательно, это завершается выводом теоремы о полной вероятности.

Вероятностные концепции

Повторное чтение

2023 Учебный план Программа CFA Уровень I Количественные методы

Концепции вероятностей

Загрузить полную версию (PDF)

Доступно для участников

Введение

Инвестиционные решения принимаются в условиях риска. Инструменты, которые позволяют нам принимать решения с последовательностью и логикой в ​​этой обстановке, основаны на концепциях вероятности.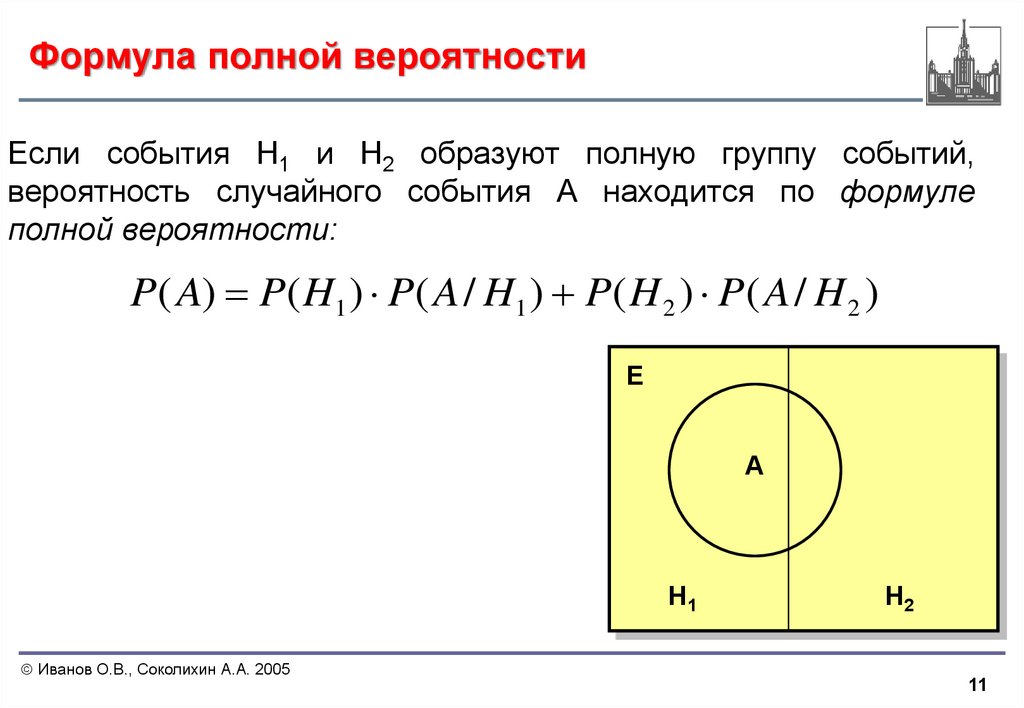 В этом чтении представлены основные инструменты вероятности, необходимые для формулирования и решения многих реальных проблем, связанных с риском. Эти инструменты применяются к целому ряду вопросов, таких как прогнозирование эффективности инвестиционного менеджера, прогнозирование финансовых переменных и установление цен на облигации, чтобы они справедливо компенсировали держателям облигаций риск дефолта. Наш фокус практичен. Мы исследуем концепции, наиболее важные для инвестиционных исследований и практики. Среди них независимость, поскольку она связана с предсказуемостью доходов и финансовых переменных; ожидания, поскольку аналитики постоянно смотрят в будущее в своих анализах и решениях; и изменчивость, дисперсия или дисперсия вокруг ожиданий как концепция риска, важная в инвестициях. Читатель приобретет определенные навыки и компетенции в использовании этих вероятностных концепций для понимания рисков и отдачи от инвестиций.

Результаты обучения

Участник должен уметь:

• определить случайную величину, результат и событие;
• определить два определяющих свойства вероятности, включая взаимоисключающие и исчерпывающие события, а также сравнить и сопоставить эмпирические, субъективные и априорные вероятности;
• описывают вероятность события с точки зрения шансов за и против события;
• вычислять и интерпретировать условные вероятности;
• демонстрируют применение правил умножения и сложения для вероятности;
• сравнивать и противопоставлять зависимые и независимые события;
• вычислить и интерпретировать безусловную вероятность, используя правило полной вероятности;
• рассчитать и интерпретировать ожидаемое значение, дисперсию и стандартное отклонение случайных величин;
• объяснить использование условного ожидания в инвестиционных приложениях;
• интерпретировать дерево вероятностей и продемонстрировать его применение к инвестиционным задачам;
• рассчитать и интерпретировать ожидаемое значение, дисперсию, стандартное отклонение, ковариации и корреляции доходности портфеля;
• рассчитать и интерпретировать ковариации доходности портфеля, используя совместную функцию вероятности;
• рассчитать и интерпретировать обновленную вероятность, используя формулу Байеса;
• определить наиболее подходящий метод для решения конкретной задачи подсчета и проанализировать задачи подсчета с использованием концепций факториала, комбинации и перестановки.

 

Резюме

В этом чтении мы обсудили основные понятия и инструменты вероятности. Мы применили вероятность, ожидаемую стоимость и дисперсию к ряду инвестиционных проблемы.

• Случайная величина — это величина, результат которой неизвестен.

• Вероятность — это число от 0 до 1, описывающее вероятность того, что указанное событие произойдет.

• Событие — это заданный набор исходов случайной величины.

• Взаимоисключающие события могут происходить только по одному за раз. Исчерпывающие события охватывают или содержать все возможные исходы.

• Двумя определяющими свойствами вероятности являются, во-первых, то, что 0 ≤ P ( E ) ≤ 1 (где P (

  E ) обозначает вероятность события E ), и, во-вторых, что сумма вероятностей любого набора взаимоисключающих а исчерпывающие события равны 1,

• Вероятность, оцениваемая по данным как относительная частота появления, является эмпирическим вероятность. Вероятность, основанная на личном или субъективном суждении, является субъективным вероятность. Вероятность, полученная на основе логического анализа, является априорной вероятностью.

• Вероятность события E , P ( E ), может быть выражена как шансы для E = P ( E )/ [1 — P ( E )] или шансы против E = [1 — P ( E )]/ P ( E )]/ P ( E ).

• Непоследовательные вероятности создают возможности для получения прибыли, согласно Голландская книжная теорема.

• Вероятность события , а не , обусловленная другим событием, является безусловной вероятностью. Безусловная вероятность события A обозначается P ( A ). Безусловные вероятности также называются маргинальными вероятностями.

• Вероятность события, данного (обусловленного) другим событием, является условной вероятностью. Вероятность события A для данного события B обозначается как P ( A | B ) и P ( A  |  B 9 0244 ) =  P ( AB )/ P ( B ), P ( B ) ≠ 0,

• Вероятность появления A и B равна совместной вероятности A и B , обозначенной P ( AB ).

• Правило умножения вероятностей: P ( AB ) = P ( A | B ) P ( B ).

• Вероятность появления A или B , или обоих, обозначается P ( A или B ).

• Правило сложения для вероятностей: P ( A или B ) = P ( A ) + P ( B ) − 902 43 Р ( АБ ).

• Когда события независимы, возникновение одного события не влияет на вероятность наступления другого события. В противном случае события зависимы.

• Правило умножения независимых событий гласит, что если A и B являются независимыми событиями, то P ( AB ) = P ( A ) P ( В ). Правило обобщается аналогичным образом на более чем два события.

• Согласно правилу полной вероятности, если S ₁ , С ₂ , …, С _n являются взаимоисключающими и исчерпывающими сценариями или событиями, тогда P ( A ) = P ( A | S ₁ ) Р ( С ₁ ) + Р ( А | С ₂ ) Р ( С ₂ ) + … + P ( A | S _n ) P ( S _n ).

• Ожидаемое значение случайной величины представляет собой взвешенное с вероятностью среднее возможного результаты случайной величины. Для случайной величины X ожидаемое значение X обозначается как E ( X ).

• Правило полной вероятности для ожидаемого значения утверждает, что E ( X ) = E ( X | S ₁ ) Р ( С ₁ ) + Е ( Х | С ₂ ) Р ( С ₂ ) + … + E ( X | S _n ) P ( S _n ), где 9 0243 С ₁ , С ₂ , …, S _n являются взаимоисключающими и исчерпывающими сценариями или событиями.

• Дисперсия случайной величины представляет собой ожидаемое значение (взвешенное по вероятности среднее) квадратов отклонений от ожидаемого значения случайной величины E ( X ): σ ² ( X ) = E {[ X − E ( X )] 9 0573 2 }, где σ ² ( X ) обозначает дисперсию X .

• Дисперсия — это мера дисперсии относительно среднего значения. Увеличение дисперсии указывает увеличение дисперсии. Дисперсия измеряется в квадратах исходной переменной.

• Стандартное отклонение — это положительный квадратный корень из дисперсии. Меры стандартного отклонения дисперсия (как и дисперсия), но измеряется в тех же единицах, что и переменная.

• Ковариация — это мера совместного движения между случайными величинами.

• Ковариация между двумя случайными величинами R _i и R _j в прямом смысле представляет собой ожидаемое значение векторного произведения отклонений двух случайных величин из их соответствующих средних значений: Cov( R _i , R _j ) = E {[ R _i − E ( R _i )][ R _j − E ( R _{j 9043 6} )]}. Ковариация случайной величины сама с собой есть ее собственная дисперсия.

• Историческая или выборочная ковариация между двумя случайными величинами R _i и R _j на основе выборки прошлых данных размером n представляет собой среднее значение произведения отклонений наблюдений на двух случайных переменных из их выборочных средних:

  Cov(Ri,Rj)=∑i=1n(Ri,t−R¯i)(Rj,t−R¯j)/(n−1)

• Корреляция — это число от -1 до +1, которое измеряет совместное движение (линейную связь) между двумя случайными величинами: , R _j )/[σ( R _i ) σ( R _j )].

• Если две переменные имеют очень сильную линейную зависимость, то абсолютное значение их корреляция будет близка к 1. Если две переменные имеют слабую линейную связь, то абсолютное значение их корреляции будет близко к 0,

• Если коэффициент корреляции положительный, две переменные напрямую связаны; если коэффициент корреляции отрицательный, две переменные обратно пропорциональны.

• Чтобы рассчитать дисперсию доходности портфеля из n активов, необходимы исходные данные: n ожидаемая доходность отдельных активов, n дисперсии доходности отдельных активов и n ( n − 1)/2 различных ковариаций.

• Портфельная дисперсия доходности равна σ2(Rp)=∑i=1n∑j=1nwiwjCov(Ri,Rj).

• Расчет ковариации в перспективном смысле требует спецификации совместной функции вероятности, которая дает вероятность совместных событий значений двух случайных величин.

• Когда две случайные величины независимы, совместная функция вероятности представляет собой произведение отдельных вероятностных функций случайных величин.

• Формула Байеса — это метод обновления вероятностей на основе новой информации.

• Формула Байеса выражается следующим образом: Обновленная вероятность события с учетом новой информации = [(Вероятность новой информации с учетом события)/(Безусловная вероятность новой информации)] × Предыдущая вероятность события.

• Правило умножения гласит, например, что если первый шаг в процесс может быть выполнен 10 способами, второй шаг, учитывая первый, может быть выполнен 5 способами, а третий шаг, учитывая первые два, можно выполнить 7 способами, то шаги можно выполнить (10)(5)(7) = 350 способами.

• Количество способов назначить каждому элементу группы размером от n до n слотов равно n ! = n ( n — 1) ( n — 2)( n — 3) … 1. (По соглашению, 0! = 1.)

• Количество способов, которыми n объектов могут быть помечены k различными метками, с n ₁ первого типа, n ₂ второго типа и так далее, с н ₁ + п ₂ + … + n _k = n , определяется как n !/( n ₁ ! п ₂ ! … н _к !).

  No related posts.